与传统机器人相比,软体机器人具有更高的安全性、适应性、灵活性、相容性以及柔顺性[1-2]。作为软体机器人的代表性材料,离子聚合物金属复合材料(ionic polymer-metal composite,IPMC)具有质量小、柔性好、变形大、响应速度快、生物亲和性好等优点。在刺激电压的驱动下,IPMC内部水合阳离子会从阳极向阴极迁移而产生向阳极的弯曲;而在外力作用下变形时,也会使IPMC两侧产生电压,因此,IPMC材料既可以用作驱动器,又可以用作传感器[3]。现阶段IPMC柔性驱动器已经被用于仿生学、生物医学、机器人学、微型机电以及航天航空等领域[4-7]。
为描述IPMC的弯曲变形特征以及相应的物理变化关系,研究者对IPMC进行了基于等效电路的建模研究。KANNO等[8]提出了一种线性模型来模拟IPMC的驱动响应特性,该模型将其分成了离散的10等份,将输入电压转化为电流,研究电流和输出位移的力学响应关系。BONOMO等[9]研究了IPMC驱动器的集总式RC等效电路,模型主要包括2个阶段,一是输入电压计算执行器上的电流,二是建立黏弹力和输出位移的关系。GUTTA等[10]提出了一种用单元局部坐标系描述单元刚体运动和弹性变形的有限元建模技术,其考虑了驱动器弯曲时大挠度梁的特点和集总RC电路的分布。CAPONETTO等[11]通过将IPMC驱动器的电学特性用分布式理论表征,建立了一种基于非整数阶的驱动模型。MOEINKHAH等[12]将悬臂式驱动器等效为分布式RC电路,将电流和电压作为执行器长度的函数,通过解析推导获得了分析函数与驱动模型。MOGHADAM等[13]提出了一种适用于离子聚合物导电复合材料执行器在经历大弯曲变形时的建模方法,该方法将电动力学模型和机械动力学模型视为RC电路刚性连接系统。SUN等[14]利用Onsager方程预测了驱动器的静态特性,并对其动态驱动进行分析,将得到的静态模型和RC电路模型相结合,推导出IPMC从输入到输出整个驱动过程的传递函数。基于IPMC驱动器特性,利用等效电路、黏弹性材料的本构方程、麦克斯韦应力、哈密顿原理、伽辽金降阶模型和拉氏变换技术,获得了考虑执行器黏弹性特性的运动控制方程[15]。以上模型在一定程度上解释了柔性驱动器的驱动特性,说明简单的等效电路模型具有一定的优势,但仍然存在非线性特性捕捉不足、复杂动态行为描述有限、多物理场耦合机制不明确等问题。因此,要实现驱动器的位置和力的精准控制,还需要开展大量工作。
本文作者充分利用传输线理论的优势,首先,根据柔性驱动器的变形驱动特点,将其等效为无数微小的电路单元,利用电流传输线原理,建立电荷密度的分析函数。然后,将驱动器的弯曲角度近似与电荷密度成比例,建立驱动器变形的动态驱动模型以及相应的传递函数。并使用最小二乘迭代算法对传递函数进行辨识降阶。最后,对提出的模型进行实验验证和分析讨论。
1 柔性驱动器的变形特征
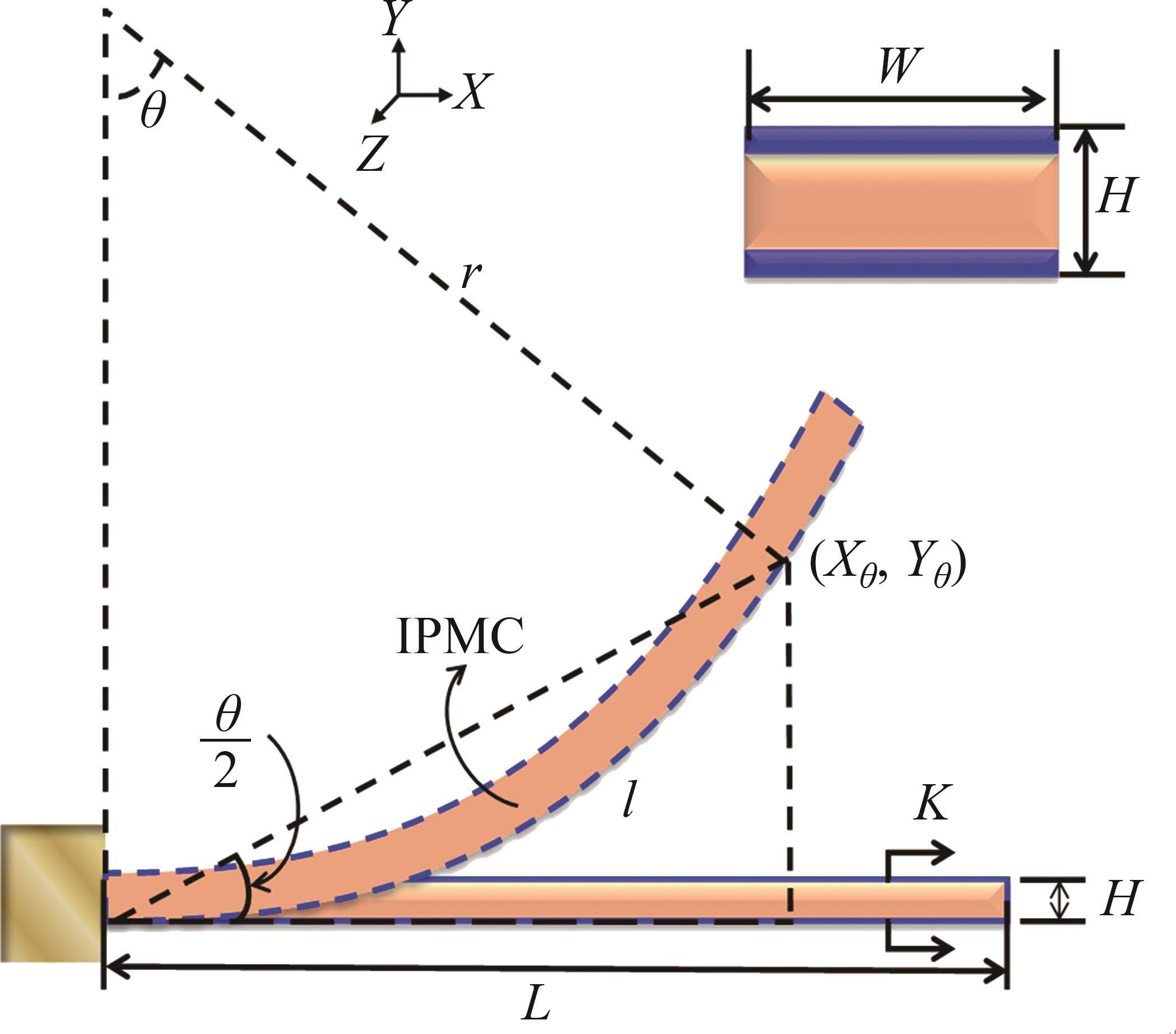
由于在柔性驱动器IPMC的两端施加电压,IPMC会发生弯曲变形,其变形过程可以看成悬臂梁结构的一端固定,另外一端发生变形。假设IPMC发生的小角度变形,其几何示意图如图1所示,其中L、W和H分别为IPMC的长度、宽度和厚度。假设施加在固定端的电压为U,其发生变形的弯曲角度为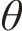
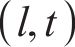
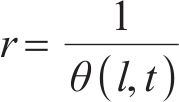
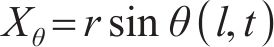
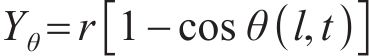
式中: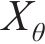
2 柔性驱动器的动态特性
2.1 传输线理论分析
柔性驱动器IPMC是由中间离子聚合物层和两边的金属电极层构成。一些研究者发现IPMC在电极层和离子聚合物层之间存在一种混合层,即电极层的部分颗粒延伸插入聚合物中,而形成了复合层或内电极层。YANG等[16]对IPMC的弹性模型建模时充分地研究了IPMC的5层结构,即外电极-内电极-离子交换膜-内电极-外电极,如图2所示。内电极层对于IPMC的弹性模量、表面电阻、驱动响应速度等有重要的影响,在建模过程中,内电极能够更加全面和准确地表征IPMC的特征和性能。基于此,本文认为在2个表面电极与膜的界面处形成了双层电容器,其电容用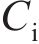
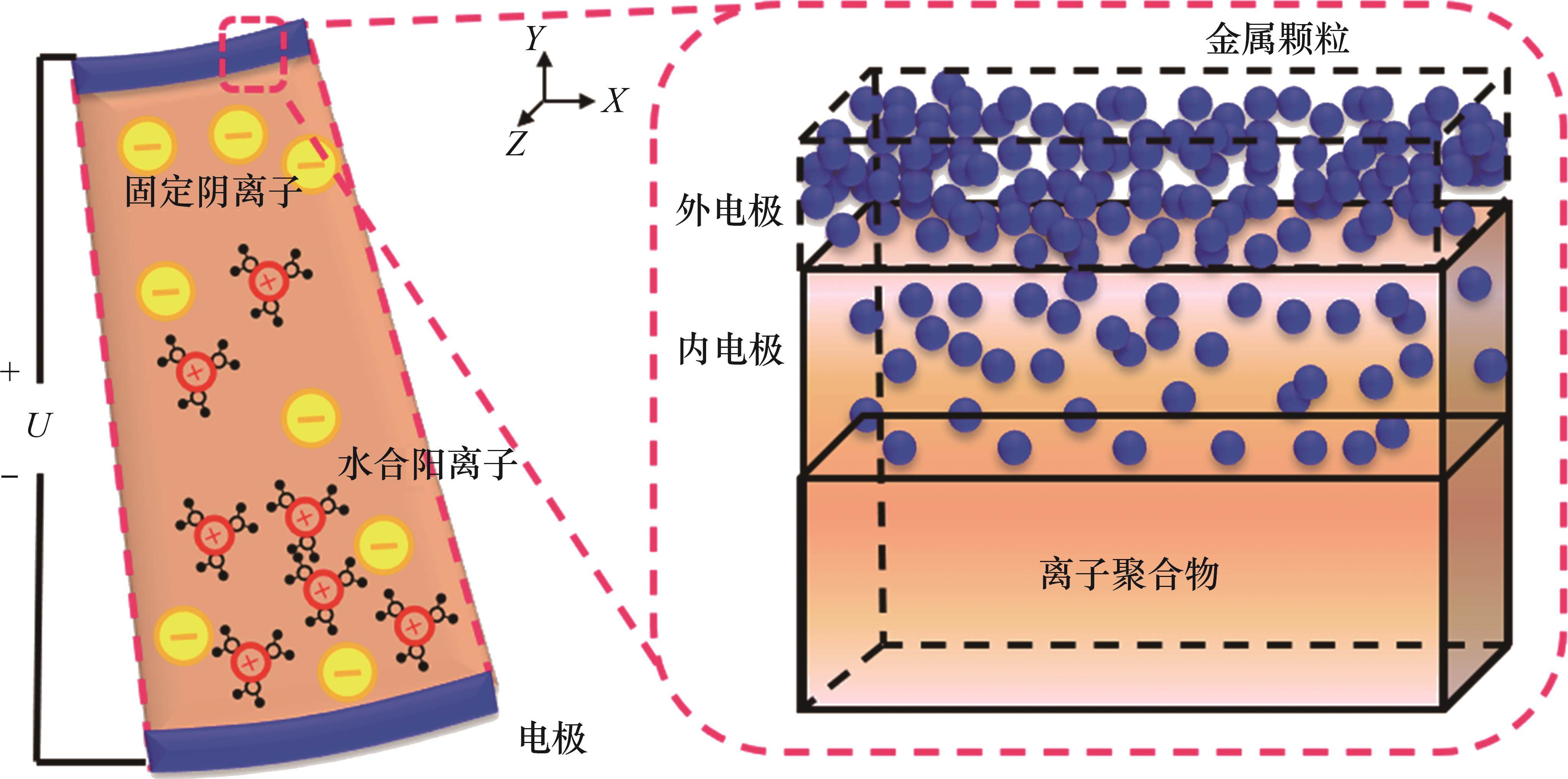
当在IPMC两侧的电极施加电压时,在电场的作用下,IPMC中的阳离子会带动水分子从阳极向阴极移动,阴离子不发生变化,使IPMC内部产生浓度差,从而引起阳极收缩、阴极膨胀,最终导致IPMC向阳极一侧弯曲变形[17],如图2所示。水合阳离子在聚合物膜中的运动在IPMC的电极之间产生电流,变形的程度主要与转移的电荷有关,本文将阳离子的运动和储存在IPMC中的电荷用双层电容(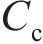
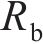
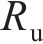
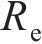
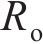
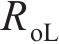
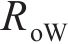
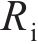
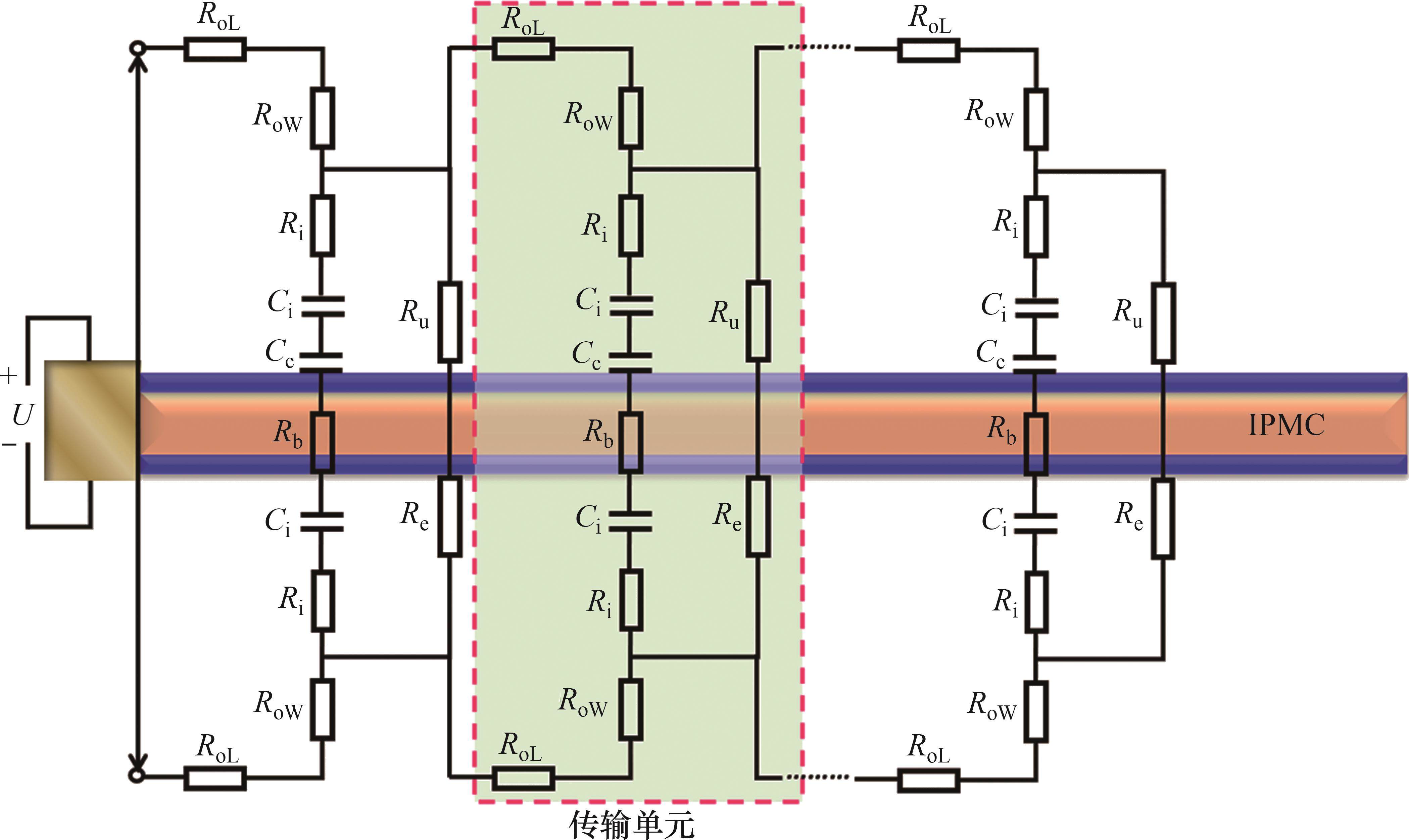
根据传输线理论,当输入电流通过电路的一端时,电流会流过整个传输线链条的所有元件,电流在电阻上会引起电压降,使得线路上的电压降低,也就是说,在给IPMC一端施加激励电压,经过传输线在另外一端会出现电压衰减的现象。水合阳离子的移动过程是电容元件进行充电的过程,电路传输线中的电压和电流都会发生变化,在水合阳离子完全在阴极侧移动,电路系统会保持在平衡状态。对于水合阳离子运动引起的IPMC的瞬态弯曲状态,本文用偏微分方程来描述。
2.2 电荷密度模型
为了简化分析IPMC的等效电路模型,从图3中分离的等效电路单元,如图4所示。将外电极不同方向的电阻进行串联,随后和内电极的电阻进行并联,因此,本文将电极层的电阻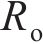
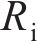
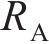
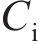
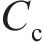

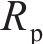
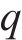
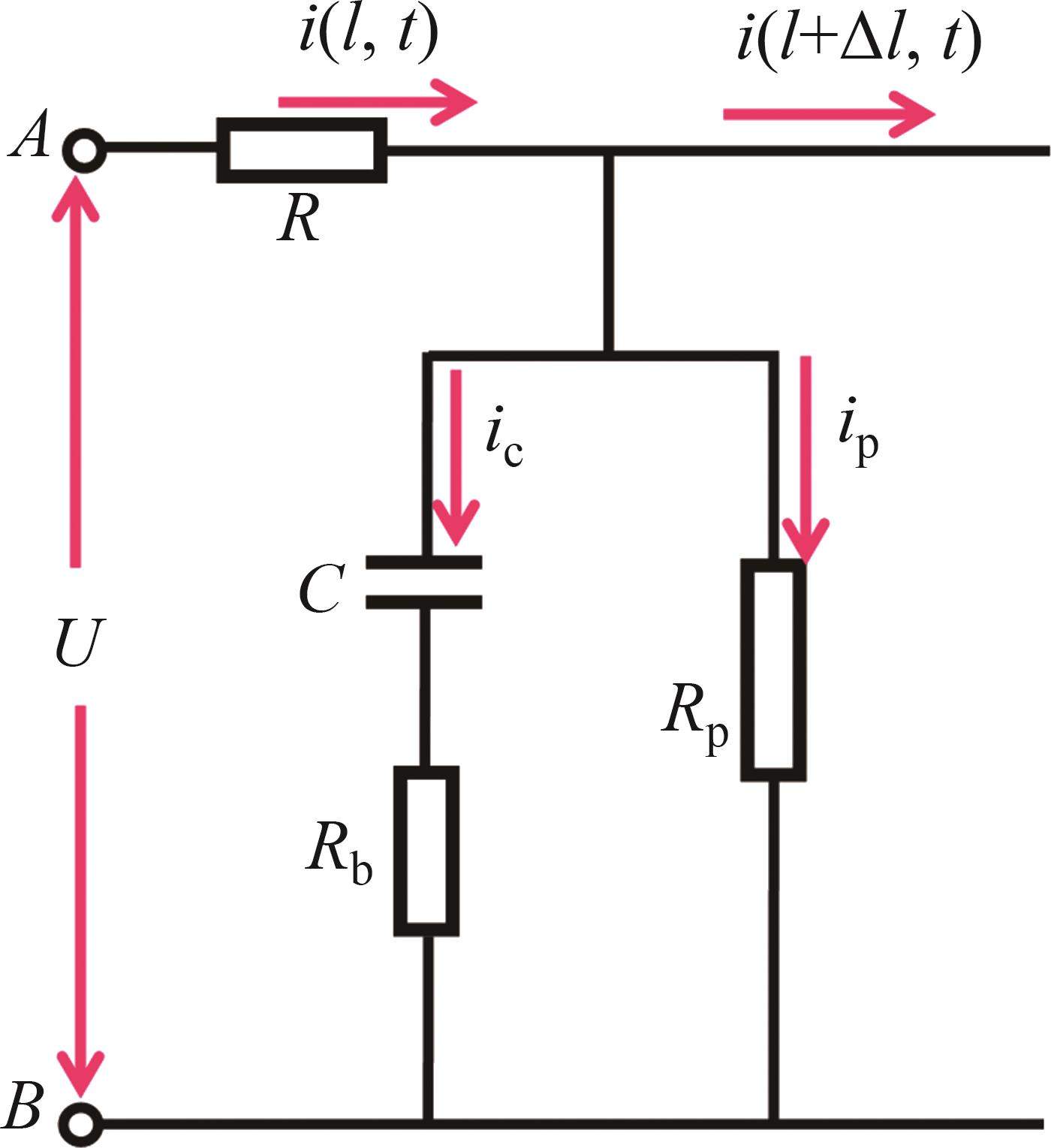
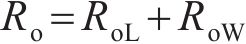
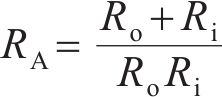

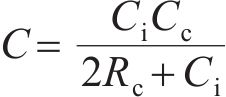
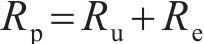
式中: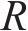
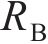
图4中,传输线电路中的电压、电流以及电荷为IPMC加持端到自由端距离(
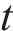
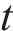
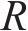
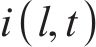
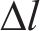
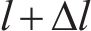
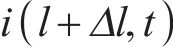
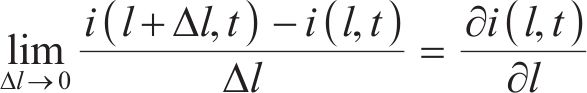
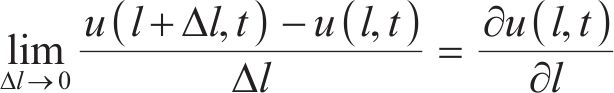
电路中的电压和电流满足基尔霍夫电压电流定律,同时根据传输线理论,电流通过电路分支的变化量等于在2个分支的电流之和,位置
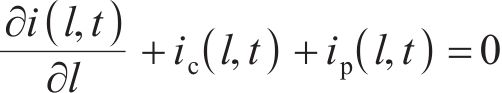
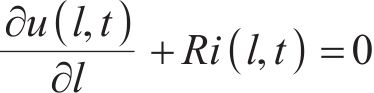
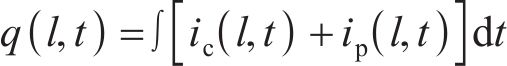
其中:
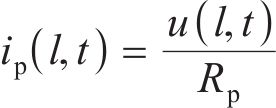
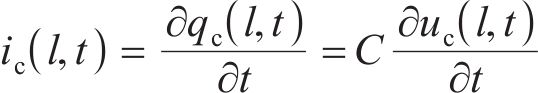
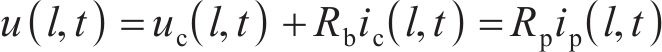
将以上各式进行变换和重新组合,经拉普拉斯变换求解,使电路中电流信号从时域(t)转换为复频域(s),设h为拉普拉斯变量,则有
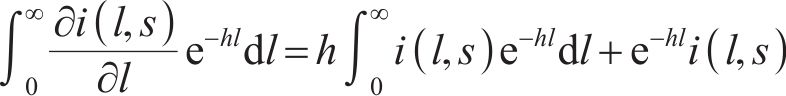
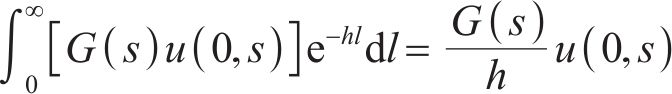
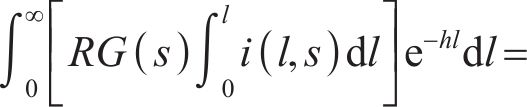
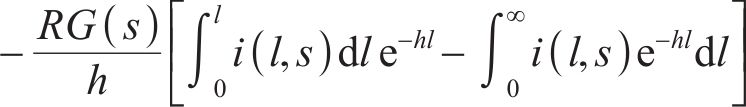
其中
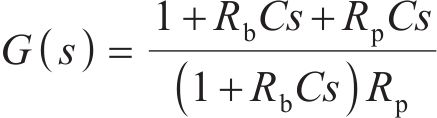
结合以上公式,有
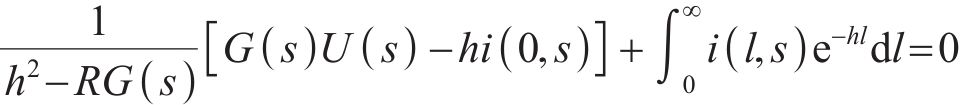
对式(21)进行反拉普拉斯变换: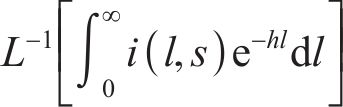
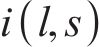
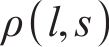
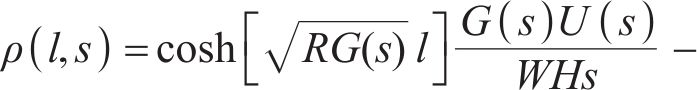
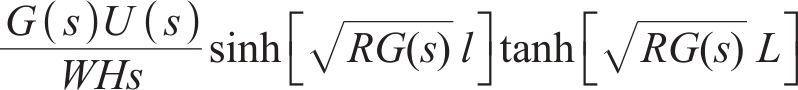
2.3 弯曲角度的动态模型
IPMC在电压激励下向阳极发生弯曲变形,除了采用弯曲位移表征其弯曲程度外,另一个重要的指标便是弯曲角度。如图4所示,据式(22),可得流入离子聚合物中的电荷量的计算公式:
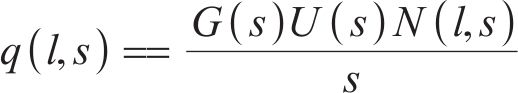
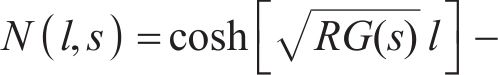
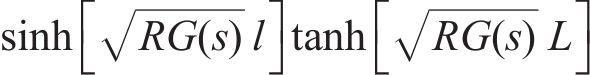
离子聚合物中的电荷量对驱动状态有很大的影响,间接决定了最终柔性驱动器变形的弯曲角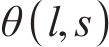
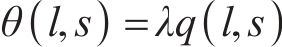
式中:
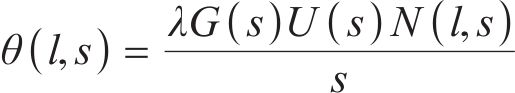
3 柔性驱动器的传递函数
3.1 传递函数的表征
变形角度(式(26))可有效地描述IPMC在驱动过程中的电机行为。在初始状态下,IPMC在没有外部激励的情况下保持不变,一旦施加电压刺激,便会发生一定程度的弯曲变形。故研究IPMC从施加电压到输出变形角度的机电转换过程具有重要意义,这是控制IPMC驱动的前提和基础。本文根据IPMC变形、输入电压、输出弯曲角的特点,定义描述这些特性之间相互作用的传递函数。为了能有效表征其动态特性特别是IPMC的磁滞特性[18],增加级联函数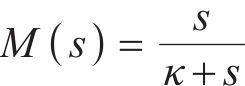
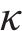


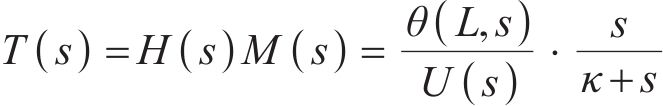
结合式(27),对式(30)进行组合和变换可以得到传递函数为
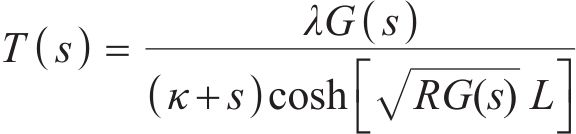
3.2 参数确定
根据2.2节IPMC的驱动单元电路的分析,结合IPMC尺寸特点,由式(4)~(6)和前期的最密堆积原理电极研究模型[19]得到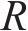
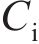
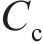

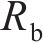
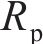
| 参数 | 数值 |
|---|---|
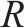 | 15.01 |
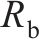 | 26 |
 | 0.000 2 |
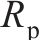 | 30 244 |
3.3 辨识算法
尽管式(26)~(28)消除了不同位置对驱动器变形的影响,但其弯曲角度仍然无法将反拉普拉斯变换为时间t的函数。其主要的原因是式(27)包括了双曲余弦函数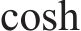
在处理动力学系统的参数辨识方面,最小二乘迭代法具有实现简单、精度高、适用性强等优势[21]。基于此,为了得到弯曲角度的传递函数,尝试优化最小二乘迭代法(least squares iteration method,LSIM)进行IPMC模型辨识。假设模型辨识的传递函数的表达式为
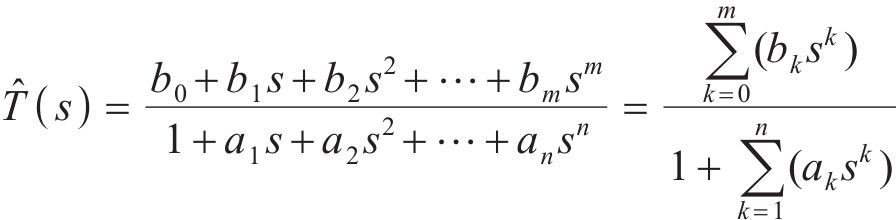
式中: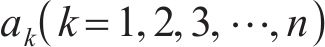
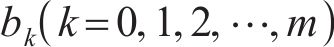
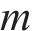
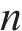
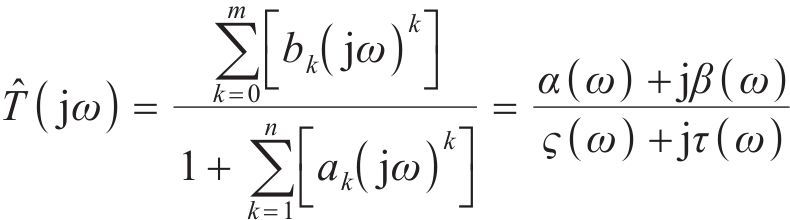
式中: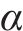
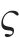
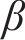

为了简化模型参数表示的复杂程度,在频率为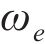
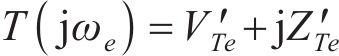
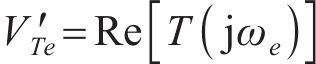
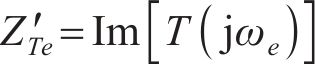
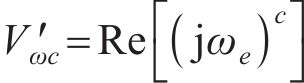
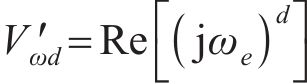
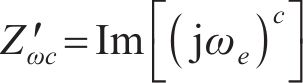
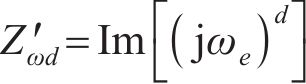
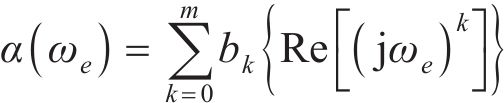
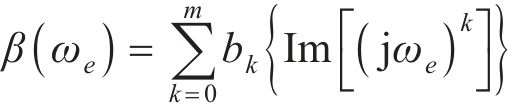
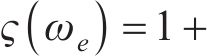
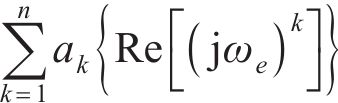
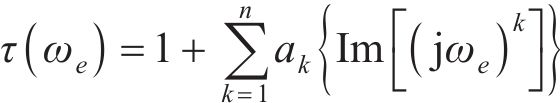
式中:
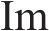
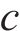
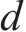
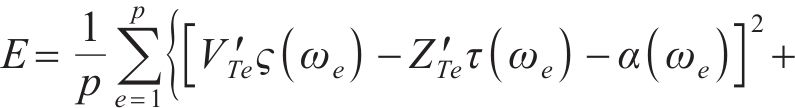
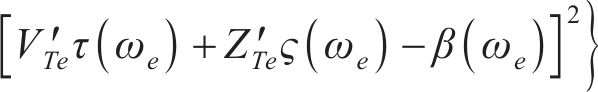
式中: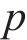
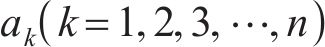
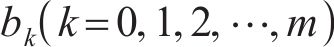
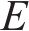
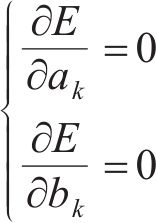
式(33)可以变换为
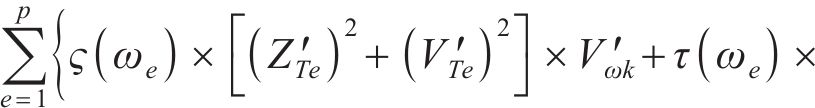
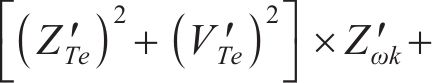
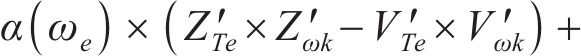
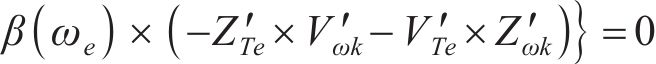
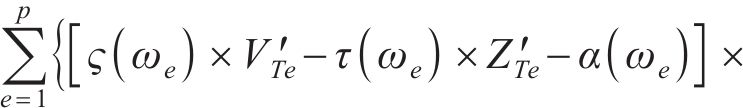
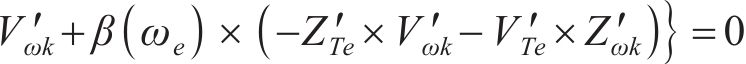
此时,
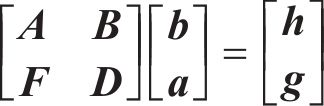
式中:
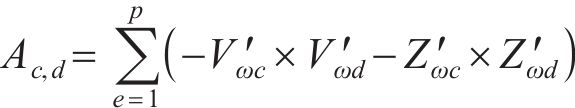
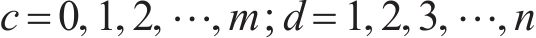
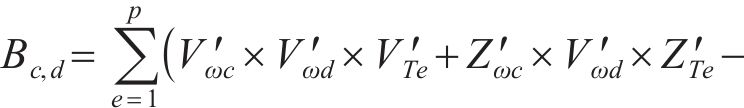
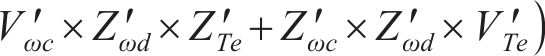
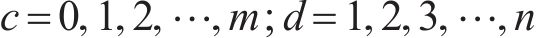
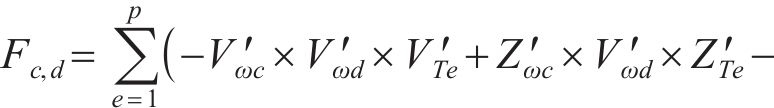
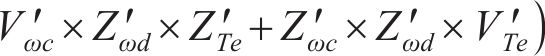
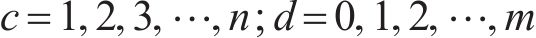
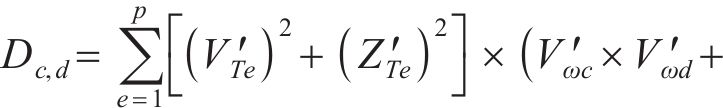
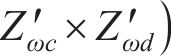
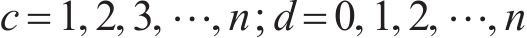
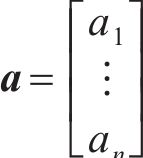
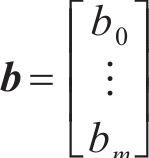
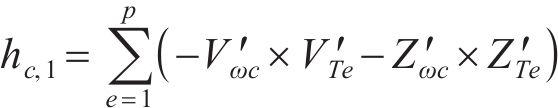
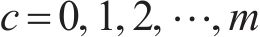
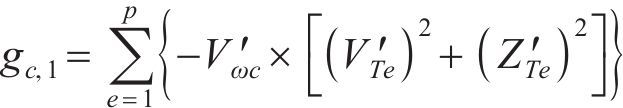
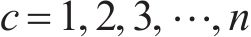
对式(36)进行求解能得到最优解,即得到了各个系数的值。此时,传递函数就从无限维转换为有限维。
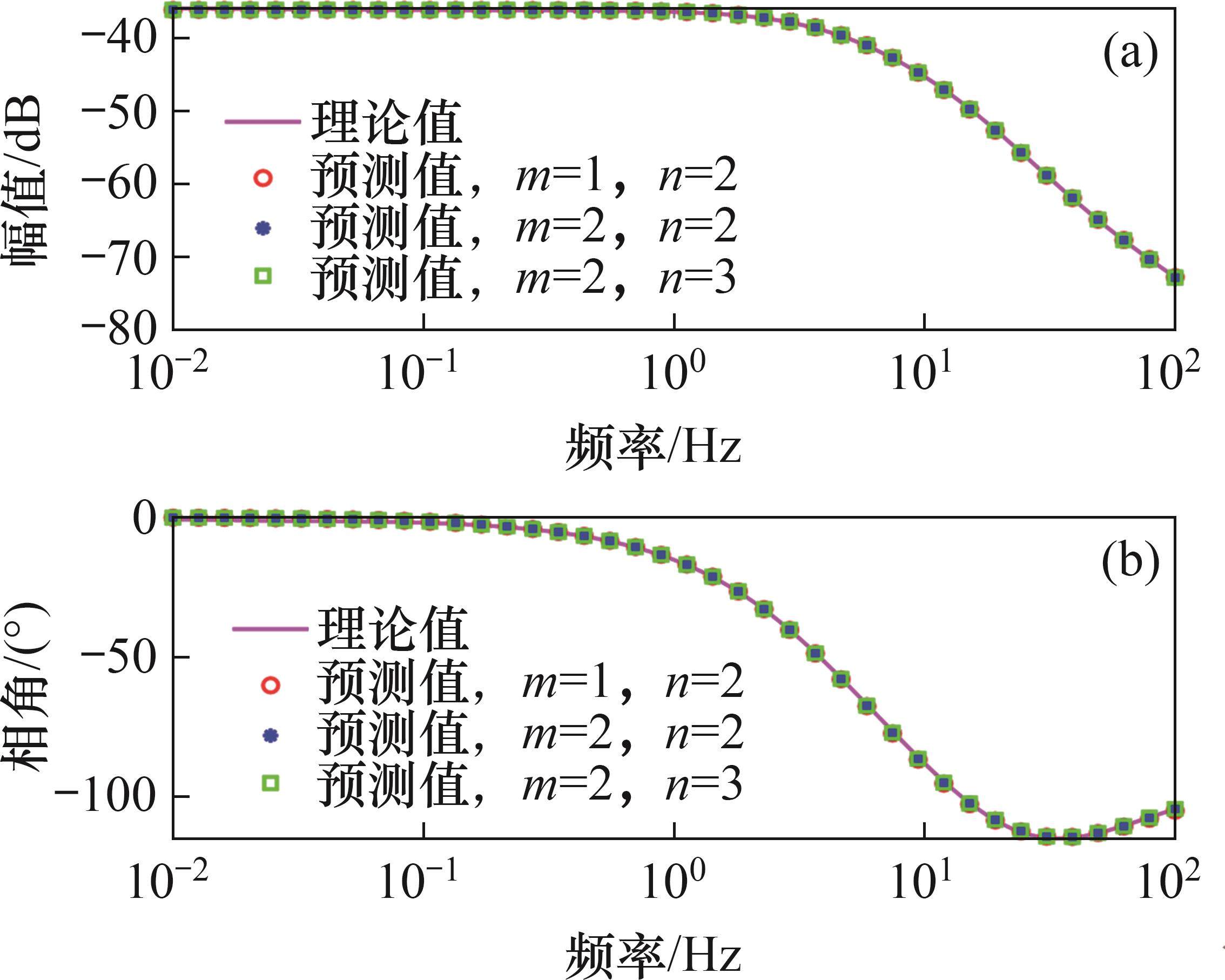
为了说明通过最小二乘迭代算法描述驱动器的驱动情况,将得到的辨识模型曲线和理论曲线进行对比。由式(29)可知:驱动器模型系统的阶数最终取决于不同的m和n。在不同阶次下,理论曲线和辨识模型的伯德图如图5所示。由图5可知:无论阶数如何变化,辨识模型的幅值和相角的预测值与理论值非常接近,不需要增加阶数对其进一步拟合,以便减小可能出现的无效解的情况。在m=1、n=2时,实际模型与辨识模型的幅值和相角的平均相对误差为1.12%,由此可知提出的模型可以有效地捕获柔性驱动器的特性。此时,得到的辨识模型为
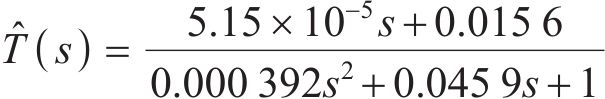
4 动态模型的降阶与实验验证
柔性驱动器的驱动模型使用最小二乘算法消除cosh函数,达到了对传递函数的降阶效果。为了得到距离和时间对动态模型的定量关系,对式(44)进行反推,以便能够得到降阶后的驱动动态模型函数。采用振幅为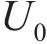
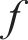
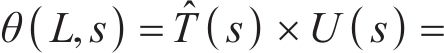
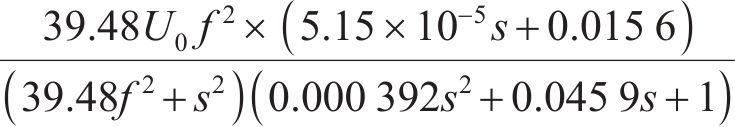
随后对式(45)进行反拉普拉斯变换,并根据 图1显示的IPMC弯曲变形特点,结合式(1)进行变换和组合,便可以得到驱动器弯曲角度的驱动模型。采用化学沉积方法[22]制备IPMC试样,建立了IPMC驱动器驱动测量实验装置,如图6所示。实验装置由信号发生器、IPMC试件、数码相机和数据采集处理模块组成。IPMC试样长×宽×高为 50 mm×10 mm×0.183 mm,采用振幅为5 V、频率为0.5 Hz的正弦驱动信号,对本文提出的驱动模型进行验证。此时,驱动器尖端处变形弯曲角度的驱动模型函数为
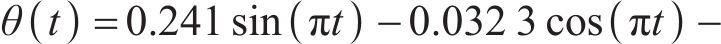
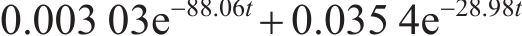
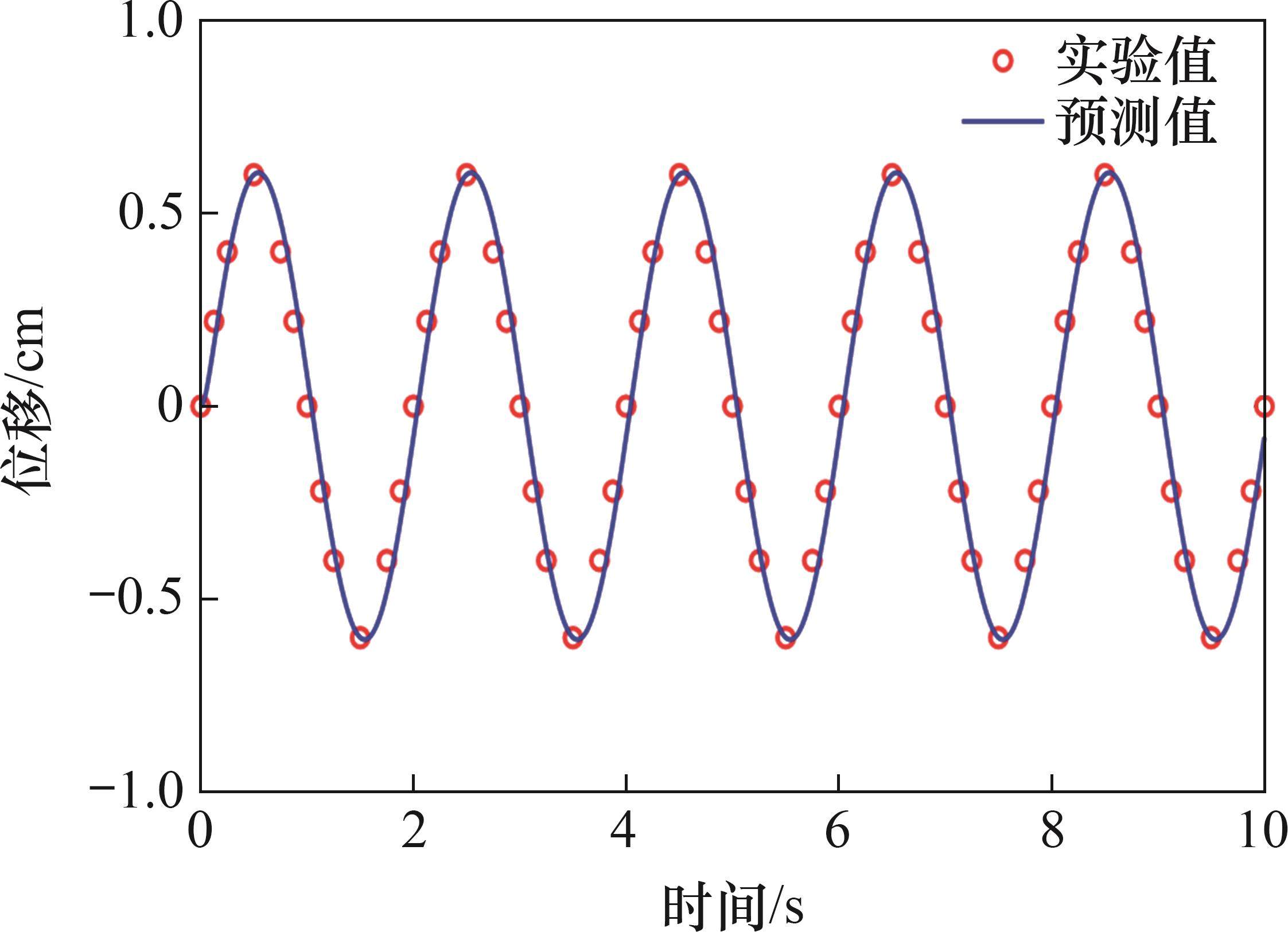
将本文提出的IPMC动态驱动模型与实验结果进行对比,如图7所示。由图7可知:本文动态模型预测的IPMC弯曲位移预测值与实验测量值非常接近,整体的变化趋势也相同,这验证了模型的有效性。同时,该模型不仅能够准确地捕捉IPMC在静态和动态电激励下的响应特性,还能够预测在不同工作条件下的IPMC驱动行为。通过建立的非线性驱动模型,可对IPMC的变形过程包括离子迁移、电荷分布和应力-应变关系等进行深入分析。此外,驱动模型为IPMC驱动器的设计和优化提供了强有力的理论支持。
5 分析与讨论
5.1 不同电压、电阻以及电容对驱动位移的影响
当驱动器受到不同的电压激励时,其驱动位移呈现规律性变化。图8所示为不同电压、电阻以及电容对驱动位移的影响。从图8(a)可以看出:外加电压幅值越大,驱动器的驱动位移越大,其驱动变形的响应时间基本没有显著的区别。尽管电压对于输出力有决定性作用,但并不是最大位移会随电压增大无限度地增加,而是存在一种临界状态[23]。超过这个临界状态后,继续增加电压将不再显著提高位移,反而可能对IPMC的性能和寿命产生负面影响。为了实现IPMC的有效驱动,需要对施加的电压进行精确控制,避免超过临界状态,同时考虑材料的电化学稳定性、热稳定性和力学稳定性,以确保IPMC驱动器的长期可靠运行。
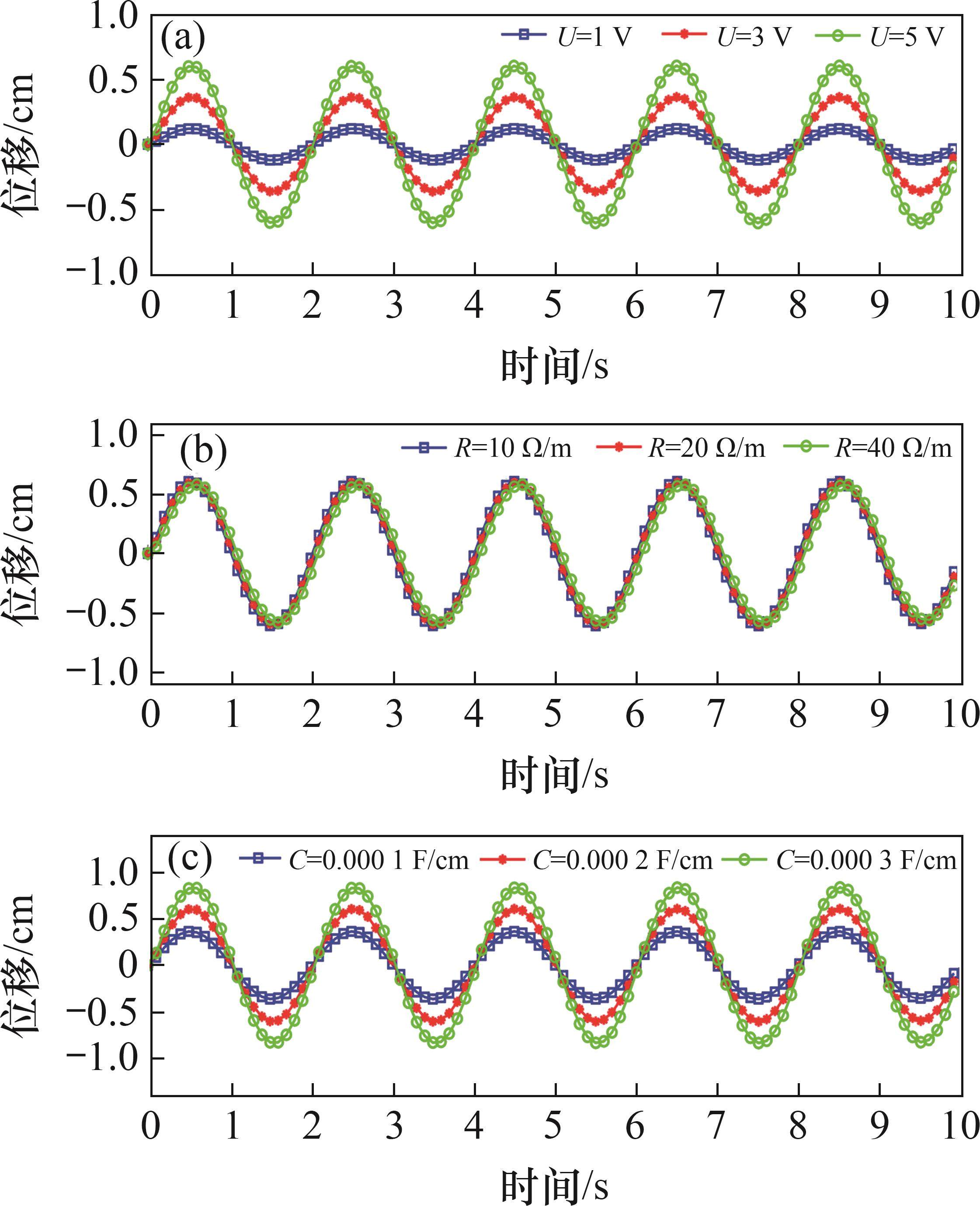
电极电阻决定了激励电压的分布,影响驱动器变形的效果[16]。在化学镀过程中必须合理采用制备工艺,才能达到预期的效果。由图8(b)可知:电极电阻对于柔性驱动器的最大位移影响不很明显,但仍然可以看出电阻越小驱动位移越大。较低的电极阻力可以促进驱动器快速变形,提高其响应速度,缩短弯曲的响应时间。其主要原因是较低的电极电阻可以使电极与聚合物基体之间的水合阳离子迁移数量增多,迁移的速度更快。由此产生的在阴阳极两侧的水合阳离子分布密度差异增大,最终导致柔性驱动器的弯曲变形位移增大。
由图8(c)可知:电容越大,输出的驱动位移越大。一方面,柔性驱动器的电容主要受表面接触面积和电极层距离的影响,界面接触面积增大和电极层之间距离减少,有利于提高驱动器的电荷存储容量,促进界面层的电荷积累[24]。另一方面,电场和诱导力进一步扩展,也会进一步导致驱动器的最大输出位移增大。另外,虽然理论上增加电容可以增加IPMC驱动位移,但实际上存在一个最优的电容范围,超过这个范围后,继续增加电容并不会显著提高位移,反而可能导致效率降低和材料受损。因此,在设计IPMC驱动系统时,需要综合考虑电容、电压、频率以及材料的特性,以实现最佳的驱动性能和效率。
5.2 不同位置处的驱动位移
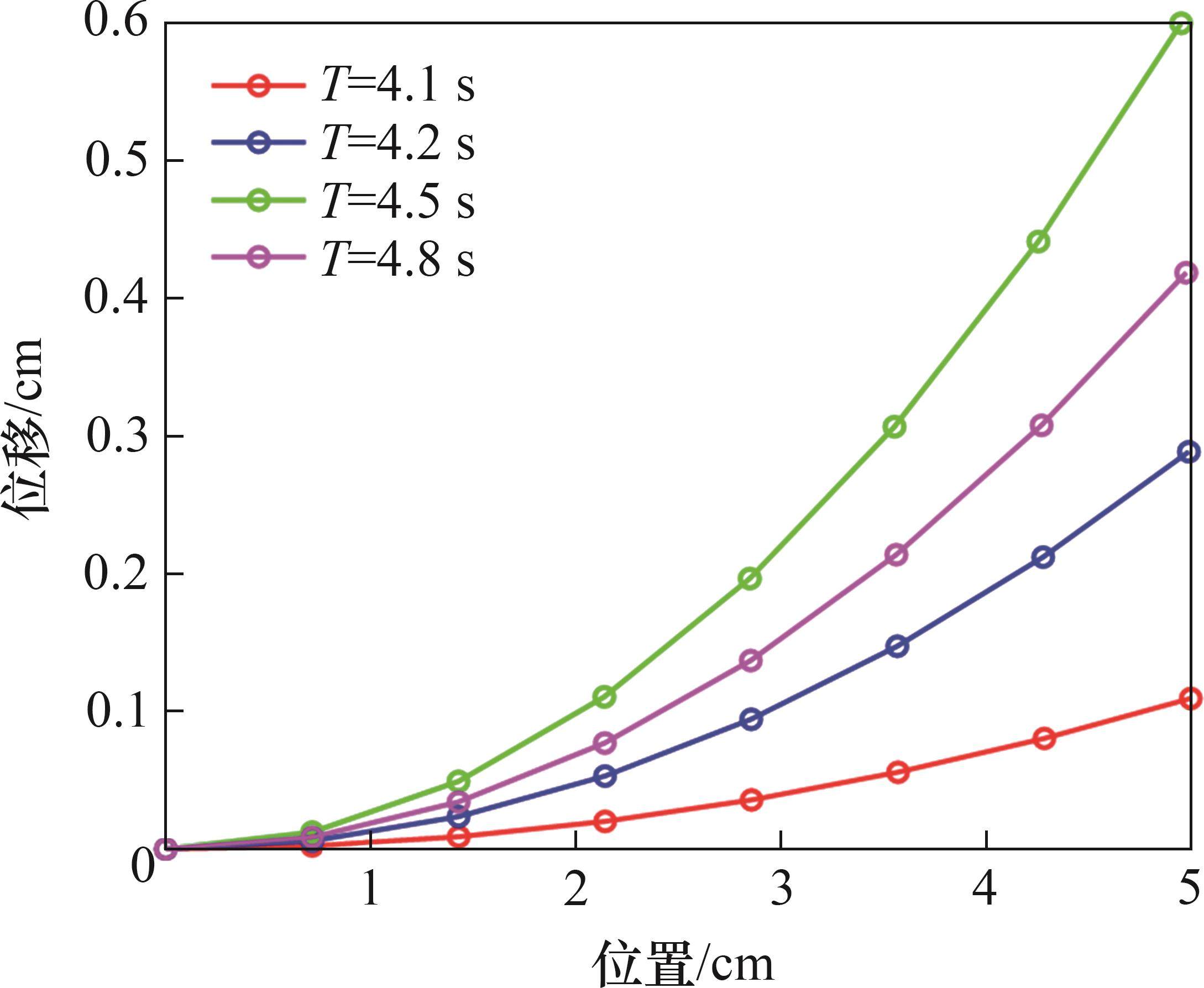
对于柔性驱动器变形的角度计算式(26),结合式(1)~(3),可以得到不同位置不同时间下、驱动器发生一定的弯曲时对应的横纵坐标。在距离夹持端不同距离的位置点,不同时刻驱动器的瞬态位移变化情况如图9所示。由图9可知:由于激励电压的作用,试样弯曲角度和末端位移的瞬态响应发生变化。随时间变化,末端位移会在一定的范围内发生变化,即位移存在一个增大值。位移增大主要是外加激励电压和水合阳离子迁移共同作用的结果。当时间为4.5 s时,距离夹持端 5 cm处位置点的最大驱动位移为0.6 cm。不同位置的驱动器试样的驱动程度也各不相同,长度越大,驱动位移越大。可见,提出的驱动动态模型可以有力地表征驱动器的驱动行为,较好地反映了其动态周期性变化特征,这对于后期柔性驱动器的尺寸设计有重要意义。
6 结论
1) 依据柔性驱动器变形特点,通过建立电荷密度函数构建非线性动态驱动模型是一种有效的方法。模型预测值与实验结果有良好的一致性,采用优化迭代算法可对传递函数进行有效辨识。
2) 基于传输线理论和驱动动力学构建的柔性驱动器动态模型可以预测不同电压、电阻以及电容对柔性驱动器驱动性能的影响,还可得到不同位置处弯曲变形的输出位移。
3) 该模型可用于解释各种物理参量对柔性驱动器性能的影响,也对离子电活性驱动器制备工艺和对应的控制器设计具有参考价值。
Modeling of ICPF(ionic conducting polymergel film) actuator: 3rd report, considerations of a stress generation function and an approximately linear actuator model
[J]. Transactions of the Japan Society of Mechanical Engineers Series C, 1997, 63: 2345-2350.杨亮, 王红, 田爱芬, 等. 基于传输线理论和驱动动力学的柔性驱动器动态特性分析[J]. 中南大学学报(自然科学版), 2024, 55(12): 4442-4451.
YANG Liang, WANG Hong, TIAN Aifen, et al. Dynamic characteristics analysis of flexible actuator based on transmission line theory and actuation dynamics[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4442-4451.

