鱼类游动经过自然的选择和进化,具有高效、规律性等的特点[1-2]。受鱼类游动行为的启发,研究者将仿生学与机械、电子信息、计算机控制等学科相结合,开发了具有高机动性的仿生水下机器鱼[3-4]。与传统的螺旋桨推进的水下机器人相比,两侧胸鳍协同推进的仿生水下机器鱼具有较强的隐蔽性,能在水下进行灵活的转弯、前进后退和俯仰等运动[5-7]。仿生机器鱼在做俯仰运动时,两侧胸鳍推进是模仿鱼类左右对称的胸鳍运动而兴起的一种推进模式,两侧胸鳍协同配合时,周围会产生复杂的流场,流场的变化对机器鱼的推进有很大的影响[8-9]。机器鱼在游动时也会受到周围流场造成的身体阻力的影响[10]。
关于仿生机器鱼的俯仰运动,文献[11]对机器鱼尾鳍摆动产生的流场结构进行了分析,讨论了俯仰运动的相位差、尾鳍摆动幅度和斯特劳哈尔数对鱼类推进性能的影响。文献[12]研究了胸鳍攻角对仿生机器鱼俯仰运动的影响,制定了机器鱼升潜运动控制规则。文献[13]数值模拟了非正弦俯仰运动下扑翼在前进方向及侧向的自主推进,研究了俯仰频率对自主推进及流场结构的影响。文献[14]研究了NACA0012翼型受到的俯仰运动,采用ANSYS有限元程序对固体运动的非线性方程组进行了求解。文献[15]设计并实现了一种新颖的非对称正弦俯仰运动,这种新颖的俯仰运动可同时提高推力和效率。文献[16]对机器企鹅进行俯仰运动学分析,采用实验研究了每个关节运动的推力特性。
仿生机器鱼俯仰运动是一种常见的游动方式,将俯仰运动应用于机器鱼的精确轨迹跟踪具有较高的价值[17] ,通过对俯仰运动和轨迹跟踪的研究,可以降低仿生机器鱼的能耗,提高其在水下任务的续航能力、灵活性、推进效率和机动性,使其在环境监测、水下资源勘探、军事侦察等领域发挥更大的作用[18-20]。以上研究对水下装置在水中做俯仰运动的流场特征进行了分析,但对于仿生机器鱼做俯仰运动时胸鳍各运动参数之间的辨识建模和定量分析较少。为此,本文采用计算流体力学(computational fluid dynamics,CFD)数值模拟了机器鱼的俯仰运动,得到俯仰运动X和Z方向的位移、鱼体俯仰角等,运用最小二乘法对绕Y轴的转角与胸鳍攻角和时间之间的关系进行拟合,得到二元二次函数关系式,为建立仿生机器鱼俯仰运动学模型奠定基础。
1 建立模型
1.1 机器鱼三维模型
为了描述仿生机器鱼的运动规律,需要对机器鱼三维模型建立坐标系。以机器鱼头尾连线与两侧胸鳍连线交点为原点创建坐标系,从头部指向尾鳍方向为X轴正方向,垂直于X轴指向鱼体左侧为Y轴正方向,竖直向下为Z轴正方向。仿生机器鱼三维模型如图1所示。
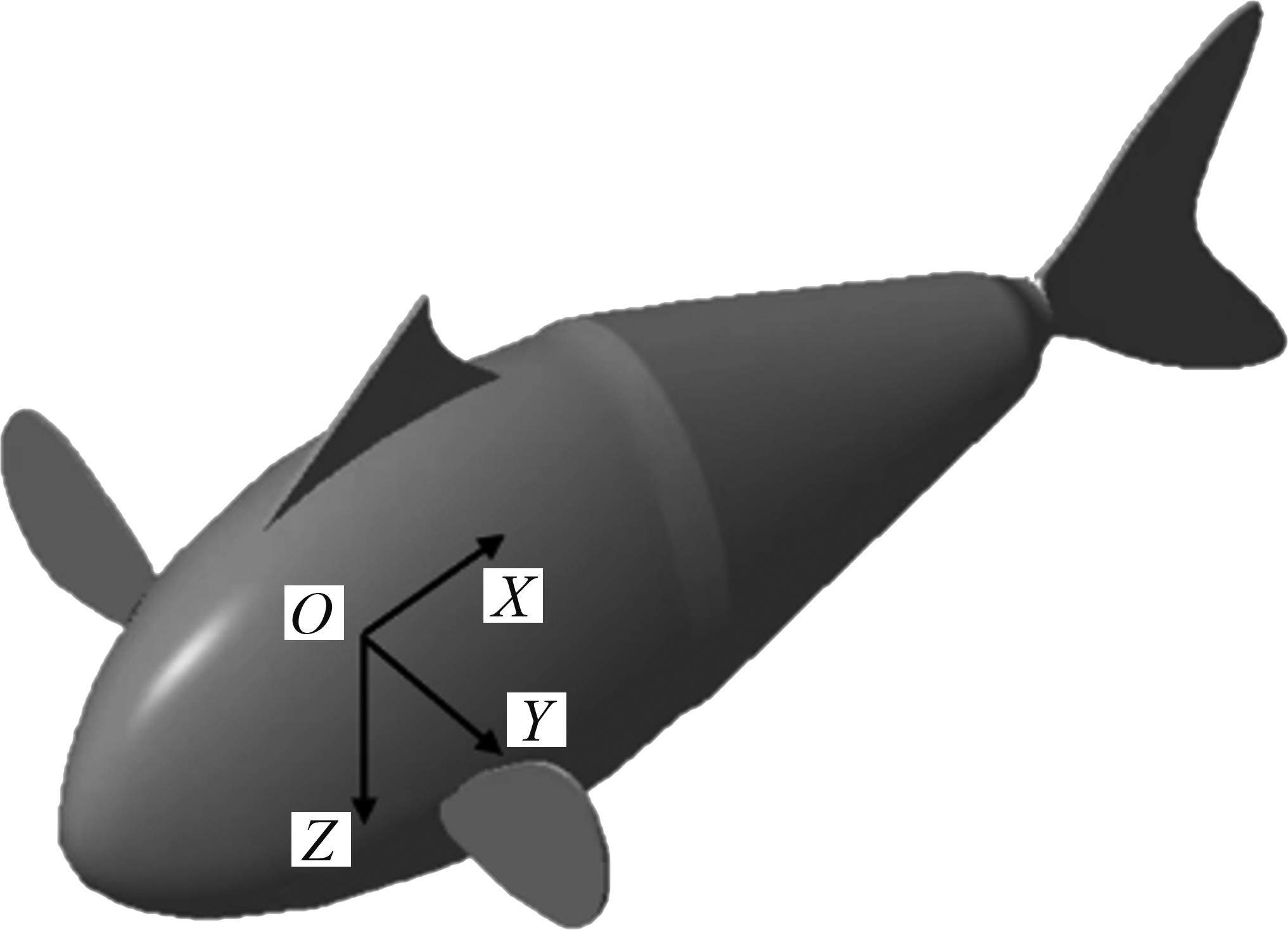
机器鱼质量约为9 kg,机器鱼的体长为693 mm,两侧胸鳍翼展总长度为458 mm,如图2所示。
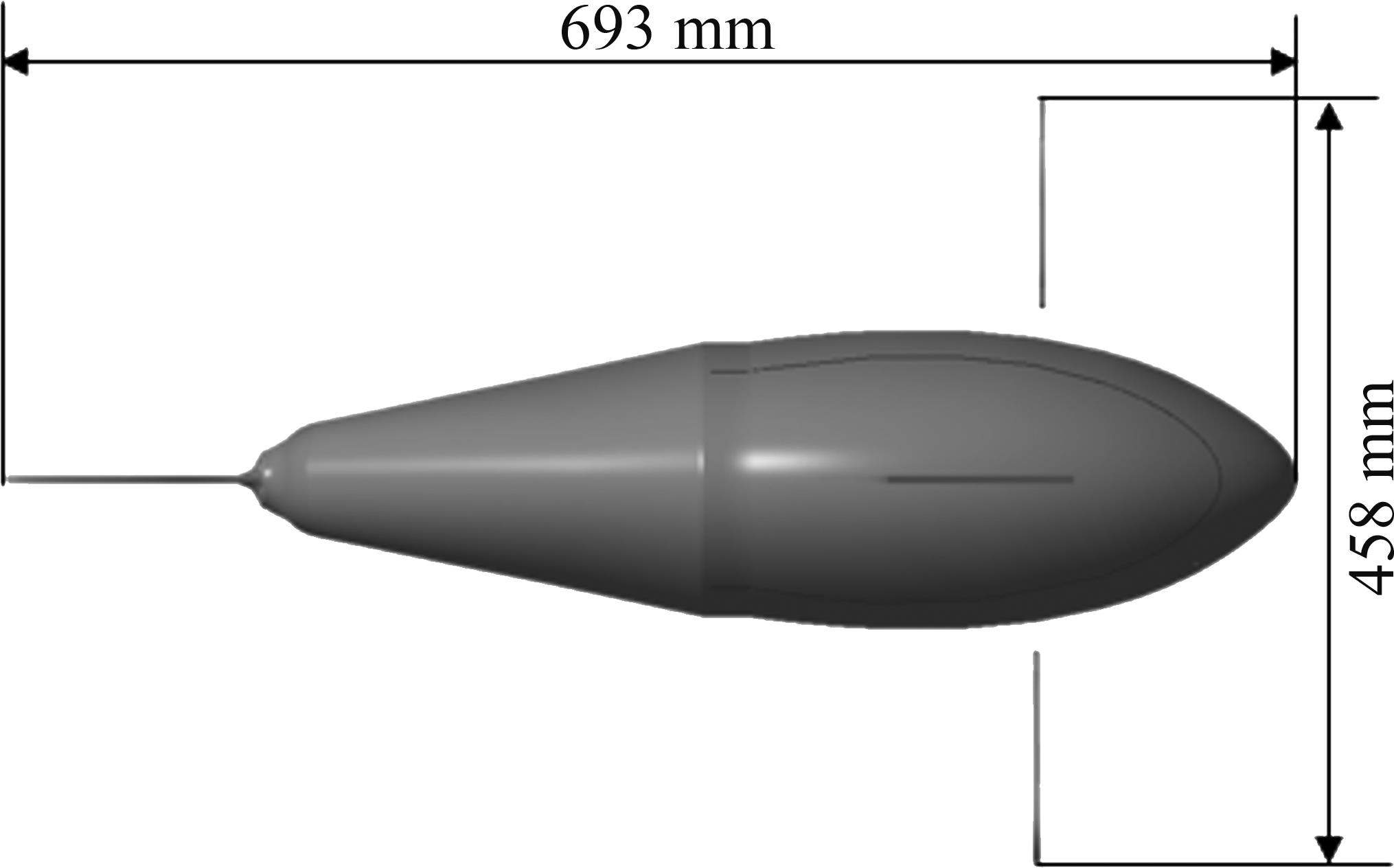
身体/尾鳍游动模式称为BCF推进模式,当前的仿生推进系统多采用BCF推进模式,该推进模式设计简单、推进效率较高[21-22],因此,本文采用BCF推进模式,由尾鳍摆动给机器鱼提供动力,两侧胸鳍协同推进完成向上或向下的俯仰运动。
1.2 胸鳍三维模型
仿生机器鱼胸鳍展长为180 mm,胸鳍弦长为105 mm,展弦比约为1.71,胸鳍整体呈均匀的板状,进行3自由度摆动。采用两侧胸鳍与鱼体的关系模仿真实鱼类,且胸鳍与实验室自制的机器鱼样机的胸鳍一致。实验室机器鱼为仿蓝圆鰺机器鱼,观察自然界真实的蓝圆鰺,分析其游动方式、身体结构以及运动特性,放大蓝圆鰺胸鳍的关键摆动特征,同时也对一些复杂的结构进行了适当简化,确保机器鱼既能够保持蓝圆鰺的基本特性,又能够适应实验室的环境和条件,研制出仿生机器鱼样机。机器鱼胸鳍三维模型如图3所示。
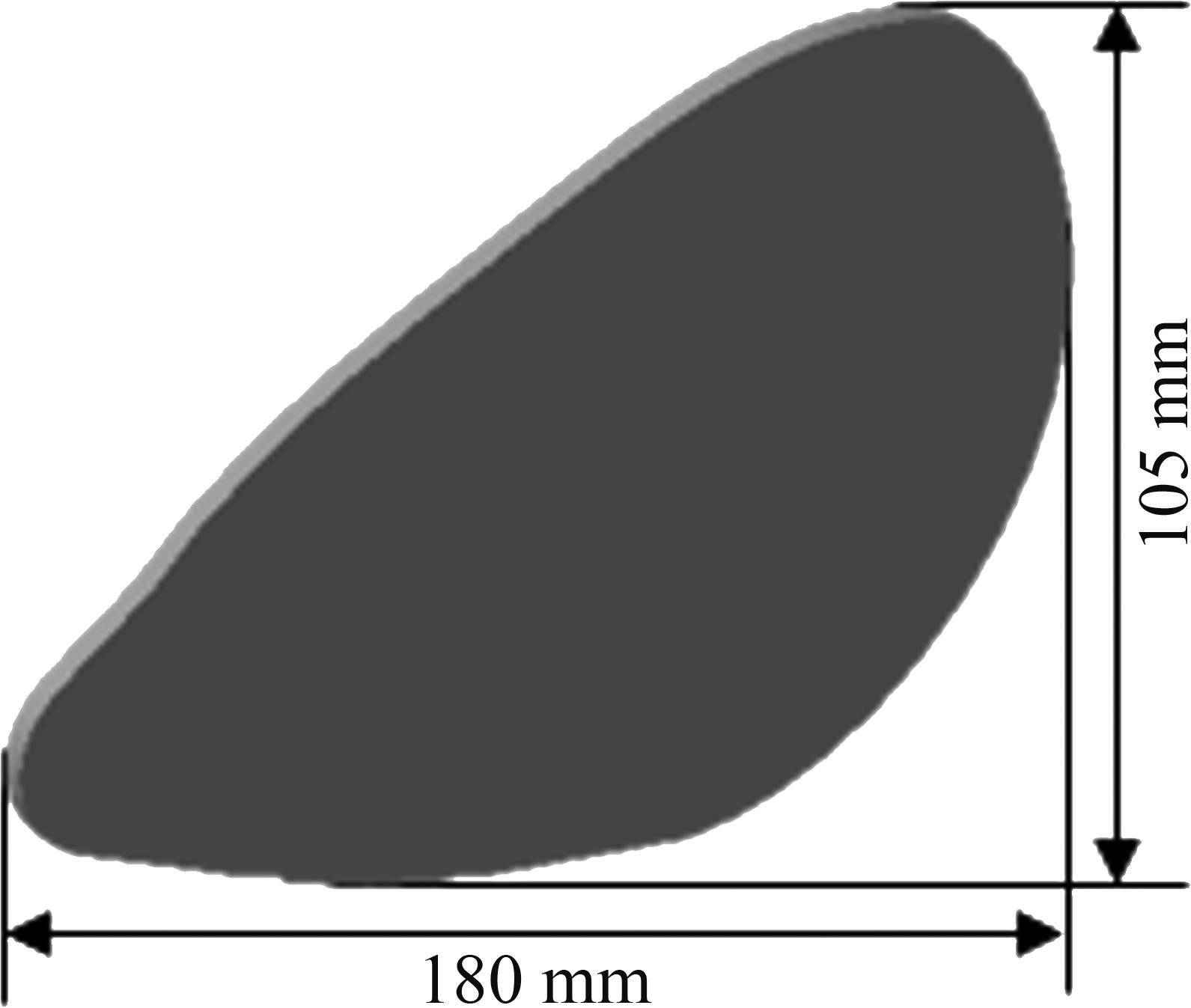
1.3 胸鳍运动学模型
为了深入研究胸鳍的摆动机制并优化其推进效率,对胸鳍的运动进行分解,即分解为绕X轴的上下拍翼、绕Z轴的前后拍翼和绕Y轴的摇翼。两侧胸鳍通过这3种自由度的运动复合协同推进,完成预期的俯仰运动[23]。在复杂的水环境中,两侧胸鳍协同推进的方式较多,能够使机器鱼轻松应对各种场景[24]。
一般来说,胸鳍的运动学模型可以由下式给出:
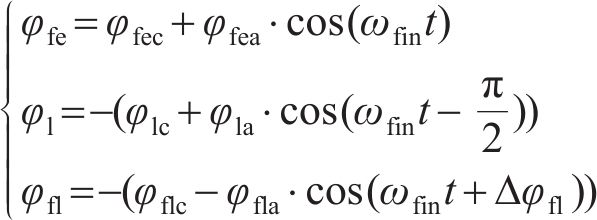
其中: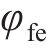
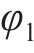
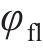
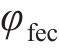
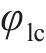
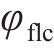
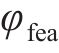
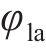
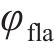
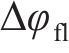
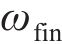
为了使机器鱼推进效率更高,采取两侧胸鳍协同推进的方式。在用户自定义函数(user-defined functions,UDF)中设定两侧胸鳍的摆动轨迹,使其遵循“椭圆”型曲线规律摆动,这种摆动规律能够有效地减小阻力,使机器鱼灵活地适应不同的水域环境,提高推进效率,最大程度地减少阻力和能量损耗。
胸鳍攻角是调整机器鱼姿态的关键参数,通过改变胸鳍的攻角可以调整鱼体的姿态,改变推力,进而实现机器鱼的上浮和下潜运动。为了描述这一角度,定义胸鳍攻角为胸鳍与平行于地面的鱼体平面之间的夹角。胸鳍原始位置为机器鱼在初始状态下未摆动时的位置,此时,胸鳍垂直于水平面。当胸鳍开始摆动时,每个时刻胸鳍的位置都不同,每个时刻对应于一个胸鳍攻角。胸鳍攻角定义如图4所示。
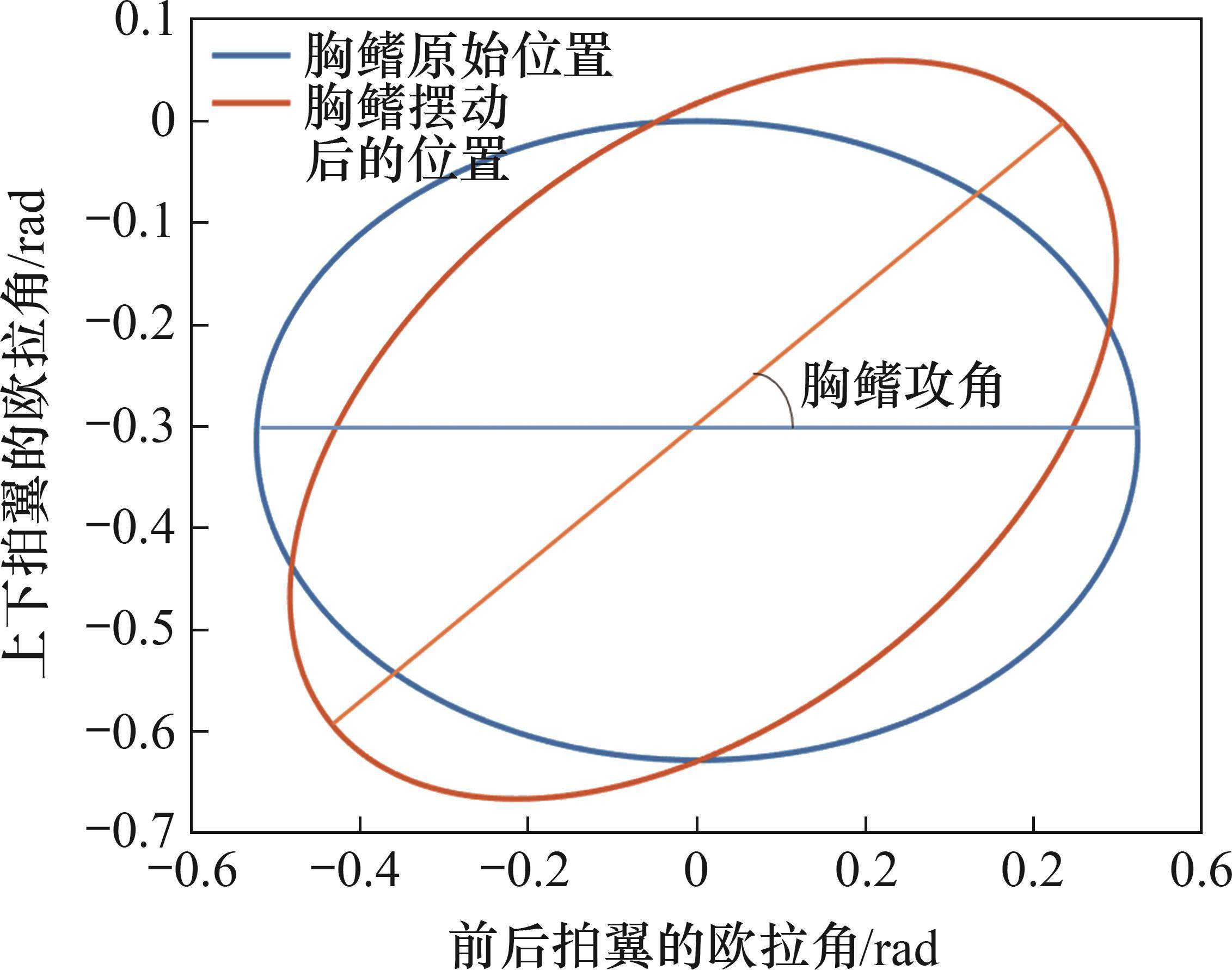
为了描述机器鱼俯仰运动与两侧胸鳍摆动角度之间的关系,改变两侧胸鳍的攻角,观察机器鱼胸鳍的摆动规律及机器鱼整体的俯仰运动。将胸鳍攻角分别设定为±15°、±30°、±45°,在不同的胸鳍攻角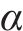
鱼体波曲线是鱼类运动学模型的简化,根据仿真中采用的动力学模型,得到鱼体波曲线方程为:
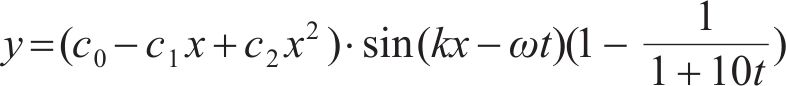
其中: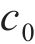
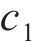
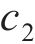
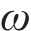
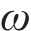
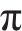
设定胸鳍攻角、机器鱼运动规律以及对鱼体波曲线方程,使机器鱼模拟真实鱼类的游动方式,并为机器鱼的运动提供更高的灵活性和可控性。
2 数值计算方法
计算流体力学(CFD)求解一般分为前处理、计算分析、计算结果后处理3个部分[25-26]。本文运用CFD模拟分析仿生机器鱼的俯仰运动,利用Fluent软件进行仿真,编写俯仰运动的UDF文件,导入Fluent进行计算。
对于黏性不可压缩流体,控制两侧胸鳍推进的Navier-Stokes方程表示为:
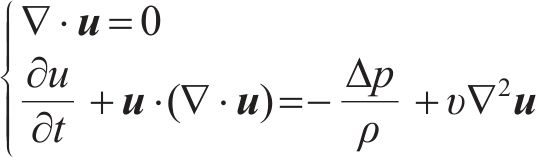
其中: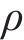
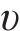
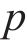
2.1 计算域网格划分
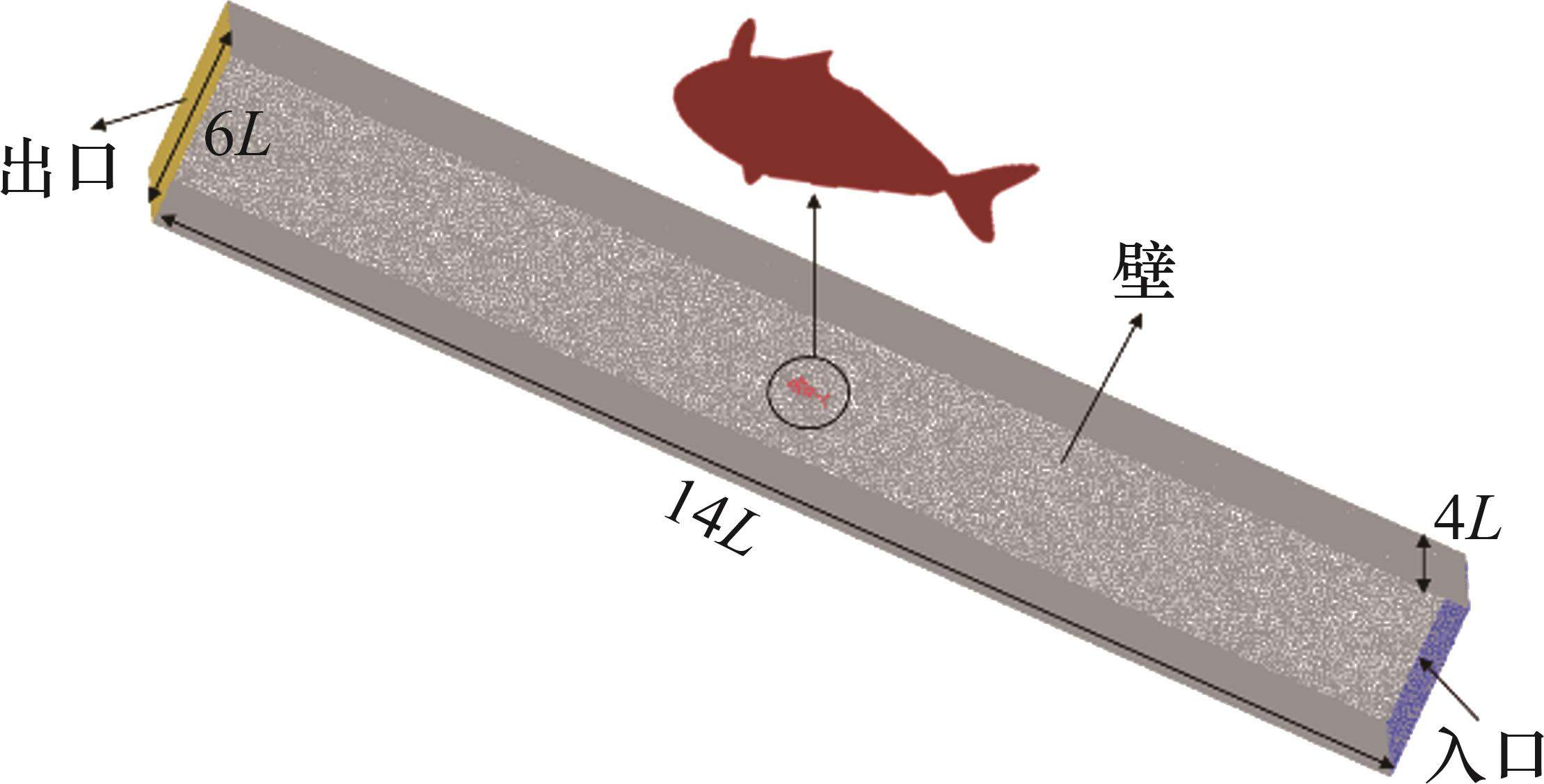
网格的划分对计算结果及精度有很大的影响,针对需求,应用ICEM CFD建立机器鱼二维几何模型,并生成均匀分布的非结构网格。对非结构网格计算时间长,但其适用范围广且划分容易。设机器鱼体长为L,长方体计算域长、宽、高分别为14L、6L和4L,鱼体位于计算域中心,计算域足够大以避免边界效应,网格数量约为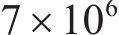
2.2 边界条件和参数设定
口流场左边界为出口,流场右边界为入口,入口速度为0.1 m/s,除了入口和出口外,其他壁面均保持无滑移边界条件。采用Fluent计算求解时,求解器采用基于压力的求解器(基于压力的求解器是针对低速、不可压缩流开发的)。动量离散采用二阶迎风格式,使用二阶精度后向隐式格式执行时间离散化,采用SIMPLE算法计算连续性方程[29]。设置时间步长为0.001 s,计算时间为4 s,以确保计算精度。Fluent数值计算参数设置如表1所示。
| 选项 | 参数设置 |
|---|---|
| 求解器类型 | 基于压力的求解器 |
| 黏性模型 | k-epsilon模型 |
| 壁面入口速度/(m·s-1) | 0.1 |
| 求解方法 | SIMPLEC方法 |
| 迭代次数 | 1 |
| 时间步长/ms | 4 |
| 步数 | 2 000 |
3 数值计算结果分析
3.1 俯仰运动步态行为分析
采用Fluent软件进行数值模拟,分析机器鱼在流场中俯仰运动时的步态行为,获得胸鳍攻角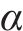
不同胸鳍攻角
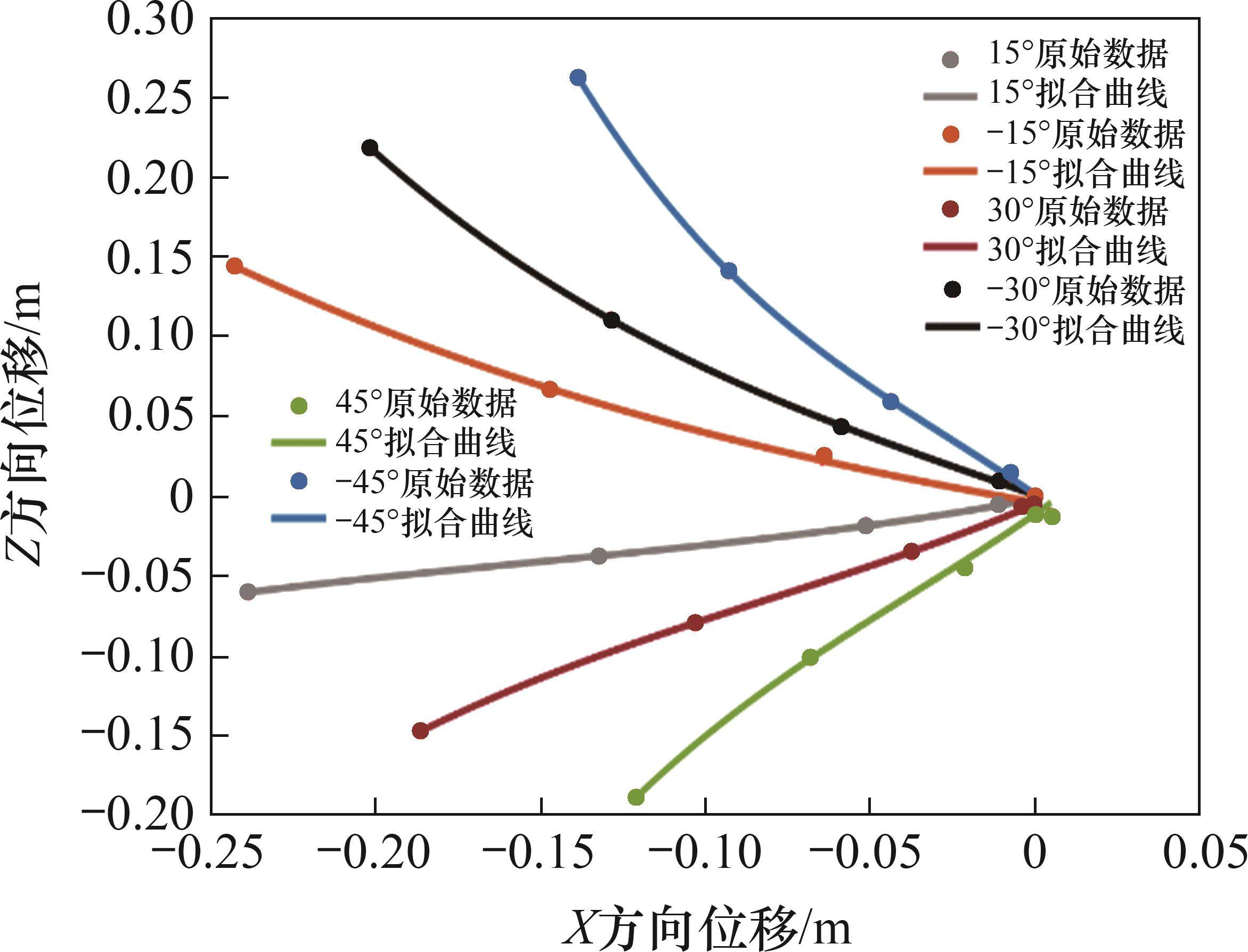
胸鳍攻角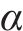
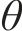
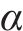
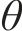
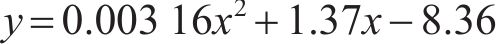
导出时间步长为0~900时绕Y轴的转角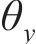
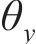
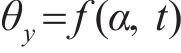
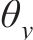
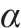 | t/s | 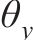 |
|---|---|---|
| -15 | 0.2(T/6) | 0.003 074 |
| -30 | 0.8(T/3) | 0.050 784 |
| -45 | 1.4(T/2) | 0.141 611 |
| 15 | 2.0(2T/3) | -0.056 606 |
| 30 | 2.6(5T/6) | -0.276 461 |
| 45 | 3.2(T) | -0.578 888 |
设拟合的曲面方程为:
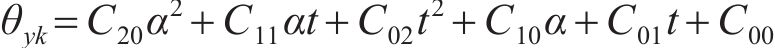
式中: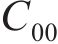
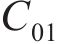
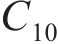
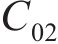
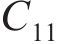
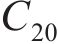
总误差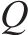
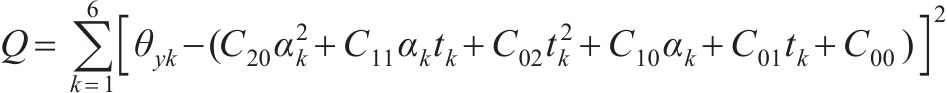
分别由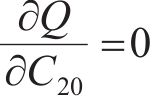
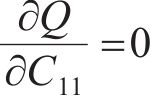
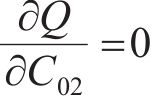
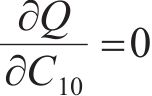
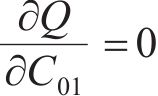
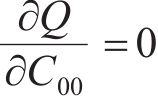
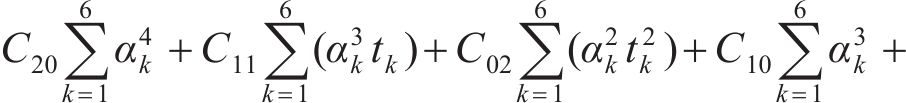
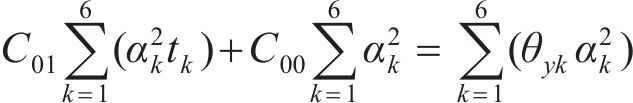
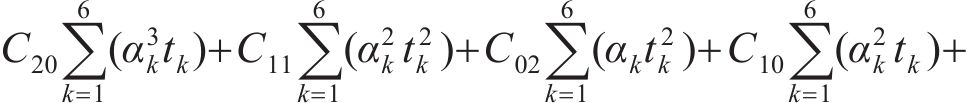
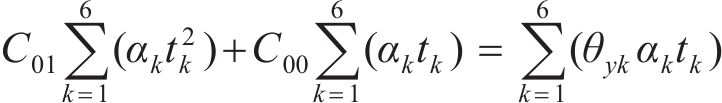
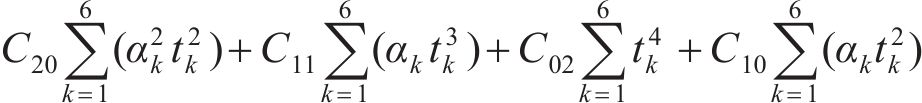
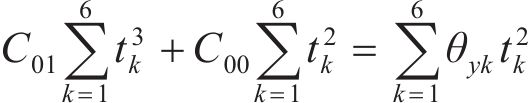
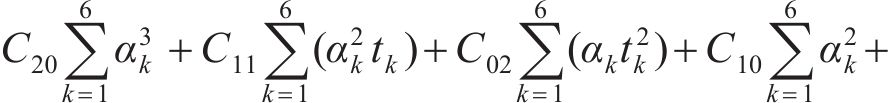
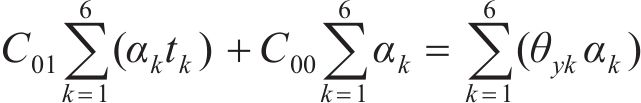
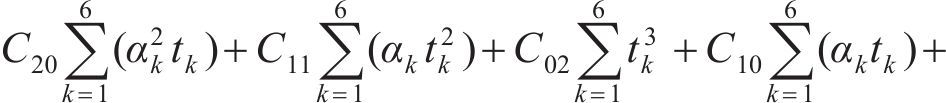
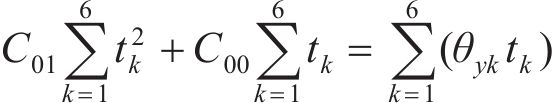
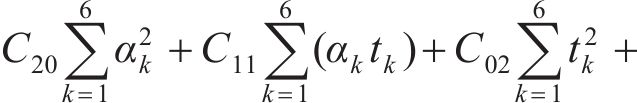
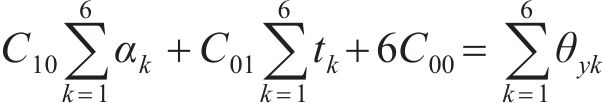
根据表2计算式(7)~(12)中的参数,并代入 式(7)~(12)可得:
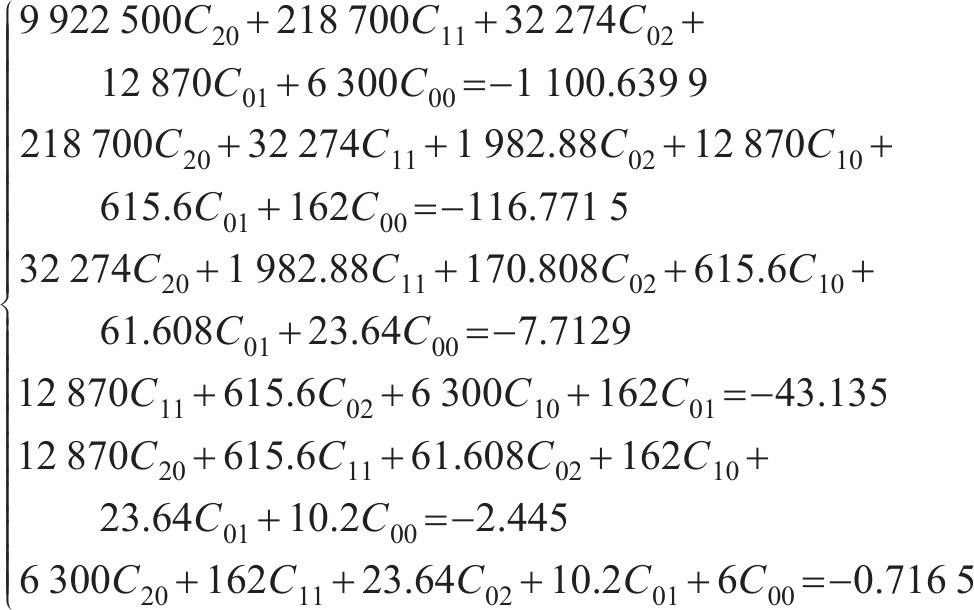
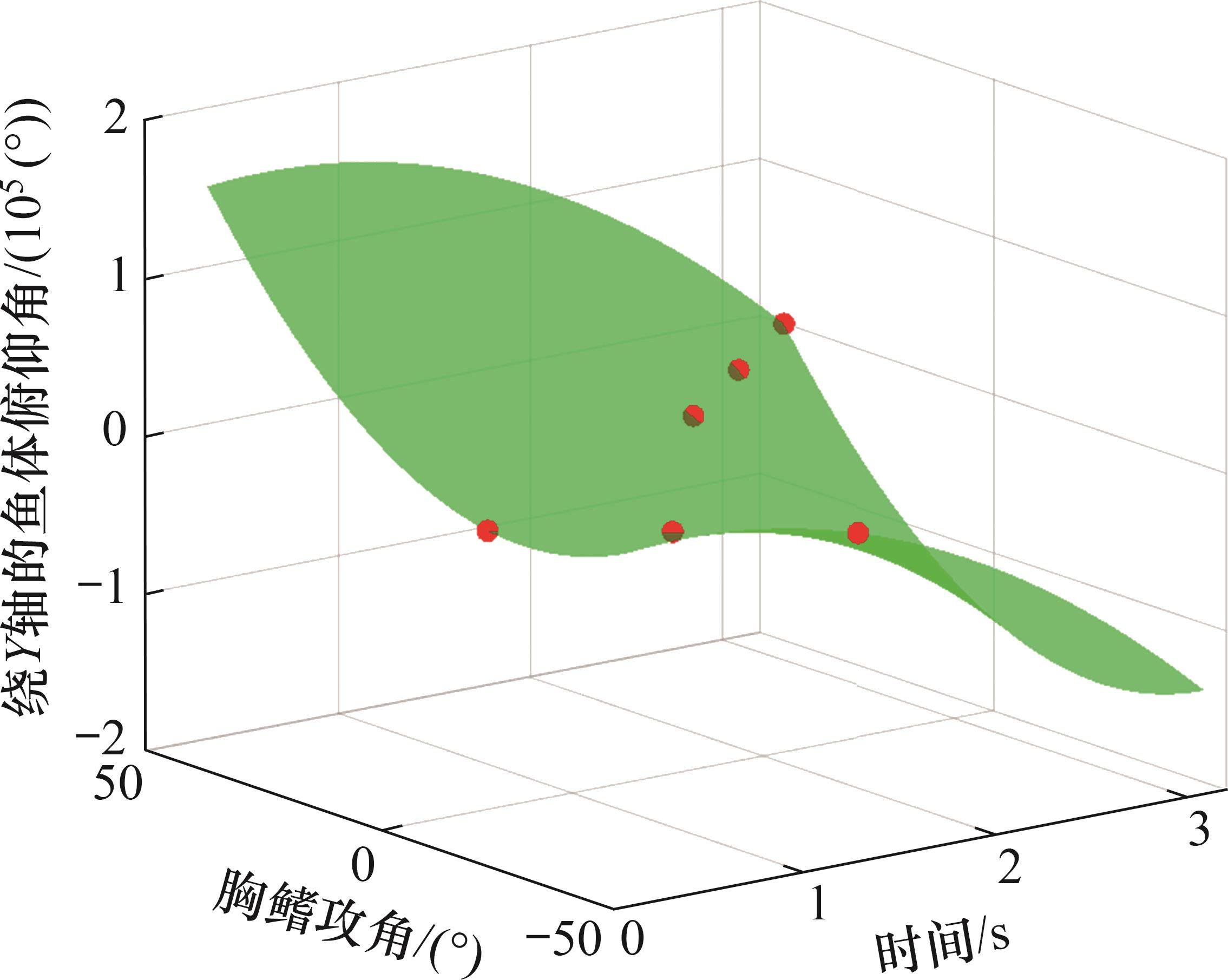
运用高斯消元法迭代拟合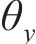
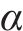
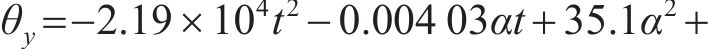
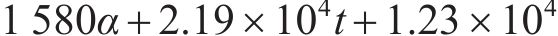
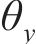
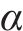
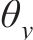
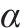
3.2 流场压力云图
当胸鳍攻角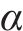
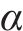
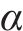
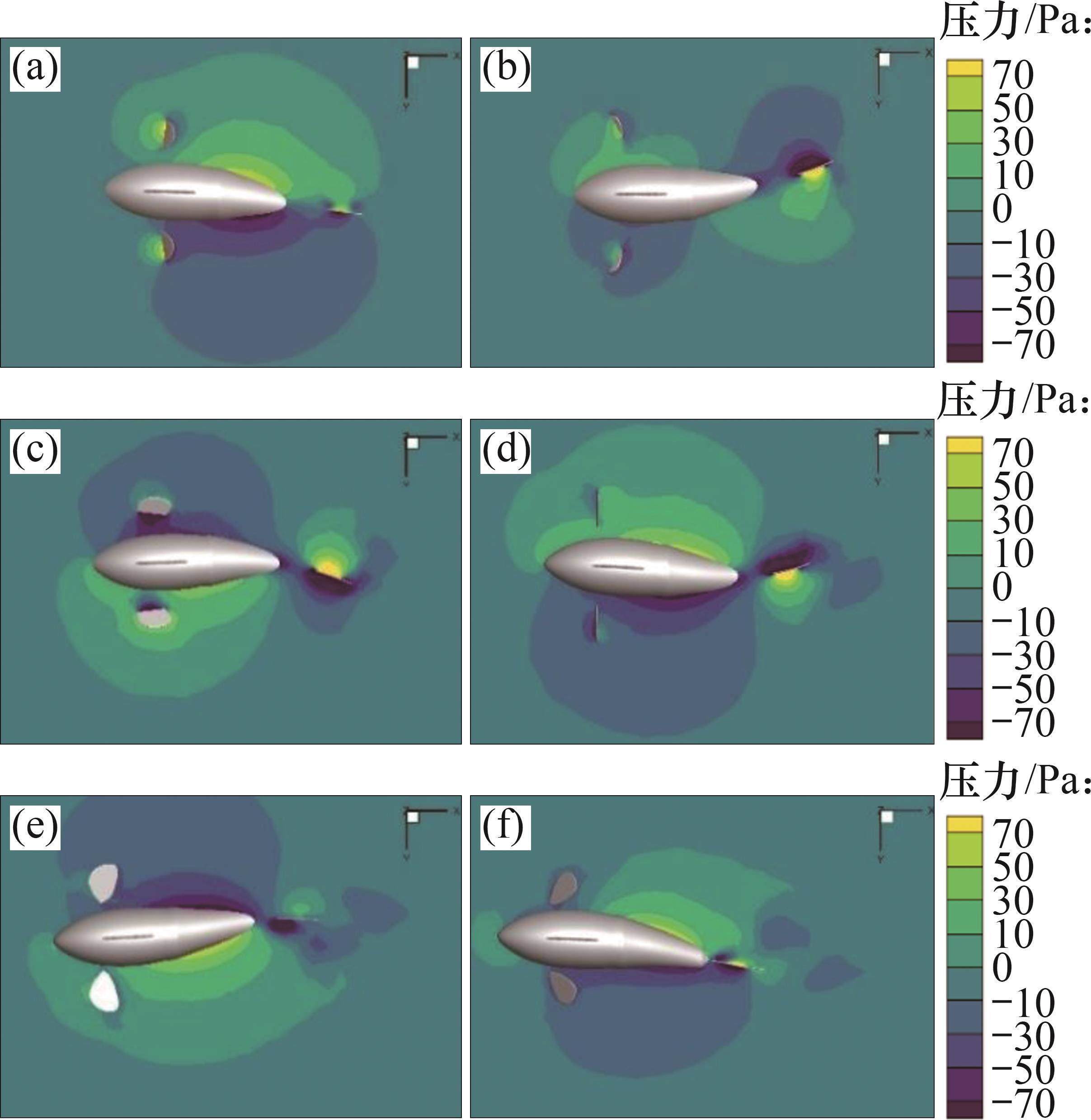
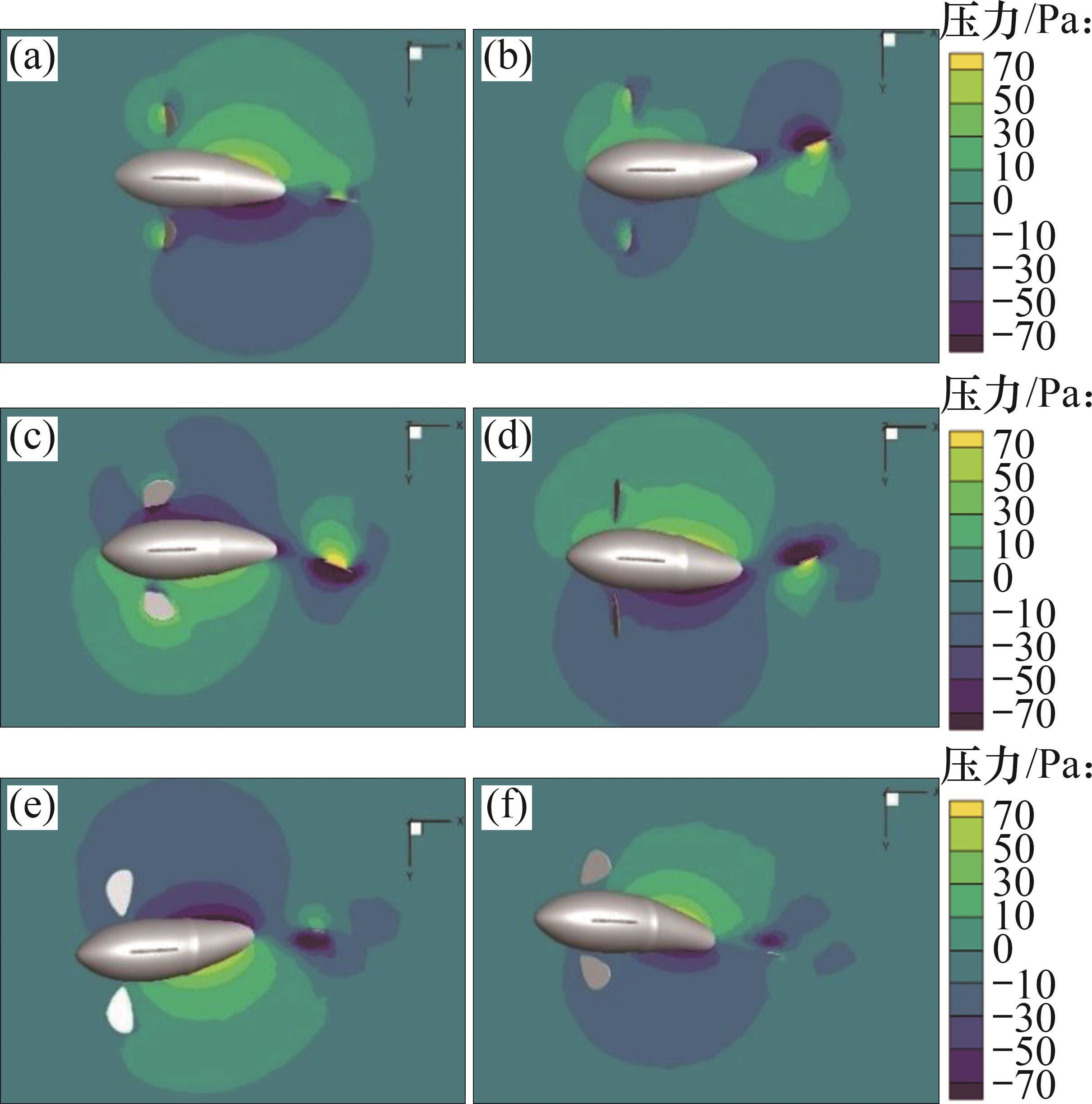
3.3 流场三维涡结构
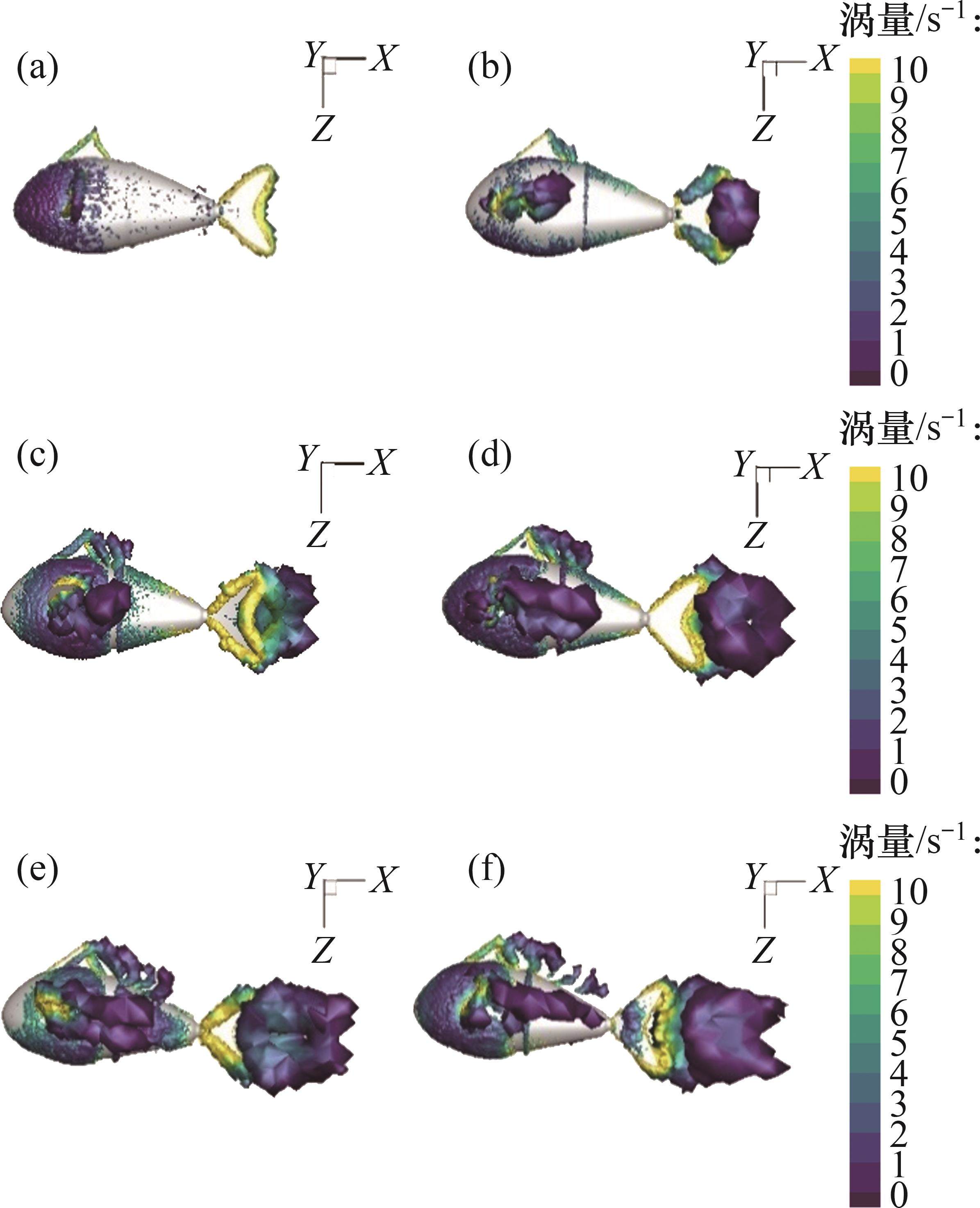
胸鳍攻角为15°时流场三维涡结构如图11所示。采用Q判据识别涡结构。从图11可见:在t=T/6时,胸鳍拍动幅度较小,未产生明显的涡环;在t=T/3时,胸鳍继续拍动,同时尾鳍持续摆动,在胸鳍后侧和上方产生涡环,而在胸鳍前侧和下方形成涡量较小的低压区,表明胸鳍前后两侧和上下两侧存在压力差,胸鳍为鱼体提供推力和升力,支持鱼体上浮;在t=T/2~5T/6时,胸鳍端涡环逐渐变大并呈现脱落趋势,尾鳍端涡环脱落趋势更加明显,此时推力和升力较大,鱼体上浮趋势较明显;在t=T时刻,胸鳍端涡环和尾鳍端涡环完全脱落,胸鳍前后、上下两侧形成较大的压差,胸鳍产生较大的推力和升力推动鱼体运动。
4 实验验证
为验证数值计算的准确性,采用实验室自主研制的仿生机器鱼进行俯仰运动实验。机器鱼外壳采用树脂材料制成,机器鱼具有三自由度胸鳍机构,柔性身体/尾鳍采用由舵机驱动的三关节串联机构。仿生机器鱼样机如图12所示。

实验平台包括室内水池(长×宽×深为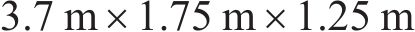

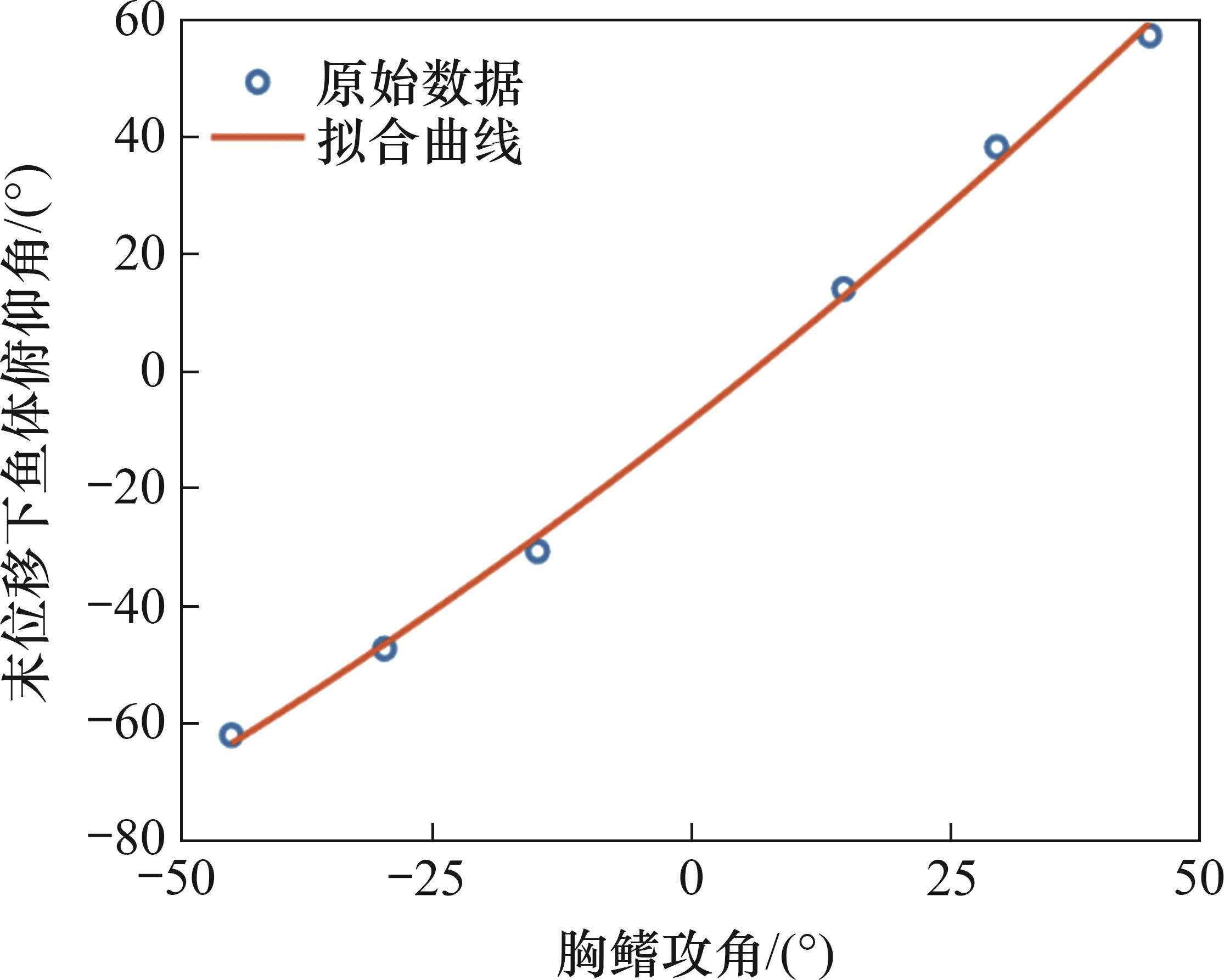
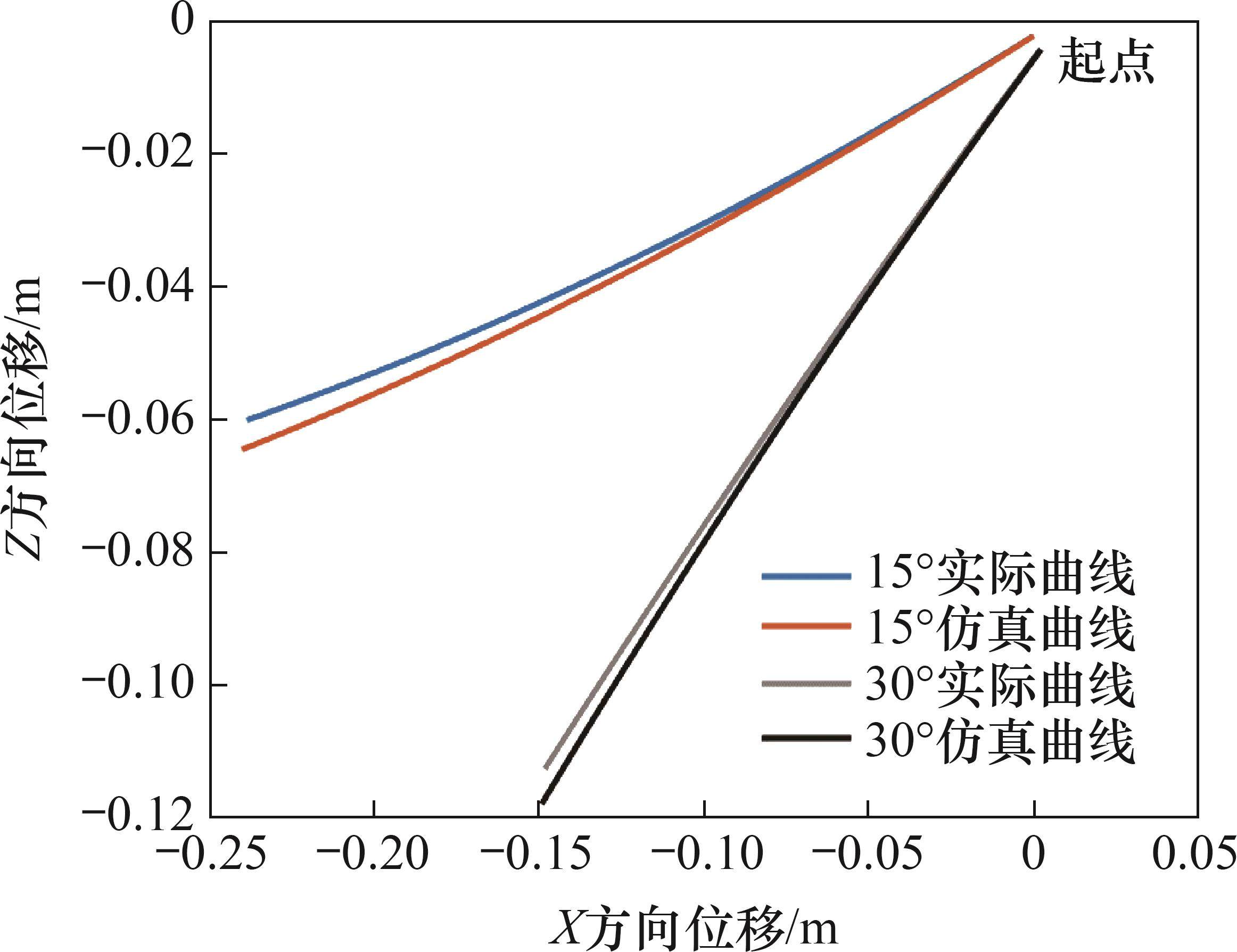
将仿真得到的位移与实验值进行分析,胸鳍攻角为15°和30°时机器鱼实际运动轨迹与仿真运动轨迹的对比如图14所示。从图14可见,仿真运动轨迹与实际运动轨迹整体差别不大,证明了仿真结果具有准确性和可靠性。
5 结论
1) 机器鱼俯仰运动需依靠胸鳍攻角的变化。当胸鳍攻角为正时,攻角越小,机器鱼下潜的幅度越大;当胸鳍攻角为负时,攻角越大,机器鱼上浮的幅度越大。
2) 当胸鳍攻角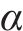
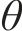
3) 运用最小二乘法拟合绕Y轴转角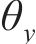
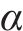
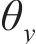
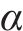
4) 机器鱼在上浮过程中,当胸鳍拍动时,胸鳍后侧和上方产生涡环,前侧和下方会形成涡量较小的低压区,表明胸鳍前后两侧和上下两侧都存在压力差,为鱼体提供推力和升力,支持机器鱼向上浮动。
5) 仿真模拟所得的机器鱼俯仰运动轨迹曲线与实验曲线相差不大,证明仿真分析结果可靠、有效。
董雅文, 李宗刚, 黎斌, 等. 仿生机器鱼俯仰运动两侧胸鳍协同推进曲线数值模拟[J]. 中南大学学报(自然科学版), 2024, 55(12): 4452-4461.
DONG Yawen, LI Zonggang, LI Bin, et al. Numerical simulation of synergistic propulsion curves of pectoral fins on both sides of a bionic robotic fish in pitching motion[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4452-4461.

