直齿轮和斜齿轮作为平行轴传动的关键元件在工业应用中广泛使用,高效率和高可靠性地传递运动和动力。其中,渐开线因其具有传动平稳性、中心距可分性、法向力方向一致性等优点成为应用最广泛的齿轮齿廓,其齿面制造方法也有很多种,如铣齿、插齿、滚齿、刮齿、磨齿等[1]。然而,它们对安装误差尤其是对交叉轴角度误差和交错轴角度误差极其敏感。错位安装导致的不连续线性传动误差会加剧齿轮的振动和噪声,且易出现边缘接触,从而降低齿轮传动使用寿命[1-2]。同时,因齿面相对滑动引发的齿面磨损和发热也不容忽视。
曲线齿线圆柱齿轮的发明距今已有100多年,相应制造技术也发展了许多年,它们最早应用于国内钢铁厂、铝厂和水泥设备厂[3]。研究人员从曲线齿线圆柱齿轮的展成方法和数学模型等角度对其接触特性、切削条件、齿面接触分析、应力分析和热弹性流体动力润滑等开展了研究[4-14]。研究表明,曲线齿线圆柱齿轮传动优点可以概括为无轴向力、润滑性能好、调心能力强和局部承载接触。然而,曲线齿线圆柱齿轮主要依赖于不同刀具和切削方法的展成法加工,其齿面几何形状仅能通过刀具几何参数进行轻微调整,且在参数选择不当时容易出现根切和齿顶变尖。
本文提出的纯滚动圆弧齿线圆柱齿轮面向非展成法加工,齿面设计不受展成法刀具参数、齿顶变尖和根切齿数等限制,具有更大的齿面设计自由度。同时,增材制造为非展成法加工的齿轮设计提供了一个粗加工选择,且可以使用如聚合物、陶瓷、金属以及纳米复合材料等多种材料[15-19]。随着增材制造精度和生产效率提升,针对特殊类型齿轮机构研究再次兴起,尤其是对新型非展成齿轮的研究成为热点。文献[20]研究了基于主动啮合线方程主动设计的非展成抛物线齿线圆柱齿轮的设计方法,并与由不同端面铣刀展成的两种传统曲线齿线齿轮进行了啮合性能和力学性能比较。这种基于啮合线方程的主动设计方法可用于平行轴、相交轴和齿条齿轮传动的非展成齿面设计[20-25],并提出了基于若干控制点的组合齿廓设计方法,根据所设定的啮合线方程形成齿面[20, 25]。
在此,本文提出了一种纯滚动圆弧齿线圆柱齿轮设计方法,其主动齿面由基于纯滚动啮合线方程及4个控制点控制的端面组合齿廓扫掠形成,并研究包括承载传动误差、接触斑痕、最大弯曲应力和齿面接触应力在内的啮合性能,将其与纯滚动抛物线齿线圆柱齿轮和齿面修形的传统渐开线斜齿轮进行了比较,以评估这种新型纯滚动圆弧齿线圆柱齿轮的优点。
1 纯滚动圆弧齿线的啮合线参数方程主动设计
图1所示为纯滚动圆弧齿线圆柱齿轮啮合坐标系。坐标系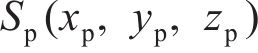
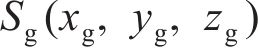
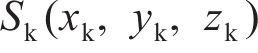
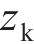
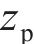
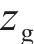
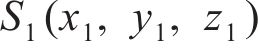
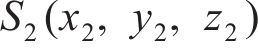
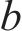
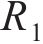
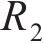
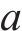
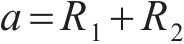
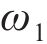
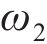
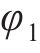
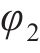

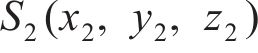
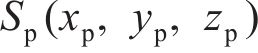
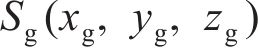
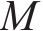
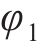
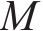
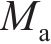
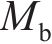
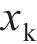
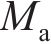
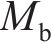
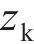
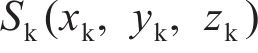
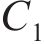
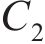
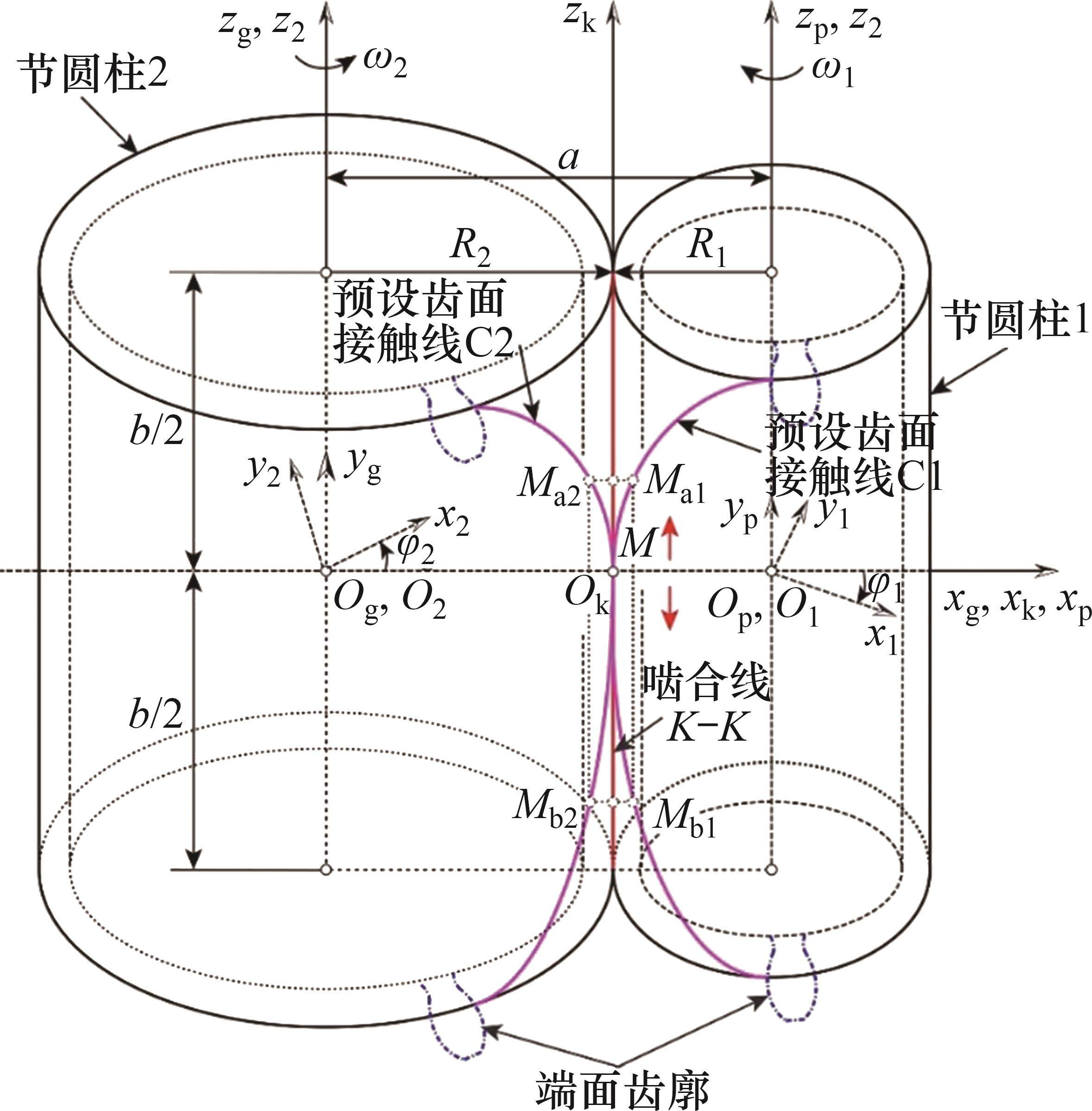
图2所示为啮合点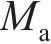
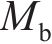
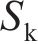
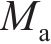
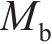
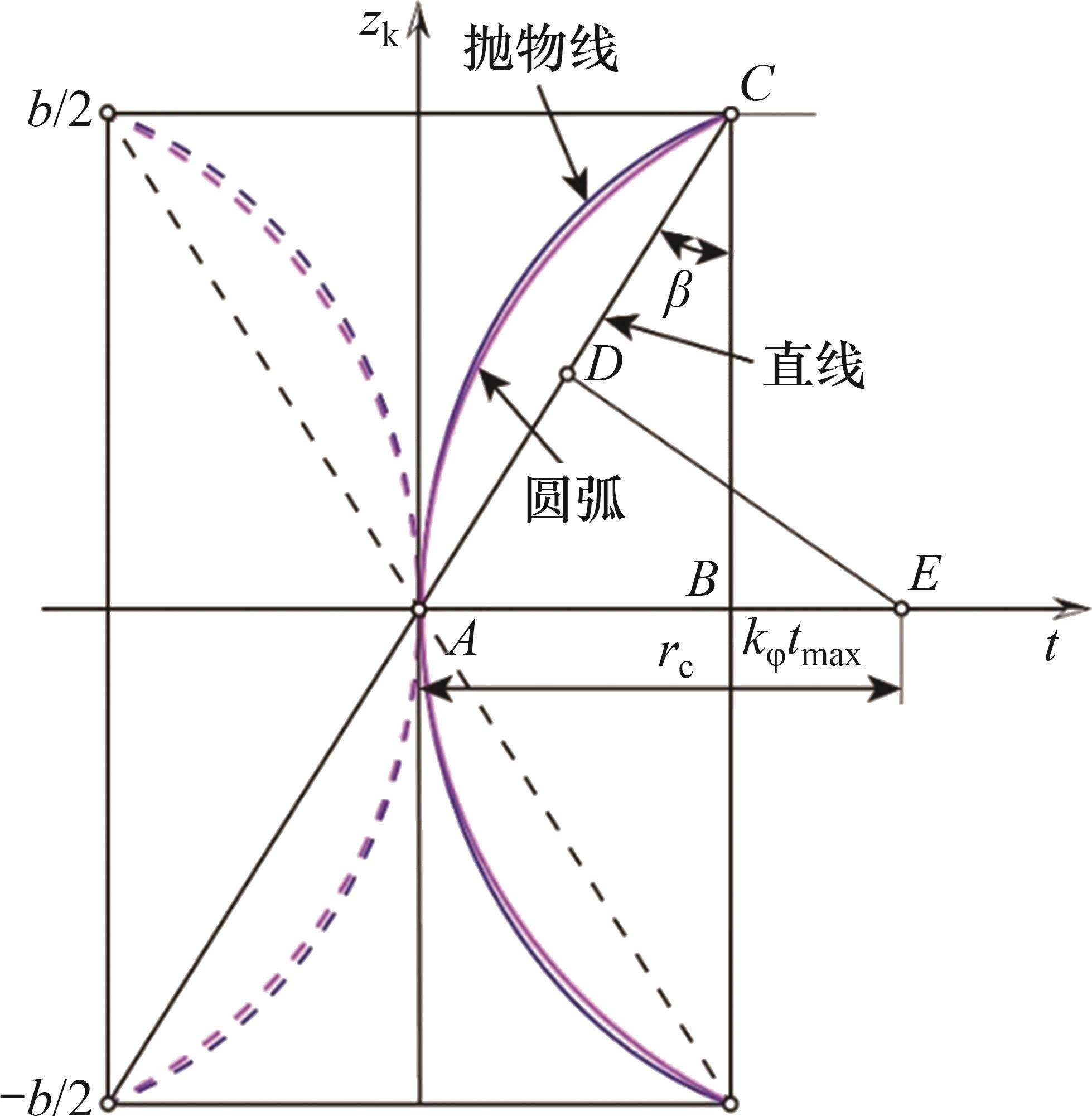
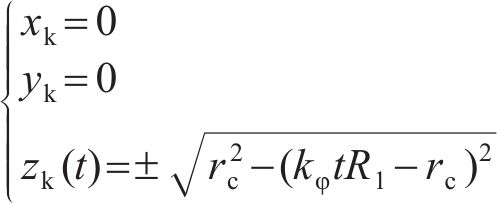
其中: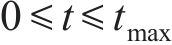
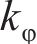
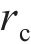
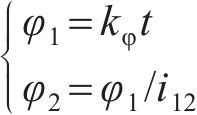
其中: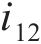
小轮齿面和大轮齿面均由端面齿廓分别沿着主、从预设齿面接触线扫掠而成。小轮齿面任意点位置矢量为:
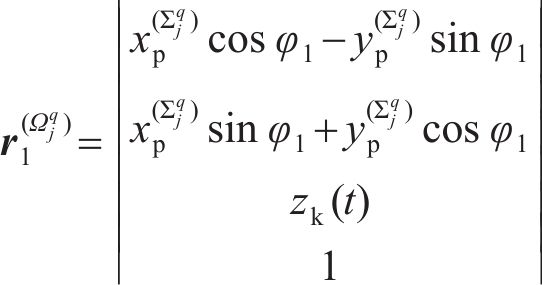
其中: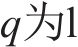
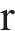
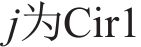


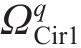
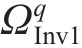

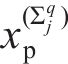
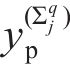
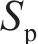
大轮齿面任意点位置矢量为:

其中: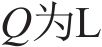
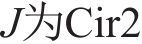


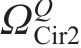
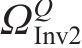

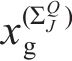
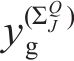
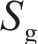
2 端面齿廓设计
从齿顶到齿根端面全齿廓由4个控制点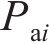
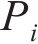
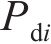
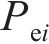
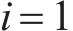
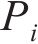
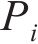
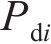
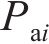
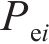
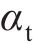
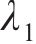
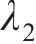
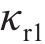
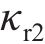
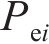
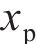
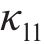
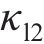
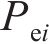
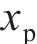
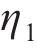
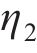
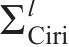
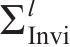
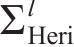
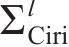
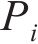
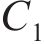
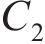
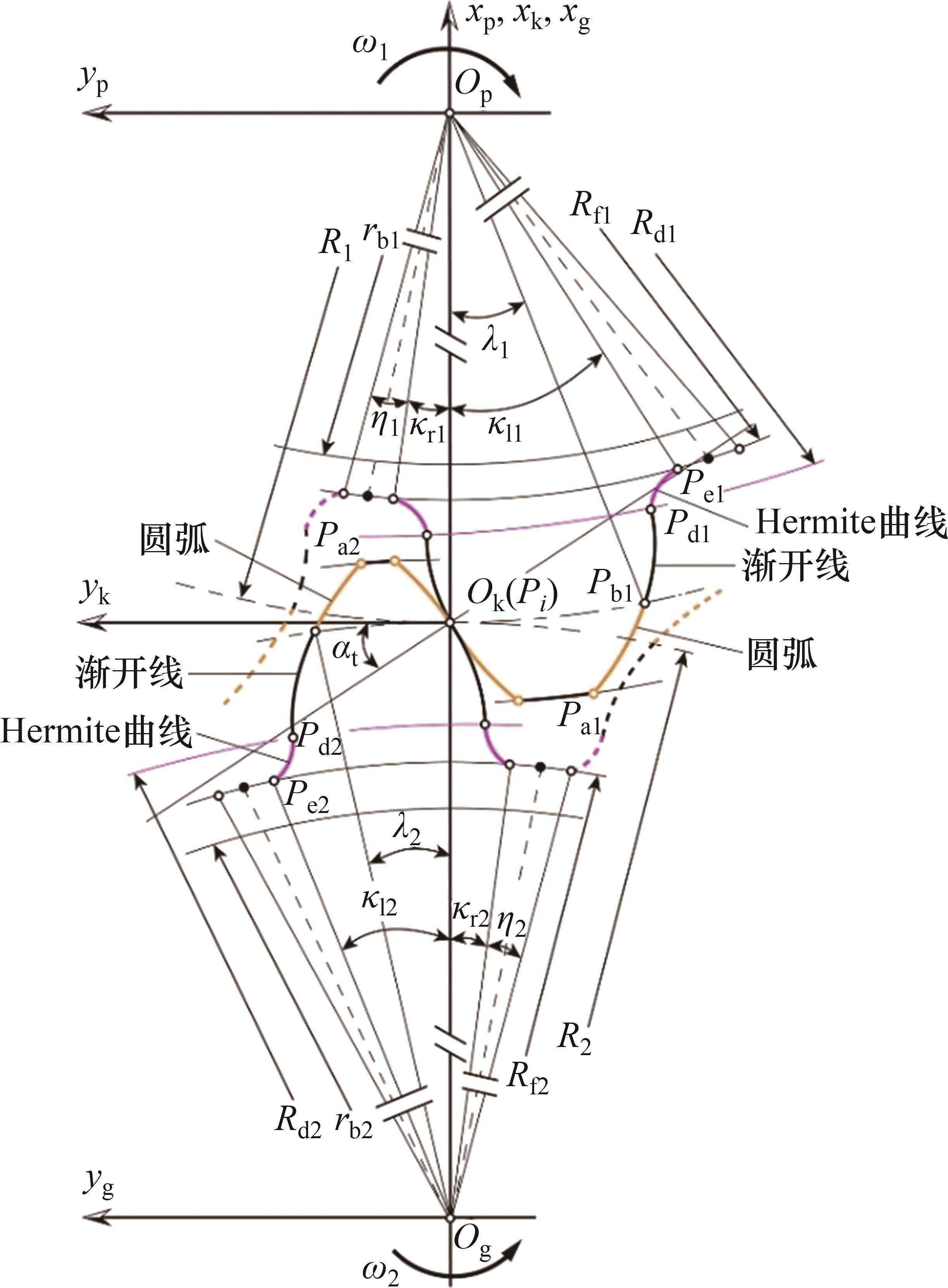
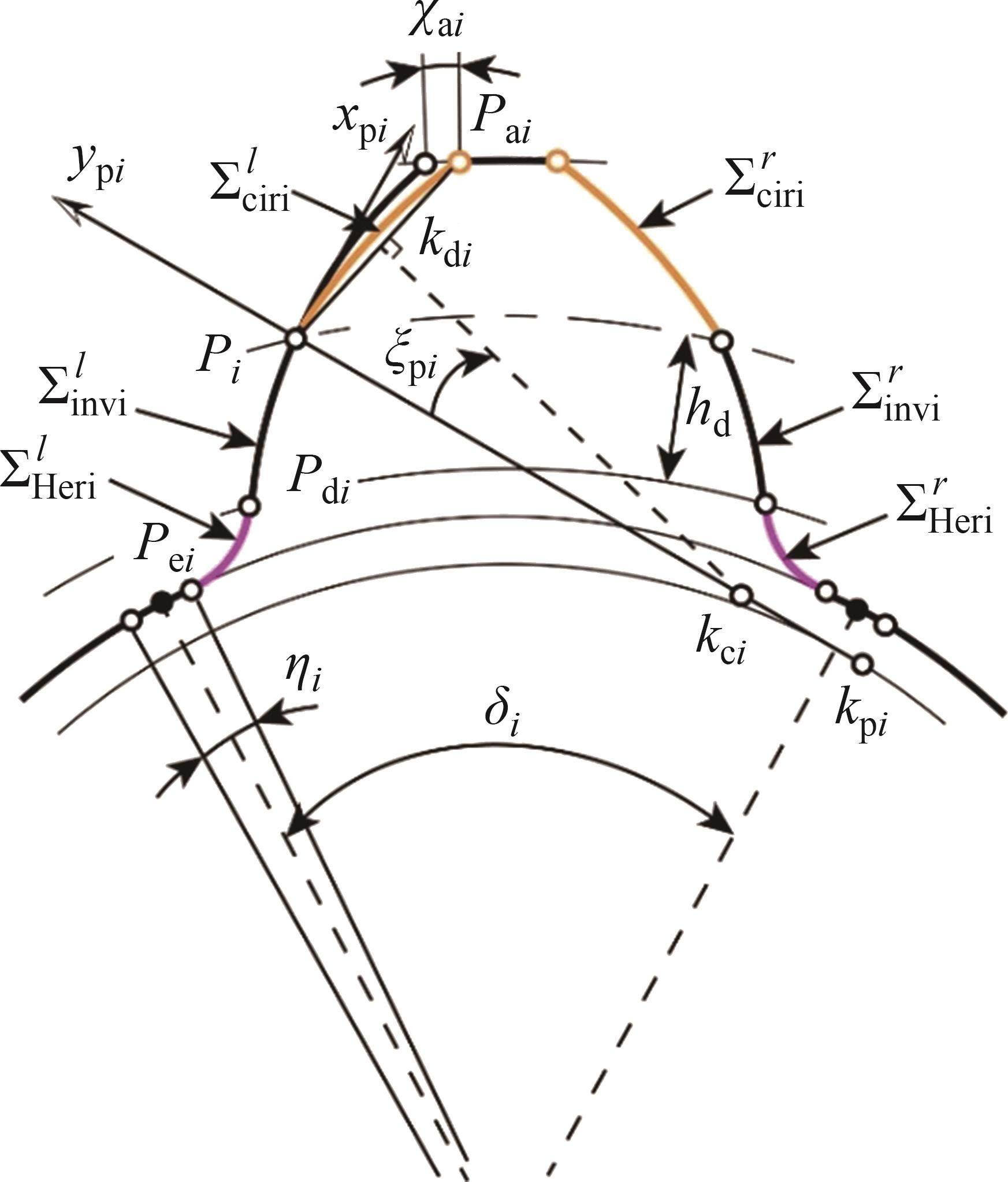
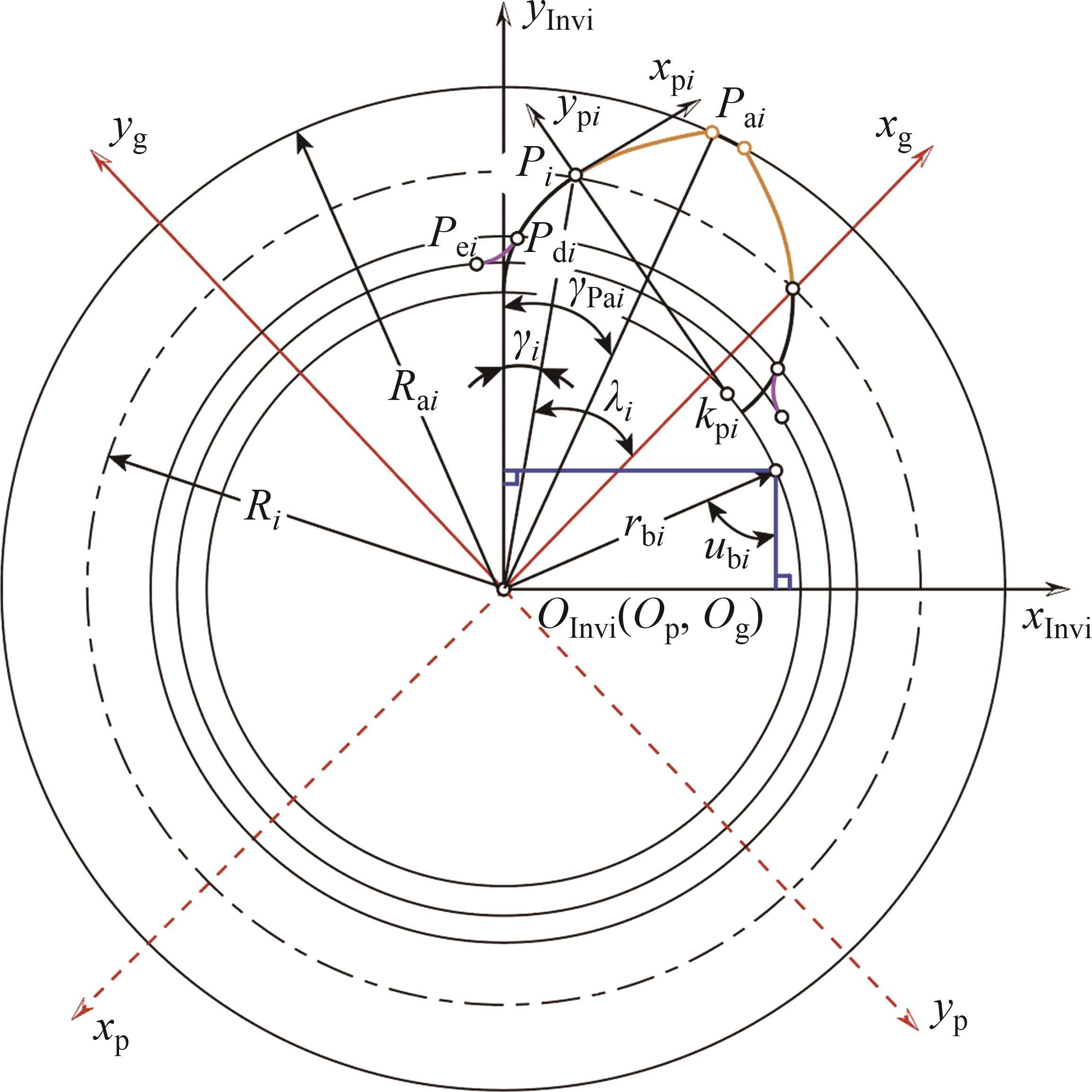
在参考渐开线的节点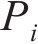
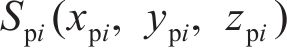
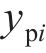
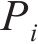
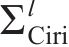
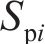
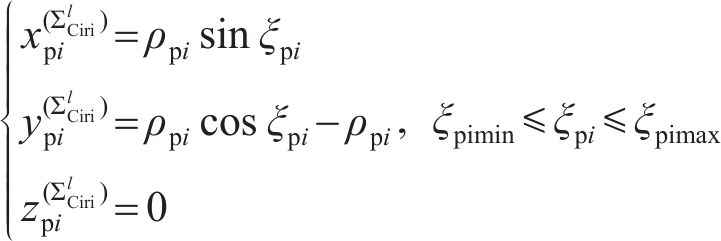
其中: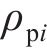
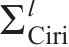
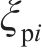
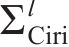
渐开线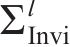

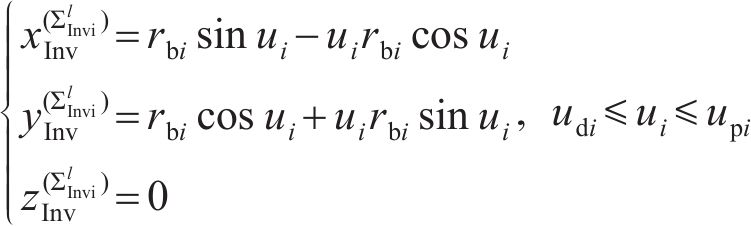
其中: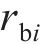
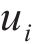
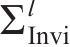
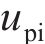
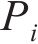
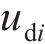
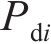
小轮和大轮齿根过渡曲线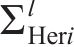
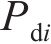
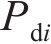
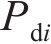
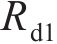
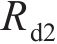
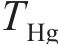
3 纯滚动圆弧齿线圆柱齿轮基本设计参数与数学模型
对4种齿轮的啮合性能和力学行为进行比较分析。实例1为纯滚动圆弧齿线圆柱齿轮,实例2为文献[20]提出的纯滚动抛物线齿线圆柱齿轮,实例3和实例4为2种不同齿面修形的传统渐开线齿轮。4对齿轮传动的设计参数如表1所示,曲线齿线圆柱齿轮的端面齿廓参数如表2所示。
| 参数 | 取值 |
|---|---|
运动系数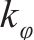 | 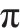 |
| tmax | 0.1 |
点Pdi位置控制系数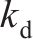 | 0.75 |
点Pa1旋转角系数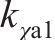 | 0.11 |
点Pa2旋转角系数 | 0.04 |
小轮Hermite曲线参数切矢权重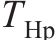 | 0.5 |
大轮Hermite曲线参数切矢权重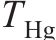 | 0.7 |
ηi的系数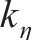 | 0.02 |
λi的系数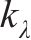 | 0.02 |
| 参数 | 数值 |
|---|---|
小轮齿数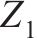 | 30 |
传动比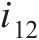 | 2.0 |
法向模数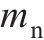 | 2.0 |
法向压力角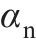 | 20 |
螺旋角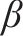 | 22.147 4 |
齿顶高系数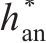 | 1.0 |
顶隙系数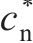 | 0.25 |
齿宽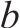 | 50 |
4组齿轮传动主要几何尺寸参数表达式如下:

其中:Z2为大轮齿数;mt为端面模数;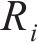
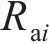
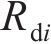
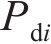
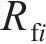
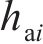
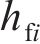

基于控制点位置的曲线齿线齿轮主要半径参数计算表达式为:
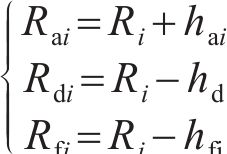
曲线齿线圆柱齿轮的端面齿厚由角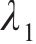
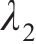
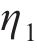
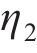
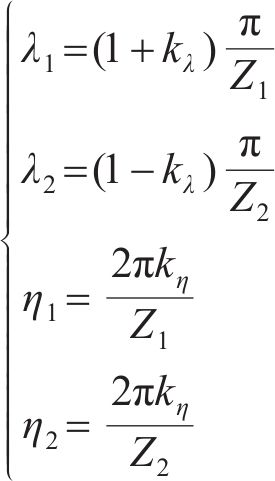
小轮和大轮左右齿廓Hermite曲线构造点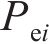
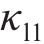
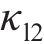
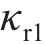
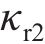
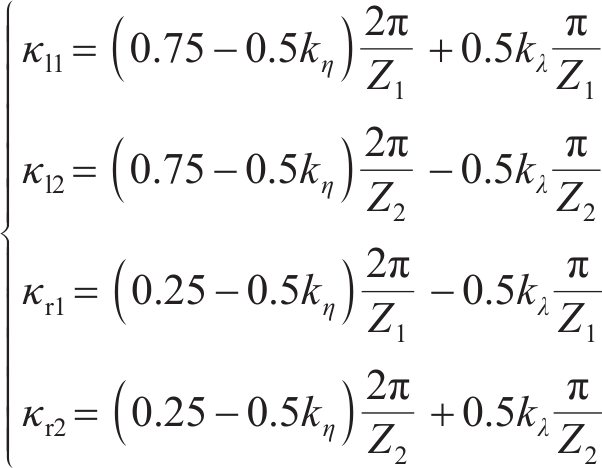
角度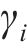
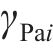
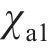
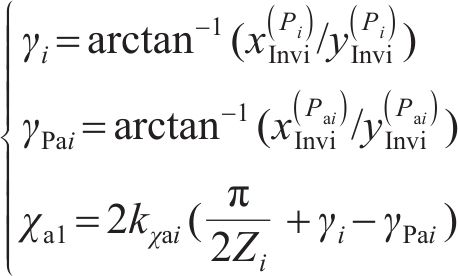
端面圆弧齿廓
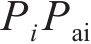
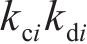
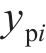
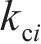
| 修形对象 | 修形类型 | 修形量/μm | ||
|---|---|---|---|---|
| 实例1和2 | 实例3 | 实例4 | ||
| 齿向 | 抛物线 | 2 | — | 10 |
| 齿廓 | 圆弧 | — | — | 60 |
| 齿向 | 圆弧 | — | 10 | — |
| 齿廓 | 抛物线 | — | 60 | — |
4 齿面接触分析
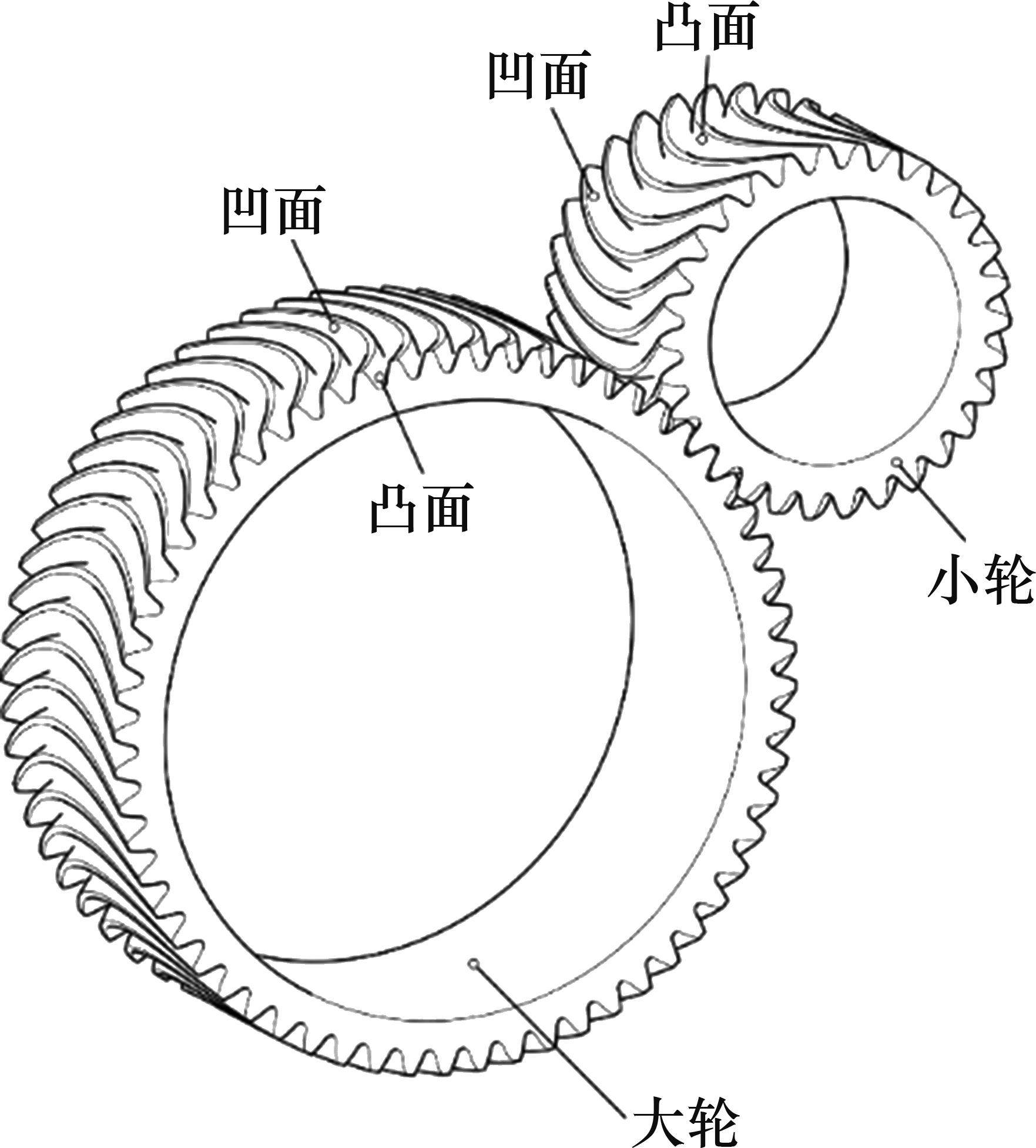
采用文献[27]提出的齿面接触分析(tooth contact analysis, TCA)算法求解并比较本文4组齿轮传动的接触斑痕和非承载传动误差曲线。在分析过程中,小轮逆时针方向(CCW)旋转2个周节角,并将其连续均匀划分为21个接触位置分别求解。图7和图8所示分别为在理想安装情况下4组实例齿轮副小轮和大轮齿面接触斑痕。


从图7(a)、(b)和图8(a)、(b)可见:实例1和实例2小轮和大轮齿面接触斑痕非常相似;实例1和实例2的接触斑痕关于轮齿中间截面对称,有助于消除轴向力。由于啮合被设计为纯滚动啮合使齿面间相对滑动最小,瞬时接触椭圆所有中心都位于节圆半径上。对实例1和实例2齿轮副而言,接触椭圆长轴长度从两端向齿面中间逐渐增加。同时,接触椭圆长轴方向与齿长方向所夹锐角从两端到齿面中间逐渐减小。
从图7(c)、(d)和图8(c)、(d)可见:齿面修形后,实例3和实例4齿轮副的瞬时接触椭圆沿齿廓方向覆盖高度与实例1和实例2的近似;实例3和实例4的接触椭圆长轴与齿长方向之间的锐角沿接触路径保持相同的大小和方向。此外,尽管进行了相同大小但不同类型的齿面修形,但实例3和实例4的接触斑痕差异非常小。
由于沿齿长方向施加了抛物线修形,实例1和实例2的非承载传动误差曲线呈现抛物线形状。对于实例3和实例4的渐开线齿轮副而言,由于同时施加了齿长方向和齿廓方向的修形,其非承载传动误差同样呈现抛物线形状。
5 轮齿应力分析
在TCA分析结果基础上,采用ABAQUS软件进行轮齿应力分析。针对实例1和实例2所述曲线齿线圆柱齿轮,建立5对轮齿的有限元模型来降低边界条件和连续接触齿对间载荷分配的影响;针对实例3和实例4所述渐开线齿轮副,因其重合度较大,建立7对轮齿有限元模型。在4组齿轮副有限元分析过程中,均将小轮-15°~9°总转角划分为21个连续均匀分布的接触位置,重点分析中间轮齿啮合全过程中的齿面接触应力和齿根弯曲应力。
图9所示为实例1纯滚动圆弧齿线圆柱齿轮有限元分析模型。研究表明:当齿长方向的网格数量达到50个、齿廓方向网格数量达到30个时,ABAQUS求解的齿面Von Mises应力已收敛。小轮和大轮齿面沿齿长方向均匀划分网格数量为65个,沿工作齿廓方向均匀划分网格数量为35个,齿根过渡区域划分网格数量为15个。小轮轮毂和两侧节点刚性约束在小轮旋转轴上的参考节点处,仅保留该节点绕齿轮旋转轴的转动自由度;大轮轮毂和两侧节点刚性约束在大轮旋转轴上的参考节点处,且限制其移动和转动。采用8节点六面体线性非协调模式单元C3D8I来改善其弯曲行为。齿轮副材料统一选择钢,其弹性模量为210 GPa,泊松比为0.3。在4组齿轮副的小轮旋转轴线参考节点施加300 N·m扭矩。以小轮齿面最大von Mises应力作为齿面接触应力,以中间轮齿齿根过渡区域最大第一主应力作为齿根最大弯曲应力。
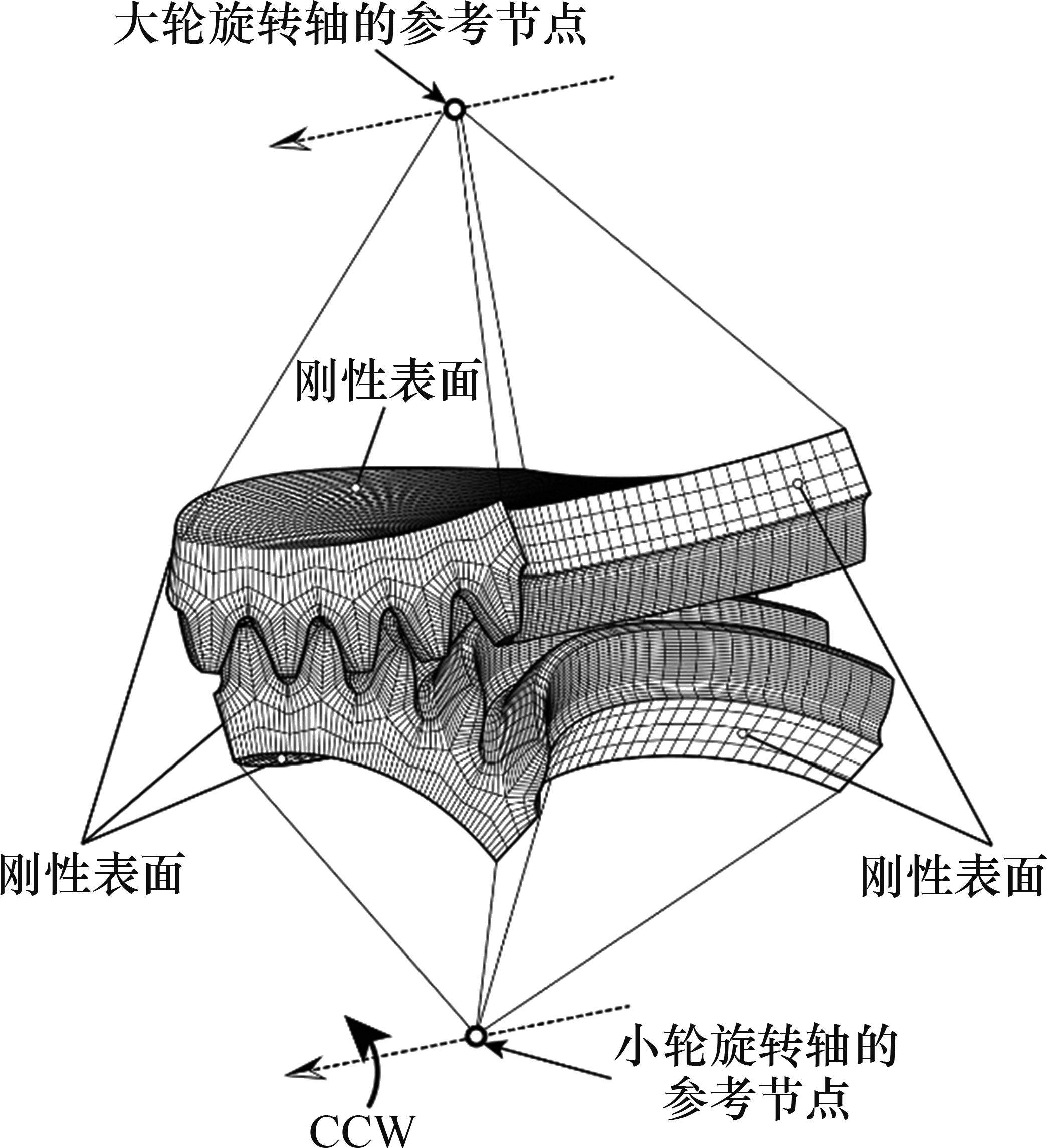
图10所示为小轮旋转2个周节角时小轮齿面最大von Mises应力沿21个接触位置的变化情况。从图10可见:实例1和实例2接触应力曲线波动及其最大值相近,实例3和实例4的接触应力曲线重合;此外,实例1和实例2的最大von Mises应力也略高于实例3和实例4的最大von Mises应力。图11所示为在接触位置11处实例1~实例4的小轮表面von Mises应力分布云图。从图11可见:4组齿轮副接触应力云图分布与TCA模拟的接触斑痕保持一致;实例1和实例2有2对齿参与啮合,齿面中间有1个长接触椭圆,相邻齿的两端各有1个小接触椭圆;实例3和实例4同时有3对齿啮合,接触椭圆具有相同的形状;实例1的最大von Mises应力最大,实例4的最大von Mises应力最小。实例2~4中小轮最大von Mises应力较实例1的分别降低了3.11%、5.34%和5.37%。
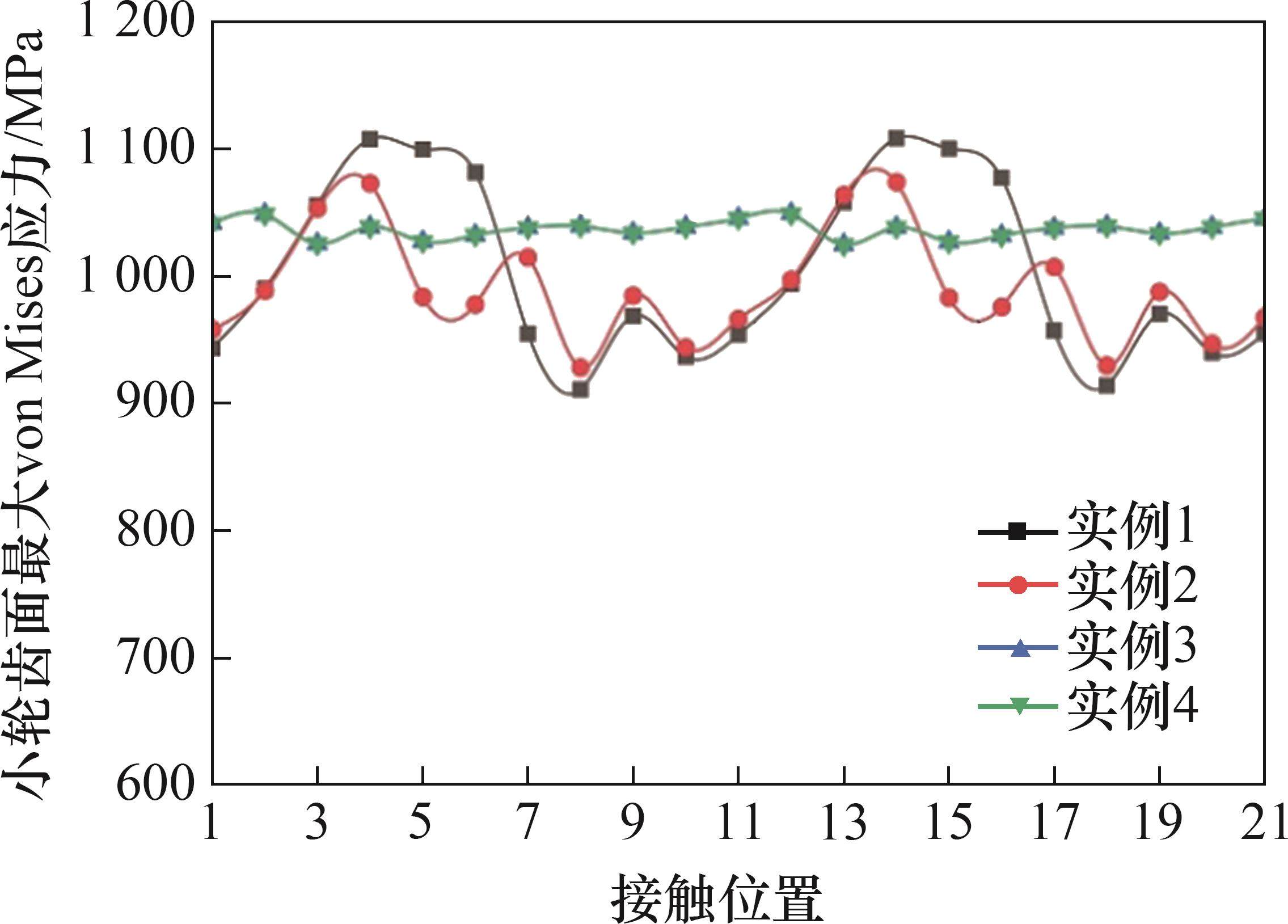

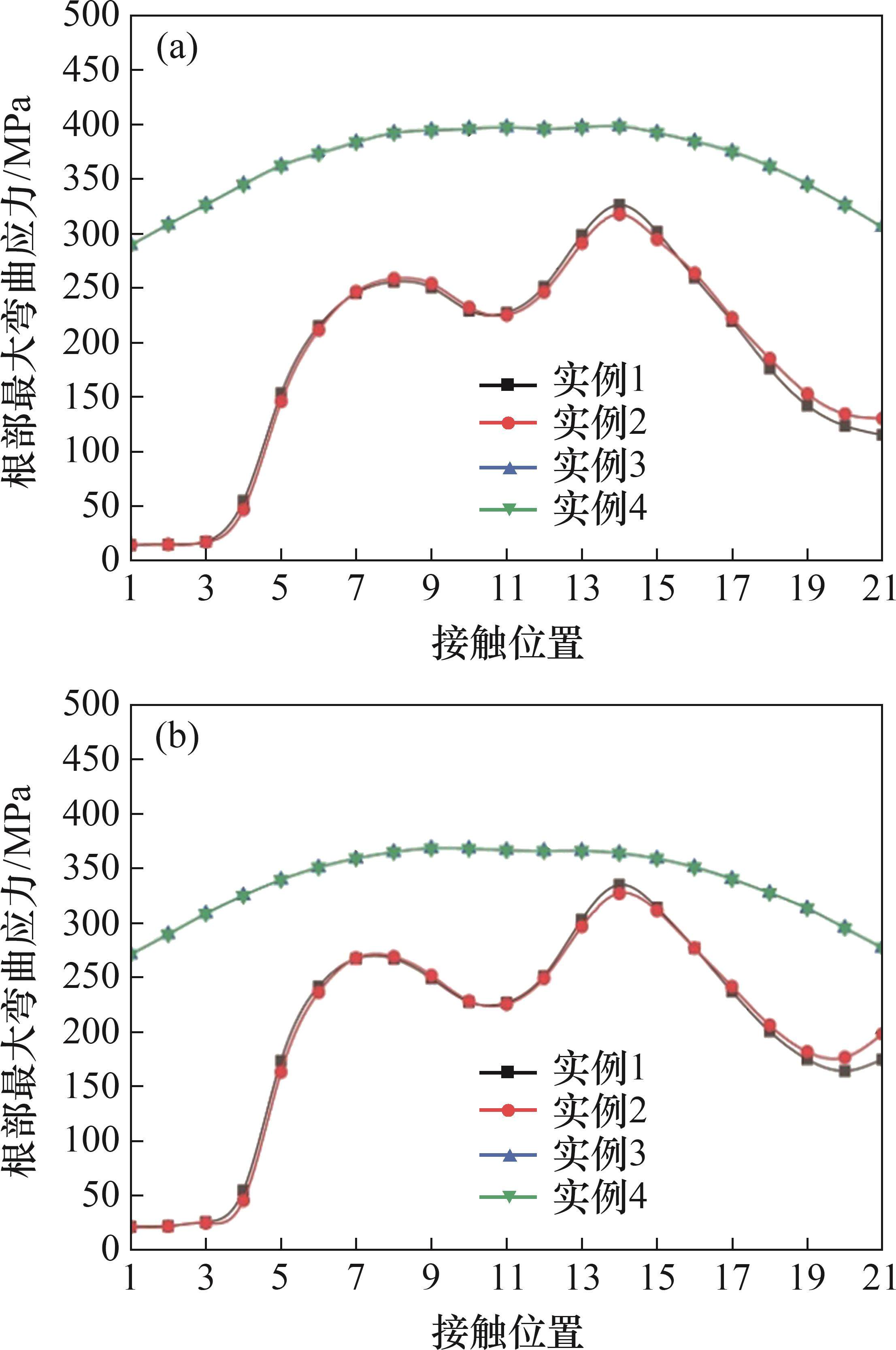
图12所示为4组齿轮副小轮和大轮齿根的最大弯曲应力变化曲线。从图12可见:实例1和实例2的小轮和大轮均具有近似的最大齿根弯曲应力曲线;实例3和实例4的小轮和大轮最大齿根弯曲应力曲线均分别重合,同时,实例1和实例2的最大齿根弯曲应力均低于实例3和实例4的最大齿根弯曲应力;此外,实例3和实例4小轮齿根的最大弯曲应力要大于大轮齿根的最大弯曲应力;实例1和实例2小轮齿根的最大弯曲应力均小于大轮齿根的最大弯曲应力。由于小轮具有更大的应力循环次数,齿轮传动设计应该降低小轮的根部最大弯曲应力而不是大轮的根部最大弯曲应力。实例2小轮和大轮齿根的最大弯曲应力最小,而实例4齿根的弯曲应力最大。实例1和实例2小轮和大轮的最大弯曲应力均出现在接触位置14处,实例3和实例4小轮齿根的最大弯曲应力发生在接触位置14处。此外,实例3和实例4大轮齿根的最大弯曲应力发生在接触位置9处。实例1、3、4小轮齿根的最大弯曲应力比实例2的最大弯曲应力分别提高了2.70%、25.40%和25.38%。此外,实例1、3、4的大轮根部最大弯曲应力比实例2的分别提高了2.36%、12.59%和12.57%。
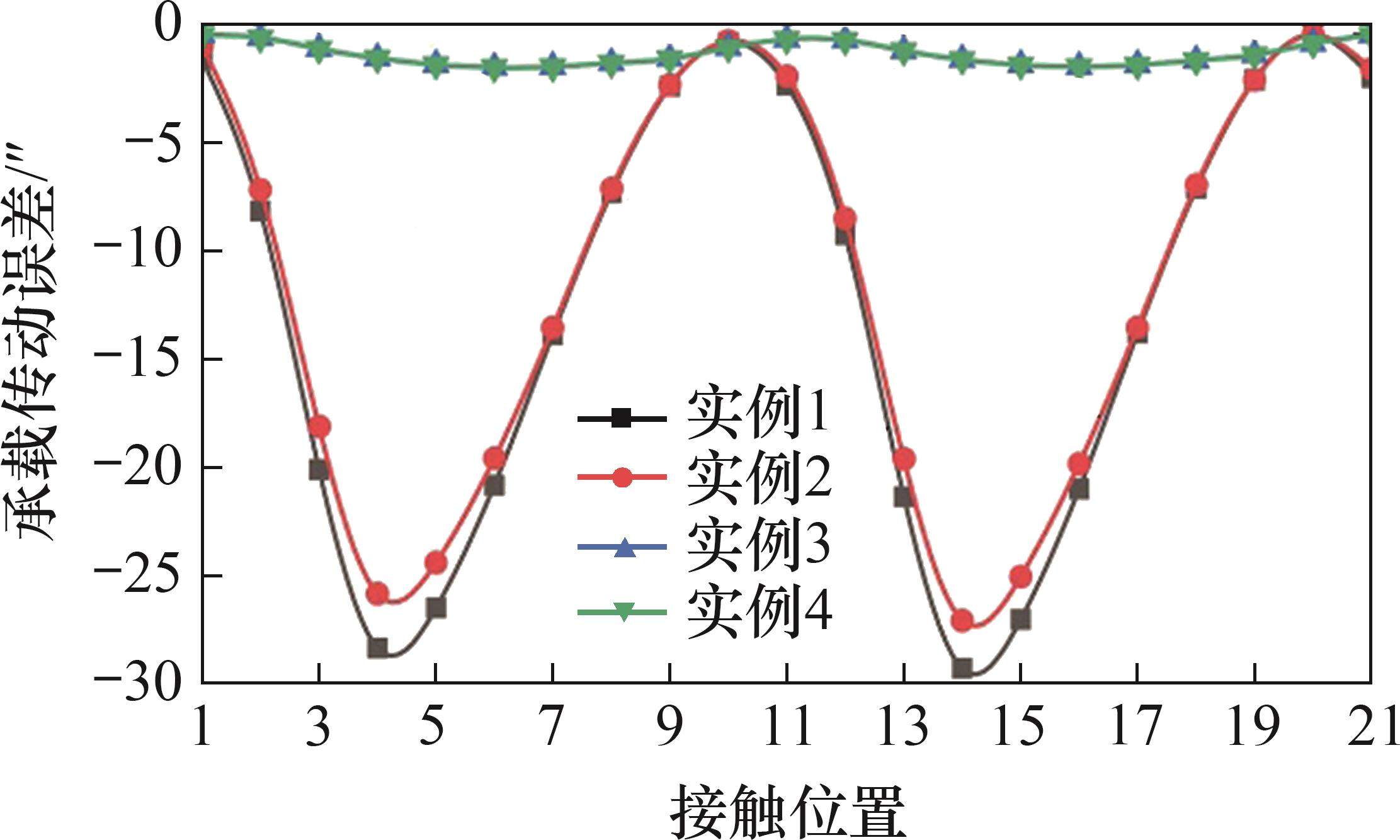
根据文献[8],在有限元分析结果基础上,考虑齿面接触变形和齿面挠度,计算4组齿轮副承载传动误差,结果如图13所示。此外,实例3和实例4的承载传动误差曲线基本重合,其幅值也相同,为1.51″。实例1和实例2的传动误差幅值比实例3和实例4的大,分别约为29″和27″。由于实例1和实例2的小轮进行了齿向抛物线修形,实例3和实例4小轮同时进行了齿廓和齿向修形,因此,4组齿轮副承载传动误差曲线均呈抛物线形状,均能够有效地降低因齿轮安装误差导致不连续线性传动误差引发的噪声和振动。
6 结论
1) 2种类型的纯滚动曲线齿线圆柱齿轮具有相似的接触斑痕、最大齿根弯曲应力、最大齿面接触应力以及承载传动误差幅值。
2) 不同于传统渐开线斜齿轮传动,纯滚动圆弧齿线圆柱齿轮的小轮比大轮轮齿具有更低的最大弯曲应力,有助于提升使用寿命。
3) 与具有相同基本设计参数和接触斑痕覆盖高度的渐开线斜齿轮传动相比,纯滚动圆弧齿线圆柱齿轮具有更低的最大齿根弯曲应力、相近的最大齿面接触应力以及更大的承载传动误差幅值。
陈祯, 李颖淇, 肖小平, 等. 纯滚动圆弧齿线圆柱齿轮设计与啮合性能分析[J]. 中南大学学报(自然科学版), 2024, 55(12): 4462-4472.
CHEN Zhen, LI Yingqi, XIAO Xiaoping, et al. Design and meshing performance analysis of pure rolling curvilinear cylindrical gears with circular arc tooth trace[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4462-4472.

