弧齿锥齿轮传动是机械动力传动的关键部件[1-2]。近年来,在高精度的齿面制造中,齿面铣削和磨削技术都得到了广泛发展,然而,对于弧齿锥齿轮热处理的研究较少[3-4]。在微尺度结构中,热弹塑性的影响很复杂[5],其中,材料属性是影响性能评价的重要因素[6]。SUGIANTO等[7]对SCr420H钢斜齿轮渗碳淬火过程进行了数值模拟和试验验证。王延忠等[8]利用DEFORM软件对渗碳淬火工艺对轮齿残余应力分布和变形的影响进行了分析。许鸿翔等[9]对20Cr2Ni4钢弧齿锥齿轮渗碳淬火磨齿后出现的磨削烧伤进行了检测与分析。DING等[10]研究了考虑渗碳-啮合耦合效应的齿面热处理工艺参数的优化方法,但并没有对考虑渗碳-啮合耦合效应的弧齿锥齿轮热处理变形进行全面测定。半解析计算方法在弧齿锥齿轮传动的相关问题中得到了应用。廖平等[11]采用半解析计算方法对弧齿锥齿轮时变啮合刚度和传动误差进行了求解。QU等[12]对数值加载接触分析(NLTCA)及其半解析测定方法进行了改进。LU等[13]提出了一种针对局部接触区域的侧重于加载接触效应的动态加载齿面接触分析。然而,对于复杂弧齿锥齿轮,还没有与半解析齿面热处理变形的相关研究报道。
齿面渗碳是弧齿锥齿轮热处理的重要步骤。在渗碳齿面啮合过程中,当齿轮受到接触压应力或冲击载荷作用时,容易发生渗碳层剥落形式的接触疲劳失效。在满足几何精度的前提下,可以采用半解析关系预测与强度和疲劳寿命密切相关的渗碳-啮合耦合效应。基于传统商业软件的热处理研究方法求解精度高,但存在效率较低的问题。而半解析方法可在兼顾一定精度的前提下更加高效地预测齿面的热处理变形,这对考虑几何精度和物理性能[3, 14]的协同制造至关重要。
本文采用一种创新的半解析计算方法预测渗碳-啮合耦合效应对弧齿锥齿轮齿面热处理变形的影响。针对弧齿锥齿轮传动复杂的齿面弯曲特性[12, 15],以由加工参数驱动的齿轮有限元模型为对象来研究考虑耦合效应的热处理变形。基于齿轮啮合的协调关系和平衡方程[16],通过数值加载接触分析(NLTCA)以获得精确的齿面接触性能[12]。通过研究齿面热处理变形,确定其与加工参数之间的驱动关系。该方法对弧齿锥齿轮的高精度几何精度控制具有重要意义[17]。
1 齿面建模与渗碳理论
1.1 齿面建模
由于弧齿锥齿轮没有标准的齿廓表达式,目前的齿面建模通过对实际加工过程的仿真模拟来实现[14]。
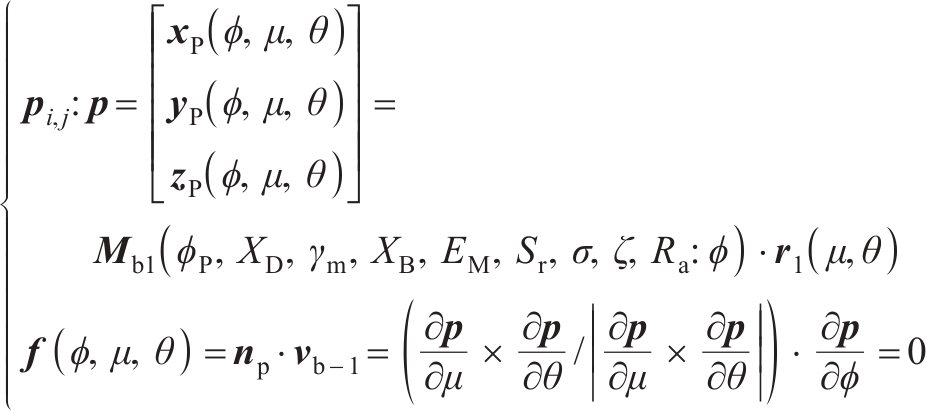
式中:μ和θ为刀具的高斯参数;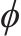
在齿面切削模拟中,采用直线形作为刀具的几何形状[18-19]。确定刀具形状后,坐标变换矩阵Mb1可表示为
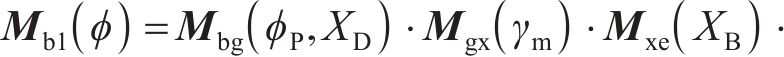
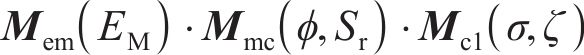
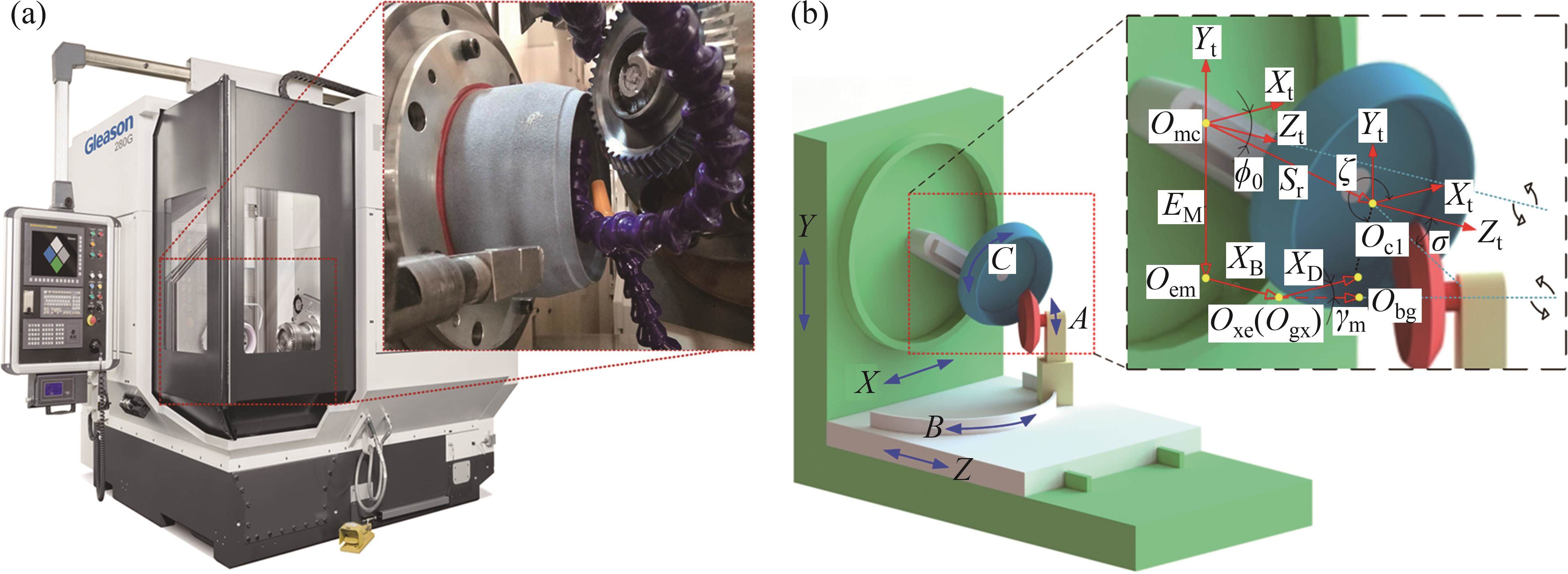
根据以加工参数表示的机床各部分的运动链,可得到由刀具轨迹的曲线族包络而成的齿面。与加工参数相关的数控机床及其运动学模型如图1所示。在当前UMC框架中[14],每项加工参数都可以用机床摇台角ϕ的多项式来表示,如基本加工参数ϕP可表示为
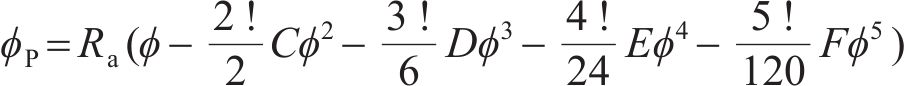
式中:
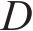
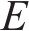

在整个切削模拟中,机床各部分的运动链分别为
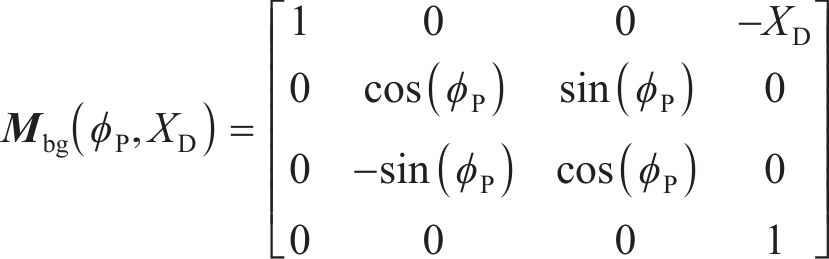
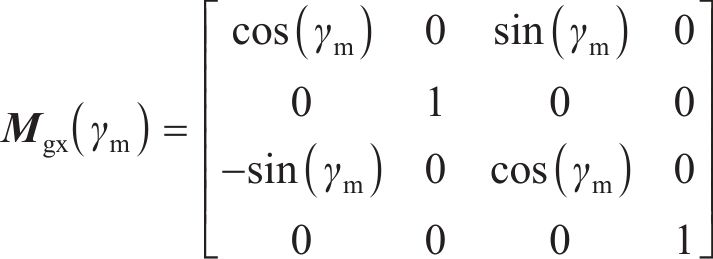
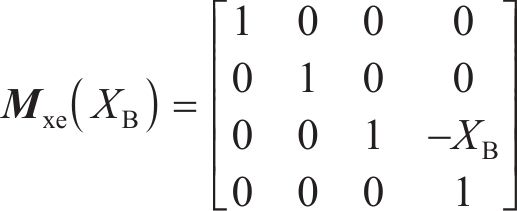
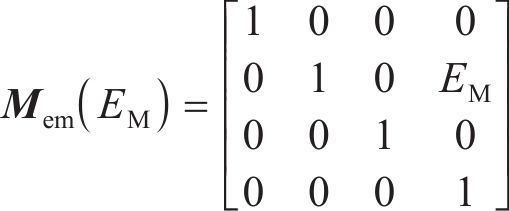
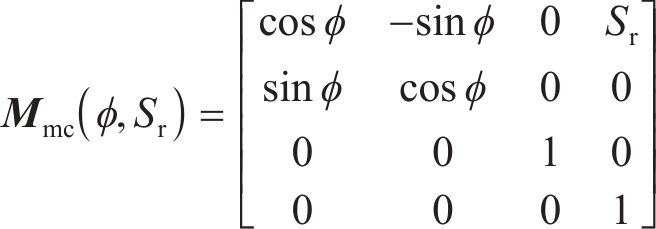
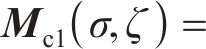
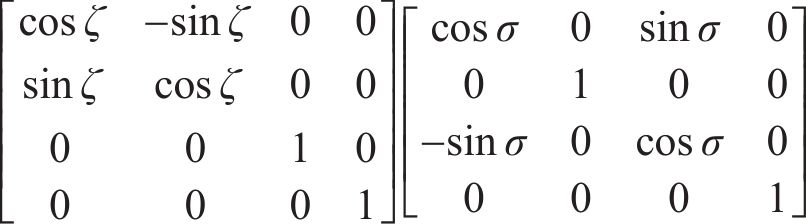
在应用双重螺旋法进行齿面加工仿真建模时,床位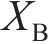
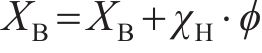
式中:χΗ为螺旋修正系数。将工作齿轮齿坯的几何形状作为齿面离散化的约束条件引入建模方程中求解,有
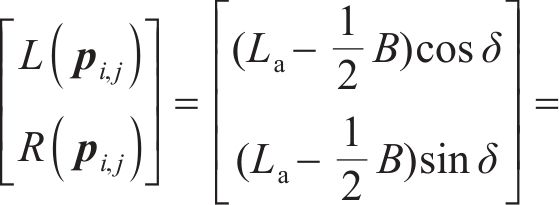
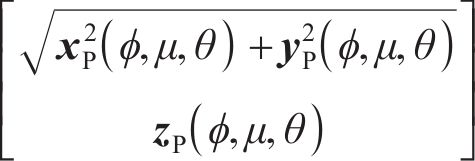
式中:(L,R)为齿面点在轴截面的坐标;La为外锥距;δ为节锥角;B为齿宽。
1.2 加载变形的NLTCA计算
采用文献[20]的DC-FFT方法对弧齿锥齿轮的载荷分布进行数值加载接触分析(NLTCA)的求解计算。NLTCA的基本求解过程见图2。将齿面pi,j∈(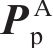
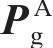
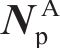
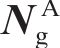
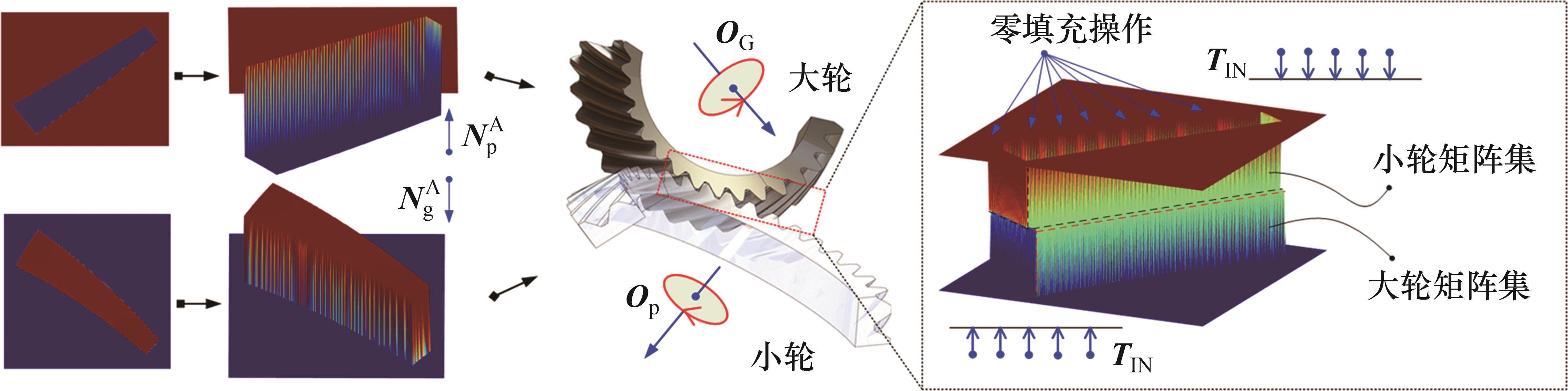
在给定的载荷条件下,根据2个齿面矩形集可分别确定2个齿面在每个网格位置上的瞬时干涉区域ΘK。控制设计变量网格密度ΔL和旋转角度步长ΔϕCP,由时变的ΘK(K=1,2,…,N)可以确定ΘLCP的整体几何形状以及时变啮合过程中的载荷分布,具体计算过程见文献[20]。
1.3 渗碳理论
渗碳是低碳钢和低碳低合金钢零件的一种表面热处理工艺。在热处理过程中,虽然表层含碳量较高,但内部仍保持着原有成分。渗碳环境中主要包含了CO和H2,在渗碳过程中,工件表面会发生气体反应。弧齿锥齿轮在渗碳过程中工件表面的气体反应见图3,图3中,C3D8R为三维有限元模型的一种网格类型,其中,C表示实体单元,3D表示三维,8为该单元所具有的节点数目,R指该单元为缩减积分单元。在兼顾全齿面的基础上,渗碳工艺的作用对象主要是承载接触区域及热力变形边界内的网格单元。气体反应式为[22]:
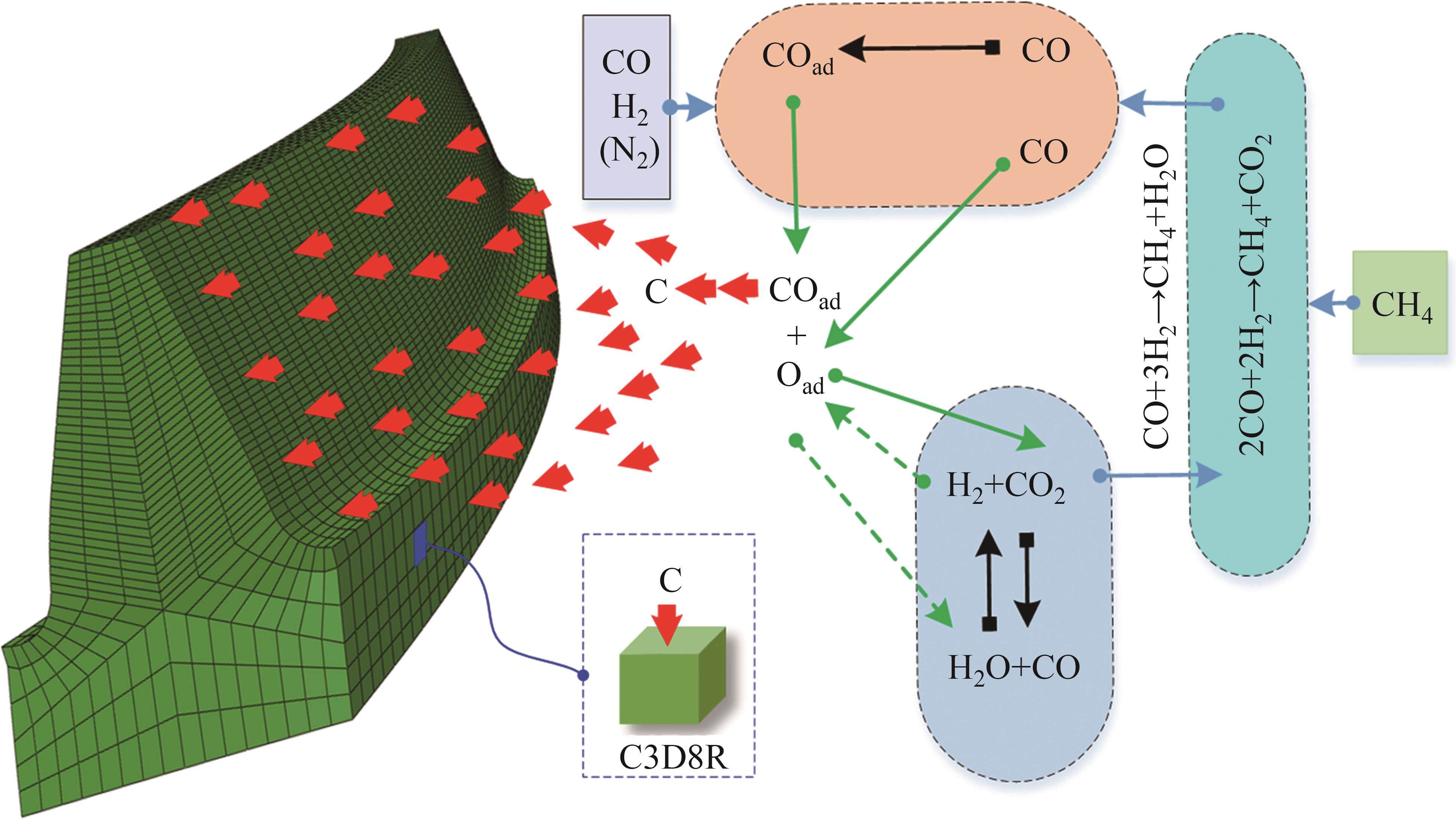

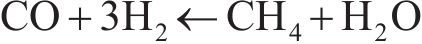
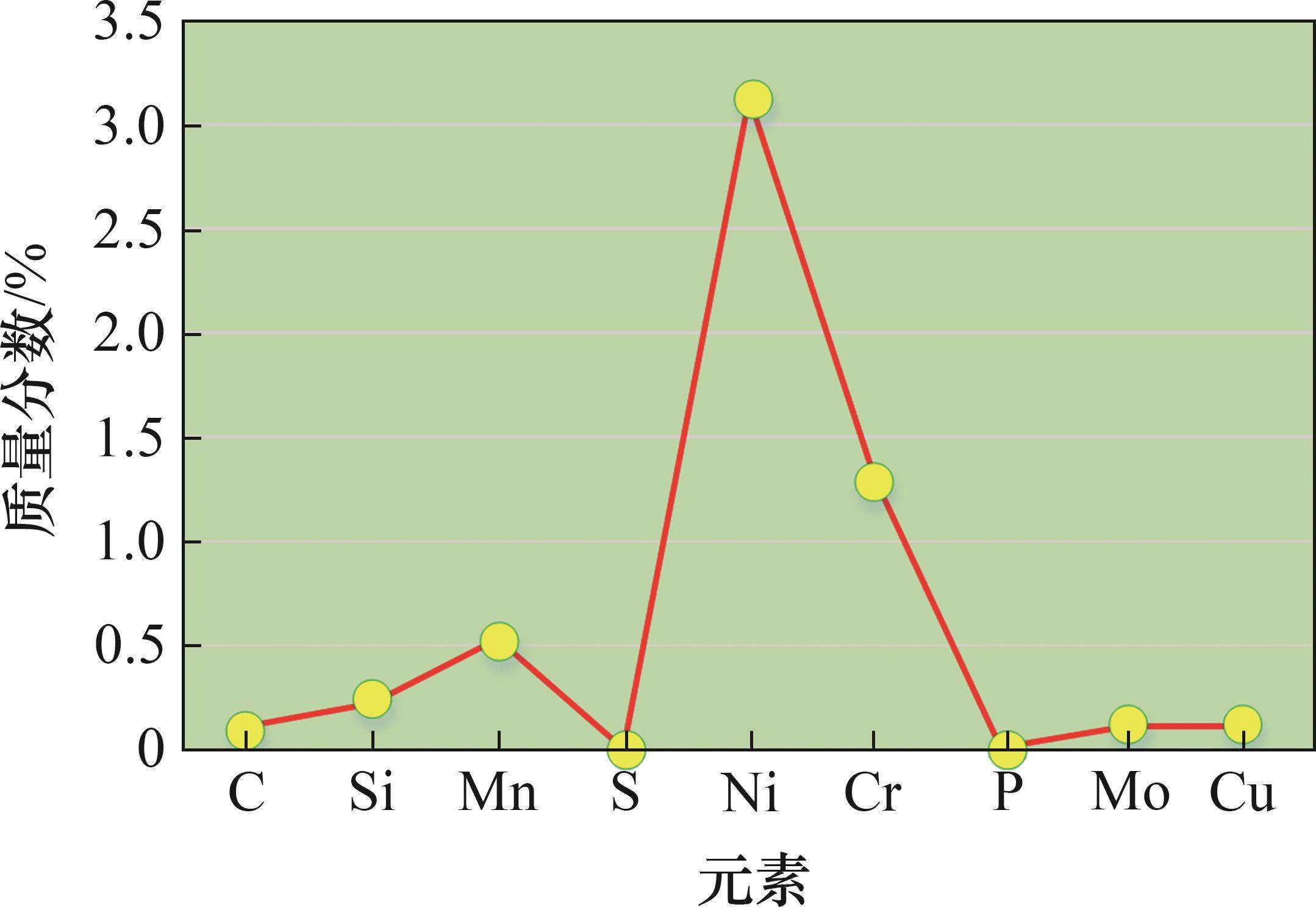
主要的化学作用过程是渗碳环境能使齿面上产生活性碳原子并扩散到齿轮部件中。航空航天工业主要应用的齿轮材料是9310钢。9310钢的材料元素质量分数见图4,其中,镍(Ni)质量分数最大,为3.13%,磷(P)质量分数最小,为0.008%。
在强渗透和扩散阶段,假设实际齿面渗碳为非稳态,则满足菲克第二定律的基本控制方程[7]:
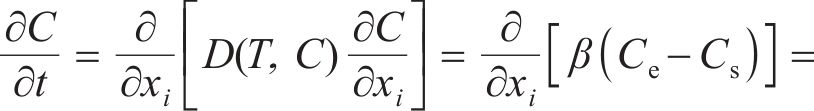
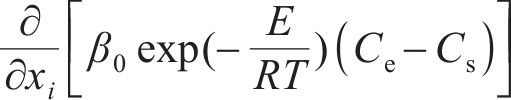
其中:C、t和xi分别为碳的质量分数、渗碳时间和沿扩散方向的距离;Ce和Cs分别为渗碳过程中反应炉中的实际碳的质量分数和齿面碳的质量分数;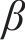
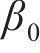
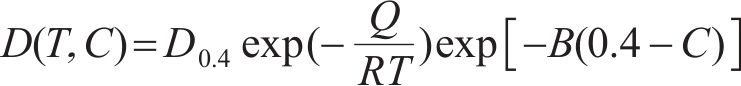
式中:D0.4为当碳的质量分数为0.4时的扩散系数;B为常数,反映扩散系数与碳浓度之间的关系;Q和R分别为碳原子扩散激活能和气体常量。
2 考虑耦合效应的热处理变形预测
文献[12]中的LTCA方程显示了加工参数与齿面啮合变形的关联规律。本文在文献[12]的基础上加入渗碳场并考虑耦合效应,提出一种基于加工参数的精准半解析预测方法,可反映更加真实的齿面热变形。在该预测中,加工参数被视为求解考虑渗碳-啮合耦合效应的热处理变形的基本未知设计参数。
2.1 渗碳-啮合耦合效应
加载接触的啮合与渗碳和机床加工参数存在直接而复杂的半解析关系。加载啮合点的几何状态和物理状态都会随加工参数变化而变化。在考虑齿面几何形貌优化的加工参数反调中,加工参数之间相互耦合的效应非常明显[14]。而在从齿面建模到加载接触啮合与渗碳的精确几何形貌设计中,存在如下加工参数的齿面变形映射关系:
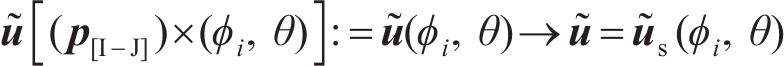
式中: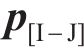

考虑渗碳-啮合耦合效应,每个有限元单元都可以在齿面渗碳过程中引入基本的齿面热变形u。对于齿面渗碳,需要对包括局部区域ΩLCP的整个齿面Φ进行约束,以作为基本的初始条件。
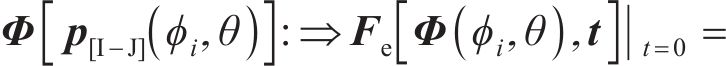
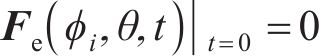
“
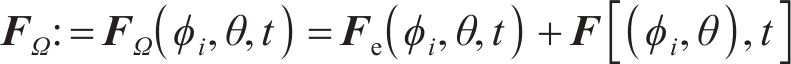
式中:Fe为考虑热变形的齿面点的力;F为考虑接触啮合变形的的齿面点的力;FΩ为考虑耦合相应的耦合力;(ϕi,θ,t)为设计参数。
对于每个点接触位置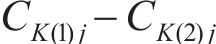
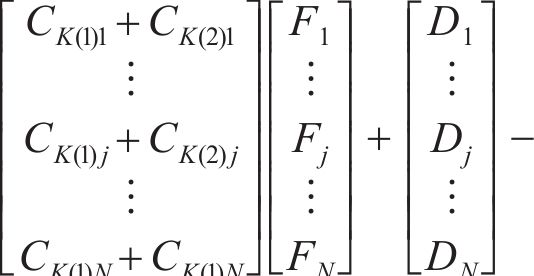

其中:CK为有限元单元中接触单元柔性系数;D为初始距离;Θ为加载接触网格变形下的相对距离;“=”表示已经接触的协调关系;“>”表示还未接触的协调关系。
在齿面接触时,加载的接触力FK(K=1,2,…,N)等同于所有外部载荷P。在每个接触的齿点对上,存在以下平衡条件[12]:
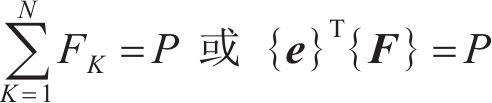
由于式(13)是不等式,为此,引入松弛变量Y,有
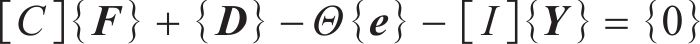
因此,根据式(15),耦合方程可以表示为
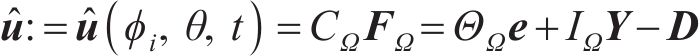
式中:Ω为对印痕齿面进行网格离散化后再对每个点进行约束的局部几何区域。式(17)可以反映热处理变形预测的基本边界条件,其中,齿面啮合过程中的渗碳-啮合耦合效应对齿面变形的影响被整合到有限元单元的变形中。采用文献[12]中的改进单纯形法求解式(17),从而确定啮合-渗碳耦合效应。需注意的是,设计参数(ϕi,θ,t)会直接影响整个齿轮齿面的热处理变形。
2.2 齿面热变形的半解析预测
考虑渗碳-啮合耦合效应的热处理变形可由下式获得:
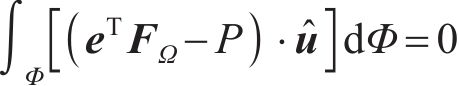
根据式(14)的平衡条件,将引起热处理变形的耦合力FΩ与输入扭矩中的外部载荷P相耦合,便可得到如式(18)所示的关于加工参数(ϕi,θ,t)的半解析优化表达。约束区域Ω
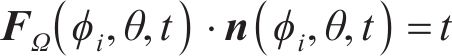
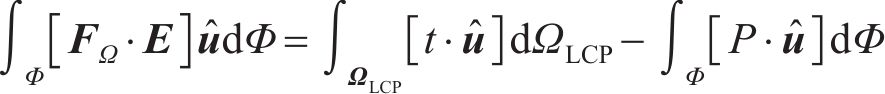
对于每个齿面点位置有
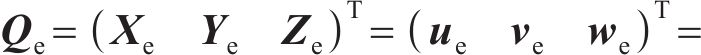
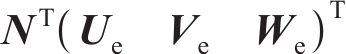
其中:N为单位形状函数。单位应变矩阵为
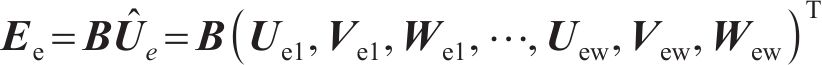
其中:B为应变-位移矩阵;Ue、Ve和We分别为X、Y、Z方向的位移矢量。
在上述计算中,引入以下迭代式:
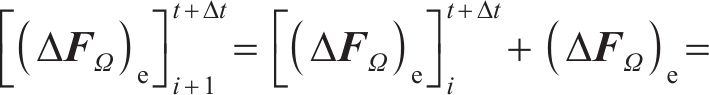
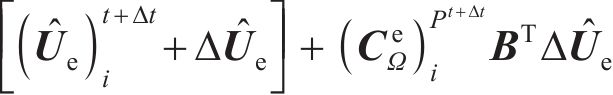
最终的平衡条件可以表示为
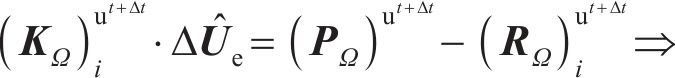
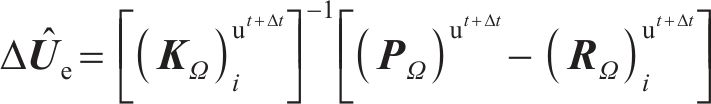
式中:(KΩ)u为全局刚度矩阵;(PΩ)u为全局等效节点载荷矢量;(RΩ)u为内部反作用力的矢量。利用上述公式,可将式(24)改写为
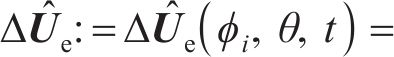
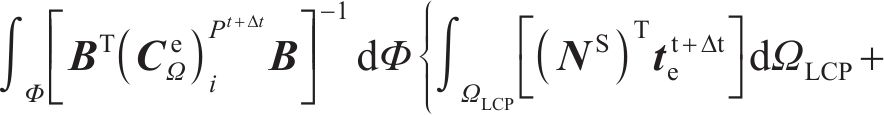
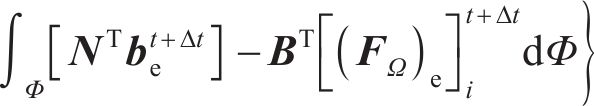
其中:te为单位牵引力矢量;be为单位力矢量。式(25)可改写为与加工参数(ϕi,θ,t)相关的半解析函数。在瞬时接触椭圆中心点进行半解析优化操作,可以确定不同方向上的啮合-渗碳耦合效应[22]。采用Newton-Raphson迭代法可以求解每个有限元的式(25)热变形方程。应用这种半解析预测可以确定整个齿面的热处理齿面几何变形的变化。
3 结果及验证
3.1 初始数据
本文以直升机传动系统中应用的非正交弧齿锥齿轮为基本对象来验证所提出方法的正确性。要获得精确的弧齿锥齿轮齿面模型及有限元模型,需要利用表1中的基本几何参数获得齿轮的齿坯设计,并利用表2中的机床加工参数进行齿面建模以及弧齿锥齿轮传动的有限元建模。具体步骤为:
| 参数 | 小轮 | 大轮 |
|---|---|---|
| 齿数/个 | 31 | 38 |
| 法向模数/mm | 5.3 | 5.3 |
| 齿宽/mm | 32 | 32 |
| 压力角/(°) | 22.5 | 22.5 |
| 外锥距/mm | 208.81 | 208.81 |
| 根锥角/(°) | 22.4 | 27.733 |
| 节锥角/(°) | 23.167 | 28.833 |
| 面锥角/(°) | 24.267 | 29.6 |
| 螺旋角/(°) | 35 | 35 |
| 旋向 | 右旋 | 左旋 |
| 齿顶高/mm | 5.09 | 3.44 |
| 齿根高/mm | 4.65 | 6.30 |
| 轴交角/(°) | 52 | 52 |
| 加工参数 | 大轮 | 小轮 |
|---|---|---|
| 滚比Ra | 2.073 214 | 2.352 220 |
| 径向刀位Sr /mm | 163.356 10 | 152.072 09 |
| 垂直轮位EM/mm | 0 | 1.953 31 |
| 床位XB/mm | -3.952 00 | -37.138 76 |
| 轴向轮位XD/mm | 0 | -15.909 14 |
| 根锥安装角γm/(°) | 27.73 | 34.34 |
| 刀倾角σ/(°) | 0.63 | 17.46 |
| 刀转角ζ/(°) | 14.83 | 106.62 |
| 角向刀位ϕ/(°) | 49.83 | 61.19 |
| 修正螺旋系数χHL | 0 | 38.952 65 |
1) 根据齿坯设计参数确定机床加工参数。加工参数通常是通过使用先进而复杂的计算软件确定的,如KLINGELNBERG提出的KIMOSTM和GLEASON提出的CAGETM。需注意的是,这些加工参数适用于齿面的磨削加工,该加工方法被称为双重螺旋法[23],具有很高的制造效率。
2) 利用加工参数进行机床运动学仿真,以建立齿面模型,并进行半解析齿面变形分析。
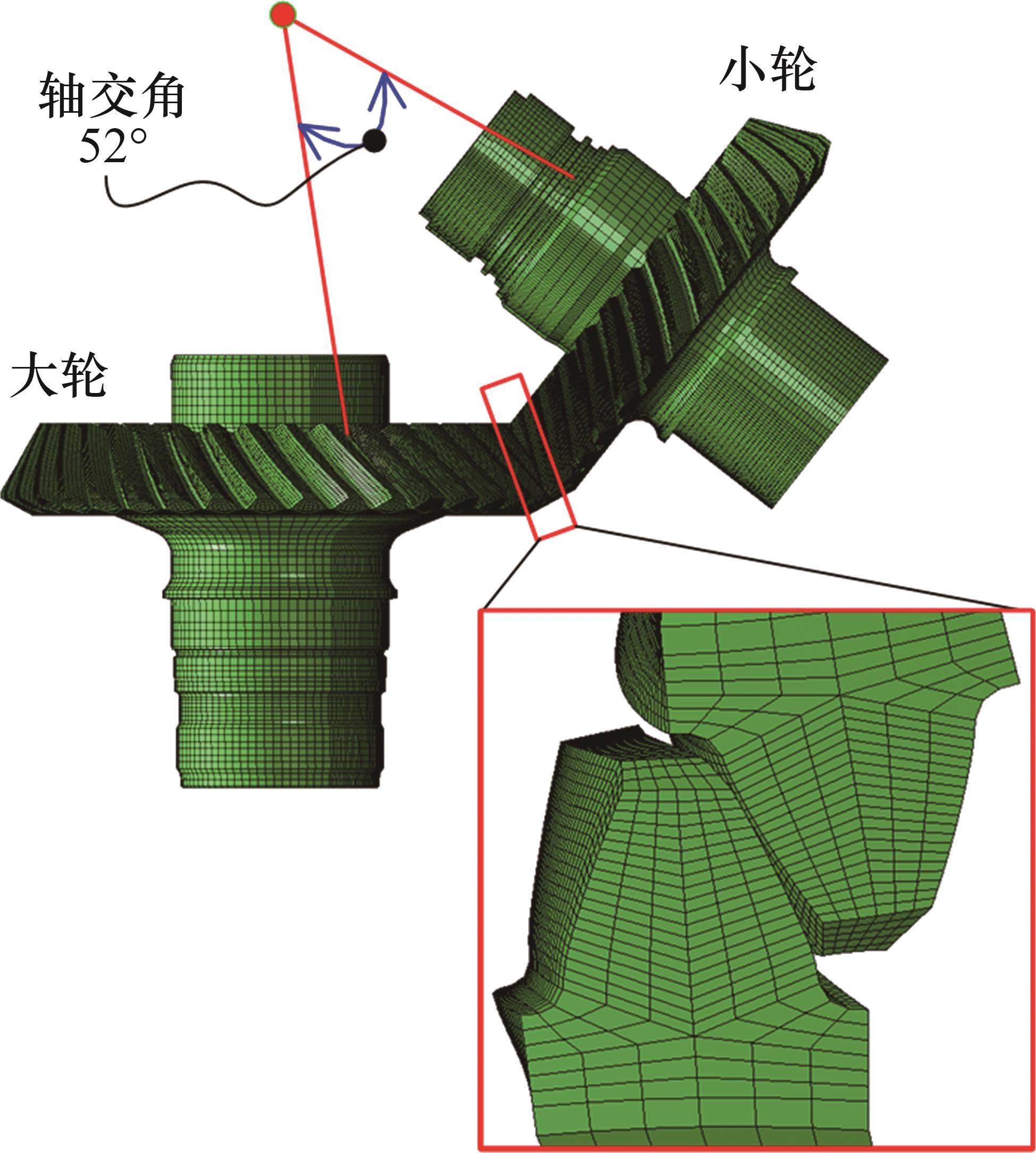
在建立精确的齿面模型后,分别确定包括齿轮小端、大端、齿顶和齿根在内的边界线。根据齿面设计要求,考虑每条边界线上的节点数,自动划分网格。可以任意改变网格密度,但也需要考虑计算效率来确定其合理范围。详细的有限元网格划分见文献[12]。图5所示为弧齿锥齿轮结构的三维有限元模型,其网格类型为C3D8,网格数量为18 000个。该弧齿锥齿轮对的轴交角较小,对加载接触性能有很强的敏感性。
3.2 未考虑耦合效应的NLTCA结果
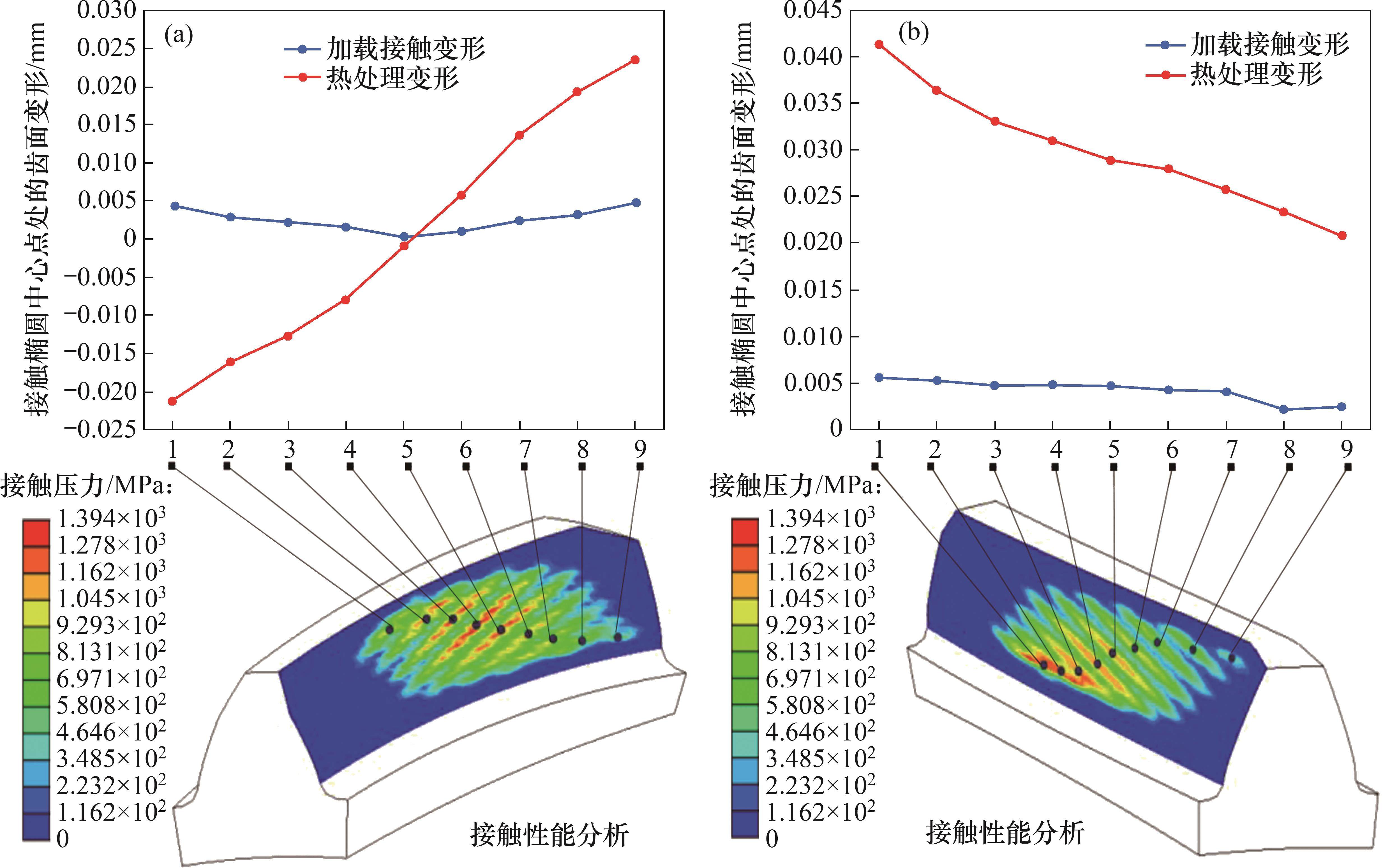
根据NLCTA解决方案[12],分别测定加载接触变性和热处理变形,给出小轮齿面和大轮齿面变形结果。图6(a)所示为以9310钢为材料的小轮齿面的NLTCA分析结果,9310钢设计参数见表3。从图6(a)可见:在第9个啮合位置,加载接触变形最大,为0.004 645 mm;第1个啮合位置的加载接触变形其次,为0.004 326 mm;在第5个啮合位置加载接触变形最小,为0.000 290 5 mm。图6(b)所示为大轮齿面的NLTCA分析结果。从图6(b)可见:从第1个啮合位置到第9个啮合位置,热变形和接触变形整体均呈下降趋势,其中,第1个啮合位置的加载接触变形最大,为0.005 546 3 mm;第8个啮合位置的加载接触变形最小,为0.002 124 9 mm。由于分开测定得到加载接触变形和热处理变形,并没有考虑渗碳-啮合耦合效应的影响,因此,这里的热处理变形结果并不准确。
| D0.4/(mm2·s-1) | Q/(kJ·mol-1) | B | β0/(mm·s-1) | E/(kJ·mol-1) |
|---|---|---|---|---|
| 25.5 | 14 | 0.8 | 0.003 47 | 34 |
3.3 考虑耦合效应的齿面热处理变形
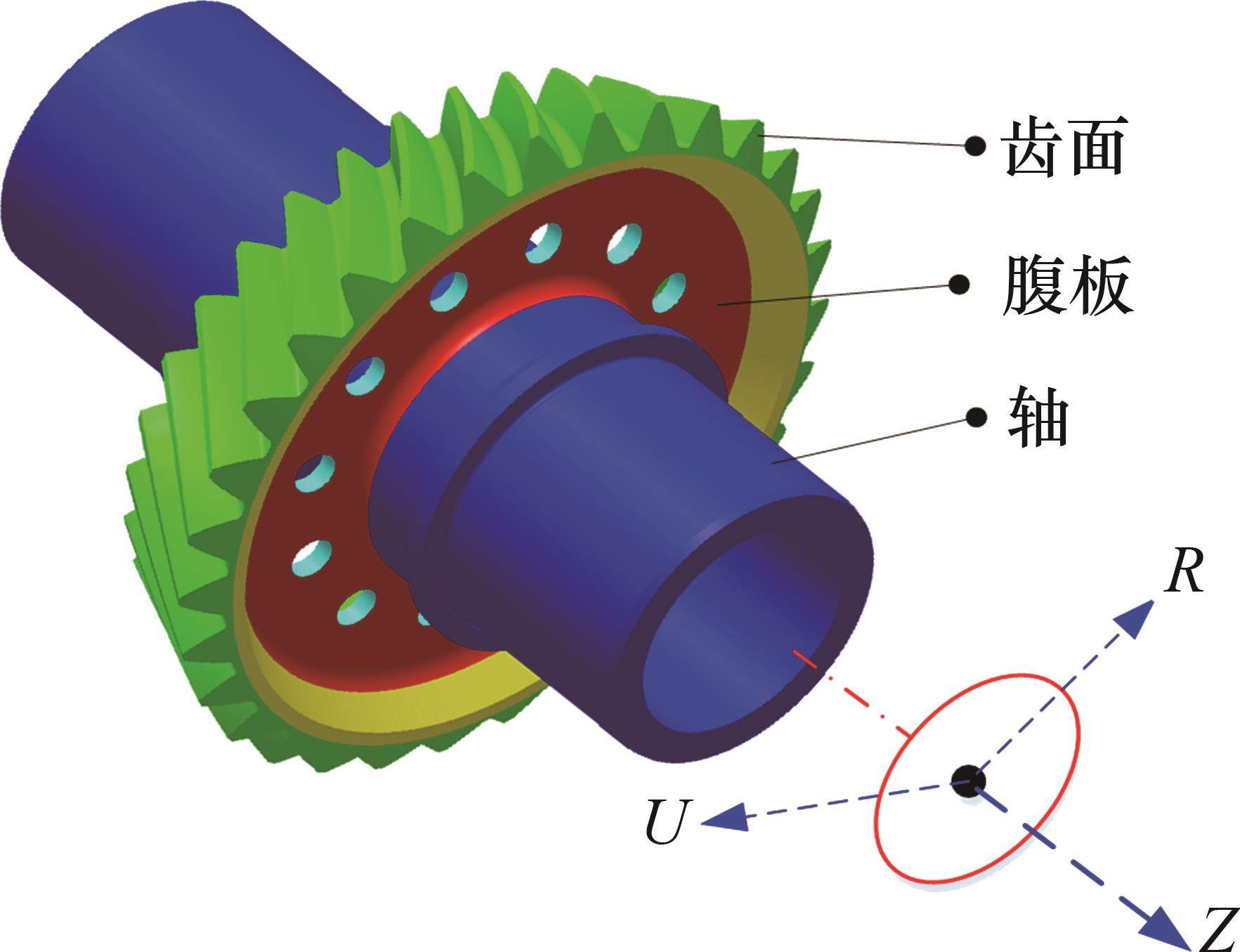
考虑到加载接触啮合和齿面渗碳的复杂耦合效应,确定齿面冷却至室温时的热变形,并将其分为径向R、轴向Z和齿面法线方向U这3个方向的分量与总量两大部分。弧齿锥齿轮在坐标系(R、Z、U)中的基本三维结构模型见图7。
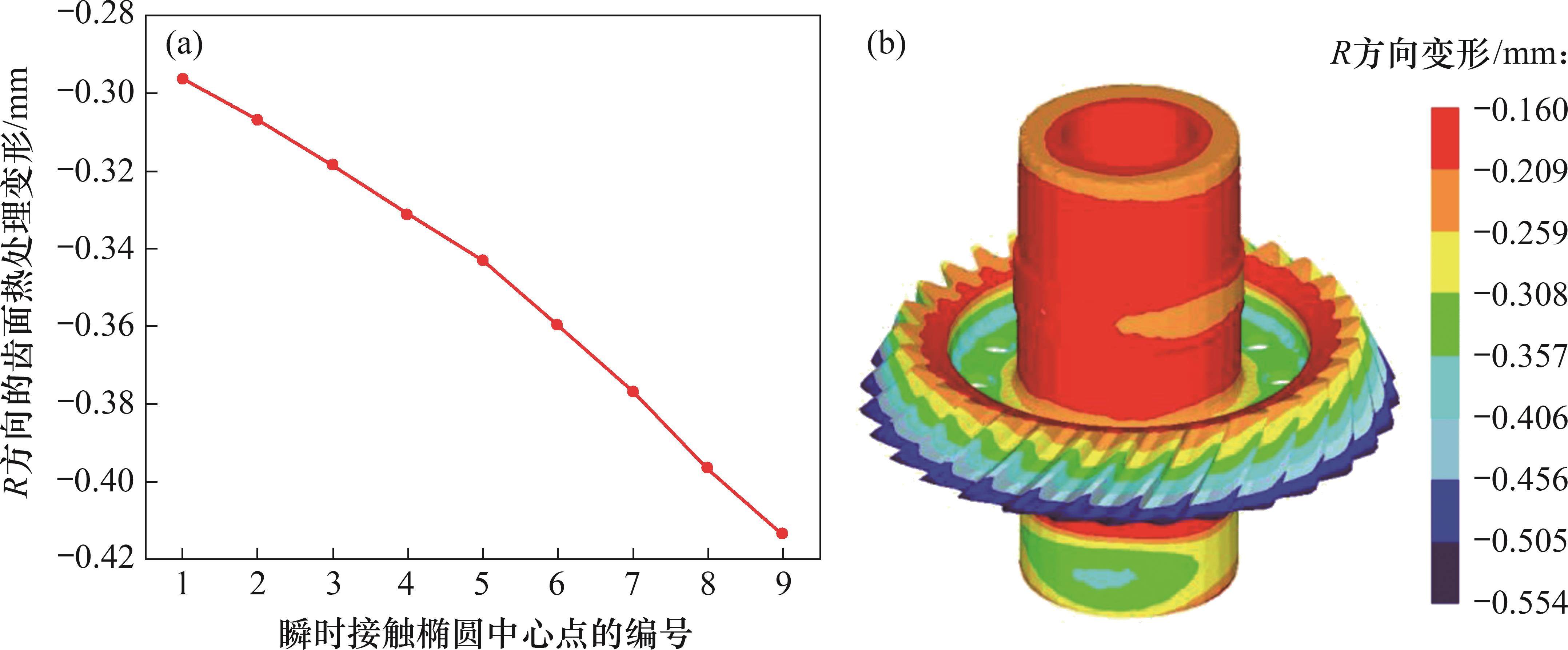
以‘+’表示正方向的变形,‘-’表示负方向的变形,以数值表示变形的大小。考虑啮合-渗碳耦合效应的小轮齿面R方向的热处理变形见图8。对于相同的取样点,对9个加载接触中心位置分别使用半解析预测方法来确定其变形。在R方向上,接触椭圆中心的热变形从第1个啮合位置的 -0.296 39 mm增加到第9个啮合位置的-0.413 32 mm。在从轮齿小端到大端的方向上,整个弧齿锥齿轮结构在R方向的热变形整体呈增大趋势。
考虑啮合-渗碳耦合效应的小轮齿面Z方向热处理变形见图9。从图9可见:在Z方向上,从开始啮合到最后啮合完毕,接触中心的齿面热变形呈现减小的趋势,这与R方向有着很大不同;在第1个啮合位置,最大变形为-0.210 98 mm,而在第9个啮合位置,最小变形为-0.184 88 mm。对于包括腹板、轮毂、齿面和轴在内的整个齿轮结构,小变形主要位于轴、轮毂和腹板,这些位置的变形明显小于齿面变形。而除齿面之外,最明显的变形则是位于轴的上端。
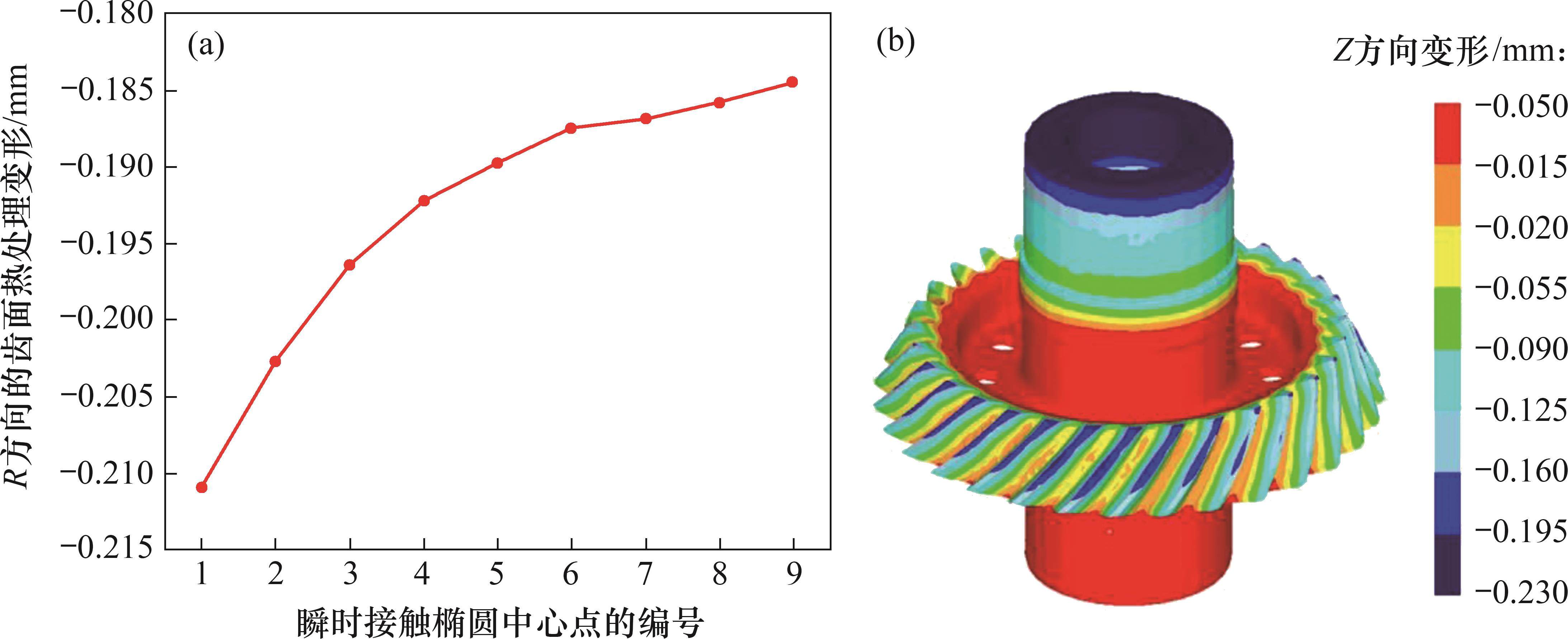
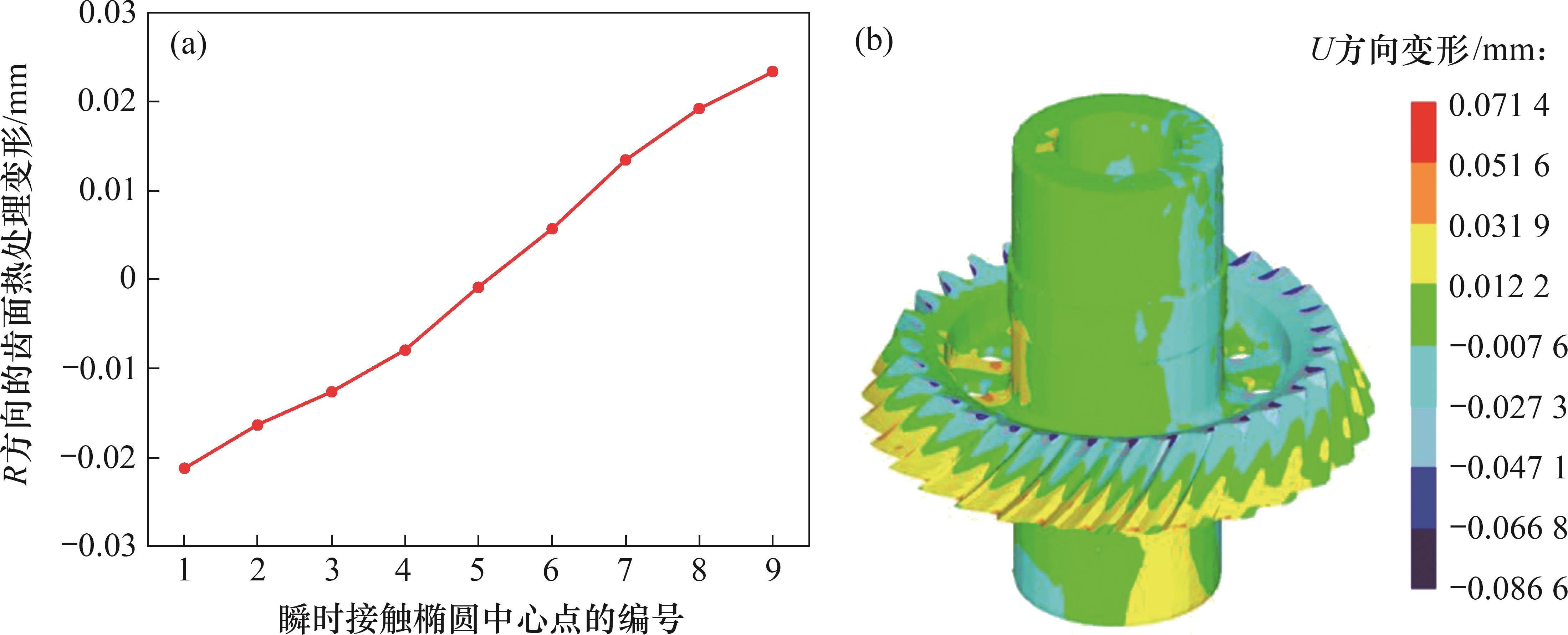
图10所示为考虑啮合-渗碳耦合效应的小轮齿面U方向热处理变形结果。从图10可见:对于第1个到第9个的接触椭圆中心点的齿面热处理变形,基本变形方向由负方向变为正方向,如第1个啮合位置的变形为-0.021 34 mm,而第9个啮合位置的变形为0.023 334 mm,且第5个啮合位置的变形最小,为-0.000 882 mm,这与其他方向的变形分布有很大不同。对于整个弧齿锥齿轮结构的U向变形而言,较小的热处理变形主要位于轴、腹板和轮毂甚至整个齿面的某些区域,而较大的变形主要位于轮齿凹面附近的小端和大端。
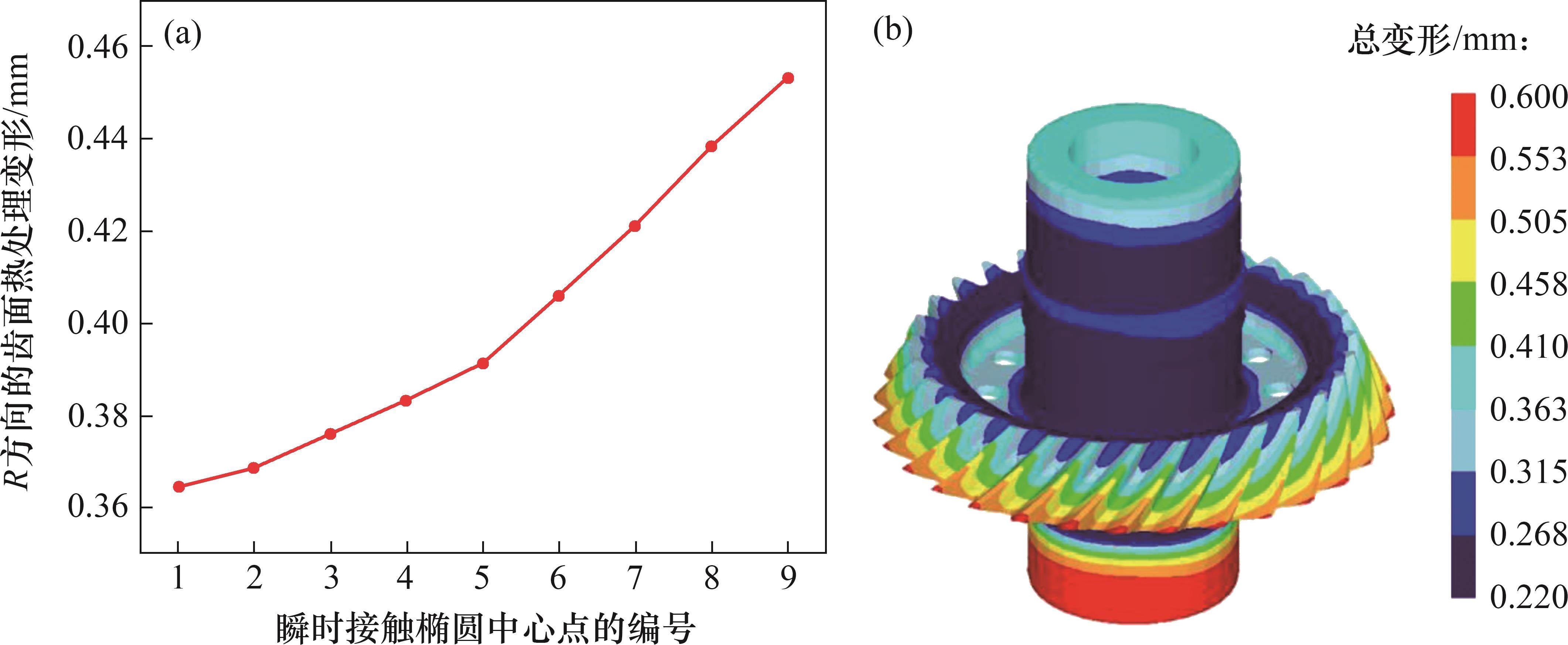
在确定3个方向的变形的分量后,齿面热处理的总变形实际上就是分量的矢量组成。考虑啮合-渗碳耦合效应的小轮齿面总热处理变形见图11。从图11可见:从啮入到啮出,接触椭圆中心点的热处理变形的变化呈上升趋势,最大变形为第9个啮合位置的0.453 224 mm,最小变形为第1个啮合位置的0.364 532 mm;对于包括腹板、轮毂、轴和齿面在内的整个弧齿锥齿轮结构,较大的齿面变形位于靠近齿顶大端处;对于齿轮轴的变形分布,最小变形位于轴的中间区域,最大变形则位于轴的下部;在轴与轮毂的重要连接部位,齿面热处理变形的变化较小,而从轮齿大端到小端部的变形变化很大。
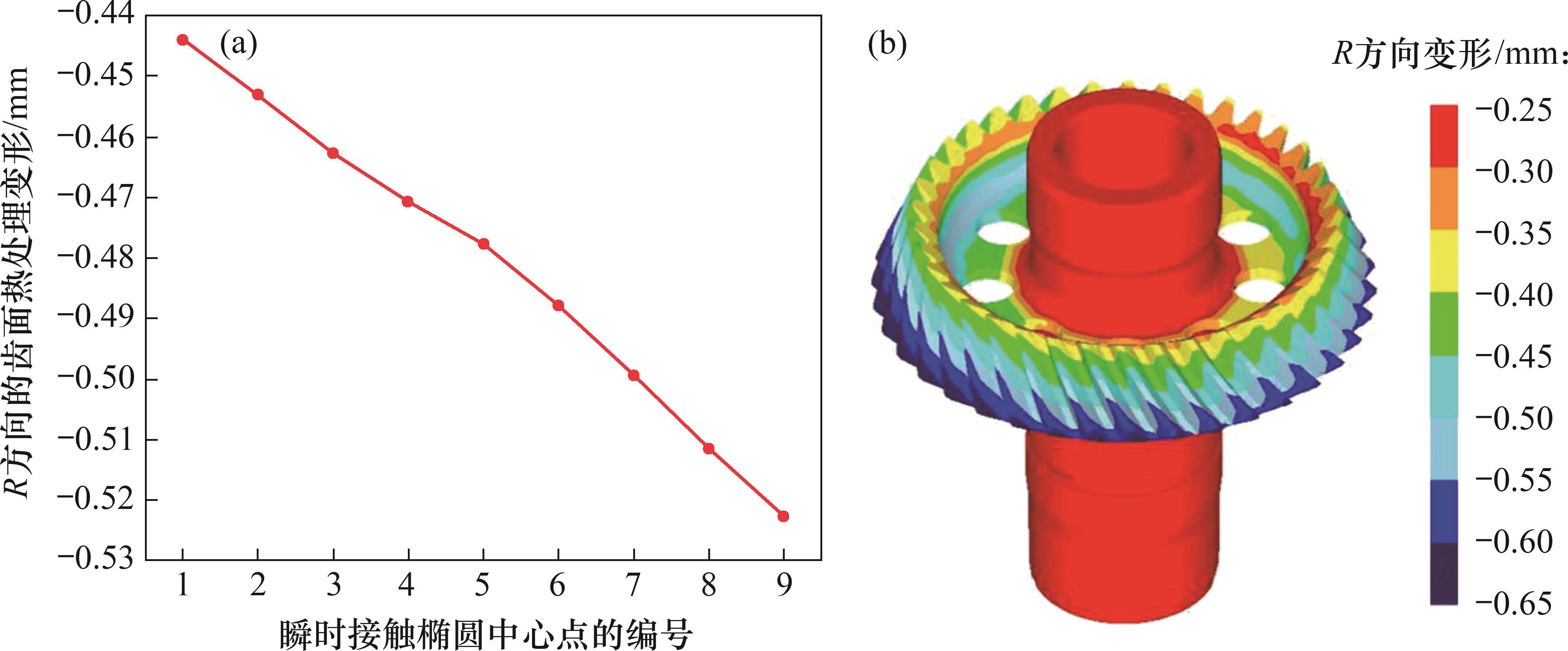
考虑啮合-渗碳耦合效应的大轮齿面R方向热处理变形见图12。从图12可见:变形从第1个啮合位置的-0.444 09 mm增加到第9个啮合位置的-0.522 85 mm,且变形基本上沿着接触路径所在的方向变化;在包括腹板、轮毂、轴和轮齿的整个航空弧齿锥齿轮结构中,齿轮轴是最小变形的主要部位。
考虑啮合-渗碳耦合效应的大轮齿面Z方向热处理变形的基本结果见图13。从图13可以看出:从第1个啮合位置到第9个啮合位置,Z方向的变形整体呈减小趋势;相较于其R方向的热处理变形,Z方向的变形呈现不同的变化趋势。如从轮齿大端指向小端的方向上,齿轮整体结构的变形呈增大趋势,且方向由“-”变为“+”;从齿顶到齿根的位置,齿面的变形逐渐增加;位于腹板、轮毂和轴上的部分变形较大,且大部分都是正方向上的变形。
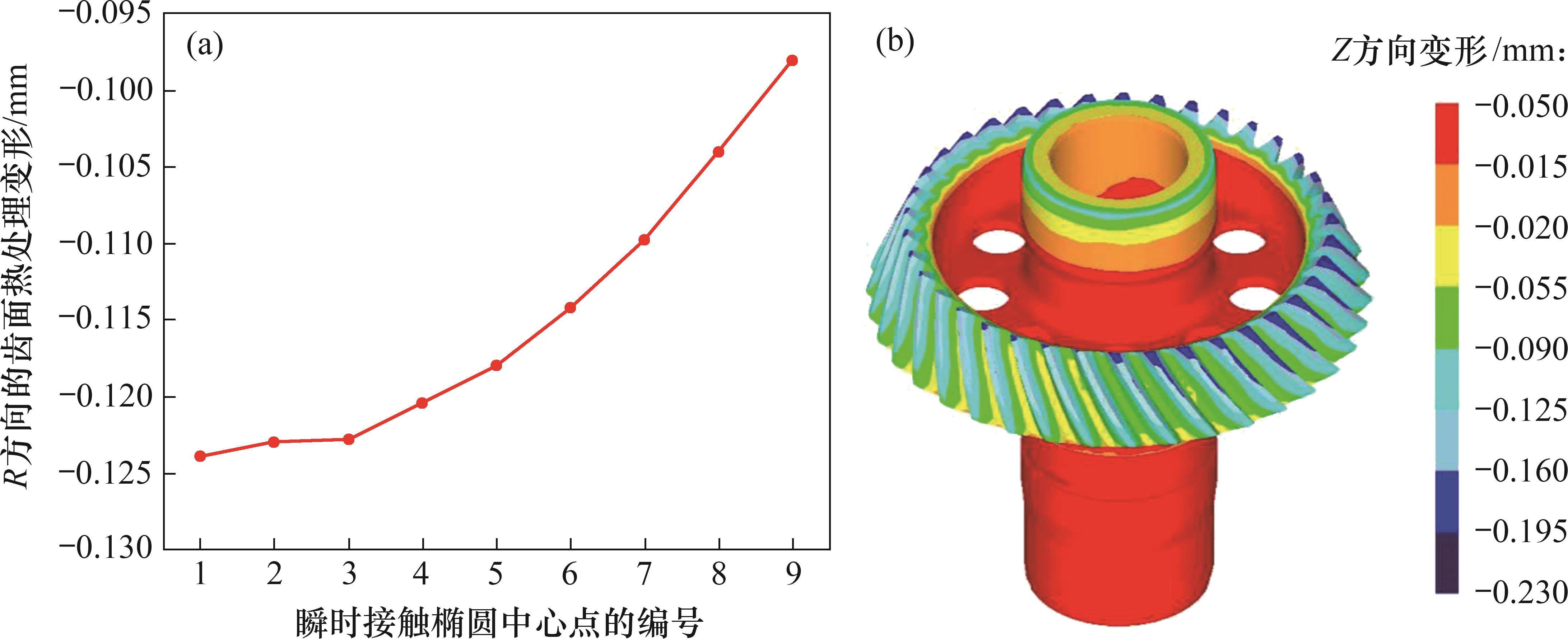
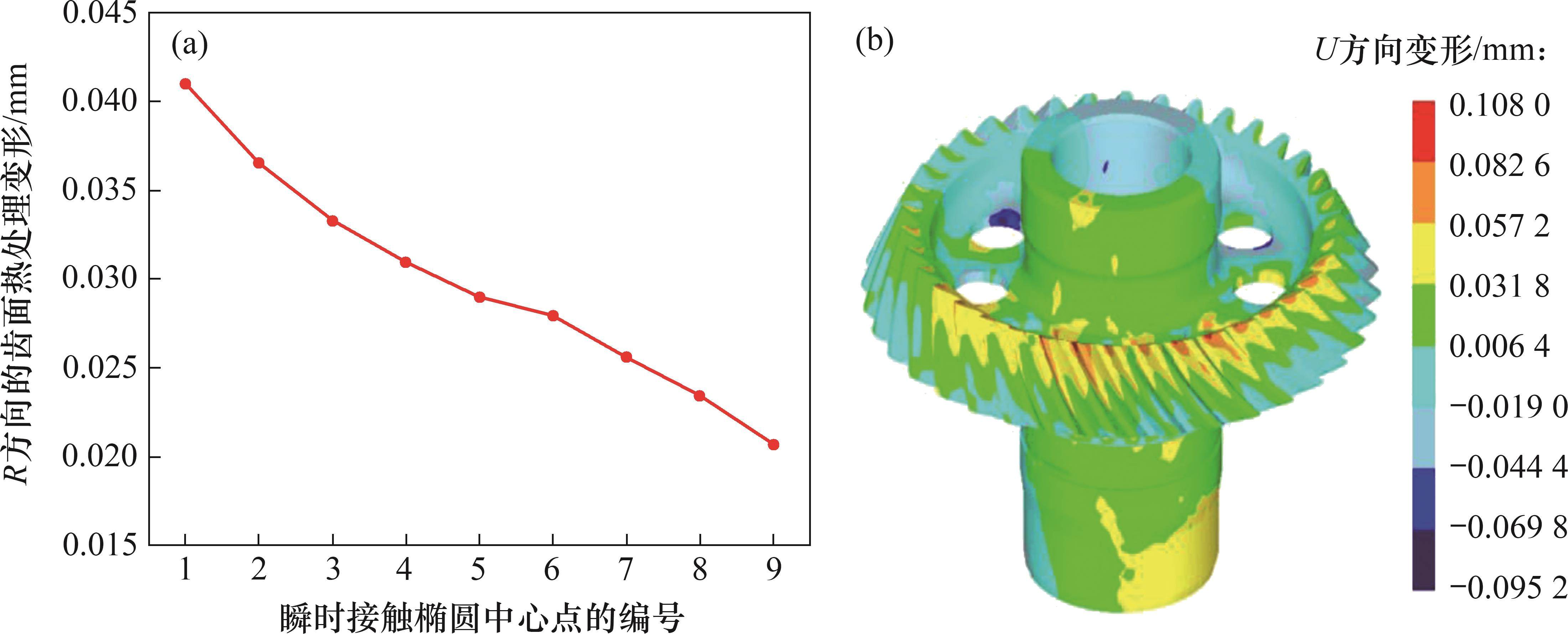
考虑啮合-渗碳耦合效应的大轮齿面U方向热处理变形见图14。从图14可以看出:从啮入到啮出,接触椭圆中心点的齿面热处理变形呈递减趋势;最后1个啮合位置的变形最小,为0.020 768 mm,第1个啮合位置变形最大,为0.040 989 mm;整个航空弧齿锥齿轮结构在U方向上的变形有很大差异;从轴的上端到下端,热变形存在由小到大的变化规律;而从轮齿大端部分到小端部分,整个齿面的变形具有明显的增加趋势,这与加载接触印痕区域的热变形变化趋势一致。
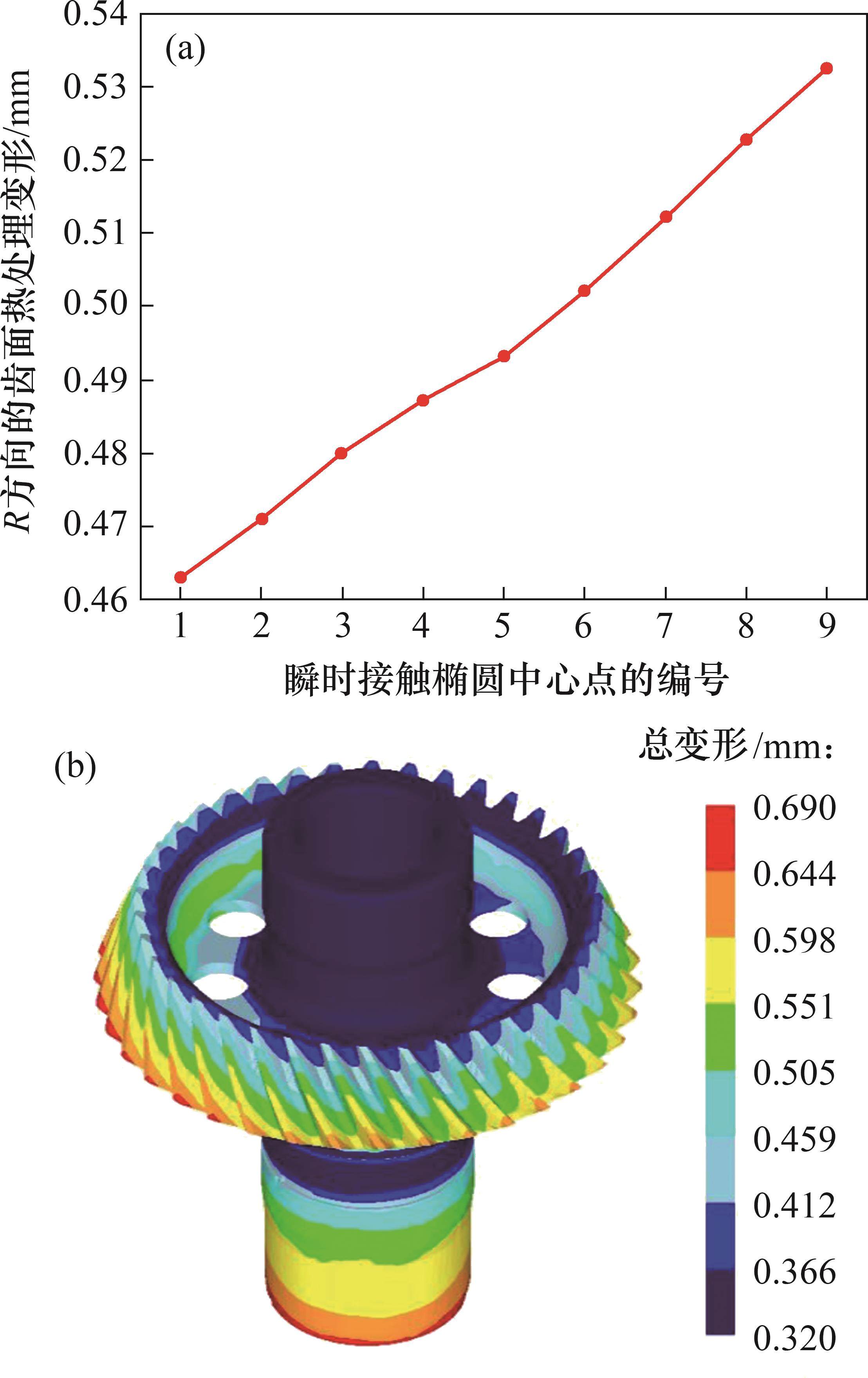
考虑啮合-渗碳耦合效应的大轮齿面的热处理总变形见图15。从图15可见:从开始啮合到啮合完毕,接触椭圆中心点处的齿面热处理变形整体呈上升趋势;最大变形为第9个啮合位置的0.532 417 mm,最小变形为第1个啮合位置的0.462 923 mm;整个航空弧齿锥齿轮结构某些部分的总变形分布也存在很大差异,如齿轮轴部分的变形由上至下逐渐增大,而从轮齿小端到大端,整个齿面的变形呈现上升趋势,其中,靠近齿顶大端的区域存在较大变形。
3.4 结果验证
为验证本文所提出的方法的准确性,以小轮和大轮的齿面法线方向U的热处理变形结果为例进行研究,并将其计算结果与文献[10]中的结果进行对比。
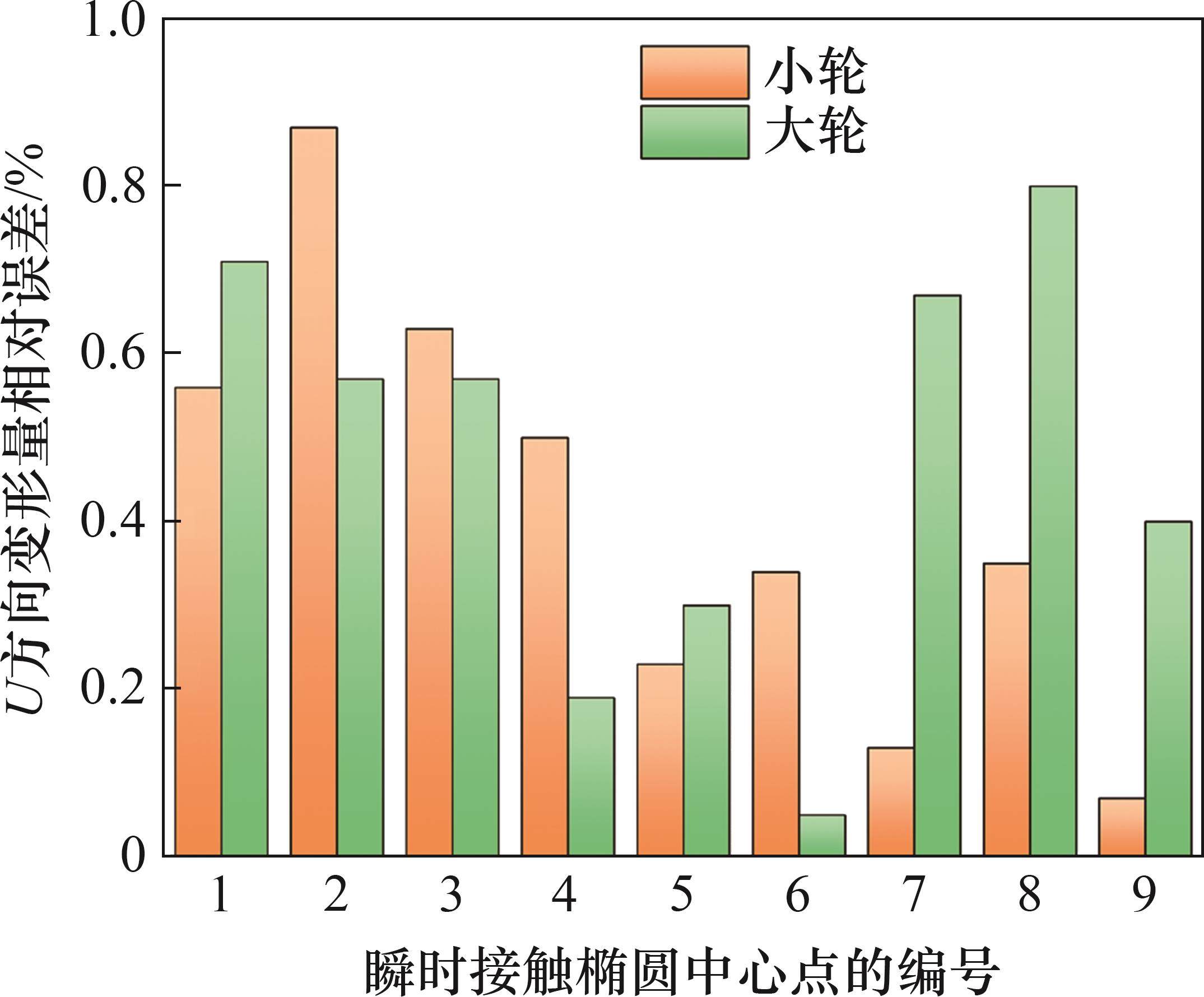
各个瞬时接触椭圆中心点U方向热处理变形与文献[10]中结果的相对误差见图16。从图16可见:第2啮合位置的小轮U向变形相对误差最大,为0.87%;第8啮合位置的大轮U向变形相对误差最大,为0.8%;所有结果的相对误差均在1%以内,验证了基于渗碳-啮合耦合效应的齿面热变形半解析预测方法的准确性和可靠性。
4 结论
1) 针对弧齿锥齿轮提出了一种新的用于预测渗碳-啮合耦合效应对齿面热处理变形影响的半解析预测方法。将NLTCA与齿面渗碳相结合,确定了机床加工参数与齿面热处理变形之间的半解析泛函关系,指导考虑宏观和微观几何形貌的实际齿面制造的加工参数的精确协同优化。
2) 所提出的方法能够高效、精确地求解齿面的热处理变形。这种半解析预测可以为具有高精度、高效率和高性能要求的弧齿锥齿轮制造提供技术参考。
3) 该方法除可用于预测几何变形外,还可以扩展到热处理的物理性能如接触应力、接触压力以及传递误差等的评估。
A data-driven programming of the human-computer interactions for modeling a collaborative manufacturing system of hypoid gears by considering both geometric and physical performances
[J]. Robotics and Computer-Integrated Manufacturing, 2018, 51: 121-138.杜文龙, 陈唐炜, 张建兴, 等. 基于渗碳-啮合耦合效应的弧齿锥齿轮热处理变形半解析预测方法[J]. 中南大学学报(自然科学版), 2025, 56(2): 487-500.
DU Wenlong, CHEN Tangwei, ZHANG Jianxing, et al. Semi-analytical prediction method for heat treatment deformation of spiral bevel gears based on carburizing-meshing coupling effect[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 487-500.

