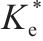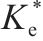软土地基具有含水率高、压缩性大、承载能力低等不良工程特性。因此,在软土地基上进行铁路、公路等工程建设时,往往需要对其进行加固或处理[1]。塑料排水板(PVD)结合预压法可加快软土固结、提高地基承载力、减小地基工后沉降,具有施工简便、成本较低等优势,在国内外均获得了广泛应用[2-4]。预压荷载下,PVD地基快速固结的同时,往往伴随有较大的变形,且由于预压荷载的不同,其侧向变形形态存在明显差别[5]。PVD地基的预压方式主要包括真空预压、堆载预压及真空联合堆载预压[6]。真空预压下,土体处于各向“被动受压”状态,产生向内收缩的侧向变形;堆载预压下,由于竖向荷载为主的压缩固结作用,土体一般发生向外膨胀的侧向变形;真空联合堆载预压下,地基变形则是真空与堆载联合作用的结果,可能存在整体向内、整体向外或浅层向内深层向外的3种侧向变形模式[7]。PVD地基过大的向外侧向变形会挤压、破坏临近结构,或导致路堤坍塌破坏[8],过大向内侧向变形则可能导致预压区边缘的劈裂破坏[9]。因此,有效预测不同预压模式下PVD地基侧向变形,对工程设计和施工具有重要的指导意义。真空预压方面,IMAI[10]基于弹性理论提出了真空预压下PVD地基侧向变形的计算方法,该方法原理清晰,但受限于弹性理论相关假定,计算结果可能存在一定偏差。CHAI等[11]根据真空预压下土体体积应变与一维压缩下相同的假定,建立了基于土体体积应变及垂直应变的水平应变计算方法,提出了真空预压下PVD地基侧向变形轮廓的计算方法,并取得较好的预测效果。WU等[12]对CHAI等[11]提出的方法及参数作了简化,进一步提升了该方法计算侧向变形效率,但该方法仍仅适用于真空预压的工况。真空联合堆载预压方面,ONG等[13]由模型试验和有限元分析得到了真空联合堆载预压下侧向变形的主要影响因素,并提出了联合预压下PVD地基平均侧向变形的预测方法,但无法得到较为关键的地基最大侧向变形。CHAI等[14]基于系列真空联合堆载预压的现场测试数据,提出了联合预压下PVD地基最大净侧向变形的预测方法,但无法获得地基的侧向变形轮廓和最大侧向变形所在深度。LU等[15]基于真空联合堆载预压的三轴试验,综合考虑各主要影响因素,提出了联合预压下PVD地基侧向变形轮廓预测方法,可分析获得PVD地基不同深度处的侧向变形;XU等[7]结合三轴试验及有限元仿真计算,进一步修正LU等[15]提出的方法,得到了较为完善的联合预压下PVD地基侧向变形轮廓的预测方法,不过该方法仅适用于联合预压的工况,无法应用于真空或堆载单独作用的工况。堆载预压方面,陈继彬等[16]基于现场数据分析,提出了堆载预压下PVD地基最大侧向变形随时间变化的经验公式,可为最大侧向变形增长趋势的分析提供参考,但该经验公式的相关参数缺乏物理含义,对工程设计的指导意义有一定局限性。XU等[17]通过系列现场测试数据的统计分析,提出了堆载预压下PVD地基最大向外侧向变形的预测方法,并由模型试验[18]对该方法进行了验证和完善,然而该方法无法预测和分析PVD地基的侧向变形轮廓及最大侧向变形深度。综上可知,现阶段仍缺乏有效预测堆载预压下PVD地基侧向变形轮廓的计算方法。鉴于此,本文基于改进三轴压缩试验,建立有限元仿真模型,并通过多工况仿真计算,研究堆载预压下PVD地基侧向变形及应力状态的主要影响因素(包括竖向应力、水平应力、加载速率及土体初始应力)。基于分析结果,提出可综合考虑以上因素及地基固结特性的综合影响因子β,最终建立堆载预压下PVD地基侧向变形轮廓的预测方法。
1 改进三轴压缩试验及仿真模型
1.1 试验装置及方法
采用自研的改进三轴试验装置开展堆载预压下径向排水的三轴压缩试验。相较常规三轴试验仪,该装置的改进主要有2点:一是移除三轴土样顶部和底部的透水石,并于圆柱体土样中心内置mini-PVD,以使土样实现径向排水;二是孔压监测点不再置于土样中心,而是置于距离试样底座中心一定距离处(本文为17 mm)。图1为改进三轴试验装置的示意图。
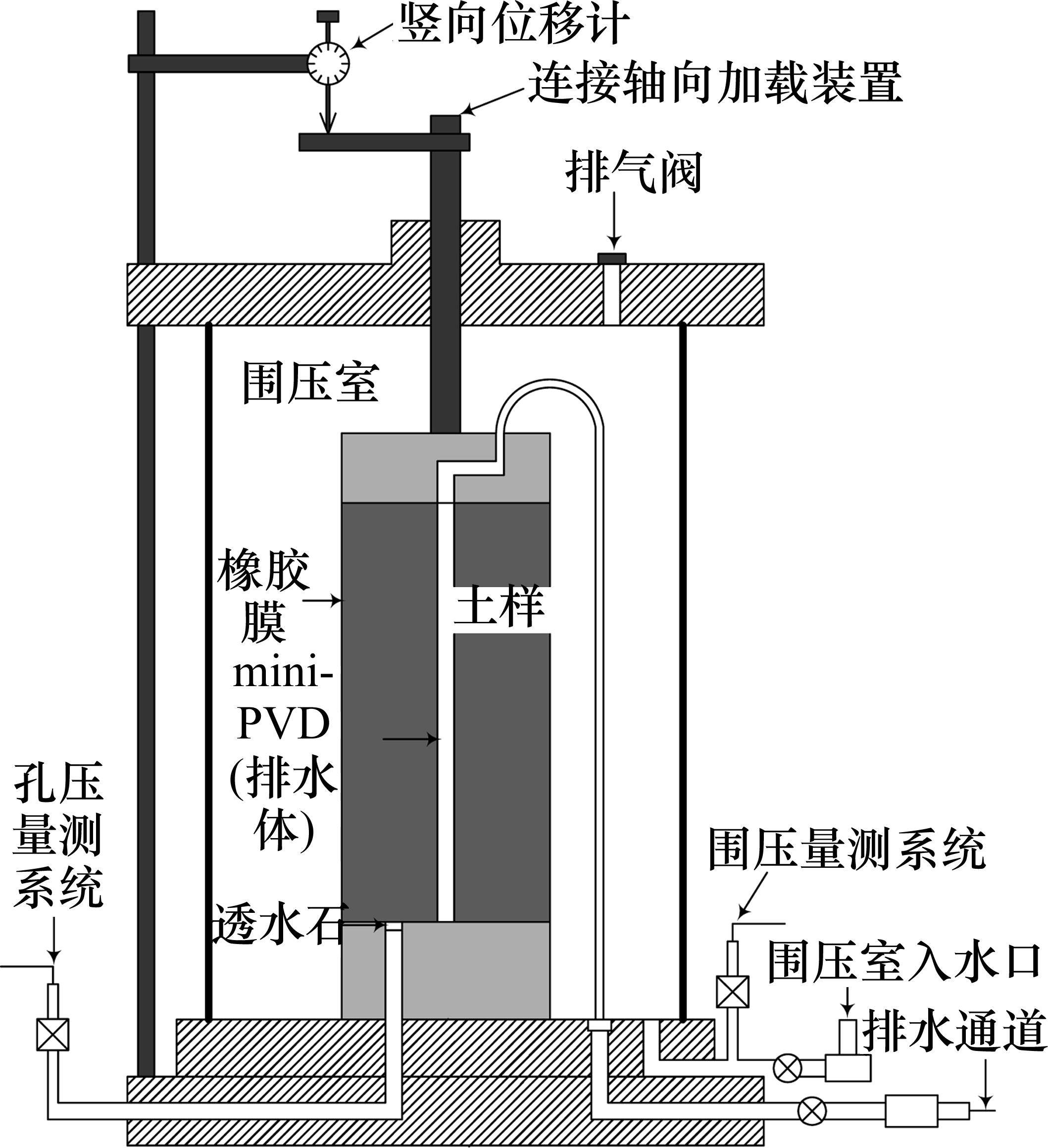
三轴试验所用土样取自广州南沙港地区淤泥质软土层。原状土取回后,首先将其加水搅拌至流塑态,并填入直径300 mm圆柱筒容器,填土高度约为300 mm。重塑土的顶部、底部及四周均设置排水土工织物,以加快其排水固结过程;随后施加30 kPa竖向荷载,直至重塑土完全固结(不少于60 d)。最后,取重塑土开展相关物理力学参数试验,并切出圆柱体标准试样用于开展三轴压缩试验;试样的高度和直径分别为125 mm和61.8 mm。试验前,用直径6 mm麻花钻头垂直向下于试样中心缓慢钻出小孔,并插入直径约6 mm由土工滤纸包裹软弹簧所制成的mini-PVD,将试样抽真空饱和24 h后即可开展试验。试验开始后,首先保持初始竖向应力30 kPa,围压18 kPa预固结1 d(试样可实现完全固结),然后进行堆载预压下径向排水的三轴压缩试验。试验施加的轴向荷载共28.5 kPa,分3级阶梯型施加,每级荷载9.5 kPa,加载时间间隔3 h。试验期间通过LVDT位移计和三轴仪数据采集系统监测试样顶部的沉降、试样排水量及孔压监测点处的超孔压。待土样变形稳定后结束三轴试验,并运用游标卡尺测量试样直径;测量时,每间隔5 mm高度在相互垂直的2个方向各测量一次,并根据试样直径的改变量分析试样的侧向变形。
1.2 三轴试验仿真模型
改进三轴试验虽能较好实现堆载预压下土单元体的径向排水试验,但土样制备时间较长,不适于开展大规模多工况试验研究。为系统分析堆载预压下,各主要影响因素对土体侧向变形及应力状态的影响,基于改进三轴压缩试验及PLAXIS 2D有限元软件,建立相应的轴对称有限元仿真模型。模型高125 mm,mini-PVD半径rw=3 mm,PVD影响半径re=30.9 mm。约束模型顶部和内侧(即试样内径边缘)的水平向位移;模型底部为固定边界,外侧为自由边界。根据改进三轴压缩试验的实际情况,模型内侧边界设置为排水边界,以模拟mini-PVD的排水效应,其余边界则均为不排水边界。图2为有限元模型的网格图,共计包含712个三角形轴对称单元和6 009个节点;具体仿真计算时,设置模型网格随分析步实时更新,以考虑土体的大变形效应。

土体采用修正剑桥模型模拟,相关土体物理力学参数如表1。表中,e0为土体初始孔隙比;λ和κ分别为修正剑桥模型中土体正常固结线及卸载线(膨胀线)的斜率,其中λ(=Cc/ln10)由土体一维压缩固结试验所得的土体压缩指数Cc转化计算而来,κ则根据既有文献推荐,取为λ的0.2倍[19];cv和ch分别为土体竖向和水平向固结系数,cv由一维压缩固结试验(25~50 kPa)沉降曲线及时间平方根法计算所得,既有研究表明,ch一般为竖向固结系数cv的1.5~4.0倍[20],本文综合考虑后取为3cv;M为修正剑桥模型临界状态线斜率,由土体静止土压力系数K0(K0=0.45)反算得出;kv为土体竖向渗透系数,根据固结试验结果,由cv反算得出;kh为土体水平向渗透系数,参考固结系数ch的取值依据,本文取为竖向渗透系数kv的3倍;ck为与渗透系数折减相关的常数,根据TAYLOR的研究[21],土体渗透系数随孔隙比而变化,变化关系为k=k0×10-(e0-e)/ck,且ck取值一般为e0的0.4~0.5倍,本文取为0.5e0。值得注意的是,由于试验中mini-PVD是由麻花钻缓慢钻孔后再小心插入,因此其机械涂抹区可忽略不计;另外,由于mini-PVD尺寸相较于试样而言可以达到较高的径向排水效率,因此三轴试样的井阻效应亦可忽略不计[15]。
| e0 | λ | κ | cv/(m2∙d-1) | ch/(m2∙d-1) | M | kv/(m∙d-1) | kh/(m∙d-1) | ck |
|---|---|---|---|---|---|---|---|---|
| 1.3 | 0.138 9 | 0.027 8 | 0.019 | 0.057 | 1.764 | 2.986×10-5 | 8.958×10-5 | 0.65 |
1.3 仿真模型验证
三轴试验预固结期间,土样会产生一定的形变和体积改变,使得土样初始高度和直径略小于标准值[15]。分析时,需对土样初始高度及直径进行修正;初始高度可由竖向位移计直接读取的高度变化按式(1)进行调整,初始直径则根据前期预固结体积变化量(即排水量)和试样高度变化按式(2)进行调整。由土样调整后的初始直径和试验结束后的最终直径,计算土体平均半径增量。
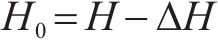
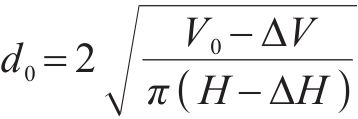
式中:H和V0分别为预固结前试样的初始高度和初始体积;ΔH和ΔV则分别为试样预固结期间的高度变化和体积变化。
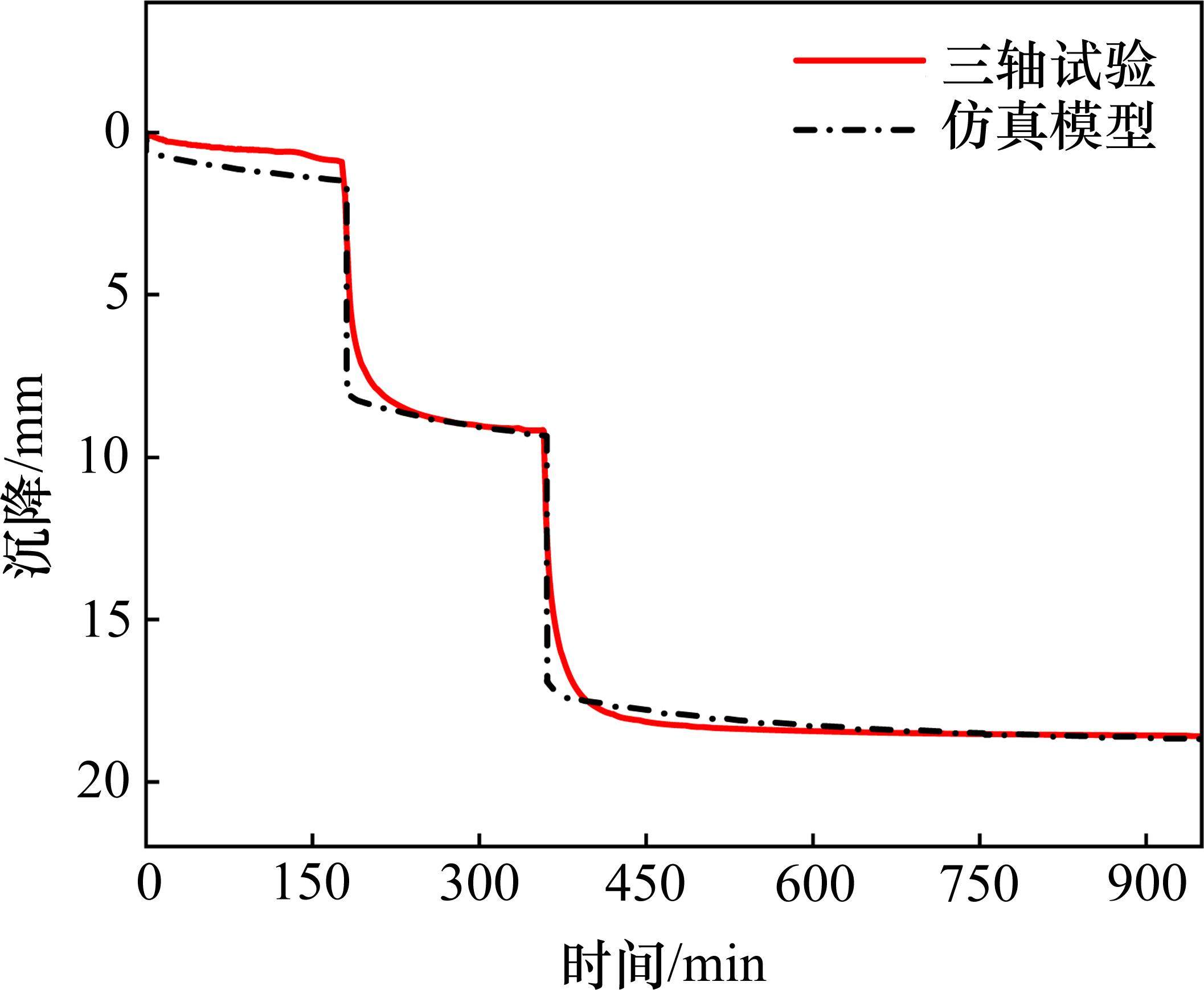
本文有限元仿真模型与三轴压缩试验实测的沉降曲线对比如图3所示,可见二者沉降大小及增长趋势均基本一致。另外,三轴试验测得的试样平均半径增量为2.94 mm,仿真模型所得平均半径增量则为2.85 mm,二者吻合较好。综上,可认为仿真模型能有效模拟径向排水三轴土样的变形特性,可用于进一步开展多工况仿真分析。
2 数值仿真分析
2.1 试验工况
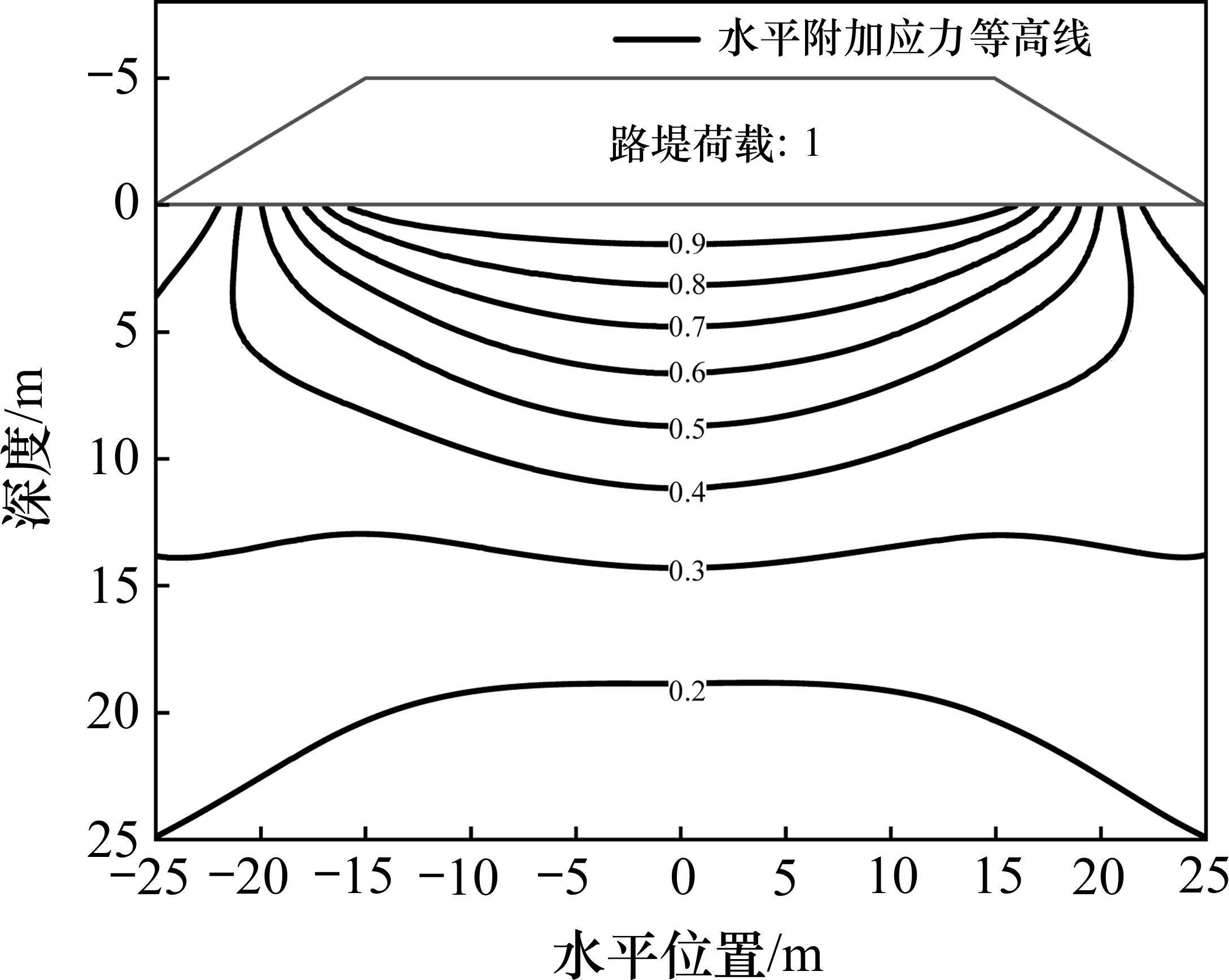
堆载预压下,影响PVD地基变形及应力状态的主要影响因素有堆载大小、堆载速率和土体固结性质等。值得注意的是,堆载的施加会同时引起土体竖向应力及水平应力的改变。现阶段,PVD地基侧向变形的分析中,较少考虑水平应力变化的影响;但由Boussinesq解[22],地基内的水平向附加应力是不容忽视的(如图4),特别是地基浅表层。因此,综合考虑以竖向应力、水平应力、加载速率及土体初始有效应力为主要影响因素开展多工况仿真分析。
参考XU等[7]关于真空联合堆载预压的仿真分析,初始围压与初始竖向应力比值调整为K0(K0=0.45,三轴试验中该比值为0.6),以使模型初始状态与实际静止土压力状态一致。另外,PVD地基堆载加荷过程,多为单级或多级线性加荷,而非三轴试验中的阶梯型加载;因此,多工况仿真分析中,荷载由阶梯型施加修改为线性施加。
值得注意的是,三轴试验中,mini-PVD尺寸相较于土样直径较大,其排水固结效率较快。因此,径向排水三轴试验中加载速率不宜太小,以保障三轴试验保持与实际PVD地基较为接近的孔压增长和消散趋势。同时,由于土体压缩性较大,当荷载28.5 kPa (试样初始应力30 kPa,加载速率9.5 kPa/180 min)时其平均水平应变即可大于0.1,土体已达到或接近破坏状态,从变形角度而言应适当减小堆载以保障试验和仿真结果的合理性。最终,综合考虑土体固结特性和变形特性,拟定的多工况仿真方案如表2。
| Case | 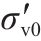 | ps/kPa | LR/(kPa∙min-1) | ph/kPa | 影响因素 |
|---|---|---|---|---|---|
| 1 | 30 | 10 | 10/60 | 1 | 初始有效应力(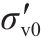 |
| 2 | 40 | 10 | 10/60 | 1 | |
| 3 | 50 | 10 | 10/60 | 1 | |
| 4 | 60 | 10 | 10/60 | 1 | |
| 5 | 30 | 4 | 10/60 | 1 | 竖向应力增量(ps) |
| 6 | 30 | 6 | 10/60 | 1 | |
| 7 | 30 | 8 | 10/60 | 1 | |
| 8 | 30 | 12 | 10/60 | 1 | |
| 9 | 30 | 14 | 10/60 | 1 | |
| 10 | 30 | 10 | 2/60 | 1 | 加载速率 (LR) |
| 11 | 30 | 10 | 5/60 | 1 | |
| 12 | 30 | 10 | 15/60 | 1 | |
| 13 | 30 | 10 | 20/60 | 1 | |
| 14 | 30 | 10 | 10/60 | 0 | 水平应力增量(ph) |
| 15 | 30 | 10 | 10/60 | 2 | |
| 16 | 30 | 10 | 10/60 | 3 | |
| 17 | 30 | 10 | 10/60 | 4 | |
| 18 | 30 | 10 | 10/60 | 5 |
2.2 主要影响因素对土体侧向变形的影响
2.2.1 竖向应力
图5为土体水平应变εh(土单元体平均直径改变量与初始直径的比值)随竖向应力增量ps的变化曲线。由图5可见,土体水平应变随竖向应力的增加呈非线性增长的规律变化;当ps较大时,荷载的微小增量即可引起土体水平应变的急剧增长;另外,水平应变随竖向加载缓慢增长与迅速增长之间具有较为明显转折点,图5所示工况中,该转折点约为10 kPa。因此,实际堆载预压工程中,当观测到侧向位移具有明显转折性增长时,或侧向位移增长速率明显增大时,应当减小堆载或放缓堆载速率,以确保地基在预压荷载下的稳定性。
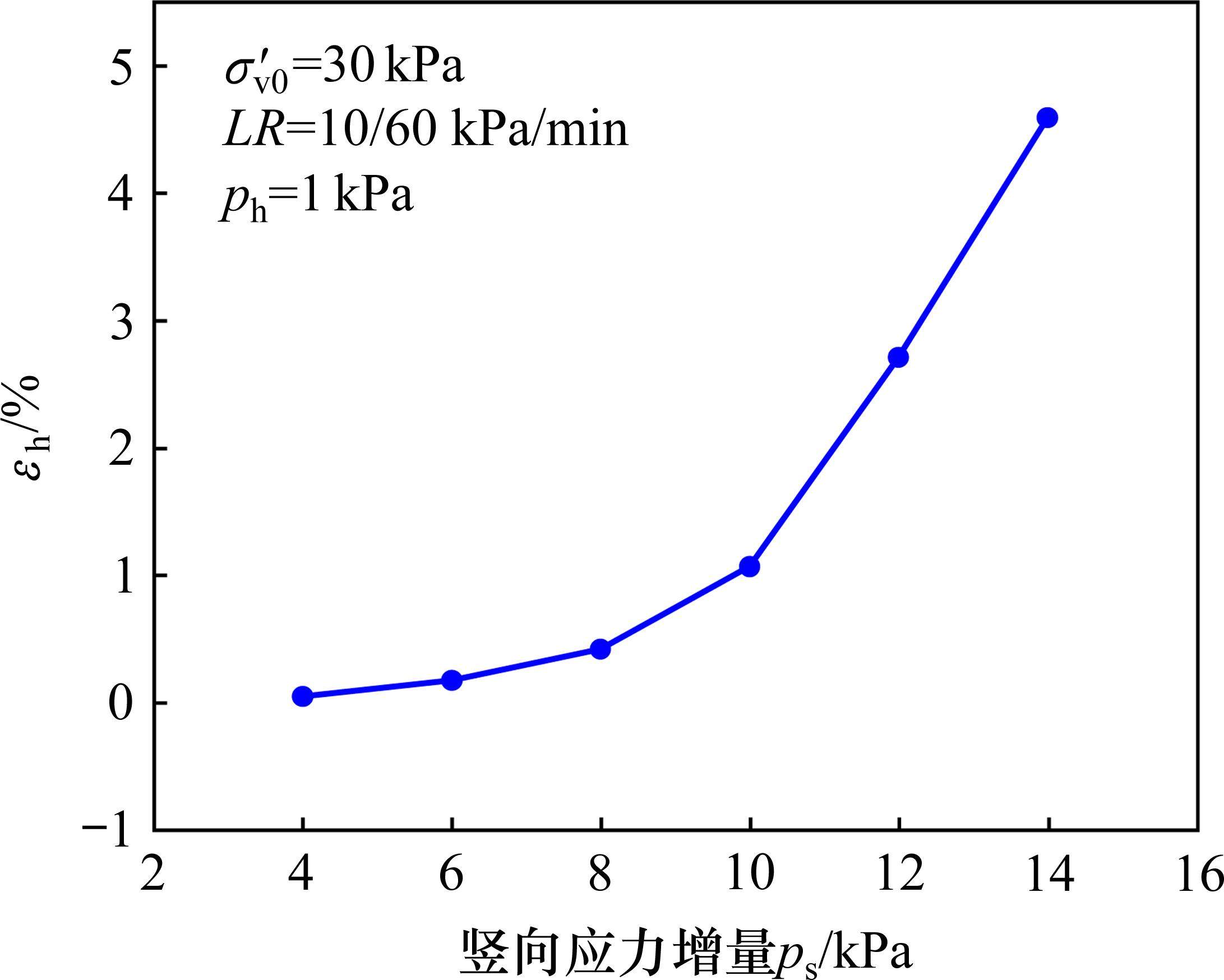
2.2.2 加载速率
图6为土体水平应变εh随加载速率LR的变化曲线。由图6可知,土体水平应变随加载速率增加而非线性增大,且当加载速率增大时,水平应变的增长率有所减缓。究其原因在于,加载速率改变对土体的直接作用为孔压增长的改变,加载速率越大,孔压增长越快且极值越大,而孔压的增长速率及极大值随着加载速率增大逐渐趋于某一较高水平,进而体现为变形随加载速率增大的增长率变缓,同时土体变形逐渐趋于某较大值或达到破坏水平。
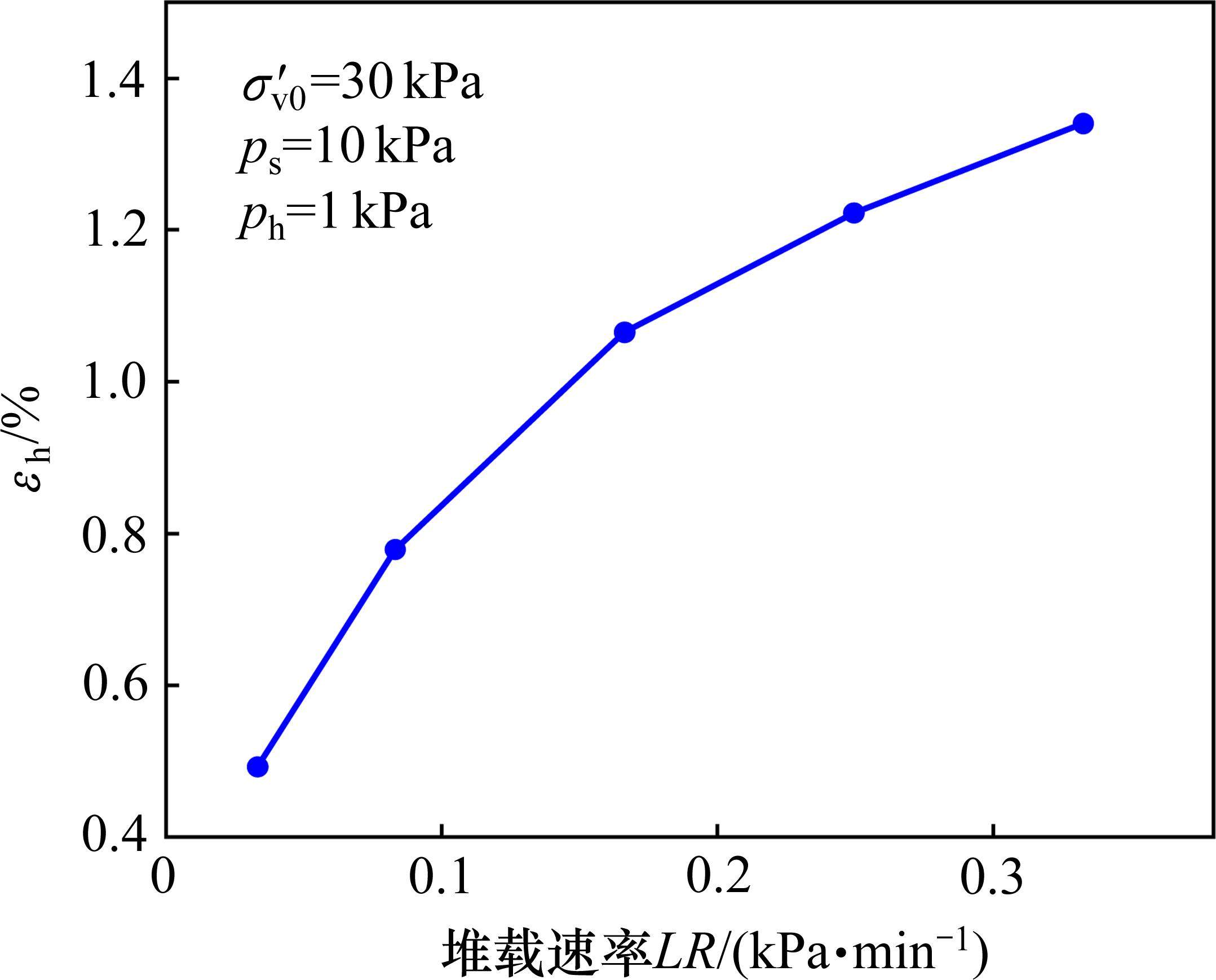
2.2.3 水平应力
图7为土体水平应变εh随水平应力增量ph的变化曲线。由图7可见,土体水平应力的增大可有效限制土体向外侧向变形的发展。由弹性理论可知,堆载预压产生的水平向附加应力与堆载大小比值在地基表层可达1.0。因此,分析堆载预压地基变形时,需要考虑综合水平向附加应力的影响。堆载预压下地基浅层分布有较大的水平向附加应力,这将一定程度约束地基向外的侧向变形,且随深度的增加,水平向附加应力对侧向变形的约束作用逐渐减弱,这亦符合堆载预压下PVD地基侧向变形在浅层随深度增加而逐渐增大的变形特性。而当地基深度增大到一定值时,地基中的竖向和水平向附加应力相较浅表层均明显减小,地基的变形则随之相应减小。因此,堆载预压下,PVD地基的侧向变形轮廓一般呈现典型的“弓”形分布。
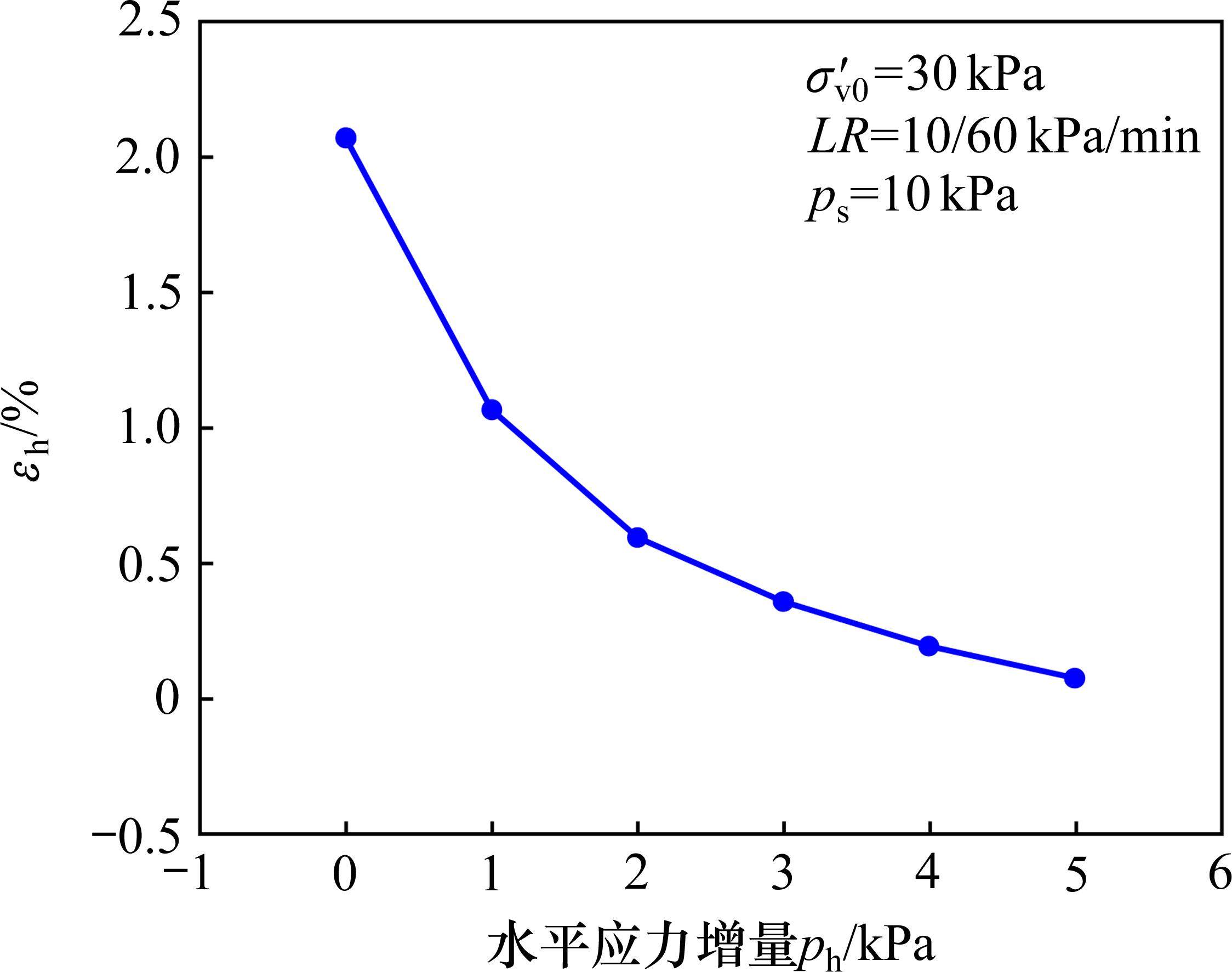
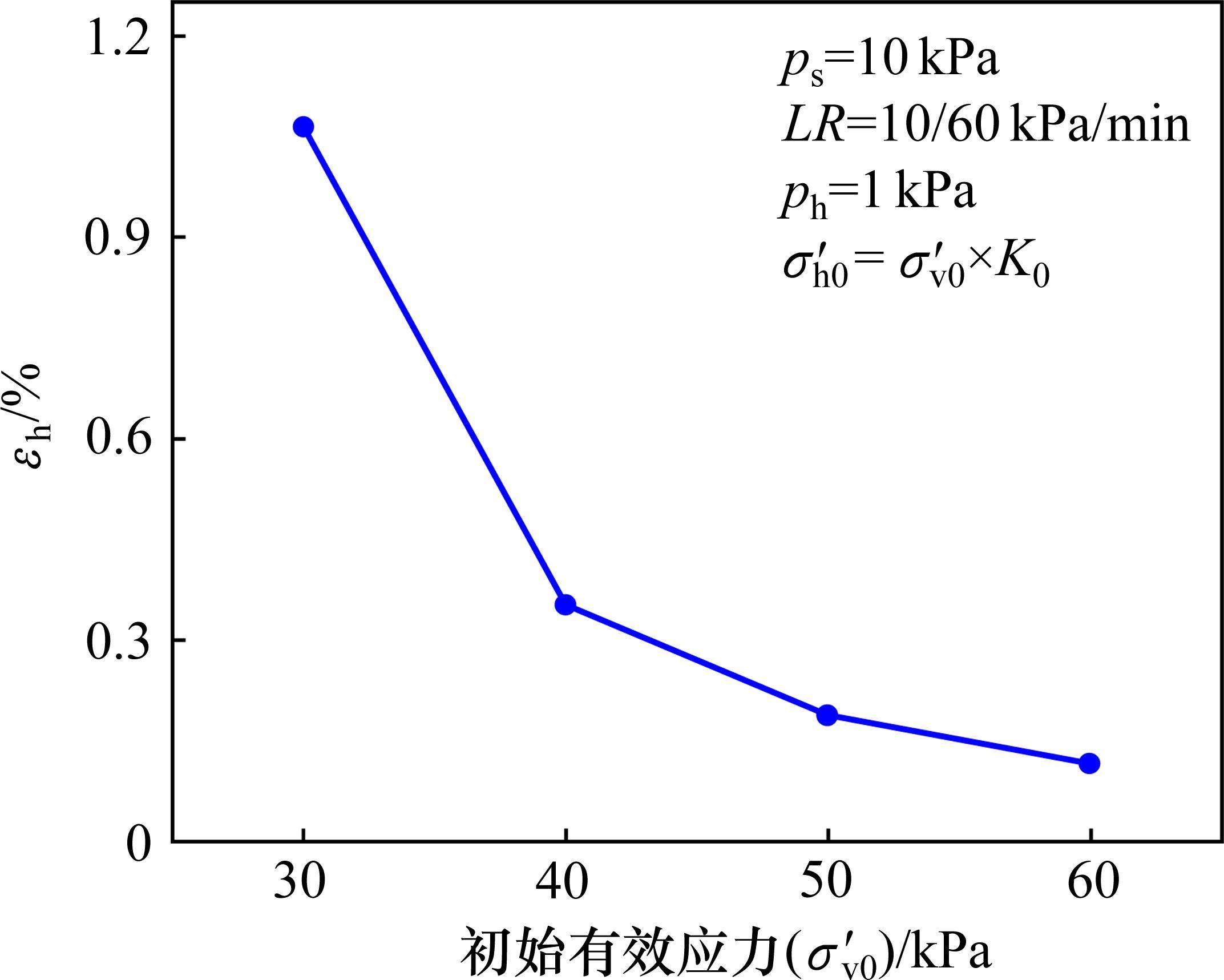
2.2.4 初始有效应力
图8为土体水平应变εh随初始有效应力(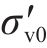
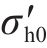
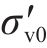
2.3 主要影响因素对土体应力状态的影响
如图9所示,土体水平有效应力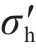
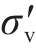
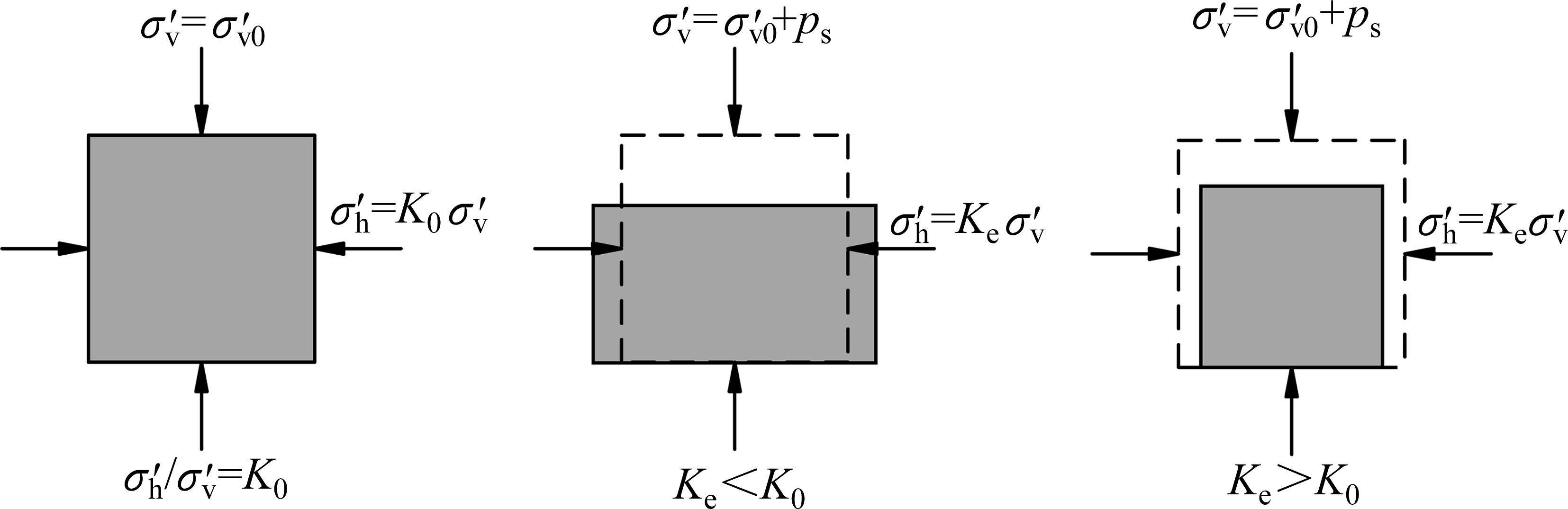
堆载预压过程中,土体应力比并非固定值,其值随超孔压的增长及消散而变化。为研究三轴试验中土体的应力比随各主要影响因素的变化关系,三轴及仿真分析中均取距离试样中心17 mm处作为超孔压ue的输出点,并按式(3)和式(4)计算土单元体的平均超孔压ua[23]。
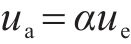
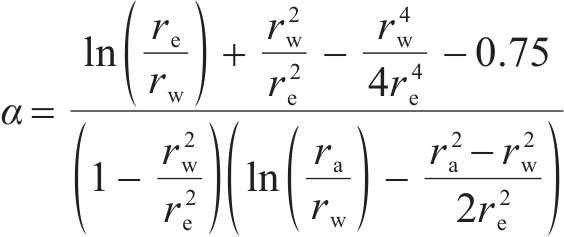
式中:ra为超孔压输出点所对应半径(本文为17 mm);rw为PVD等效半径;re为PVD影响范围半径。根据三轴试验相关尺寸参数,计算得α=1.011 8。
土体的竖向有效应力及水平有效应力则可分别按式(5)和式(6)进行计算。
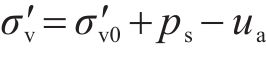
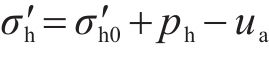
图10为某仿真工况输出的超孔压ue时程曲线,可见超孔压随堆载的施加逐渐增长,当堆载达到最大时超孔压亦达到最大,随后的预压固结阶段,超孔压则逐渐消散。图11为基于输出超孔压计算得到的堆载预压下土单元体应力比Ke的时程曲线。由图可见,加载阶段土体应力比Ke随堆载的增加由K0开始迅速减小,后续固结阶段则逐渐增大至一稳定值,且稳定时的应力比与静止土压力系数K0不同,其值与竖向附加应力及水平向附加应力有关。综合考虑Ke的变化过程,后续土单元体应力比分析中,选取土体固结阶段超孔压的中值点(图10中点a)所对应的应力比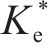
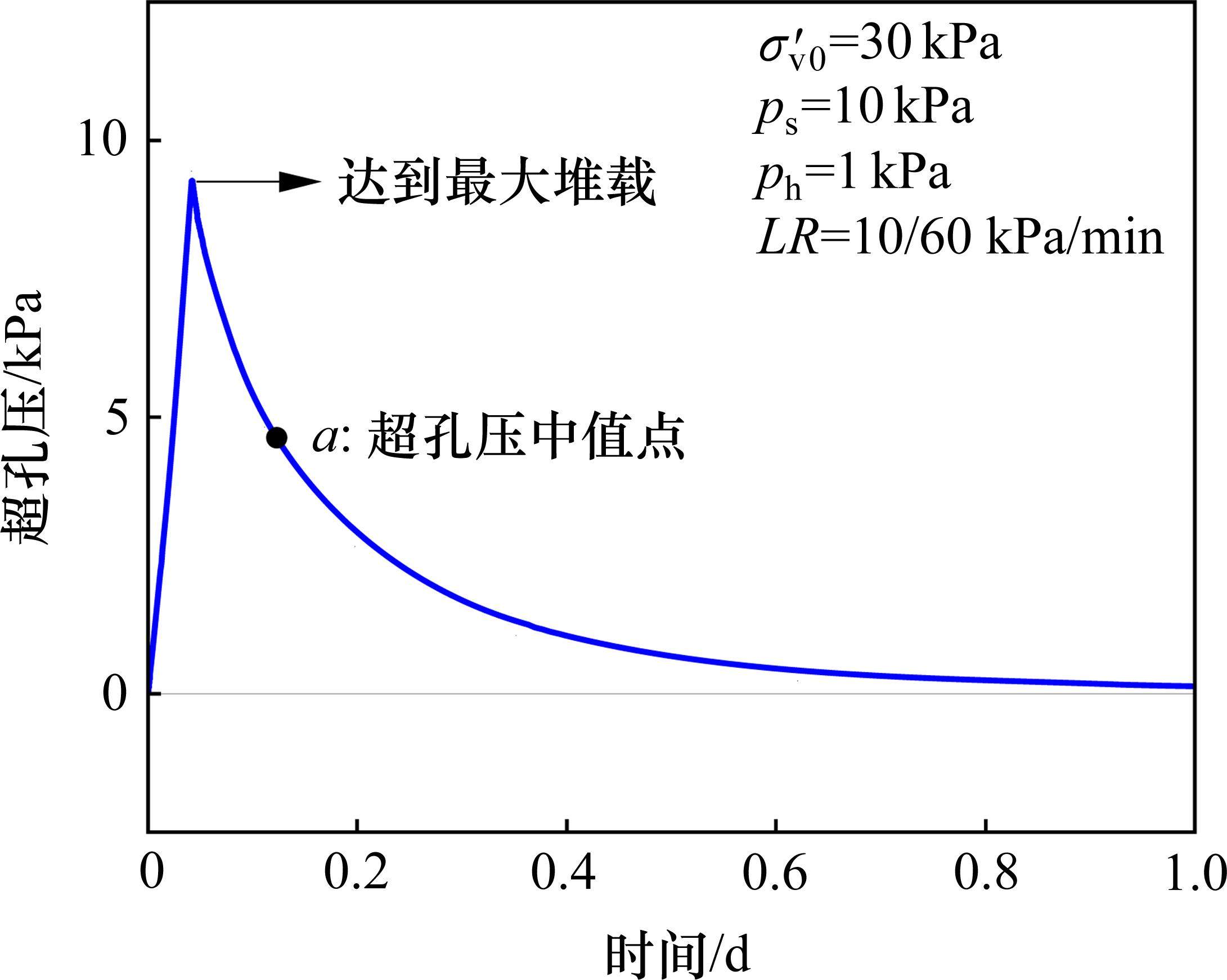
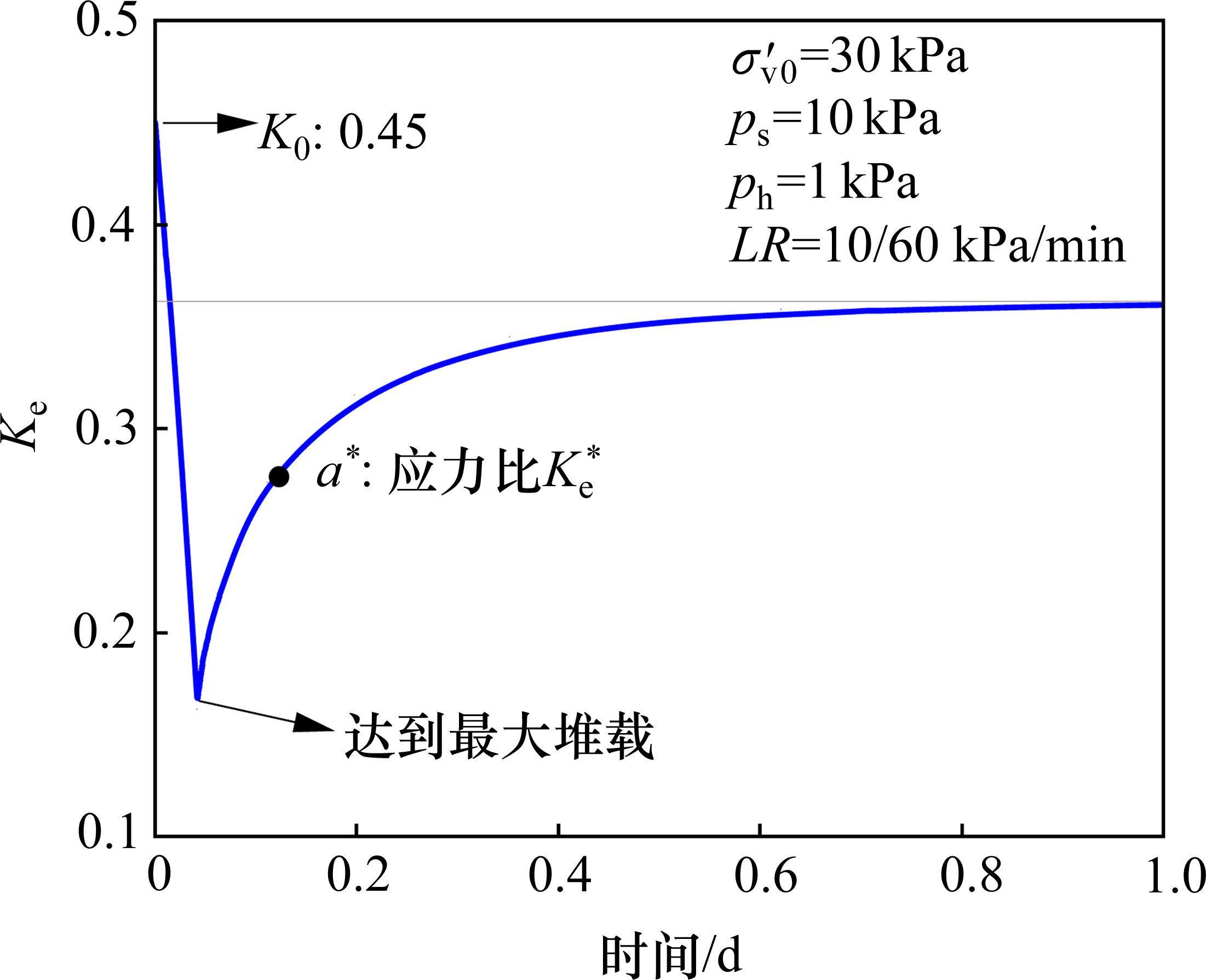
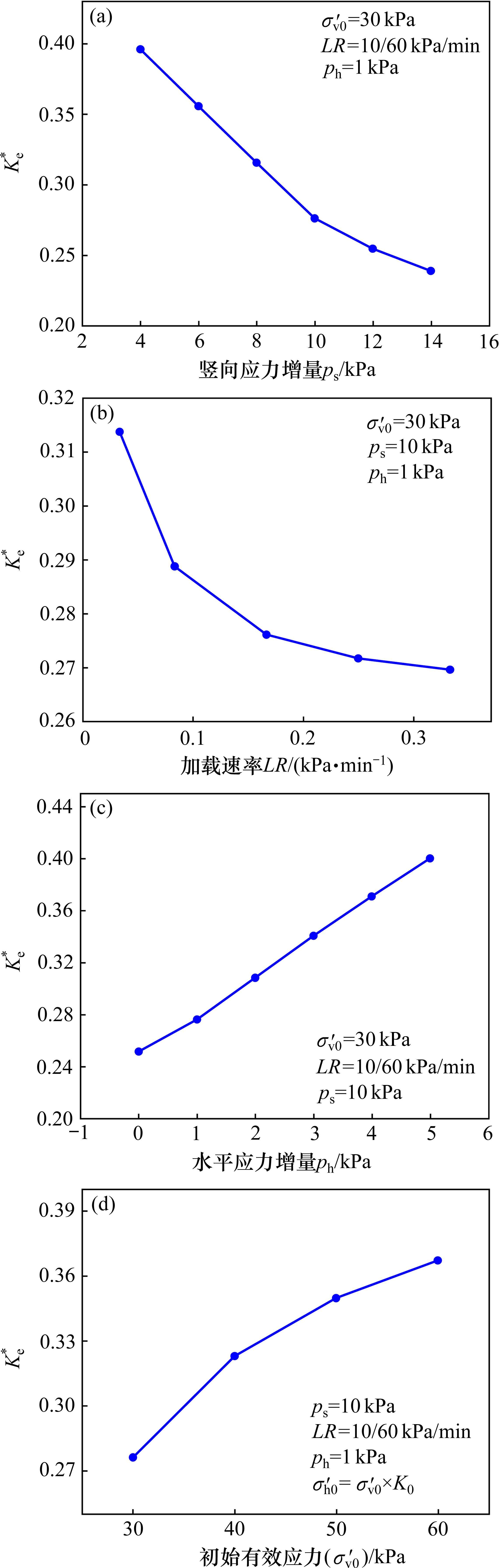
图12(a)~图12(d)分别为竖向应力、加载速率、水平应力及初始有效应力变化对土体应力比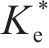
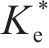
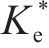
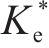
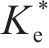
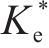
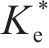
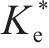
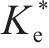
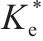
3 堆载预压下PVD地基的侧向变形预测方法
3.1 土体水平应变εh与应力比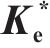
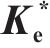
为系统研究不同条件下土体水平应变εh与应力比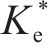
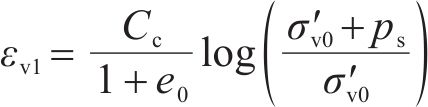
最终,根据多工况仿真计算结果,分析可得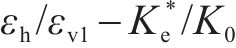
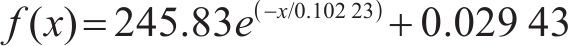
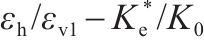
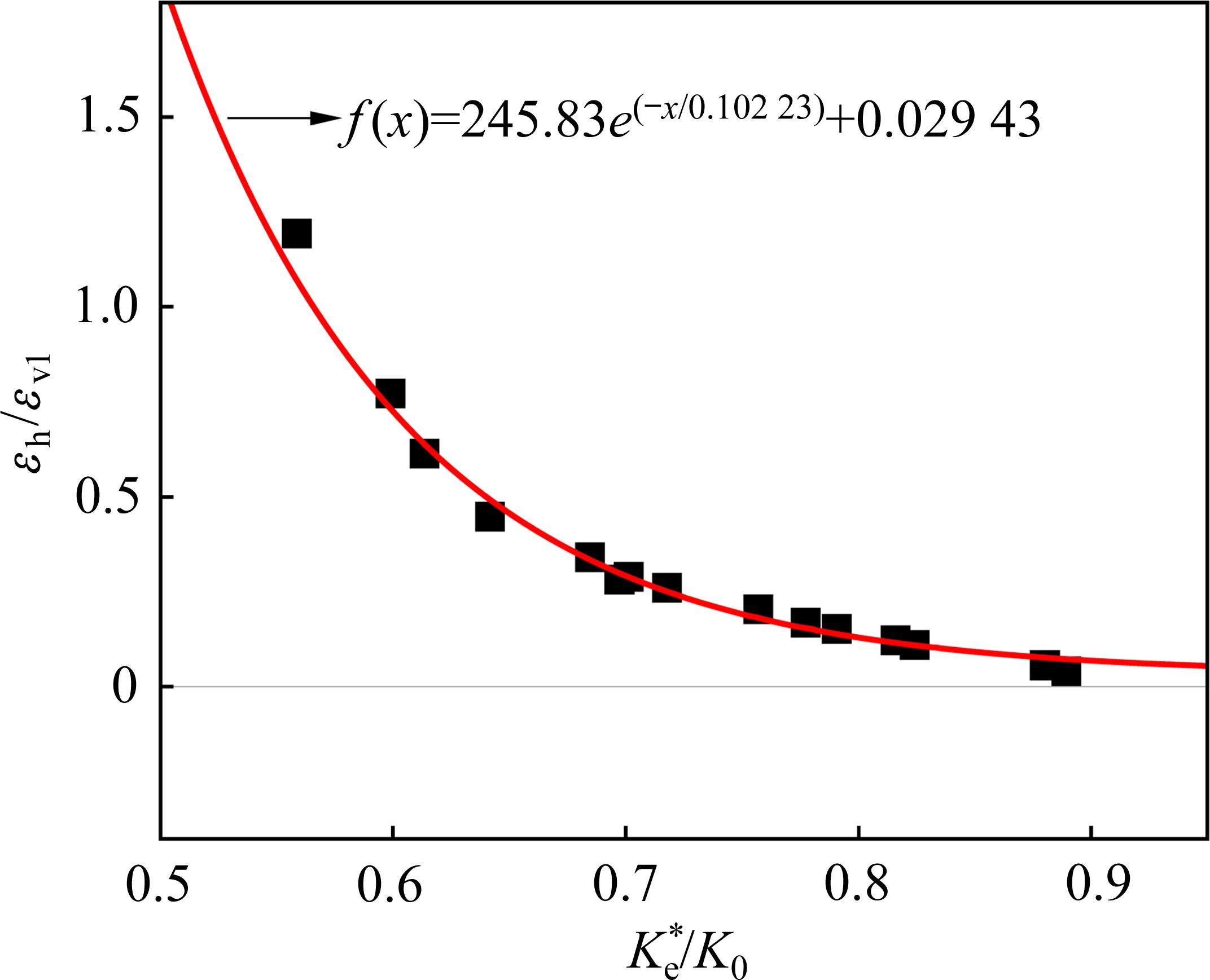
3.2 应力比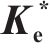
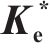
由应力比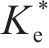
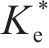
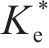
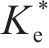
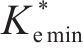
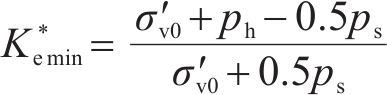
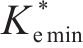
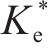
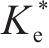
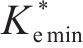
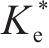
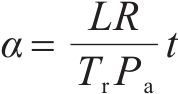
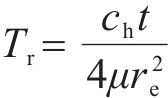
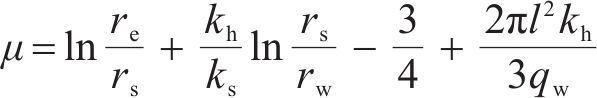
式中:Tr为径向固结的时间因子;pa为标准大气压强;t为时间;μ为考虑涂抹效应及井阻效应的无量纲因子;rs和ks分别为涂抹区半径及涂抹区渗透系数;l为PVD长度;qw为PVD排水能力。
由上述分析可知,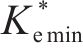
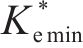
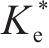
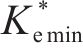
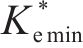
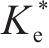
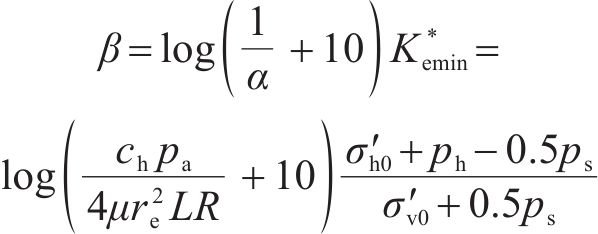
三轴试验中,虽然插入mini-PVD引起的机械涂抹效应及mini-PVD的井阻效应较小,可忽略不计,但土体单元的非均匀固结仍会引起等效涂抹效应[25]。对此,参考XU等[7]关于径向排水三轴试验中等效涂抹效应的考量,令rs/rw=2,可反算得kh/ks=7。经计算分析可得,β与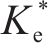
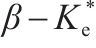
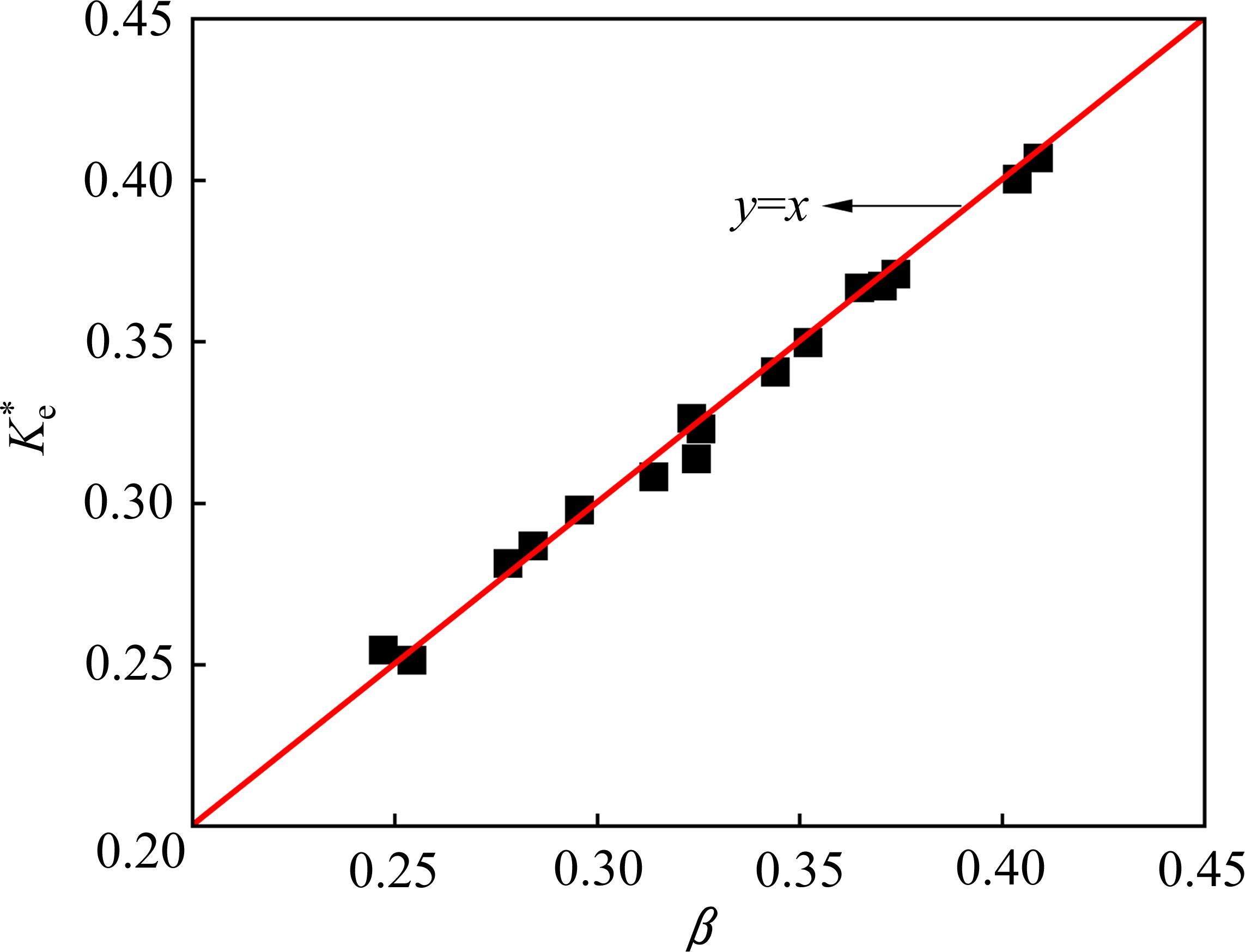
3.3 堆载预压下PVD地基侧向变形的计算步骤
基于所提出的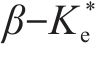
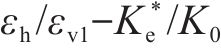
1) 由地勘资料及土体基本物理力学参数试验确定各土层初始有效应力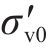
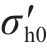
2) 根据Boussinesq解,计算堆载预压下地基内的竖向附加应力ps及水平向附加应力ph。竖向附加应力可取路堤中心线处进行计算[15],而水平附加应力分布形式与竖向应力有较大差异,其影响主要集中于地基浅层,同一深度下沿水平向变化较为明显(参见图4),综合考虑后,折中取距离路堤中心线1/8路堤底宽处水平附加应力值进行计算。
3) 由式(12)计算无量纲参数μ,再由式(13)计算综合影响因子β,按β与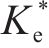
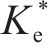
4) 由式(7)计算土体一维压缩应变εv1,再由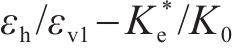
5) 根据水平应变按式(14)计算地基侧向变形。
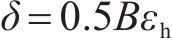
式中:δ为地基的侧向变形;B为预压区宽度。
值得注意的是,本文预测方法是基于三轴模型建立;因此,当该方法用于平面应变工况下时,计算所得水平应变应按式(15)进行修正。
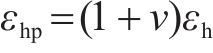
式中:ν为土体泊松比;εhp为平面应变条件下的水平应变。
4 工程应用
4.1 案例1
案例1位于杭嘉湖平原中部,郭庆海等[26-27]报道了该路堤工程相关数据。路堤和地层截面及参数如图15所示,图中,γt为土体重度,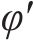
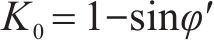
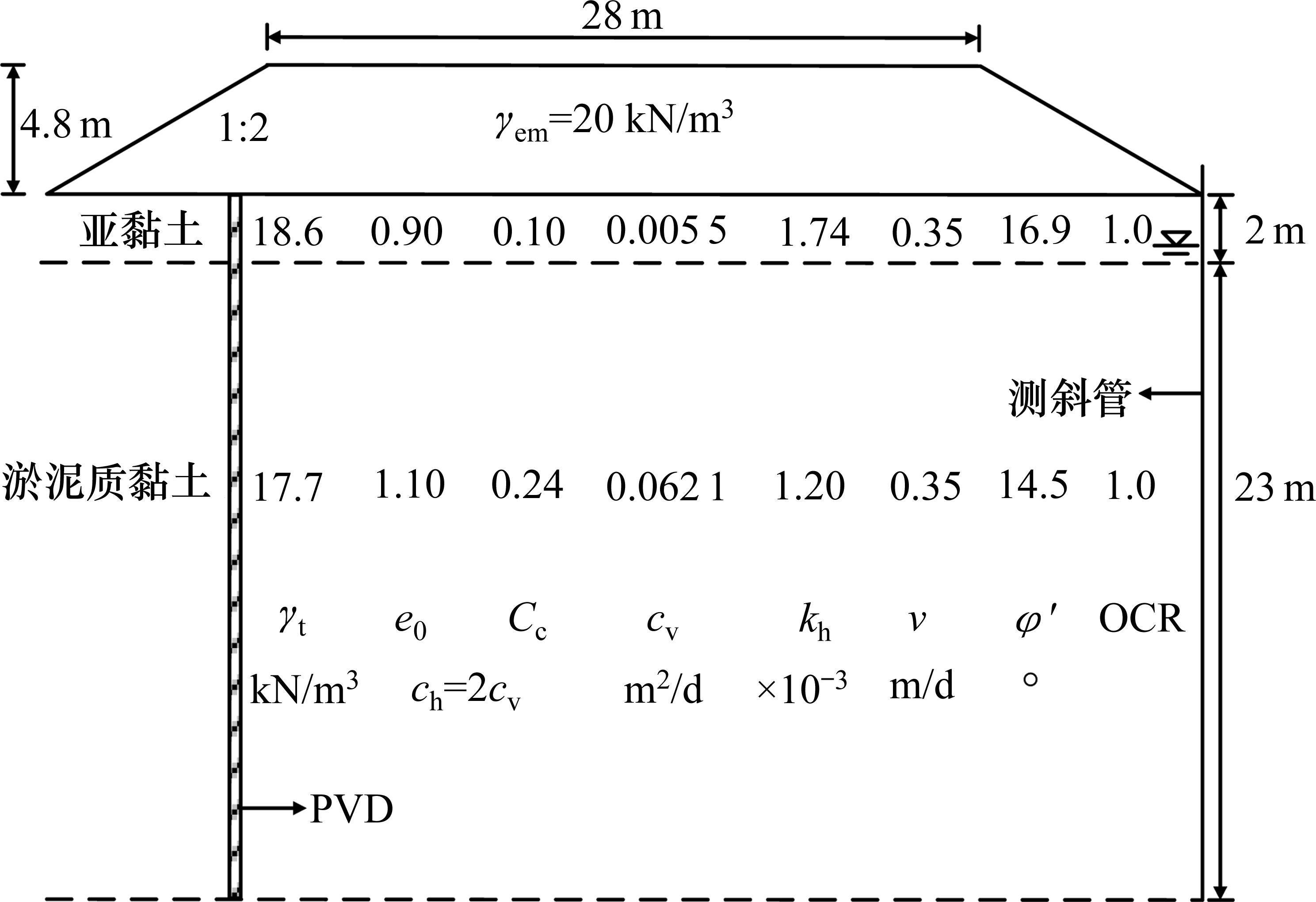
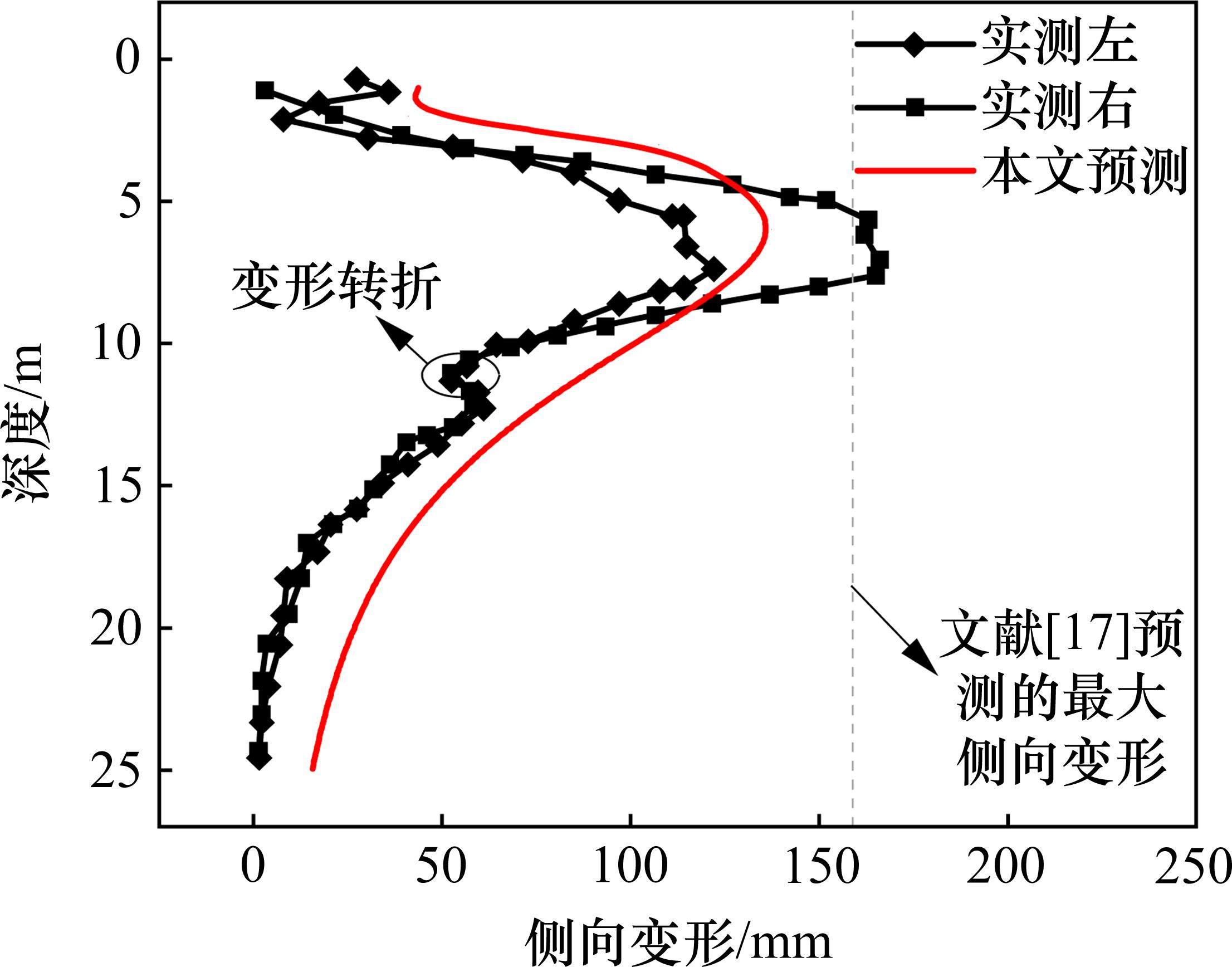
图16为案例1地基侧向变形预测轮廓与实测轮廓的对比结果,图中同时以虚线展示文献[17]方法预测所得的地基最大侧向变形。由图16可见,文献[17]仅能预测地基的最大侧向变形,其预测值较为接近路堤右侧的最大侧向变形实测值,而与路堤左侧实测值偏差较大。本文预测方法则可完整地预测地基的侧向变形轮廓,所得地基最大侧向变形接近于路堤左右两侧最大侧向变形均值,整体而言预测结果与实测数据较为吻合,地基最大侧向变形及侧向变形随深度的发展趋势与实测数据均较为一致。地基深层侧向变形预测结果略偏大则可能是地层参数单一所导致。实测数据表明,10 m深度左右地基侧向变形存在转折,一般而言这代表土层性质有所变化,而由报道数据无法更为准确确定土层性质如何改变,因此使用同一土层参数预测地基2~25 m的侧向变形,可能引起深层预测偏差。而地基表层预测结果偏大的原因可能有以下2点:一是填土路堤与地基表层间的相互作用可能影响地基表层的侧向变形,但本文预测方法暂未能全面兼顾该相互作用的影响;二是表层亚黏土为硬壳层,现有数据可能仍低估了其强度和刚度性质。
4.2 案例2
案例2是位于杭州湾南岸的某路堤工程,CHAI等[28-29]报道了相关工程细节。路堤顶宽26 m,高5.88 m,边坡坡率1∶1.5,砂垫层及路堤填土重度约20 kN/m3,最终堆载约117.6 kPa,填筑至设计高度用时257 d,平均堆载速率约0.46 kPa/d,路堤具体截面及土层参数如图17所示。塑料排水板呈梅花型布置,布置间距1.5 m,插设深度19 m,排水板等效直径dw=0.053 m,涂抹区直径ds=0.355 m,PVD影响范围直径de=1.575 m,涂抹区与非涂抹区渗透系数之比为1/13.8,排水板排水能力qw=100 m3/year。由于相关文献并未报道土体的有效内摩擦角,因此,基于弹性力学理论,根据土体泊松比按K0=ν/(1-ν)估算土体的静止土压力系数[22]。

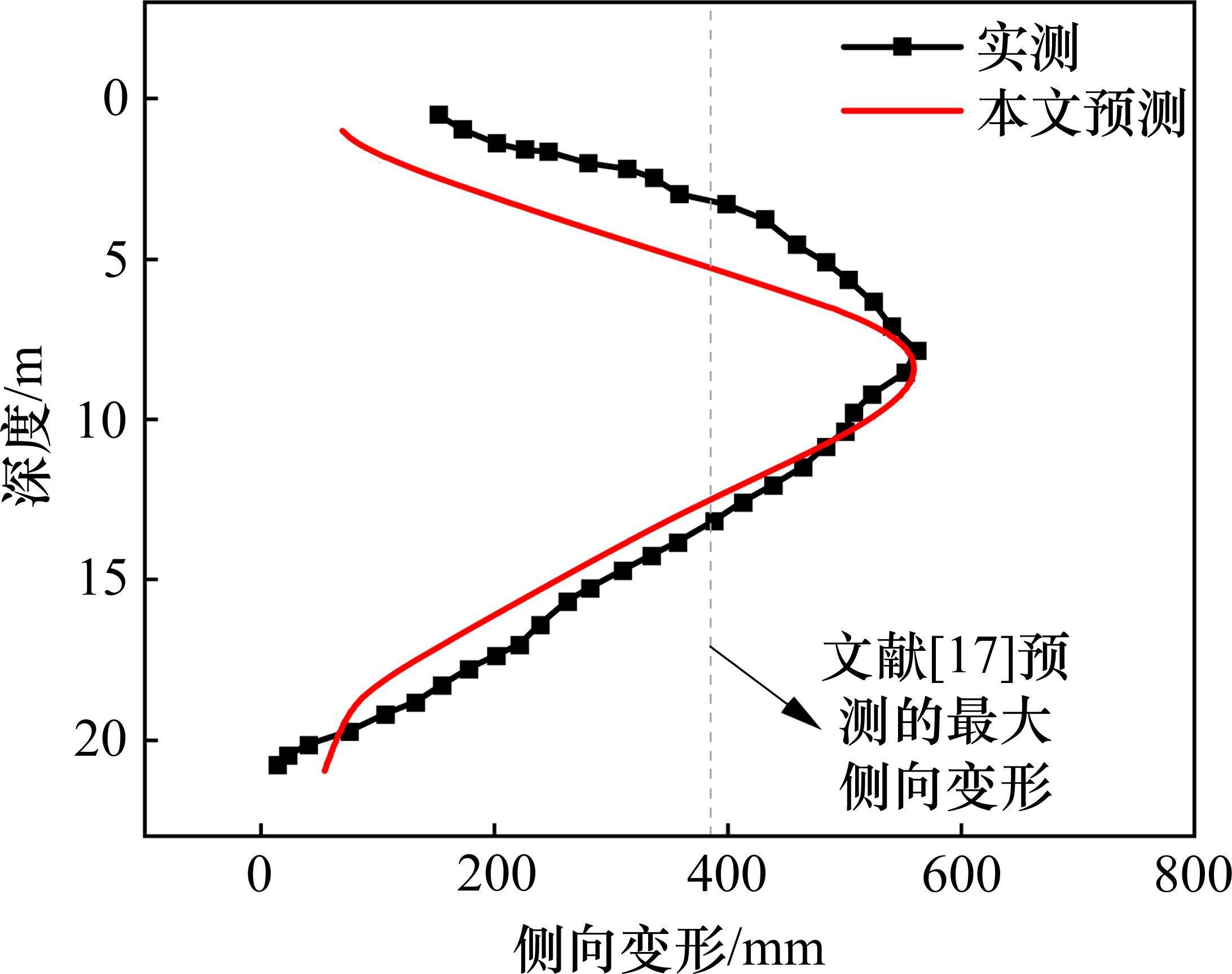
图18为案例2地基侧向变形预测轮廓与实测轮廓的对比结果,图中虚线为文献[17]方法预测所得的地基最大侧向变形。由图18可见,相较于文献[17]方法预测结果,本文方法所得最大侧向变形更为接近实测值,且本文方法预测所得PVD地基侧向轮廓与实测结果较为一致。浅层预测结果相较实测偏小的可能原因是:本文预测方法暂未考虑机械、施工等荷载的影响,然而堆载预压期间,若施工荷载(如大型施工机械、临时堆土等)存在较大扰动,可能引起浅层土体侧向变形偏大。
5 结论
1) 增加堆载及堆载速率会使土体应力比减小,并引起土体的向外侧向变形非线性增大,而增加水平应力和初始有效应力则可使土体应力比增大,并有效抑制土体向外的侧向变形。
2) 堆载预压下,水平附加应力对地基侧向变形的影响不容忽视,土体水平和竖向附加应力的共同作用,使得PVD地基侧向变形沿深度呈先增加后减小的变形特性。
3) 基于仿真分析结果,引入土体一维压缩应变εv1及静止土压力系数K0,建立了归一化的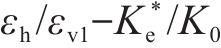
4) 考虑堆载预压的加载因素、土体初始应力状态及固结特性,提出综合影响因子β,并分析获得了β与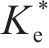
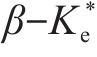
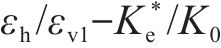
5) 将所提出的侧向变形预测方法用于分析2个实际工程案例,均取得了较好的预测结果,说明该方法可较为有效地预测堆载预压下PVD地基的侧向变形轮廓。
徐方,吴其长,门小雄等.堆载预压下塑料排水板地基的侧向变形预测方法[J].铁道科学与工程学报,2025,22(01):416-428.
XU Fang,WU Qichang,MENG Xiaoxiong,et al.Prediction method for lateral deformation of prefabricated vertical drains improved ground under surcharge preloading[J].Journal of Railway Science and Engineering,2025,22(01):416-428.