机匣结构是航空发动机的重要组成部分,它支承转子,固定静子叶片及附件,构成气流通道和传递发动机推力[1-3]。航空发动机每一级机匣主要由机匣壳体和法兰边组成,通过螺栓结合部可将各级机匣的法兰边连在一起形成完整的机匣连接结构。由于机匣受力极为复杂[4-6],必须对机匣连接结构合理设计才能保证其优越的动力学性能,尤其要充分考虑法兰边上螺栓结合部的影响。而要实现上述目标,需要在考虑螺栓力学特性的基础上研究机匣连接结构的动力学建模方法。
当前对机匣连接结构动力学建模已有一些研究,例如,MIR-HAIDARI等[7-8]建立了航空发动机机匣组件的有限元模型,进行了前、后压气机机匣的动力学分析,并通过试验验证了模型的有效性和准确性。SCHWINGSHACKL等[9]基于ANSYS软件建立了机匣模拟件的有限元模型,分析了机匣结构的动力学特性。HUANG等[10]建立了由高压压气机机匣、静子支撑结构和燃烧室机匣组成的机匣连接结构有限元模型,对其固有特性进行了分析,并通过试验验证了模型的合理性。目前,对于航空发动机机匣这类复杂结构,有限元法是最主要的研究方法。但是,在当前的研究中并未充分考虑各级机匣之间的螺栓结合部力学特性,这将影响机匣连接结构动力学建模与分析的精度。
合理地引入机匣法兰边上各螺栓结合部的力学特性,才能创建准确预估机匣连接结构动力学特性的分析模型。当前,对螺栓结合部的力学建模的研究可以大致分为实体模型及简化模型。例如,孙伟等[11]建立了基于三维实体单元的螺栓结合部有限元模型,预测了螺栓结合部的静态迟滞特性,并为辨识其刚度及阻尼提供了方法。ASKRI等[12]在给定轴向预载荷、摩擦因数的情况下创建了螺栓结合部的实体单元模型,分析了结合部的等效刚度。上述基于实体模型的螺栓结合部建模,计算工作量通常较大(尤其是用于动力学分析时),因而,一些学者为了提高计算效率提出了简化的螺栓结合部模拟方法。EKH等[13]采用梁单元和连接件的节点对螺栓结合部进行建模,并通过试验结果证明了模型的合理性。GRAY等[14]建立了由梁单元耦合到刚性接触面的螺栓结合部模型,刚性表面表示螺栓的接触面,同样通过试验验证了模型的合理性。蒋国庆等[15]采用若干个弹簧阻尼单元模拟单个螺栓结合部,并对上述参数进行了辨识。JALALI等[16]用3个方向弹簧单元模拟螺栓结合部,用弹簧刚度表示预紧力,分析了不同预紧力下螺栓连接梁的振动特性。ZHANG等[17]在ABAQUS软件中建立了基于虚拟材料的螺栓结合部模型,分析了接触参数对螺栓结合部动态响应的影响。LIU等[18]采用虚拟材料模型对螺栓结合部进行了模拟,研究了不同激励水平下螺栓薄板的振动特性。上述研究主要侧重于螺栓结合部的力学建模,并未将其引入形如机匣连接结构这样复杂的结构中,因而包含螺栓结合部力学特性复杂结构动力学建模还应进一步深入研究。
本文以两级机匣连接结构模拟件为对象,在考虑螺栓力学特性的基础上,描述了采用ANSYS软件对其进行有限元建模的方法。分别采用实体单元、刚性耦合的梁单元、弹簧单元、虚拟材料4种方式模拟机匣法兰边上螺栓结合部并给出了其引入机匣连接结构的方式;然后进行实例研究,用包含不同螺栓结合部模型的两级机匣连接结构有限元模型求解固有频率及模态振型,并用试验证明上述建模的合理性;最后对比分析对应不同螺栓结合部模型的两级机匣连接结构动力学分析精度及计算效率。相关结果可为实际机匣连接结构建模及动力学分析提供参考。
1 机匣连接结构模拟件有限元建模
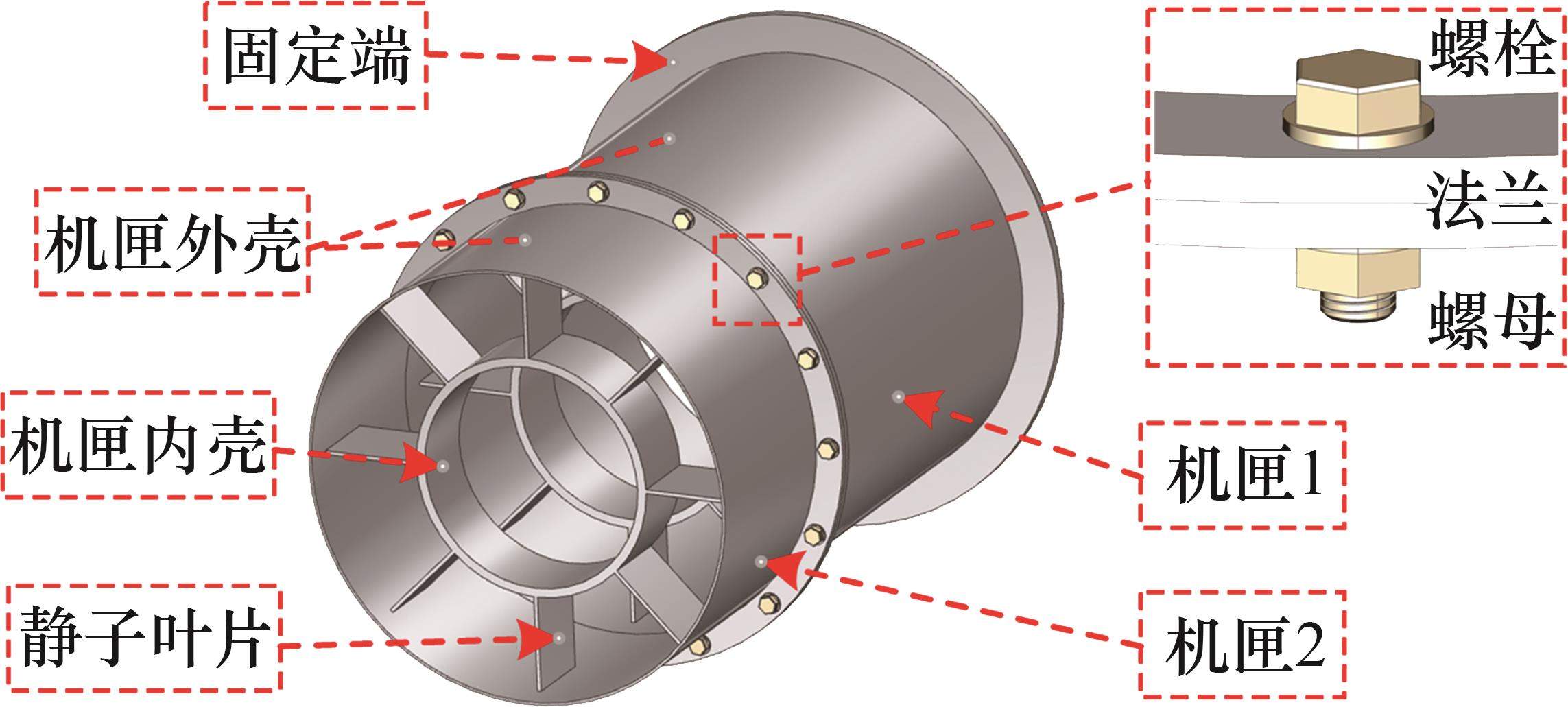
实际机匣包括外机匣、叶片以及与叶片相连接的内机匣等构件。包含上述特征的两级机匣连接结构模拟件如图1所示。为了便于描述,将外机匣命名为机匣外壳(包含法兰边),与叶片相连接的内机匣等结构命名为机匣内壳,两者之间为静子叶片。该两级机匣连接结构的有限元建模方法包括机匣内、外壳的模拟、静子叶片的模拟以及法兰边上螺栓结合部的模拟。
1.1 机匣内、外壳模拟
机匣内、外壳是构成机匣结构的主要部分,承担着支撑和传递力作用。为了较精确地模拟机匣内、外壳的力学特性,采用三维实体单元建模,如选用SOLID185单元,同时为了提高求解精度,打开SOLID185单元非协调开关选项。后续静子叶片有限元建模是也采用相同的三维实体单元。
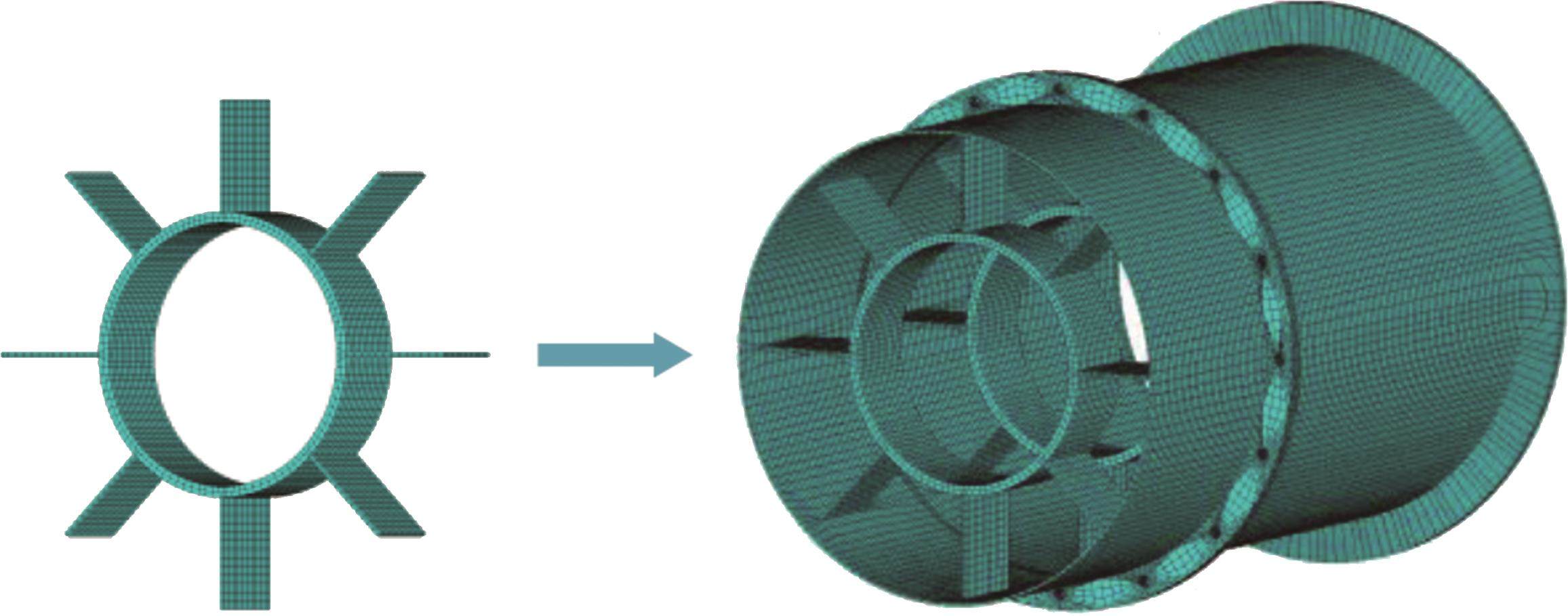
采用拉伸圆环成体的方法对机匣内、外壳进行几何建模,如图2所示。首先,拉伸出机匣外壳的薄壁圆筒以及法兰边,并采用体搭接的命令去掉多余生成的体;然后,在两个机匣连接处的法兰边上建立螺栓孔(由于机匣固定端法兰边上螺栓数量较连接处多,且本文着重考虑连接处螺栓结合部建模方式对分析结果的影响,因而,这里忽略固定端法兰边上的螺栓孔的建模);最后,在外壳里面拉伸出机匣内壳结构。
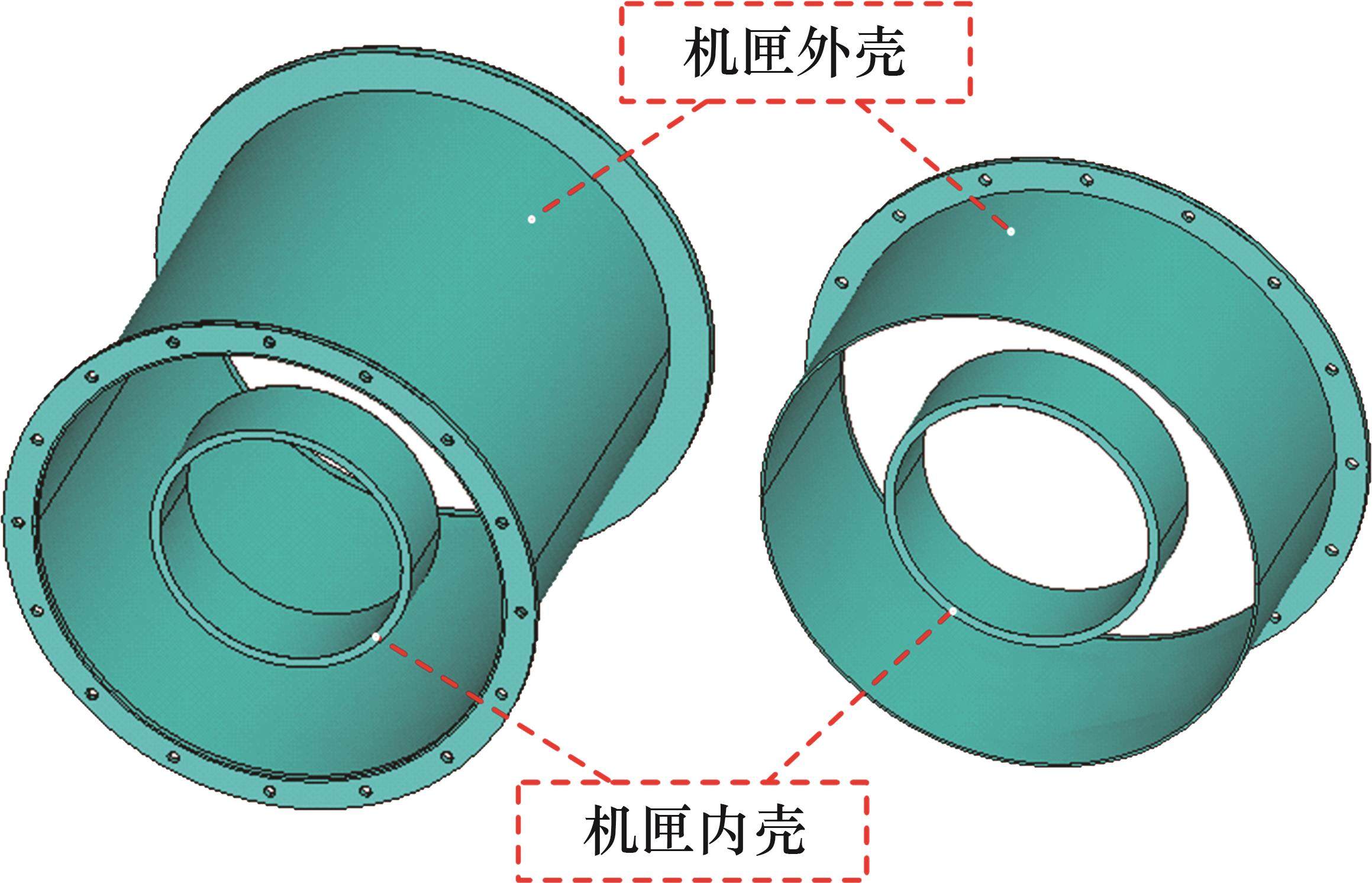
由于连接处法兰边上存在螺栓孔结构,且螺栓孔附近应力较集中,因而,在对机匣内、外壳进行分网时,需要精细化处理螺栓孔区域的网格。可将螺栓孔位置均匀切分,进一步划分形成闪射状的体扫掠网格,如图3所示。进行分网的命令为“VSWEEP”。
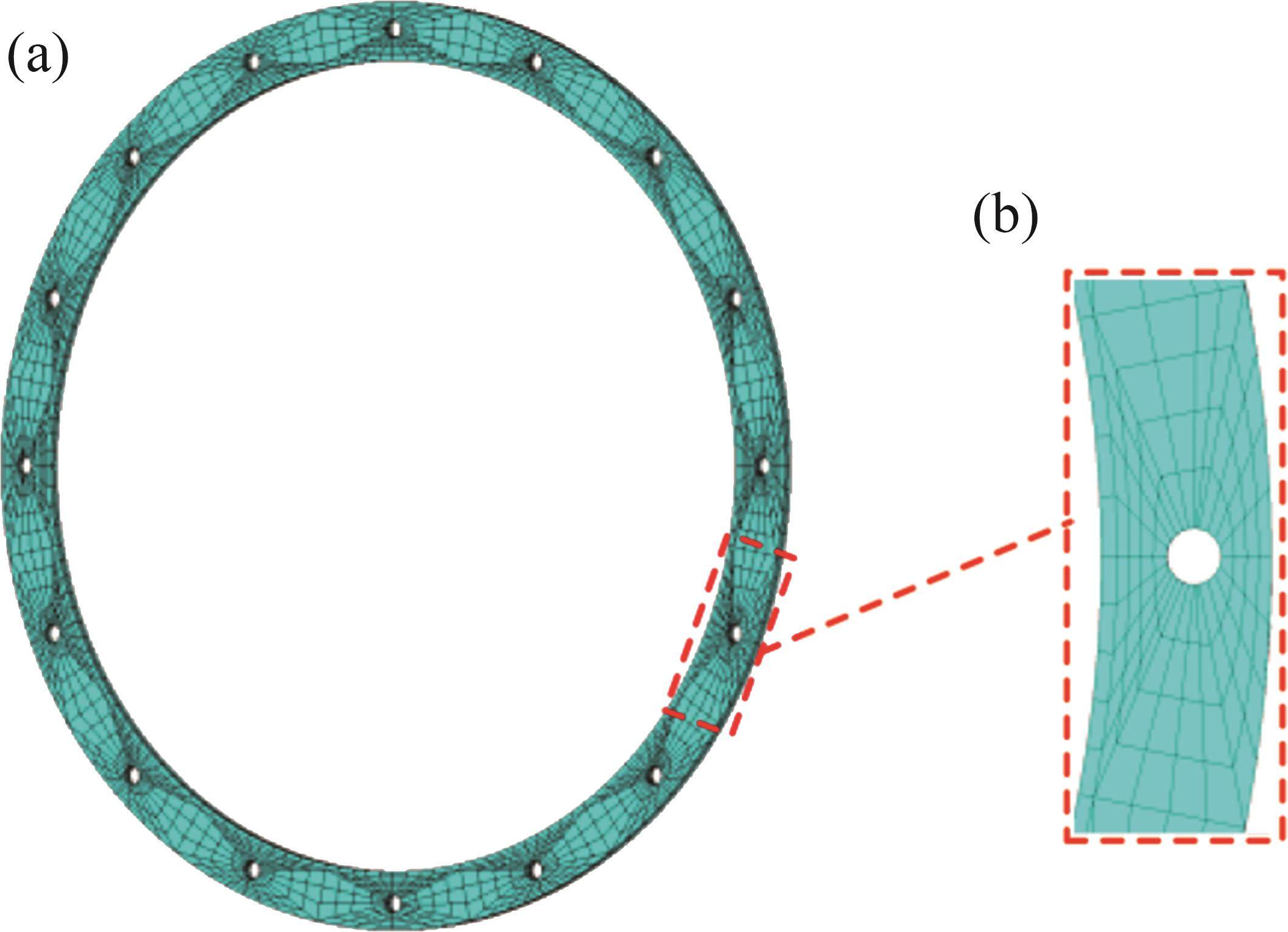
1.2 静子叶片模拟
静子叶片是构成机匣连接结构的重要部分,负责连接机匣内、外壳,对转子叶片压缩过来的气流进行整流和扩压,同样也承担着支撑和传递力作用。静子叶片结构沿周向方向是均匀分布的,因此,在ANSYS软件中进行几何建模时,只需要建立1个叶片,其余叶片均可通过复制得到,具体生成过程见图4。首先,在机匣内壳圆周面上绘制叶片的拉伸线,并在线的一端绘制叶片截面;接着,将叶片截面沿拉伸线生成叶片实体;最后,采用VGEN命令将单个叶片沿圆周方向复制N次,生成全部的叶片。
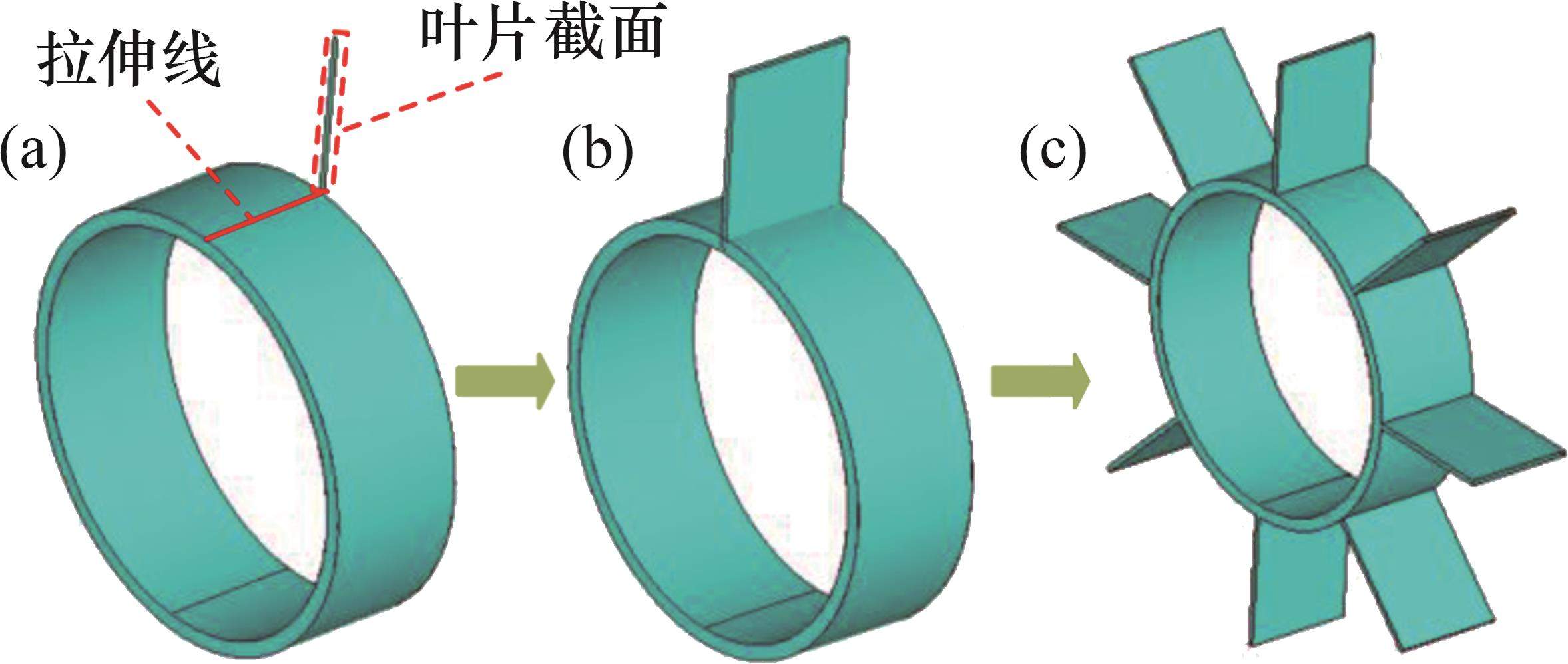
在生成全部叶片后,还需将叶片与机匣内、外壳进行合并才能模拟叶片与机匣内、外壳同时产生的形变,且变形谐调。进行叶片与机匣内、外壳合并的命令为“AADD”和“VADD”。
合并后,静子叶片与机匣内、外壳形成一个相对完整结构。由于机匣结构复杂,对不同部位的网格尺寸要求不同,因此,在实际分网时,需对机匣内、外壳和静子叶片3个部分进行独立分网。此外,可以考虑先对静子叶片进行扫掠分网,再对内、外壳进行分网,使得网格划分比较清晰、整齐,具体过程如图5所示。
1.3 螺栓结合部模拟
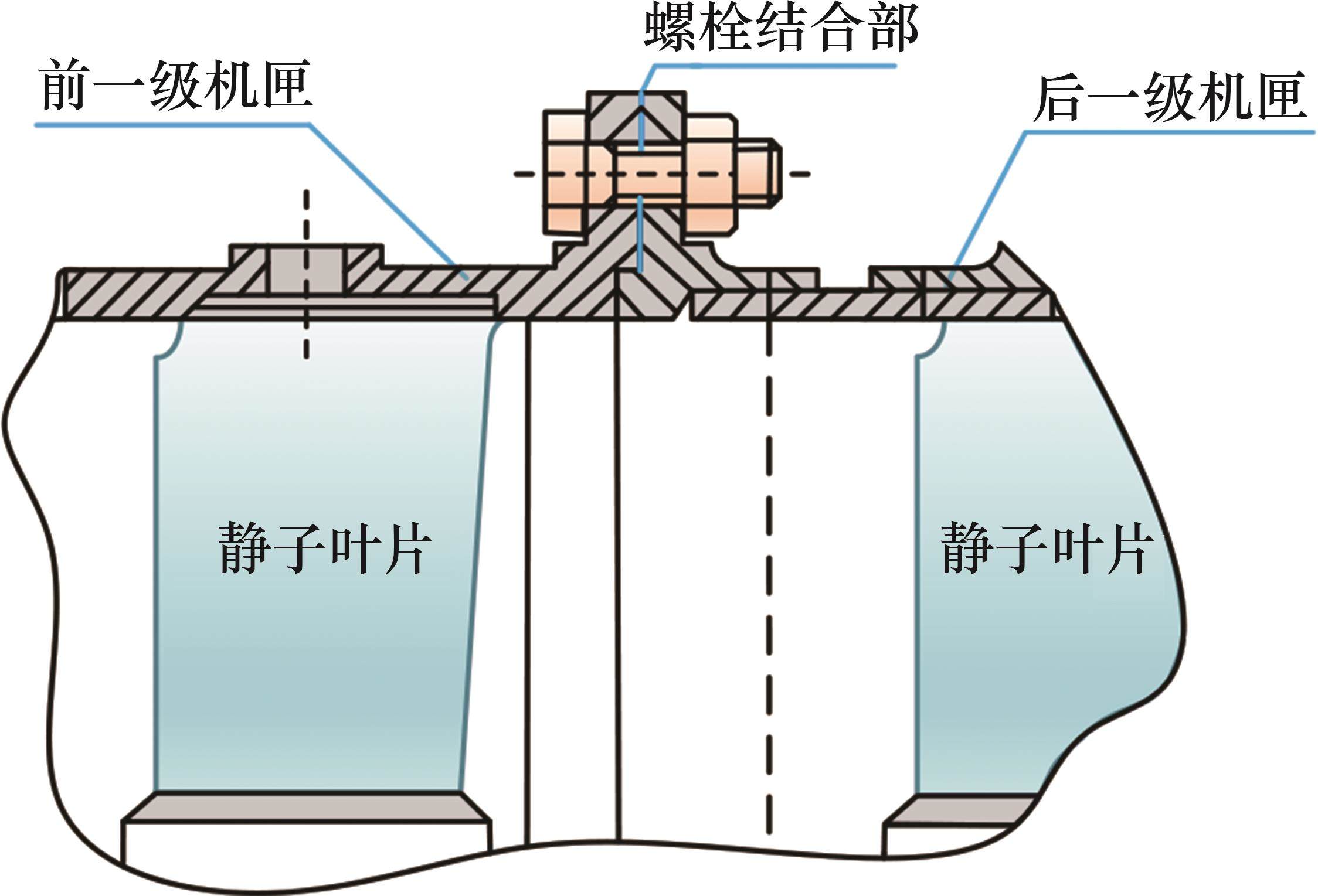
图6所示为典型的机匣螺栓-法兰连接的真实结构,前后两级机匣通过法兰边上的螺栓进行连接。为完成有限元建模,还需要对螺栓结合部的力学特性进行模拟。分别采用实体单元、刚性耦合的梁单元、弹簧单元、虚拟材料4种方式模拟机匣法兰边上螺栓结合部并给出其引入机匣连接结构的方式。
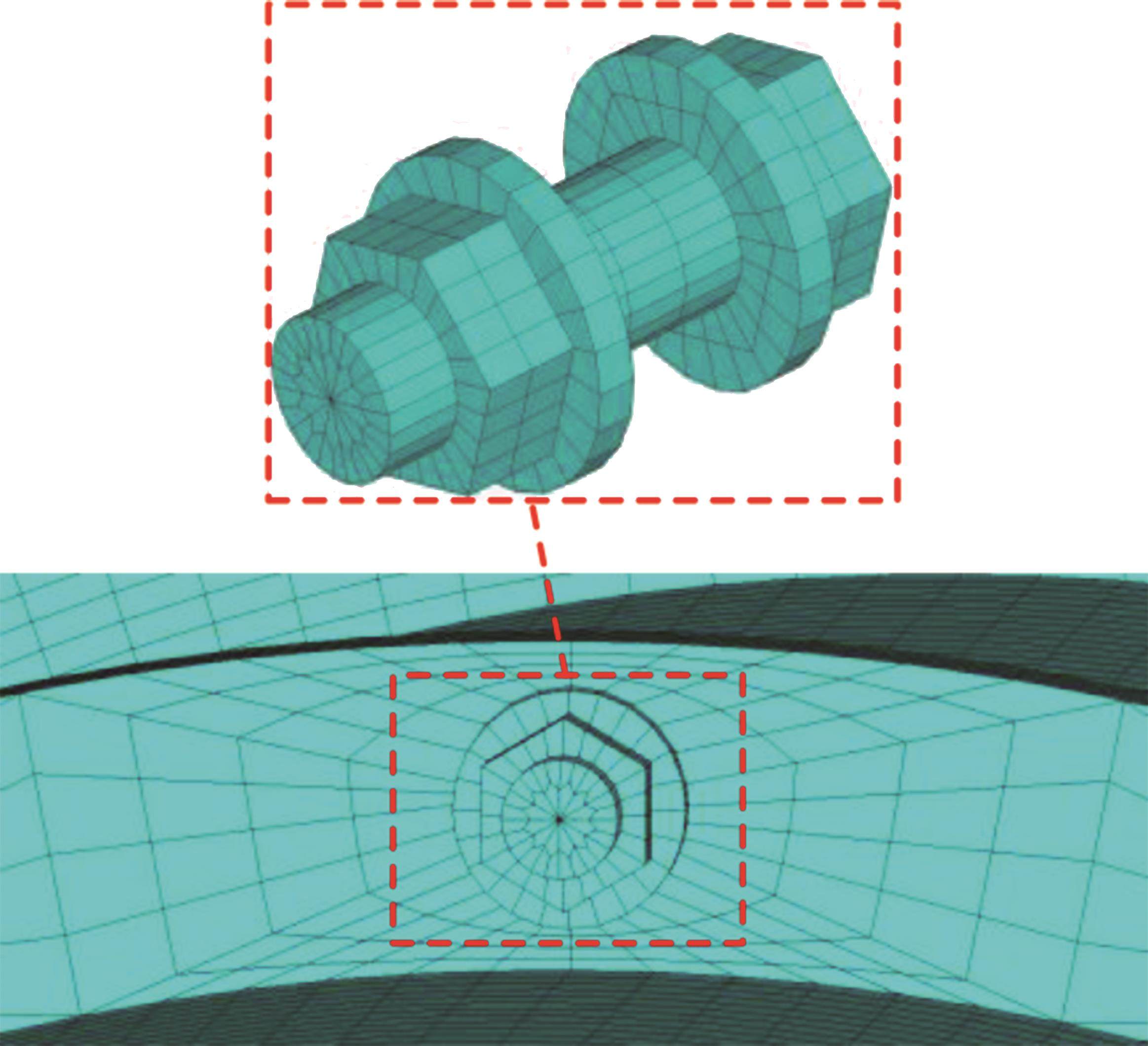
1.3.1 实体单元模型
用实体单元模型模拟螺栓结合部需考虑螺杆和螺母等螺栓特征,并且在连接界面之间建立接触单元。螺栓结合部实体单元模型如图7所示。将每个螺栓(包括螺栓、垫圈和螺母)建成一个整体几何模型,以便在计算过程中减少接触个数。进一步,采用SOLID185三维实体单元对螺栓整体几何模型进行映射网格划分,每隔30°切分1次,划分成六面体网格,从而更好地模拟螺栓预紧力对结构的影响。
利用PRETS179预紧单元,模拟每个螺栓上施加的预紧力,螺栓预紧力模拟方法如图8所示,在螺栓杆中某一轴向位置处形成一个预紧的截面,并通过命令“SLOAD”设置预紧力。
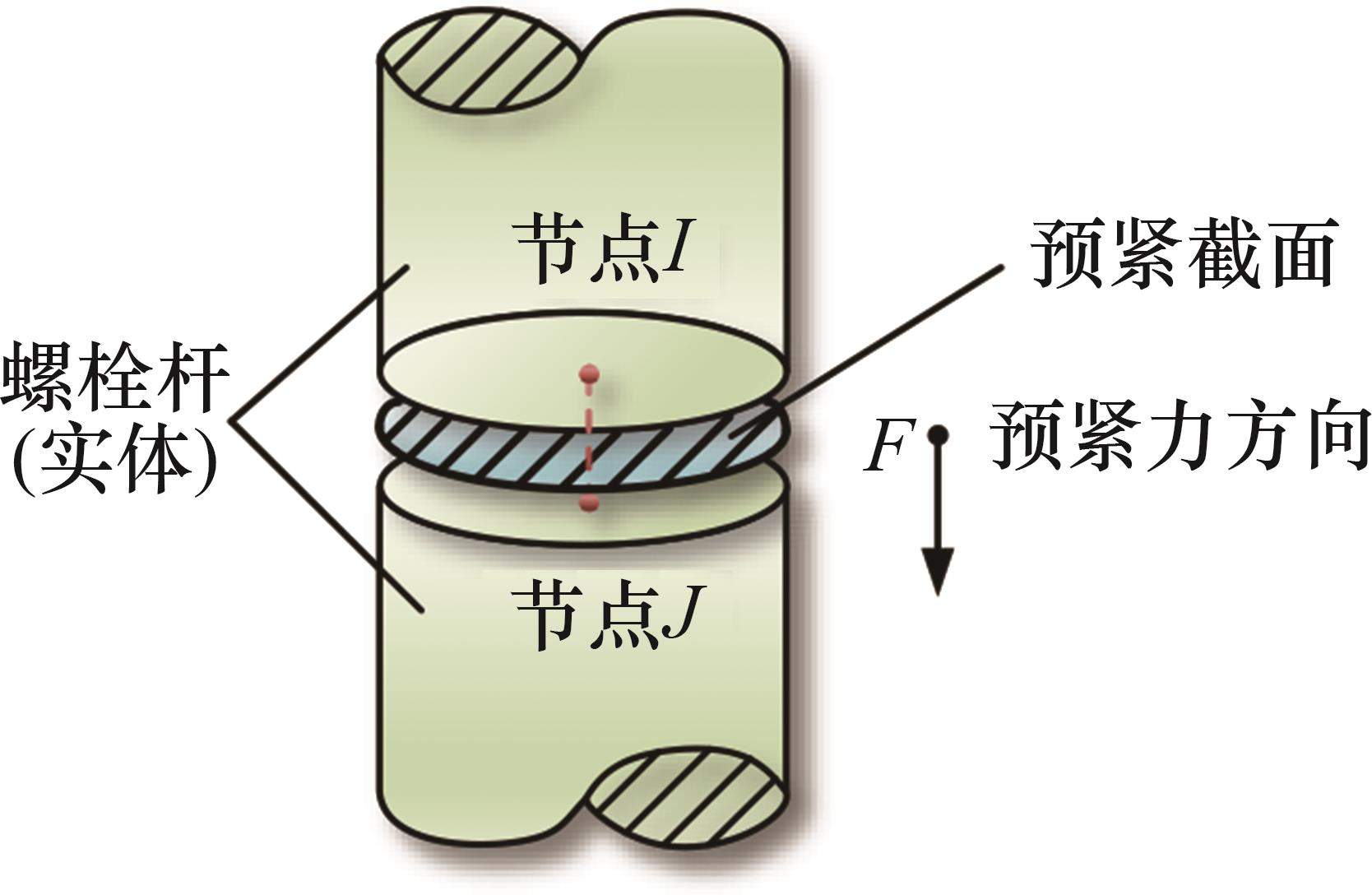
在两级机匣连接结构装配中,通常使用定力矩扳手对螺栓施加相同拧紧力矩来实现拧紧。拧紧力矩和预紧力的换算公式为
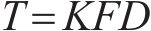
式中:T为螺栓预紧力矩;F为螺栓预紧力;K为螺栓扭矩系数,近似为0.2;D为螺栓螺纹的公称直径。
最后,通过创建各实体螺栓模型与法兰边的接触,将螺栓结合部的力学特性引入两级机匣连接结构中。图9所示为法兰边上每个螺栓结合部涉及的接触面,对每个螺栓结合部都设置了3个接触对,分别为螺栓头垫片-法兰接触对、法兰-法兰接触对和螺母垫片-法兰接触对。
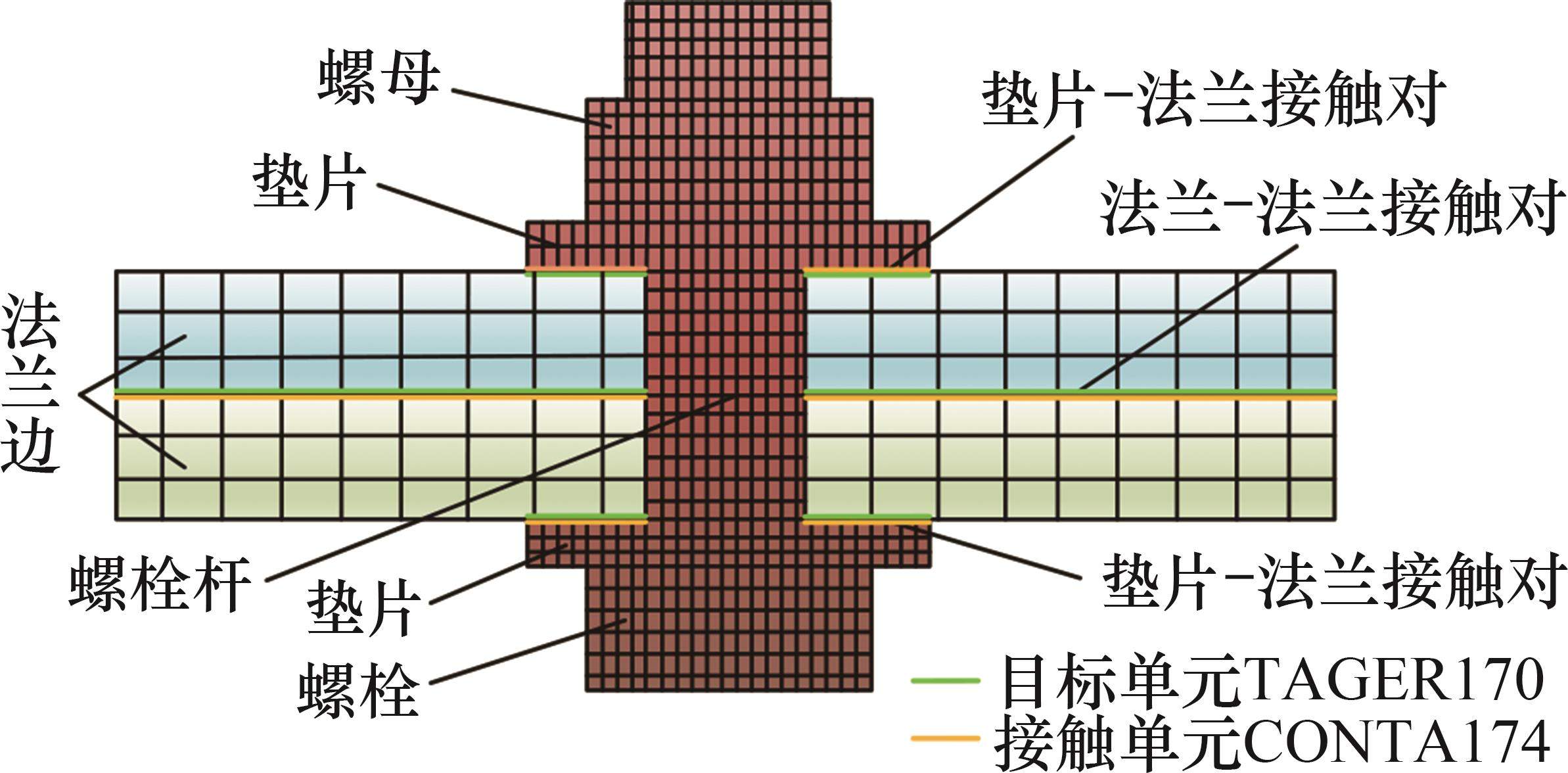
1.3.2 刚性耦合的梁单元模型
采用刚性耦合的梁单元模型是指螺栓用一根耦合到刚性接触面的梁单元表示,梁两端的节点分别与螺栓垫片范围内的节点通过节点耦合的方式连接以模拟螺栓头和螺母。
首先,在每个螺栓孔圆心处建立梁单元节点,将上下对应的两个梁单元节点相连从而形成梁单元(梁单元个数决定于周向所分布的螺栓个数)。接着,对每个梁单元节点与相应螺栓垫片外径范围内所有节点建立刚性区,最终形成用刚性耦合的梁单元模型模拟螺栓结合部。
螺栓结合部刚性耦合梁单元模型如图10所示。将螺栓结合部刚性耦合梁单元模型引入两级机匣连接结构中。通过建立刚性区(命令为“CERIG”)并用梁单元(可选用BEAM188梁单元)连接的方式来模拟螺栓与法兰之间的刚性耦合。
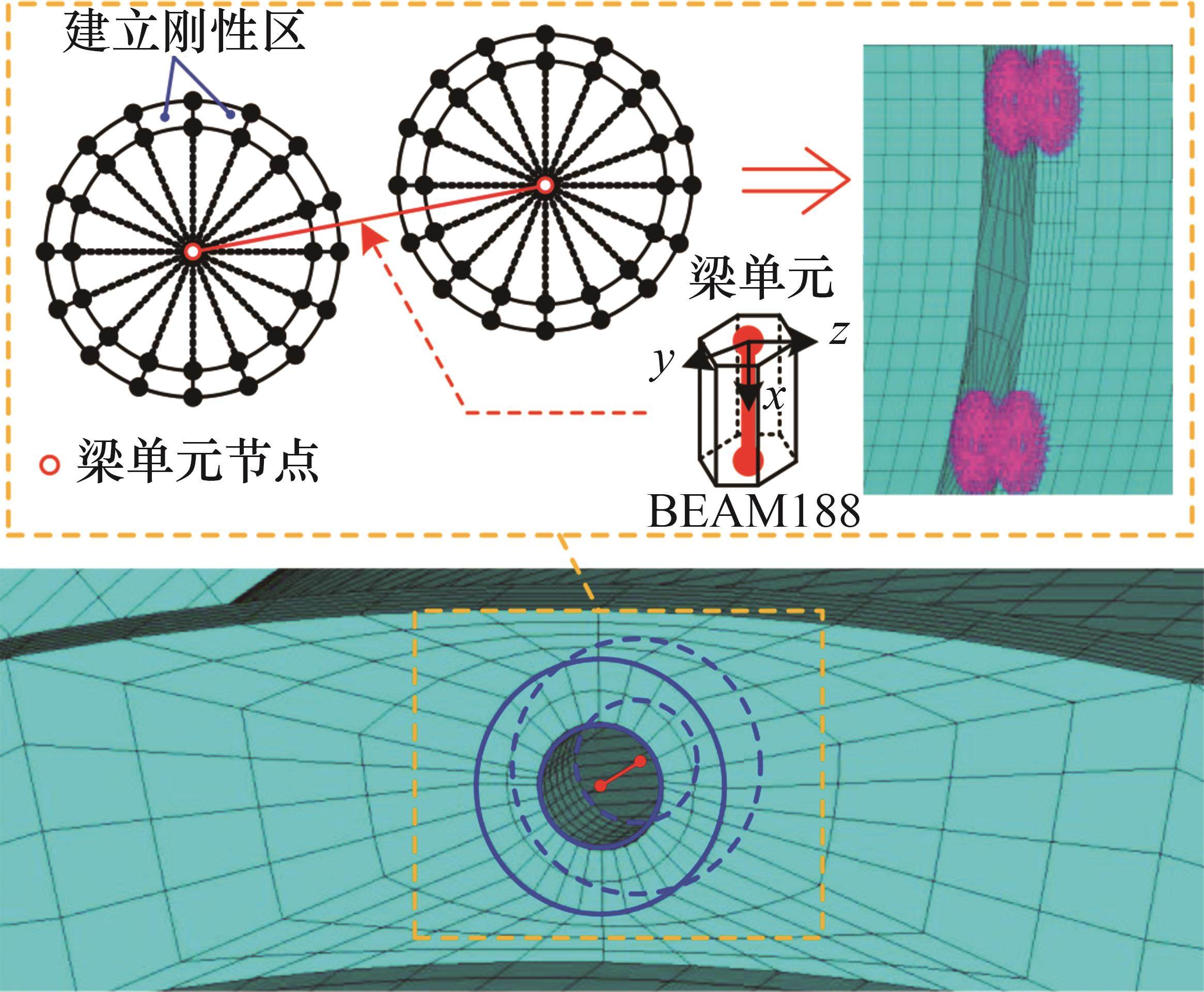
1.3.3 弹簧单元模型
弹簧单元模型主要通过在被连接结构的接触面上建立若干个弹簧单元来模拟结合部的力学特性。通过调整弹簧单元的个数、弹簧单元的类型以及弹簧单元在接触面上的分布情况来调整不同螺栓结合部的力学特性差异。
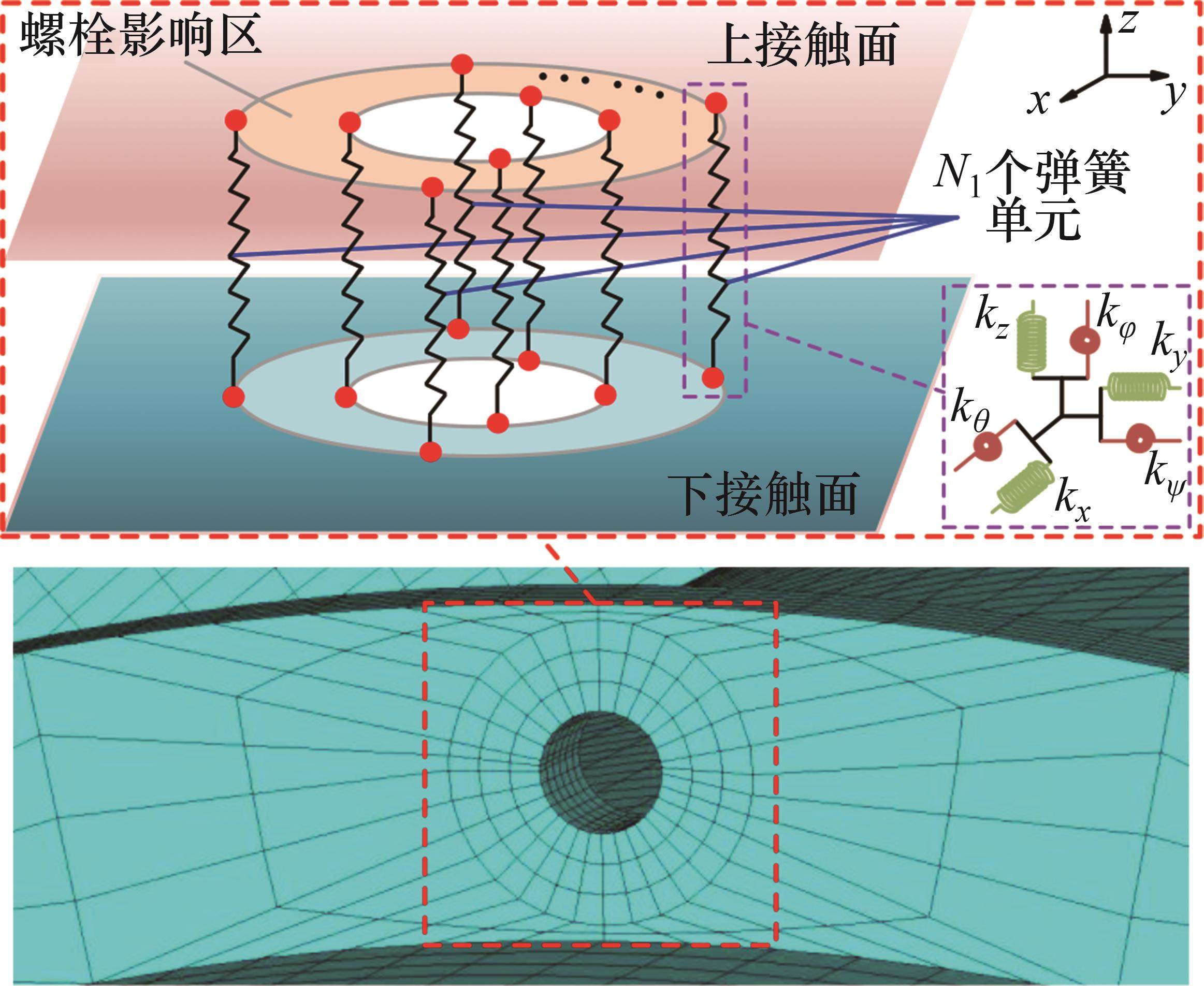
研究表明[19-21],螺栓在紧固时会产生一个以螺栓杆轴心为中心的圆形压力区域,称为螺栓影响区。可选用COMBIN14弹簧单元对螺栓结合部进行模拟。在每个螺栓结合部中上、下两个接触面的螺栓影响区内、外圈周向选取相对应的节点,直接相连创立弹簧单元。在螺栓影响区内、外圈周向上使用N1个弹簧单元的均布方式,每个弹簧含有x、y、z、θ、ψ和φ方向的刚度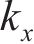
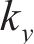
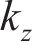
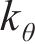
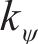
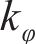
螺栓结合部弹簧单元模型见图11。通过给定弹簧单元的刚度参数,将螺栓结合部的力学特性引入两级机匣连接结构中。弹簧单元支撑刚度可以采用反推辨识法[22-24]确定。在ANSYS中,面向COMBIN14弹簧单元可以使用实常数命令“R”分别定义各个方向的弹簧刚度。
1.3.4 虚拟材料模型
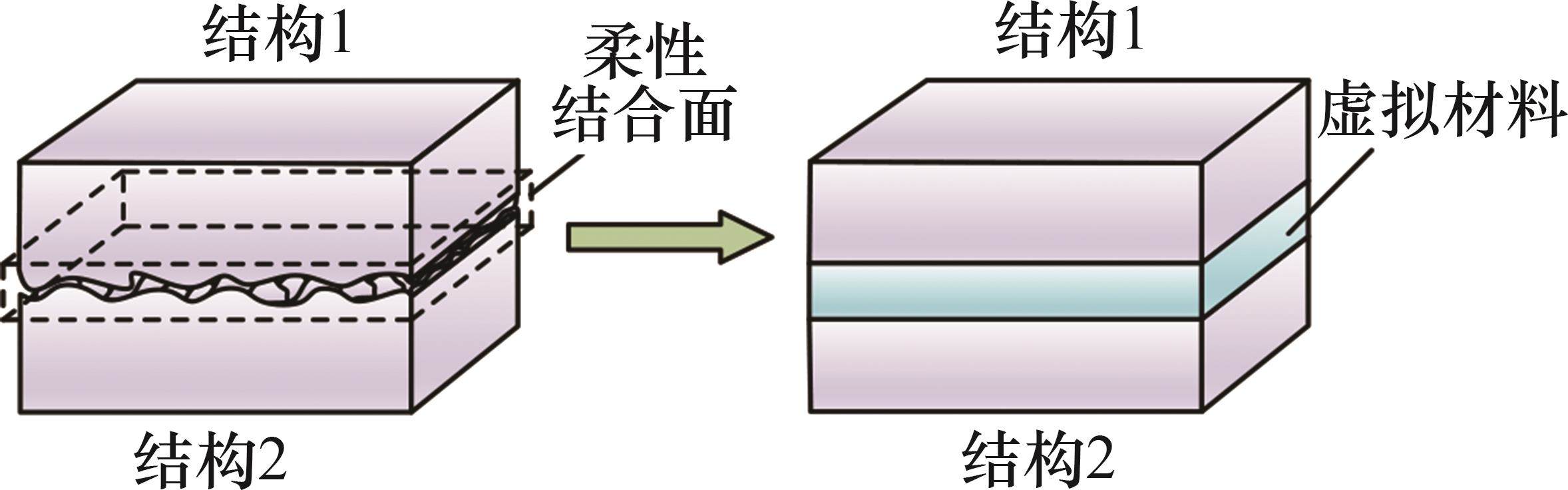
基于虚拟材料的螺栓结合部建模理念为:螺栓结合面的接触实际上是由无数个微凸体的接触构成,如图12所示,将所有微凸体的接触等效成具有一定厚度的虚拟材料层;通过改变虚拟材料的弹性模量、泊松比、密度和厚度来模拟螺栓结合部的力学特性。
参照文献[25],并考虑所研究的两级机匣连接结构的尺寸及螺栓结合部的形式,选取虚拟材料层的厚度h为1 mm。
虚拟材料层的密度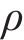
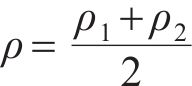
其中,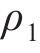
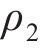
采用反推辨识法,将弹性模量、泊松比设置为输入参数,将仿真固有频率和目标函数设置为输出参数,通过相关的辨识算法获得螺栓结合部虚拟材料的弹性模量、泊松比。
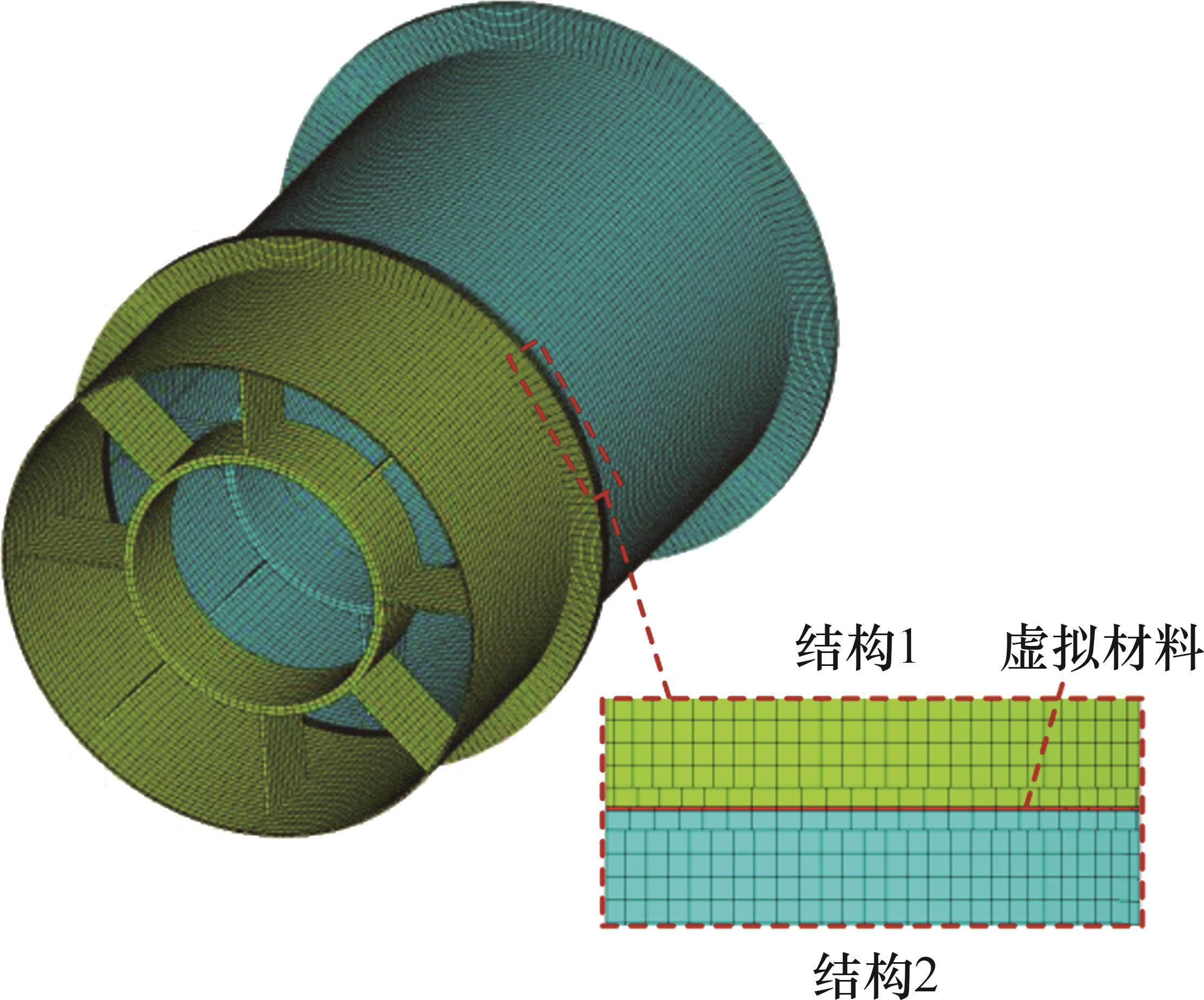
虚拟材料层的几何建模与机匣法兰边的几何建模类似,通过拉伸圆环面直接生成,这里选用SOLID185实体单元进行扫掠划分网格。虚拟材料层两侧与机匣法兰端面均通过固定连接,即在ANSYS中采用GLUE操作。两级机匣连接结构的局部有限元模型如图13所示。最后,通过输入虚拟材料层的弹性模量和泊松比,将螺栓结合部的力学特性引入两级机匣连接结构中。
1.4 固有特性求解
4种不同螺栓结合部建模方式的两级机匣模拟件的有限元模型见图14。
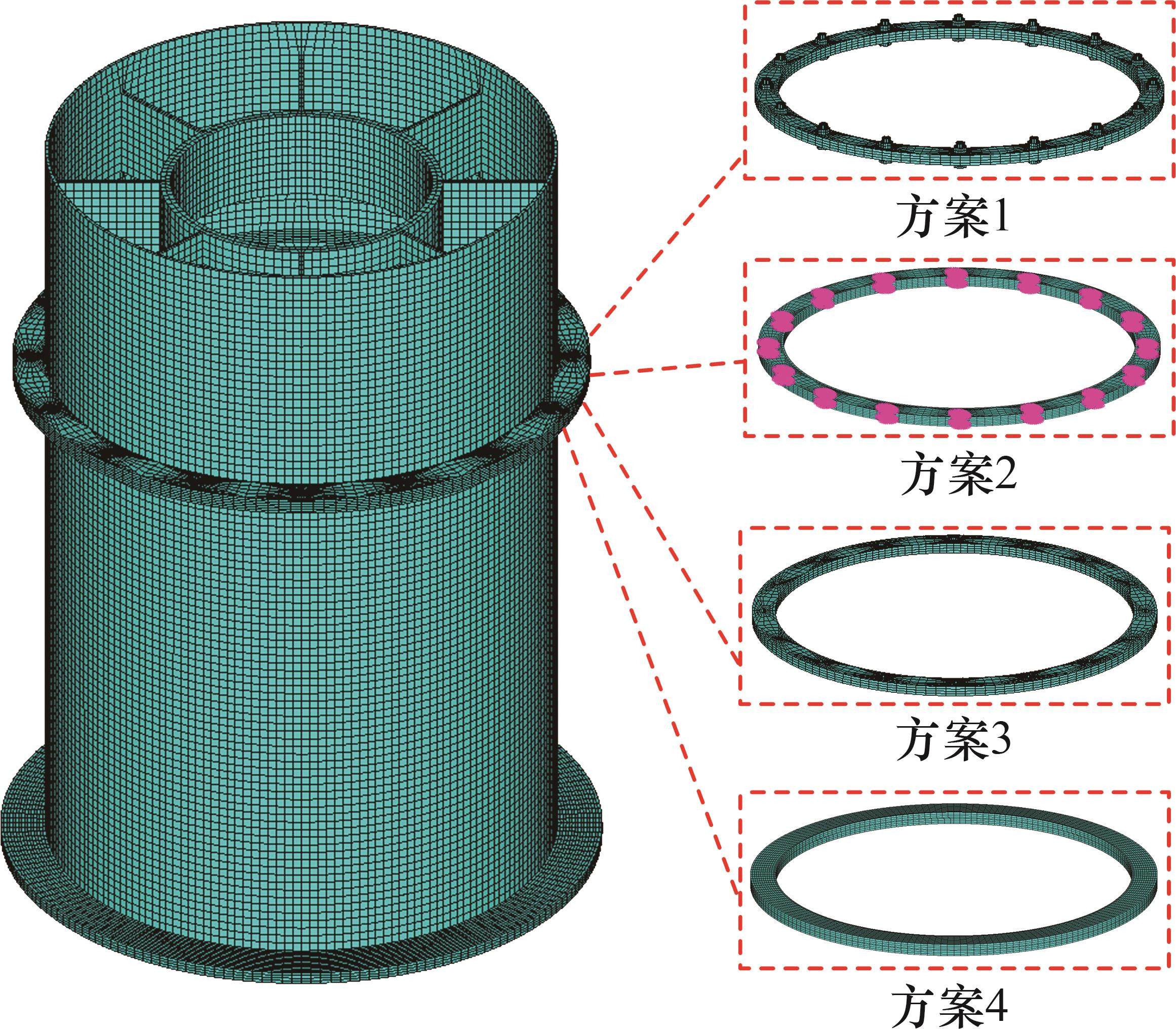
完成两级机匣连接结构有限元建模后,还需要设置边界条件。两级机匣连接结构有限元模型边界条件的模拟如图15所示。机匣1的法兰边是固定端,采用螺栓连接固定在夹具上,采用弹簧单元模拟两级机匣与夹具之间的弹性约束。具体建模方法如下:将机匣1固定端法兰边均分N2份,每一个扇形区域代表一个螺栓影响区,在每个螺栓影响区内建立由n2个弹簧单元组成的弹簧弧段。弹簧单元的建立方法与前面的连接处螺栓结合部弹簧单元模型建立方法相同,通过设定合理的弹簧刚度值来模拟这个弹性约束边界条件。
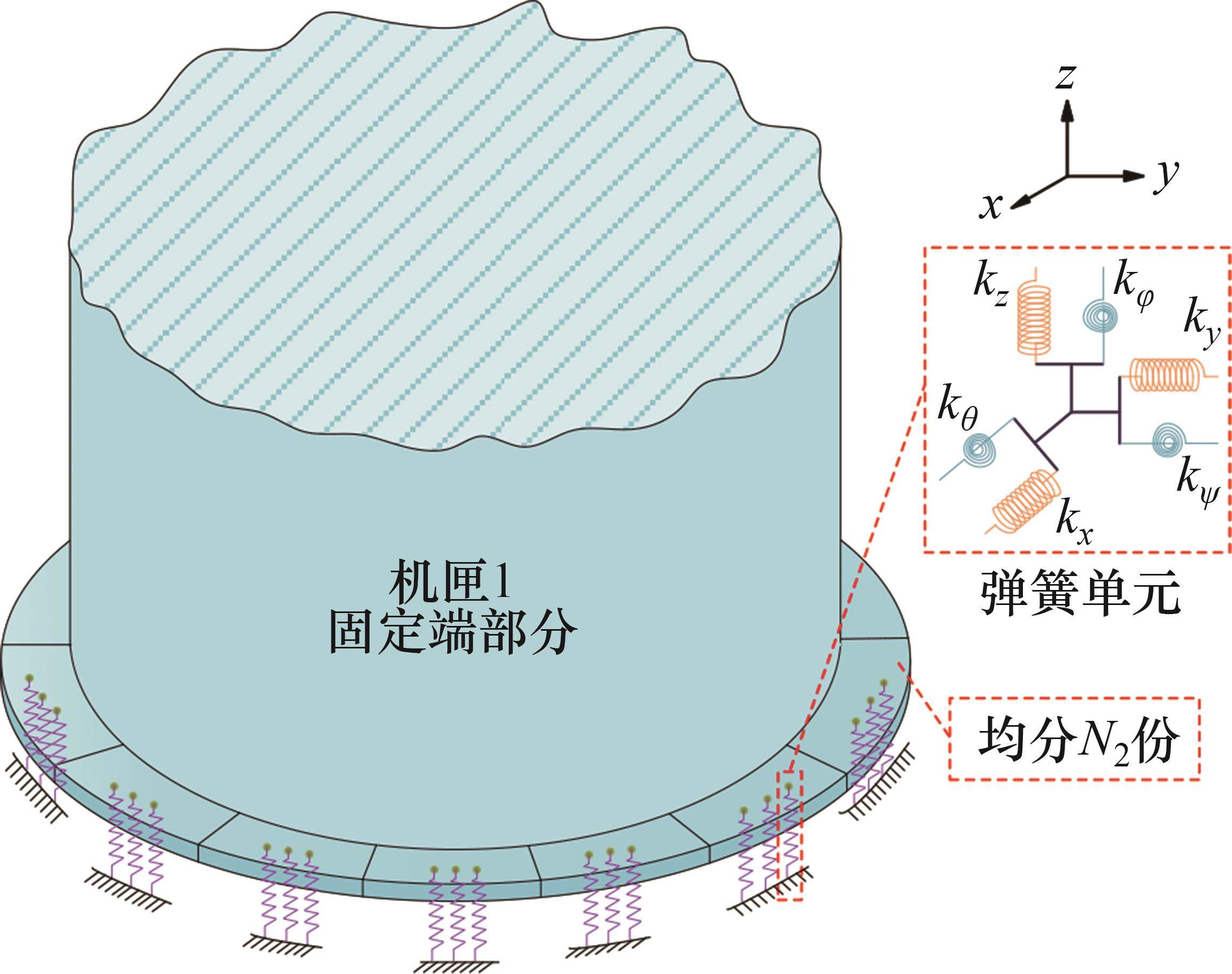
基于创建的包含弹性约束边界条件的两级机匣连接结构模拟件有限元模型,可采用分块兰索斯模态求解方法,提取两级机匣连接结构模型的固有频率和模态振型。
2 两级机匣连接结构固有特性测试
利用建立的实验系统对两级机匣连接结构的固有特性进行测试。首先,测试单个机匣(机匣1)的固有特性,获得机匣与夹具之间模拟弹性约束边界条件的弹簧单元参数。然后,安装另一个机匣,对两级机匣连接结构的固有特性进行测试,得到其固有特性以及两级机匣连接处螺栓结合部的参数。辨识获得的螺栓结合部参数用于后续机匣连接结构有限元建模,获得的固有特性用于模型正确性验证。
2.1 机匣试验件
两级机匣连接结构的基体材料均为45号钢,其材料参数如下:弹性模量为2.06×1011 Pa,泊松比为0.269,密度为7 850 kg/m³。固定端法兰轴向长为 8 mm,外径为202 mm;中间连接处法兰轴向长为10 mm,外径为194 mm,其余几何尺寸见表1。
| 机匣 | 参数 | 机匣外壳 | 机匣内壳 | 静子叶片 |
|---|---|---|---|---|
| 机匣1 | 长度/mm | 365 | 60 | 60 |
| 内径/径向长 | 170 | 88 | 75 | |
| 厚度/mm | 2 | 7 | 3 | |
| 机匣2 | 长度/mm | 165 | 60 | 60 |
| 内径/径向长 | 170 | 88 | 75 | |
| 厚度/mm | 2 | 7 | 3 |
2.2 单机匣固有特性测试
建立面向机匣1的单机匣实验测试系统,如图16所示。该实验系统主要包括PCB SN 30272模态力锤、B&K4517加速度传感器、LMS SCSDAS数据采集前端和LMS.Testlab笔记本工作站等。将机匣1用32个M12的螺栓固定在实验台夹具上,机匣与夹具之间的螺栓预紧力为40 N·m。

为了获得机匣1的固有特性,在外壳上均匀地布置120个锤击点,在静子叶片及机匣内壳布置了48个锤击点,共168个测点。实验中,使用PCB SN 30272模态力锤对机匣进行锤击实验,最终获得300~1 200 Hz范围内结构的各阶频率及模态振型。此外,需要说明的是,机匣1模态振型测试主要用于校验机匣1有限元模型的合理性,并不参与确定边界条件参数,因而,后续并没有给出机匣1的模态振型结果。
2.3 两级机匣固有特性测试
在单机匣实验测试系统的基础上安装机匣2,用16个M8的螺栓连接,螺栓预紧力矩为4 N·m,建立两级机匣固有特性测试系统,如图17所示。

根据仿真得到的振型特点,在两级机匣连接结构的机匣外壳上均匀地布置192个锤击点,在静子叶片及机匣内壳均匀地布置了96个锤击点,共288个测点。
同样地,使用模态力锤对两级机匣连接结构进行锤击实验,最终获得300~1 200 Hz范围内结构的各阶频率和模态振型。
3 固有特性分析及螺栓模型比较
3.1 边界条件确定
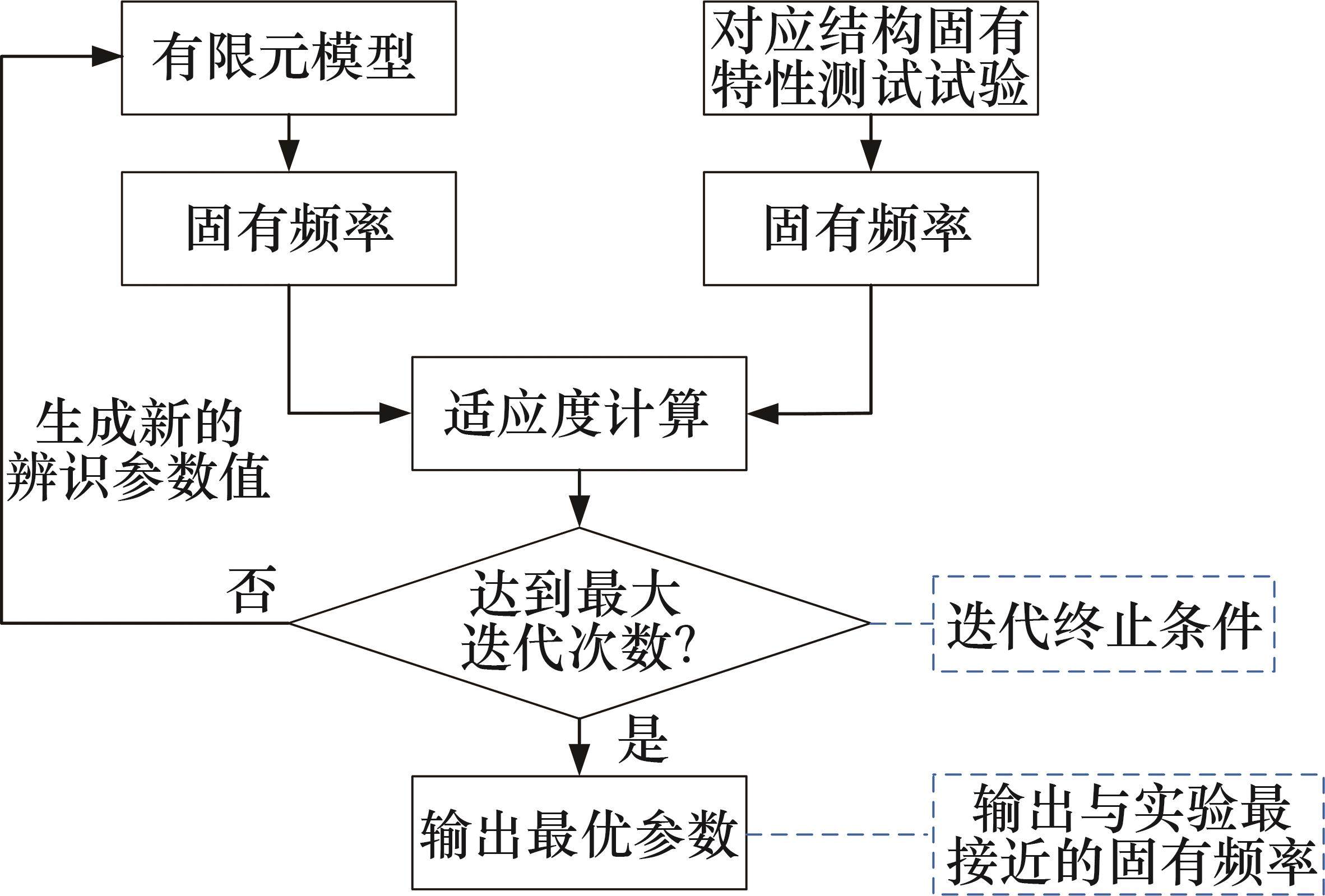
仅针对机匣1进行有限元建模,在每个螺栓位置布置3个弹簧单元用于模拟边界条件,且为了简化,各弹簧单元之间刚度相同,每个弹簧的参数也相同。进一步,基于单机匣实验测试获得的固有频率进行反推辨识来确定模拟边界条件的弹簧单元参数。基于遗传算法[26-29]进行相关参数的反推辨识(相关流程见图18),将弹簧单元参数定义为设计变量,通过适应度计算不断地对设计变量进行修正,使利用ANSYS软件计算得到的单机匣固有频率与实验结果逐渐一致,最终反推出待识别参数。在进行适应度计算时,定义的优化模型为
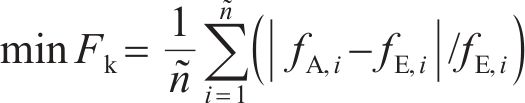
其中: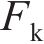
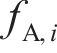
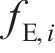
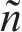
选择机匣1模型前2阶固有频率参与适应度函数的计算,将得到的辨识参数用于其他阶次的固有频率计算,最终得到两级机匣连接结构模型约束端的弹簧单元线刚度为2.05×1010 N/m,扭转刚度为2.05×1010 N·m/rad。
表2所示为实验及仿真获得的机匣1前5阶固有频率对比。从表2可以看出:采用弹簧单元模拟边界条件,实验与仿真模型获得的机匣1固有频率最大偏差为2.763%,最小偏差为0.157%。因此,可以证明反推辨识得到的弹簧单元参数模拟边界条件时能够较准确地反映两级机匣连接结构的底部约束状态。
| 阶次 | 实验频率fE/Hz | 仿真频率fA/Hz | 偏差/% |
|---|---|---|---|
| 1 | 338.551 | 338.019 | -0.157 |
| 2 | 434.614 | 424.129 | -2.413 |
| 3 | 780.034 | 785.634 | 0.718 |
| 4 | 872.645 | 866.519 | -0.702 |
| 5 | 908.218 | 883.128 | -2.763 |
3.2 不同螺栓模型仿真结果与实验结果对比
将反推辨识获得的边界条件参数应用于4种不同螺栓结合部模拟方法的两级机匣有限元模型中,计算两级机匣连接结构的固有频率和模态振型,从计算精度、耗时、建模的复杂程度三方面对比分析连接处各螺栓结合部模拟方法的优缺点。
对于连接处采用实体单元创建螺栓结合部的分析模型,可根据式(1)计算得到螺栓预紧力为 2 500 N。参照预紧力模拟方法(图8),对螺栓施加轴向拉伸方向的预紧力。由于分析过程中考虑了螺栓结合部的预紧力,因此,对两级机匣连接结构固有特性进行分析时,需考虑预应力效应的影响,即先对静力学进行分析,再对预应力模态进行分析。
对于连接处采用刚性耦合的梁单元创建螺栓结合部的分析模型,根据实验所用的螺栓垫片外径(16 mm),在法兰处选出该尺寸范围内的所有节点与梁单元两端节点形成刚性区。同时,定义截面几何尺寸为螺栓孔半径(4 mm),对固有特性进行分析。
对于连接处采用弹簧单元模拟螺栓结合部的分析模型,根据经验公式得到螺栓影响区的面积,并在每个螺栓的影响区内建立弹簧单元。通过尝试调整弹簧单元数量,最终采用在螺栓影响区面积内、外圈上周向均匀分布4个弹簧的模拟方式。为了简化,各弹簧单元之间刚度相同,每个弹簧的弹簧参数也相同。根据实验值反推辨识获得上述弹簧单元线刚度数2×108 N/m,扭转刚度为2×108 N·m/rad,利用辨识的参数对最终的固有特性进行分析。参数的辨识方法以及其余反推辨识方法与图18所描述的一致。
对于连接处采用虚拟材料模拟螺栓结合部的分析模型,取虚拟材料层厚度为1 mm,根据式(2)计算得到密度为7 850 kg/m³。材料为各向同性材料,根据实验结果反推辨识出虚拟材料层的其余材料参数:弹性模量为1.80×1011 Pa,泊松比为0.285。同样利用辨识的参数对最终的固有特性进行分析。
3.2.1 计算精度对比
4种螺栓结合部模型获得的固有频率和模态振型仿真值与实验值对比如表3和表4所示。
| 阶次 | 实验频率fE/Hz | 实体单元模型 | 刚性耦合的梁单元模型 | 弹簧单元模型 | 虚拟材料模型 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 仿真频率fA/Hz | 偏差/% | 仿真频率fA/Hz | 偏差/% | 仿真频率fA/Hz | 偏差/% | 仿真频率fA/Hz | 偏差/% | ||
| 1 | 312.060 | 319.956 | 2.530 | 322.647 | 3.393 | 320.379 | 2.666 | 312.753 | 0.222 |
| 2 | 339.180 | 344.608 | 1.600 | 347.648 | 2.496 | 345.372 | 1.825 | 334.043 | 1.514 |
| 3 | 402.154 | 385.996 | -4.017 | 394.055 | -2.013 | 392.959 | -2.286 | 390.624 | -2.866 |
| 4 | 565.840 | 556.817 | -1.594 | 571.508 | 1.001 | 546.410 | -3.434 | 610.743 | 7.935 |
| 5 | 611.133 | 609.372 | -0.288 | 626.327 | 2.486 | 600.875 | -1.678 | 655.639 | 7.282 |
| 6 | 790.966 | 788.712 | -0.285 | 797.856 | 0.871 | 787.496 | -0.438 | 791.067 | 0.013 |
| 阶次 | 1 | 2 | 3(n=2) | 4(n=4) | 5(n=5) | 6(n=6) |
|---|---|---|---|---|---|---|
| 实体单元模型 | ||||||
刚性耦合的 梁单元模型 | ||||||
| 弹簧单元模型 | ||||||
| 虚拟材料模型 | ||||||
| 实验 |
从表3可以看出:对于连接处采用实体单元、刚性耦合的梁单元、弹簧单元模拟螺栓结合部的分析模型其固有频率与实验结果均较接近,而连接处采用虚拟材料模拟螺栓结合部的分析模型其固有频率与实验结果相差较大,最大偏差为7.935%。
利用均方根误差

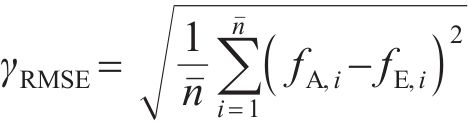
其中: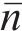
将表3中的数据代入式(4),获得对应4种螺栓结合部模拟方式的两级机匣连接结构有限元模型的前6阶固有频率

| 模拟方式 |  |
|---|---|
| 实体单元模型 | 8.587 |
| 刚性耦合的梁单元模型 | 9.659 |
| 弹簧单元模型 | 10.699 |
| 虚拟材料模型 | 26.321 |
从表5可以看出:4种螺栓结合部模拟方式的两级机匣连接结构有限元模型仿真与实验前6阶固有频率的
从表4可见:第1~2阶振型主要是静子叶片及机匣内壳的振动,而第3~6阶振型主要是机匣外壳的振动。实验与仿真获得的4种螺栓结合部模拟方式的两级机匣连接结构有限元模型前2阶内部模态振型对比如表6所示。从表6可以看出:实验与仿真获得的前2阶振型一致,都是静子叶片在振动。
| 模型 | 1阶 | 2阶 |
|---|---|---|
| 实体单元模型 | ||
| 刚性耦合的梁单元模型 | ||
| 弹簧单元模型 | ||
| 虚拟材料模型 | ||
| 实验 |
3.2.2 计算耗时对比
4种不同螺栓结合部建模方式计算两级机匣连接结构固有特性所需的时间见表7。从表7可知,4种螺栓结合部模拟方式的两级机匣连接结构有限元模型的固有频率计算时间由低到高依次是虚拟材料模型、刚性耦合的梁单元模型、弹簧单元模型、实体单元模型。实体单元模型由于考虑了螺杆和螺帽等螺栓特征,且在固有特性分析时进行了预应力分析,使得求解步骤较为复杂,耗时最长;虚拟材料模型在建模时忽略了复杂的螺栓结构,使得单元数量大幅度减少,耗时最少;刚性耦合的梁单元模型和弹簧单元模型虽然忽略了螺杆和螺帽等螺栓特征,但保留着螺栓孔,使计算时间相对增加。
| 模拟方式 | 计算时间/s |
|---|---|
| 实体单元模型 | 692 |
| 刚性耦合的梁单元模型 | 384 |
| 弹簧单元模型 | 568 |
| 虚拟材料模型 | 111 |
3.2.3 建模复杂程度对比
从螺栓结合部建模的复杂程度上分析,实体单元模型在建模时考虑了螺杆和螺帽等螺栓特征,而实体螺栓的建模和分网往往较为复杂。并且在连接界面之间建立了接触单元,整体网格数量较多,计算时间较大并且占用较大的内存空间,是4种螺栓结合部模型中最复杂的模型。刚性耦合的梁单元模型和弹簧单元模型在建模过程中完全一样,都需要造螺栓孔,整体建模难度不大。虚拟材料模型是4种螺栓结合部模型中建模最简单的模型,没有螺栓孔、实体螺栓等复杂结构,简化了建模过程,加快了求解分析过程。
综上可知,刚性耦合的梁单元是一种高效的螺栓结合部模拟方法,与实体单元模拟螺栓结合部的方法相比,时间减少了44.5%。因而,在实际机匣连接结构有限元建模时,可优先选用这种螺栓结合部建模方式。
4 结论
1) 基于ANSYS软件平台,从机匣内、外壳的模拟、静子叶片的模拟以及法兰边上螺栓结合部的模拟三方面描述了两级机匣连接结构有限元建模方法。针对连接处法兰边上螺栓结合部,分别采用实体单元、刚性耦合的梁单元、弹簧单元以及虚拟材料对其建模,并给出了引入两级机匣结构的方式。
2) 以给定几何尺寸的两级机匣连接结构为对象进行了实例研究。分别测试了单级及两级机匣结构固有频率及模态振型,获取的结果用于确定弹性约束边界条件以及校验两级机匣连接结构有限元模型的合理性。结果表明:对于4种螺栓结合部模拟方式的两级机匣有限元模型,仿真计算的前6阶固有频率与实验值最大偏差为7.935%,模态振型基本一致,从而证明了所描述的两级机匣结构有限元建模方法的合理性。
3) 采用实体单元、刚性耦合的梁单元、弹簧单元模拟螺栓结合部的分析模型计算精度都较高,而连接处采用虚拟材料模拟螺栓结合部的分析模型计算精度与实验结果相差较大;计算耗时由低到高依次是虚拟材料模型、刚性耦合的梁单元模型、弹簧单元模型、实体单元模型;实体单元模型最复杂,刚性耦合的梁单元模型和弹簧单元模型难度相似,虚拟材料模型最简单。综合上述对比,在实际机匣连接结构有限元建模时,可优先选用刚性耦合的梁单元,其计算精度与实体单元的计算精度最相近,但时间减少44.5%。
Analysis of the similarity design and vibration transmission characteristics of typical support structures of an aero-engine
[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2022, 236(17): 9441-9458.李浩, 孙伟, 徐昆鹏, 等. 考虑螺栓力学特性的两级机匣连接结构有限元建模及振动分析[J]. 中南大学学报(自然科学版), 2025, 56(2): 501-513.
LI Hao, SUN Wei, XU Kunpeng, et al. Finite element modeling and vibration analysis of two-stage casing connection structure considering mechanical properties of bolts[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 501-513.

