路基作为列车运营的下部基础设施,通常用一定规格的填料填筑而成,路堤上面施工轨道结构。为满足线路平顺性,高速铁路对路基工后沉降提出了非常严格的要求。根据TB 10621—2014《高速铁路设计规范》[1],无砟轨道路基工后沉降应符合线路平顺性、结构稳定性和扣件调整能力的要求,一般不宜超过15 mm。因此,为了达到路基工后沉降要求,路基填料的材质、级配、水稳定性等都必须适宜。通常缺乏优质填料,且农田用地珍贵,但若采用“以桥代路”的方式,则所需投资巨大[2]。在此背景下,开发一种新型的路基结构,以适应高速铁路高速行车的建造要求具有重要的意义。
1 路基结构形式
在高速铁路的工程实践中,我国工程师提出了一种箱式路基结构的概念[3],其主要是由顶板、底板和侧板所形成的一种钢筋混凝土结构物。箱式路基采用钢筋混凝土结构取代了传统的松散体碎石、土体填料。与传统高填方路基相比,箱式路基不仅强度和稳定性得到了显著提高,而且极大地降低了施工成本和减少了耕地占用面积,具有明显的经济性和实用性,被视为一种新型绿色路基结构。中铁一、二、三、四设计院针对箱式路基结构均进行了设计,但结构上存在一定差异[4]。
参照TB 10092—2017《铁路桥涵混凝土结构设计规范》[5]关于箱梁的规定,建议箱式路基顶面宽取12.6 m,下部地基采用“CFG桩+垫层”复合地基设计。其中,垫层的加固面积需比箱式路基底面积大,四周宽出基底的部分不宜比垫层的厚度小,故取厚度为0.6 m,如图1所示。在一般地段,箱式路基结构的轴线与线路走向相同;在需要设置涵洞的位置,箱式路基结构还可以垂直线路方向设置,即箱式路基同时起排水涵洞作用。
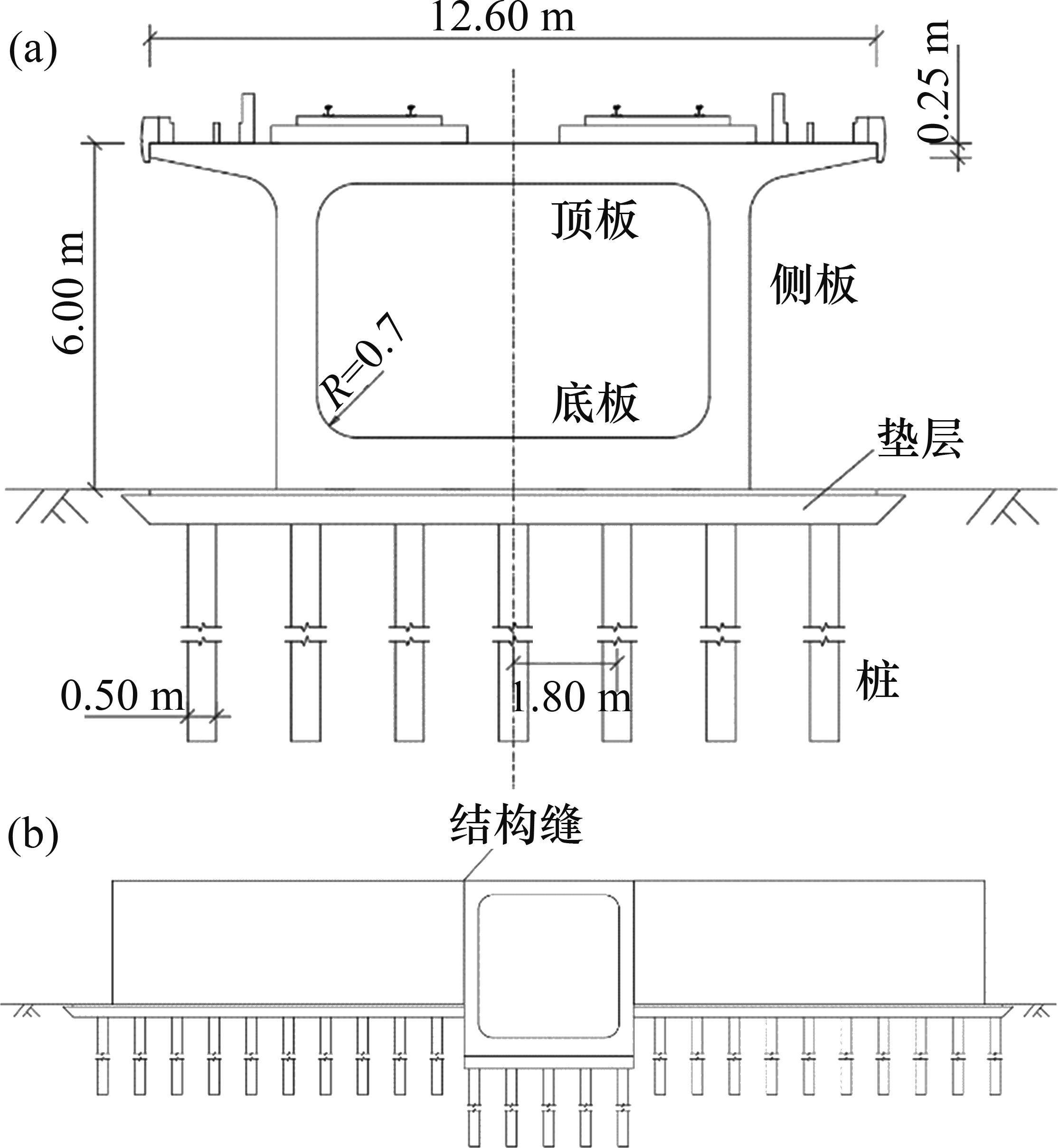
目前,箱式路基还处于早期研发阶段,仅在部分工程中得到应用,设计分析理论尚未系统开展,在列车长期荷载作用及温度作用下的工作特性、受力传递、变形规律等均不清晰,更没有行业规范。基于此,本文作者在对箱式路基结构的特点和适用条件分析的基础上,借鉴相关行业标准和研究成果,探讨箱式路基设计荷载分类与组合,对其主要结构尺寸进行分析,同时,建立车辆-轨道-箱式路基-复合地基耦合模型,研究箱式路基工作特性与荷载传递特点,以便为箱式新型路基结构推广应用提供理论参考。
2 箱式路基荷载分类及组合
箱式路基是介于普通土质路基和桥梁结构之间的一种结构构筑物,因此,其兼具土质路基和桥梁结构的特点。在对其进行设计计算时,应根据结构特性,考虑施工阶段和运营阶段等多种荷载作用[6]。综合列车作用下的土质路基和桥梁结构受力特点,提出箱式路基结构荷载如表1所示。
| 荷载分类 | 荷载名称 |
|---|---|
| 恒载(主力) | 结构自重 |
| 二期恒载 | |
| 混凝土收缩 | |
| 基础变位的影响 | |
| 活载(主力) | 列车竖向静活载 |
| 列车竖向动力作用 | |
| 离心力 | |
| 横向摇摆力 | |
| 附加力 | 制动力或牵引力 |
| 风力 | |
| 温度变化的作用 | |
| 特殊荷载 | 列车脱轨荷载 |
| 施工临时荷载 | |
| 地震力 |
箱式路基的荷载组合工况可分为主力(恒载+活载)、主力+附加力、主力+特殊荷载。当考虑2种及2种以上附加力与主力组合时,应当注意附加力种类的选择及取值折减。当特殊荷载与主力组合时,只考虑一种特殊荷载,且不考虑与附加力进行组合。
3 箱式路基设计计算
作为一种新型路基结构,箱式路基的结构尺寸不仅决定了其安全性、稳定性,也直接影响着其经济性,进而决定了其推广应用价值。箱式路基的长、宽、高、厚度等尺寸对其受力安全都有影响,本节重点讨论其长度和底部结构厚度[7]。
3.1 纵向长度确定
箱式路基结构在确定其纵向长度时,应考虑以下3个原则[8]:
1) 箱式路基的纵向长度应考虑与外界环境的适应性[9]。箱式路基结构的箱体属于单元式钢筋混凝土结构,存在热胀冷缩效应,其纵向长度需满足温度荷载引起的伸缩变形需求。
2) 箱式路基的纵向长度应考虑与地形地质条件的适应性。箱式路基的纵向长度应综合考虑其施工性和连续性,能很好地适应复杂的下部地形地质条件。若箱式路基纵向长度分段过短,则会影响施工效率和经济性;若过长,则其适应地形能力差,同时将面临防裂问题[10]。
3) 箱式路基的纵向长度应考虑与上部轨道结构的匹配性。箱式路基长度应与其上轨道板分块长度的模数相对应,即宜为轨道板分块长度的整数倍,这样既可满足铁路建设配板要求,还可避免轨道板由于跨缝设置的受力复杂性[11]。
综合上述3种原则,当温度发生变化时,考虑最不利情况,即箱体产生自由伸缩,箱体的收缩量为
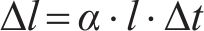
式中:α为材料的线膨胀系数,钢筋混凝土材料取10-5;l为结构长度;Δt为温度变化量;Δl为长度变化量。
参考TB 10002—2017《铁路桥涵设计规范》[12]桥梁设计计算的全年温度分布图,中国全年最高设计温度为28 ℃,最低设计温度为-30 ℃,传统桥梁设置伸缩缝为20 mm。由于箱式路基底部与桩土之间的作用属于摩擦作用,即两端伸缩,则通过式(1)计算,箱式路基最大长度为17.24 m。以CRTS III型板式无砟轨道为例,考虑到上述配板需求,一般地段箱式路基长度初步设置为铺设3块P5600轨道板;当下部地形起伏变化较大时,还可采用1块或2块轨道板。
3.2 底部构造设计
在设计箱式路基底部构造时,主要考虑以下2个原则:
1) 箱式路基在横风荷载、离心力和横向摇摆力等横向最不利荷载组合条件下不发生侧滑,此时,箱式路基受力如图2所示。
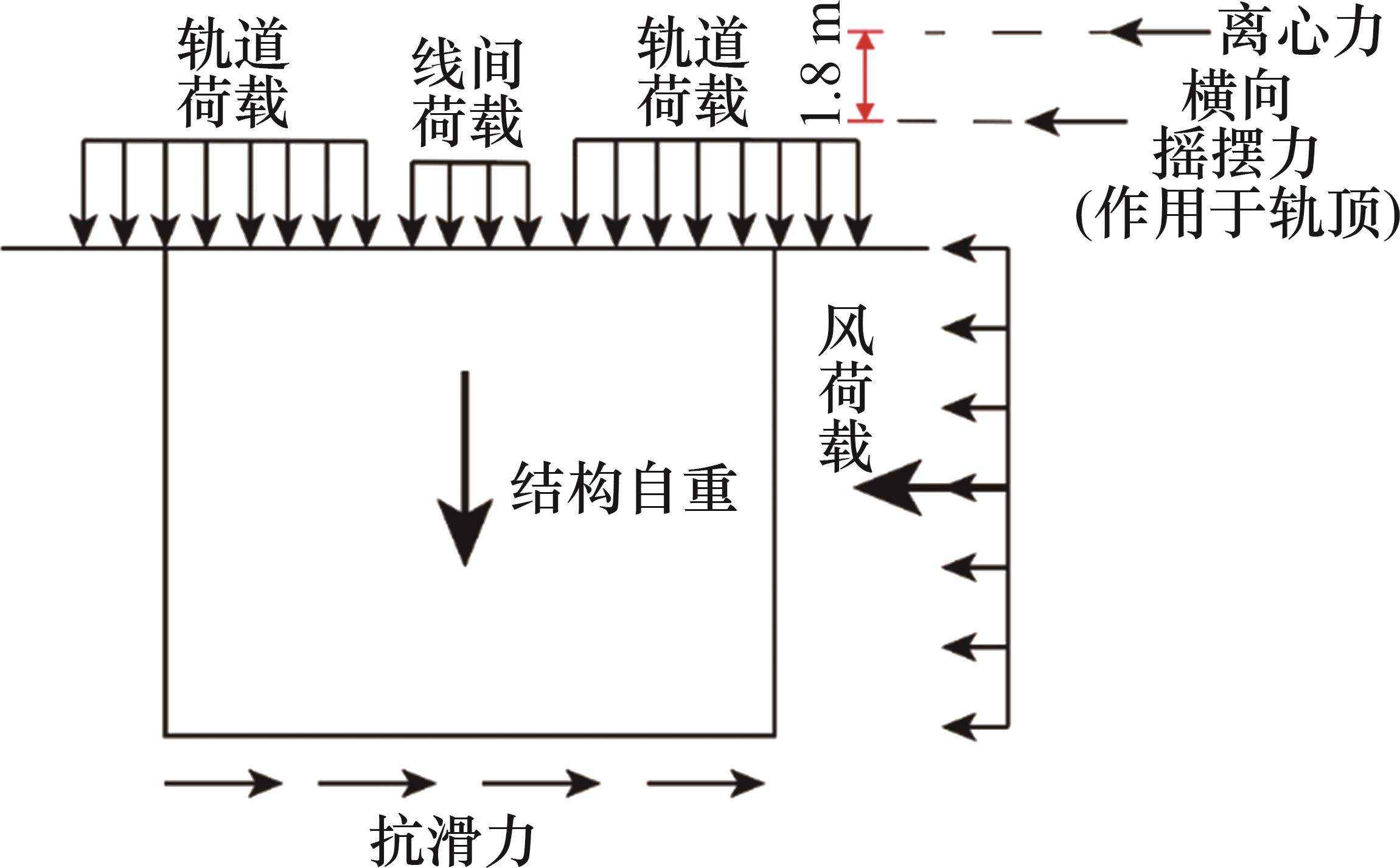
参考TB 10093—2017《铁路桥涵地基和基础设计规范》[13]中基础滑动稳定的检算标准,滑动稳定系数应按下式计算:
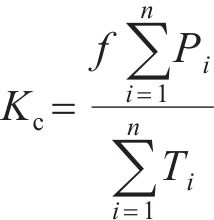
式中: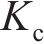
参考规范[13],考虑下雨后地基土湿滑最不利情况,基底摩擦因数f=0.25,竖向力主要考虑结构自重,轨道结构以均布荷载形式作用于箱式结构路基面上,双线轨道荷载(CRTS III型板式)为84.94 kN/m;线间均布荷载为4.37 kN/m;防护墙及外侧基础结构荷载为35.2 kN/m;整体式栏杆基础 荷载为16.2 kN/m;箱式路基荷载为542.74 kN/m,结构自重总计683.45 kN/m。
水平力主要考虑风荷载Pw、离心力Pc和横向摇摆力,其中,横向摇摆力取80 kN,其他各荷载计算方法如下:
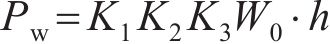
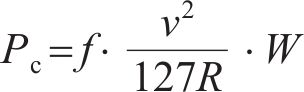
式中: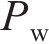
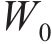
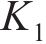
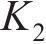
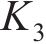
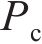
综上,考虑最不利情况,依据式(2)计算获得箱式路基基底滑动稳定系数Kc=1.49,比规定要求的1.30大,故在正常运营条件下,箱式路基不会发生侧滑。
2) 箱式路基底部不因发生较大的应力集中使而结构被破坏[14]。
考虑最不利情况,即箱式路基下无垫层,荷载直接由下部桩承担[15]。以底板单元单桩抗冲切强度确定底板厚度。参考GB 50010—2002《混凝土结构设计规范》[16],在集中反力作用下,箱式路基底板的抗冲切承载力按下式计算:
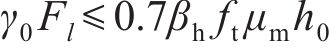
式中: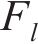
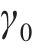
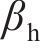
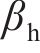
考虑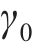
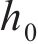
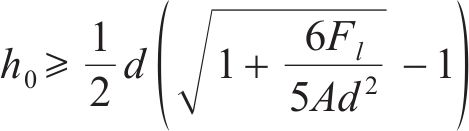
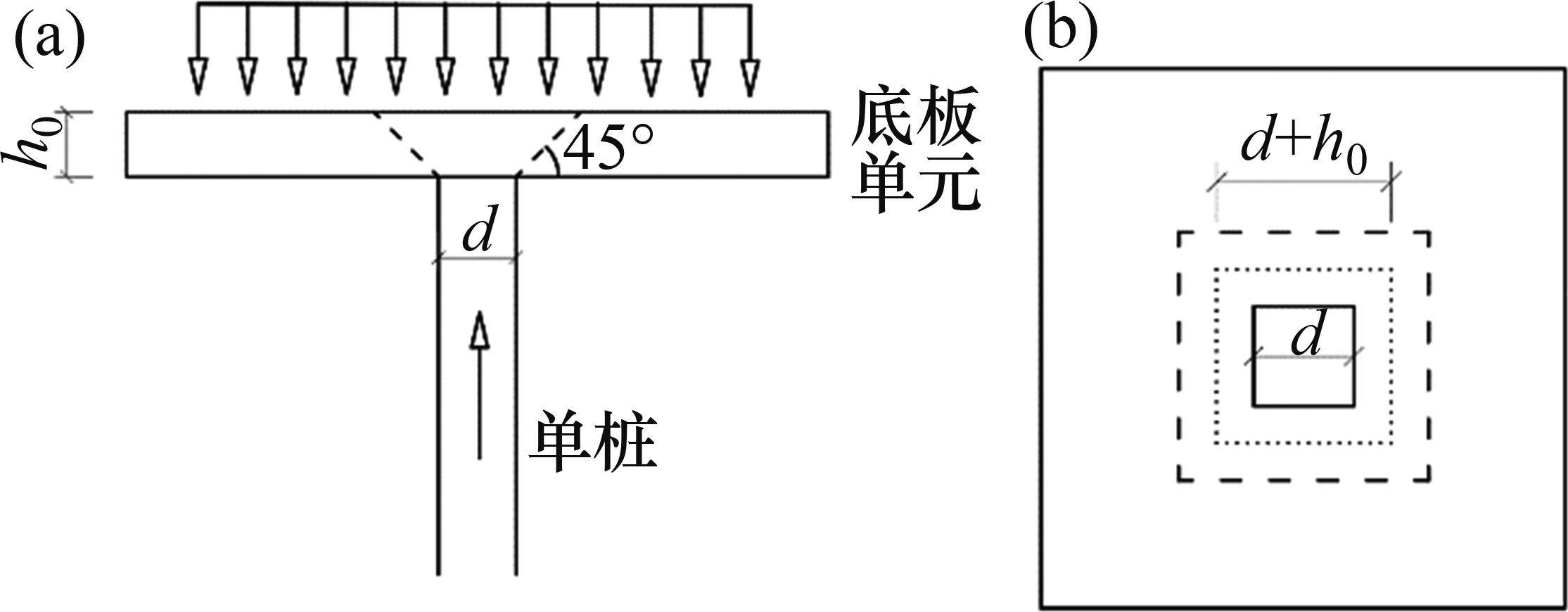
计算的单桩冲切力设计值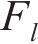
4 有限元建模
综合考虑箱式路基实际工作时与其上轨道结构和其下地基结构的相互作用关系,基于列车-轨道耦合动力学理论[18],建立车辆-轨道-箱式路基-复合地基空间动力学模型,如图4所示,对箱式路基的工作特性展开研究。
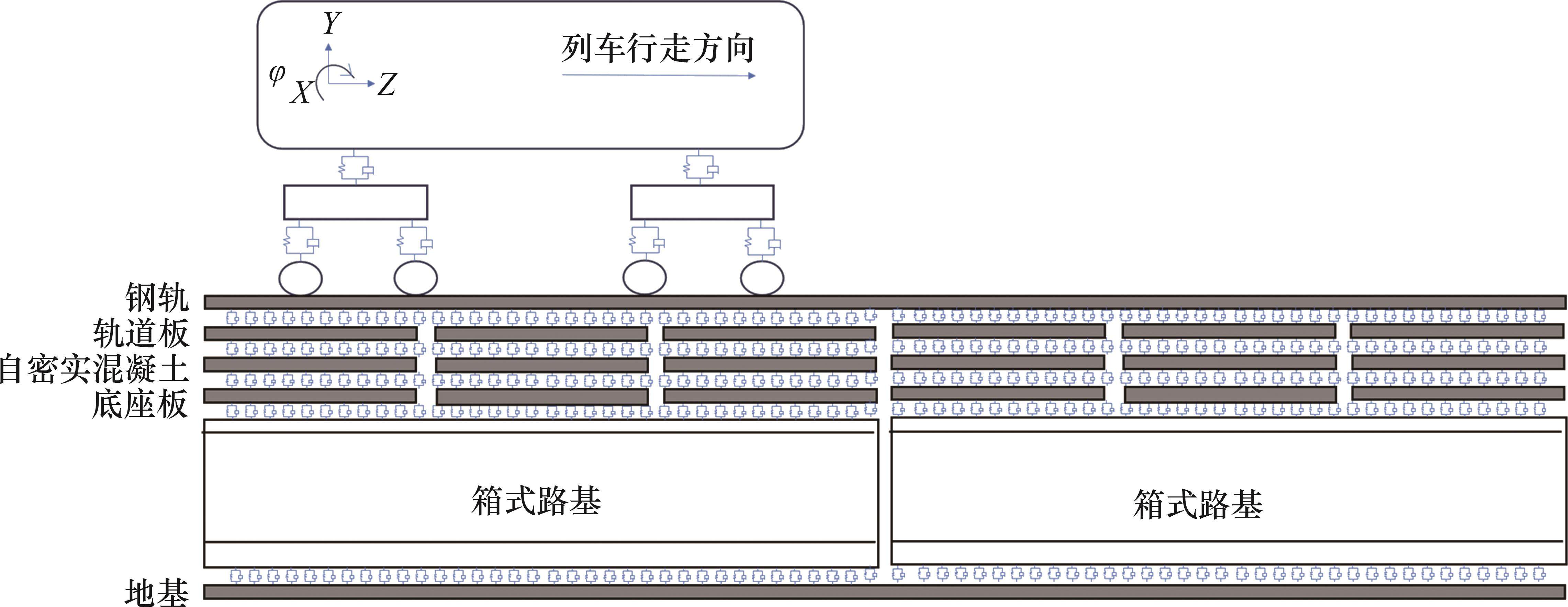
4.1 车辆模型
为了便于建立模型和分析计算,对原始系统进行简化。车辆模型由1个车体、2个转向架、4个轮对及一系和二系悬挂组成。考虑车体、转向架的沉浮、点头、横移、侧滚和摇头运动,以及每一轮对的沉浮、横移、侧滚和摇头运动,共31个自由度[19]。一、二系悬挂等参数由线性弹簧和阻尼来模拟。车辆参数选取动力学计算常用的CRH3型高速列车,运行速度为350 km/h。
4.2 轨道结构
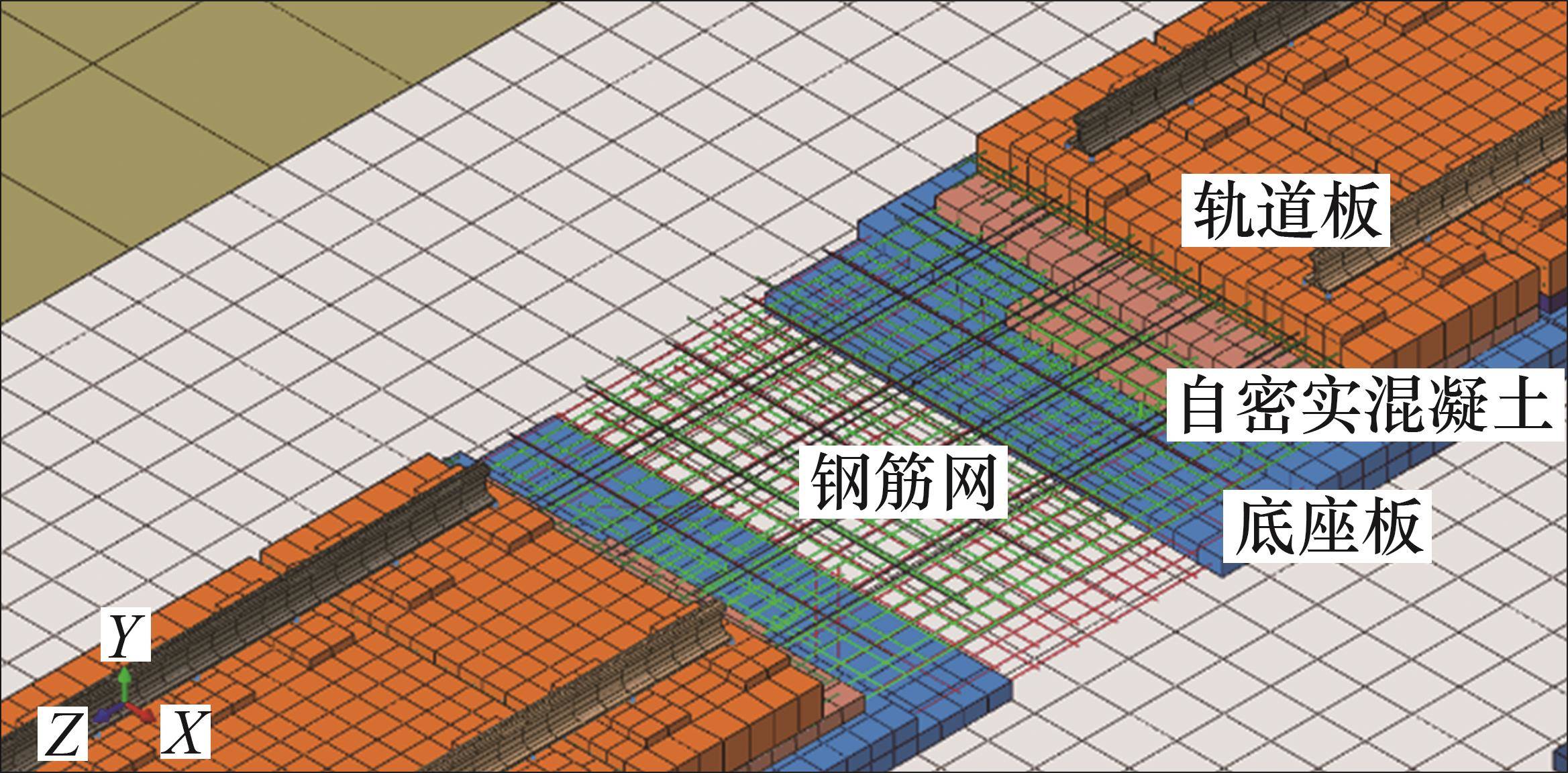
选用我国自主研发的CRTS III型板式无砟轨道,由上至下依次为钢轨、扣件、轨道板、自密实混凝土以及底座板。本文基于有限元软件ABAQUS对无砟轨道进行精细化建模,各轨道部件采用8节点实体单元(C3D8R)网格模拟,钢筋采用T3D2单元模拟,扣件采用弹簧阻尼单元模拟,间距为0.63 m,竖向动刚度为50 MPa,横向动刚度为40 MPa。
在实际工程中,轨道板与自密实混凝土层间使用门型钢筋紧密连接,故模拟中采用绑定约束;自密实混凝土与底座板之间模拟中采用面面接触的方式。参考桥梁上CRTS III型板的尺寸与布置[20],具体参数如表2所示,所建立的模型如图5所示。
| 轨道部件 | 密度/(kg∙m-3) | 弹性模量/Pa | 泊松比 |
|---|---|---|---|
| 钢筋 | 7 800 | 1.90×109 | 0.300 |
| 钢轨 | 7 850 | 2.10×1011 | 0.300 |
| 轨道板 | 2 500 | 3.60×1010 | 0.167 |
| 自密实混凝土 | 2 000 | 3.00×109 | 0.167 |
| 底座板 | 2 500 | 3.25×1010 | 0.167 |
4.3 轮轨接触
按照实际情况建立磨耗型(LM)踏面的轮对,钢轨按照60 N轨为原型建立。通过空间迹线方法确定车轮踏面与钢轨的相对位置,再根据Hertz非线性接触理论计算得到任意时刻各个轮对的轮轨间法向接触力,见式(7),据文献[21],摩擦因数取0.3。最后按照Kalker线性理论计算横向蠕滑力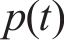
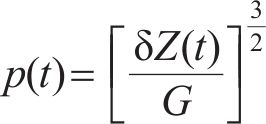
式中: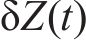
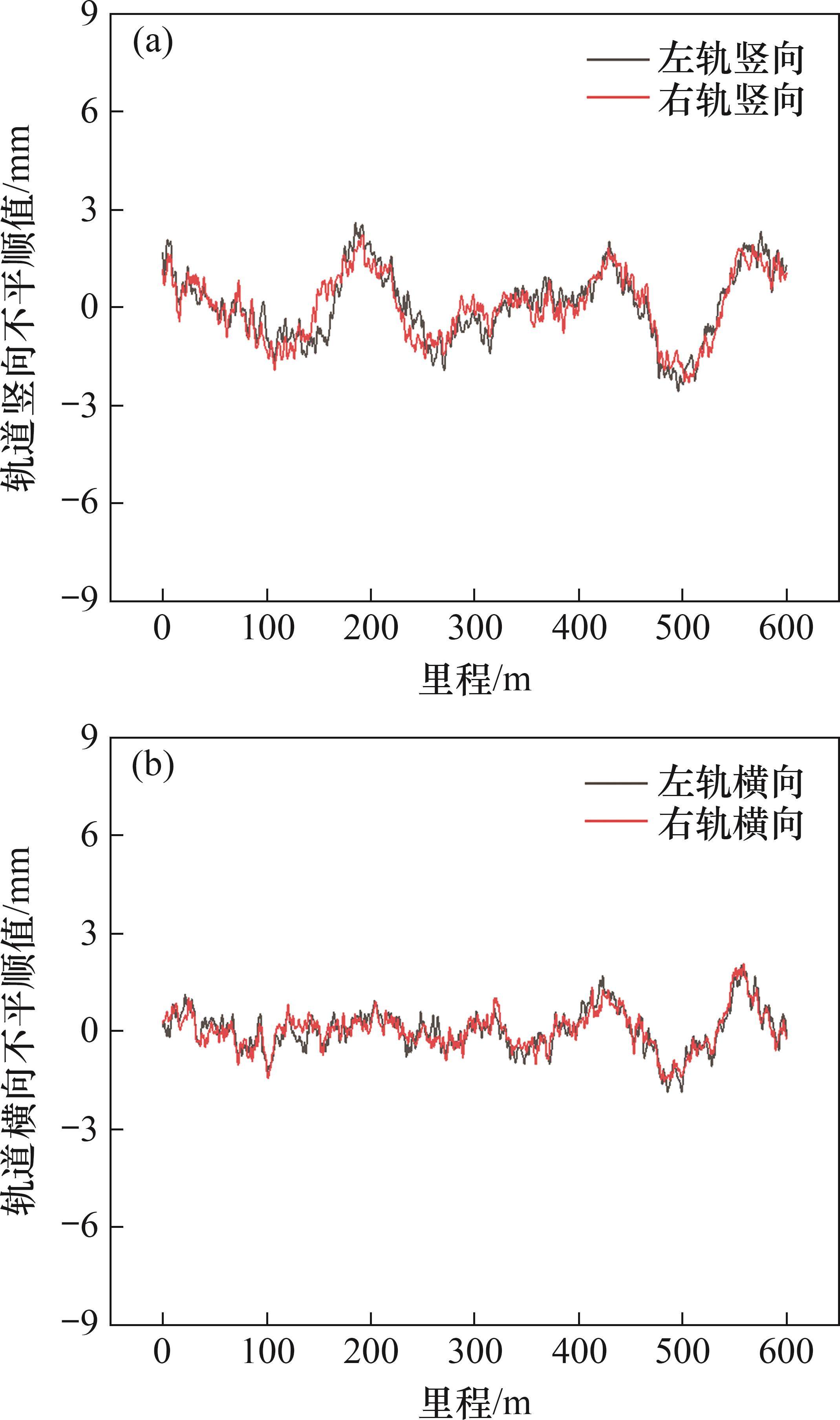
为了更加真实、准确地模拟车轨系统实际工作状态,模型中考虑轨道不平顺的存在。在数值分析中,通常采用实测不平顺数据或者按照轨道不平顺功率谱进行逆傅里叶转换[23]。本文采用我国高速铁路无砟轨道不平顺谱,如图6所示。
4.4 耦合模型
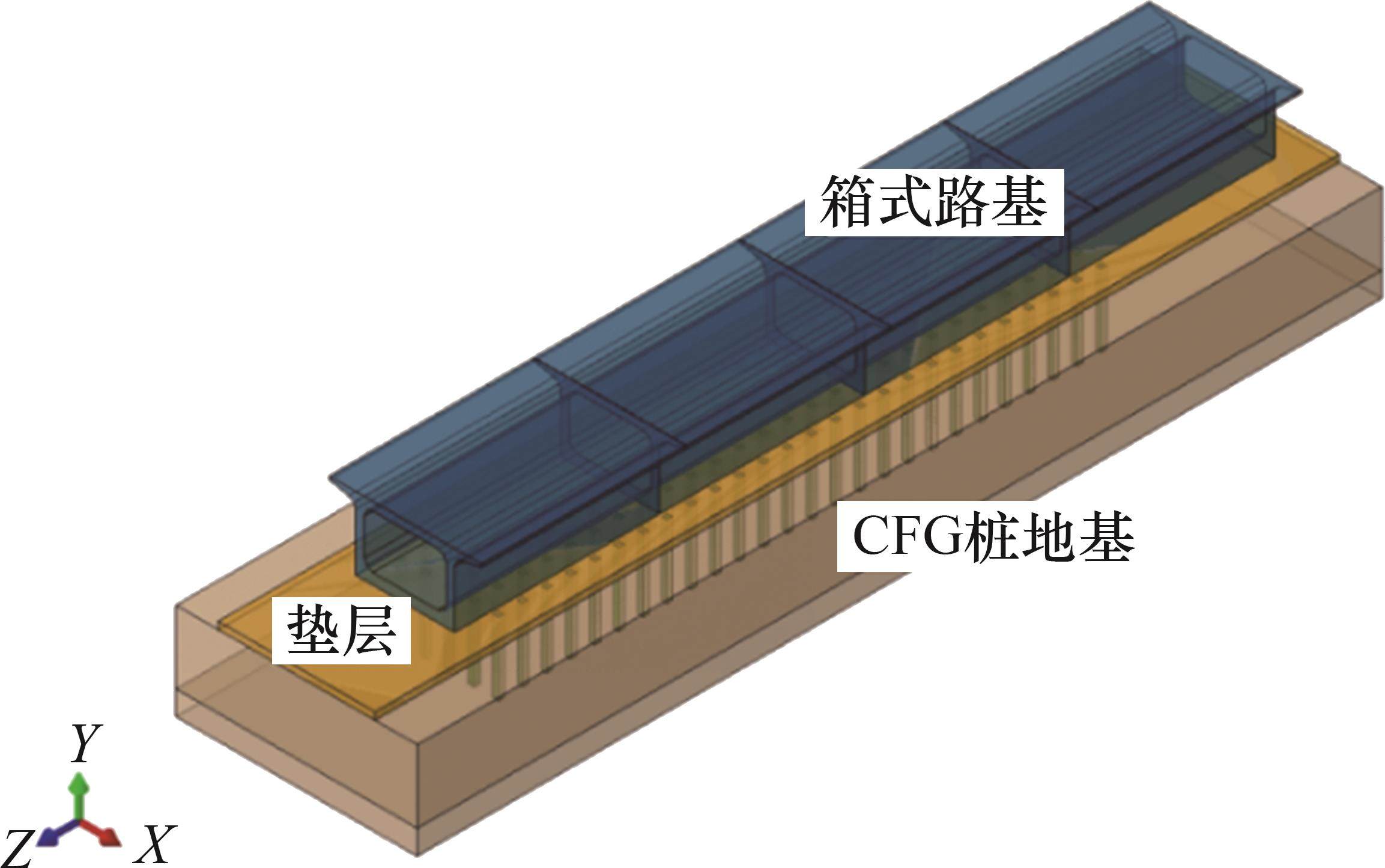
建立的模型由上至下依次为箱式路基、垫层和CFG桩地基,如图7所示,各部件材料属性[24]如表3所示,箱式路基采用C45混凝土,碎石垫层和地基采用摩尔-库仑弹塑性材料。单元网格采用8节点实体单元(C3D8R)模拟。箱式结构和垫层按照原型建立,地基土简化为厚度为8 m的2个土层,表层为厚度为5 m的粉质黏土,底层为厚度为3 m的中风化泥岩。CFG桩长为6 m,直径为0.5 m,无桩帽,采用矩形布置,桩横向间距×纵向间距为2.0 m×1.8 m,桩底打入持力层1 m。
| 部件结构 | 密度/(kg∙m-3) | 弹性模量/Pa | 泊松比 | 体积模量/Pa | 剪切模量/Pa | 黏聚力/Pa | 内摩擦角/(°) |
|---|---|---|---|---|---|---|---|
| 箱式路基 | 2 500 | 3.35×1010 | 0.167 | — | — | — | — |
| 垫层 | 2 150 | 6.00×107 | 0.200 | 3.33×107 | 2.50×107 | 4.5 | 30 |
| 桩 | 2 300 | 2.80×1010 | 0.167 | — | — | — | — |
| 粉质黏土 | 1 810 | 2.00×107 | 0.300 | 1.67×107 | 7.70×106 | 12.0 | 10 |
| 中风化泥岩 | 2 100 | 1.00×108 | 0.200 | 5.56×107 | 4.17×107 | 5.0 | 35 |
综合考虑模型边界条件以及确定列车行驶在箱式路基上的最不利情况,建立4节箱式路基长度,即51.01 m作为模型计算长度,模型断面宽度通过试算确定为3倍计算深度,取24 m。箱式路基与其上轨道板结构的接触采用绑定约束,与底部垫层按面面接触约束[25];在模型两端、地基土四周及底部均设置黏弹性边界[26]。考虑现场实际施工过程,在计算箱式路基之前,先对地基模型进行初始地应力平衡。
5 箱式路基工作特性
5.1 温度作用下箱式路基工作特性
箱式路基是一种钢筋混凝土结构,在温度作用下会产生热胀冷缩变形,这是结构设计时需重点考虑的因素。考虑到箱式路基在结构形式上类似于桥涵结构,参考TB 10002—2017《铁路桥涵设计基本规范》[12]中桥梁设计计算的全年温度分布图可知,中国全年最高设计温度为28 ℃,最低设计温度为-30 ℃,本文箱式路基温度范围取±30 ℃。热膨胀系数钢筋混凝土取0.000 01,钢轨取0.000 011 8。根据TB 10092—2017《铁路桥涵混凝土结构设计规范》[5],计算内力时取混凝土受压弹性模量,计算降温温差时取混凝土受压弹性模量的0.8,计算变形时取混凝土受压弹性模量的0.8。
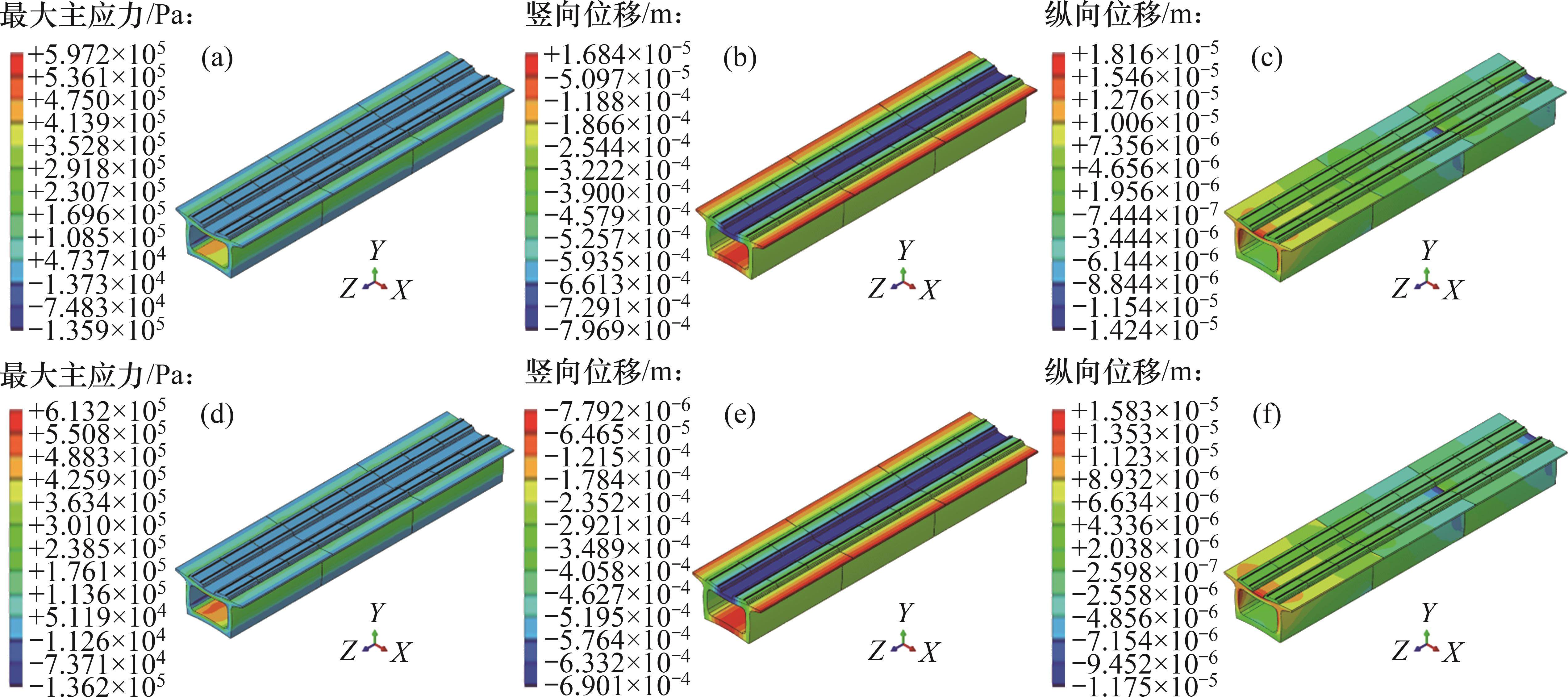
计算获得升降温荷载作用下箱式路基内力变形分布云图如图8所示。由图8可以看出:在降温或升温作用下箱式路基受力变形分布呈对称性,结构受力与变形规律相协调;箱式路基内力与位移分布相似。其内力与变形计算结果见表4。表4中内力正值为拉应力,负值为压应力。由表4可知:箱式路基结构最大主应力位于顶板底面中部,升温作用下最大主拉应力为0.613 MPa,降温作用下最大主拉应力为0.597 MPa,均比C45混凝土轴心抗拉强度标准设计值1.800 MPa小,箱体内无明显应力集中情况。此外,在升降温作用下,箱体结构整体伸缩位移较小。
| 项目 | 降温荷载 | 升温荷载 |
|---|---|---|
| 最大主应力/MPa | 0.597/-0.136 | 0.613/-0.136 |
| 横向应力/MPa | 0.597/-0.626 | 0.638/-0.613 |
| 竖向应力/MPa | 0.296/-1.294 | 0.304/-1.285 |
| 纵向应力/MPa | 0.121/-0.343 | 0.122/-0.343 |
| 横向位移/mm | 0.196/-0.262 | 0.167/-0.223 |
| 竖向位移/mm | 0/-0.794 | 0.017/-0.687 |
| 纵向位移/mm | 0.011/-0.142 | 0/-0.012 |
| 轴向力/kN | 33.310 | -30.980 |
| 弯矩/(kN·m) | 18.397 | 18.397 |
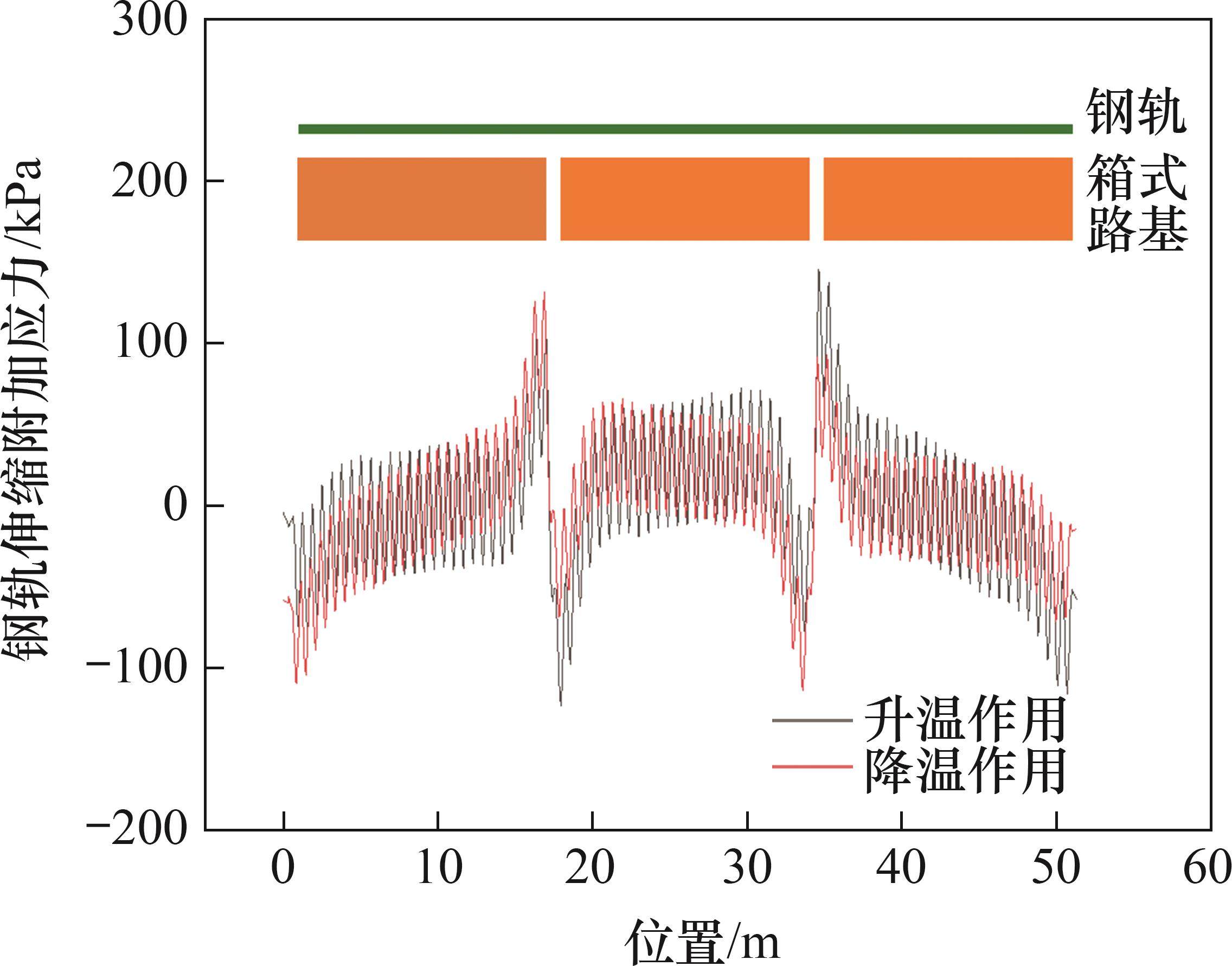
由于箱式路基与无缝线路的相互作用,钢轨会产生伸缩附加力。提取升降温作用下钢轨伸缩附加应力分布,如图9所示。由图9可见:钢轨最大伸缩附加应力为130 kPa,满足规范要求。但在箱式路基结构缝处钢轨存在应力峰,因此,在对该处的扣件选型设计及建成后的养护维修时应予以关注。
5.2 箱式路基模态分析
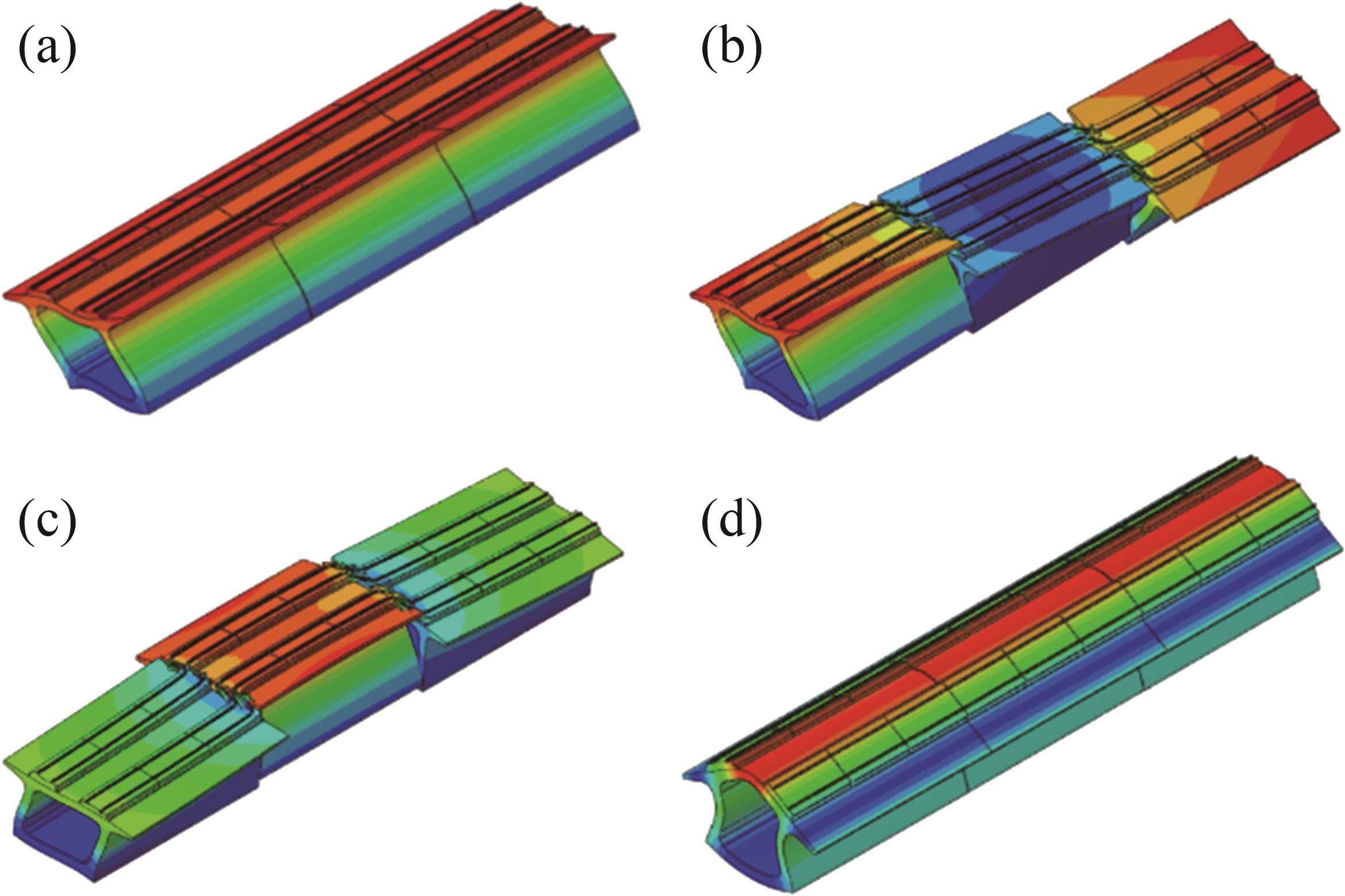
为进一步探究高速列车行驶在箱式路基上的安全性和平稳性,对箱式路基模态进行分析。提取箱式路基前10阶约束模态,统计频率和变形状态见表5,本文仅展示前4阶模态振型云图,见图10。
| 阶次 | 频率/Hz | 箱式路基变形状态 |
|---|---|---|
| 1 | 9.24 | 横向左右变形 |
| 2 | 10.74 | 横向左右变形 |
| 3 | 13.84 | 横向左右变形 |
| 4 | 23.10 | 竖向上下变形 |
| 5 | 23.21 | 竖向扭转变形 |
| 6 | 24.64 | 竖向扭转变形 |
| 7 | 25.00 | 水平扭转变形 |
| 8 | 26.15 | 水平扭转变形 |
| 9 | 27.19 | 竖向扭转变形 |
| 10 | 27.50 | 竖向扭转变形 |
根据已有研究[27],高速列车对桥梁的周期性激振规律主要与运行速度和车辆长度有关。对于我国高速铁路CRH系列动车组,车长为25 m,相应的激振频率f=0.011v(其中v为列车速度,km/h)。我国高速列车速度范围为200~350 km/h,故列车激振频率为2.2~3.85 Hz。
将箱式路基竖向自振频率与杨宜谦等[27-28]采用环境微振动法测试和跳击法在张家院子中桥 (24 m+32 m+32 m)实测的竖向自证频率进行对比,如表6所示。由表6可见:箱式路基竖向自振频率比我国常用跨度桥梁的竖向自振频率大,为23.10 Hz,远比列车激振频率大。因此,箱式路基能满足高速列车的安全平稳运行,不存在共振风险。
| 梁体 | 竖向自振频率/Hz |
|---|---|
| 箱式路基 | 23.10 |
| 24 m简支梁 | 11.25 |
| 32 m简支梁 | 8.08 |
5.3 箱式路基动力响应分析
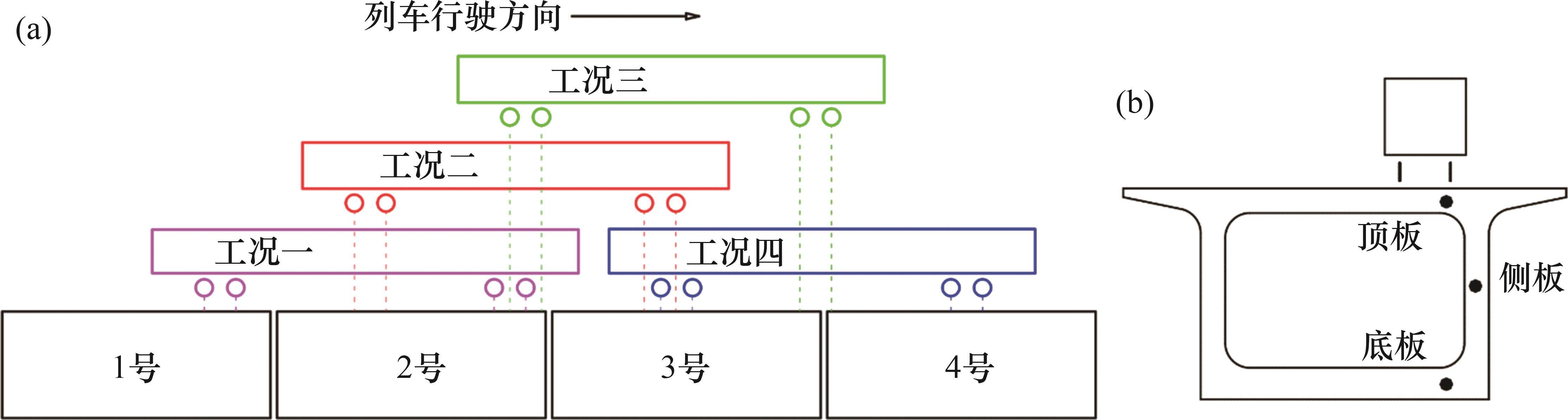
基于前文建立的车辆-轨道-箱式路基-复合地基空间非线性动力学模型,可计算得到箱式路基在行车作用下的动力响应结果。提取列车行驶在箱式路基上的4个工况,如图11所示,对比4个工况处箱式路基最大主应力和最大竖向动位移,如表7所示。由表7可知:工况一为最不利工况,即高速列车前后转向架分别位于箱式路基前后端结构缝处时,受力变形最大。此外,在工况三时,箱式路基受力变形也较大,接近于工况一的结果。因此,建议在进行箱式路基设计时,可将工况一、三作为重点检算箱式路基结构的分析工况。限于篇幅,下文主要针对最不利工况(即工况一)分析箱式路基受力变形分布规律,提取最不利截面并关注结构顶板、侧板和底板的特征点的动力响应情况。
| 工况 | 最大主应力/MPa | 最大竖向动位移/mm |
|---|---|---|
| 工况一 | 0.205 | 0.132 |
| 工况二 | 0.127 | 0.109 |
| 工况三 | 0.201 | 0.130 |
| 工况四 | 0.138 | 0.114 |
5.3.1 箱式路基动应力
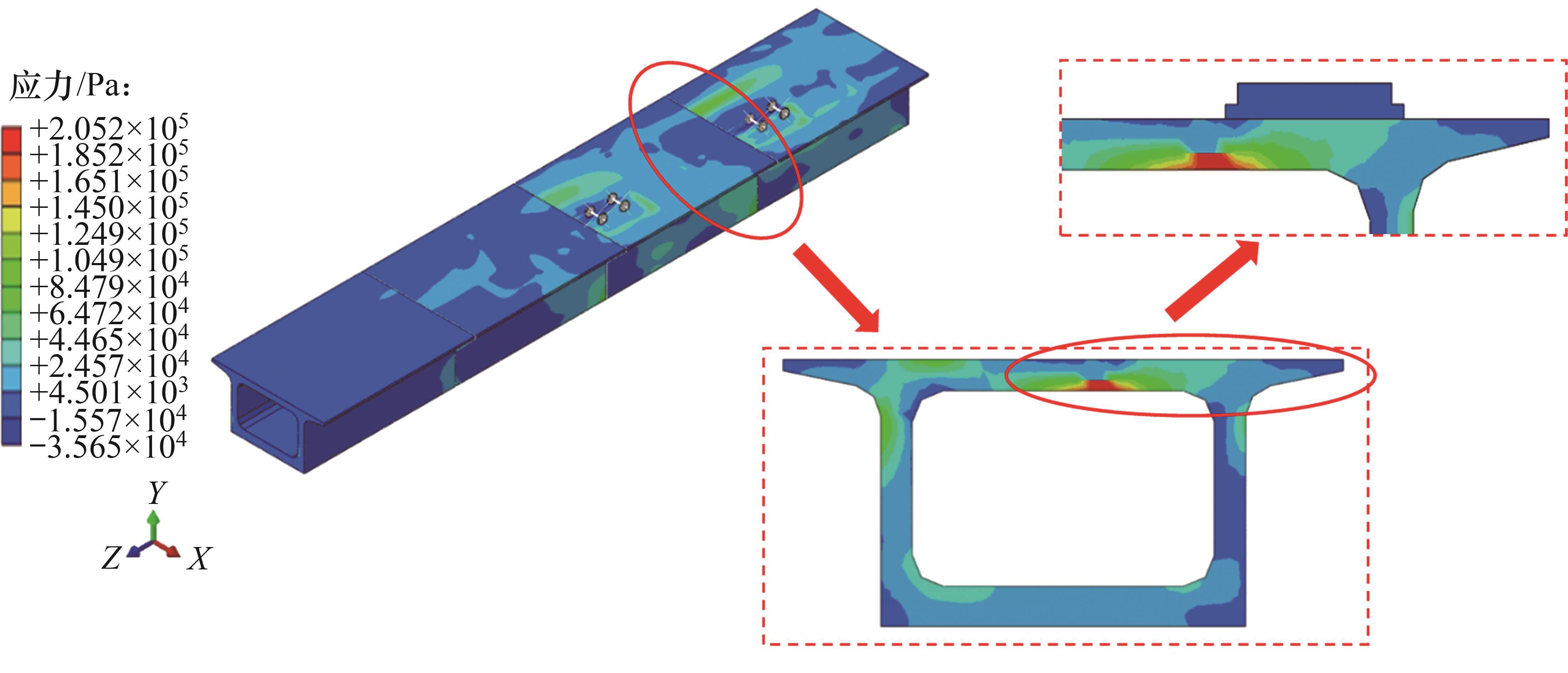
箱式路基最大主应力位于第1节箱式路基结构缝处端面,提取最不利端面,如图12所示。由图12可知:在列车荷载作用下,顶板底面中部存在一定的应力集中,最大值为0.205 MPa,比C45混凝土轴心抗拉强度标准设计值1.800 MPa小,因此,满足规范要求;侧板内侧受压,外侧与翼缘连接处存在拉应力,最大值为0.105 MPa,远比限值小;底板整体受压,两端梗腋处存在拉应力,最大值为0.05 MPa,远比限值小。
5.3.2 箱式路基动位移
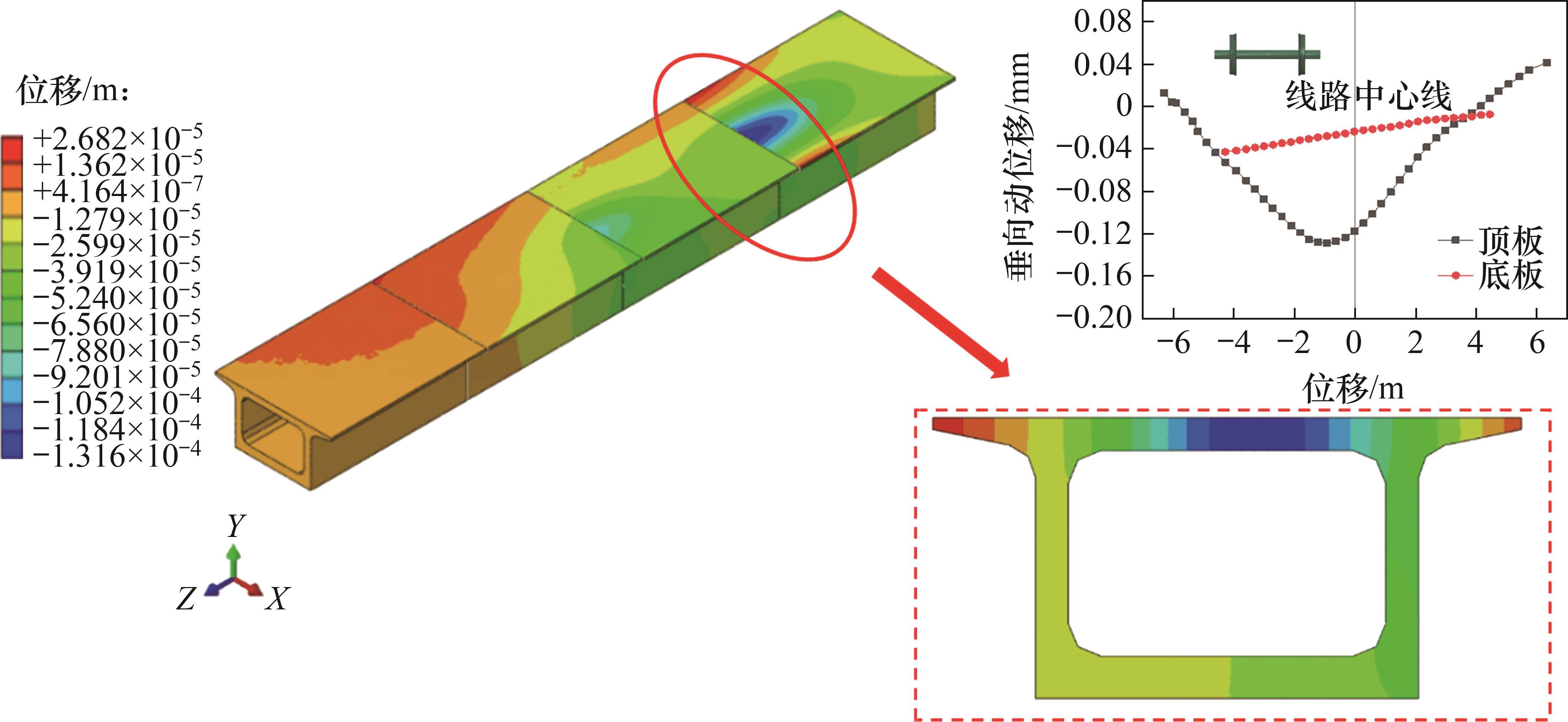
图13所示为最不利工况下箱式路基动位移分布云图。由图13可以发现:列车所在位置箱体向下弯曲变形。提取最不利截面,可知顶板中部竖向动位移最大,约为-0.13 mm(负号表示方向与坐标系正方向相反);整体上在顶板中部凹陷,在两端翼缘翘起。提取顶板和底板竖向变形曲线,可以发现双线箱式路基在单侧高速列车移动荷载作用下,顶板中心向下凹型变形,呈抛物线形状,而底板整体向下沉降变形。箱式路基由于结构整体刚度较大,在列车荷载的作用下,结构变形远比限值要求小。
为进一步探究箱式路基动位移响应规律,提取顶板、侧板、底板处的竖向动位移时程曲线,如图14所示。由图14可以发现:箱型路基竖向动位移时程曲线呈“波浪”形,在列车轮对作用处出现峰值;箱式路基顶板变形最大,侧板变形次之,底板变形最小。此外,对比顶板、侧板、底板的图形可知:由上向下,动位移逐渐由双峰曲线变为单峰曲线,表明箱式路基具有良好的荷载传递性能,结构振动趋于均匀化。
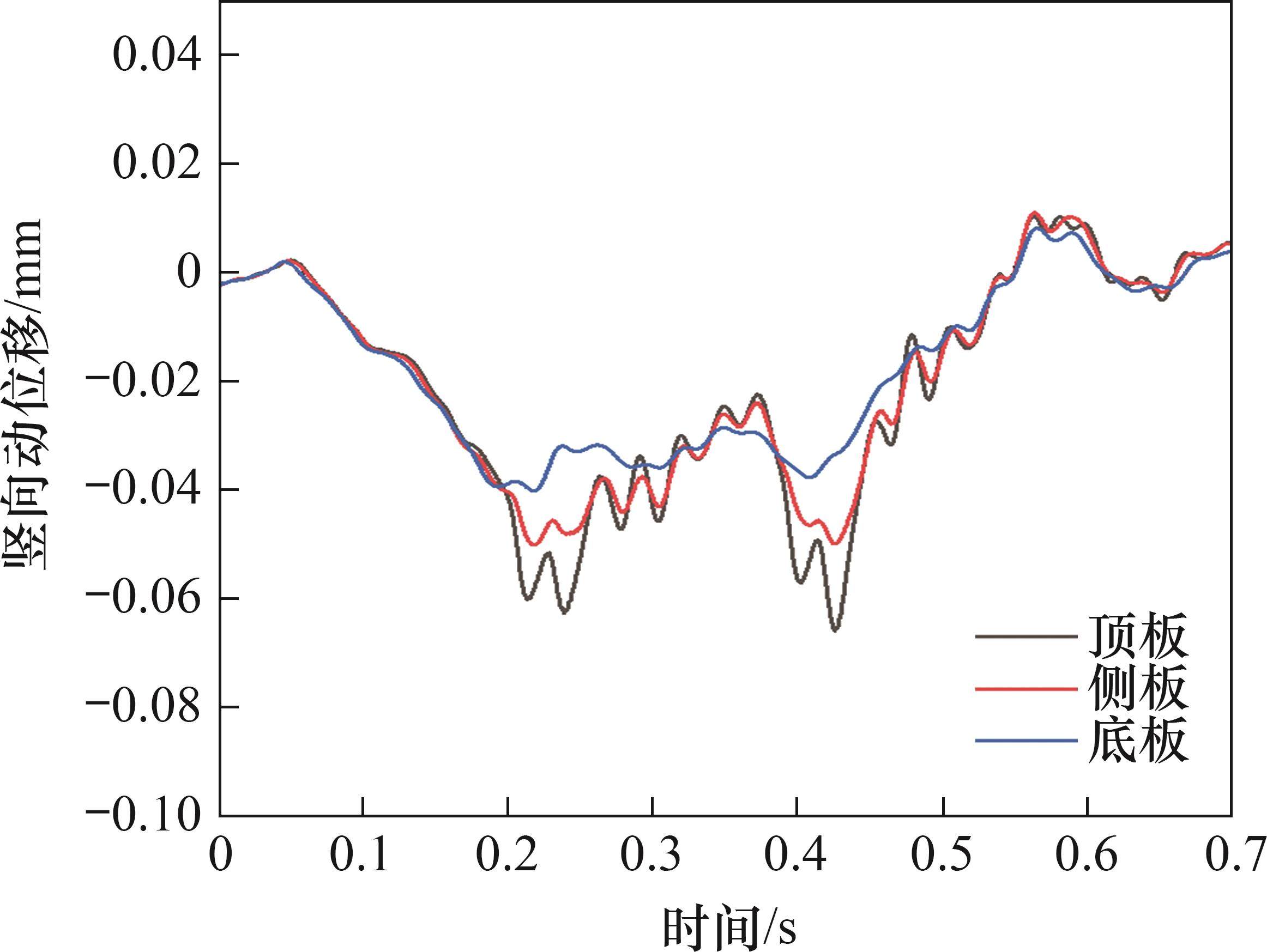
5.3.3 箱式路基动加速度
为保证列车安全运行以及结构工作性能,TB 10621—2014《高速铁路设计规范》[1]规定桥面竖向振动加速度要小于5 m/s2。提取箱式路基顶板、侧板和底板处的竖向和横向加速度,如图15所示。由图15可以看出:箱式路基动加速度最大值位于顶板处,为3.325 m/s2,横向加速度最大值为1.687 m/s2。对比文献[29]中我国传统简支梁桥振动加速度检测结果,当行车速度为350 km/h时,桥面竖向振动加速度最大值为0.800 m/s2,横向加速度最大值为0.620 m/s2。可以发现,箱式路基振动加速度较大,但比规范限值小。
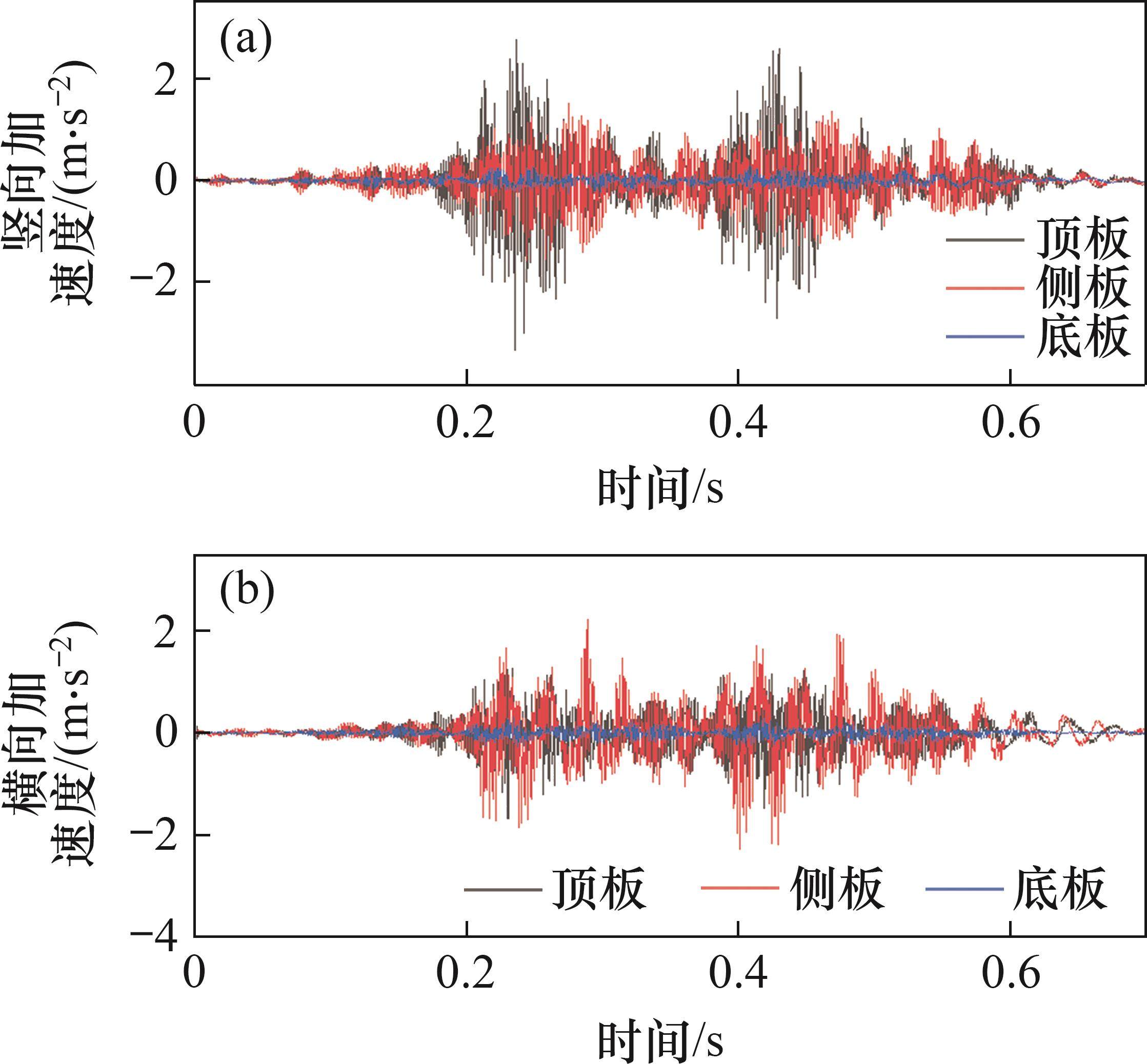
为进一步研究箱式路基荷载传递效应,提取箱型路基钢轨正下方不同深度的竖向加速度,结果如图16所示。由图16可知:加速度在钢轨扣件处急剧减小,衰减率高达97.37%,这主要是因为无砟轨道扣件本身具有减振性能,且箱式路基的整体质量大,因此,加速度会明显减小。对比箱式路基不同位置的加速度可知,顶板加速度为3.325 m/s2,底板加速度仅为0.27 m/s2,箱体内衰减率高达91.88%,到路基垫层时,已衰减93.43%。同时,由文献[30]可知,传统土质路基竖向加速度在6.7 m路基范围内衰减率为80%,至路基底面时为1.5 m/s2。经对比可知,对于同等高度的箱式路基和传统土质路基,箱式路基对列车动荷载的吸收和耗散效果更好。
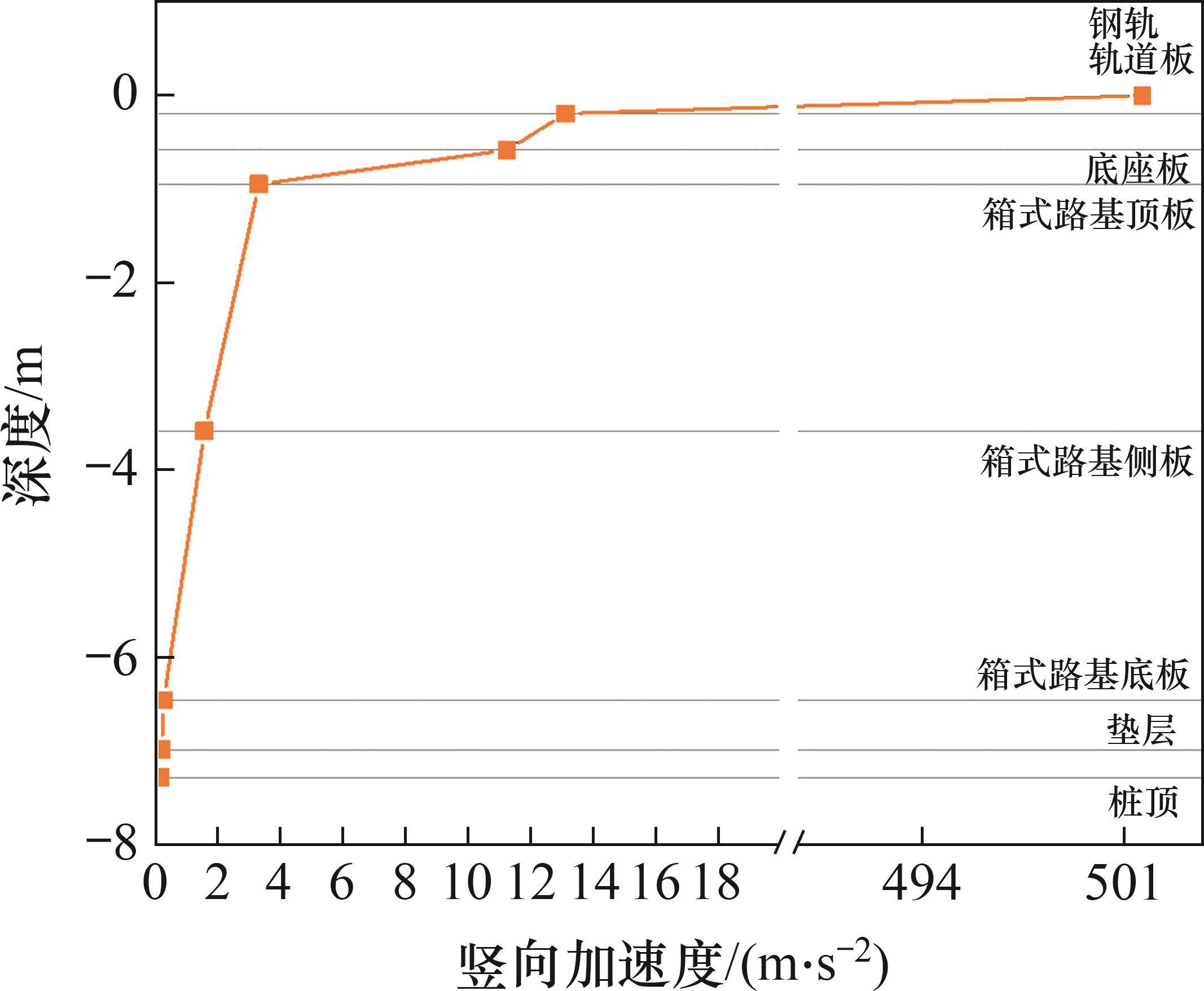
6 结论
1) 分析了箱式路基的结构特点,明确了箱式路基结构组成及形式,提出了箱式路基设计荷载及荷载组合。
2) 针对箱式路基结构特点,分别提出了纵向长度和底部厚度确定原则,并通过计算分析,建议箱式路基结构长度为16.99 m,底板厚度不小于500 mm。
3) 建立了车辆-轨道-箱式路基-复合地基空间非线性力学分析模型,确定了最不利荷载作用位置,即高速列车前后转向架分别位于箱式路基前后端结构缝处时受力变形最大。
4) 一般情况下,箱式路基受温度的涨缩作用较小,但在箱式路基端缝处存在钢轨应力峰。
5) 箱式路基自振频率比我国常用跨度桥梁的自振频率大,为23.10 Hz,且远比列车激振频率大,能满足高速列车的安全平稳运行,不存在共振风险。
6) 在列车作用下,顶板底面中部存在应力集中,但满足梁体强度设计要求;箱式路基整体刚度较
大,动位移远比限值小;在速度为350 km/h时,箱式路基动加速度最大值位于顶板处,为3.325 m/s2,比我国传统简支梁桥振动加速度大,但比规范限值小;对比传统土质路基,箱式路基对动荷载的吸收和耗散能力更强,到路基垫层时,已衰减93.43%,因此,设计箱式路基底部复合地基时可不考虑列车动荷载的影响。
肖宏, 陈盈盈, 宋绪国, 等. 高速铁路箱式路基新型结构研究[J]. 中南大学学报(自然科学版), 2025, 56(2): 769-781.
XIAO Hong, CHEN Yingying, SONG Xuguo, et al. Study on new structure of high-speed railway box-type subgrade[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 769-781.
http://dx.doi.org/10.11817/j.issn.1672-7207.2025.02.030

