树脂锚固技术广泛应用于矿山支护、隧道工程、边坡支护等岩土工程领域[1-3]。随着煤炭资源的开采逐渐进入深部阶段,锚杆锚固体面临的地层环境更复杂,深部巷道高温热害和高地压造成深部软岩巷道锚固支护效果降低[4-5]。锚固剂-围岩界面作为软岩巷道锚固支护系统中相对薄弱的部分,易发生脱黏滑移[6]。为减少锚固界面失效滑移情况的发生,工程上一般采用增加锚固长度的方式提高锚杆支护张拉失效破坏的阈值。但在地温、地压环境下,不同锚固长度锚固体荷载传递、应力分布及锚固界面失稳机理不明。因此,研究温压环境下不同锚长锚固体受力特征及荷载传递规律具有重要意义。
为探究锚固体受力特征及拉拔荷载传递规律,国内外学者开展了大量研究。针对拉拔荷载在锚固段荷载传递规律,李怀珍等[7]基于锚固剂-围岩界面脱黏失效滑移模型,推导了弹性阶段锚固界面剪应力分布公式;尤春安[8]基于Mindlin解析法,得到了拉拔荷载作用下的锚杆轴力和剪应力沿锚杆分布的解析式;张季如等[9]采用弹性理论分析法,分析了预应力锚索锚固段剪应力分布规律。针对不同锚固长度锚固体受力特征研究,王洪涛等[10]建立了不同锚固长度下巷道围岩力学分析模型,研究了锚杆应力分布规律;姚强岭等[11]通过室内拉拔试验得到了不同锚固长度锚固段剪应力和轴力变化规律;肖同强等[12]针对软岩锚固体利用锚杆拉拔测试系统,得到了不同锚固长度锚杆的受力特征;黄明华等[13]采用荷载传递法分析了锚固长度对锚杆受力的影响,得出了临界锚固长度计算方法。
以上学者采用室内试验和理论分析等方法探讨了拉拔荷载在锚固段的荷载传递规律及不同锚固长度锚固体受力特征,取得了许多有价值的成果。但深部巷道锚固支护系统受地温、地压影响,锚杆失锚率增大,针对地温、地压环境下锚固体受力特征及锚杆拉拔过程中锚固体系传力规律的研究还不完善。为此,本文作者采用理论分析、室内试验和数值模拟相结合的方法研究了在温-压耦合环境拉拔荷载作用下,锚固段弹性变形阶段锚固剂-围岩界面剪应力、锚杆轴力分布特征和拉拔过程中锚杆荷载传递规律,研究成果可为优化深部软岩巷道锚杆支护参数提供参考。
1 锚固段弹性拉拔阶段荷载分布理论分析
拉拔荷载作用下锚固段剪应力分布不均,但因研究方法、锚固因素、分析模型的不同,剪应力具体分布形式不同[14-15]。且锚固界面的剪应力与温度、侧压系数、围岩强度、锚固长度等锚固因素相关,以影响因子ζ表征锚固因素对剪应力的影响,代入锚固微元段平衡方程。锚固段受力模型如图1所示,图1中,τ(x)为剪应力;F为任意锚固微元段的轴向荷载;P为锚杆轴向载荷。
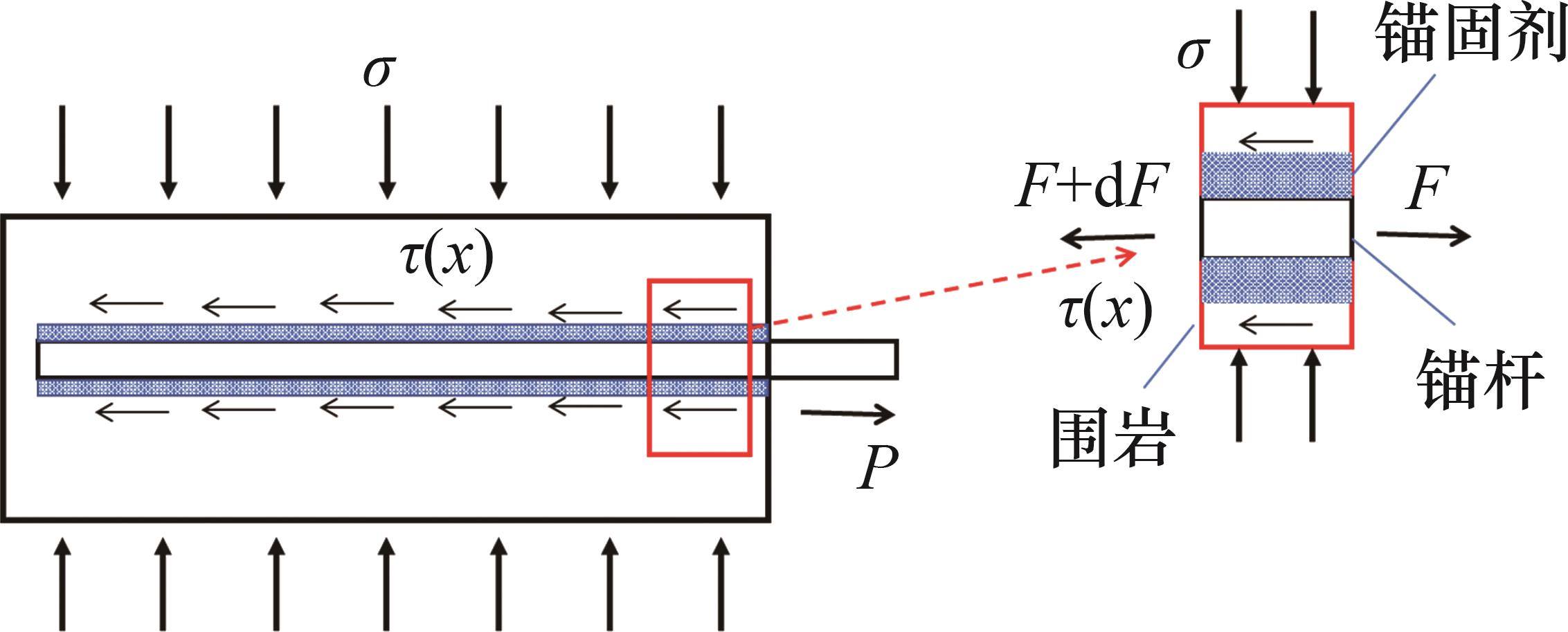
对锚固微元段进行受力分析,建立平衡公式:
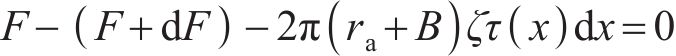
式中:ra为锚杆的半径;B为破坏后锚杆黏结树脂层的厚度。
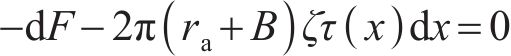
根据胡克定律,锚杆在轴向荷载作用下产生的轴向位移为:
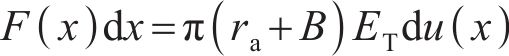
式中:ET为锚固体复合弹性模量,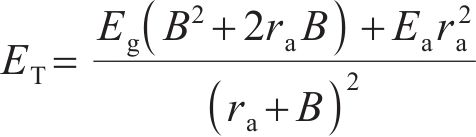
联立式(2)和(3)得:
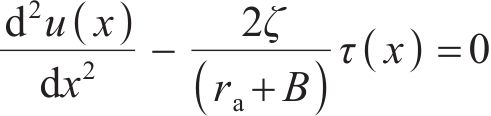
为简化分析过程,基于BENMOKRANE等[16]提出的三阶段线性函数对锚固界面剪应力-剪切位移关系进行描述。简化三段式模型曲线如图2所示。
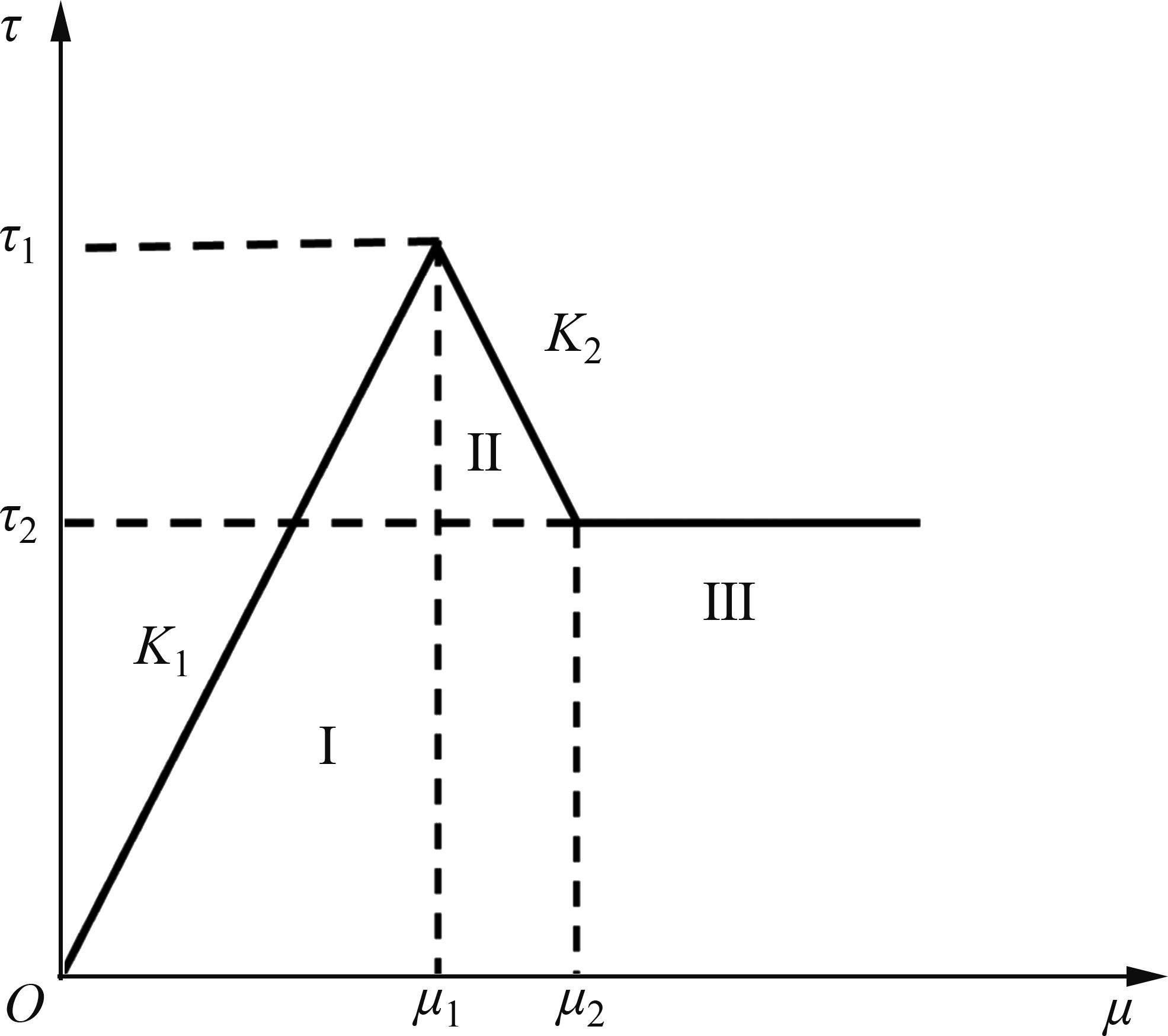
由三阶段线性函数可知,弹性阶段锚固段的荷载传递函数为:
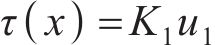
式中: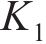
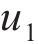
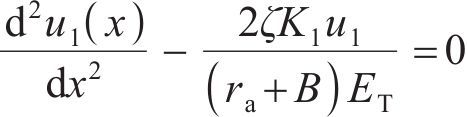
令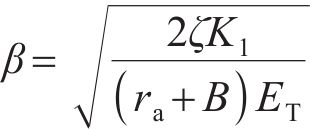
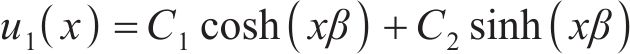
将边界条件锚固段起始端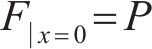

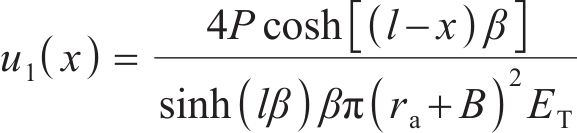
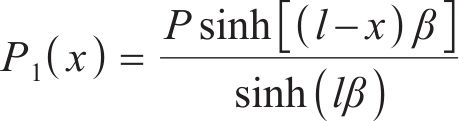
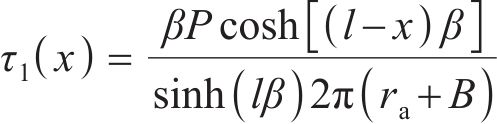
根据锚固段拉拔位移对参数β进行求解。在锚固段弹性变形阶段,锚杆端部的位移包括锚杆自由段位移和锚固段位移。锚杆端部的位移为s,锚杆自由段位移为u2,可求得锚固段位移u1:
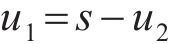
由胡克定律得锚杆自由段位移:
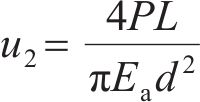
式中:L为锚杆自由段长度;d为锚杆直径。
锚固段始端x=0的变形量u1(0)为:
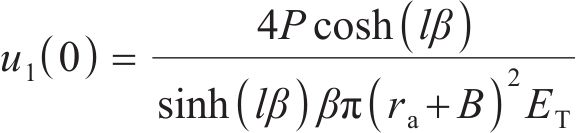
由式(11)求得锚固段端部的变形量u1(0),计算参数β。将β代入锚固界面剪应力和锚杆轴力方程,得到弹性阶段不同锚固条件下锚固剂-围岩界面的剪应力和锚杆的轴力方程。
2 不同锚固长度锚固体拉拔试验
2.1 试验模型制作
深部巷道地质环境复杂,在温压锚固环境下,深部软岩巷道围岩稳定性控制是亟待解决的难题[17-18]。配制抗压强度较小的围岩模拟深部软岩研究温压作用下软岩锚固体受力变形和拉拔荷载传递规律。以普通河沙作为填料,石膏和P.O32.5普通硅酸盐水泥为胶凝材料。为延缓围岩材料凝结,选用聚羧酸作为缓凝剂,用量为胶凝材料质量的1%。经多次试配,得到锚固体围岩的配比,如 表1所示。按照配比浇筑锚固体试件A、B、C,锚固体模型长×宽×高为500 mm×150 mm×150 mm,锚孔直径为16 mm,选用直径为10 mm的螺纹钢筋作为锚杆。在锚杆两侧开槽,槽中安放5个应变片,相邻应变片间隔9 cm。为防止锚固和拉拔过程中应变片和导线受损,采用硅橡胶和环氧树脂保护应变片和导线。为减少锚固阻力,采用流动性较好的全长树脂锚固剂进行锚固,锚固时调整锚杆位置,使锚杆位于锚孔中心。
| 试样编号 | 砂、水泥、石膏质量比 | 水的质量分数/% | 抗压强度/MPa |
|---|---|---|---|
| A | 5꞉2꞉9 | 20 | 3.10 |
| B | 6꞉4꞉6 | 25 | 6.08 |
| C | 3꞉4꞉4 | 26 | 9.02 |
2.2 试验装置及试验方案
采用温压加载装置对锚固体施加荷载,利用拉拔装置对锚杆进行拉拔,研究拉拔过程中荷载传递规律。试验装置包括围压加载装置、温度加载装置、拉拔装置、数据采集系统。试验装置及锚固试件制作如图3所示。

1) 围压加载装置。为了实现对锚固体围压加载,采用万能试验机和千斤顶对锚固体施加围压。万能试验机和千斤顶的最大输出荷载均为1 000 kN。万能试验机对锚固体竖直方向施加压力,采用应力控制,加载速度为0.01 MPa/s。利用油泵和数显压力控制器控制千斤顶对锚固体水平方向施加压力。在锚固体和加压顶头之间垫放厚铁板均分压力。千斤顶底部作用在工字钢反力架上。
2) 温度加载装置。温度加载装置包括长×宽×高均为200 mm×150 mm×20 mm的铸铝加热板4块、温度控制器1个和温度传感器1个。将铸铝加热板和K型温度传感器连接温度控制器,K型温度传感器感温端插入锚固体底部预留测温孔内。利用加热板对锚固体加热,温度传感器感温端反馈锚固体内部温度,当温度达到预设温度时,温度控制器停止对铸铝加热板供电,加热停止。
3) 拉拔装置。采用最大输出荷载为300 kN的手动锚杆拉拔仪对锚杆进行拉拔。为记录拉拔过程中张拉应力变化情况,利用压力变送器和数显压力记录仪实时采集压力数据,采集频率为1次/s。
4) 数据采集系统。数据采集系统包括数据采集仪和数显压力记录仪,分别采集应变、位移及拉拔仪压力。
对深井软岩巷道的锚固单元受力进行分析,巷道中的锚固单元受“三向五面”应力作用。将锚固体承受的水平和竖向围压按侧压系数划分为第一或第二主应力。锚固体底部围岩较稳定,受力较小,作为第三主应力。试验中对锚固体水平和竖向施加荷载,锚固体底部采用钢板约束其膨胀变形,钢板对锚固体的反作用力作为第三主应力。采用铸铝加热板进行加热,模拟锚固体承受的地温环境。考虑温度、侧压系数、锚固长度和围岩抗压强度4个因素,设计正交试验,并按锚固体围岩强度将锚固试件分成3组,试验方案如表2所示。
| 编号 | 锚固方式 | 围岩抗压强度/MPa | 温度/℃ | 侧压系数 |
|---|---|---|---|---|
| A1 | 端锚 | 3.10 | 30 | 0.8 |
| A2 | 全锚 | 3.10 | 45 | 1.2 |
| A3 | 加长锚 | 3.10 | 60 | 1.0 |
| B1 | 加长锚 | 6.08 | 30 | 1.2 |
| B2 | 端锚 | 6.08 | 45 | 1.0 |
| B3 | 全锚 | 6.08 | 60 | 0.8 |
| C1 | 加长锚 | 9.02 | 45 | 0.8 |
| C2 | 端锚 | 9.02 | 60 | 1.2 |
| C3 | 全锚 | 9.02 | 30 | 1.0 |
试验过程:1) 在试验平台上组装试验装置;2) 调整万能试验机和千斤顶对锚固体施加预应力,使加载铁板和锚固体贴紧;3) 使用温度加热装置将锚固体加热至预设温度;4) 按侧压系数对锚固体施加围压,达到设定围压后,稳定围压;5) 利用拉拔仪对锚杆施加拉拔荷载至锚杆脱锚;6) 保存试验数据。
2.3 试验结果与分析
2.3.1 锚杆拉拔荷载-位移关系
锚杆拉拔荷载-位移关系如图4所示。由图4可知,拉拔过程大致分为3个阶段:1) 弹塑性阶段,锚杆的拉拔荷载与位移呈线性增长,拉拔荷载增速较快,随着拉拔荷载增大,锚固界面逐渐进入塑性阶段;2) 失效破坏阶段,达到极限拉拔荷载后,锚固剂-围岩界面发生脱黏失效,拉拔荷载明显下降;3) 残余应力阶段,锚固界面脱黏失效后,锚杆位移快速增大,随着锚固层被拉出,摩阻力缓慢降低。
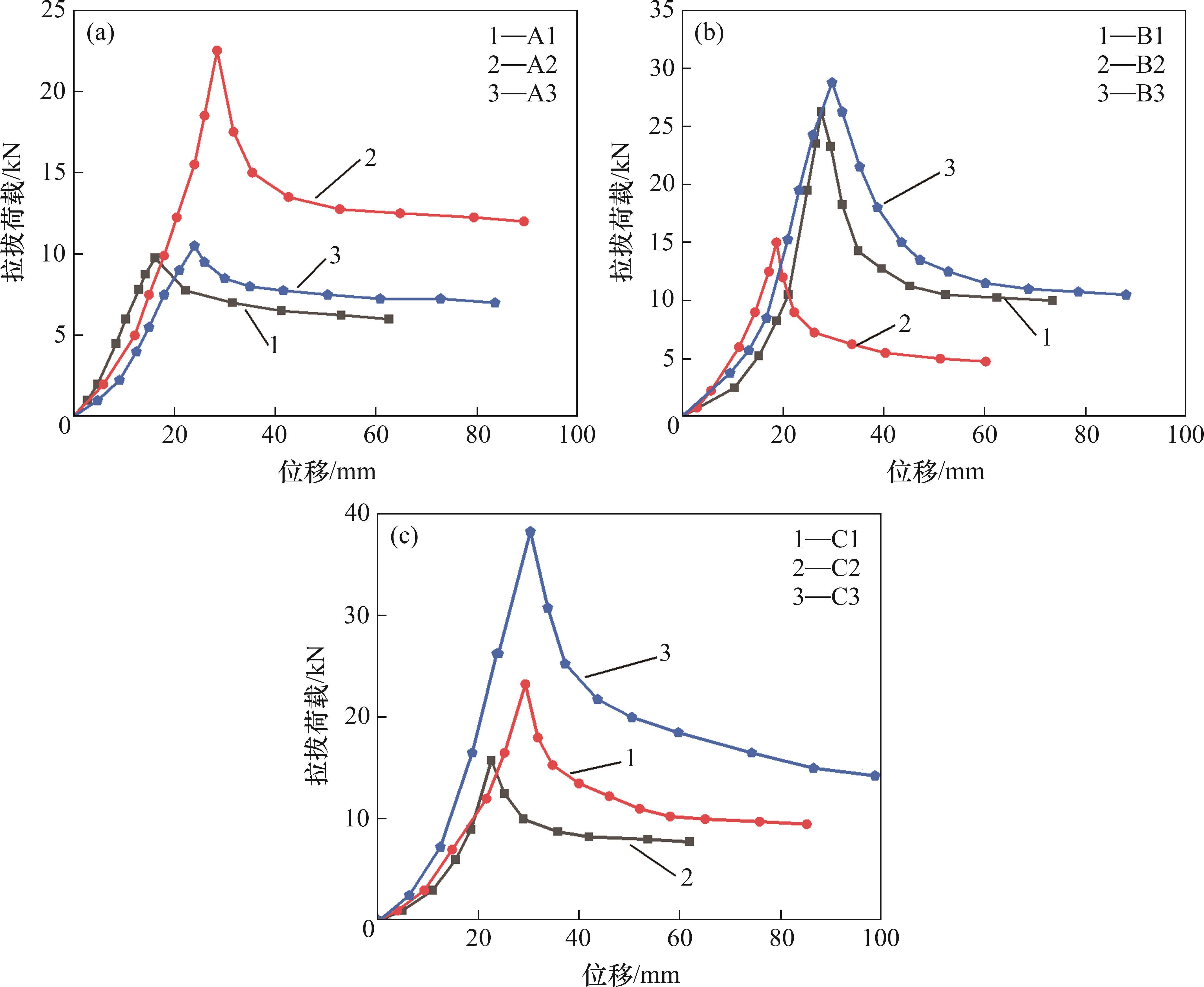
在锚固段弹性变形阶段,不同锚固长度锚固界面剪应力分布特征类似,但锚固剂-围岩界面的剪应力受锚固因素影响,参数β不同。根据拉拔荷载-位移关系和弹性阶段锚固段轴向位移公式,得到不同锚固条件的参数β如表3所示。
| A1 | A2 | A3 | B1 | B2 | B3 | C1 | C2 | C3 |
|---|---|---|---|---|---|---|---|---|
| 0.992 | 0.645 | 0.594 | 0.885 | 0.884 | 0.671 | 0.686 | 0.800 | 0.676 |
根据三阶段线性函数,锚固界面失效滑移前,锚固段处于弹性变形状态。将参数β代入弹性阶段的锚固剂-围岩界面剪应力和锚杆轴力方程,得到锚固剂-围岩界面剪应力分布图和锚杆轴力分布图,如图5所示。锚固剂-围岩界面的剪应力分布不均,剪应力呈下凹趋势递减。随着锚固剂不断深入锚固体内部,剪应力递减速度减缓,剪应力衰减速率先快后慢,在锚固段尾端剪应力曲线近似水平。由图5可知,锚杆轴力由锚固始端至锚固末端近似呈线型单调递减分布。
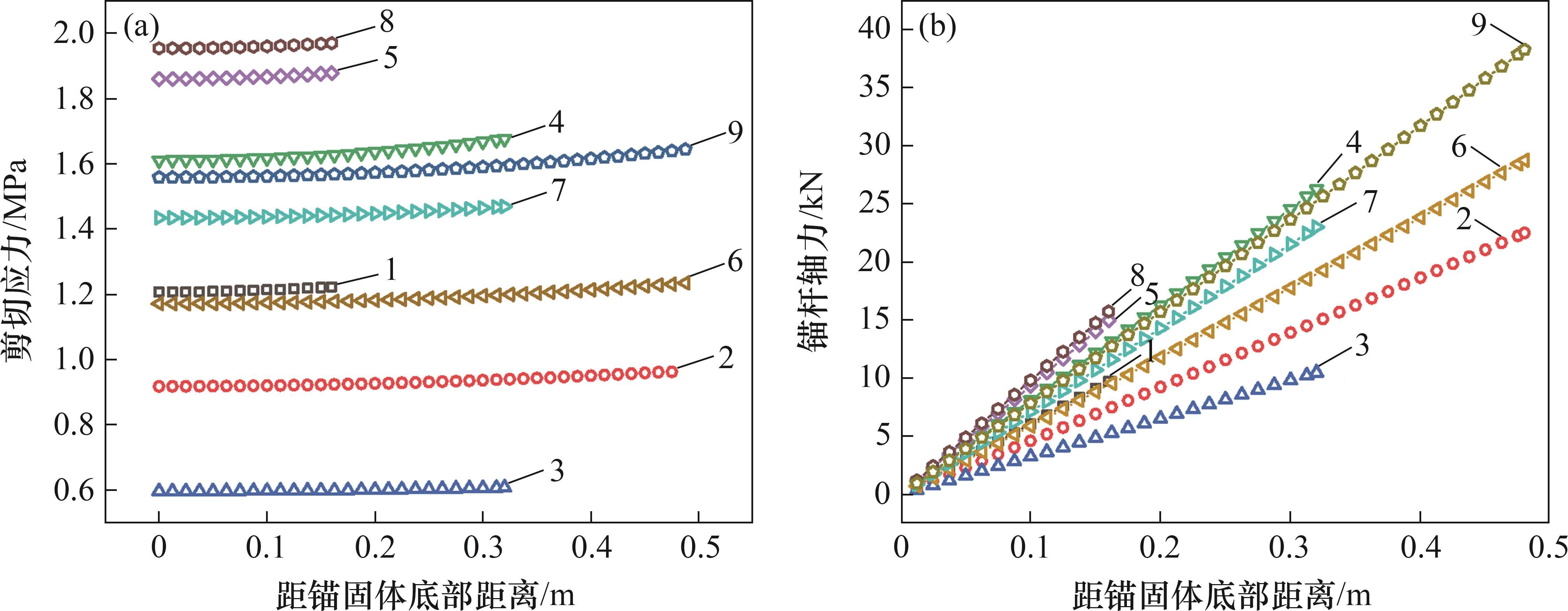
2.3.2 锚固体受力破裂及锚固失效特征
在温压条件下,锚固体受拉拔荷载作用,不同锚长锚固体受力变形情况不同。锚固体临空面变形特征如图6所示。从图6可见:在围压加载过程中,锚固体向临空自由面膨胀变形;在不均匀应力作用下,围岩强度较弱的锚固体临空面出现裂纹。其中,端部锚固体变形破裂特征较为明显,临空面出现竖向裂缝,裂缝向锚固体内部延伸,但延伸距离较小,锚孔未发生严重破坏(图6(a));加长和全长锚固体未出现明显的裂纹;全长锚固体锚固层被拉出,锚固剂层表面有与围岩摩擦产生划痕(图6(b)和(c))。

2.3.3 拉拔荷载传递规律
锚杆受力变形如图7所示。
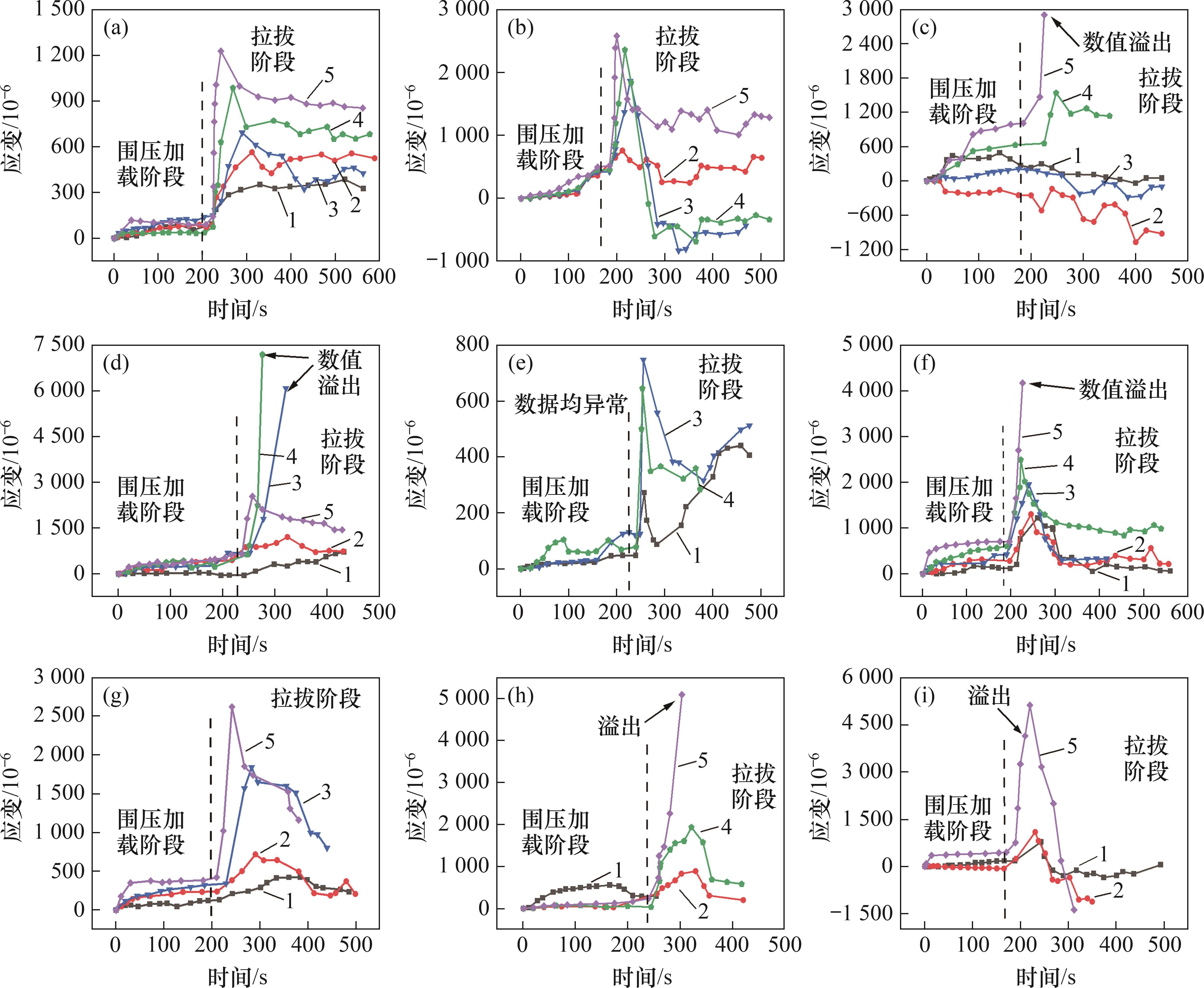
端部锚固仅有测点1(图3(b))在锚固层内部,围压加载过程中锚固体向临空面膨胀变形,在锁具限制下,锚杆处于张拉状态。应变片在张拉应力作用下,发生不同程度变形。由于锚固段锚杆张拉受限,位于锚固剂内部的应变片变形较小。拉拔阶段各测点应变快速增长,由外向内应变呈衰减趋势,说明拉拔荷载在传递过程中不断衰减。锚固界面发生失效滑移后应变快速下降,然后,保持较小波动,此时,锚固体在拉拔荷载和摩擦力的作用下处在相对平衡状态。
加长锚固测点1、2、3(图3(b))位于锚固层内部,受围压作用,锚固段内锚杆受力较为复杂,在拉、压、剪的应力共同作用下,锚固段内部分测点应变出现负值。自由段锚杆受力以锚固体向临空面膨胀产生的拉力为主,锚杆变形由外向内逐渐减小。拉拔阶段自由段的锚杆应变快速增大,部分应变出现溢出的情况。拉力传递至锚固层衰变明显,锚固层内测点应变较小。处在锚固层外或临近锚固层的应变片受脱锚影响,应变波动较大。
全长锚固体在围压加载过程中各测点受围岩膨胀变形的张拉作用,锚杆拉力向锚固体内部传递,各测点应变逐渐衰减。在拉拔过程中,拉力逐渐向锚固体内部传递,应变相继到达峰值,应变片变形由外向内呈递减状态,且随着不断深入锚固体内部,锚杆变形衰减增快。受脱锚的影响,峰后应变出现较大差异但最终趋势呈平稳状态。锚固层内的应变片的变形较小,锚固越深锚杆变形受限越明显,应变片受脱锚的影响越小。
由此可见,在不同温度、侧压系数、锚固长度和围岩强度下,锚杆受力由外向内逐呈渐减小的趋势,当拉拔荷载传递至锚固段锚杆时,变形受限,锚杆受力减小。
2.3.4 锚固体极限拉拔荷载多元线性回归分析
为探究极限拉拔荷载与锚固因素的关系,对锚固体极限拉拔荷载进行多元线性回归分析,得到锚固长度、温度、围岩强度、侧压系数与锚固体极限拉拔荷载的多元线性回归方程,并对多元线性回归方程进行验证。
在弹性变形阶段,锚固微元段的轴向拉拔荷载和锚固界面剪切力平衡。锚固剂-围岩界面的剪应力随着拉拔荷载的增大而增大。通过分析温度、围岩强度、侧压系数与极限拉拔荷载之间的关系,进一步得到锚固剂-围岩界面峰值剪应力与温度、围岩强度和侧压系数的关系。
设多元线性回归模型为:
式中:FM极限拉拔荷载;σ、λ、T、L分别为围岩抗压强度、侧压系数、温度、锚固长度;β0为常量,β1、β2、β3、β4分别为围岩强度、侧压系数、温度和锚固长度的系数;ε为残差。
室内拉拔试验得到的极限拉拔荷载如图8所示。
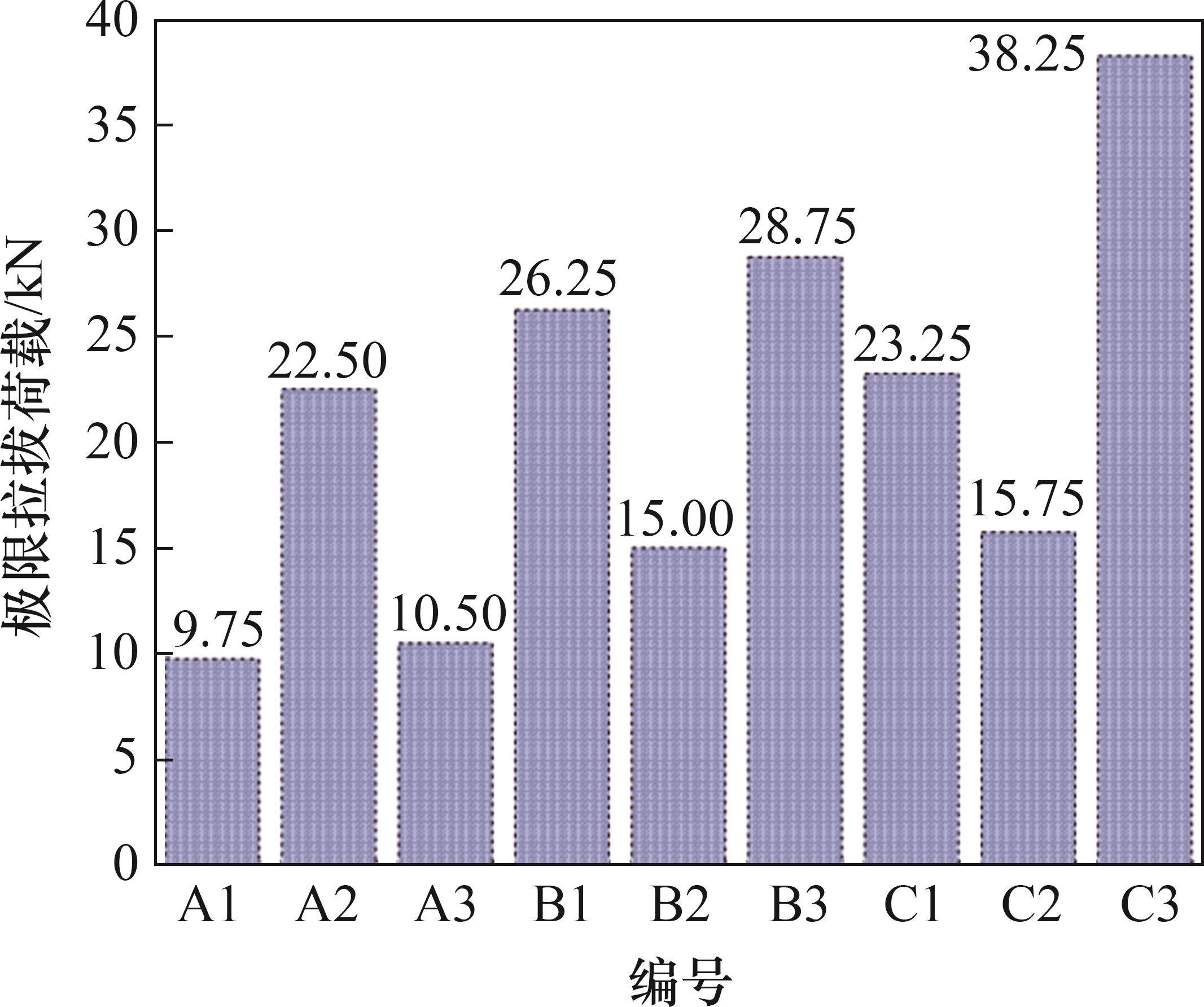
多元线性回归分析结果显示,模型的决定系数R2=0.977,具有较高可信度。由锚固因素回归系数可知,极限拉拔荷载与侧压系数、围岩强度、锚固长度呈正相关,与温度呈负相关;锚固剂-围岩界面的峰值剪应力与围岩强度和侧压系数呈正相关,与温度呈负相关。由模型的标准化系数可知,各锚固因素对软岩锚固体的极限拉拔荷载的影响程度从大到小依次为锚固长度、围岩抗压强度、温度、侧压系数排列。极限拉拔荷载的多元线性方程为FM=0.611+1.917σ+2.292λ-0.214T+0.510L。
采用参考文献[19]中的数据对极限拉拔荷载方程预测结果进行验证,结果表明,对较软弱的C20围岩锚固体极限拉拔荷载的预测较准确。由于仅对软岩和极软岩进行拉拔试验,因此,极限拉拔荷载方程对硬岩锚固体失锚值的预测偏差较大。但当温度为20 ℃和50 ℃时,对围岩抗压强度较大的锚固体的失锚预测值偏小。由此可知,当预测值达到锚固力要求时,锚固体的实际锚固值满足要求;当温度为70 ℃时,由于温度对锚固剂强度影响较大,锚固剂锚固力明显下降,预测值偏大,因此,现场锚固应在预测值的基础上增大锚固长度。极限拉拔荷载多元线性回归方程可用于判断锚固体锚固力是否达到锚固要求。文献[19]中的极限拉拔荷载与方程预测值对比如表4所示。
3 不同锚固长度锚固体数值分析
3.1 锚固模型的建立和模拟方案
通过FLAC3D数值模拟软件建立锚固体实体数值模型,为验证拉拔试验得到荷载传递规律,模型尺寸及模拟方案与室内拉拔试验的尺寸及模拟方案一致。模型的底部采用位移边界条件固定,模型的X和Z方向按拉拔试验方案施加对应压力。将锚固体围岩和锚固剂视为均质、连续、各向同性的材料,赋予摩尔-库仑本构模型。锚杆赋予弹性本构模型,不考虑锚杆横肋的影响。温度传导采用各向同性热传导模型。在锚固剂-锚杆、锚固剂-围岩之间建立接触面。
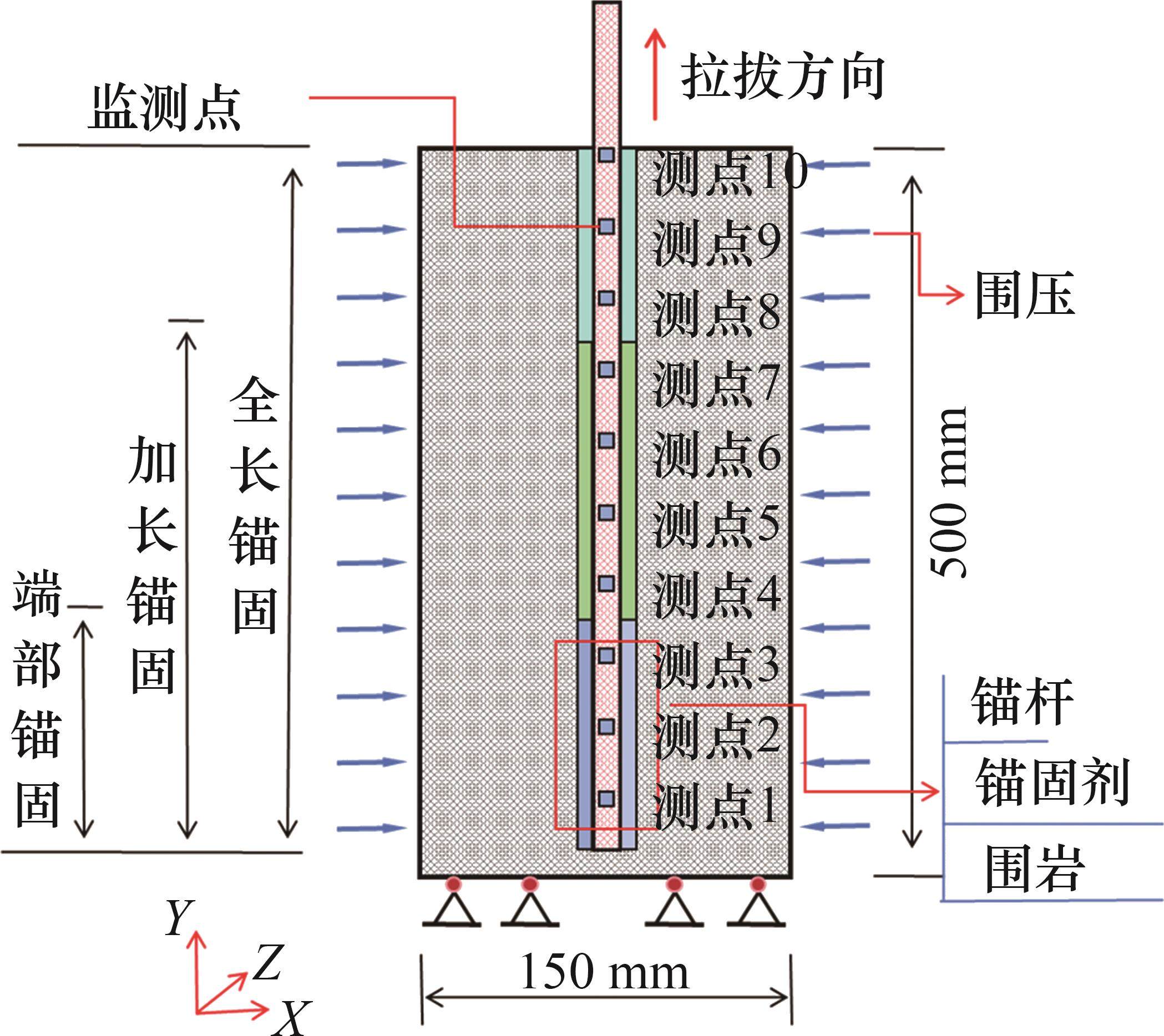
在模拟的温度范围内,围岩和锚杆的力学性质变化较小,温度对树脂锚固剂力学性质的影响较大,为减少计算时间,围岩初始温度设置为预加载的温度,模拟时仅考虑锚固剂和锚杆的温度传导。通过软件自带的热力分析模块,对锚固剂受热产生的膨胀应力进行模拟计算[20]。利用fish语言分析锚固剂力学性质随温度变化而变化的特性。首先对锚固体进行温压加载,加载完成后,在锚杆端部施加逐渐增大拉拔荷载,直至锚固剂层完全发生塑性破坏。锚固的数值模型如图9所示。
| 材料 | 本构模型 | 弹性模量/GPa | 泊松比 | 黏聚力/MPa | 内摩擦角/(°) |
|---|---|---|---|---|---|
| 围岩A | 摩尔-库仑 | 0.5 | 0.22 | 0.6 | 23 |
| 围岩B | 摩尔-库仑 | 1 | 0.25 | 0.8 | 25 |
| 围岩C | 摩尔-库仑 | 1.2 | 0.23 | 1.2 | 26 |
| 锚杆 | 弹性 | 200 | 0.3 | — | — |
3.2 数值模拟结果及分析
3.2.1 锚杆轴向应力分布
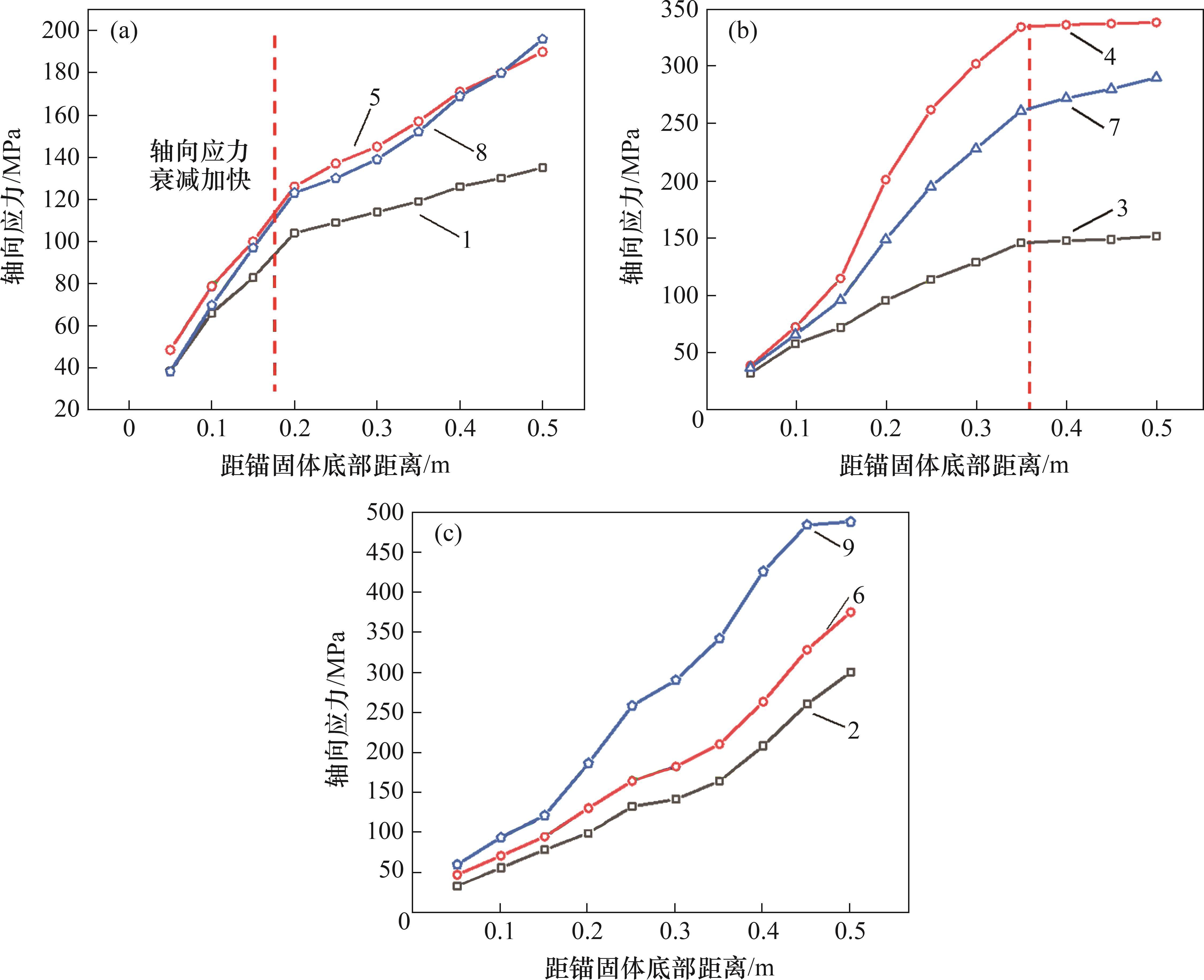
锚杆失锚后监测点轴向应力分布如图10所示。由图10可知:不同锚固长度锚杆轴向应力在传递过程中不断衰减,锚杆自由段轴向应力衰减幅度较小,传递至锚固段,受锚固层的约束影响,锚杆轴向应力迅速衰减,锚固层深部的锚杆受力较小;当锚固方式为端部锚固时,锚杆自由段较长,锚杆自由段轴向应力的衰减特征相较于加长锚固和全长锚固更明显。由于锚固长度较短,轴向应力衰减速率逐渐增大。当锚固长度增加至加长锚固时,锚杆拉拔位置距锚固段较近,锚固段锚杆的轴向应力在自由段衰减幅度较小。当应力传递至锚固层后,应力衰减速率增大。随着轴向应力在锚固段内部不断衰减,当应力传递一定距离后,锚固段的应力衰减速率逐渐减小。锚固段的应力衰减速率整体呈先快后慢的变化趋势。当锚固长度增加至全长锚固时,轴向应力在锚固段端部迅速衰减,但随着应力向锚固段内部渗透,轴向应力不断减小,应力衰减速率随之减缓。全长锚固的轴向应力衰减规律与加长锚固的轴向应力衰减规律相同。
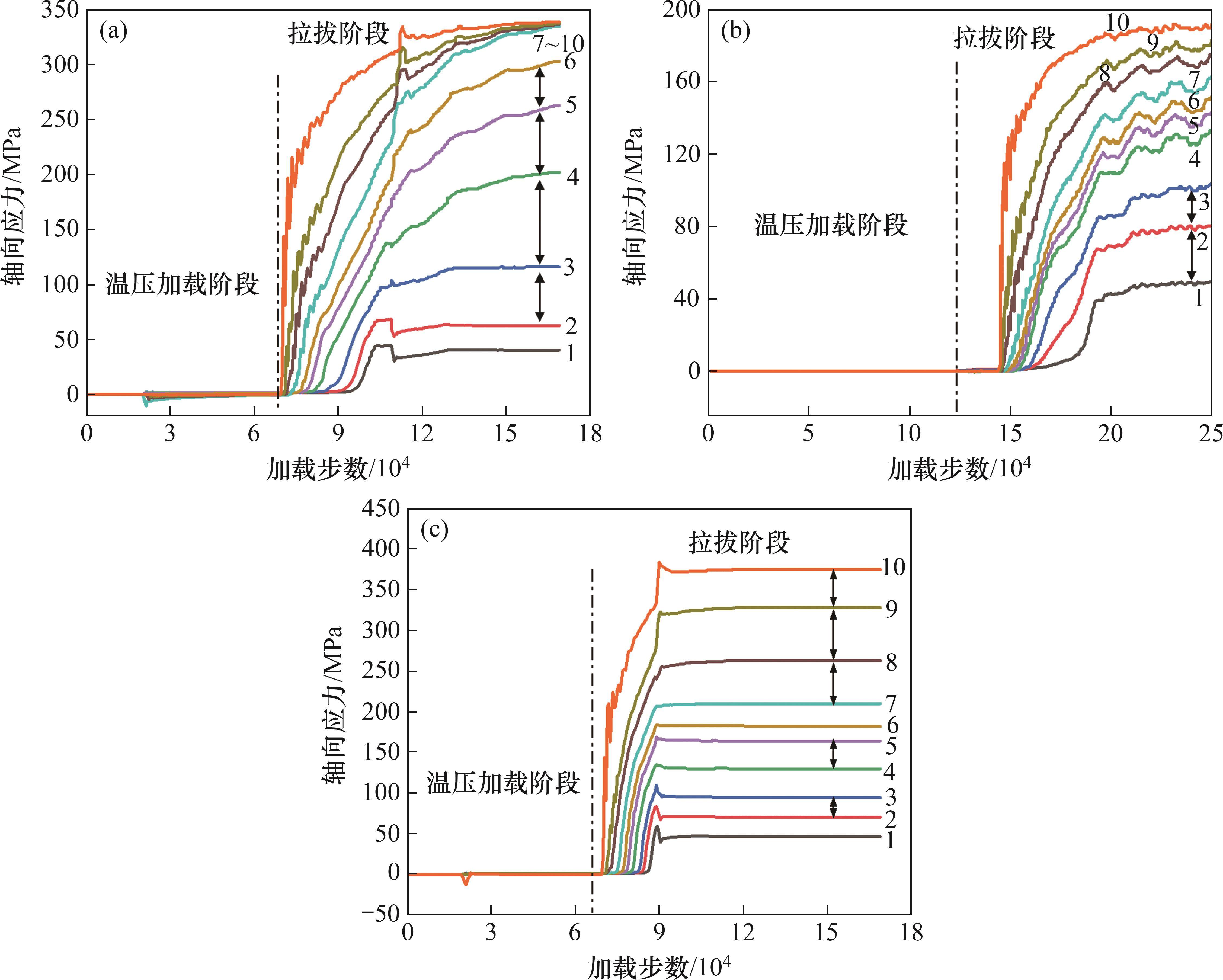
3.2.2 锚杆轴向应力变化特征
不同围岩强度锚杆轴向应力变化特征类似,以B组锚杆轴向应力变化为例,在温压加载和拉拔过程中,B组锚杆轴向应力变化如图11所示,其中,测点1~10位置见图9。从图9可见:在温压加载阶段,锚杆轴向应力变化较小,锚固剂膨胀挤压锚杆和围岩,但由于锚固剂层较薄,锚杆和围岩受力较小;在围压加载阶段,当侧压系数不为1时,锚固体受力不均,在不均匀围压作用下,部分监测点轴向应力出现负值;在拉拔阶段,锚杆轴力逐渐向锚固体内部传递,锚固层在拉拔荷载作用下,逐渐进入塑性状态。在拉拔荷载作用下,锚固层逐渐进入塑性状态;端部锚固时,拉拔过程中锚杆轴向应力快速增加,然后保持水平。由于轴向应力较小,失锚时,应力下降不明显,荷载传递曲线未出现较明显的脱锚现象。但最终轴向应力呈现水平状态,观察锚固层的塑性发育状况可知锚固体已失锚;加长锚固时,在拉拔过程中,应力逐渐向锚固体内部渗透,各监测点轴向应力逐个达到峰值然后保持水平;全长锚固时,拉拔荷载渗透速度较快,应力达到峰值后,有小幅下降,然后保持水平,锚固层发生塑性破坏。
4 结论
1) 基于三阶段线性函数和荷载传递法,推导了不同锚固条件下锚固段弹性变形阶段锚固剂-围岩界面剪应力和锚杆轴力分布公式。由理论推导公式结合拉拔试验发现锚固剂-围岩界面剪应力沿锚固方向呈下凹型递减分布,锚杆轴力呈近似线型单调递减分布。
2) 在温压耦合环境下,拉拔荷载在传递过程中不断衰减,锚杆自由段荷载衰减幅度较小。当荷载传递至锚固段后,受锚固层的约束作用,拉拔荷载迅速衰减。
3) 锚杆轴向应力在锚固段传递过程中,当锚固长度较短时,轴向应力在锚固段衰减速率逐渐增大。随着锚固长度增加,锚固段轴向应力衰减速率呈先快后慢变化趋势。
4) 极限拉拔荷载与温度呈负相关,与侧压系数、围岩强度、锚固长度呈正相关。各锚固因素对软岩锚固体的极限拉拔荷载的影响从大到小依次为锚固长度、围岩抗压强度、温度、侧压系数排列。
王佳奇, 姚直书, 刘小虎, 等. 温压耦合不同锚固长度锚固体受力特征及拉拔荷载传递规律研究[J]. 中南大学学报(自然科学版), 2024, 55(12): 4628-4640.
WANG Jiaqi, YAO Zhishu, LIU Xiaohu, et al. Study on stress characteristics and pull-out load transfer law of anchorage body with different anchorage length under temperature-pressure coupling[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4628-4640.

