随着经济的快速发展以及城市人口的不断增长,城市轨道交通一直保持着较快的发展速度。截至2023年12月底,我国地铁运营总里程达8 600多km,新增地铁线路600多km。地铁给人们出行带来方便的同时,也会带来一些不良影响,比如环境振动问题[1-4]等。针对地铁引起的环境振动问题,国内外许多学者对扣件减振做了大量研究[5-8]。目前地铁小半径曲线段行车速度较快,大部分都是欠超高,外轨时常出现车轮轮缘贴靠行为,外轨受到的轮轨横向力较大。现有的减振扣件类减振轨道的扣件横向刚度较低,外轨存在轨头侧向外扭转及横向位移,导致其轮轨接触关系与普通整体道床差异较大,实测减振轨道接触光带的位置与宽度跟普通整体道床存在差异。因此有必要开展减振扣件系统的横向力传递特性研究。现有针对地铁小半径曲线段减振扣件系统横向力传递特性的研究几乎没有,并且在仿真计算中大多数学者将减振扣件系统横向刚度取某个特定值进行轮轨动力学分析[9-12]。实际上,减振扣件系统相较于普通扣件系统部件更多,各部件之间的碰撞摩擦会产生强非线性行为,这就会导致减振扣件系统的服役横向刚度具有明显的非线性特征。因此本文以地铁常见的上部锁紧式双层非线性减振扣件系统作为研究对象,分析列车过地铁小半径曲线段时减振扣件系统横向力的传递特性。首先,通过室内试验测试其服役横向刚度,得到荷载-位移曲线;其次,建立可考虑网格尺寸、材料类型和摩擦接触的上部锁紧式双层非线性减振扣件系统精细化有限元模型,在与试验对比验证正确后,研究其在横向荷载作用下得到的荷载-位移曲线相应节点含义,并分析其内部的横向力传递过程,从而为今后减振扣件系统的横向刚度设计优化及轮轨动力学仿真计算提供实验依据和理论指导。
1 减振扣件系统横向力传递试验测试
列车经过地铁小半径曲线段减振扣件系统正上方时,外轮会贴靠曲线外轨,形成2点接触,钢轨轨头同时受到垂向和横向轮载力,因此模拟真实轨道工作情况,本试验采用对钢轨轨头施加垂横向荷载方式,测定得到的横向荷载-位移曲线为后续仿真分析上部锁紧式双层非线性减振扣件系统横向力内部传递过程作铺垫,以钢轨轨头产生单位横向位移所受到的横向力作为上部锁紧式双层非线性减振扣件系统的服役横向刚度。
1.1 服役横向刚度测试试验
按照如图1所示的荷载分担作用示意图[13],轮载力P会被分配到5根轨枕上,其中40%的轮载力被分配到车载正下方的轨枕上,20%被分配到相邻的两轨枕上,10%被分配到两端轨枕上。而此试验研究的是单轮轴(设计轴重P=16 t)经过单跨减振扣件系统正上方时横向荷载-位移变化过程,故取0.4P作为垂向荷载,即32 kN。同时文献[14]的研究表明,横向轮载力为垂向轮载力的25%左右,故取垂向荷载的1/4作为横向荷载,即8 kN。

1.2 试验准备与过程
测试对象为上部锁紧式双层非线性减振扣件系统,主要包括60短钢轨、弹条、8号轨距块(非工作边使用)、10号轨距块(工作边使用)、轨下垫板、上铁垫板、中间弹性垫板、下铁垫板、锚固螺栓及弹簧垫圈等;测试工装为用来固定上部锁紧式双层非线性减振扣件系统同时也便于液压千斤顶施加荷载的扣件系统横向力加载试验装置;测试仪器为用于对钢轨轨头施加荷载的液压千斤顶及用于测定钢轨轨头产生位移的百分表。整个减振扣件系统服役横向刚度测试组装如图2所示。

首先,将上部锁紧式双层非线性减振扣件系统实体按照图纸进行组装,将其固定在扣件系统横向力加载试验装置上,使之达到设计安装状态。其次,如图2(a)所示,在钢轨轨头上方位置安装液压千斤顶,加载位置为偏离钢轨轨顶中心线15 mm[15]处的位置,即对钢轨偏心加载,同时在钢轨轨底4个角处安装百分表,确保加载时同一侧的位移差一致,防止钢轨发生偏转,加载到32 kN,模拟正常过车时行为。接着,如图2(b)所示,在钢轨轨头工作边一侧安装液压千斤顶,加载位置为偏离钢轨轨顶10 mm[15]处正中间的位置,以确保钢轨轨头均匀受力,同时在钢轨轨头非工作边一侧两端各安装一个百分表,确保加载时位移差一致,防止钢轨发生偏转,中间安装一个百分表,与加载位置平齐,测量横向加载后的钢轨轨头横向位移。最后,以1 kN的横向荷载为间隔进行正式加载,每次加载待液压千斤顶加载示数值稳定后,再读取并记录百分表的示数,当加载到8 kN并记录对应的钢轨轨头横向位移后试验结束。试验结束后重复进行多次测试,最终选取一组均匀性较好的试验数据作为上部锁紧式双层非线性减振扣件系统横向刚度的测试结果。需要特别注意的是,在每次正式加载前,要先对整个减振扣件系统进行预压,观察钢轨轨头非工作边一侧两端百分表的示数是否接近,如果不接近说明钢轨在加载的过程中发生了偏转,需要重新调整液压千斤顶加载的位置,直至钢轨轨头非工作边一侧两端百分表的示数接近,以减少因钢轨发生偏转而引起的试验误差。
1.3 试验结果
上部锁紧式双层非线性减振扣件系统在有垂向荷载情况下的服役横向刚度测试结果如图3所示,由图中可以看出,该减振扣件系统的服役横向刚度具有明显的非线性特征,整个荷载-位移曲线存在着明显的拐点,根据拐点可将整个曲线划分成3段斜率不同的曲线,因此该减振扣件系统的服役横向刚度应以每段曲线的割线刚度进行表征。当加载到4 kN时, 钢轨轨头产生了0.62 mm的横向位移,可以明显地发现横向荷载-位移曲线的斜率发生了改变,此时减振扣件系统的服役横向刚度约为7.84 kN/mm。当横向荷载继续增加时,曲线斜率有所降低,当加载到6 kN时,钢轨轨头共产生了1.14 mm的横向位移,可以发现横向荷载-位移曲线地斜率再度发生改变,此时减振扣件系统的服役横向刚度约为4 kN/mm,达到最小。当横向荷载继续增加时,曲线斜率显著增大,加载到8 kN时钢轨轨头共产生了1.38 mm的横向位移,此时减振扣件系统的服役横向刚度约为22.6 kN/mm。
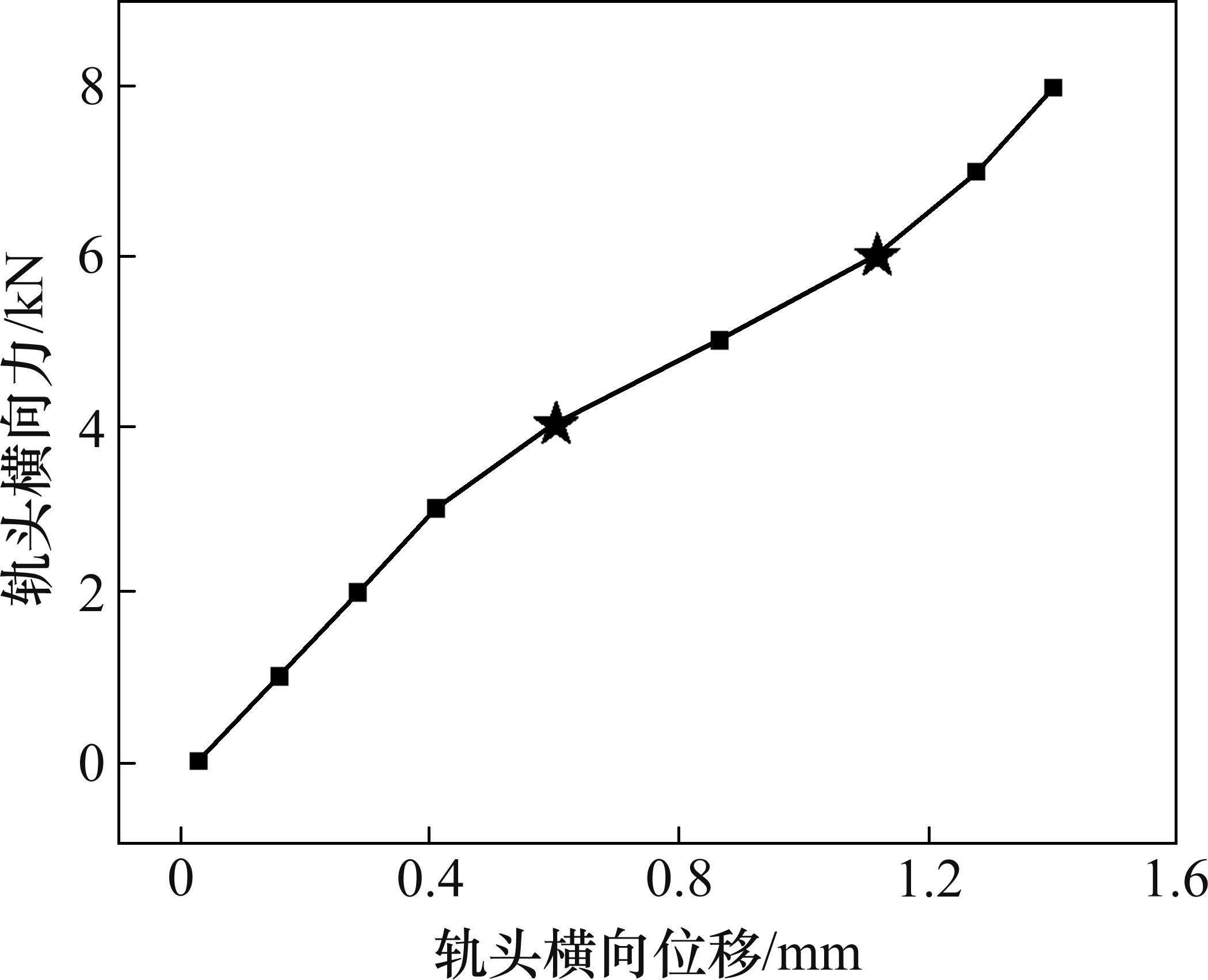
综上所述,上部锁紧式双层非线性减振扣件系统在垂向和横向荷载的作用下,横向力的内部传递过程较为复杂,表现出明显的非线性特征。每个阶段的刚度大小不一,显然如果以单一的割线刚度(线性刚度)来表征服役横向刚度会严重偏离减振扣件系统的实际服役横向刚度,因此在实际工程中或轮轨动力学仿真计算中应对其分阶段分别设计。但根据现有的试验条件仅能展现出减振扣件系统宏观层面上的荷载-位移变化规律,并不能展现减振扣件系统内部横向力的传递过程以及各个拐点的含义。因此,需要借助有限元仿真的方法,对整个减振扣件系统进行微观层面的分析,研究各个部件在内部横向力传递过程中的受力情况,明确横向力的传递过程。
2 减振扣件系统横向力传递仿真分析
2.1 减振扣件系统精细化有限元模型
本节按照上部锁紧式双层非线性减振扣件系统实际尺寸在SOLIDWORKS中建立了减振扣件系统三维实体几何模型,主要包括60钢轨、弹条、8号轨距块(非工作边使用)、10号轨距块(工作边使用)、轨下垫板、上铁垫板、中间弹性垫板、下铁垫板、锚固螺栓及底板连接套等部件,然后将几何模型导入到HyperMesh中划分网格,最后将网格导入到ABAQUS进行仿真计算。整个减振扣件系统全部部件均扫描生成六面体网格,共划分145 898个C3D8R实体单元和191 331个节点。有限元模型如图4所示。

按照设计图纸,钢轨轨底与非工作边轨距块留有1 mm左右的间隙。轨下垫板和中间弹性垫板的材料均为天然橡胶,考虑了其超弹性材料性质,近似为不可压缩的各向同性的材料,采用Mooney-Rivlin双参数模型并带入等效应变能函数和体积应变能密度公式,其中C01取0.001 797 3 MPa,C10取0.210 57 MPa。轨距块和底板连接套的材料均为玻纤增强聚酰胺66,上铁垫板和下铁垫板的材料均为QT450-10,螺栓的材料为Q235A,弹条的材料为60Si2MnA弹簧钢,同时考虑到弹条可能会出现塑性变形,故采用理想线性强化弹塑性模型模拟弹条[16],模型各部件具体材料参数见表1所示。
| 部件 | 弹性模量/MPa | 泊松比 | 密度/(kg∙m-3) |
|---|---|---|---|
| 钢轨 | 206 000 | 0.3 | 7 850 |
| 弹条 | 207 000 | 0.3 | 7 850 |
| 轨距块 | 6 200 | 0.35 | 1 400 |
| 轨下垫板 | 6 | 0.49 | 1 300 |
| 上、下铁垫板 | 193 000 | 0.3 | 7 850 |
| 中间弹性垫板 | 10 | 0.49 | 900 |
| 螺栓 | 200 000 | 0.3 | 7 800 |
| 底板连接套 | 6 200 | 0.35 | 1 400 |
为了真实模拟整个减振扣件系统模型中各部件的受力状态,各部件之间建立面-面接触,相互作用关系设为摩擦接触,接触算法采用罚函数法。各部件之间具体接触边界对设置见表2所示。
| 部件1 | 部件2 | 摩擦因数 |
|---|---|---|
| 钢轨 | 轨距块 | 0.45 |
| 轨距块 | 上铁垫板 | 0.45 |
| 钢轨 | 轨下垫板 | 0.55 |
| 轨下垫板 | 上铁垫板 | 0.5 |
| 上铁垫板 | 中间弹性垫板 | 0.5 |
| 中间弹性垫板 | 下铁垫板 | 0.5 |
| 弹条趾端 | 轨距块 | 0.35 |
| 弹条中肢 | 上铁垫板插孔 | 0.3 |
| 弹条跟端 | 上铁垫板承台 | 0.3 |
由于试验中通过锚固螺栓将整个减振扣件系统固定在横向力加载试验装置上,故在仿真中对下铁垫板底面设置固定约束进行模拟。同时为了消除边界条件的影响,在钢轨两端设置对称约束。
2.2 减振扣件系统精细化有限元模型验证
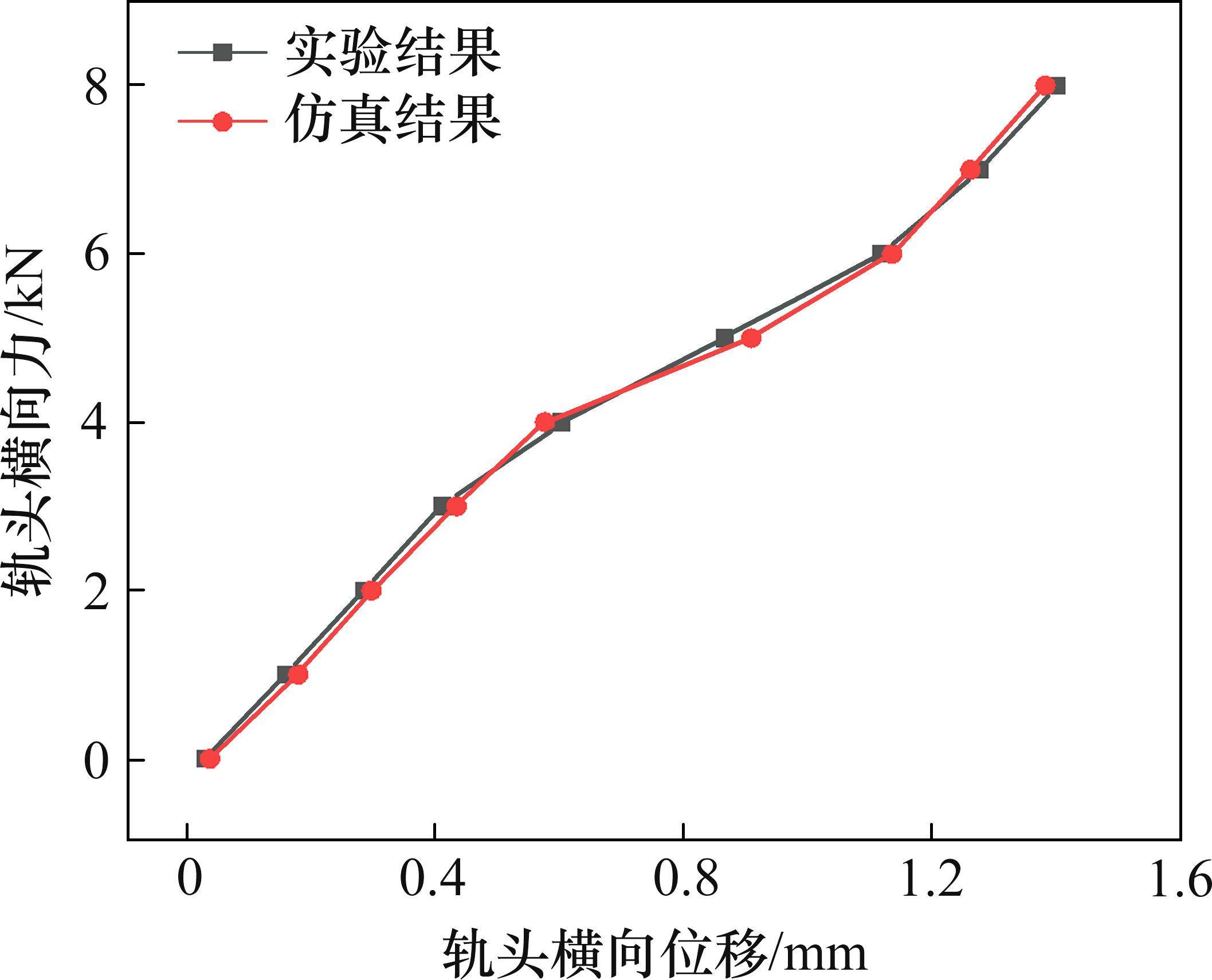
为了更好地分析地铁小半径曲线段减振扣件系统在真实有轮载情况下的内部横向力传递过程,考虑2点接触。仿真中先按上节所提到的方法使弹条达到正常安装状态后,再对偏离钢轨轨顶10 mm处的位置施加以0.01 kN为间隔的横向荷载,逐步加载到8 kN,与此同时,对偏离钢轨轨顶中心线15 mm处的位置施加以0.01 kN为间隔的垂向荷载,逐步加载到32 kN,计算得到钢轨轨头的横向荷载-位移曲线如图5所示。与试验结果相比,2条曲线基本吻合,每段横向刚度相差较小,因此验证了减振扣件系统精细化有限元模型的正确性,可以进行后续的横向力传递过程分析。
2.3 减振扣件系统横向力传递过程分析
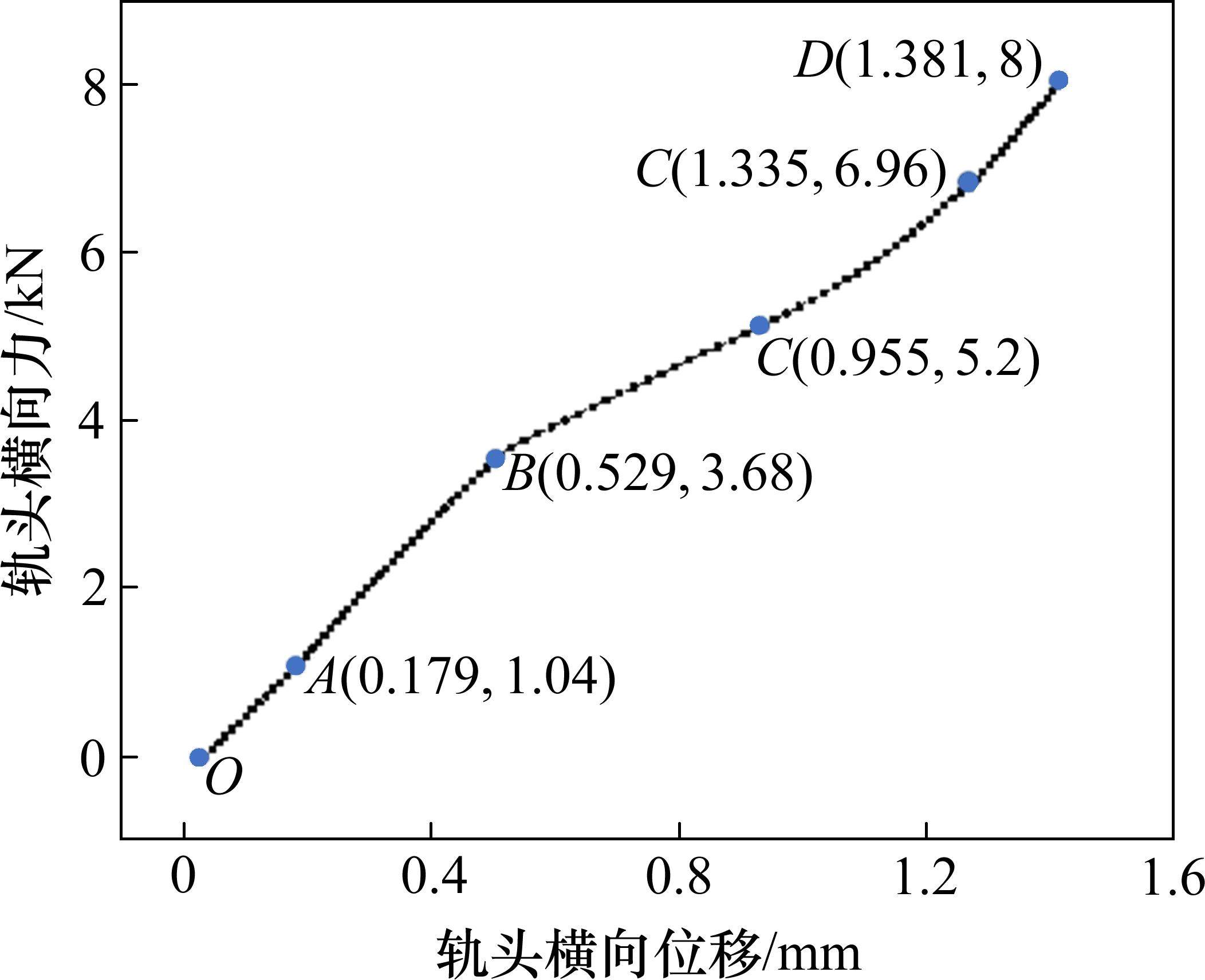
根据仿真结果提取了关键部件之间的相互作用力,其变化情况具体反映在横向荷载-位移曲线的相应节点上,如图6所示。同时各个部件的受力情况见图7。本节结合图6和图7详细阐释减振扣件系统的横向力传递过程。
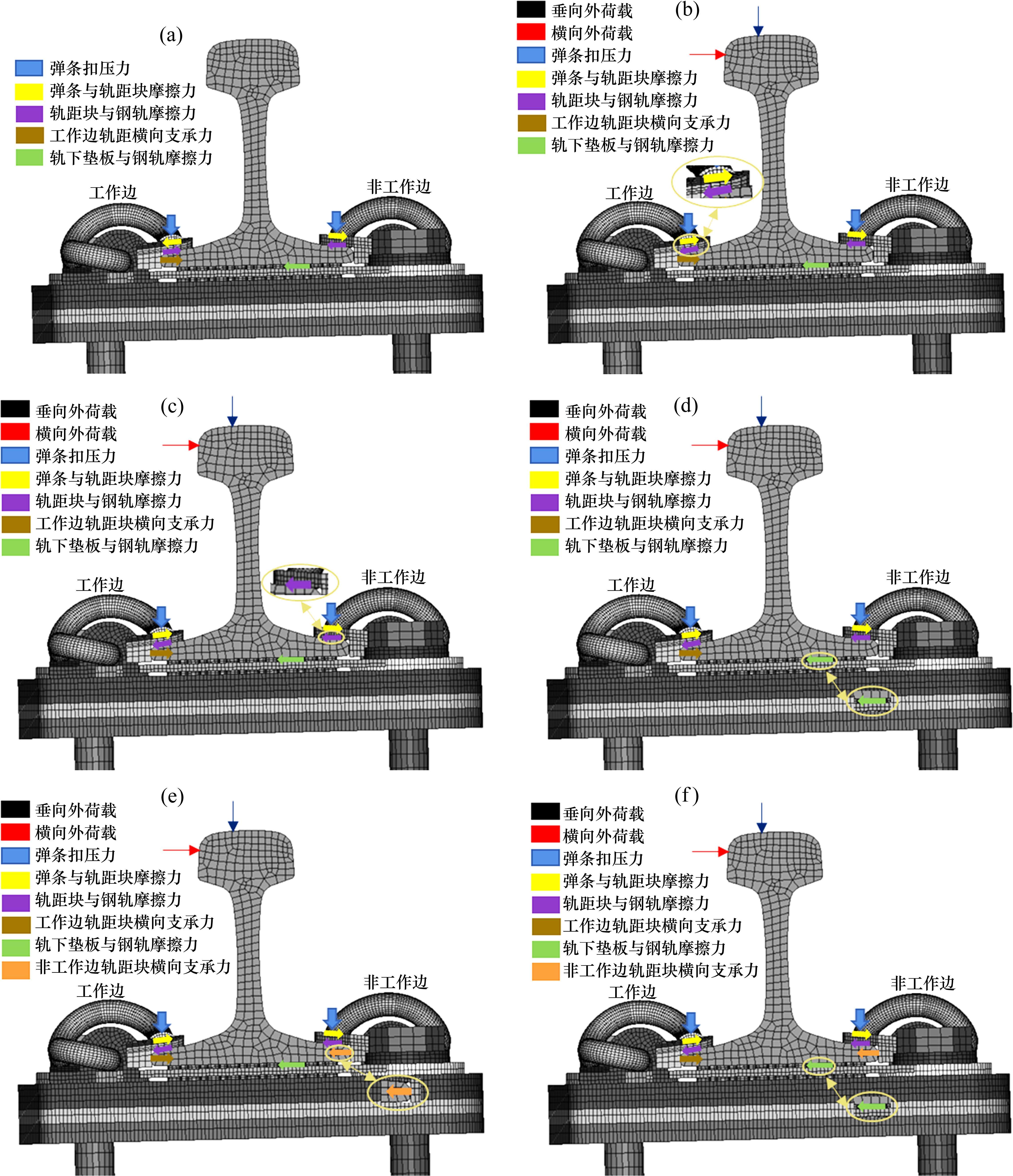
从图7(a)中可看出,在未施加横向荷载时,整个扣件系统在弹条的扣压力作用下已经产生了部分横向作用力,主要靠工作边弹条与工作边轨距块上下表面接触的静摩擦力、非工作边弹条与非工作边轨距块上下表面接触的静摩擦力、工作边轨距块与钢轨轨底上下表面接触的静摩擦力、非工作边轨距块与钢轨轨底上下表面接触的静摩擦力、工作边轨距块横向支承力、钢轨轨底与轨下垫板上下表面接触的静摩擦力提供,大小分别为0.24,0.28,0.84,1.63,0.92和0.05 kN。
施加横向荷载后,整个横向传力过程分为工作边轨距块静摩擦力被克服、非工作边轨距块静摩擦力被克服、非工作边侧轨下垫板压缩变形、非工作边轨距块横向支承、轨下垫板静摩擦力增幅减缓5个阶段。
其中OA段表示工作边轨距块由最大静摩擦力变为动摩擦力阶段(见图7(b)),加载到1.12 kN过程中,工作边轨距块与钢轨轨底上下表面接触的静摩擦力及工作边弹条与工作边轨距块上下表面接触的静摩擦力逐渐达到最大静摩擦力,同时非工作边轨距块与钢轨轨底上下表面接触的静摩擦力逐渐增大,A点表示钢轨轨底与工作边轨距块开始产生滑移,此时扣件系统横向力主要靠非工作边轨距块与钢轨轨底上下表面接触的静摩擦力、工作边轨距块横向支承力、轨下垫板的静摩擦力提供,大小分别为1.77,1.07和0.11 kN。
AB段表示非工作边轨距块由最大静摩擦力变为动摩擦力阶段(见图7(c)),加载到2.32 kN过程中,非工作边轨距块与钢轨轨底上下表面接触的静摩擦力逐渐达到最大静摩擦力,同时非工作边侧轨下垫板的压缩刚度逐渐增大,B点表示非工作边轨距块与钢轨轨底开始产生滑移,此时扣件系统横向力主要靠非工作边轨距块与钢轨轨底上下表面接触的滑动摩擦力、工作边轨距块与钢轨轨底上下表面接触的滑动摩擦力、工作边轨距块横向支承力、轨下垫板的静摩擦力提供,大小分别为3.51,0.71,1.35和0.45 kN。
BC段表示非工作边侧轨下垫板压缩变形阶段(见图7(d)),加载到4.64 kN过程中,在轨下垫板压缩变形下,钢轨轨底相对2个轨距块上下表面接触区域发生滑移,导致钢轨轨底逐渐贴靠非工作边轨距块内侧,两者之间的空隙逐渐闭合,B点表示刚好贴靠上,此时扣件系统横向力主要靠非工作边轨距块与钢轨轨底上下表面接触的滑动摩擦力、工作边轨距块与钢轨轨底上下表面接触的滑动摩擦力、工作边轨距块横向支承力、轨下垫板的静摩擦力提供,大小分别为3.42,1.52,1.61和1.45 kN。
CD段表示非工作边轨距块提供横向支承阶段(见图7(e)),加载到5.92 kN的过程中,在横向力的作用下,钢轨发生倾覆,非工作边侧轨下垫板在钢轨轨底向下倾覆的作用下压缩量逐渐加大,导致钢轨轨底挤压非工作边轨距块内侧,轨距块产生的横向支承力从0逐渐加大,此时扣件系统横向力主要由非工作边轨距块与钢轨轨底上下表面接触的滑动摩擦力、工作边轨距块与钢轨轨底上下表面接触的滑动摩擦力、工作边轨距块横向支承力、轨下垫板的静摩擦力、非工作边轨距块的横向支承力、工作边弹条与工作边轨距块的上下表面接触静摩擦力提供,大小分别为3.23,2.19,2.13,2.09,1.07和1.09 kN。
DE段表示轨下垫板静摩擦力增幅减缓阶段(见图7(f)),加载到8 kN过程中,在横向力的作用下,钢轨继续发生倾覆,非工作边侧轨下垫板在钢轨轨底向下倾覆的作用下压缩量继续加大,导致钢轨轨底挤压非工作边轨距块内侧的同时,非工作边轨距块沿着与铁垫板两接触面向下滑移,而工作边轨距块在钢轨轨底向上倾覆的作用下沿着与铁垫板两接触面向上滑移,轨下垫板出现静摩擦力增幅减缓现象,此时扣件系统横向力主要由非工作边轨距块与钢轨轨底上下表面接触的滑动摩擦力、工作边轨距块与钢轨轨底上下表面接触的滑动摩擦力、工作边轨距块横向支承力、轨下垫板的静摩擦力、非工作边轨距块的横向支承力、工作边弹条与工作边轨距块上下表面接触的静摩擦力提供,大小分别为3.12,2.35,2.46,2.12,2.31和1.04 kN。
3 减振扣件系统横向力传递行为影响因素分析
摩擦因数的改变进而导致关键部件之间的摩擦接触行为发生变化,因此,有必要分析钢轨轨底与轨距块以及钢轨轨底与轨下垫板之间的摩擦因数对整个减振扣件系统的横向力传递行为的影响规律。此外,由于在现场安装减振扣件系统弹条时难免会出现施工误差,具体体现在扣压力增大或减小,因此,还需要考虑扣压力对整个扣件系统的横向力传递行为的影响程度。
3.1 钢轨轨底与轨距块之间的摩擦因数
根据已有研究[17],本节取0.25、0.45、0.65的摩擦因数,对比分析钢轨轨底与轨距块之间不同的摩擦因数对横向力传递行为的影响,对比结果如图8所示。
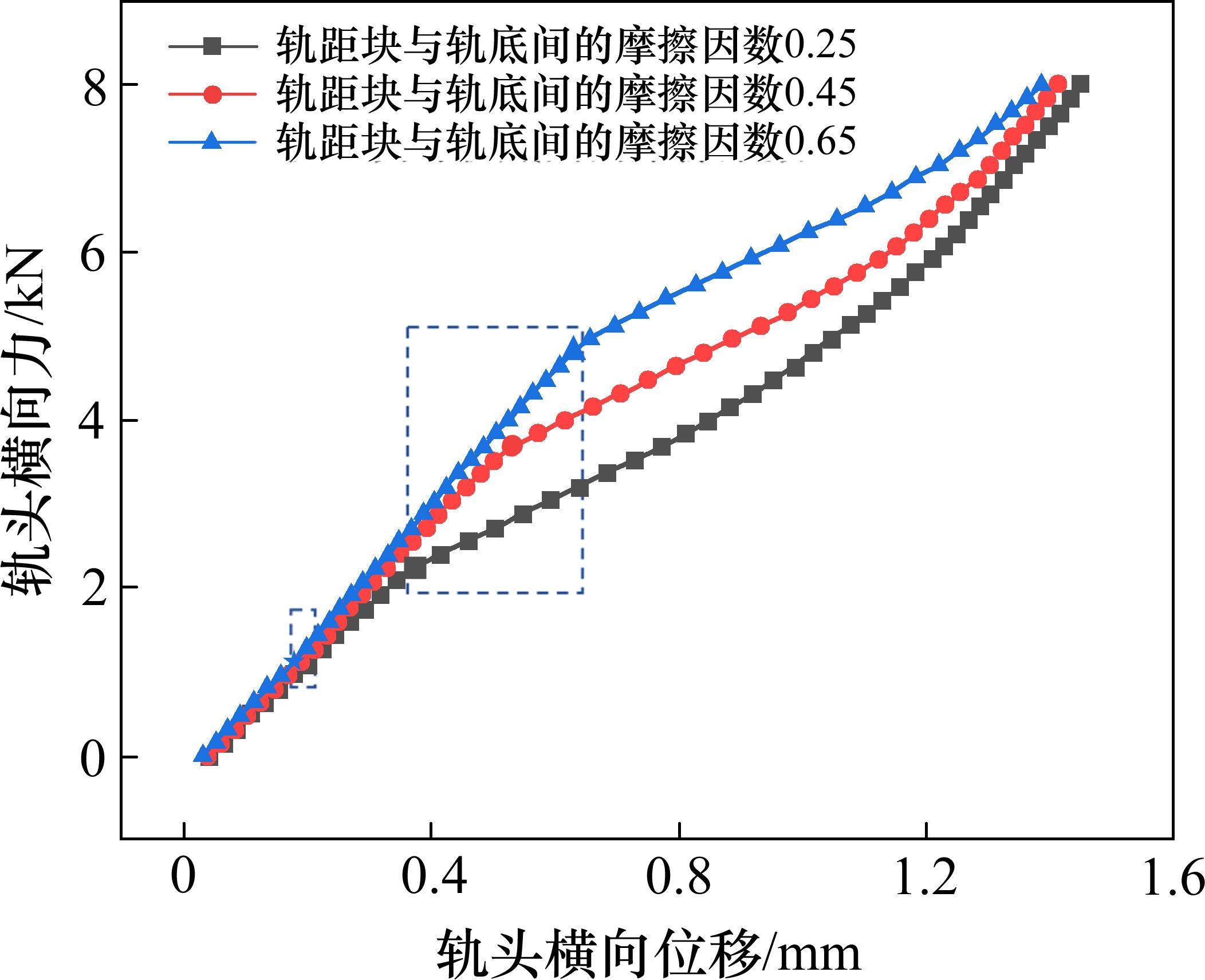
摩擦因数控制着摩擦性能,当钢轨轨底与轨距块之间的摩擦因数增大时,两者之间的摩擦力也会随着增大,继而提高了工作边轨距块和非工作边轨距块由最大静摩擦力变为动摩擦力所需要的横向力。
由图8可知,同时施加垂向和横向荷载时,摩擦因数由0.25逐渐增加到0.45和0.65,工作边轨距块由最大静摩擦力变为动摩擦力所需要的外荷载由0.88 kN增大到1.04 kN和1.12 kN,分别增加了18%和8%。非工作边轨距块由最大静摩擦力变为动摩擦力所需要的外荷载由2.24 kN增大到3.68 kN和4.8 kN,分别增加了64%和30%。而第3阶段曲线趋于重合,这是由于钢轨轨底与轨距块进入了动摩擦状态,两者不再随横向力的变化而变化,因此钢轨轨底与轨距块之间的摩擦因数对第3阶段的影响很小。
3.2 钢轨轨底与轨下垫板之间的摩擦因数
在不同的工作状况下,钢轨轨底与弹性垫板之间的摩擦因数为0.15~0.9[18-19],故本节取0.35、0.55和0.75的摩擦因数,对比分析钢轨轨底与轨下垫板之间不同摩擦因数对横向力传递行为的影响,对比结果如图9所示。
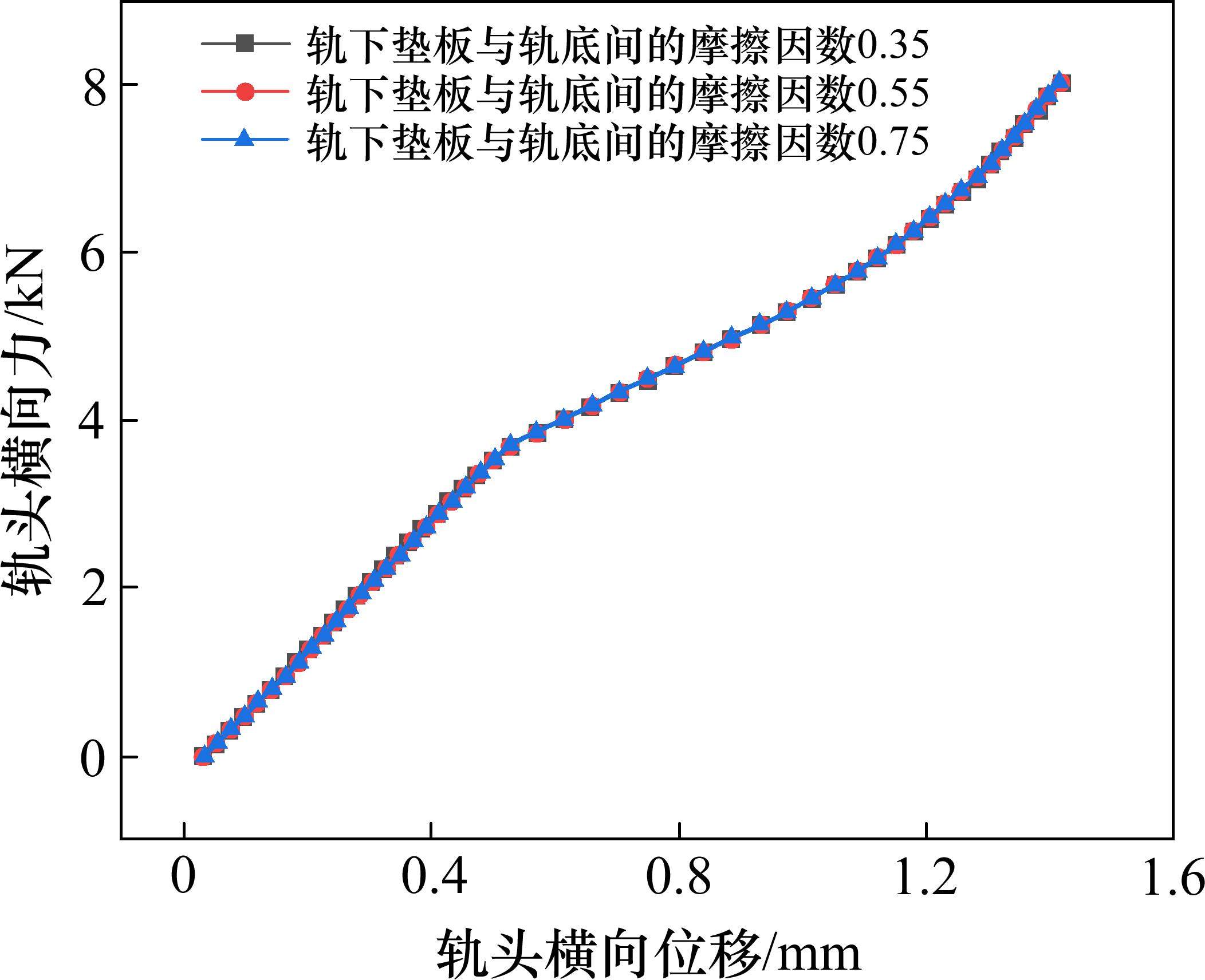
从图9中可以看出,钢轨轨底与轨下垫板之间的摩擦因数对减振系统的横向力传递行为影响较小,这是因为钢轨轨底与轨下垫板之间一直都是静摩擦力,削弱了因摩擦因数的变化对整个横向力传递过程的影响。
3.3 扣压力
不同的弹程对应不同的扣压力[20],故本节取6,8和10 kN的扣压力,对比分析不同的扣压力对横向力传递行为的影响程度,对比结果如图10所示。
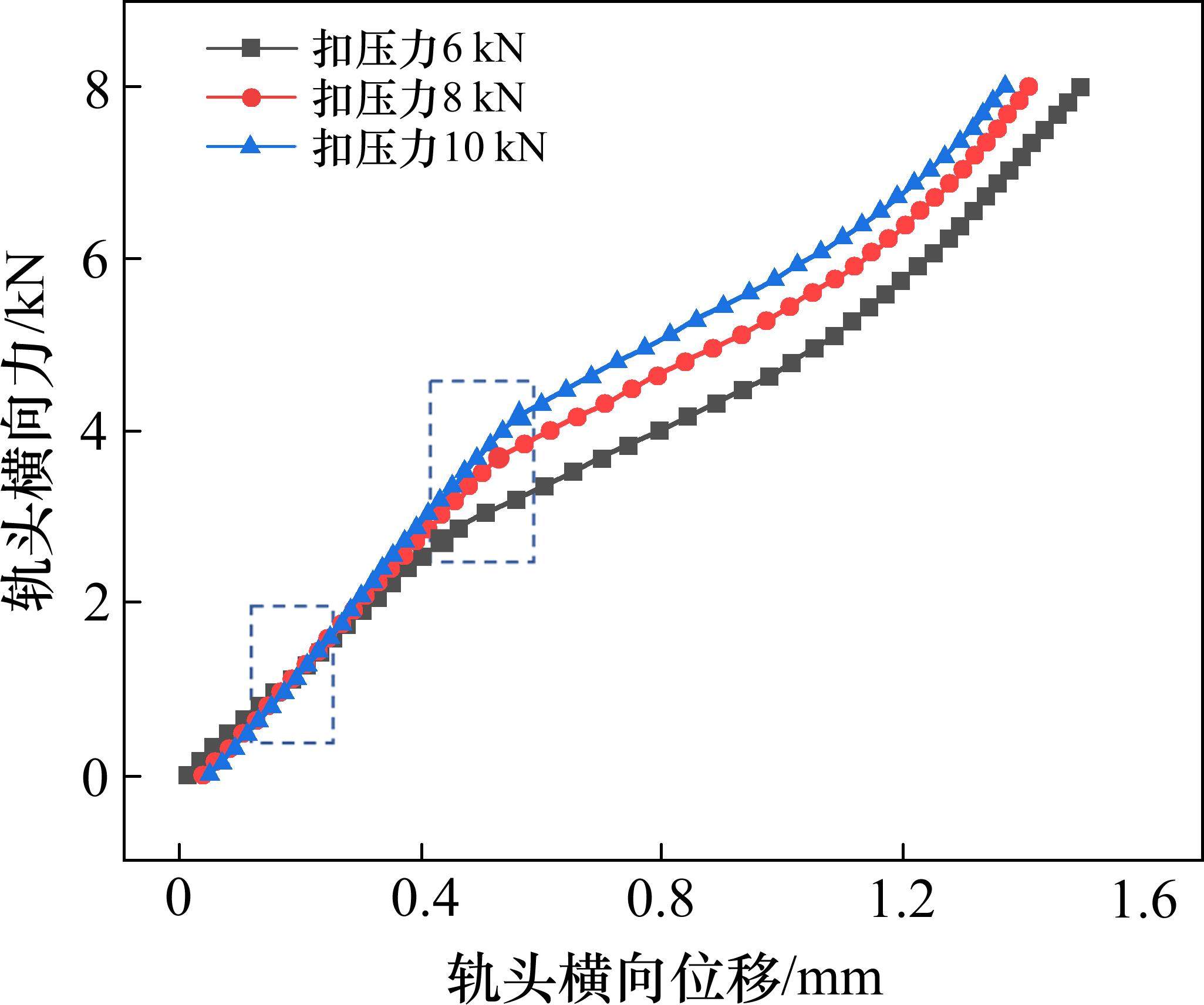
扣压力的变化相当于改变了垂直于轨距块上的正压力,扣压力越大,克服工作边轨距块最大静摩擦力及非工作边轨距块最大静摩擦力所需要传递的最大荷载越大。同时钢轨轨底与轨下垫板之间的摩擦力也越大,轨下垫板静摩擦力增幅减缓阶段随之推延。整体而言,当轨头产生相同大小的横向位移时,较大扣压力的工况所需要的横向外荷载高于较小扣压力的工况。
由图10可知,同时施加垂向和横向荷载时,扣压力由6 kN增大到8 kN和10 kN,工作边轨距块由最大静摩擦力变动摩擦力所需要的外荷载由0.56 kN增大到1.04 kN和1.52 kN,分别增加了86%和46%。非工作边轨距块由最大静摩擦力变动摩擦力所需要的外荷载由2.8 kN增大到3.68 kN和4.16 kN,分别增加了31%和13%。各个阶段的横向刚度都有所提高。
4 结论
1) 室内试验测试得到的横荷载-位移曲线,表明该减振扣件系统的服役横向刚度具有明显的非线性特征,横向力的内部传递过程较为复杂,整个荷载-位移曲线存在着明显的拐点,显然如果以单一的割线刚度(线性刚度)来表征横向刚度会严重偏离减振扣件系统的实际服役横向刚度。
2) 为了更好地分析地铁小半径曲线段减振扣件系统在真实有车载情况下的内部横向力传递过程,考虑2点接触,仿真中对减振扣件系统精细化有限元模型施加横向荷载的同时施加垂向荷载,结果表明减振扣件系统的整个横向传力过程分为工作边轨距块静摩擦力被克服、非工作边轨距块静摩擦力被克服、非工作边侧轨下垫板压缩变形、非工作边轨距块横向支承、轨下垫板静摩擦力增幅减缓5个阶段。
3) 钢轨轨底和轨距块之间的摩擦因数、扣压力是影响轨距块由最大静摩擦力变为动摩擦力所需要外荷载大小的关键因素,摩擦因数越大,所需要的外荷载越大;而钢轨轨底与轨下垫板之间的摩擦因数对减振系统的横向力传递行为影响较小。
赵才友,张明凯,赵炎南.地铁小半径曲线段双非减振扣件系统横向力传递特性分析[J].铁道科学与工程学报,2024,21(11):4487-4496.
ZHAO Caiyou,ZHANG Mingkai,ZHAO Yannan.Analysis of transverse force transfer characteristics of double-non-vibration damping fastener system in small radius curve section of subway[J].Journal of Railway Science and Engineering,2024,21(11):4487-4496.

