城市轨道交通运营过程中产生的振动和噪声会对设备的稳定性、安全性和使用寿命造成损害,甚至对人类的身体健康造成潜在的威胁。这种振动和噪声通常以弹性波的形式传播,低频弹性波(低于20 Hz)虽然人类无法感知,但它仍然可以对结构和系统产生物理影响。地铁运行过程中若与建筑结构产生共振,极大概率会破坏地铁隧道和相关基础设施的结构完整性,特别是对线路中的精密仪器产生极大危害。抑制低频弹性波的传递始终是工程中的巨大挑战,核心问题是结构中弹性波传播的调控。目前地铁与高铁的减振降噪措施以声屏障为主[1-2],但是却无法针对低频弹性波进行隔绝。近年来,有许多学者通过声子晶体的带隙特性来控制振动与噪声。已有研究发现声子晶体作为一种人工制造的周期性介质材料的声学超材料[3-8],具有特殊的力学或声学特性,即某些频段内的弹性波在周期性波导中能够无需外界阻尼或能量的抑制,出现完全阻隔弹性波传播的效应,将这种特殊现象所对应的频段称为“带隙”[9-13]。因此,诸多学者基于超材料带隙的原理,通过设计调整超材料结构的形状及材料等,实现定向控制弹性波的目的,从而为阻隔振动及噪声提供了新颖的思路和理论支撑。国内外学者已对超材料结构抑制弹性波进行了大量研究,通过设计不同的几何构型和选取不同的材料参数,可使不同频率范围内的弹性波得到衰减和隔离。ZHANG等[14]发现,周期性隔振屏障(PVIB)的埋深和排数对地铁列车引起的地面振动影响较大。XIANG等[15]对具有宽低频带隙的周期隔振基础进行了深入研究。BRÛLÉ等[16]利用在地面周期性钻孔的方法表明所设计的超材料结构能够隔离特定方向上50 Hz左右的Rayleigh波,体现了超材料结构在实际抗震应用上的可行性。PALERMO等[17]设计了埋入土体的单元谐振器,能够对Rayleigh地震波进行衰减,使用更紧凑的小型单元简谐器保护建筑物免受Rayleigh波的影响。SHI等[18]设计了一个由周期性排列的空心桩组成的桩屏障,其中填充软质或硬质填充材料,可以产生低频或中频的衰减区域。PU等[19]设计了填充式沟槽,对列车引起的地面振动进行了现场实验,探究了周期性填充沟槽中表面波的衰减区域。薛富春等[20]利用超弹性材料本构关系模拟橡胶垫片的大变形行为,补充了将超弹性材料应用在超材料领域的力学特性。但是对于抑制20 Hz以下的弹性波而设计的超材料结构带隙起始频率不够低,带宽不够大,导致隔振效果并不理想[21-22]。上述研究难以进行低频宽带的铁路振动噪声衰减控制,针对地铁模式下的低频超材料设计仍面临诸多挑战[23-25]。因此,本文在前有研究的基础上,利用超材料的局域共振带隙机理设计出针对地铁的可实现低频宽带减振降噪超材料波阻垫;同时结合理论解析与数值仿真研究进行了相关的讨论与验证。
1 模型建立与带隙分析
1.1 单胞模型设计
基于超材料结构的带隙特性,本研究为抑制频率低于20 Hz的弹性波设计了如图1(b)所示的控制低频振动的新型超材料波阻垫。由于结构具有周期性,可先选取一个如图1(a)所示的单胞进行研究。单胞由内部钢振子、环形橡胶、外部钢振子和环形钢片组成,通过周期性排布形成波阻垫。
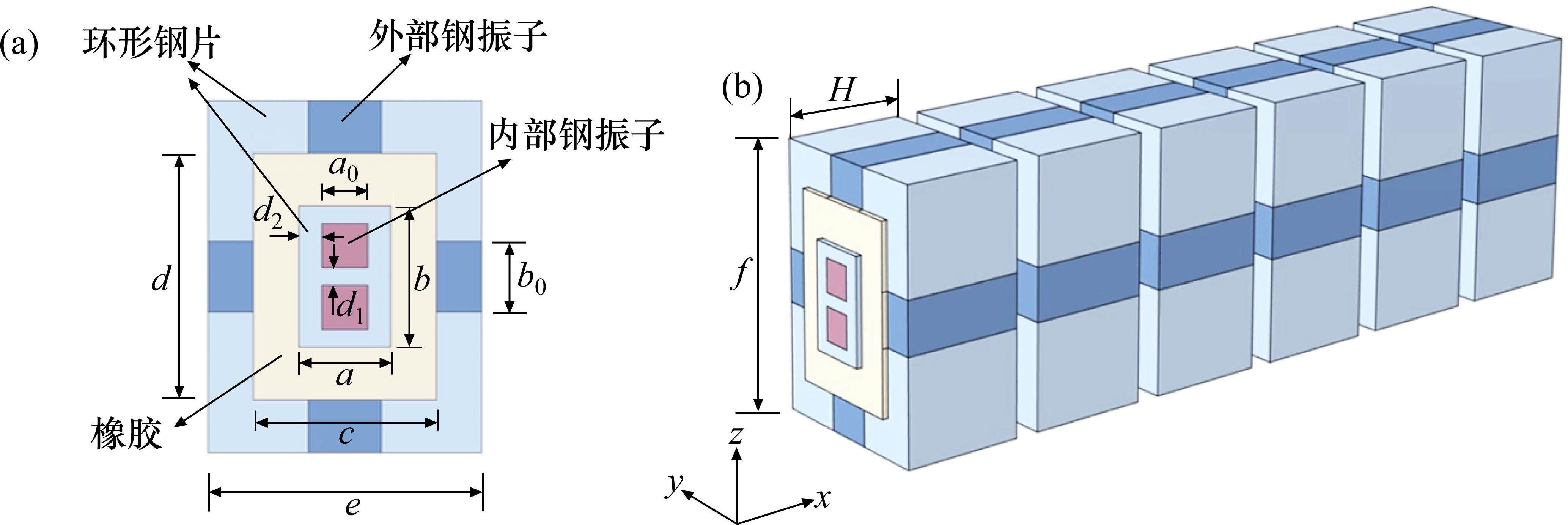
单胞的几何参数为:内部钢片a=0.5 m,b=0.8 m;内部正方形钢振子边长a0=0.25 m;环形橡胶c=1 m,d=1.4 m;外部钢片e=1.5 m,f=2 m;外部钢振子b0=0.4 m;内部钢振子间距d1=0.125 m,d2=0.1 m,厚度H=1 m。波阻垫单元模型的材料参数如表1所示。
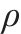 | E/MPa | 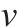 | |
|---|---|---|---|
| 钢 | 7 850 | 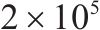 | 0.3 |
| 橡胶 | 1 300 | 3 | 0.47 |
1.2 能带结构
根据Bloch-Floquet定理[26],在单元结构的X方向和Y方向施加Bloch边界条件,沿着不可约Brillouin区
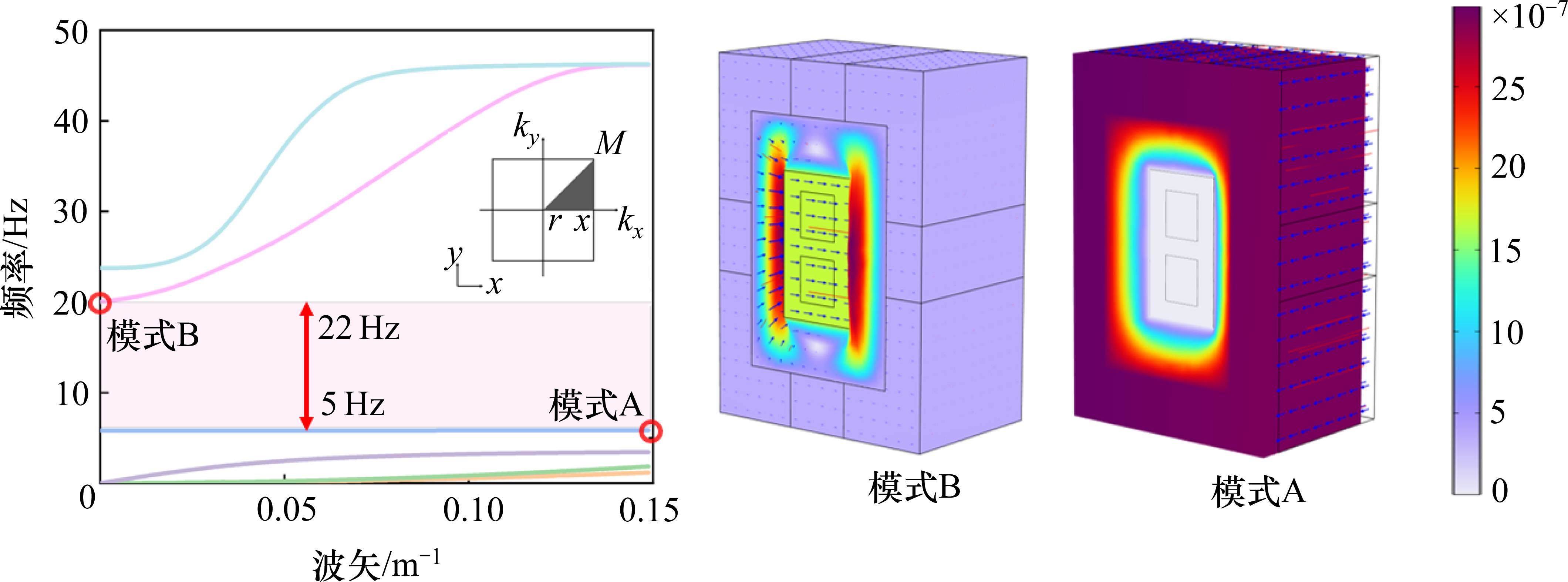
1.3 带隙机理分析
为进一步研究超材料波阻垫振动带隙的边界频率,本小节继续对元胞进行带隙特性分析。如图2的导波模态振型所示,决定起始频率的导波模式表现为外部钢片带动橡胶发生反相位共振,而内层钢片的振动几乎为0,因此起始频率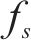
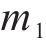
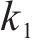

决定截止频率的导波模式表现为内层钢片与橡胶的连接与外层钢片发生反相位共振,外层钢片的振动较小,截止频率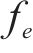
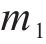
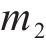
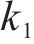
起始频率与截止频率的公式为
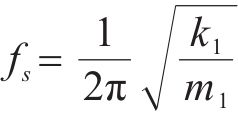
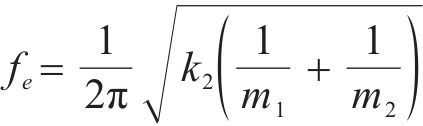
利用材料力学的公式,可算出橡胶的剪切刚度k,为了消除误差,故使用不同的剪切刚度k1,k2进行起始频率与截止频率的计算:
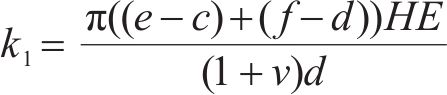
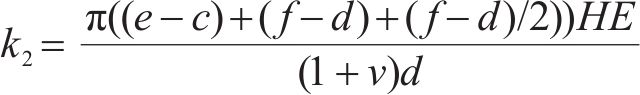
外层钢片的质量m1为
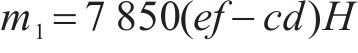
内层钢片和橡胶的质量和m2为
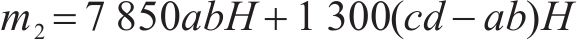
结合弹性波运动方程,波阻垫完全带隙的起始频率和截止频率如式(7)和式(8)所示:
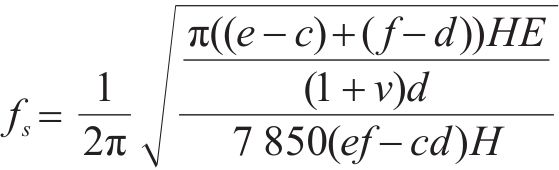
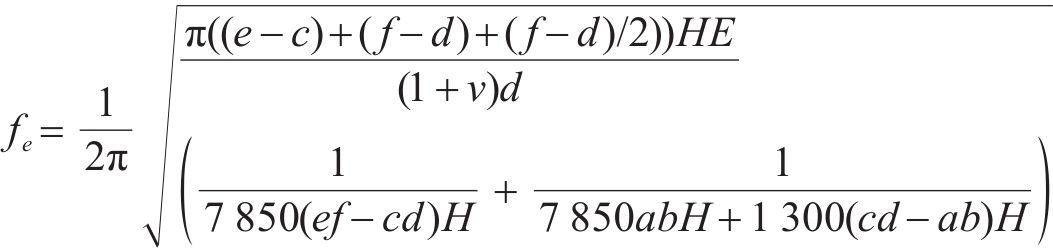
代入第1节中的参数,式中计算结果为: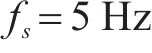
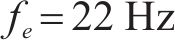
1.4 带隙影响规律
波阻垫内部不同结构的几何参数与带隙的频率紧密联系,在保持其他参数不变的情况下,调节波阻垫的几何参数:内部钢片、外部钢片、环形橡胶的长宽,内部正方形钢振子边长可以相应地改变波阻垫的带隙,另外还研究了橡胶材料的弹性模量和泊松比对于带隙的影响,可以使得波阻垫根据不同环境的需求达到理想效果。取5个不同参数的波阻垫对比带隙的变化,图4(a)为内部钢振子宽度a=0.3,0.5,0.7,0.8,0.9 m,图4(b)为环形橡胶宽度c=0.6,0.8,1,1.2,1.3 m,图4(c)为橡胶泊松比ν=0.4,0.42,0.45,0.47,0.49,图4(d)为橡胶弹性模量E=2.5,3,3.5,4,4.5 MPa时的带隙起始频率、截止频率以及带隙宽度的变化规律。
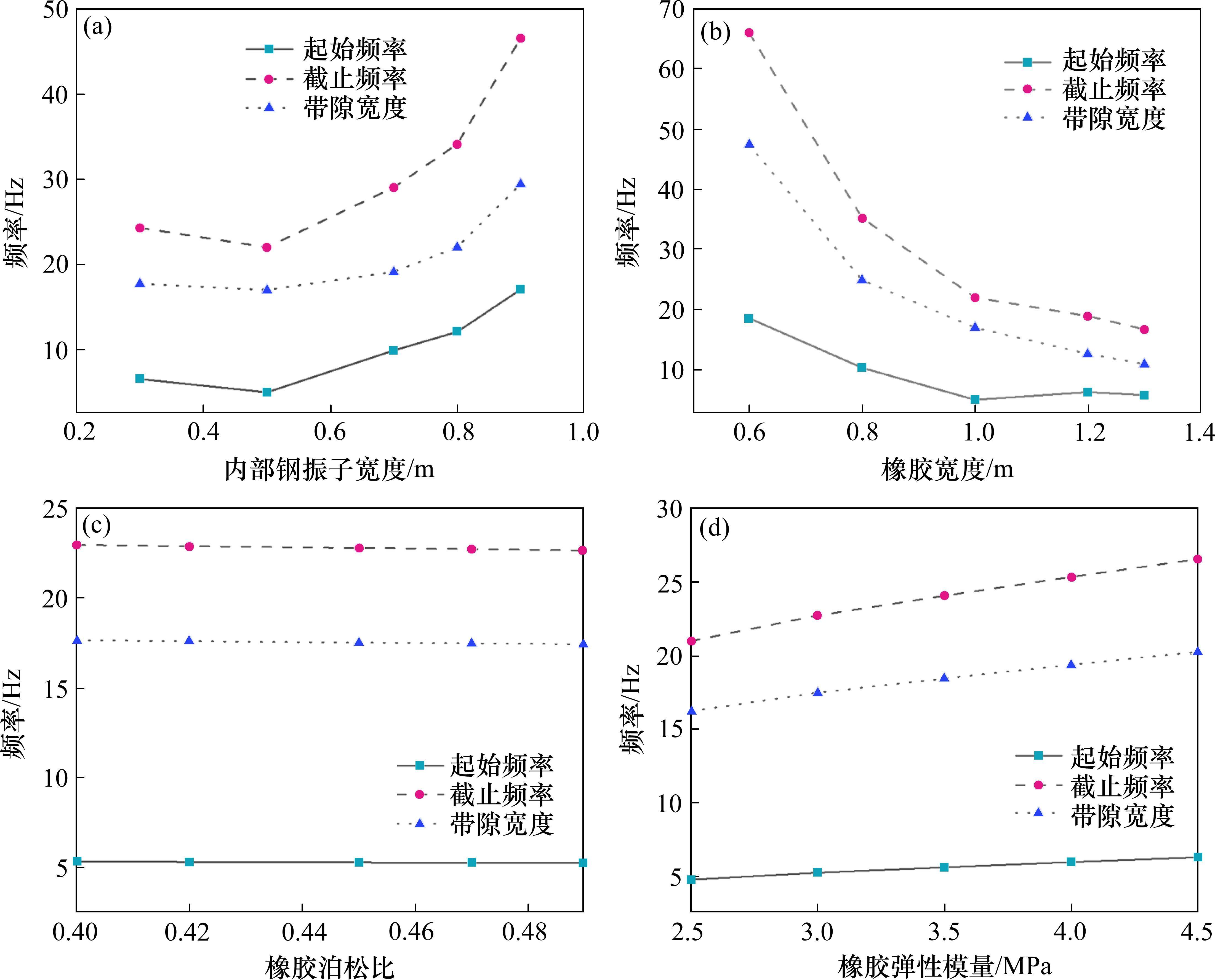
如图4(a),随着内部钢振子宽度的增加,波阻垫带隙的起始频率逐步升高,截止频率显著升高,带隙的宽度呈现先减小后增大的趋势。可以看出在宽度为0.5 m时,起始频率和截止频率为最低点。从整体上看,带隙的起止频率始终在升高,产生这个变化规律的原因是因为内部钢振子宽度增加时,结构整体的刚度增大,导致频率升高。
如图4(b),波阻垫带隙的起止频率均随着环形橡胶宽度的增加而呈现不断降低的趋势,带隙宽度也随之降低。从带隙起止频率及带宽变化趋势来看,橡胶的宽度越小,带隙频率越高,故若想要抑制低频必须增大橡胶宽度。其原因是由于环形橡胶宽度增加导致刚度减小,柔度增大,质量和刚度的变化均导致带隙的频率下降。
从图4(c)可以看出,由于橡胶材料的泊松比波动不大,所以对带隙几乎没有影响。图4(d)波阻垫带隙的起始和截止频率均随着橡胶弹性模量的增大而提高,带隙宽度有少量增大,故可以衡量带隙频段与带隙宽度的需求从而选取合适的橡胶材料。
此外,为了探究阻尼对带隙特性的影响,设置了不同损耗因子进行带隙计算,带隙变化如表2所示。由表中可看出阻尼的增加对带隙宽度的影响不大,这是因为阻尼对中低频的影响较为显著,对超低频几乎没有影响。
| 阻尼损耗因子 | 带隙/Hz | 阻尼损耗因子 | 带隙/Hz |
|---|---|---|---|
| 0 | 5.42~22.16 | 0.6 | 5.48~22.40 |
| 0.2 | 5.43~22.29 | 0.8 | 5.52~22.48 |
| 0.4 | 5.46~22.34 |
2 振动传递损失分析
为了验证超材料波阻垫产生的带隙,建立如图5所示的几何模型,沿X方向周期组合排列6个单元结构。在X方向施加1N/m2的边界载荷来激发在土壤中传播的体波和弹性波。为了防止土体下方位移产生影响,在土体下方施加固定约束。在土壤右侧响应处拾取位移幅值响应,得到频率响应函数曲线如图5所示。
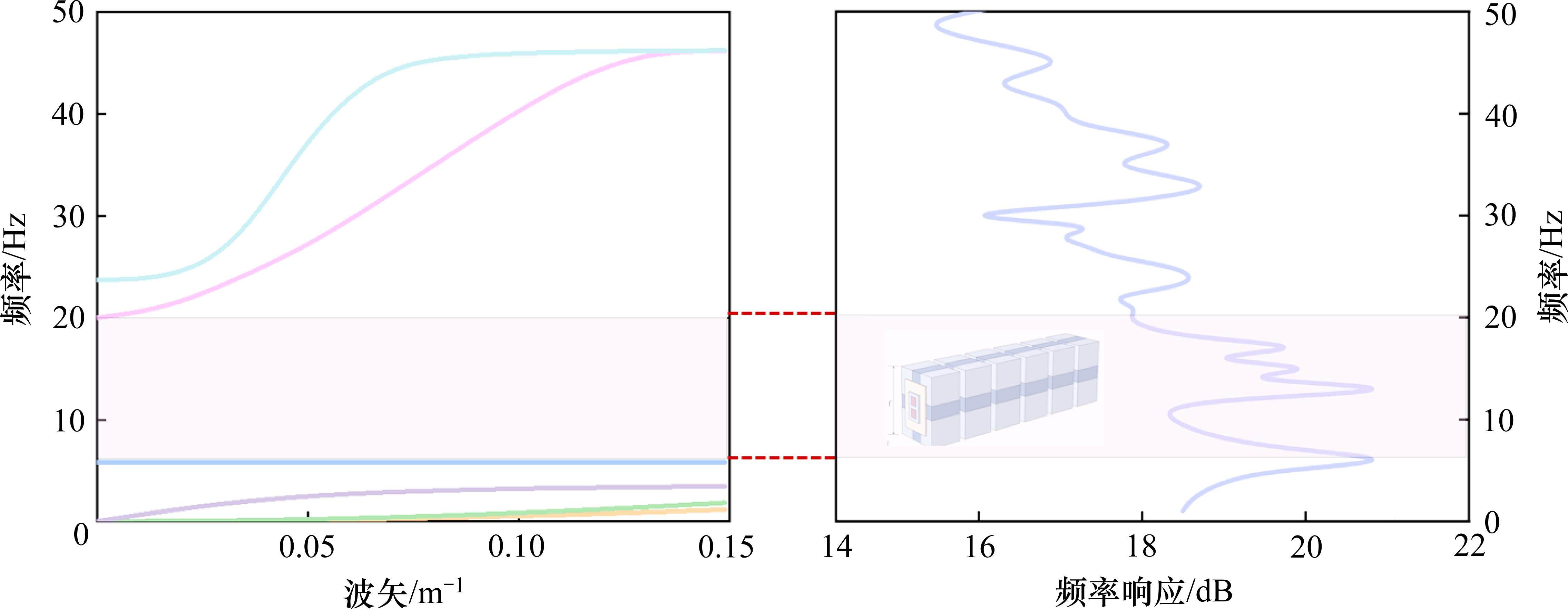
频率响应函数表征了有限超材料结构中输入与输出幅值的比值与频率之间的关系,通过计算频率频响函数可以有效描述屏障的减振效果。定义频率频响函数的传递率TL为
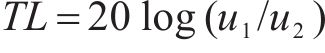
式中: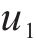
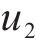
3 超材料波阻垫在地铁隧道-建筑物工况仿真
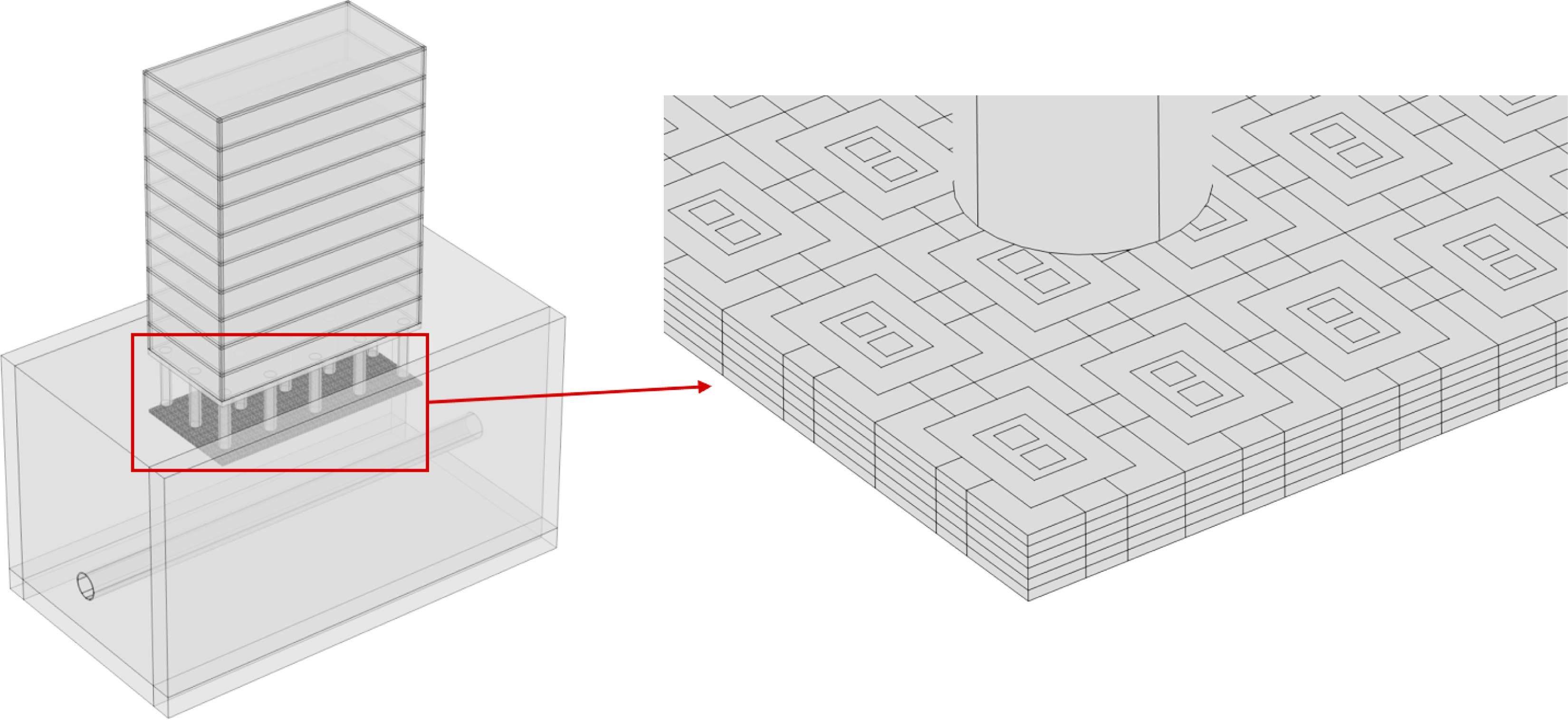
为了模拟本文所设计的超材料波阻垫在地铁隧道运行中吸收弹性波的效果,本节利用COMSOL Multiphysics 6.1多物理场软件,建立了一个地下列车隧道与建筑物的简化模型,在建筑物的地基下方放置设计6层如图6所示的超材料波阻垫。通过添加指定位移源的激励方法,验证地铁隧道、固体土壤域和混凝土建筑的隔振效果。利用声-固结构边界多物理场耦合,模拟声学和振动问题。由于实际模型尺寸庞大,建模时通过建筑的对称性来减少边界条件和完美匹配层(PMLs)的自由度数量。
3.1 建筑物声压级与土地位移变形对比
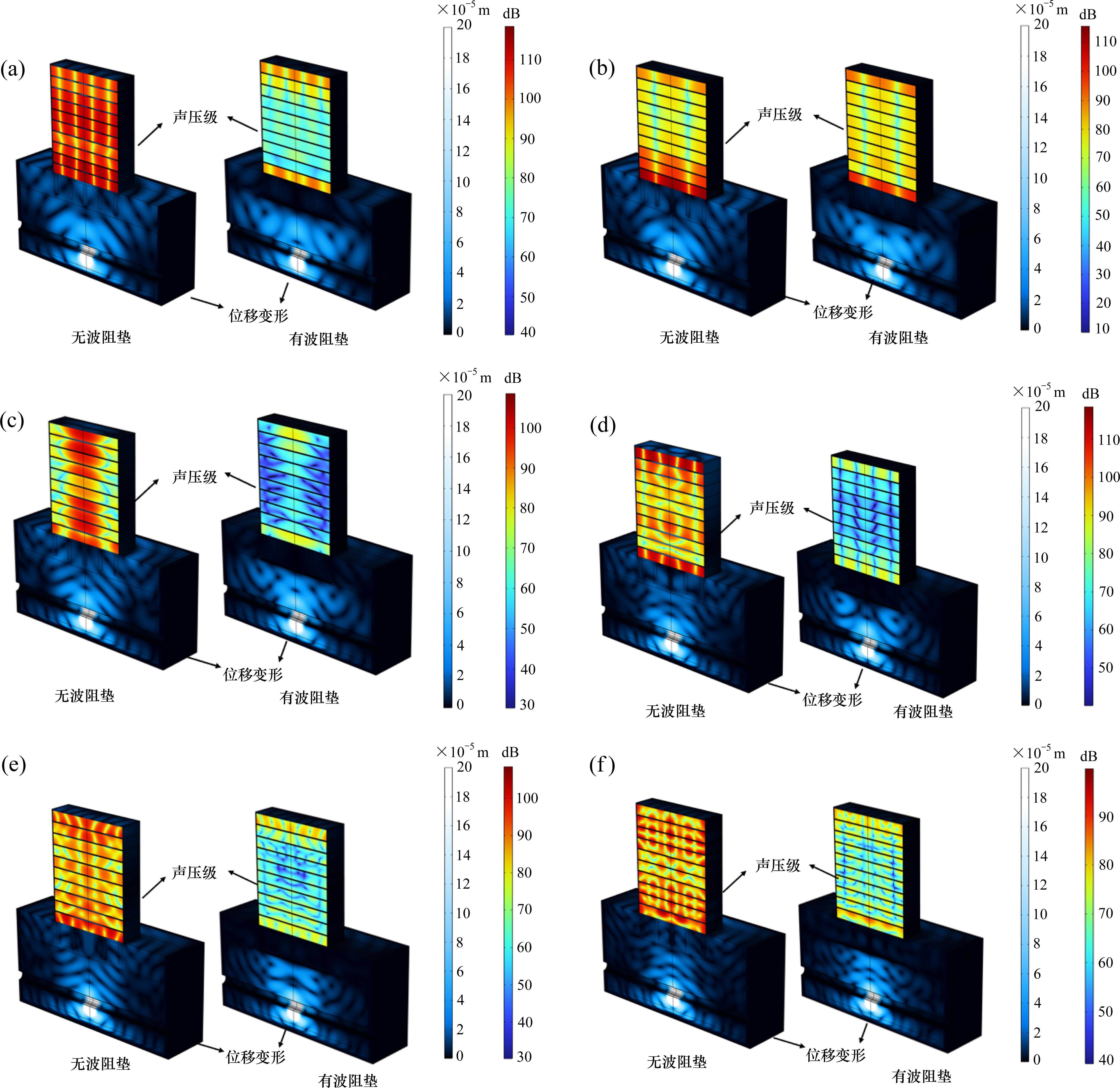
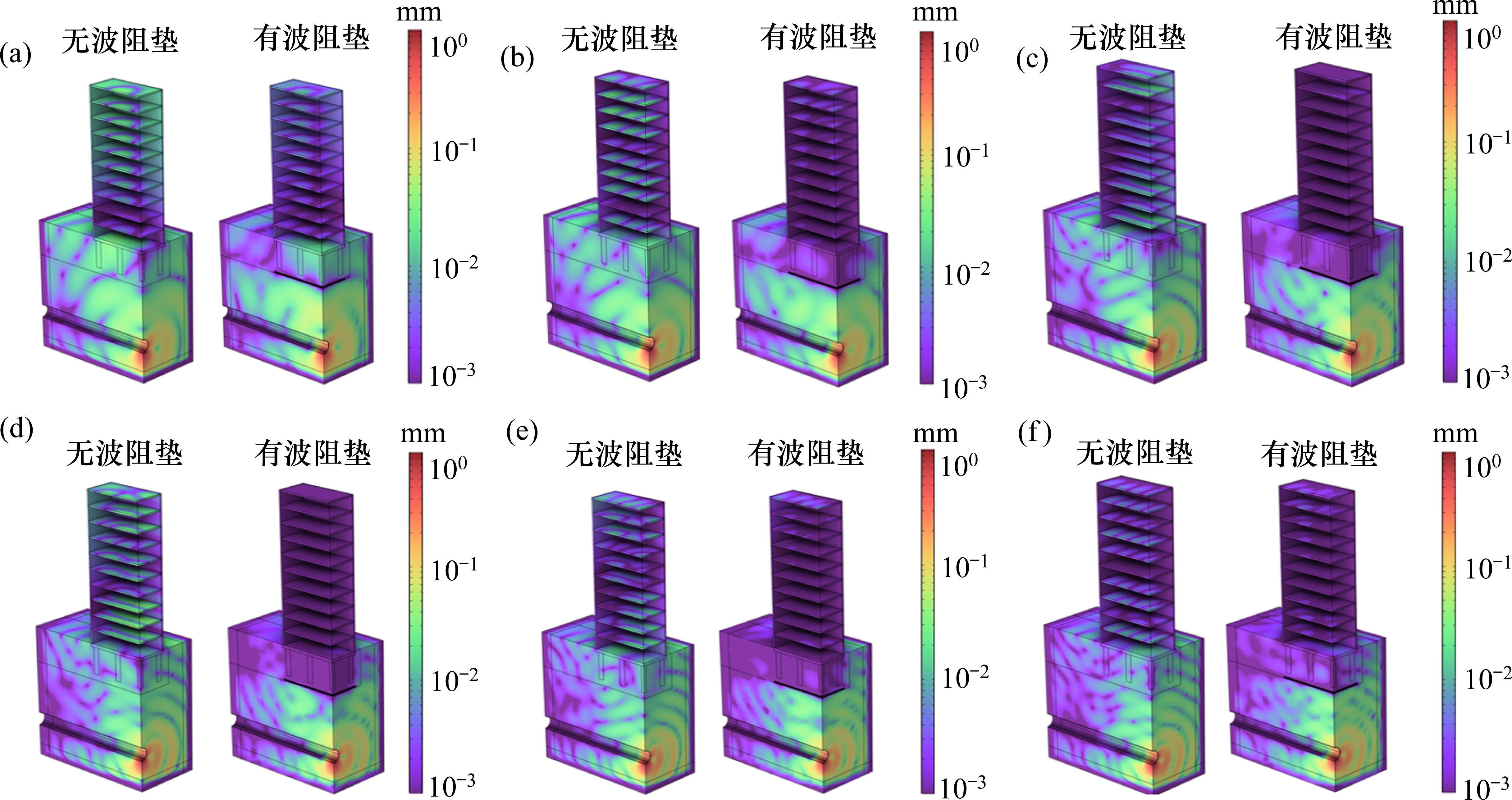
图7(a)~图7(f)分别为带隙范围内17.5,20,22.5 Hz以及通带内25,27.5,30 Hz时的超材料波阻垫的建筑物声压级和土体位移变形在comsol中的计算结果图。3个带隙范围内的频率:从图7(a)中,在17.5 Hz下未施加波阻垫的建筑物中最大声压级达到118 dB,而施加了超材料波阻垫后建筑物的最大声压级为102 dB,降低了16 dB。图7(b)中,在20 Hz下未施加波阻垫的建筑物中最大声压级达到115 dB,而施加了超材料波阻垫后建筑物的最大声压级为100 dB,降低了15 dB。图7(c)中,在22.5 Hz下未施加波阻垫的建筑物中最大声压级达到100 dB,而施加了超材料波阻垫后建筑物的最大声压级为80 dB,降低了20 dB。3个通带内的频率:图7(d)中,25 Hz时施加超材料波阻垫后的建筑物声压级比未施加波阻垫时降低了24 dB,图7(e)中施加波阻垫后声压级在27.5 Hz时降低了12 dB,图7(f)中施加波阻垫后声压级在30 Hz时降低了10 dB。可以得出结论,超材料波阻垫在17.5~30 Hz频段内可以有效降低地铁引起的建筑物振动,衰减量在25 Hz达到最大,为24 dB;平均衰减量为16 dB,与图5计算得到的声衰减曲线基本一致。而土体部分可以看出,在不同频率下施加超材料波阻垫后桩基础部分的位移变形几乎为0,而未施加波阻垫时的桩基础土体的位移变形为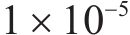
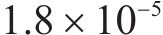
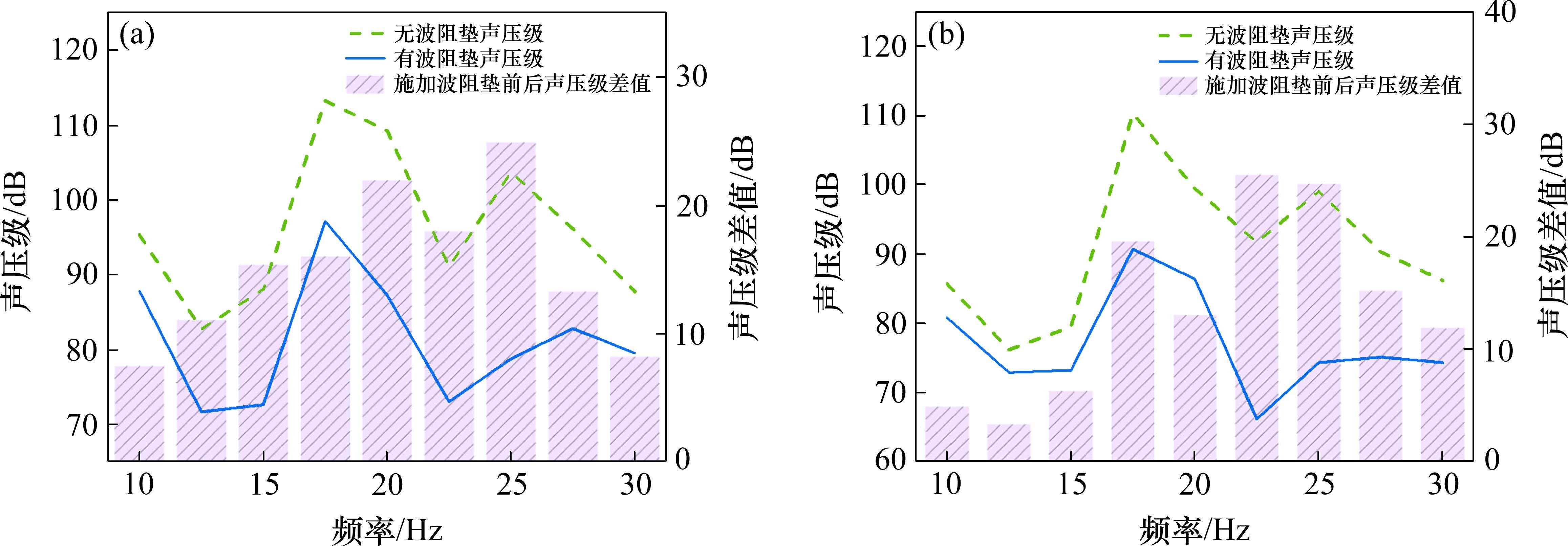
为了更加直观地看出施加超材料波阻垫后建筑物声压级的变化,取出了所有楼层的声压级平均值和地面层的声压级平均值进行对比,如图8所示。图8(a)为地面层的平均声压级折线,图8(b)为所有楼层的平均声压级折线。图中绿色虚线为没有施加波阻垫时,不同频率下的平均声压级;图中蓝色实线为施加波阻垫后,不同频率下的平均声压级;紫色的柱形部分为不同频率下施加波阻垫前后的平均声压级差值。由图8(a)可以看出施加超材料波阻垫后10~30 Hz时的平均声压级都有明显降低,在带隙频段10~22 Hz内降低较多,带隙频段外也存在小幅减振效果,效果最好的频段为15~28 Hz。由图8(b)可以看到施加超材料波阻垫后所有楼层的平均声压级均有下降,在17~28 Hz内效果最佳,最多降低了25 dB。
3.2 建筑物位移变形对比
图9为带隙频段内外的建筑物的位移变形结果,图9(a)~9(d)为带隙频段内,图9(e)~9(f)为带隙频段外。图9(a)中,在10 Hz时建筑物的位移变形相对较大,无波阻垫时最大达到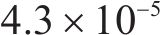
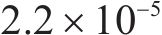
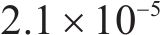
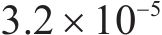
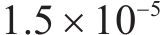
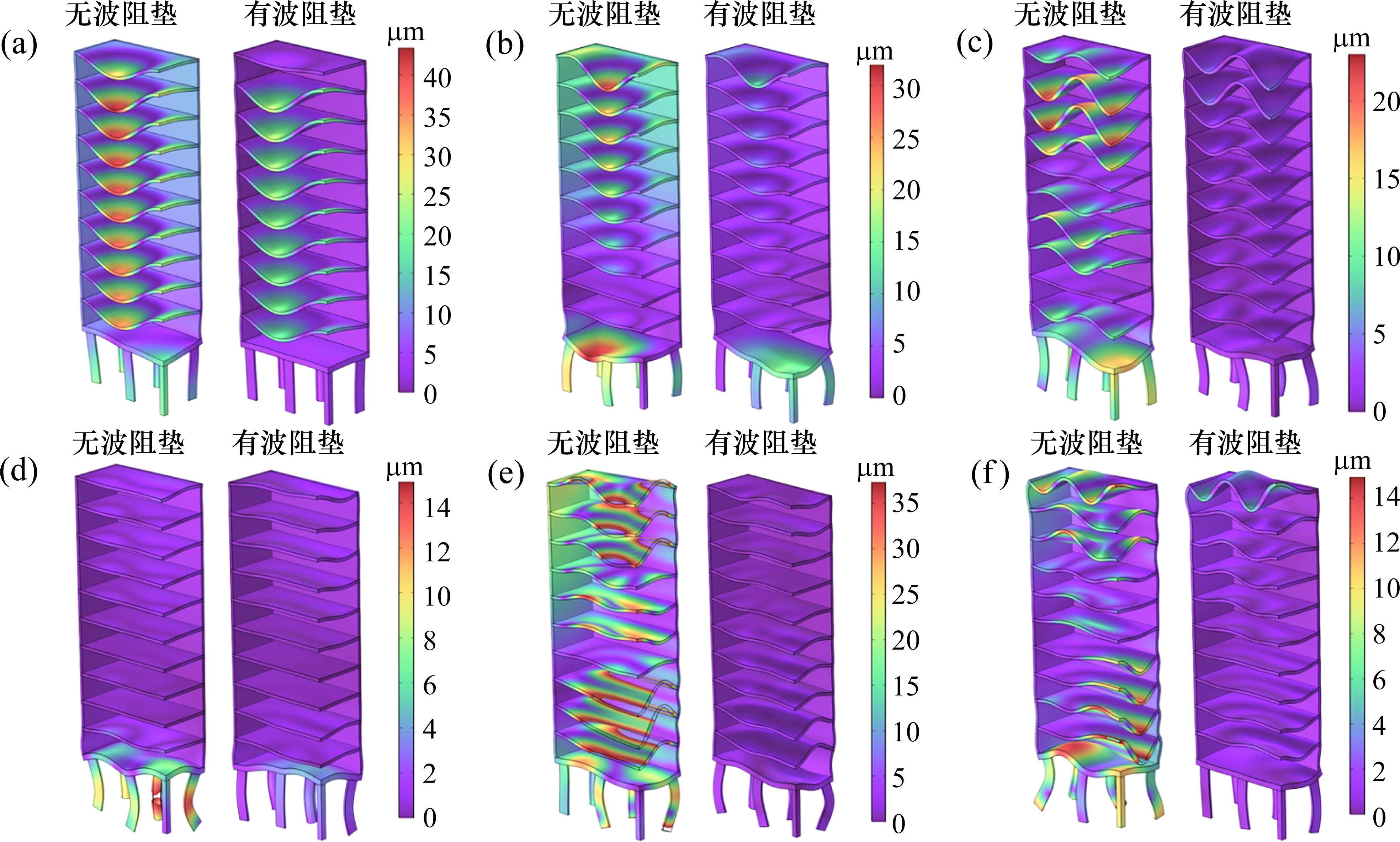
3.3 建筑物振级对比
图10为土体和建筑物的振级计算结果,在15 Hz时,无波阻垫的建筑物基本每层楼都存在振动,楼层的振动最大达到0.03 mm,而施加超材料波阻垫后振动控制在最大为0.01 mm,振级降低了0.02 mm。在17.5 Hz时,没有设置波阻垫的建筑物振动最大达到0.02 mm,而施加波阻垫后振动几乎为0。在17.5~30 Hz之间的频率范围内,施加超材料波阻垫后的建筑楼层内基本没有振动,效果显著。
4 实验验证
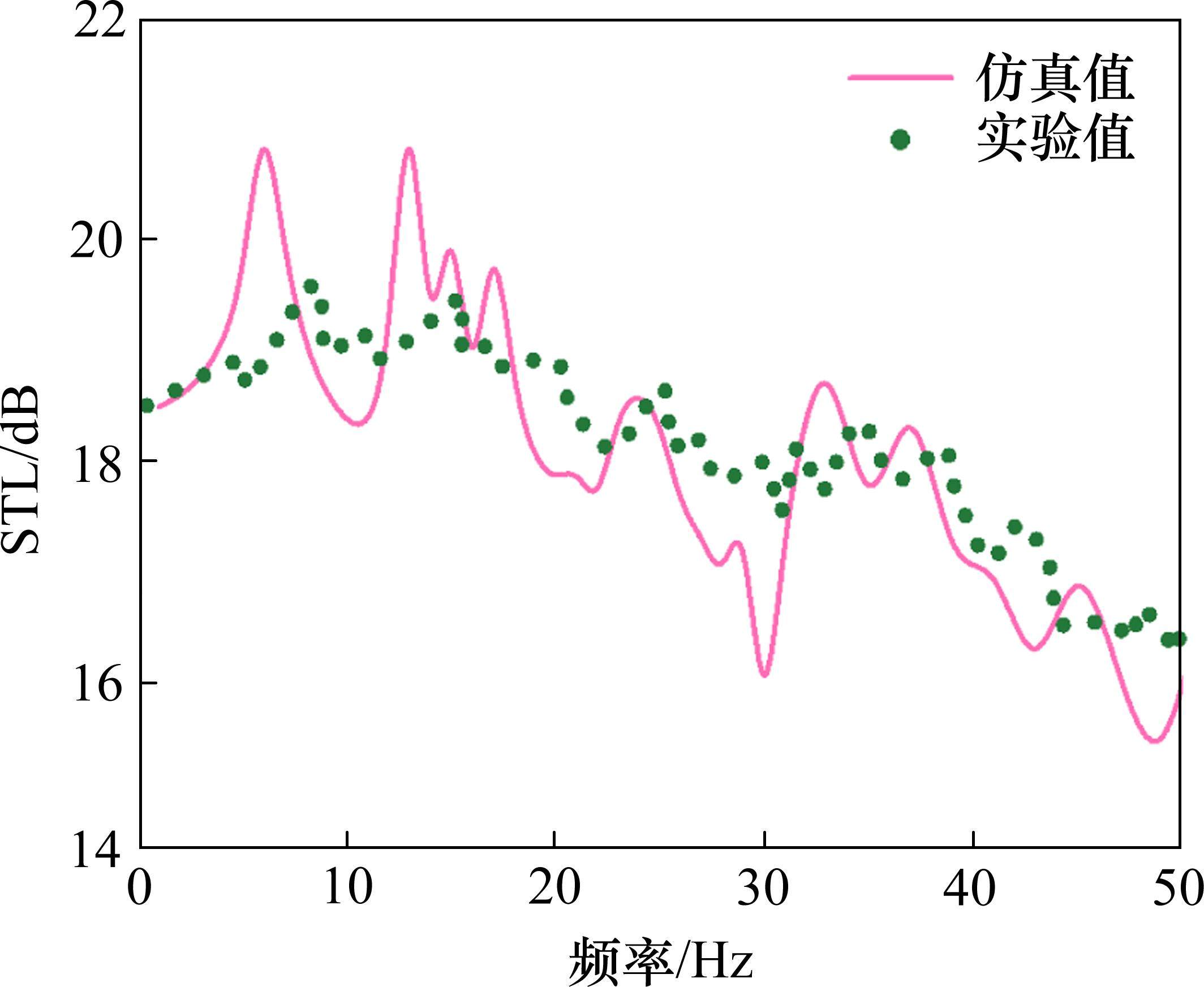
为了验证超材料波阻垫的隔振性能,制作了如图11所示的缩尺超单元模型来测量样品的传递损失。采用3D打印技术制备大楼模型,材料为光敏树脂。由于原结构尺寸过大,进行的缩尺实验为原模型等比例缩放0.006倍。将制备出的超材料波阻垫埋入土体,大楼放置在波阻垫正上方,振动传感器分别放置在大楼的顶层和底层,运行大楼后方轨道上的小车,利用采集仪收集放置波阻垫前后的测试数据。通过测试得到的传递损失值如图12所示,在0~50 Hz下实验结果和仿真结果大致一致,验证了超材料波阻垫的隔振性能。

5 结论
1) 根据局域共振原理采用有限元法设计了一种新型超材料波阻垫。该结构能够抑制20 Hz以下的低频环境振动和宽频域的噪声辐射。其中带隙范围可达5~22 Hz,同时进行了参数化分析和带隙的振动衰减验证。
2) 讨论了超材料波阻垫结构的带隙产生机理,推导出了带隙预测的理论解析公式,与数值仿真结果相符合。
3) 建立了地铁隧道-建筑物的声学-固体力学多物理场耦合模型,对比施加超材料波阻垫前后的环境振动与建筑物噪声的空间及频率分布规律。结果表明,施加超材料波阻垫后,在带隙范围内所有楼层的平均噪声声压级均有下降,最多降低了25 dB,平均下降16 dB,带隙范围之外声压级也有小幅降低;建筑楼层内振动位移显著减小,平均降低了13 μm。
4) 进行缩尺实验对超材料波阻垫进行验证,发现实验和仿真结果表现出较高的一致性,验证了超材料波阻垫的减振性能与工程可行性。
上述研究证明了,超材料波阻垫可有效实现低频振动控制,从而控制地铁列车诱发的环境振动及建筑物二次噪声,本文提出的超材料设计方法,也可为有减振降噪需求的各类工程应用提供新的技术和理论支撑。
余奇,赵才友,张鑫浩等.铁路超材料波阻垫设计与低频减振降噪应用研究[J].铁道科学与工程学报,2024,21(12):5221-5231.
YU Qi,ZHAO Caiyou,ZHANG Xinhao,et al.Research on the design and application of low-frequency vibration and noise reduction of railroad metamaterial wave-resistant pads[J].Journal of Railway Science and Engineering,2024,21(12):5221-5231.

