基于OTFS的城轨T2T通感一体化信号设计与优化

智能制造与装备

基于OTFS的城轨T2T通感一体化信号设计与优化

杨骞，

苏宏升，

刘大为，

魏伟

铁道科学与工程学报

第21卷, 第12期

pp.5209-5220

纸质出版 2024-12-28

DOI：10.19713/j.cnki.43-1423/u.T20240292

中图分类号：U283.5

400

为了在B5G/6G商用频谱资源紧缺的环境下，对现有城市轨道交通列车运行控制设施基础上进行改造，以实现基于车-车通信的列车信息传递，提出基于正交时频空(OTFS)调制的通信感知一体化信号设计。首先提出单符号和多符号OTFS时域信号模糊函数模型，对两者的距离模糊性和速度模糊性进行仿真对比，以验证原始多符号OTFS信号感知性能的优越性。再提出蚁群优化(ACO)算法与经典选择映射法(SLM)的结合ACO-SLM算法，设计应用ACO-SLM算法的OTFS系统发射机结构，用来对原始OTFS信号的高峰均功率比进行抑制，并将抑制作用通过仿真实验进行横向和纵向对比。最后经过ACO-SLM算法处理后的OTFS时域信号模糊性与传输误比特率进行仿真分析。研究结果表明：改变算法参数进行横向对比显示，16QAM星座调制作为输入序列，用相位因子组数为16的ACO-SLM算法处理OTFS信号，峰均功率比为6.03，为最低水平；纵向对比显示，ACO-SLM算法相比于其他传统算法，对峰均功率比有更好的抑制作用。对ACO-SLM算法处理的多符号OTFS时域信号进行模糊性仿真分析，显示其测距和测速性能有所提升，且传输误比特率与传统算法处理后的OTFS信号相比，几乎不受影响。研究结果为面向B5G/6G的城轨车-车通信感知一体化实现和基于车-车通信的列车运行控制提供了理论依据。

通感一体化正交时频空蚁群优化选择映射法峰均功率比

目前，城市轨道交通主要依靠基于通信的列车控制(Communication Based Train Control，CBTC)系统保证其运行控制，在CBTC系统的发展过程中，车-地之间的高效率、高可靠性通信是信息传输、列车运行控制的重要保证^[1-2]，在CBTC的基础上，下一代基于车-车通信的列车运行控制系统的智能化和自动化程度将会提高^[3]，列车之间的可靠信息传输是实现高效列车运行控制的基础。车-车(Train-to-Train, T2T)通信的技术实现方式分为2种：一是通过传统车-地链路的改进，间接实现T2T通信；二是利用专用铁路通信频段，配合天线技术，建立T2T空口无线链路，实现列车间的直接通信。在T2T的通信方案研究上，SONG等^[4]提出了一个T2T数据通信系统的系统结构，该系统不仅可以实现数据通信，还可以提供训练距离测量的列车。徐纪康^[5]提出的VBTC系统改进了列车的自动控制方式，降低了系统控制模块间的耦合，提高了系统运行效率，降低了成本。WANG等^[6]介绍了利用LTE-T2T通信的城市轨道交通系统的通信策略，系统以列车为控制中心，新的on-ZC取代传统的区域控制器，成为信息中转的关键。这些都是利用地面设备作为信息中转，先完成T2X，再去完成T2T的通信，陈启香等^[7]基于超短波实现了列车间的直接通信。未来在B5G(Beyond 5th Generation)/6G(6th Generation)通信技术应用过程中，会出现商用频谱资源紧缺的情况，因此将重点研究基于通信感知一体化实现的城市轨道交通列车运行控制^[8]。考虑到由于列车高速移动产生的多普勒频移问题，基于正交时频空(Orthogonal Time Frequency Space, OTFS)的T2T无线通信系统是有效的解决方案之一。在OTFS应用方面，RANGAMGARI等^[9]将OTFS的使用环境置于高速车辆的通信场景，从OFDM的角度可视化OTFS，仿真结果验证OTFS在开销和抗子载波干扰方面都优于块OFDM。RAVITEJA等^[10]在OTFS单帧的末端只添加了一个循环前缀，显著降低了导频开销。WANG等^[11]在传统OTFS调制的基础上，提出了一种基于加权型分数傅里叶变换的具有二维可调参数和强可扩展性的集成波形框架。HOSSAIN等^[12]基于窗口重组设计了OTFS系统，保证了通信质量和效率的同时，有更好的高迁移率场景适应性。而T2T无线通信过程，其中一项特征就是高迁移率场景，OTFS已被证明比OFDM更适用于B5G/6G通信场景。基于通信的通感一体化信号设计，近些年的多数研究工作都集中在基于4G的OFDM调制系统方面。谷亚彬等^[13]选用基于通信的OFDM雷达-通信一体化信号模型，仿真验证相关函数共享信号处理算法在高多普勒频移环境下，对调制信号主、旁瓣峰值的积极影响。余显斌等^[14]分别从感知和通信的角度讨论了一体化波形设计及优化策略，提出太赫兹波段基于OFDM的一体化信号，通过实验对测速、测距和无线通信性能进行测试。GAUDIO等^[15]对基于OTFS调制的通感一体化系统的雷达参数估计部分，推导了一个有效的近似极大似然算法和相应的距离和速度估计的下界，仿真证明OTFS等多载波数字格式可以实现与最先进的雷达波形一样精确的雷达参数估计。在OFDM和OTFS调制信号的传输性能指标方面，高峰均功率比(Peak-to-Average Power Ratio, PAPR)会造成传输过程中的信号畸变，信号非线性失真，从而导致系统性能下降。针对上述问题，NAVEEN等^[16]基于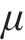律压缩技术将OTFS的PAPR比原始OTFS信号降低2.5 dB，但传输误码率相比于原始OTFS信号略有升高。CHENNAMSETTY等^[17]验证了选择映射(Selected Mapping, SLM)技术对OTFS调制信号的PAPR的抑制作用，并将所得结果与OFDM调制进行了比较，结果表明OTFS信号性能要优于OFDM信号。在采用优化算法与经典SLM算法结合对PAPR进行抑制方面，INSOO^[18]将遗传算法(Genetic Algorithm, GA)与SLM算法结合对OFDM信号的PAPR进行处理，但遗传算法维度高、复杂度高，参数选择严重依靠经验。白菊蓉等^[19]将粒子群优化(Particle Swarm Optimization, PSO)与SLM算法结合对OTFS信号的PAPR进行抑制，XU等^[20]将帝国主义竞争算法(Imperialist Competition Algorithm, ICA)与SLM算法结合对OTFS信号的PAPR进行抑制，PSO与ICA优化算法都易过早收敛，而陷入全局最优。上述研究，在基于OTFS的通信感知一体化信号设计和性能优化2个方面均未做到结合研究并做出改进，基于此本文主要工作如下：

1) 设计以通信为基础的，基于OTFS调制的通感一体化信号。对OTFS信号的单符号及多符号信号进行雷达模糊性仿真。仿真验证单符号OTFS信号的速度模糊性的缺失，但距离模糊性良好；多符号OTFS信号在速度模糊性和距离模糊性上均有良好表现，具备作为城轨T2T通感一体化信号的能力。

2) 提出一种蚁群优化(Ant Colony Optimization, ACO)算法与经典SLM算法相结合的ACO-SLM算法，对发射机的OTFS调制信号进行PAPR优化，抑制PAPR对时域信号传输的影响，并与其他现有研究的PAPR抑制算法结果进行仿真对比，以此验证该算法抑制PAPR能力的突出。

3) 将经过ACO-SLM算法处理的时域信号再次进行模糊性分析，验证优化后的OTFS信号的距离和速度模糊性仍旧良好。通过对信号传输误比特率(Bit Error Rate, BER)的对比分析，说明ACO-SLM算法处理后的信号，其误比特率仍能保持较优水平。

1 通感一体化信号模型与模糊性分析

1.1　OTFS信号模型

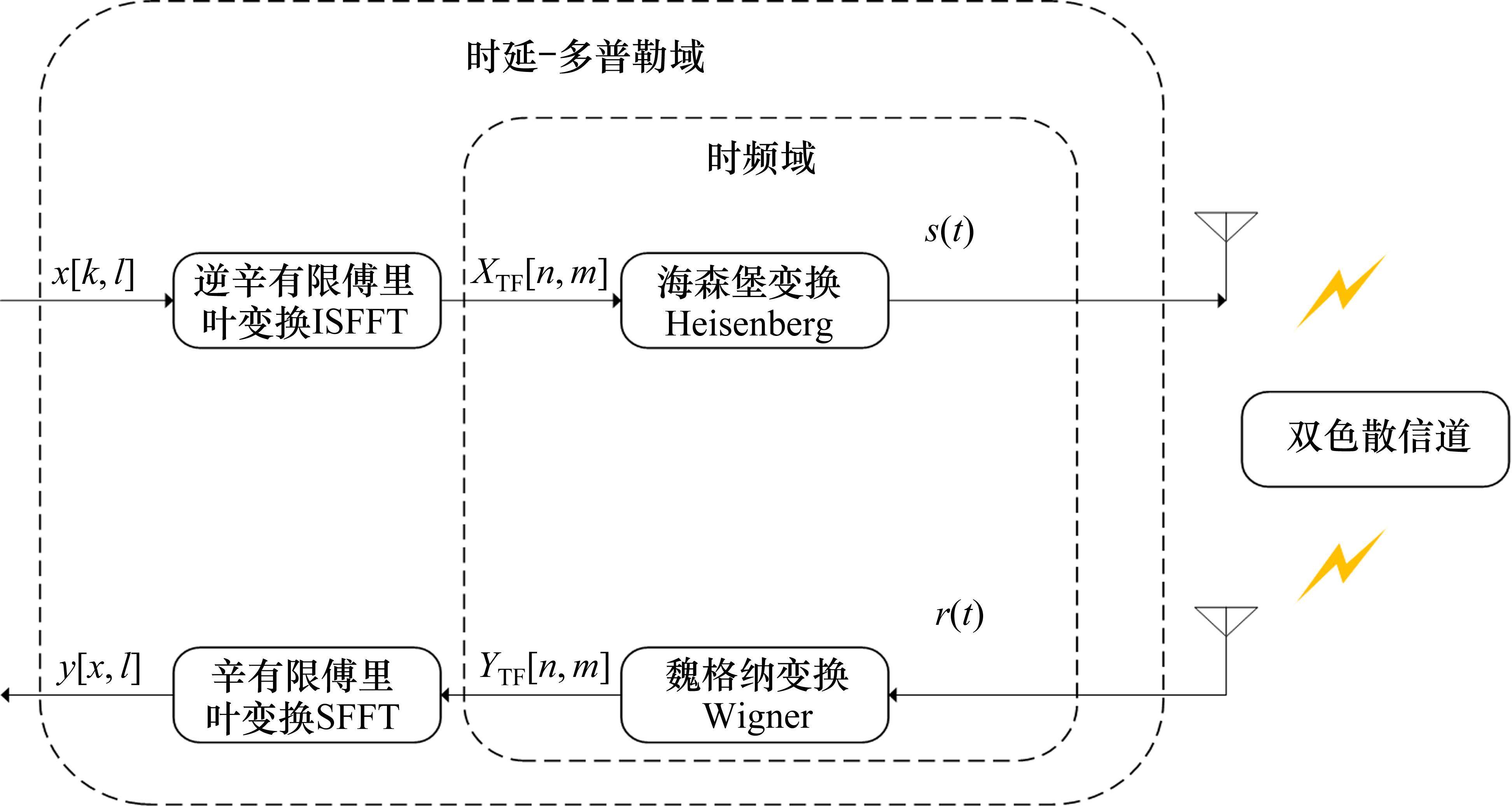
图1展示了OTFS调制的发射端和接收端二维变换的级联关系^[21]。

图1

OTFS调制解调过程

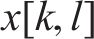
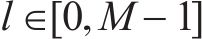
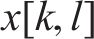
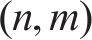
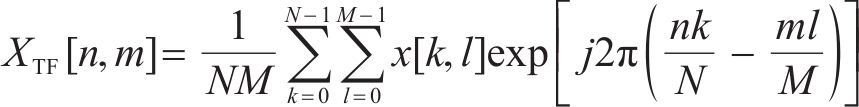
若待发送信息为，其中为延迟域序号，为多普勒域序号，信息符号是置于DD域的QAM符号，在经过ISFFT后，得到TF域第个信息符号：

(1)

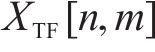
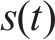
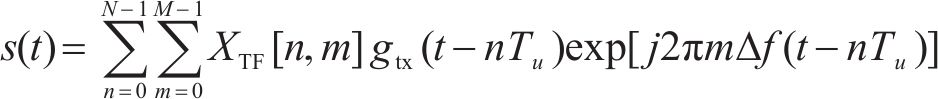
其中，，。时频域符号通过Heisenberg变换转换为时域信号，过程如下。

(2)

其中，是单帧内的符号数；是子载波个数；是子载波带宽；是单个信息符号持续时间，则无线信号传输系统的带宽，发射数据总时长为。

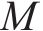
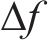
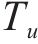
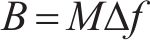
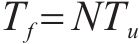
1.2　OTFS信号模糊性分析

为实现城轨T2T的通感一体化，需验证OTFS信号的速度模糊性和距离模糊性^[22]。若式(2)是基于通信的通感一体化OTFS时域信号，设其复模糊函数为

(3)

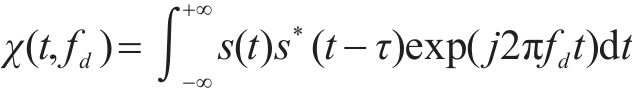
其中，为时间延迟；是多普勒频移；为式(2)中发送端输出信号的复共轭函数表示，即雷达回波信号。

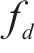
1.2.1　单符号OTFS信号模糊性分析

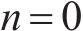
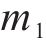
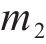
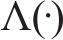
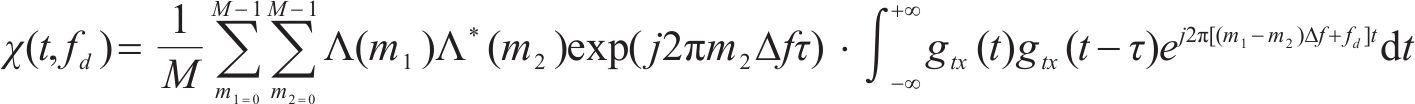
将式(2)代入式(3)中，令，表示发射出的信号子载波数，表示反射回波信号中的子载波数，引入表示延迟网格内的子载波块，则

(4)

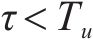
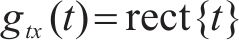
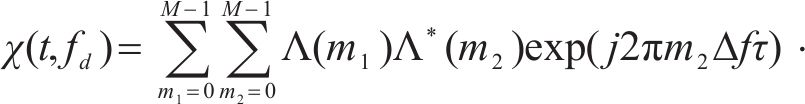
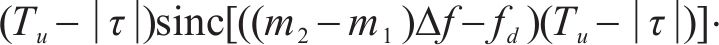
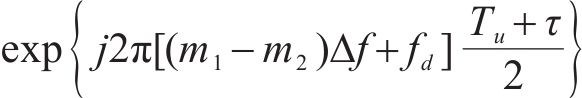
设时延，加窗函数为矩形脉冲，即，则式(4)可表示为

(5)

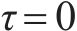
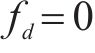
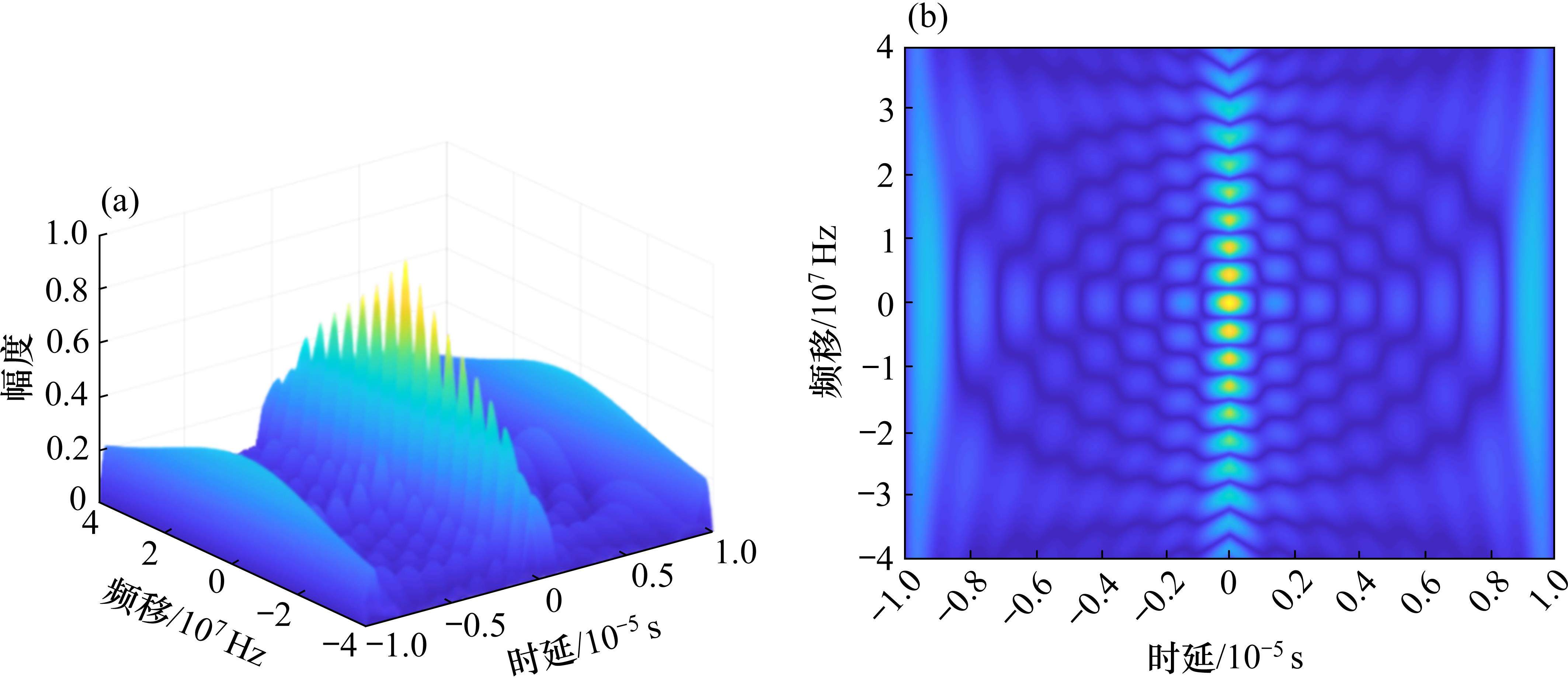
图2对单符号OTFS信号模糊函数进行仿真。当时延时，沿多普勒频移轴有多个峰值的出现，单符号OTFS信号的速度模糊性不佳，不具备良好的测速能力。当多普勒频移，沿时延轴只出现单个峰值，单符号OTFS信号有很好的距离模糊性，即测距定位能力良好，可用于对列车定位。

图2

单符号OTFS信号模糊性分析

1.2.2　多符号OTFS信号模糊性分析

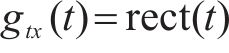
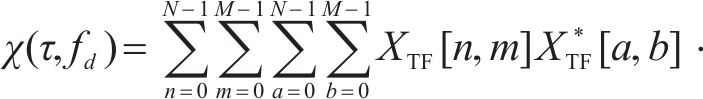
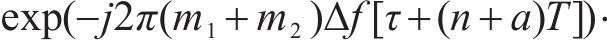
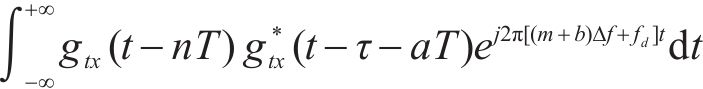
设加窗函数为矩形脉冲，即，将式(2)代入(3)中

(6)

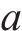
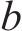
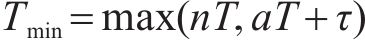
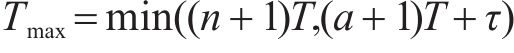
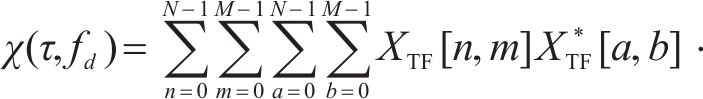
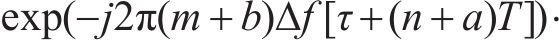
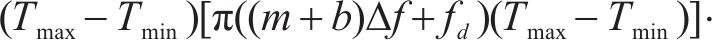
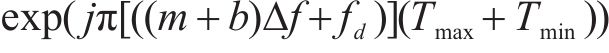
其中，为回波信号符号数；为回波信号子载波数。设含有雷达回波信号的时域边界，，则式(6)可写为

(7)

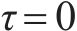
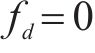
图3对多符号OTFS信号模糊函数进行仿真。当时，信号波形仅在频移0点出现峰值；当时，信号仅在时延0点出现峰值。2个一维0点处，子载波波形具有良好的正交性，故多符号OTFS信号同时具备良好的抗延迟和多普勒频移的特性，理论上有良好的测速和测距定位能力，符合面向T2T的通感一体化信号波形设计需求。但在图3中可以看到旁瓣区域仍有较高幅值，故需对基于OTFS的通感一体化波形进行优化，本文将对一体化信号的PAPR进行干预抑制，从而达到优化一体化信号传输性能的目的。

图3

多符号OTFS信号模糊性分析

2 OTFS一体化信号优化

2.1　OTFS信号的PAPR

对式(2)进行奈奎斯特采样，时域信号离散化之后得到^[23]

(8)

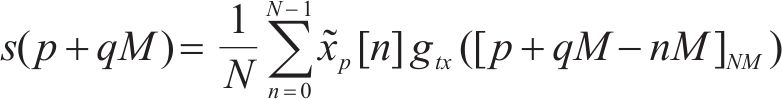
其中，，，。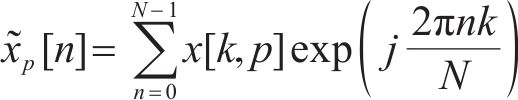

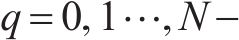
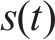
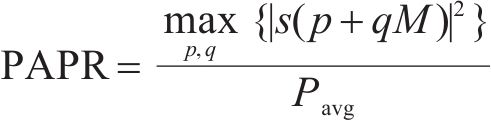
时域信号在发射机末端将通过高功率放大器后进入信道，OTFS信号随着符号数的增加，在信道传输过程中非线性失真造成的传输性能降低将会越加严重，在发射机末端降低PAPR是有效降低时域信号非线性失真的办法。单帧离散时域OTFS信号的PAPR表示如下^[24]_：

(9)

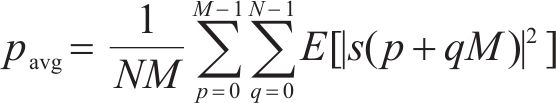
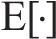
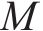
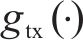
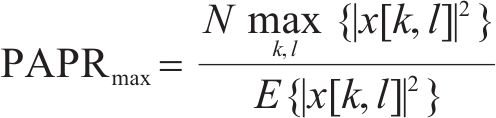
其中，，为期望运算。将式(8)代入式(9)，当和足够大，且为理想的矩形脉冲函数的时候，可得到PAPR的临界峰值为

(10)

式(10)中：PAPR的上限随着OTFS信号的多普勒网格数N，即符号数线性增长。在实践过程中N过大将导致严重的解码延迟，故一般选择。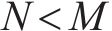

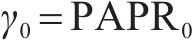
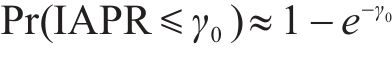
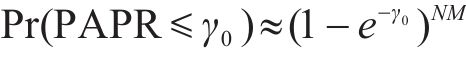
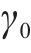
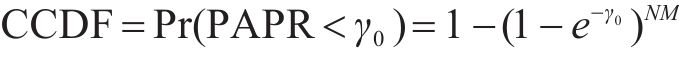
瞬时平均功率比(instantaneous-to-average power ratio, IAPR)为指数分布，设其阈值为，IAPR不超过阈值的概率为，根据奈奎斯特采样次数，可将PAPR不超过阈值的概率定义为。PAPR的优化问题转化为互补累计分布函数(Complementary Cumulative Distribution Function, CCDF)值的优化问题，将其设定为PAPR超过阈值的概率，所以优化问题的表述如下：

(11)

上述CCDF只是近似值，但当接近于无穷大时，实际的CCDF值收敛于式(11)的近似值。

2.2　经典SLM

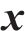
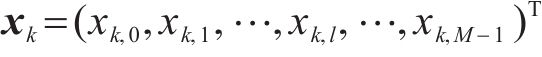
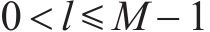
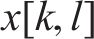
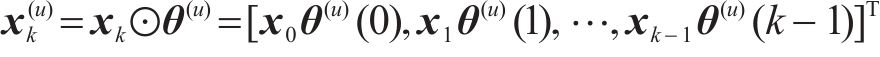
经典SLM是将输入发射机的正交调幅(Quadrature Amplitude Modulation, QAM)信号进行转置，并与转向向量点乘，然后逐个对处理后的每个符号进行OTFS调制，调制后的时域信号进入SLM模块进行筛选，最后选择最低的PAPR信号从末端发出^[17]。设为第k个OTFS符号的输入符号向量，表示为，。N个带有M个子载波的多符号信号表示为，将相位旋转的输入符号向量表示为

(12)

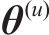
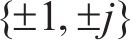
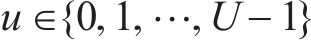
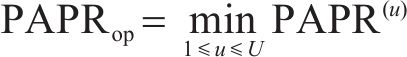
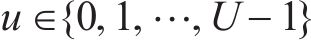
相位序列是由集合中的单位大小的复数随机选取，为可变的相位因子组数，可以理解为SLM算法的系数，SLM算法即是在诸多点乘转置后映射至时域的信号中，选取PAPR最低的信号发出，可表述为

(13)

其中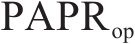，为最优PAPR。传统SLM方法是基于增加备选时域信号的数量，最终选择最优PAPR的时域信号进行传输，从而达到抑制PAPR的目的。

2.3　ACO-SLM算法对最优PAPR时域信号的确定

将蚁群算法与经典的SLM相结合，对进入信道的OTFS时域信号进行PAPR优化。经典蚁群算法是蚂蚁用“信息素”标记行走路径，随着时间推移，蚁群逐渐选择被标记次数最多的路径，即“信息素”浓度最高的路径，进行食物搜索，整个搜索过程是一个正反馈的机制，最终的目标是搜索获得食物的最佳路径。图4为本文采取的ACO-SLM算法OTFS信号发射机的结构。

图4

基于ACO-SLM算法的发射机结构

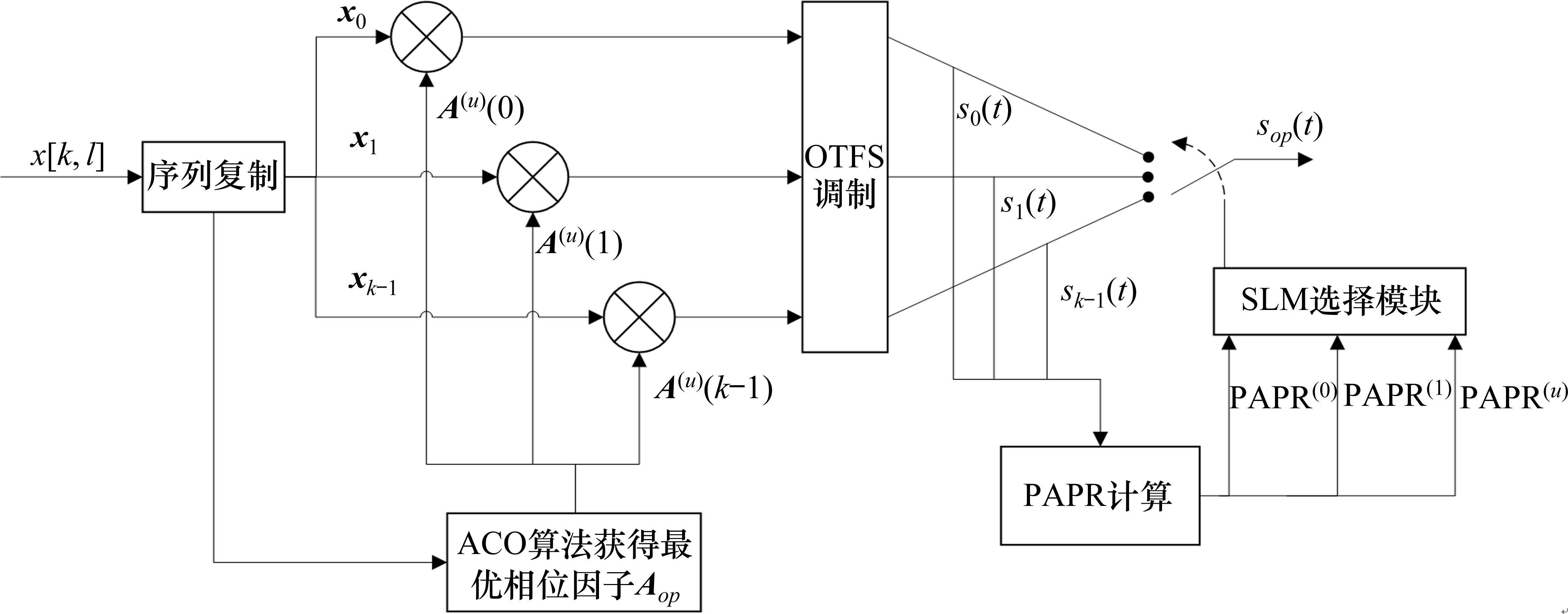
2.3.1　ACO算法模块对最优相位因子组的选择

QAM符号经过序列复制后，再通过S/P模块输出至ACO算法模块，求解使每次迭代后的全局最优PAPR的相位因子，经过多轮的迭代搜索之后，找到利于SLM寻找全局最优PAPR时域信号的最优解，确定最优相位因子。在进入OTFS调制前的信号矩阵可表示为

(14)

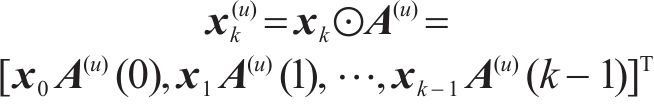
其中，相位序列是经蚁群算法进行搜索，在限定迭代次数时，得到的适应于全局PAPR最小化的相位因子。ACO模块的算法步骤描述如下。

步骤1：初始化set ；为时刻蚂蚁从相位因子搜索走到相位因子路径上标记的信息素量，，设，为最大信息素量；相位因子当前搜索次数(所有蚂蚁搜索完一次加1)，设置搜索循环最大次数为；蚂蚁总数为，禁忌表代表第个蚂蚁的禁忌表，，对最优相位因子遍历走索一次，更新一次禁忌表。

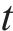
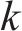
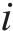
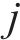
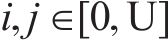
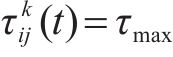
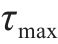
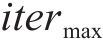
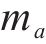
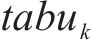
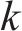
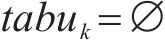
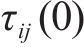
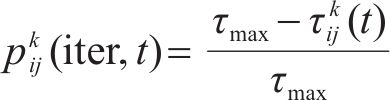
步骤2：随机生成蚁群的初始位置，信息素为初始适应度函数值，计算状态转移概率

(15)

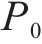
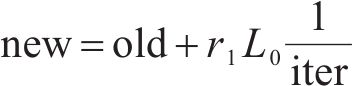
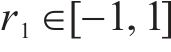
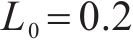
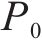
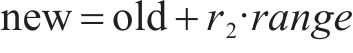
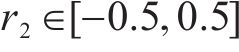
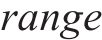
步骤3：进行蚂蚁的位置更新。当状态转移概率小于概率常数时，进行局部搜索，搜索公式为

(16)

为即将搜索的新位置，为当前位置，为随机局部搜索系数，为搜索步长；当状态转移概率大于概率常数时，进行全局搜索，搜索公式为

(17)

为随机全局搜索系数，为相位因子所处区间。

步骤4：计算新的蚂蚁位置的适应度函数值，判断蚂蚁是否继续移动，更新信息素

(18)

为信息素挥发因子。

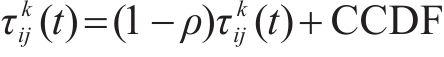
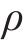
步骤5：判断是否满足终止条件(适应度函数值收敛稳定或达到最大迭代次数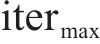)。若满足，则输出最优相位因子；若不满足，则继续进行迭代搜索。

2.3.2　ACO-SLM联合算法

发射机ACO-SLM联合算法的步骤如下。

输入：原始QAM信号，，。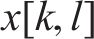

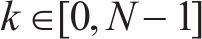
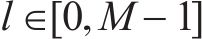
输出：输出最优相位因子，输出优化得到的时域信号。

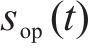
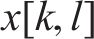
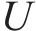
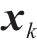
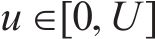
步骤1：将进行序列复制组，得到符号向量，。

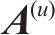
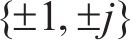
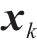
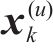
步骤2：将上述符号向量输入ACO算法模块，设定相位因子取值在集合中，将其与符号向量相乘，得到信号矩阵。

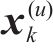
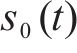
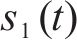
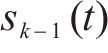
步骤3：将信号矩阵输入OTFS调制模块，得到输出时域信号,,…,。

步骤4：计算步骤3中各输出时域信号的。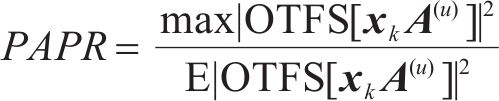

步骤5：进行迭代计算，并在每次计算后，更新全局最优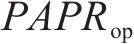，并更新与之相对应的相位因子进行输出。

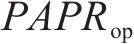
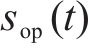
步骤6：将所计算所得的各PAPR值输入SLM的选择模块，选择全局最优解的对应的时域信号进行输出。

2.3.3　算法复杂度分析

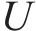
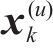
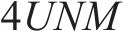
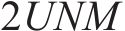
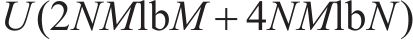
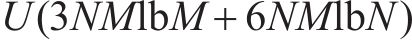
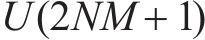
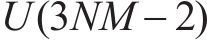
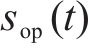
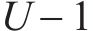
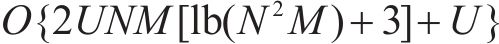
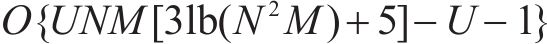
图4所示基于ACO-SLM算法的发射机OTFS信号计算复杂度主要取决于逆辛有限傅里叶变换(ISFFT)、海森堡变换、ACO算法、SLM算法的计算复杂度。传统SLM算法中，若有组相位因子，相位序列的计算需次乘法和次加法，OTFS的信号变换需次乘法和次加法，输出时域信号的PAPR计算需次乘法和次加法，最后为了选取最优PAPR的，需要次加法器运算。计算可得最终需要复杂度为次乘法运算和次加法运算。

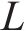
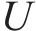
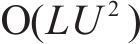
ACO算法需要大量的蚂蚁和迭代来提高解决方案的质量，并获得资源分配的最终解决方案，也就是寻求符合设计方案的近似最优解，而不是精确最优解的过程。因此，与其他元启发式算法类似，ACO优化的时间复杂度大于传统算法，但与需要指数时间的最优穷举搜索相比，ACO策略的时间复杂度要小得多。在迭代次数同为、相位因子组数同为时，ACO算法的时间复杂度即为信息素更新，ACO-SLM的算法复杂度略高于传统SLM算法，但ACO-SLM算法对PAPR的抑制效果远远优于SLM算法。

3 仿真分析

仿真环境设定为城轨T2T通信模型，发送机加窗脉冲和信道脉冲函数均为理想矩形单位脉冲函数，配合实验的接收机采用最小均方误差的方法对信号进行检测。表1是仿真实验参数具体设置。

仿真实验参数

实验参数	赋值
星座调制	16QAM
两列车相对移动速度v/(km∙h^-1)	120
输入信号帧数	500
单帧符号数N，子载波数M	8，128
载波频率/GHz	4
子载波间距/kHz	15
蚁群算法蚂蚁个数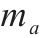	50
最大迭代次数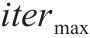	200
信息素因子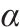	1
启发因子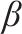	5
信息素挥发因子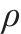	0.5
最大信息素量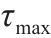	1 000

展开更多

3.1　PAPR优化分析

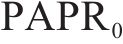
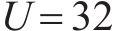
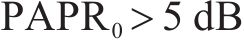
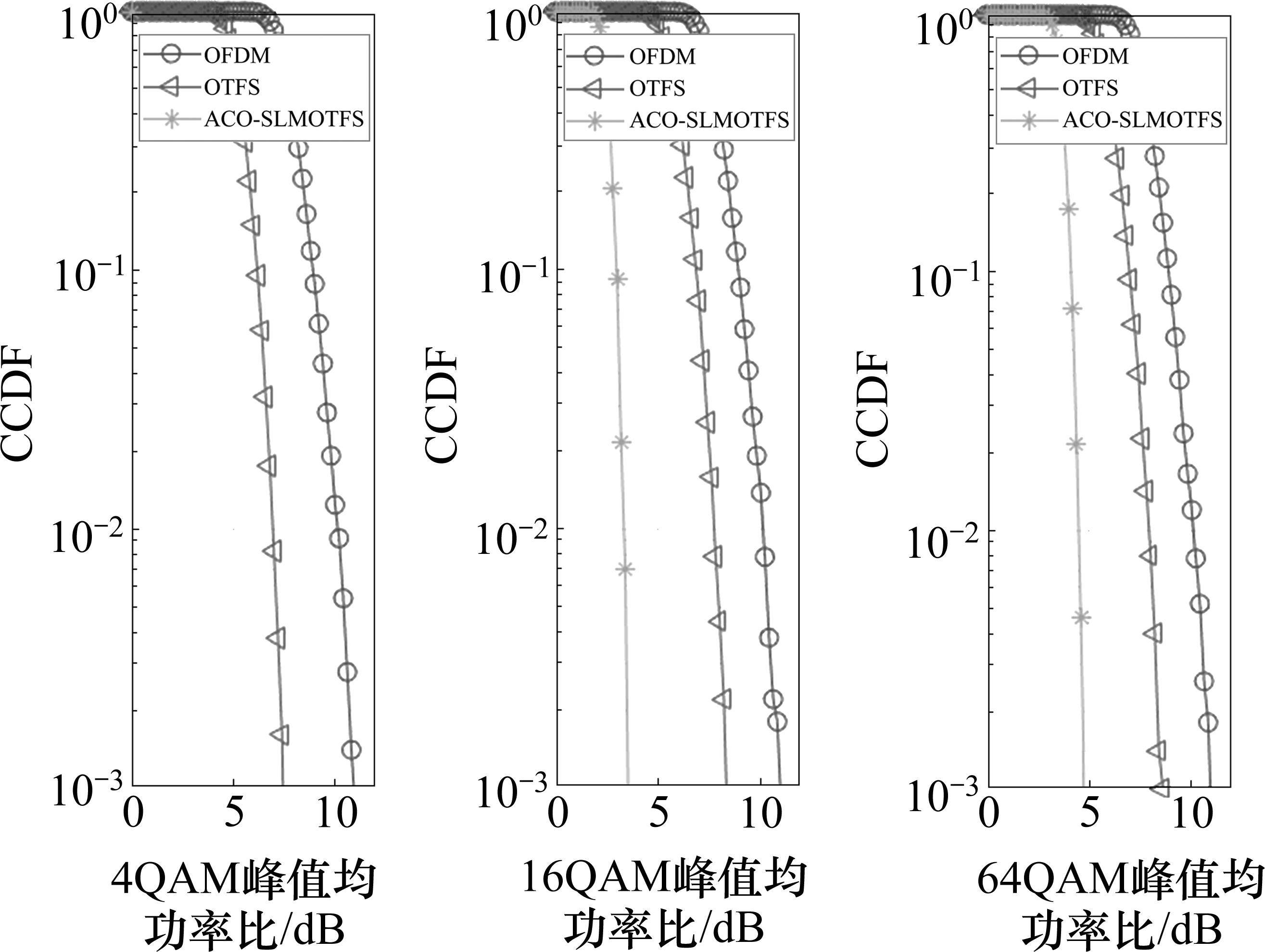
如图5所示，为三种星座调制信号的PAPR对比，分别用了4QAM、16QAM和64QAM调制信号作为发射机输入信号，横轴是PAPR的阈值，纵轴CCDF为实际PAPR值大于所设阈值的概率，图中ACO-SLM OTFS信号的相位因子组数。当输入信号为4QAM调制时，OTFS信号和经过ACO-SLM算法处理的OTFS信号的CCDF变化趋势几乎重合，当时，两者的CCDF都要低于未经过处理的OFDM；当输入信号为64QAM调制，CCDF=10^-3时，经过ACO-SLM算法处理的OTFS信号的PAPR比传统OFDM信号低6.4 dB，而比OTFS信号低4.1 dB；当输入信号为16QAM调制时，ACO-SLM算法OTFS信号的PAPR远远小于OFDM和OTFS，CCDF=10^-3时，PAPR低至4.1 dB。对比来看，OTFS的PAPR要优于OFDM，而经过ACO-SLM算法筛选后从发射机输出的信号PAPR整体要低于原始的OFDM和OTFS信号。

图5

ACO-SLM OTFS与原始OFDM、OTFS的PAPR对比

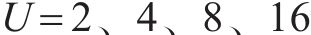
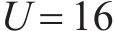
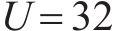
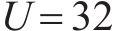
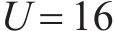
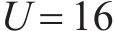
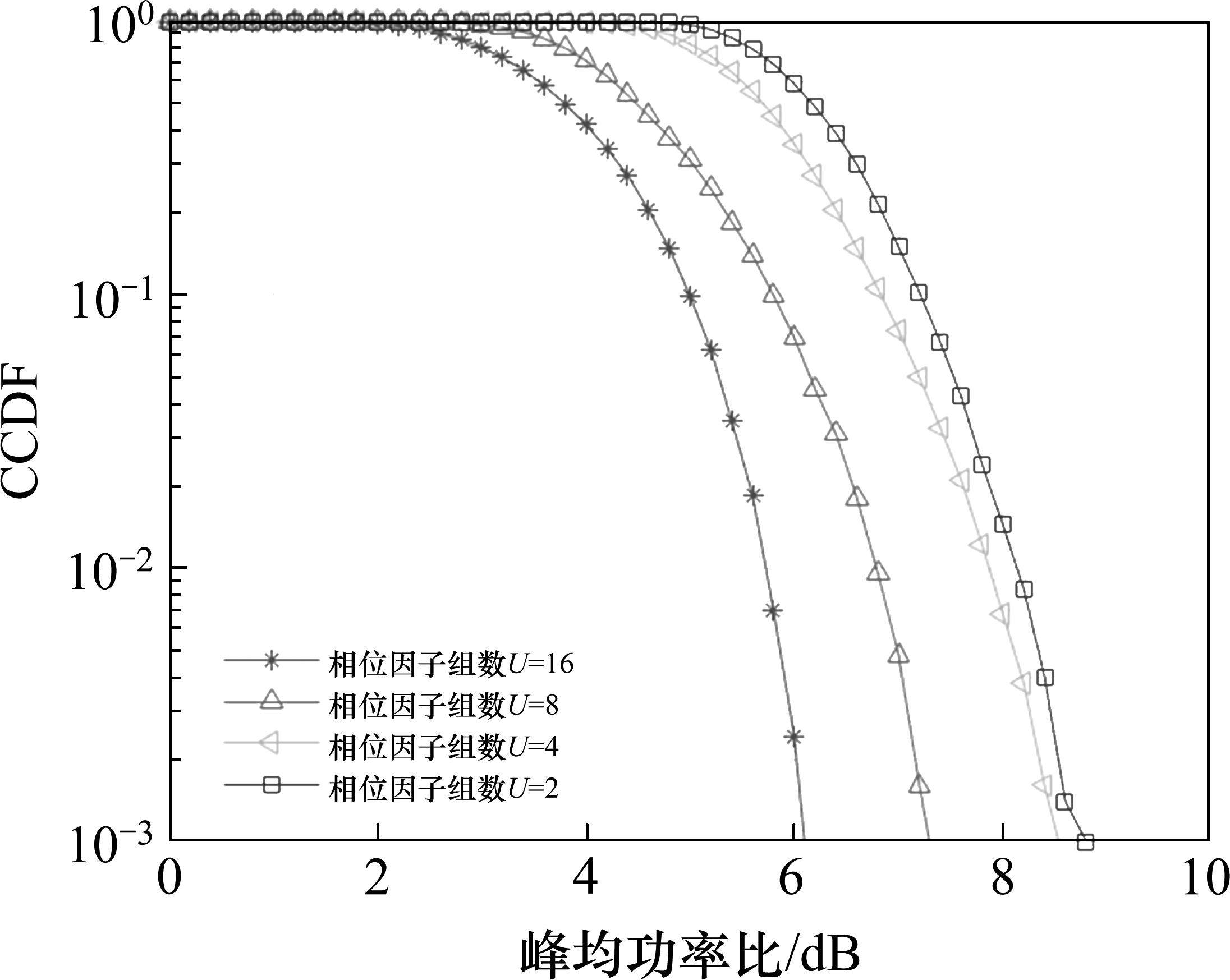
如图6所示，为采用不同相位因子组数，即时，ACO-SLM算法的PAPR结果与原始OTFS信号对比，输入信号为16QAM信号。相位因子取值为[1,-j]，当相位因子组数成倍增长时，PAPR性能逐步改善，但随着U的增加，ACO-SLM OTFS发射机的复杂度会逐步增加，尤其在ACO算法优化相位因子的过程中，收敛速度变慢，ACO算法会呈现极低的效率，所以在图4发射机的设计过程中，需要通过实验获得最佳U值的确定。时，PAPR值为6.03，大于图5中时，16QAM信号的PAPR。实验过程中，相位因子时收敛时长明显大于，综合考虑，对OTFS一体化信号PAPR做优化处理时，ACO-SLM算法的相位因子组数定为。

图6

ACO-SLM OTFS不同相位因子组数的PAPR对比

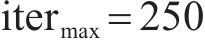
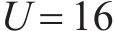
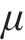
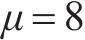
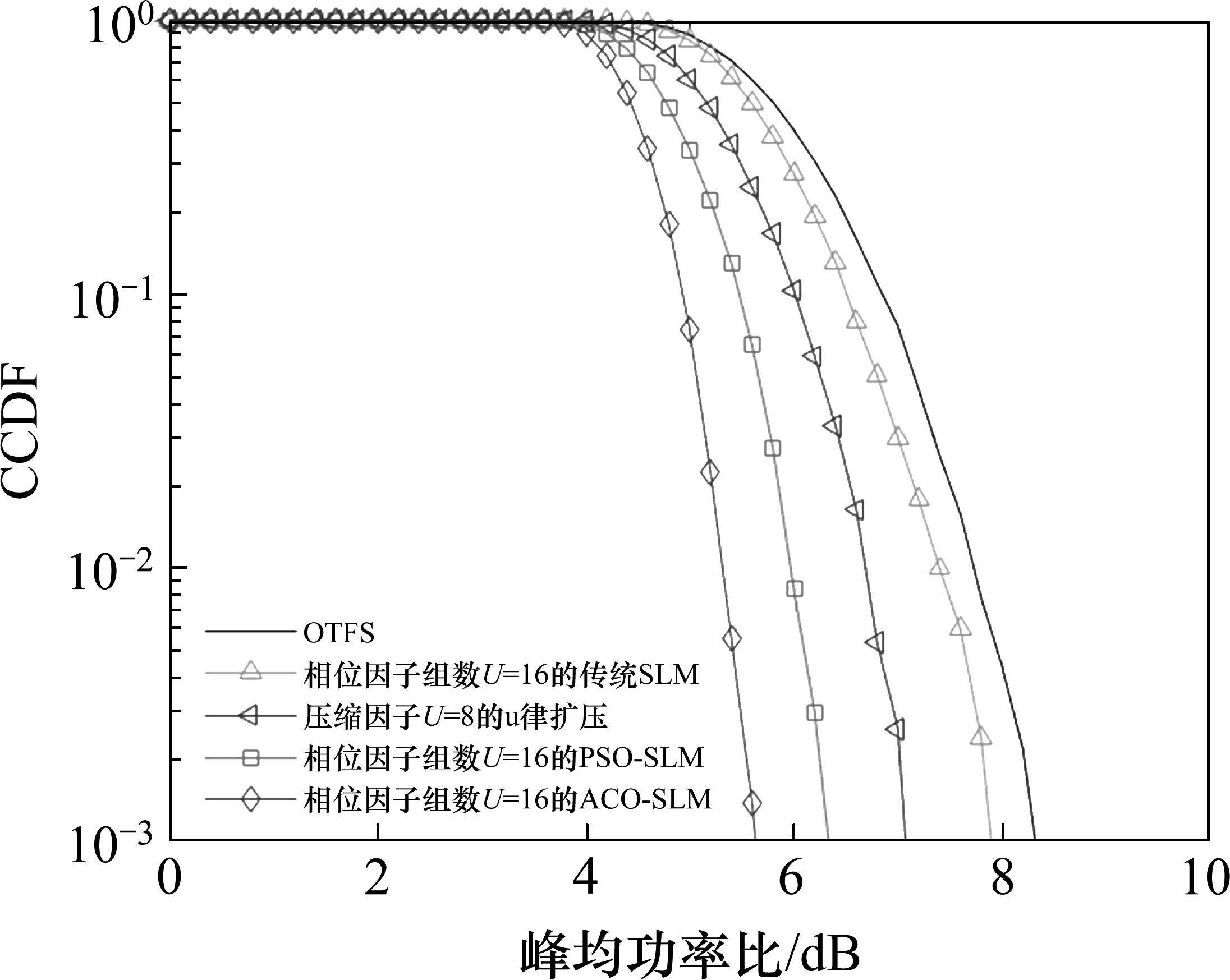
图7展示了不同OTFS信号PAPR抑制算法的性能对比。PSO-SLM算法^[19]与本文提出的ACO-SLM算法对比，两者均采用了仿生算法来对最优相位因子进行搜索，在参数选择合适的前提下，仿生算法具有较好的全局搜索结果和鲁棒性。当继续试探ACO-SLM算法的优化极限时，将最大迭代次数提升至，相位因子组数选取，ACO-SLM算法处理后的OTFS信号PAPR低至5.74 dB，比PSO-SLM算法6.27 dB低0.53 dB，比经典SLM算法7.89 dB低2.15 dB。文献[18]中提出的律压扩技术，当压缩因子时，PAPR为7.11 dB，ACO-SLM算法的PAPR比其低1.37 dB。

图7

不同OTFS信号PAPR抑制算法性能对比

表2中对比了两种算法模式接近的仿生算法，即ACO-SLM与PSO-SLM算法，在不同的迭代次数下PAPR结果。可以看到，ACO-SLM算法在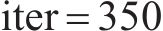时，PAPR值开始趋于收敛；PSO-SLM算法在时，PAPR值趋于收敛。实验过程中，ACO算法收敛所用时长为13.27 s，PSO算法收敛所用时长为9.73 s，但ACO-SLM算法对PAPR的抑制极限更佳，收敛PAPR极限值约为3.86 dB。

不同迭代次数iter下ACO-SLM和PSO-SLM算法的PAPR对比

iter	ACO-SLM	PSO-SLM
50	8.068 4	8.141 2
100	7.578 5	7.871 1
150	7.024 7	7.365 2
200	6.037 5	6.578 9
250	5.735 7	6.265 7
300	4.265 8	5.045 2
350	3.856 1	4.863 2
400	3.698 5	5.069 6
450	3.869 8	4.824 8
500	3.646 7	5.081 1

展开更多

3.2　ACO-SLM算法对OTFS通感一体化信号的影响

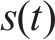
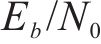
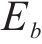
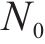
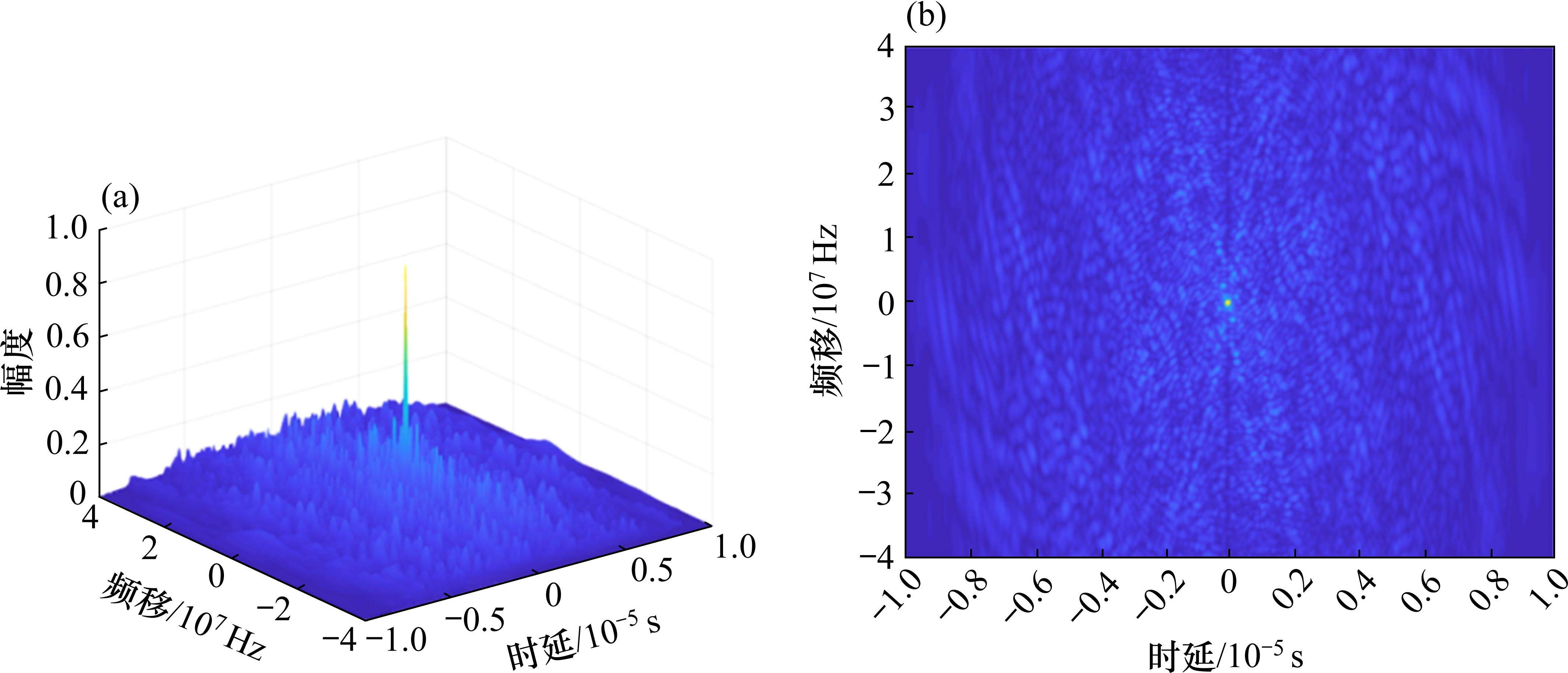
在利用ACO-SLM算法对OTFS调制后的时域信号进行优化后，进行模糊性分析，并在接收端利用最小均方误差法进行检测，对接收端的BER随比特信噪比的变化进行分析，来反映各调制算法对信号在多径衰落时变信道中传输性能的影响，其中为信号的比特能量，为接收端高斯白噪声功率谱密度。

图8展示了对经过ACO-SLM算法处理后的OTFS时域信号的模糊函数进行仿真分析，图8中OTFS信号旁瓣值得到明显抑制。图8(a)中在时延轴0点处，出现了单峰，说明处理后的时域信号有良好的测距性能；图8(b)中在频移轴0点处，出现了单峰，说明处理后的时域信号有良好的测速性能。

图8

ACO-SLM算法处理后的OTFS信号模糊性分析

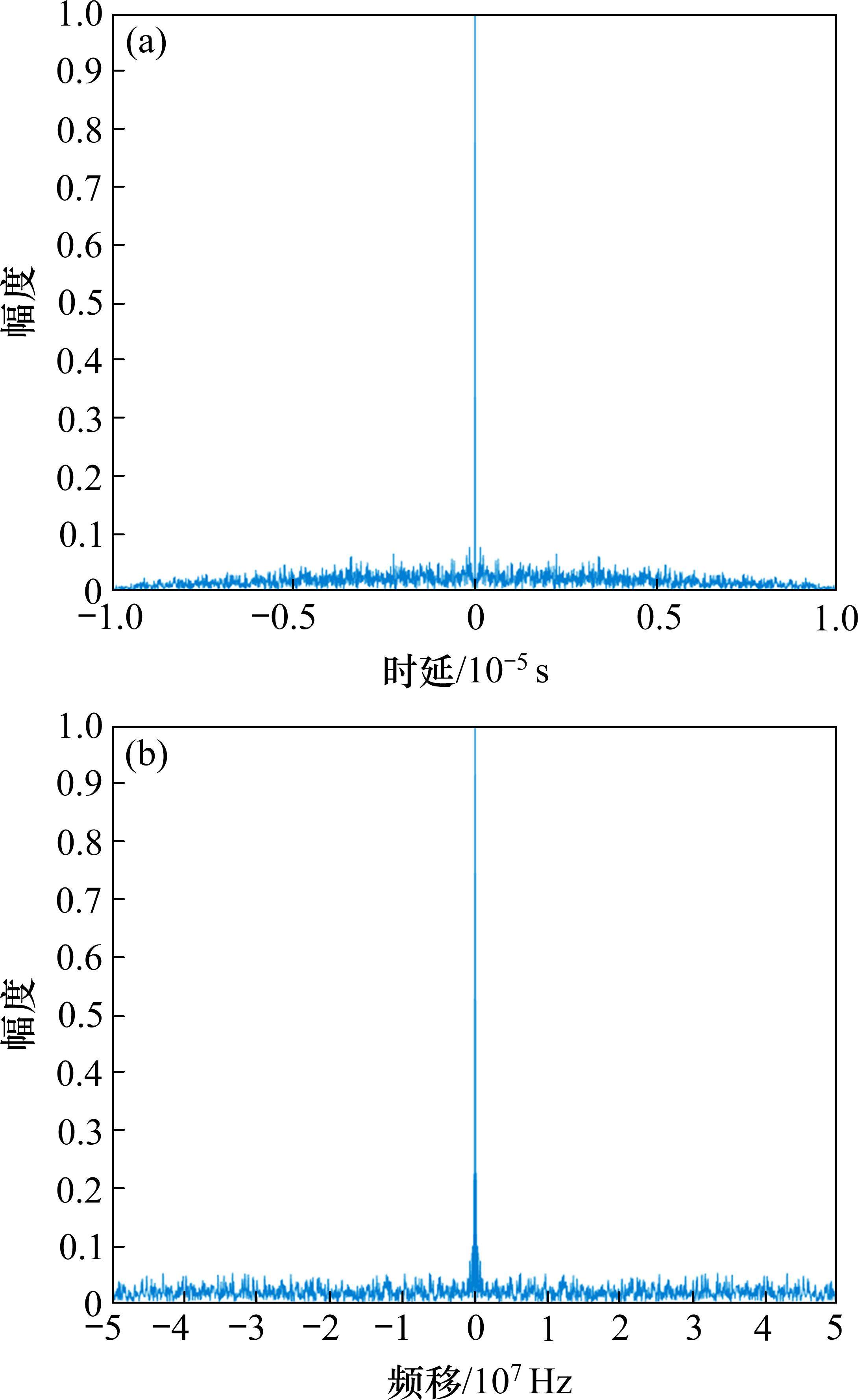
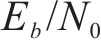
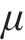
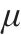
图9对几种调制算法处理后的时域信号在接收端检测出的误比特率性能进行了对比，随着的升高，即信噪比升高，算法处理后的信号传输误比特率降低。ACO-SLM算法、PSO-SLM算法处理后的OTFS信号在AWGN信道中传输的误比特率性能与原始OTFS时域信号几乎相同，但三者要优于律压扩技术处理后的OTFS信号。

图9

OTFS、ACO-SLM OTFS、PSO-SLM OTFS和

律压扩技术OTFS信号BER对比

4 结论

1) 单符号OTFS调制信号具有良好的距离模糊性，即测距性能，可用于面向T2T的列车运行控制中的列车定位作用，但几乎没有测速能力；多符号OTFS信号在距离模糊性和速度模糊性方面表现良好，具备较好的测距、测速能力。多符号OTFS信号可作为基于OTFS调制的通感一体化信号的设计基础，但需对其性能进行干预优化。

2) 在实验室PAPR抑制过程中，16QAM信号作为输入序列，结合ACO-SLM算法在对OTFS信号进行PAPR抑制方面，对比传统算法，表现出较好的抑制能力，ACO-SLM算法在相位因子组数时，PAPR低至6.03。相位因子组数，与同为仿生算法作为基础的PSO-SLM算法相比，ACO-SLM算法收敛时长较长，故相位因子取值16，可相对提升ACO算法的效率，在算法效率和PAPR抑制优化结果中取得平衡。

3) ACO-SLM算法处理后的OTFS信号，展现出良好的距离模糊性和速度模糊性，T2T通信中对列车的实时位置和速度进行感知获取，在系统接收端检测误比特率，与原始OTFS信号接近，ACO-SLM算法并没有降低OTFS信号在多径衰落时变信道中的传输性能。上述实验证明，ACO-SLM OTFS信号可作为B5G/6G环境下城轨T2T通感一体化的基础信号。

参考文献

ZHU Li, YU F R, TANG Tao, et al.

An integrated train-ground communication system using wireless network virtualization: security and quality of service provisioning

[J]. IEEE Transactions on Vehicular Technology, 2016, 65(12): 9607-9616.

百度学术

谷歌学术

PASCOE R D, EICHORN T N.

What is communication-based train control?

[J]. IEEE Vehicular Technology Magazine, 2009, 4(4): 16-21.

百度学术

谷歌学术

李强, 陈子健.

基于车车通信的列控系统后备模式研究

[J]. 铁道科学与工程学报, 2022, 19(11): 3407-3416.

百度学术

谷歌学术

SONG Haifeng, SCHNIEDER E.

Availability and performance analysis of train-to-train data communication system

[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(7): 2786-2795.

百度学术

谷歌学术

徐纪康

基于车-车通信的新型CBTC系统分析

[J]. 铁道通信信号, 2014, 50(6): 78-80.

百度学术

谷歌学术

WANG Xiaoxuan, LIU Lingjia, TANG Tao, et al.

Next generation train-centric communication-based train control system with train-to-train (T2T) communications

[C]// 2018 International Conference on Intelligent Rail Transportation (ICIRT). Singapore. IEEE, 2018: 1-5.

百度学术

谷歌学术

陈启香, 李茂青, 林俊亭.

基于超短波的列车间直接通信技术研究

[J]. 计算机工程, 2013, 39(12): 5-10.

百度学术

谷歌学术

ITU.

ITU-T technical report - representative use cases and key network requirements for network 2030

[R]. ITU, 2020.

百度学术

谷歌学术

RANGAMGARI V, TIWARI S, DAS S S, et al.

OTFS: interleaved OFDM with block CP

[C]// 2020 National Conference on Communications (NCC). Kharagpur, India. IEEE, 2020: 1-6.

百度学术

谷歌学术

RAVITEJA P, HONG Yi, VITERBO E, et al.

Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS

[J]. IEEE Transactions on Vehicular Technology, 2019, 68(1): 957-961.

百度学术

谷歌学术

WANG Zhenduo, CHEN Xingyu, NING Xiaoyan.

BER analysis of integrated WFRFT-OTFS waveform framework over static multipath channels

[J]. IEEE Communications Letters, 2021, 25(3): 754-758.

百度学术

谷歌学术

HOSSAIN M N, SUGIURA Y, SHIMAMURA T, et al.

Waveform design of low complexity WR-OTFS system for the OOB power reduction

[C]// 2020 IEEE Wireless Communications and Networking Conference Workshops (WCNCW). Seoul, Korea (South). IEEE, 2020: 1-5.

百度学术

谷歌学术

谷亚彬, 张林让, 周宇, 等.

采用相关函数的OFDM雷达通信共享信号处理算法

[J]. 西安电子科技大学学报, 2018, 45(4): 12-17, 105.

百度学术

谷歌学术

余显斌, 吕治东, 李涟漪, 等.

太赫兹感知通信一体化波形设计与信号处理

[J]. 通信学报, 2022, 43(2): 76-88.

百度学术

谷歌学术

GAUDIO L, KOBAYASHI M, CAIRE G, et al.

On the effectiveness of OTFS for joint radar parameter estimation and communication

[J]. IEEE Transactions on Wireless Communications, 2020, 19(9): 5951-5965.

百度学术

谷歌学术

NAVEEN C, SUDHA V.

Peak-to-average power ratio reduction in OTFS modulation using companding technique

[C]// 2020 5th International Conference on Devices, Circuits and Systems (ICDCS). Coimbatore: IEEE Press, 2020: 140-143.

百度学术

谷歌学术

CHENNAMSETTY S, BODDU S, CHANDHAR P, et al.

Analysis of PAPR in OTFS modulation with classical selected mapping technique

[C]// 2023 15th International Conference on COMmunication Systems & NETworkS (COMSNETS). Bangalore, India. IEEE, 2023: 319-322.

百度学术

谷歌学术

SOHN I.

New SLM scheme to reduce the PAPR of OFDM signals using a genetic algorithm

[J]. ICT Express, 2016, 2(2): 63-66.

百度学术

谷歌学术

白菊蓉, 宋朝阳, 兰琳, 等.

基于PSO-SLM算法的OTFS系统峰均比抑制

[J]. 西安邮电大学学报, 2023, 28(1): 30-36.

百度学术

谷歌学术

XU Xiangnan, YANG Ping, ZHANG Bo, et al.

An improved PAPR reduction method based on imperialist competition algorithm for OTFS system

[C]// 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall). London, United Kingdom. IEEE, 2022: 1-6.

百度学术

谷歌学术

HADANI R, RAKIB S, TSATSANIS M, et al.

Orthogonal time frequency space modulation

[C]// 2017 IEEE Wireless Communications and Networking Conference (WCNC). San Francisco, CA, USA. IEEE, 2017: 1-6.

百度学术

谷歌学术

LI Shuangyang, YUAN Weijie, LIU Chang, et al.

A novel ISAC transmission framework based on spatially-spread orthogonal time frequency space modulation

[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1854-1872.

百度学术

谷歌学术

SURABHI G D, AUGUSTINE R M, CHOCKALINGAM A.

Peak-to-average power ratio of OTFS modulation

[J]. IEEE Communications Letters, 2019, 23(6): 999-1002.

百度学术

谷歌学术

SHANG Huichao, CHEN Ruifeng, ZHANG Haoxiang, et al.

OTFS modulation and PAPR reduction for IoT-railways

[J]. China Communications, 2023, 20(1): 102-113.

百度学术

谷歌学术

注释

杨骞,苏宏升,刘大为等.基于OTFS的城轨T2T通感一体化信号设计与优化[J].铁道科学与工程学报,2024,21(12):5209-5220.

YANG Qian,SU Hongsheng,LIU Dawei,et al.Design and optimization of ISAC signal for urban railway T2T based on OTFS[J].Journal of Railway Science and Engineering,2024,21(12):5209-5220.

论文推荐

1 通感一体化信号模型与模糊性分析

1.1　OTFS信号模型

1.2　OTFS信号模糊性分析

2 OTFS一体化信号优化

2.1　OTFS信号的PAPR

2.2　经典SLM

2.3　ACO-SLM算法对最优PAPR时域信号的确定

3 仿真分析

3.1　PAPR优化分析

3.2　ACO-SLM算法对OTFS通感一体化信号的影响

4 结论

参考文献

基于OTFS的城轨T2T通感一体化信号设计与优化

1 通感一体化信号模型与模糊性分析

1.1 OTFS信号模型

1.2 OTFS信号模糊性分析

1.2.1 单符号OTFS信号模糊性分析

1.2.2 多符号OTFS信号模糊性分析

2 OTFS一体化信号优化

2.1 OTFS信号的PAPR

2.2 经典SLM

2.3 ACO-SLM算法对最优PAPR时域信号的确定

2.3.1 ACO算法模块对最优相位因子组的选择

2.3.2 ACO-SLM联合算法

2.3.3 算法复杂度分析

3 仿真分析

3.1 PAPR优化分析

3.2 ACO-SLM算法对OTFS通感一体化信号的影响

4 结论

1.1　OTFS信号模型

1.2　OTFS信号模糊性分析

1.2.1　单符号OTFS信号模糊性分析

1.2.2　多符号OTFS信号模糊性分析

2.1　OTFS信号的PAPR

2.2　经典SLM

2.3　ACO-SLM算法对最优PAPR时域信号的确定

2.3.1　ACO算法模块对最优相位因子组的选择

2.3.2　ACO-SLM联合算法

2.3.3　算法复杂度分析

3.1　PAPR优化分析

3.2　ACO-SLM算法对OTFS通感一体化信号的影响