推进器技术作为发展高性能船舶的关键技术,逐渐成为各国船舶领域研究的重点。混流式喷水推进泵具有流量大、扬程高、高效运行区宽等特点,随着喷水推进器向着大型化和高速化方向发展,逐渐成为当前大型喷水推进装置主要采用的推进泵型[1]。叶轮作为转子机械的核心水力部件,其流动结构对泵的性能起着重要的作用,因此,准确获取推进泵叶轮内部流场特性、空化流动、涡结构是研究喷水推进泵性能优化的前提[2]。
在叶顶间隙处,由于叶片吸力面和压力面间存在压力梯度,在压差作用下形成叶顶泄漏流TLF(tip leakage flow)。叶顶泄漏流从叶尖与叶轮室端壁间的间隙压出,流入叶片吸力面时,受主流扰动在叶片表面发生卷吸,形成主导叶顶间隙流场的叶顶泄漏涡TLV(tip leakage vortex)。WU等[3]利用二维和三维粒子图像测速技术(SPIV),发现喷水推进泵叶尖泄漏涡瞬时结构是由不稳定的涡丝向叶片通道尖端区域卷吸缠绕形成的,叶尖区域湍流结构是由沿吸力面卷起并向相邻叶片移动的叶尖泄漏涡、壁面附着空化和涡旋破裂主导的。FEI等[4]发现在空化发展阶段,叶轮内部的能量损失主要是由尾迹流和叶顶泄漏涡引起的。在完全空化后,流动分离和由空化引起的二次叶尖泄漏涡导致了主要的能量损失。JI等[5]基于熵产分析研究了混流泵不同叶顶间隙下的能量特性,发现叶顶泄漏流的增加导致叶轮内能量损失增大,而导叶区水力损失减小。
近年来,随着计算机性能的提高和数值模拟方法的完善,计算流体力学CFD(computational fluid dynamics)在预测水力机械空化流动方面取得显著成果。雷诺平均Navier-Stokes(RANS)方法作为一种最简单的湍流模型,在大多数湍流流动计算中效果很好,因此,得到广泛应用,但其对于一些不稳定或复杂流动的计算结果与实际结果有较大误差。DECAIX等[6]发现RANS模型能够捕捉叶尖泄漏涡运动轨迹和速度变化,但无法计算泄漏涡涡核区域压降,因此,直接数值模拟DNS(direct numerical simulation)和大涡模拟LES(large eddy simulaton)更多地应用于湍流流动的预测。程怀玉等[7]通过大涡模拟研究了空化对叶顶泄漏涡特性的影响,发现叶尖泄漏涡强度主要受片空化演变行为影响,同时,涡心气核分布受空化影响程度取决于叶尖泄漏涡结构的稳定性及强度。HAN等[8]使用大涡模拟方法较好地预测了转子叶片周围的非定常空化涡,通过涡量输运方程进一步分析,发现涡旋结构的发展主要受拉伸项、膨胀项和斜压矩项的影响。BAI等[9]使用大涡模拟结合zwart-gerbera-belamri(ZGB)空化模型,计算了直水翼产生的尖端泄漏涡流空化流,得出的涡旋结构与实验结果具有一致性,并表征了不同涡旋识别方法(Q准则、Ω方法和Liutex方法等)的适用性。虽然DNS和LES能够提供较高精度的湍流计算结果,但由于计算量很大,目前在工程计算中还未普及使用。
为了解决湍流流动工程计算的困难,SPALART[10]提出了结合RANS和LES两者优点的分离涡模拟(detached eddy simulation,DES)方法,该方法可以通过调整控制参数,在大量流动分离发生的区域采用高解析度的LES方法,在端壁区附近则使用RANS方法进行模拟,以减少计算量。USTA等[11]基于SST k-ω湍流模型,采用DES方法研究了水翼和螺旋桨的非定常空化流动,模拟结果与试验结果一致,证明了该方法在模拟空化流动上的可靠性。YUAN等[12]基于DES湍流模型和ZGB空化模型准确捕捉了泵喷螺旋桨的叶尖间隙区涡核结构和其动态流动特性。LONG等[13]使用延迟分离涡模拟DDES(delayed detached-eddy simulation)准确地预测了螺旋桨空化湍流对船底压力脉动的影响结果。SU等[14]采用数值计算研究了跨音速转子的泄漏涡破碎现象,发现分离涡方法的结果比RANS方法的结果更精细,成功捕捉了近失速工况点处转子叶尖区螺旋形涡破碎的现象。上述研究均表明了DES模型在流体机械领域的应用前景特别是在预测叶尖泄漏流方面的优势,但与RANS方法相比,DES方法在求解大型工程项目时并未体现出明显的速度优势,因此,目前的应用场景仍较少。
近年来,一方程湍流模型因计算速度快、成本低,能满足大多数的工程计算,得到广泛应用[15]。Wray-Agarwal (WA)单方程湍流模型在预测复杂湍流结构方面具有准确性和高效性,在工程计算中受到广泛关注。JI等[16]将WA模型、标准 k-ε模型、RNG k-ε模型和SST k-ω模型对离心泵内外特性预测结果与试验数据进行对比,发现WA湍流模型计算结果更接近试验结果。HAN[17]应用hybrid WA-DES方法模拟NASA wall-mounted hump、backward facing step等多个标准算例,发现使用WA-DES方法的结果比原始WA和SA模型结果精度更高,为精确计算壁面分离流提供了更好的选择。HAN等[18]进一步提出了基于WA模型的延迟DES方法,将使用WA模型的延迟DES方法结果与实验结果进行对比发现,该模型能较好地预测流动中的壁面摩擦分布、压力分布以及分离特性[19]。ZHANG等[20]在WA-DES模型中考虑了旋转曲率修正,其最终结果优于其他RANS模型的结果。
为进一步评价WA-DES方法预测混流式喷水推进泵性能的精度及可靠性,本文比较了WA-DES模型和SST k-ω湍流模型推进泵的外特性及内部流场,并分析了两种计算结果的差异和精度。同时,重点分析了两种模型叶轮叶片不同跨度上的压力分布以及高剪切、强湍流作用下的轮缘区流场。
1 WA-DES湍流模型
WA-DES湍流模型是以DES模型为基础建立在WA湍流模型上的一种模型,WA湍流模型是基于k-ε模型闭合方式推导出来的一种单方程模型,该模型中与涡旋黏度有关的变量R(R=k/ω)的输运方程可表示为[21]
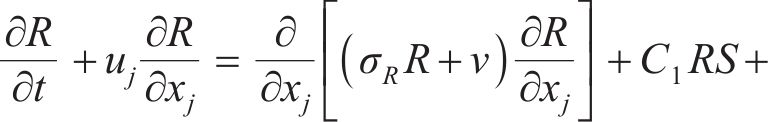
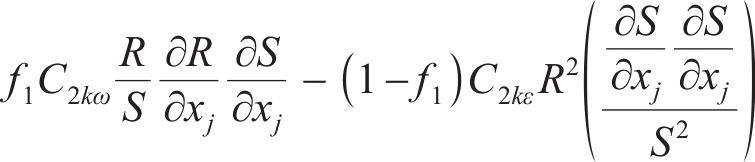
其中,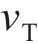
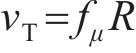
S为平均应变率,
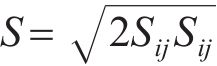
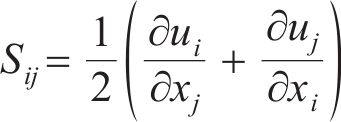
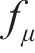
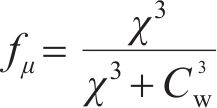
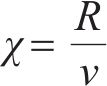
转换函数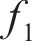
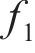
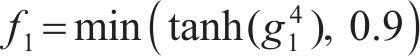
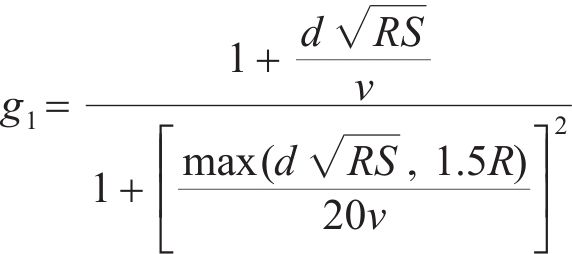
式中:d为流体到壁面的最小距离。
为了评估喷水推进泵流动过程中的能量损耗,评估湍动能k和湍流耗散率ω的表达式分别为
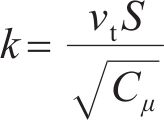
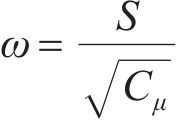
式中: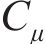
在WA-DES模型中,需要将湍流模型中的长度尺度改写成与网格相关的网格尺度,从而将一个雷诺方程的湍流模型变成一个亚格子模型。在本文中需要使用新的长度尺度代替原模型输运方程中的d。参考SA-DES模型对长度尺度的处理方式,WA-DES湍流模型的输运方程表示为
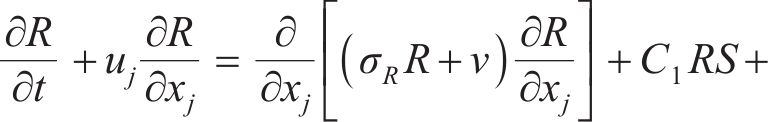
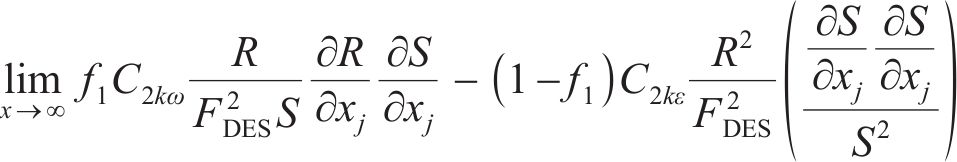
其中,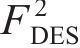
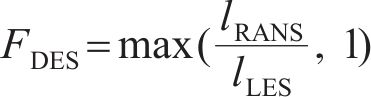
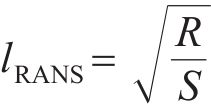
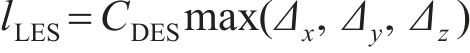
式中:
| 参数 | 数值(或表达式) | 参数 | 数值(或表达式) |
|---|---|---|---|
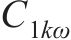 | 0.082 9 | 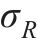 | 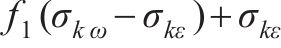 |
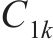 | 0.112 7 | 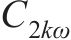 | 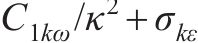 |
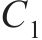 | 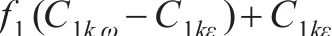 | 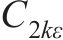 | 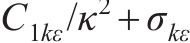 |
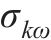 | 0.72 | 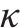 | 0.41 |
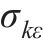 | 1.0 | 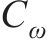 | 8.54 |
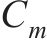 | 8.0 |
2 计算模型与网格划分及边界条件
2.1 计算模型
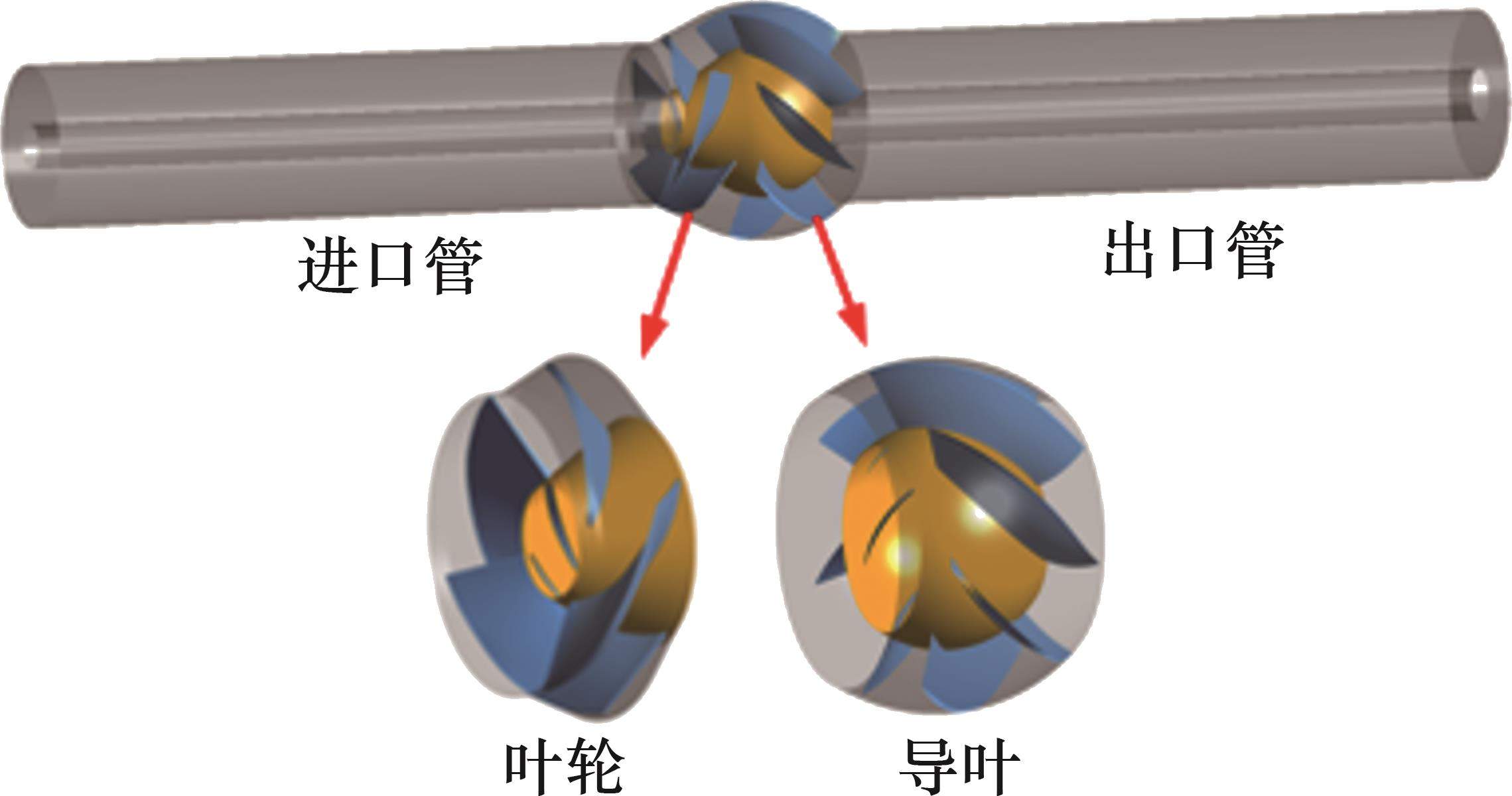
本文的研究模型为江苏大学自主研发的喷水推进泵模型,由进水流道、叶轮、导叶和喷口组成,建模使用UG软件完成。为提高不同湍流模型空化性能及叶轮内空化流动结果的精确性,检验其结果之间差异性,将模型原有的进水弯管和喷口改为直管道进出,管道长度为进出口直径的4倍。装配后混流式喷水推进泵计算模型如图1所示,喷水推进泵模型基本参数如表2所示。
| 参数 | 值 |
|---|---|
| 设计流量Qdes/(m3∙h-1) | 320 |
| 设计扬程H/m | 14 |
| 额定转速n/(r∙min-1) | 2 900 |
| 安装高度Hduct/mm | 180 |
| 叶轮出口直径D1/mm | 120 |
| 叶轮进口直径D2/mm | 156 |
| 叶轮叶片数Z | 4 |
| 导叶叶片数Zd | 7 |
2.2 网格划分
使用ICEM CFD软件对装配后的流体域进行网格划分,为提高数值计算的准确性,所有部件均采用六面体结构网格。根据叶轮和导叶旋转阵列式的布置方式,分别采用J-O型和H-O型拓扑结构对其进行网格划分,并对轮缘间隙和叶顶近壁面区域进行网格加密,确保壁面y+满足 WA-DES湍流模型的计算要求。计算域网格划分如图2所示,其中,PS为压力面;SS为吸力面;Shroud为盖板;Hub为轮毂。
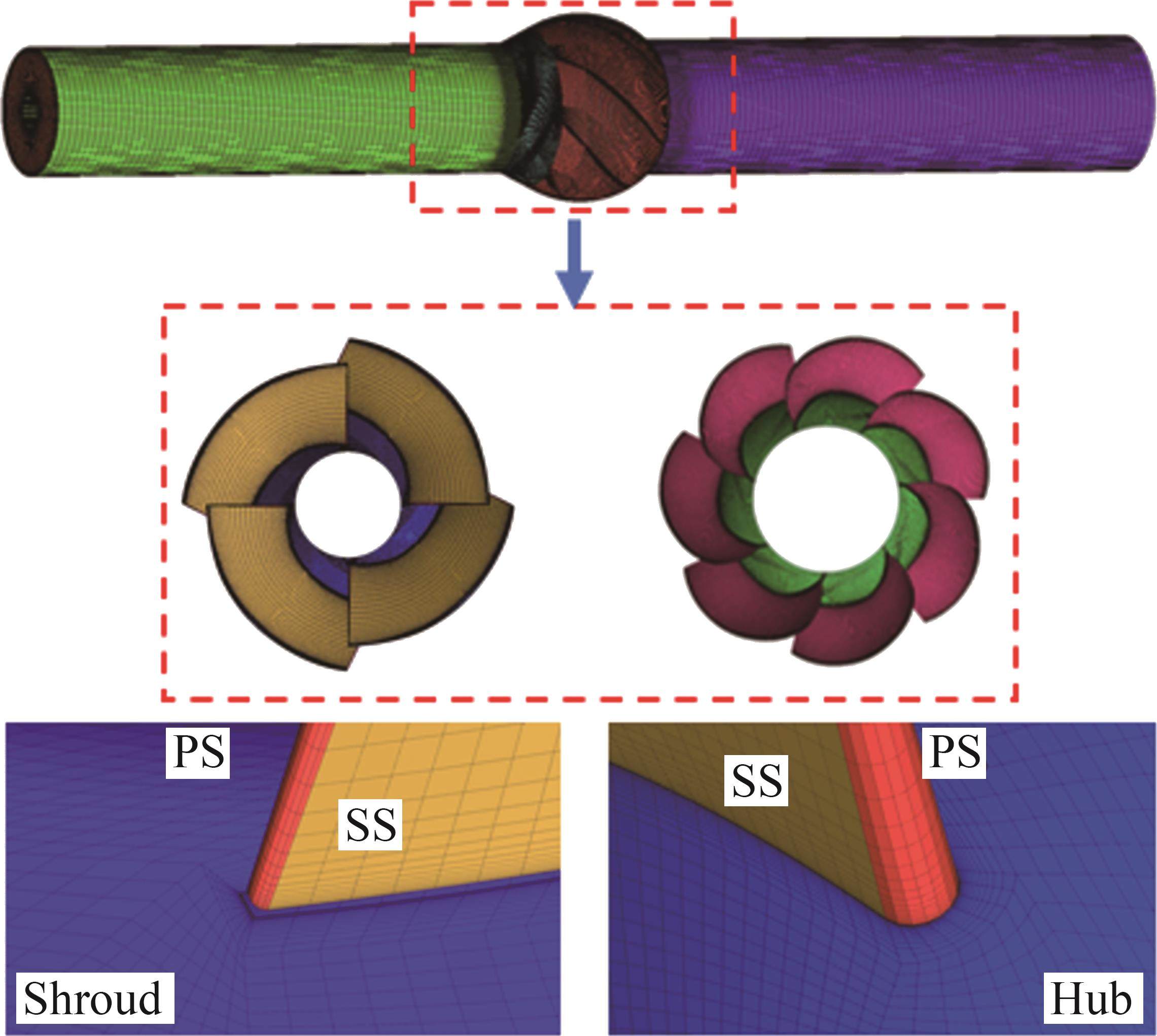
网格越精密,捕捉内部流动更精准,但对计算资源需求较大。在保证叶轮流场计算结果准确性的基础上,需综合考虑计算资源,选择合适的网格数量。为此,分别采用SST k-ω湍流模型模拟了5种叶轮网格密度下喷水推进泵的性能。不同叶轮网格数下扬程计算结果如表3所示。由表3可见:当叶轮网格数量超过230万个时,泵的扬程变化波动小于1%,满足计算稳定要求。因此,选择方案3作为叶轮网格。
| 网格方案 | 网格数量/个 | 扬程结果 |
|---|---|---|
| 方案1 | 1 332 567 | 13.91 |
| 方案2 | 1 892 532 | 14.22 |
| 方案3 | 2 376 329 | 14.41 |
| 方案4 | 2 876 941 | 14.48 |
| 方案5 | 3 303 660 | 14.43 |
2.3 边界条件
本文基于Fluent软件对混流式喷水推进泵内流场进行数值计算。在非空化定常计算中,进口设置为质量流量进口,通过调节不同质量流量进口以改变泵的工况,出口设置为压力出口,施加固定的静压以模拟大气压力。叶轮区域位于旋转坐标系中,转速n=2 900 r/min,设置为Frame motion,其余计算域均设置为静止域,叶轮域两侧的交界面设置为Rotor Stator以适应滑移网格的General Grid Interface(GGI)界面,采用无滑移壁面条件,收敛精度设置为1×10-5,同时监测泵的扬程和效率,当扬程和效率趋于稳定且残差低于收敛精度时,可认定计算收敛结果良好。在空化数值计算中,给定温度为298 K时液相和气相的物理参数:水的密度ρl为997 kg/m3;水蒸气的密度ρv为0.023 08 kg/m3;饱和蒸气压pv为3 169 Pa;采用ZGB空化模型,进口选择总压进口,初始液相和气相的体积分数分别设置为1和0,初始压力设定为2×105 Pa,通过减小进口压力,以降低装置汽蚀余量,出口采用质量流量出口。
3 结果与分析
3.1 非空化模拟结果
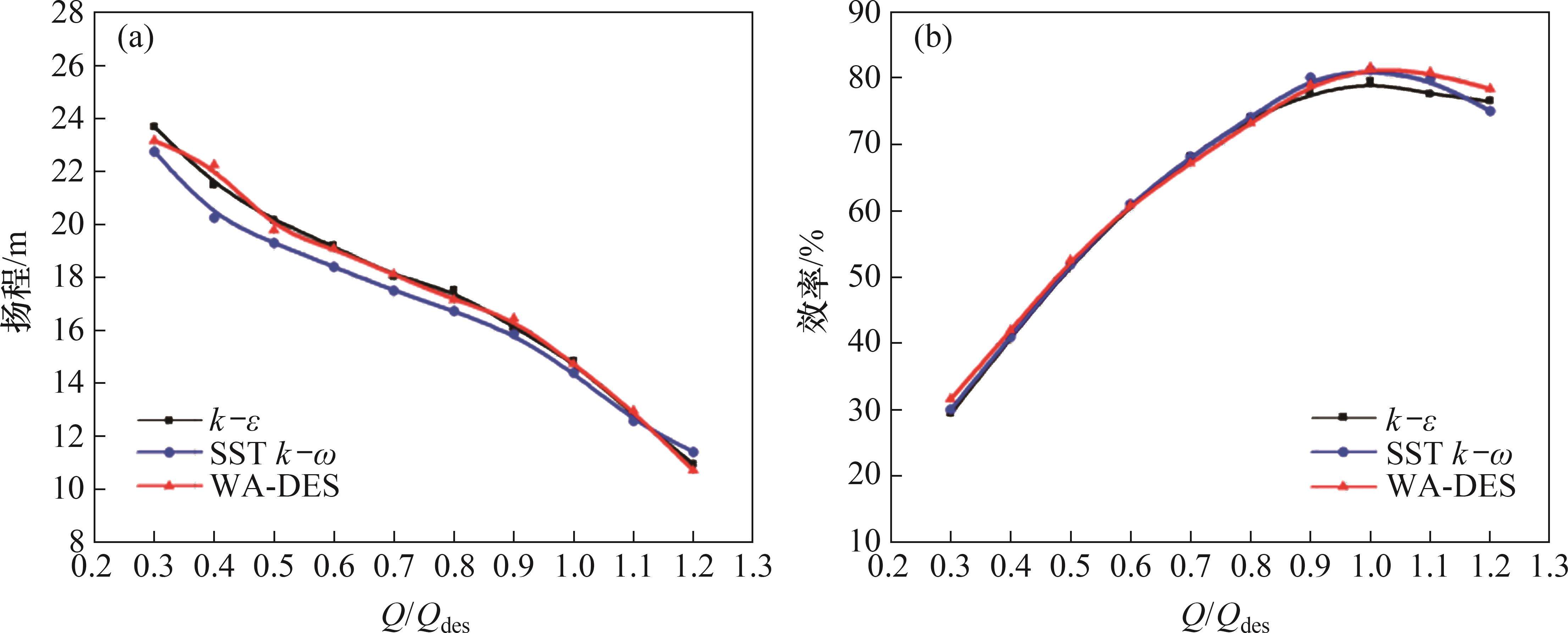
扬程和效率是喷水推进泵重要的外特性参数,扬程和效率公式分别为
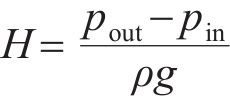
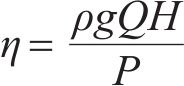
式中:H为推进泵扬程,m;Q为体积流量,m3/s;ρ为水的密度,ρ=997 kg/m3;g为重力加速度, g=9.81 m/s2;pout为推进泵出口总压,Pa;pin为推进泵进口总压,Pa;η为推进泵效率;P为轴功率,kW。
不同湍流模型扬程和流量曲线如图3所示,图中,Qdes为设计流量。由图3可见:WA-DES模型在(0.9~1.1)Qdes点区间内流量的变化对预测的效率影响较小,波动小于另外2种湍流模型的波动;3种湍流模型预测的扬程和效率随流量变化的趋势基本一致,表明了在预测泵性能曲线上,WA-DES模型与传统湍流模型基本一致。
叶片几何定义如图4所示,其中,正方向为叶片前缘到尾缘,负号代表相反方向。叶片弦长分数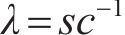
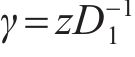
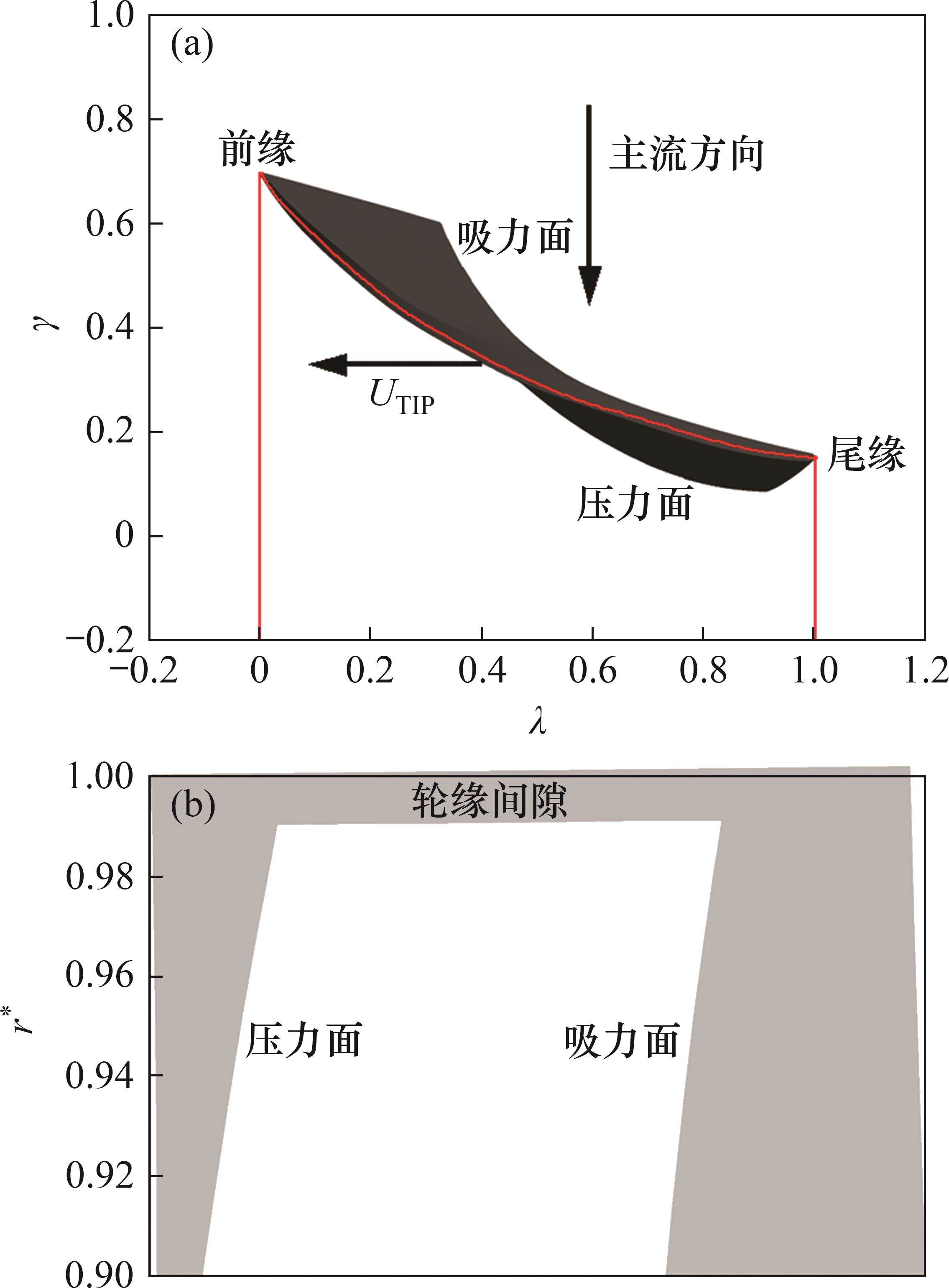
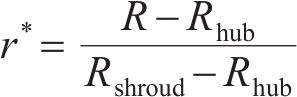
式中:R为叶轮特定位置半径;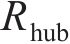
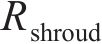
轮缘泄漏流和泄漏涡结构是混流式泵叶轮内最具特征的流动结构,也是造成叶轮内能量损失的重要因素。因此,轮缘泄漏流或泄漏涡结构的预测精度及其在叶轮内造成的能量损失,是评价湍流模型适用性的重要标准之一。使用Ω方法进行叶轮泄漏涡可视化,选择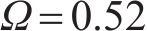
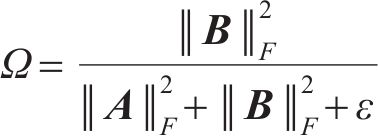
式中:Ω为旋转部分涡量占总涡量比例,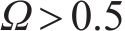
叶顶泄漏涡结构和涡量分布如图5所示。由 图5可见:随着流量增加,泄漏涡尺度和强度逐渐发展;在3种流量工况下,2种湍流模型对轮缘泄漏流和泄漏涡结构的预测差异较大,其中最明显的是,与WA-DES模型相比,SST k-ω模型预测的泄漏涡尺度更大、卷吸强度更强、沿圆周方向的背离叶片吸力面的距离更大。因为SST k-ω模型的上级轮缘泄漏流会与下级泄漏流形成干涉,即部分上级泄漏流会进入下级叶片轮缘间隙内,并泄漏到下级流道中。此时,WA-DES模型预测的泄漏涡沿叶片型线方向未大范围偏离叶片吸力面,也未与下级泄漏流形成干涉效应。尽管这2种模型预测的泄漏涡空间差异明显,但从叶轮轮缘区截面内的涡量分布来看,由轮缘泄漏导致的涡量高值区范围差距不大,且这2种模型预测的涡量在1个数量级之内。

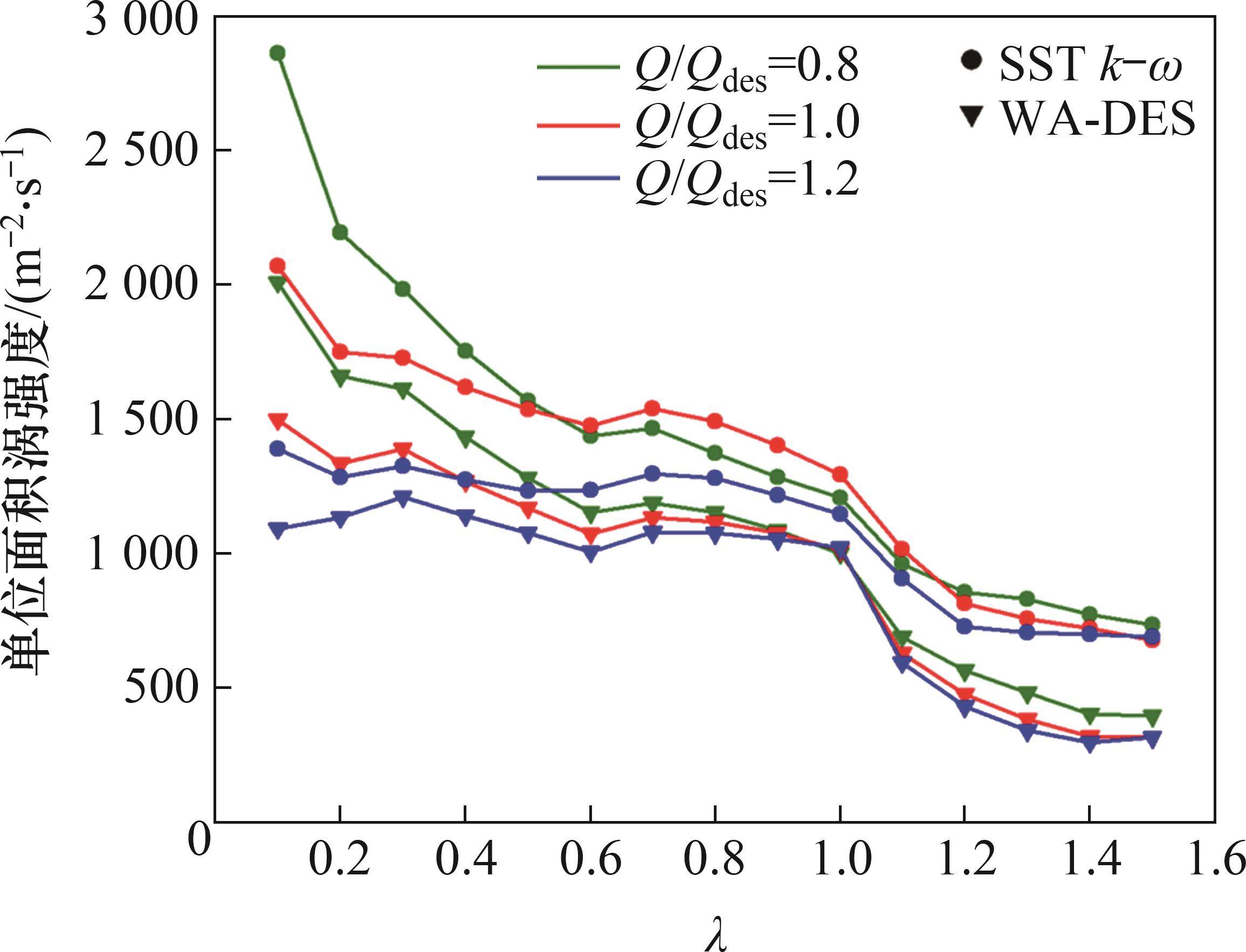
涡强度的变化可以表征不同流量工况下涡旋演变规律。沿叶片弦长径向截面单位面积涡强度ΔΓ如图6所示。由图6可见:在相同流量下,SST k-ω模型计算出径向截面上ΔΓ明显大于WA-DES模型截面上ΔΓ,ΔΓ整体上从前缘到尾缘逐渐降低,这2个模型预测的ΔΓ变化趋势一致;随着流量增加,WA-DES模型预测的相同弦长的截面ΔΓ逐渐减小;SST k-ω模型在λ为0.6~1.2的径向截面上,1.0Qdes工况点的ΔΓ大于0.8Qdes工况点的ΔΓ,与WA-DES模型结果有明显差异,但两者预测的ΔΓ差距不大。
当λ=0.5时,径向截面压力系数分布如图7所示。压力系数Cp表达式为[22]
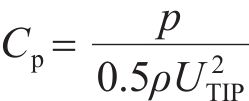
式中:p为压力,Pa;UTIP为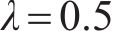
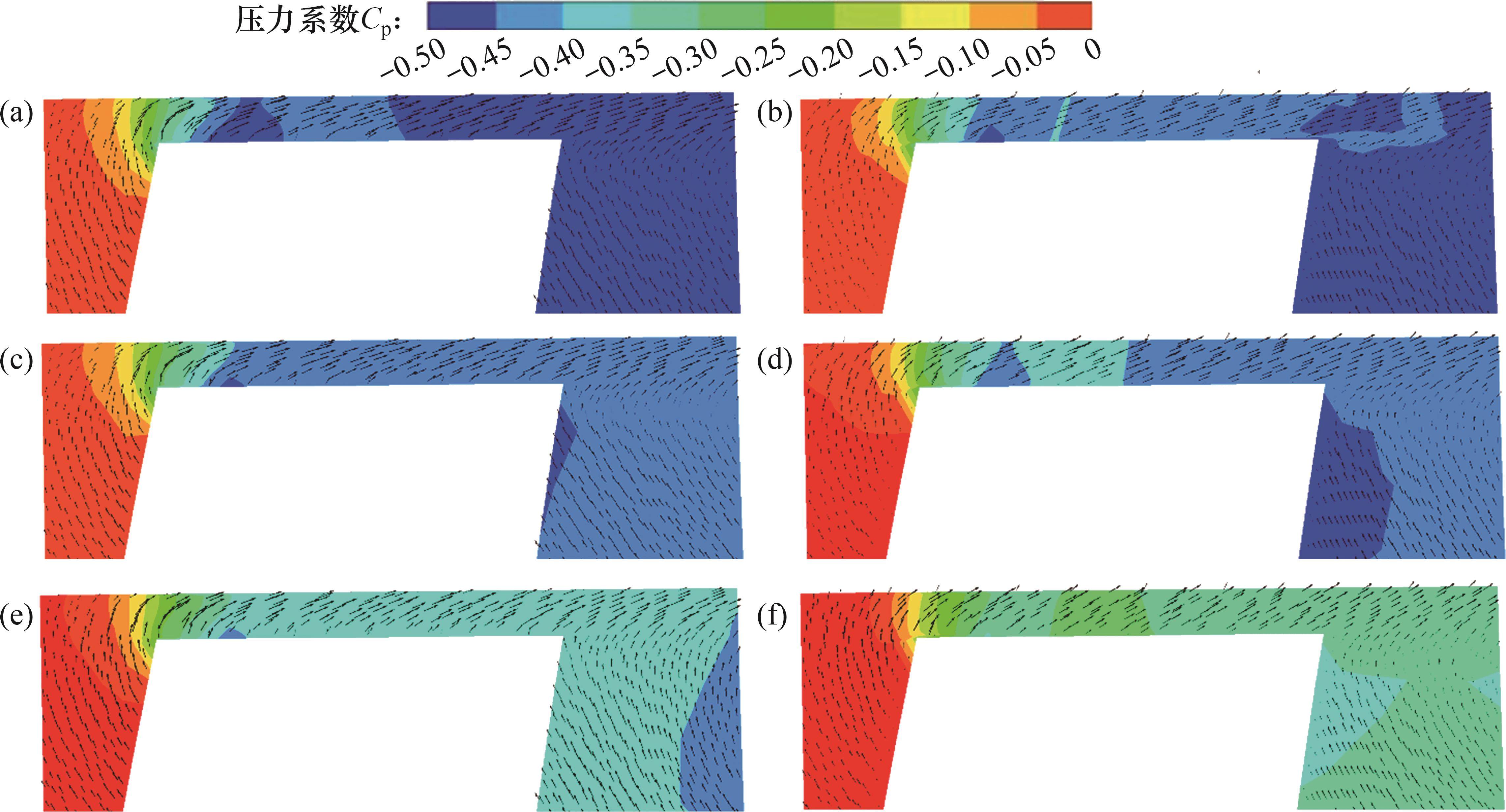
由图7可见:低压区集中在轮缘区和叶片吸力面处,靠近压力面叶顶区域压力系数出现明显的变化梯度;随着流量增加,压力系数逐渐增大,SST k-ω和WA-DES这2个湍流模型预测的压力值分布基本一致。
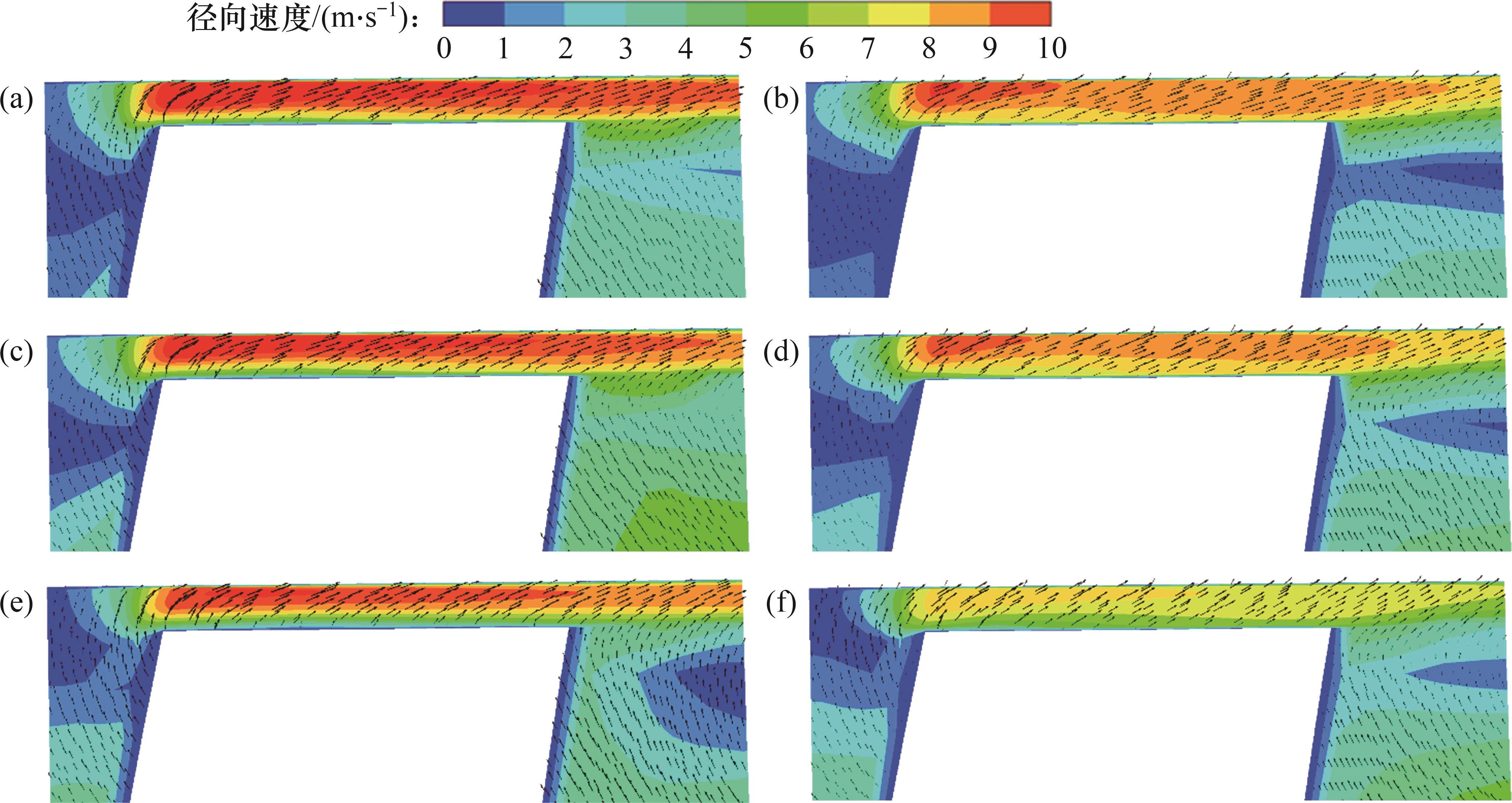
当λ=0.5时,径向截面轴向速度分布如图8所示。由图8可见:由于压力面和吸力面的压差作用,轴向速度的峰值出现在间隙泄漏流的起始段;由于主流和回旋涡流的共同作用导致吸力面叶顶下方轴向速度较大,间隙内靠近压力面叶顶处的轴向速度梯度大,叶尖内湍动能分布与轴向速度分布一致;WA-DES模型预测的轴向速度峰值小于SST k-ω模型预测的轴向速度峰值,但这2个模型高值区预测结果基本一致。
当λ=0.5时,径向截面湍动能分布如图9所示。由图9可见:高湍动能区域集中在叶顶间隙和泄漏剪切层,并沿流动方向湍动能逐渐减小;随着流量增加,间隙区内速度梯度降低,高湍动能区域减小;与SST k-ω模型相比,WA-DES模型预测的高湍动能区域沿叶片型线方向偏离叶片吸力面距离更大,两者预测的叶顶流场湍动能随流量变化的演变规律一致。
3.2 空化模拟结果
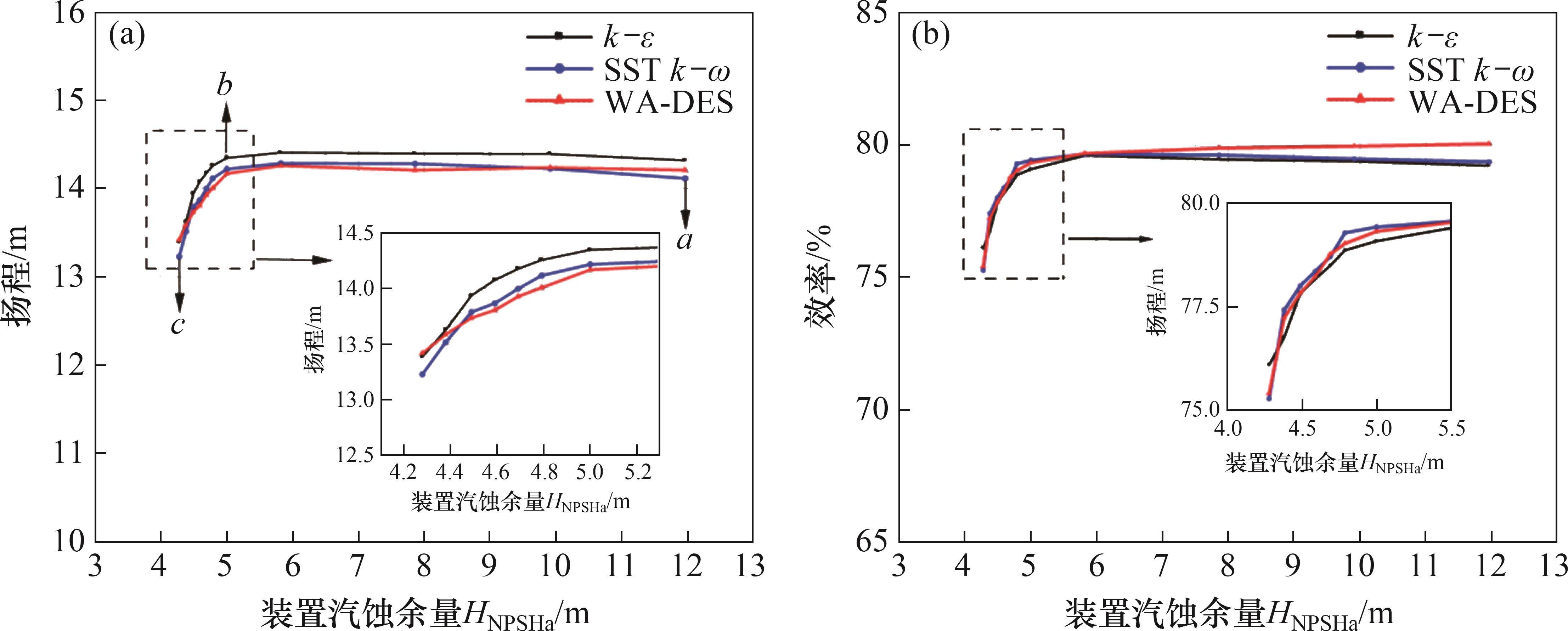
空化性能曲线如图10所示。由图10可见:当扬程下降3%时,有效汽蚀余量与k-ε和SST k-ω的装置汽蚀余量(HNPSHa)一致,保证了在相同空化条件下,不同湍流模型计算结果的可比性。本文选取空化扬程曲线中a(HNPSHa=11.96 m)、b(HNPSHa=5.00 m)、c(HNPSHa=4.28 m)作为典型空化工况点,对比不同湍流模型叶轮内空化流动。
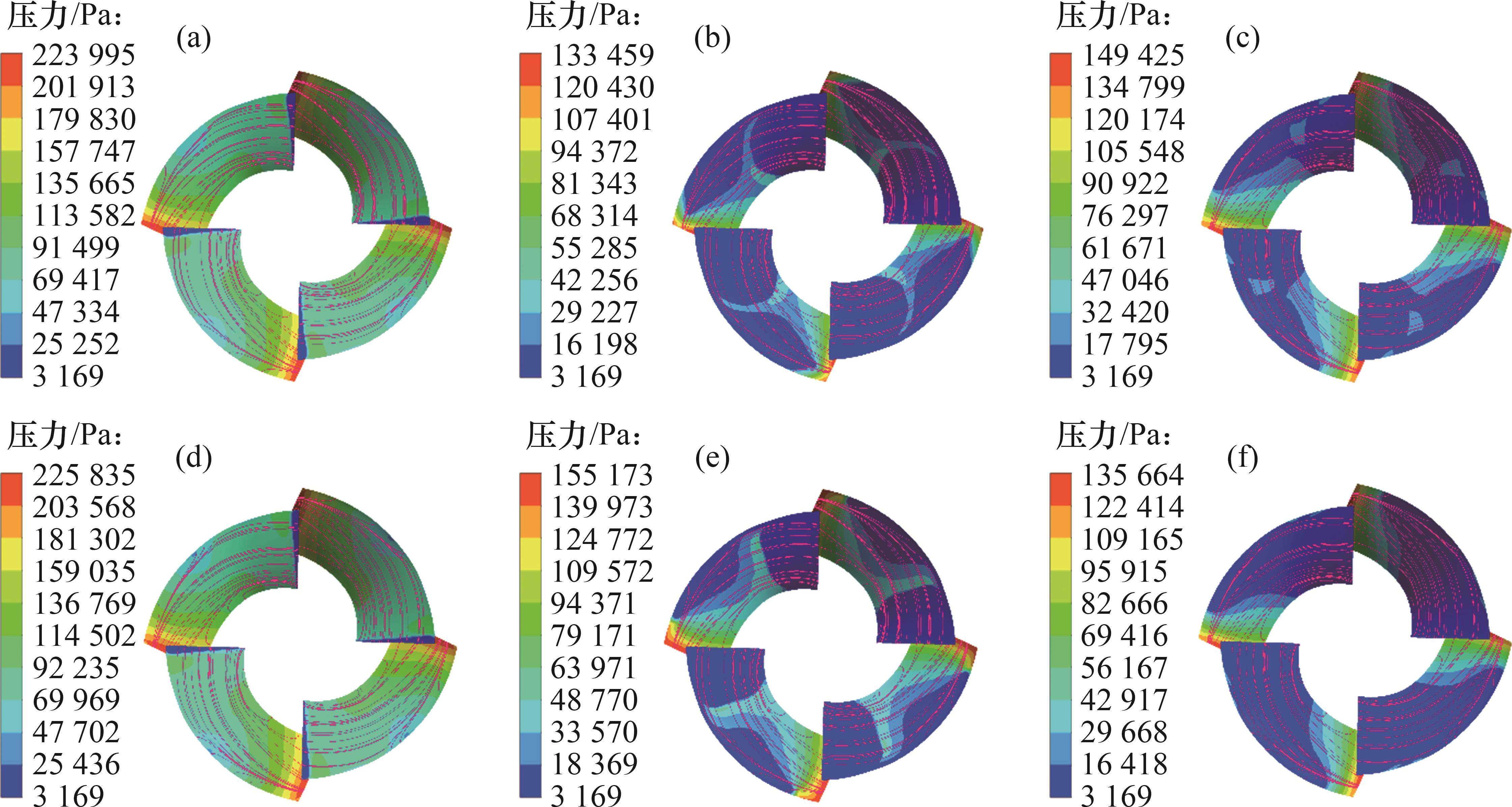
分别使用这2种湍流模型模拟泵在3种空化点下叶轮叶片背面的压力分布和流线分布,如图11所示。由图11可见:当HNPSHa=11.96 m时,低压区只集中在叶片前缘进口边,叶顶区域由于压力梯度发生流动分离;随着装置汽蚀余量的下降,前缘低压区域向后缘发展,叶顶处的低压区也逐渐向轮缘拓展;当HNPSHa=4.28 m时,吸力面大部分区域被低压区覆盖,此时,空化得到充分发展,叶轮做功能力明显下降。这2种模型预测的背面低压区域位置和面积随空化发展的变化趋势基本相同,在相同空化条件下,WA-DES模型计算的吸力面压力区间与SST k-ω模型计算的吸力面压力区间差异性较小,这2种模型对吸力面流动情况预测高度一致,证明了WA-DES模拟结果的可靠性。
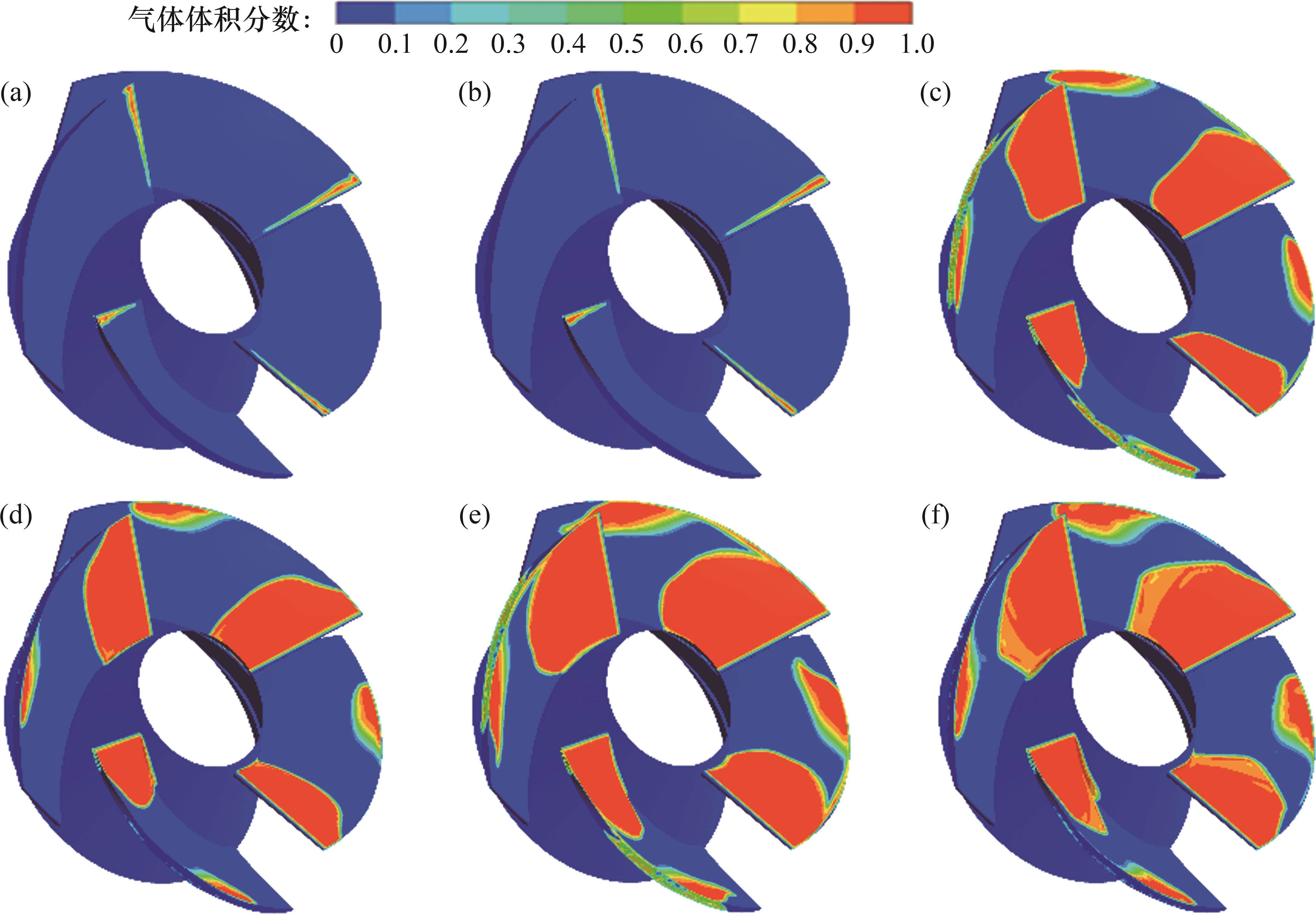
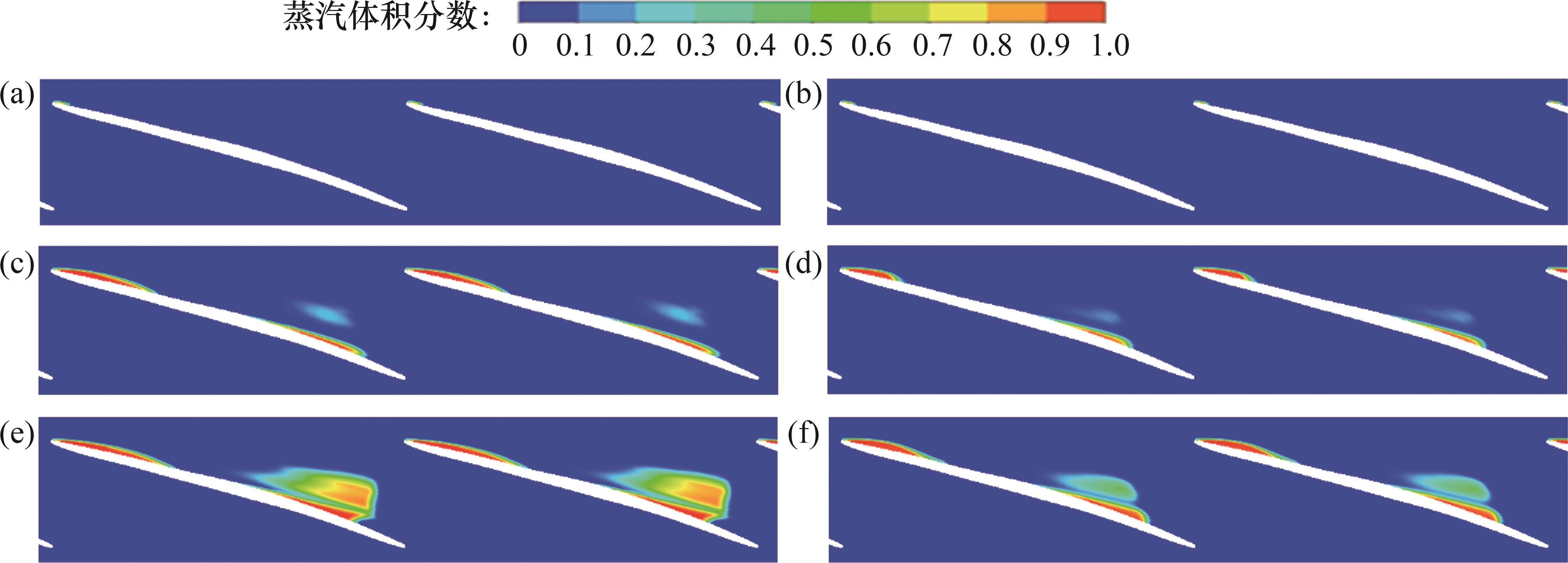
在3种空化点下,不同湍流模型计算出的叶轮流道中(面朝来流方向)蒸汽体积分数分布情况如图12所示。由图12可见:空化首先出现在轮缘间隙和靠近轮缘的叶片前缘处,随后在叶顶间隙处,空泡沿叶片背面向轮缘发展,空泡的尺寸增加,叶片前缘空泡向吸力面中、后缘发展,逐渐占据叶片表面大部分面积。这2种湍流模型预测的空化发展位置和趋势基本一致,蒸汽体积分数的分布区域与叶片背面低压区域相对应。
叶轮轮缘区0.9span截面上叶片间的蒸汽体积分数分布如图13所示。从图13可见:空泡首先在轮缘区进口边产生;随着HNPSHa减小,进口边产生的空泡逐渐向出口延伸,同时,叶片近轮缘边伴随空泡产生并向轮毂扩散。在3种空化点下,不同湍流模型显示出的叶片间的空泡体积分布与叶轮流道内的空泡体积分布大体上相似,而WA-DES湍流模型预测的靠近轮缘叶片边缘蒸汽区范围与SST k-ω模型预测的靠近轮缘叶片边缘蒸汽区范围略有差异,这主要是因为WA-DES湍流模型对湍动能和湍流耗散率的处理方法不同,可能导致对空化现象的预测产生差异,但两者预测的高蒸汽含量位置基本一致,表明了WA-DES湍流模型预测空化性能的可靠性。
轮缘泄漏流和泄漏涡结构是混流泵叶轮内最具特征的流动结构,也是造成叶轮内能量损失的重要来源。因此,轮缘泄漏流或泄漏涡结构的预测精度及其在叶轮内造成的能量损失,是评价湍流模型适用性的重要因素。
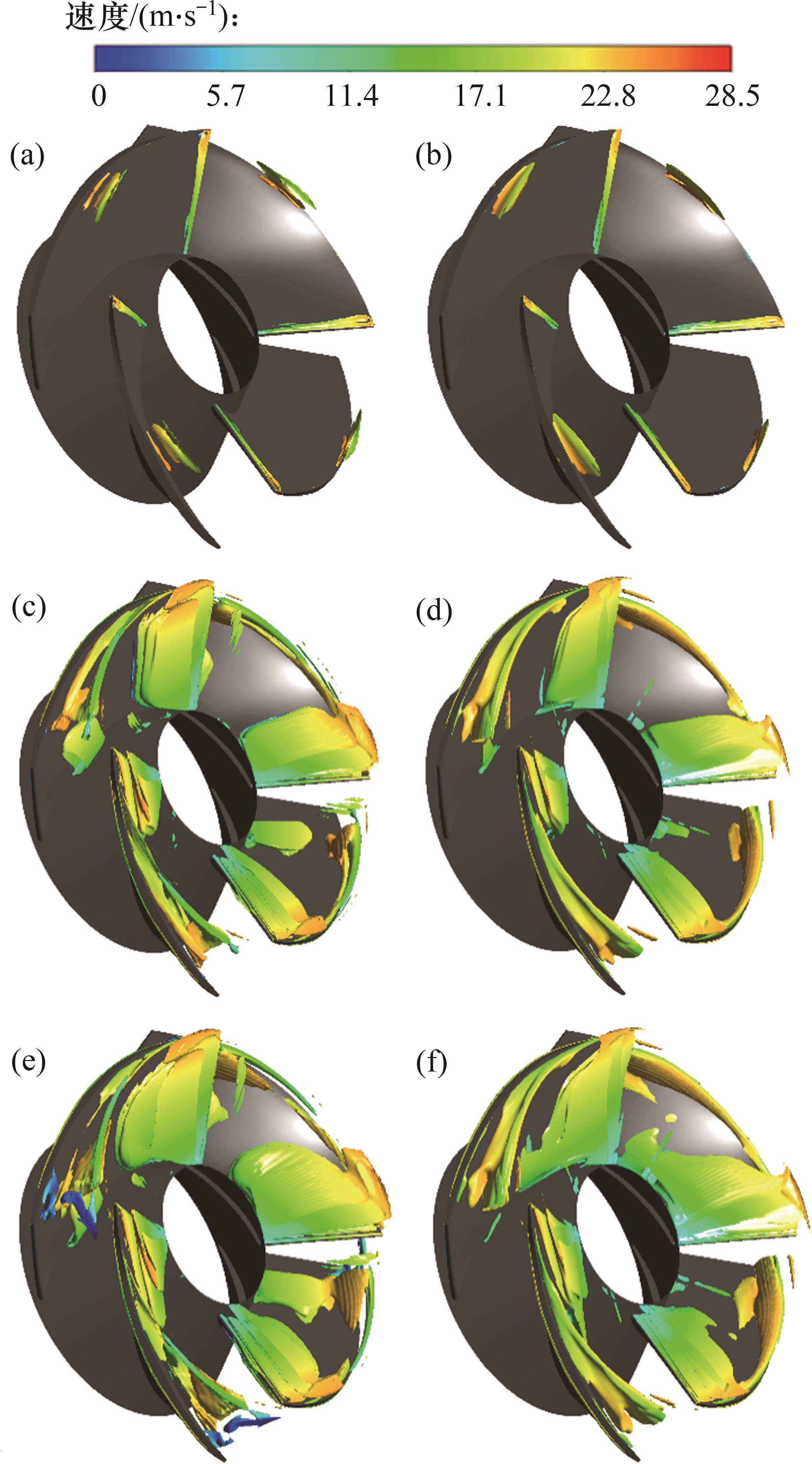
不同空化条件下叶轮内空化涡结构如图14所示。由图14可见:当HNPSHa=11.96 m时,叶片进口边存在附着涡,叶顶前缘靠近轮缘区域出现强度和尺度都较小的叶顶泄漏涡,附着在叶顶处;当HNPSHa=5.00 m时,由于压力降低,吸力面低压区出现大片云空化,泄漏涡尺度变大和强度增强,周向尺寸等增大,泄漏涡逐渐向相邻叶片的压力面发展;当HNPSHa=4.28 m时,叶顶泄漏涡尺度和强度增大,泄漏涡尾缘空化涡脱落并溃灭,形成与叶片表面垂直的空化涡,未溃灭的空化涡与相邻叶片压力面相互作用,导致叶片表面流动分离,从而引起泵的性能大幅下降。WA-DES模型和SST k-ω模型预测的叶顶泄漏涡结构随空化程度变化而变化的规律一致。
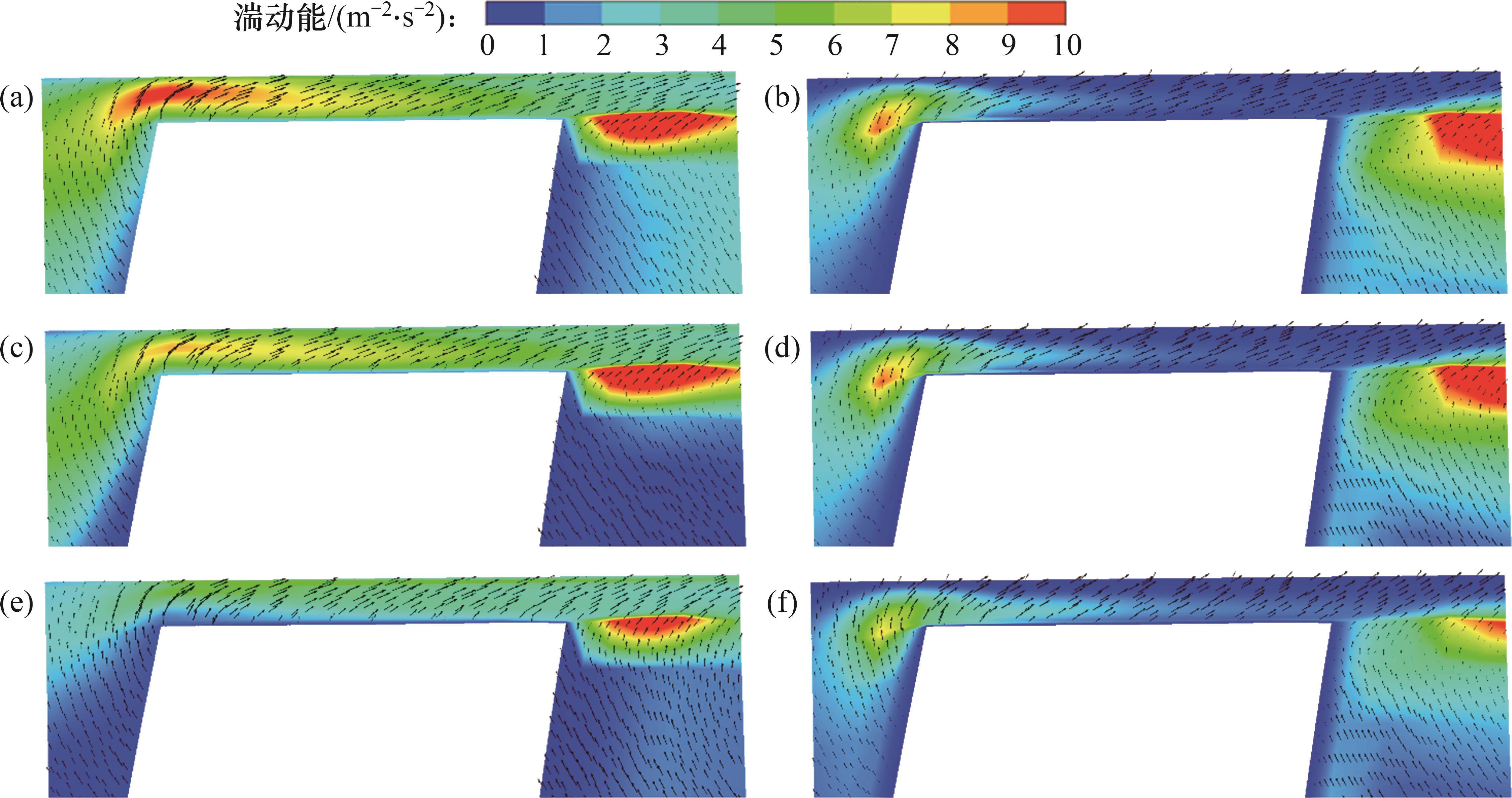
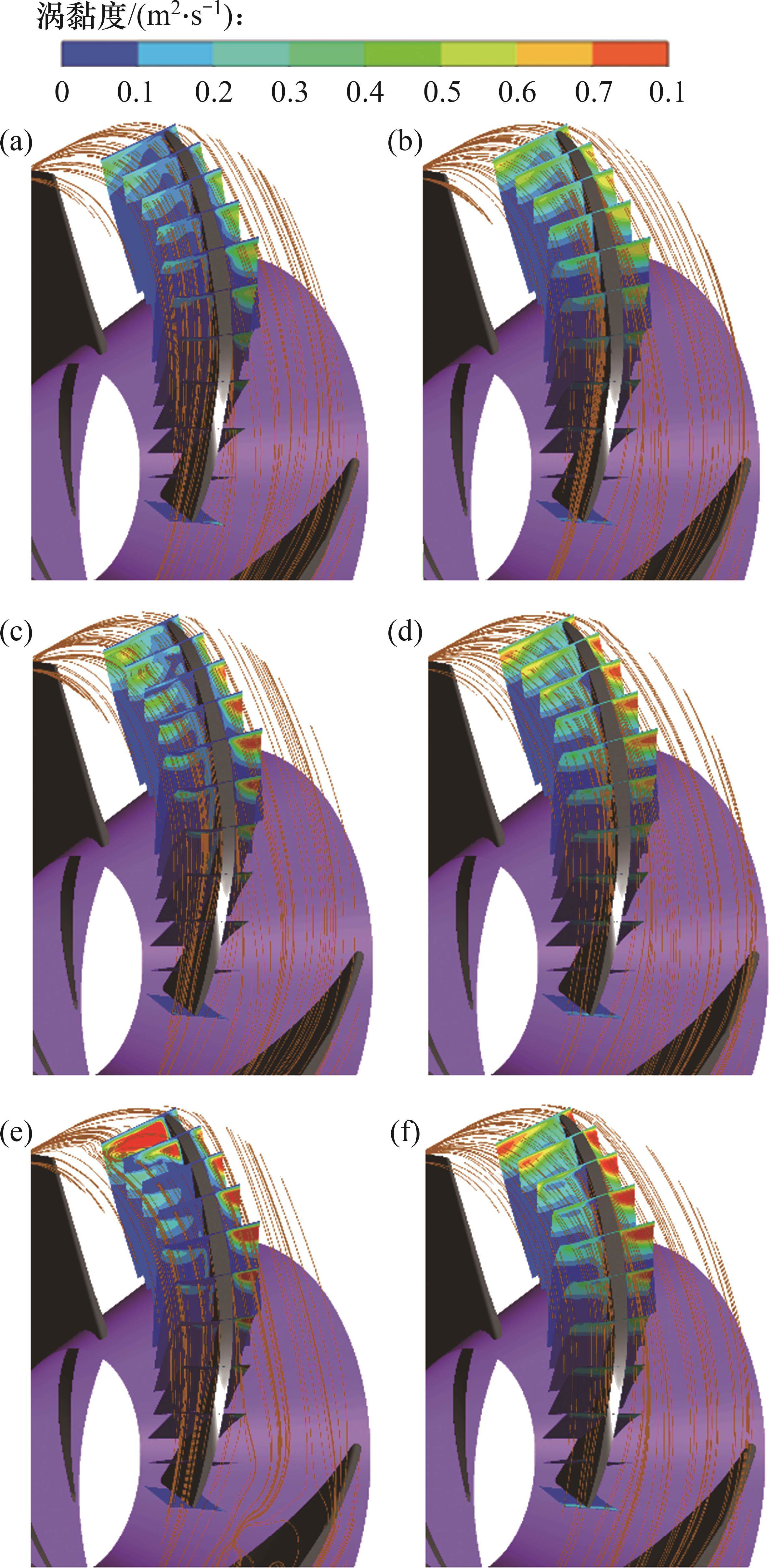
叶顶区涡黏度和流线分布如图15所示。由图15可见:这2种模型预测的泄漏涡空间结构差异明显,从叶轮径向截面内的湍流涡黏度分布来看,在HNPSHa=11.96 m和HNPSHa=5.00 m时,混流式喷水推进泵处于未完全空化状态,由叶顶泄漏涡导致的湍流涡黏度高值区范围差距不大,且这2种模型预测的涡黏度值在1个数量级之内,表示WA-DES预测的叶顶区湍流结构与SST k-ω预测的叶顶区湍流结构一致;从叶顶流线分布来看,当空化到最大程度时,SST k-ω模型的叶顶流场出现涡旋结构,而WA-DES模型并未出现这一现象,证明SST k-ω模型预测的流动分离程度大于WA-DES模型预测的流动分离程度。
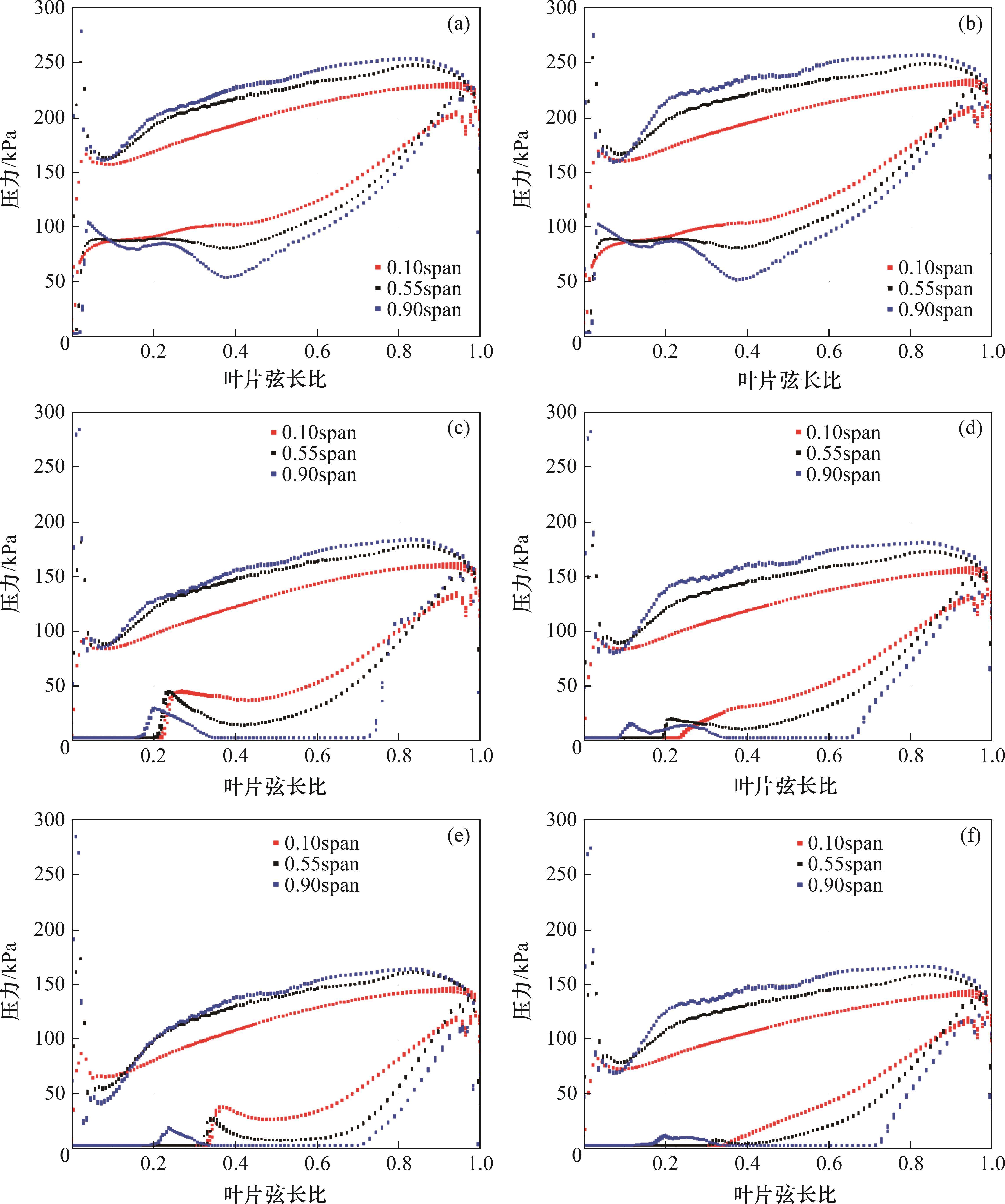
不同跨度下叶片吸力面和压力面沿叶弦压力分布如图16所示。从图16可见:在不同空化条件下,轮缘侧压力高于轮毂侧压力,吸力面压力波动明显大于压力面压力波动,0.9span处的压力分布表明轮缘比轮毂更早产生低于汽化压力的低压力区;随着HNPSHa的减小,叶片工作面和背面压力降低,叶片背面压力突变区域逐渐向尾缘靠近,湍流模型预测的不同弦长上压力变化趋势与叶片背面空泡发展相关,空化的不断发展导致叶轮流道内压力和速度分布发生变化,叶片工作面压力降低,低压区面积增大。
4 结论
1) WA-DES模型能较准确地预测喷水推进泵外特性和空化性能,预测结果与k-ε和SST k-ω湍流模型预测结果差异性不大,说明WA-DES的预测精度较高。
2) 采用Ω涡识别法对SST k-ω和WA-DES模型在非空化和空化条件下的叶轮涡结构进行可视化,两者预测的涡结构演化规律呈现较高的相似度,预测流动分离的差异性导致了涡在空间尺度上存在一定区别,沿弦长的径向截面上的单位面积涡强度分布表明SST k-ω模型预测的涡生成量大于WA-DES模型预测的涡生成量。
3) 对比分析了弦长分数为0.5时叶顶流场中SST k-ω和WA-DES的流动特性,WA-DES模型与SST k-ω模型预测的压力系数、轴向速度和湍动能分布的高值和低值区域以及随工况变化的发展趋势基本一致。
4) WA-DES和SST k-ω模型对空化条件下叶片吸力面压力和叶轮内空泡体积分数分布的计算结果表明,在设计流量条件下,空化首先出现在叶片吸力面靠近轮缘的前缘。随着进口压力的降低,空化区域向尾缘扩展,蒸汽体积分数逐渐增大。
5) 在对轮缘泄漏涡空间结构的预测中,WA-DES模型和SST k-ω湍流模型差异较大,但这2种湍流模型对轮缘湍流涡黏度预测的一致性弱化了泄漏涡在空间尺度上的差异造成的影响,这是这2种模型预测的轮缘区涡粘损失相近以及预测的泵性能差异不大的重要原因。
陈俊宝, 李伟, 胡敬宁, 等. WA-DES湍流模型在喷水推进泵数值预测中的适用性研究[J]. 中南大学学报(自然科学版), 2025, 56(2): 744-758.
CHEN Junbao, LI Wei, HU Jinning, et al. Applicability of WA-DES turbulence model in numerical prediction of water jet pump[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 744-758.

