桥面铺装作为钢桥结构的重要组成部位,不仅起到了分散车辆荷载、防止雨水侵入的作用,而且可以满足人们对行车安全性、耐久性、平整性和舒适性的要求[1-3]。常用于钢桥面的3种典型的铺装材料分别是环氧沥青混凝土(EA)、沥青马蹄酯碎石混凝土(SMA)和浇筑式沥青混凝土(GA)[4-5]。近年来,钢桥面铺装因交通流量大、超重荷载和质量缺陷等引发病害频发而备受关注[6-7]。以环氧沥青铺装层为例,其强度高、高温抗车辙性能和韧性好,但在低温条件下显现脆性、抗断裂性能差,存在低温开裂的隐患,致使施工工艺和使用环境要求极高,投入运营后不可避免地出现各类病害[8-9]。此外,环氧沥青显示出明显的偏析和马歇尔稳定性下降,摊铺过程的初始阶段易受振动的影响[10]。近20年发展起来的聚氨酯因具有极强的基团和聚酯柔性链,可为聚氨酯材料提供强度高、抗氧化、耐磨、耐光、耐化学等优异性能[11-12],已广泛应用于家用电器、建材、日用品交通运输等领域[13-14]。为探索更优的路面材料,宁波路宝科技实业集团有限公司开发了一种新型经济节能优化型混凝土(Ecology Conservation Optimization Concrete,简称ECO混凝土)。因具有良好的路面使用性能,ECO混凝土已在沈阳浑河长青大桥、福州螺洲大桥等国内多座桥梁中得到应用[15-16]。目前,关于ECO混凝土的研究较少,主要集中于研究其自身的力学性能,如不同温度条件下的抗压性能[17]和抗拉性能[18-19]、低温性能[20]和耐久性[21]等。在桥面铺装工程中,铺装层与桥面板的交界面相对薄弱,长期交通荷载和外界环境的作用易造成界面破坏,如脱粘、滑移等[22-23]。针对ECO混凝土铺装层界面,现有研究主要集中于不同温度条件下钢-ECO混凝土的斜剪性能及黏结-滑移模型[24],法向性能的研究则比较缺乏。因此,为全面研究钢-ECO混凝土交界面的力学性能,为ECO混凝土在铺装工程中的应用提供有效的理论依据,本文对钢-ECO混凝土交界面试件进行四点弯曲试验,以研究其法向力学性能。针对已有线性-抛物线和指数型模型的不足,提出了一种适用于描述钢-ECO混凝土交界面法向力学性能的内聚力模型,基于对试验数据的回归分析和断裂边界条件确定模型系数。并通过对比分析,验证了本文所提模型模拟钢-ECO混凝土交界面法向开裂的合理性和适用性。
1 试验概况
1.1 试验材料与配合比
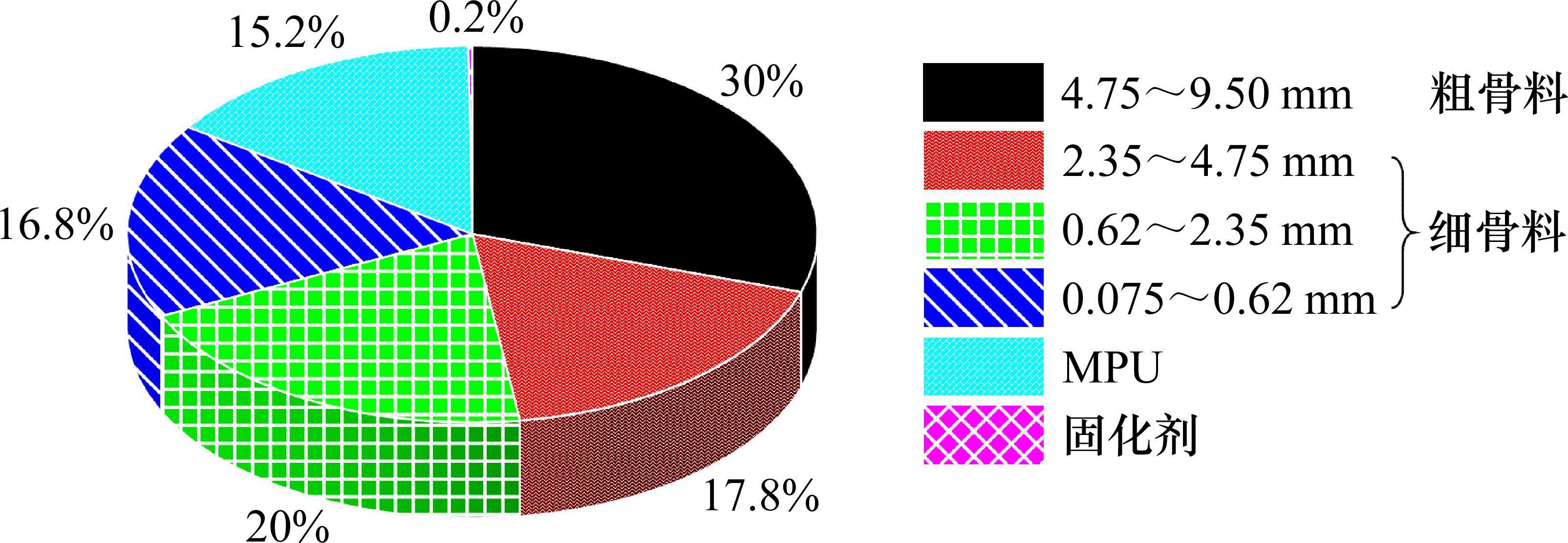
为研究钢-ECO混凝土交界面的力学性能,设计制作钢-ECO混凝土交界面试件,试件所需材料包括钢板和ECO混凝土。钢板采用Q235钢材,ECO混凝土的主要成分包括骨料、改性聚氨酯结合料(MPU)和固化剂。其中,骨料由含水率均少于0.3%的粗骨料和细骨料按最大密度曲线混合而成:粗骨料以连续级配的天然砾石为主,粒径范围为4.75~9.5 mm,细度模数约3.4,表观密度约2 600 kg/m³,且颗粒表面圆润光滑,针状颗粒的含量不超过8%;细骨料以连续级配的天然河砂为主,粒径范围为0.075~4.75 mm,细度模数约2.5,表观密度约2 580 kg/m³。具体粒径及配合比如图1所示。MPU是通过添加硅烷偶联剂(SCA)对聚氨酯(PU)进行改性而得到的一种热固性高分子聚合物材料。固化剂用以加速MPU的固化,由甲苯二异氰酸酯、六亚甲基二异氰酸酯和乙酸乙酯等材料按比例混合而成。本次试验所采用的材料均由课题合作单位宁波路宝科技实业集团有限公司提供。
1.2 试件制备
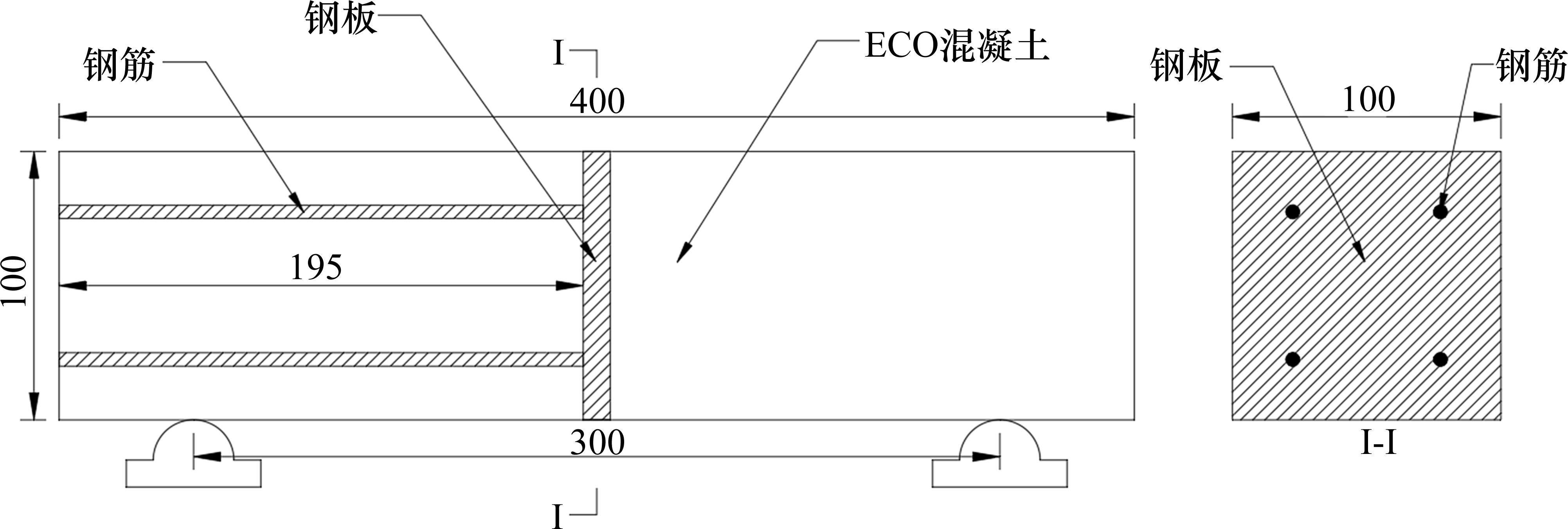
考虑到钢-ECO混凝土交界面的特殊性、拉伸试验的复杂性,试验采用钢板全嵌入式四点弯曲梁试验,制作的试件形状与尺寸参数如图2所示。试件整体尺寸为400 mm×100 mm×100 mm,其中,钢板的尺寸为100 mm×100 mm×10 mm,且钢板的左侧焊接钢筋,用以确保试验中左侧的ECO混凝土不与钢板发生脱粘,使钢板与ECO混凝土交界面的破坏发生在右侧。
试验中,采用聚氨酯黏结剂粘接钢板与ECO混凝土,用量为0.15 kg/m2。与普通黏结剂相比,聚氨酯黏结剂可以与MPU发生化学反应,形成网状结构。该试件的制备方法如下。
1) 将钢筋焊接在钢板一侧,如图3(a)所示,随后将钢板两面的粗糙度抛光至50~100 μm;

2) 将黏结剂均匀涂抹在钢板两侧,放入模具中,如图3(b)所示;
3) 根据配合比制备ECO混凝土,将混合后的ECO混凝土浆体倒入模具中,使用振动台振动,并用刮刀抹平,室温静置3 h后脱模、编号,固化成型后如图3(c)所示。
1.3 试验装置
所有试件在标准养护条件下养护28 d后进行试验,试验装置采用微机控高刚度拉压电液伺服试验机,型号为WAW-2000EDC,最大试验力为2 000 kN。采用位移控制的加载方式进行准静态加载,加载速率为0.05 mm/min。同时,为防止试验过程中支座发生滚动滑移,设计并制作了用于该试验的工装。试验使用装置如图4所示。
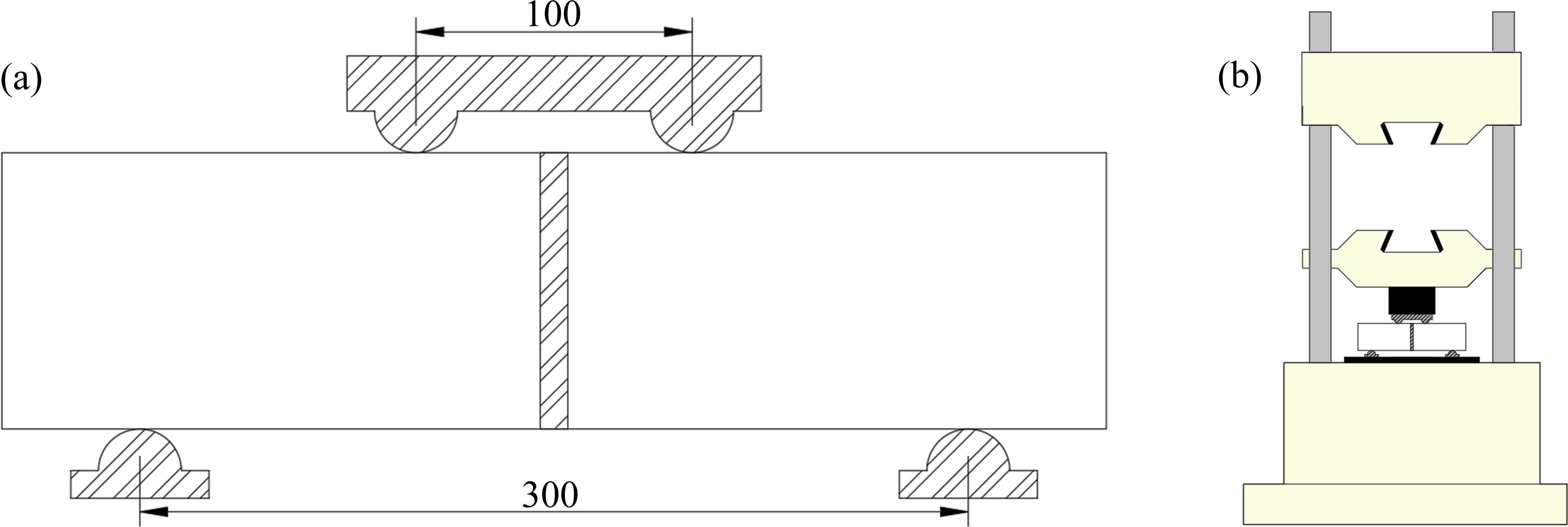
测量的物理量:竖向荷载值P和界面法向张开位移δ,其中竖向荷载值P通过试验机自带的采集系统采集,界面法向张开位移δ通过数字图像相关(DIC)技术同步采集、处理后得到。
2 试验结果及分析
2.1 试验现象
根据试验数据,绘制各试件的荷载-张开位移曲线如图5所示。在加载初期,试件并没有明显的变化,整个钢-ECO混凝土交界面处于弹性阶段(图5中OA段)。随着荷载的不断增大,达到临界荷载Pc时,钢-ECO混凝土最底部未焊接钢筋侧的交界面达到黏结强度后开始软化,使得交界面刚度下降,交界面进入过渡阶段(图5中AB段)。随着荷载的继续增加,当荷载达到极限荷载Pu时,最底部未焊接钢筋侧的交界面达到极限张开位移后失效,交界面底部开始产生细微裂纹,使得整个钢-ECO混凝土交界面的承载能力下降,交界面进入破坏阶段(图5中BC段)。随着继续加载,底部的张开位移不断增大,裂缝持续沿交界面向上扩展,承载能力持续下降,直至达到失效荷载Pr时,发出“砰”的一声,整个交界面破坏,裂缝贯穿至整个交界面。由图6(a)可以看出,试验过程中,裂缝仅出现在未焊接钢筋一侧的交界面处,而两侧的ECO混凝土和钢板均未产生细微裂纹,说明两侧材料的黏结强度大于钢-ECO混凝土交界面的黏结强度,交界面破坏失效是交界面的法向黏结应力达到了其黏结强度而导致的。同时,观察试件的断面可以发现,断裂侧钢板的表面附着少量从ECO混凝土上剥离下来的砂浆颗粒,大部分为聚氨酯黏结剂,如图6(b)所示。由此可见,在此荷载作用下,钢板与ECO混凝土的交界面破坏属于脱粘破坏。
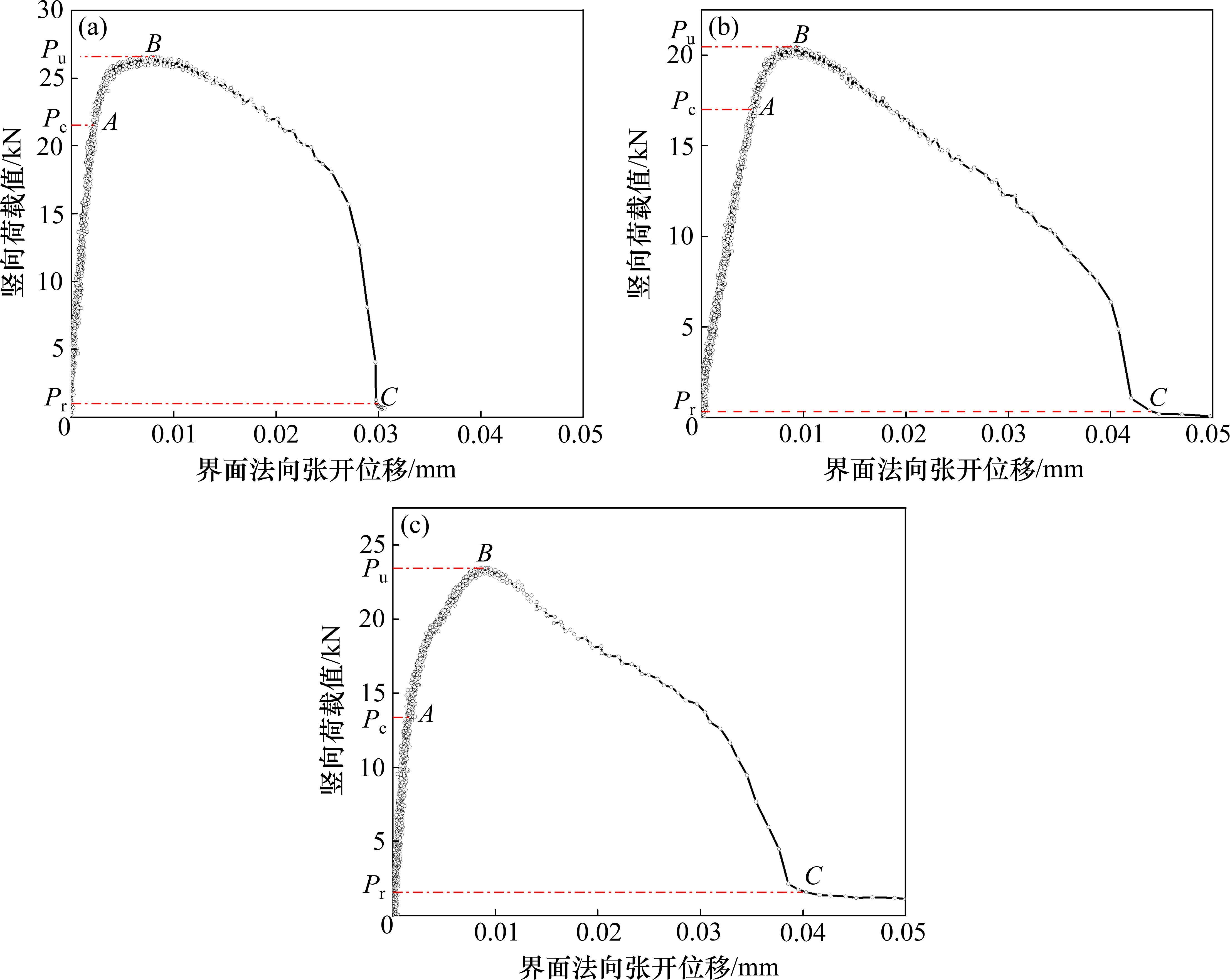

2.2 法向应力-位移曲线
根据试验现象可知,当试件处于极限开裂状态时,裂缝贯穿整个交界面,如图7(a)所示,此时作用的荷载值是失效荷载Pr,在此荷载作用下,界面法向张开位移为δm。此时:
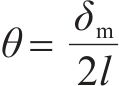
式中:θ为ECO混凝土开裂面与垂直方向的夹角;l为交界面完全脱粘的长度,等于试件的高度h,为100 mm。
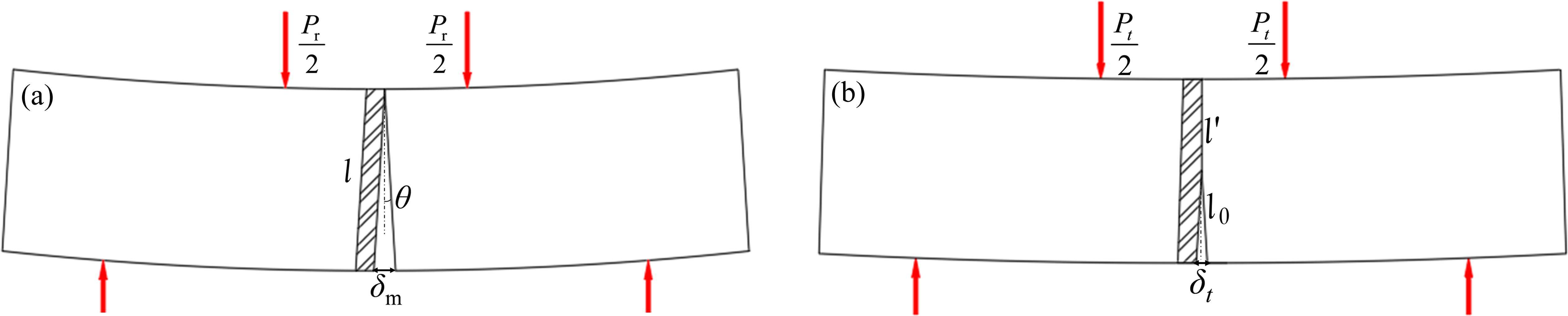
由于界面完全开裂时产生的张开位移极小,由式(1)可知,界面开裂后产生的夹角θ非常小。因此,如图7(b)所示,试验过程中,某时刻荷载Pt作用下,界面法向张开位移为δt,此时:
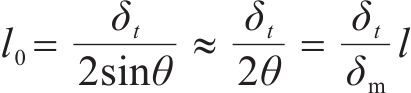
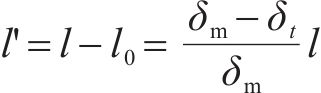
式中:l0为界面脱粘长度;l'为界面未脱粘长度。
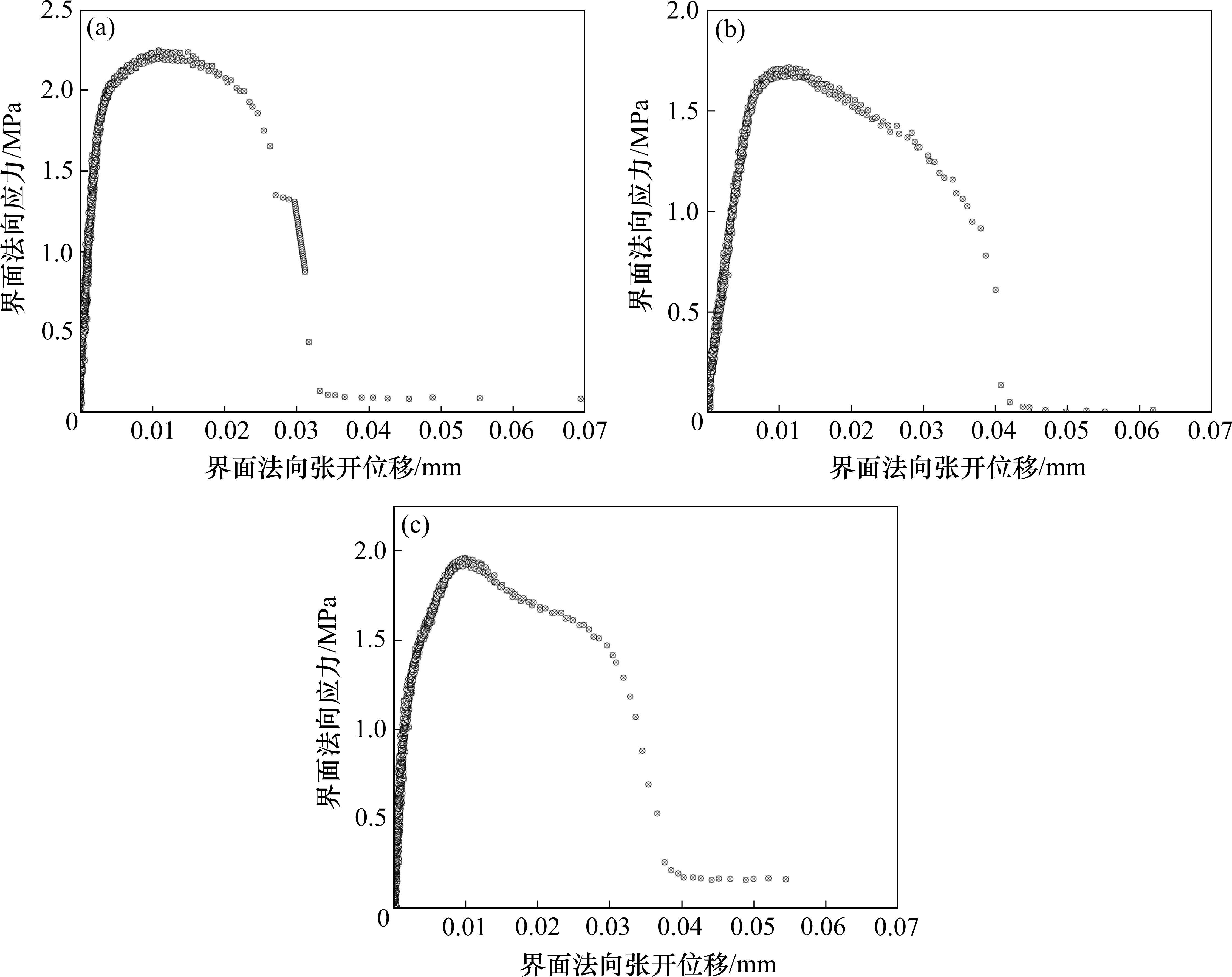
根据双线性本构关系可知,界面未开裂时试件处于弹性状态。因此,假定试验过程中未脱粘部分仍处于弹性状态,则未脱粘界面的法向应力随荷载作用的表达式见式(4)。根据式(4)处理后得到各试件的界面法向应力-张开位移关系曲线,如图8所示。
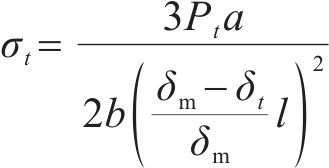
式中:a为荷载距同侧支座的距离;b为试件的宽度。
2.3 交界面力学性能参数
为研究钢-ECO混凝土交界面的力学性能,需要对试验数据进行分析处理以确定界面法向开裂的力学性能参数:黏结强度σn、界面刚度kn、损伤起始临界位移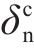
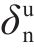
| 试件编号 | 黏结强度/MPa | 界面刚度/(MPa∙mm-1) | 损伤起始临界位移/mm | 极限张开位移/mm | 临界断裂能/(J∙m-2) |
|---|---|---|---|---|---|
| 1 | 2.245 | 873.5 | 0.011 | 0.034 | 72.0 |
| 2 | 1.717 | 286.2 | 0.011 | 0.043 | 53.5 |
| 3 | 1.960 | 612.5 | 0.010 | 0.040 | 59.2 |
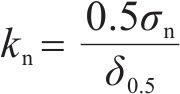
式中: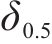
由表1可知,相同加载条件下不同试件计算得到的交界面刚度离散性较大,主要是由于试件在制作过程中存在着混凝土浇筑不均匀(骨料随机分布)、黏结剂用量及涂抹厚度不一致引起的。因此,钢-ECO混凝土交界面的法向开裂力学性能参数通过取平均值得到,计算结果如表2所示。可以发现,与普通钢-混凝土交界面相比,钢-ECO混凝土交界面的黏结强度、刚度和极限张开位移分别提高了289.3%、368.4%和160.0%,说明钢-ECO混凝土交界面具有更好的力学性能。
| 界面 | 黏结强度/MPa | 界面刚度/ (MPa∙mm-1) | 极限张开位移/mm |
|---|---|---|---|
| 钢-ECO混凝土 | 1.974 | 590.7 | 0.039 |
| 钢-混凝土[26] | 0.507 | 126.1 | 0.015 |
3 钢-ECO混凝土交界面内聚力模型
3.1 常见界面内聚力模型适用性分析
相比采用复杂的断裂力学计算强度因子进而计算界面刚度、强度的方法,建立内聚力模型更加简单、直接。目前,关于内聚力模型,国内外已有众多学者展开了研究,就张力-位移关系而言,ALFANO[25]探究了双线性、线性-抛物线、指数和梯形等内聚力模型的准确性与收敛性。由图8可知,钢-ECO混凝土交界面的张开破坏属于弹塑性开裂。因此,采用线性-抛物线内聚力模型和指数型内聚力模型对试验数据进行拟合,拟合方法采用最小二乘法,拟合得到的界面临界断裂能分别为33.1 J/m2、56.8 J/m2,结果如图9所示。此时的试验结果由各试件的试验数据取平均值得到。
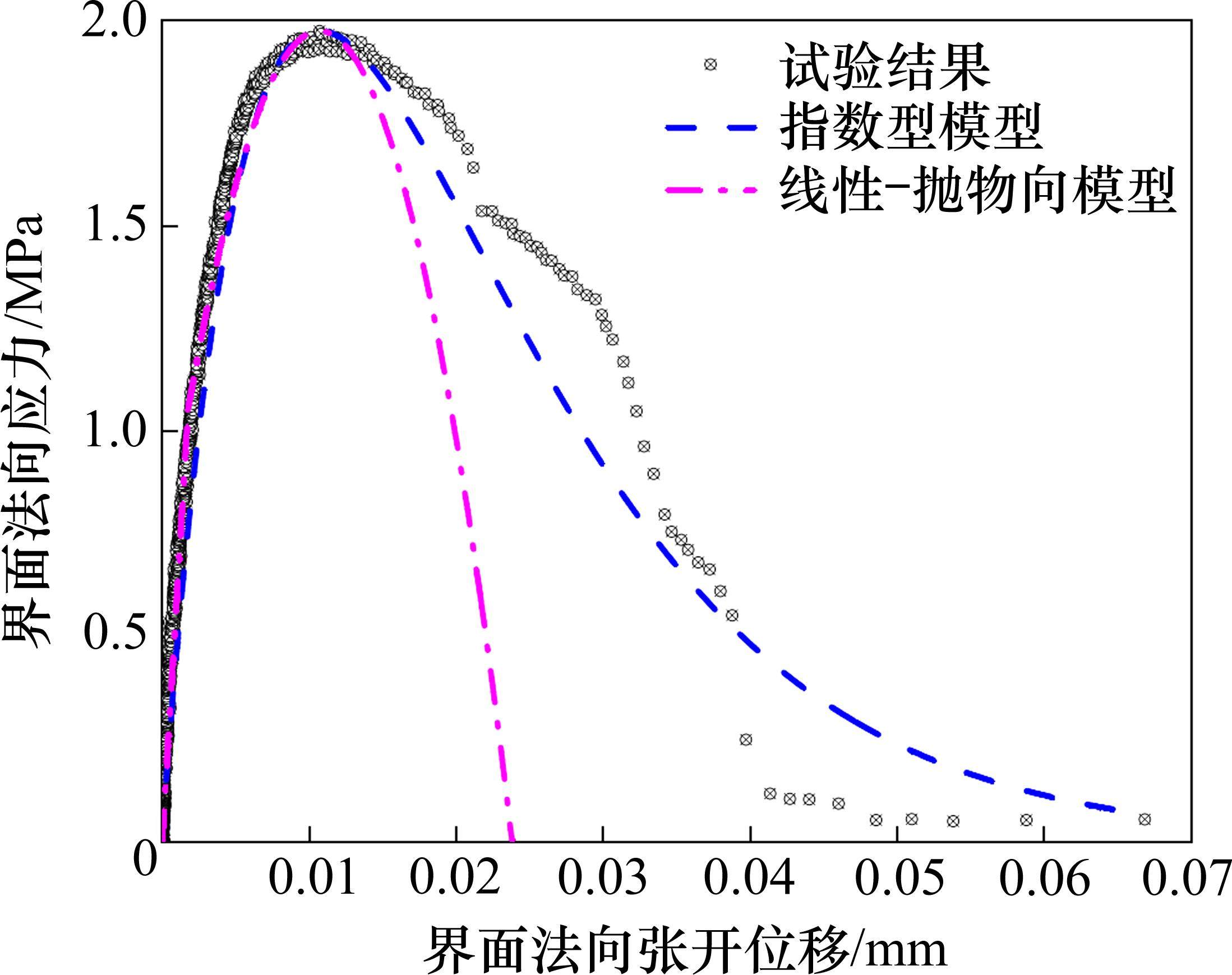
由图9可知,线性-抛物线模型下降段衰减速率极快,与钢-ECO混凝土交界面下降段的试验数据完全偏离,指数型模型下降段虽衰减速率较慢,但下降趋势与试验数据仍有较大偏差,二者均无法准确描述钢-ECO混凝土交界面的法向开裂损伤行为。因此,为准确描述钢-ECO混凝土交界面法向开裂损伤的机理,有必要建立新的内聚力模型,以表征钢-ECO混凝土界面法向开裂损伤的萌生和发展过程。
3.2 本文提出的内聚力模型
通过分析已有模型的适用性发现,上升段线性-抛物线内聚力模型的变化速率与试验数据更为接近,下降段拟合效果均较差。因此,根据下降段试验数据的变化趋势,参考Butterworth滤波器函数,提出一种新的内聚力模型,用以描述钢-ECO混凝土交界面的宏观断裂行为。建立这一模型时,需保证满足以下断裂边界条件。
1) 当交界面法向张开位移δ达到界面极限张开位移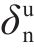
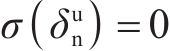
2) 当交界面法向张开位移δ达到界面损伤起始临界位移(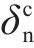
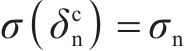
3) 交界面法向应力-张开位移曲线与坐标轴围成的面积应等于界面临界断裂能Φn,即:
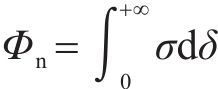
4) 当界面法向张开位移δ达到界面损伤起始临界位移(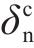
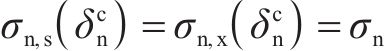
在满足上述断裂边界条件的前提下,引入相关系数来改善交界面断裂过程中的非线性特征,使其符合钢-ECO混凝土交界面法向开裂损伤的萌生和发展。本文提出的交界面内聚力模型,其法向应力-张开位移关系表达式为:
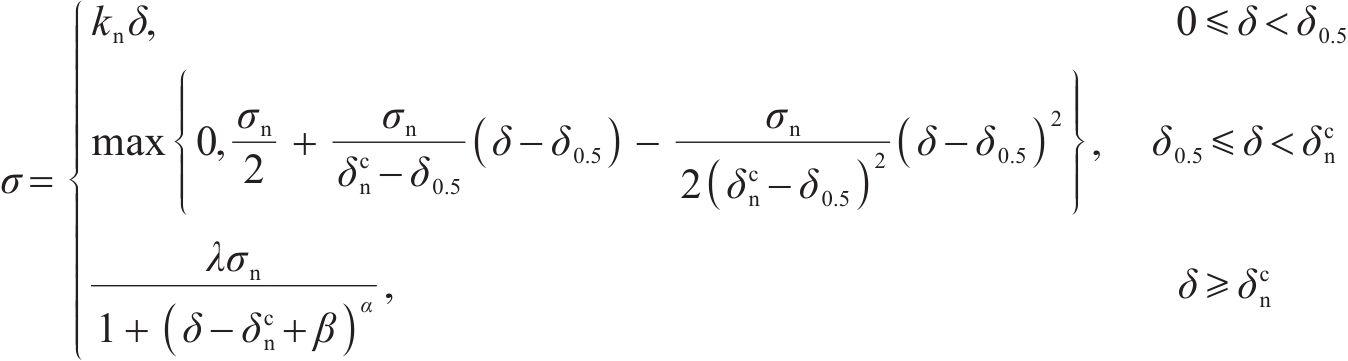
式中:α、β、λ均为内聚力模型下降段的待定系数,其中λ按式(11)计算。
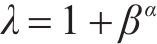
利用本文提出的内聚力模型对试验数据进行拟合,结果如图10所示。采用最小二乘法分别拟合上升段和下降段的试验数据,并结合断裂边界条件确定模型系数,进而得到钢-ECO混凝土交界面的力学性能参数,即:黏结强度、刚度、损伤起始临界位移、界面临界断裂能。由拟合结果得到本文提出的内聚力模型下降度系数α、β、λ分别为209.5、0.979、1.012。此时,界面临界断裂能为58.2 J/m2。
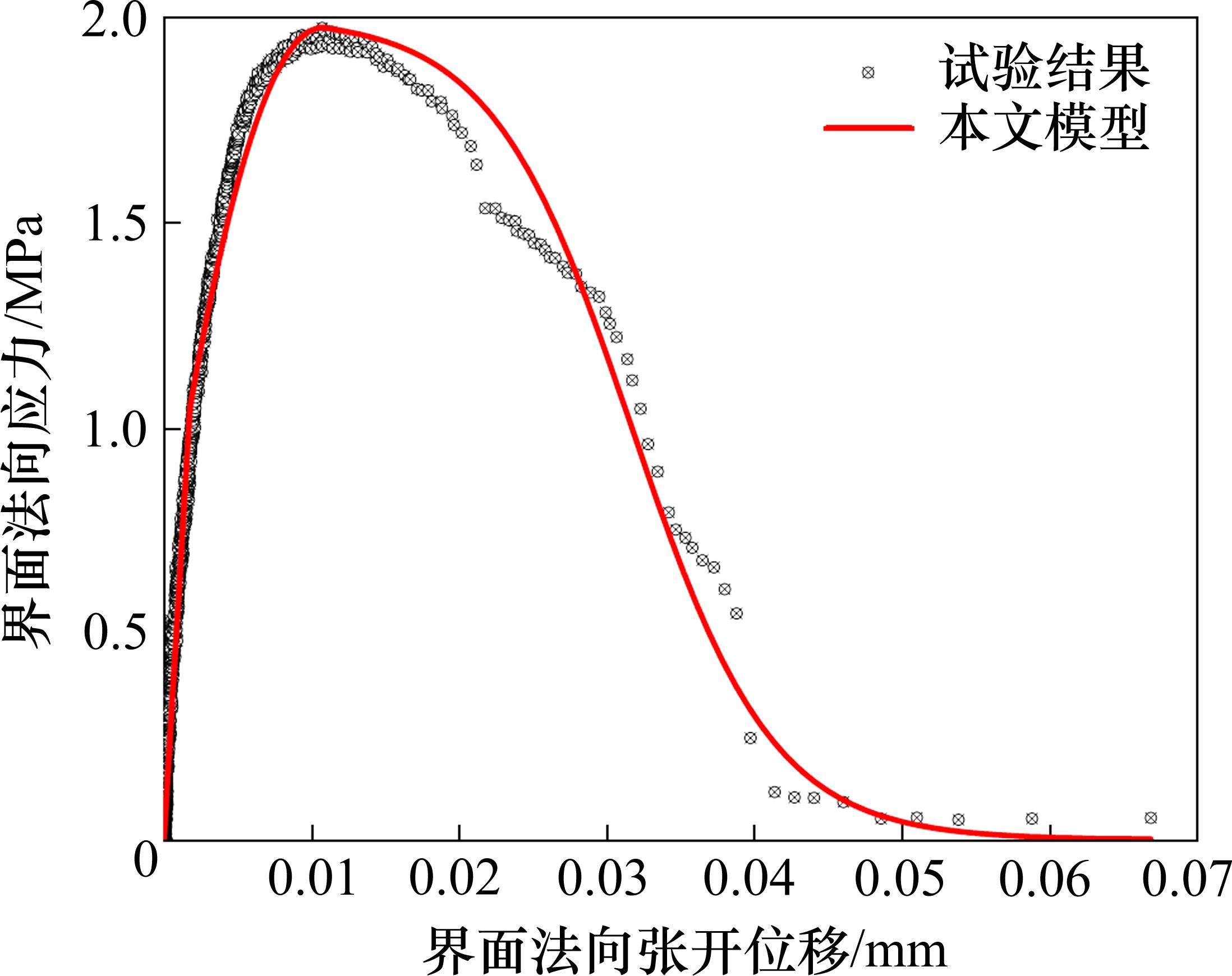
为验证本文提出的内聚力模型模拟钢-ECO混凝土交界面损伤开裂行为更具合理性,将各种内聚力模型得到的交界面力学性能参数与试验得到的参数进行对比,结果如表3所示。由表3可知,线性-抛物线模型和指数型模型的临界断裂能比试验所得临界断裂能分别减少了43.0%和2.2%,本文提出的内聚力模型的临界断裂能增加了0.2%。由此可见,本文提出的内聚力模型计算的临界断裂能与试验数据拟合曲线围成的临界断裂能更为接近。同时,对比图9和图10可知,本文提出的内聚力模型下降段的变化趋势与试验曲线更贴合,更能表征钢-ECO混凝土交界面法向开裂的萌生和发展过程。因此,本文提出的内聚力模型模拟钢-ECO混凝土交界面损伤开裂行为更具合理性。
| 类型 | 黏结强度/MPa | 损伤起始临界位移/mm | 界面刚度/(MPa∙mm-1) | 临界断裂能/(J∙m-2) |
|---|---|---|---|---|
| 线性-抛物线 | 1.974 | 0.011 | 590.7 | 33.1 |
| 指数型 | 1.974 | 0.011 | — | 56.8 |
| 本文 | 1.974 | 0.011 | 590.7 | 58.1 |
| 试验 | 1.974 | 0.011 | 590.7 | 58.2 |
3.3 内聚力模型计算值与试验值对比分析
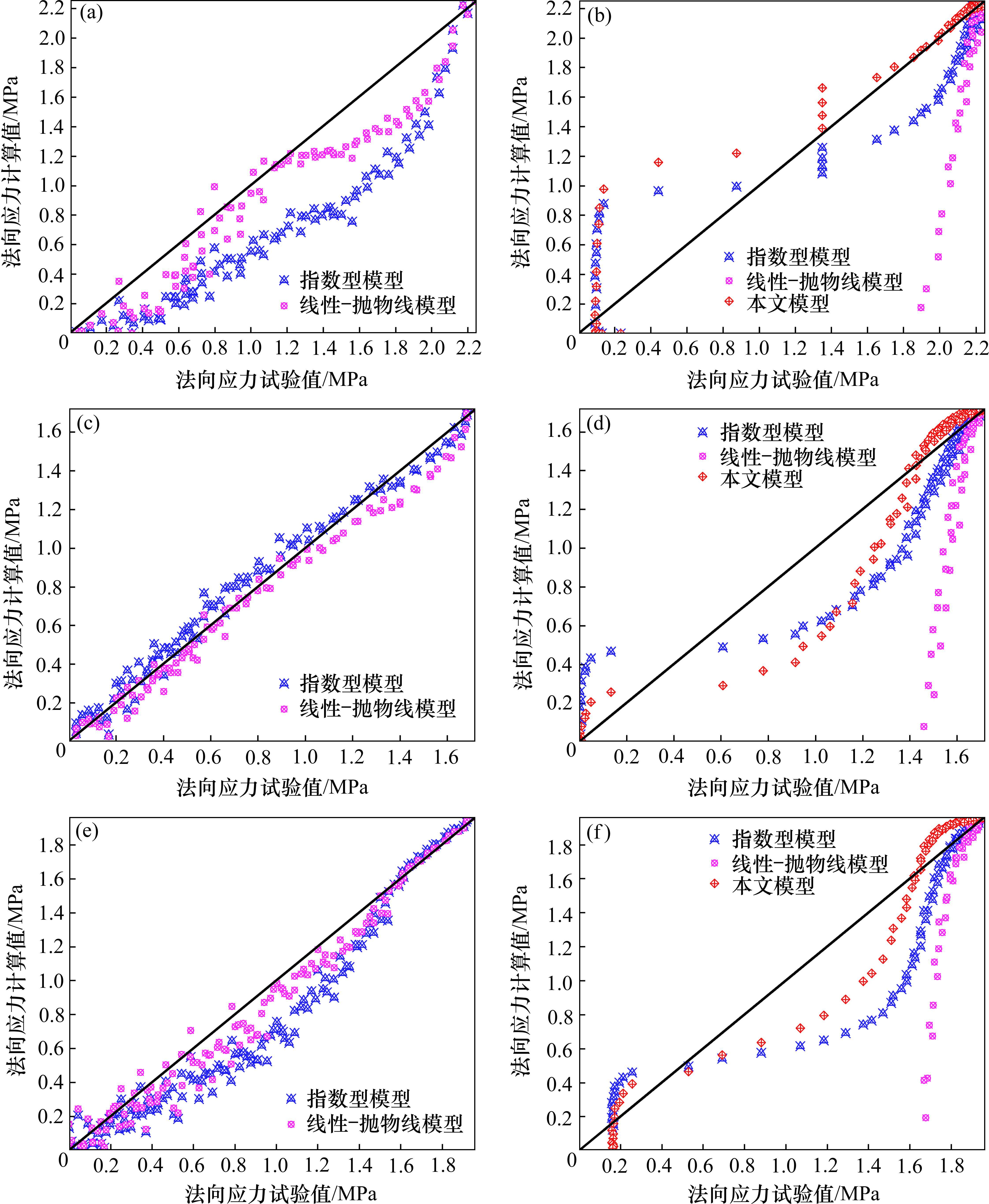
由表1可知,各个试件得到的交界面刚度离散性较大,反映出钢-ECO混凝土试件的离散性很大。由于试件试验数据存在随机性和较大离散性,上述合理性的验证在各试件试验数据取算术平均值的基础上进行。因此,将内聚力模型应用于离散性很大的各个试件中,并与试验数据进行对比,以验证本文提出的内聚力模型模拟钢-ECO混凝土交界面法向开裂损伤行为的适用性。为准确比较各内聚力模型的适用性,将上升段和下降段的对比结果分开考虑,其试验值与计算值的对比如图11所示,相关参数见表4。
| 试件编号 | 分段 | 相关系数R2 | 均方误差MSE | ||||
|---|---|---|---|---|---|---|---|
| 线性-抛物线 | 指数型 | 本文 | 线性-抛物线 | 指数型 | 本文 | ||
| 1 | 上升段 | 0.860 | 0.444 | 0.860 | 0.059 | 0.191 | 0.059 |
| 下降段 | -0.150 | 0.821 | 0.930 | 0.389 | 0.075 | 0.032 | |
| 2 | 上升段 | 0.973 | 0.978 | 0.973 | 0.006 | 0.005 | 0.006 |
| 下降段 | -0.164 | 0.794 | 0.916 | 0.237 | 0.050 | 0.027 | |
| 3 | 上升段 | 0.963 | 0.894 | 0.963 | 0.013 | 0.039 | 0.013 |
| 下降段 | 0.086 | 0.821 | 0.958 | 0.196 | 0.070 | 0.019 | |
由图11和表4可知,描述钢-ECO混凝土交界面的法向开裂损伤行为时,线性-抛物线模型对试验数据上升段的对比结果明显优于指数型模型,但对试验数据下降段的对比结果来说,线性-抛物线模型的拟合效果非常差,计算值明显偏小,均方误差明显偏大,而指数型模型拟合相对较好。与指数型模型相比,提出模型应用于各试件下降段的均方误差分别减少了57.3%、46.0%和72.9%,显著提高了内聚力模型的精度。因此,本文提出的内聚力模型能更好地表征钢-ECO混凝土交界面法向开裂的损伤行为,具有更高的计算精度。
4 结论
1) 相比其他学者研究的普通钢-混凝土交界面,钢-ECO混凝土交界面的黏结强度、刚度和极限张开位移分别提高了289.3%、368.4%和160.0%,具有更高的强度、刚度和延性性能。
2) 线性-抛物线和指数型内聚力模型拟合试验数据,上升段线性-抛物线内聚力模型拟合效果更好,其变化速率与试验数据基本一致,下降段指数型模型拟合效果更好,但仍存在较大的误差,无法准确描述钢-ECO混凝土交界面法向开裂损伤的萌生与发展。与指数型模型相比,本文提出的内聚力模型应用于各试件下降段的均方误差分别减少了57.3%、46.0%和72.9%,显著提高了内聚力模型的精度。
3) 本文提出的内聚力模型不仅可以简便计算钢-ECO混凝土交界面的黏结强度、刚度和临界断裂能,而且能准确表征钢-ECO混凝土交界面的法向开裂损伤的萌生和发展过程。
黄方林,廖静雯,高英杰等.钢-ECO混凝土交界面力学性能及内聚力模型研究[J].铁道科学与工程学报,2024,21(12):5198-5208.
HUANG Fanglin,LIAO Jingwen,GAO Yingjie,et al.Research on the mechanical properties and cohesive zone model of the steel-ECO concrete interface[J].Journal of Railway Science and Engineering,2024,21(12):5198-5208.

