钢桁系杆拱桥充分发挥拱肋抗压和系杆抗拉的力学特性,在形成自平衡体系的同时具有自重轻、强度大等优点,广泛应用于桥梁建设[1-3]。作为内部高次超静定结构,钢桁拱桥在线形控制方面有着较高的要求,其预拱线形(无应力线形)获取是设计、施工的关键环节。无应力线形设计不合理将导致成桥线形与设计线形不符、结构产生附加应力等问题,甚至直接影响桥梁的正常使用[4-6]。一般地,桥跨结构应设置预拱度以抵消其承受恒载和一半活载产生的挠度[7-8]。从设计线形出发,结合计算预拱度进行起拱设计,是普遍采用的预拱度设置思路。钢桁桥梁的预拱度设置方法主要有几何起拱法、温度法、位移荷载法和无应力起拱法等。几何法[9-10]直接根据桁架杆件间的几何关系建立上弦杆的伸缩量与预拱度的关系,无需对杆件进行内力计算,但仅适用于结构相对简单的钢桁梁桥,且需要反复试算。温度法[11]将杆件的伸缩量等效为温度的变化,从而控制节点位移逼近预拱度,对于超静定结构,采用升降温法进行起拱计算会产生附加内力和支点反力。位移荷载法[12-13]将预拱度等效为输入荷载,输出杆件的伸缩量,达到设置预拱度的目的。无应力状态起拱法[14-15]基于分阶段成型结构力学平衡方程,建立各杆件伸缩量与节点位移间的数学表达式,进而实现桁架结构起拱计算,且不会产生附加应力。总体而言,现有预拱度设置方法虽能获取钢桁拱桥的预拱线形和节点空间位置,但由于其在起拱设计时仅以起拱后的线形与计算预拱度相符为目标,不能保证起拱后的线形经设定荷载作用变形后达到设计线形。因此,这类方法无法获取钢桁拱桥的精准无应力线形。也有部分学者开展了根据设计线形直接计算无应力线形的研究。但启联等[16]基于势能驻值原理建立了结构线形控制方程,以钢桁梁设计目标状态作为输入,直接求解各杆件的无应力长度,进而得到钢桁梁的无应力线形。但该方法未考虑结构几何非线性效应,不适用于大跨度钢桁拱桥。朱勇战[17]以钢桁梁桥桥面坐标为目标线形开展迭代计算,得到杆件长度和拼装坐标,实现桥面成桥线形和内力与设计状态吻合。这种方法可以在一定程度上考虑结构几何非线性,但其迭代目标仅为桥面线形,无法直接获取桁架结构的拼装位置。目前,直接获取大跨钢桁系杆拱桥无应力线形的研究较少。由于成桥水平系杆力对钢桁系杆拱桥变形量计算的影响不可忽略[18-20],当设计线形确定时,水平系杆力的取值将直接影响系杆拱桥拱肋无应力线形的计算结果。本文针对钢桁系杆拱桥无应力线形获取问题,考虑平衡拱脚处水平推力这一水平系杆力取值目标[21],开展基于多目标控制的钢桁系杆拱桥无应力状态计算研究。以系杆拱桥在无应力状态下经荷载作用变形后得到的空间位置信息与设计值之间的差值和拱脚位移均趋近于0为迭代计算目标,将设计线形作为初始无应力状态输入,计算其经荷载作用变形后的空间位置信息与设计参数的差异和拱脚位移,根据计算结果同步更新拱肋无应力线形和水平系杆无应力长度,进行多次计算直至满足迭代目标,从而得到钢桁拱桥精准无应力线形和合理成桥水平系杆力。该方法可直接精准获取钢桁系杆拱桥无应力线形和节点空间位置,并且充分考虑结构几何非线性,适用于大跨度钢桁系杆拱桥结构精准线形设计。结合某大跨钢桁系杆拱桥设计参数,计算其无应力状态,验证本文方法的可行性。
1 系杆拱桥无应力状态特征
一般地,系杆拱桥上部结构主要承重构件包括拱肋、水平柔性系杆索、主梁,如图1所示。其拱肋结构以节段拼装施工为主要施工方式,准确的节段制作(节点空间位置、构件尺寸等信息)是确保桥梁精准施工的关键环节。各节段制作则依据无应力状态下结构几何信息而定,无应力状态下桥梁结构经体系转换、荷载作用后转化为成桥状态,其桥梁线形、空间位置、结构内力均达到成桥状态设计值。对于系杆拱桥,拱肋和水平柔性系杆索作为前期承力构件,主要承受恒载和活荷载作用;主梁作为后期储备受力构件,在成桥之前承担的荷载作用较少,其无应力状态下尺寸信息与成桥状态下尺寸差异不大。
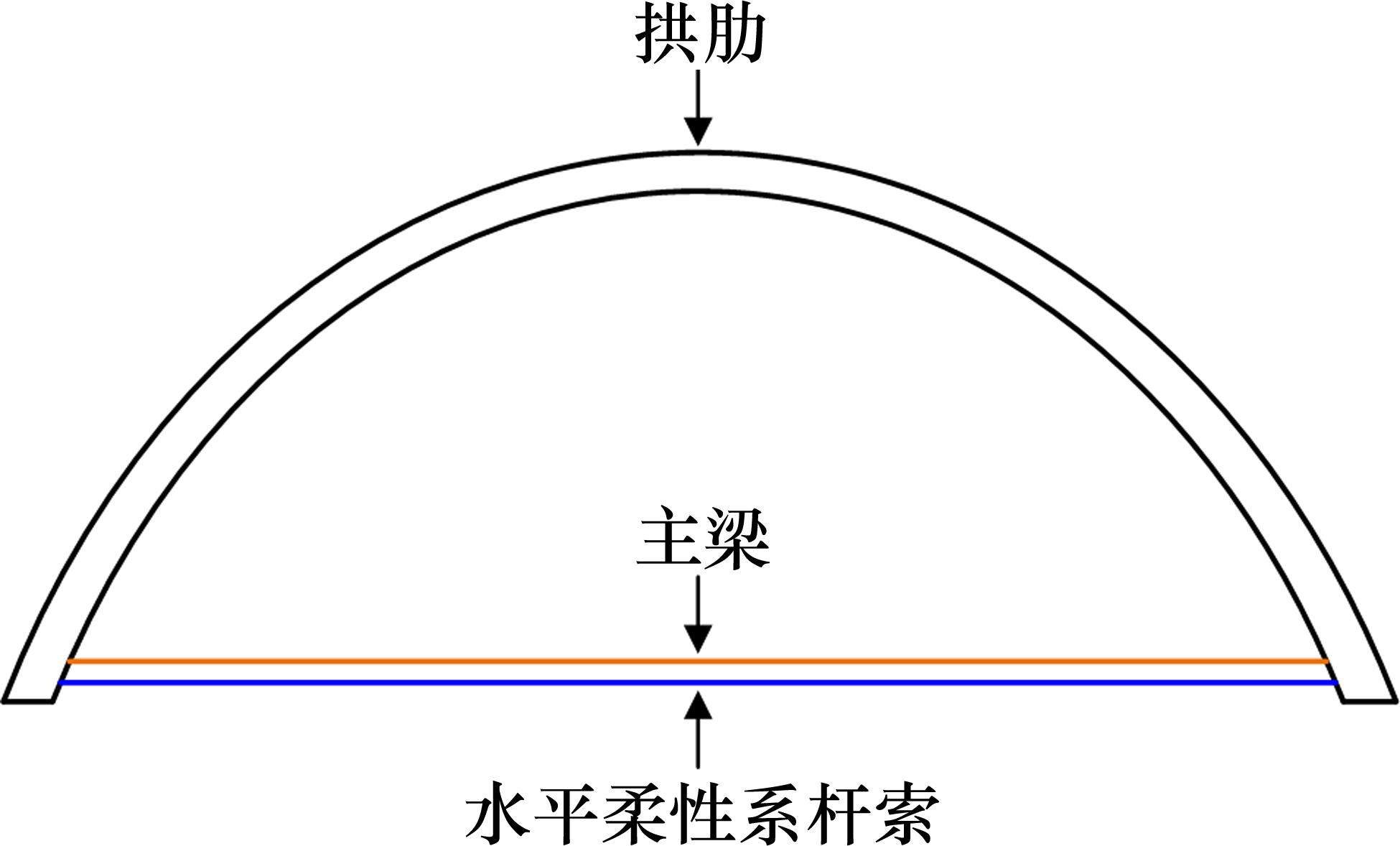
拱肋构件受力复杂,除产生拉压变形外,还承受横向荷载和弯矩导致的弯曲变形,其无应力状态下节点空间位置均与成桥状态下位置存在偏差;水平索作为主要承拉构件,其无应力状态下长度小于成桥状态长度。不同构件在无应力状态与受力状态下几何尺寸信息转换计算关系式有所不同。
针对拱肋构件,将其视为梁单元(如图2所示),则其无应力长度l0为单元处于无应力状态时的节点轴向距离,无应力曲率ki0,kj0为单元无应力时的挠度曲线曲率[6]。具体计算如下式:
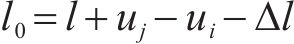
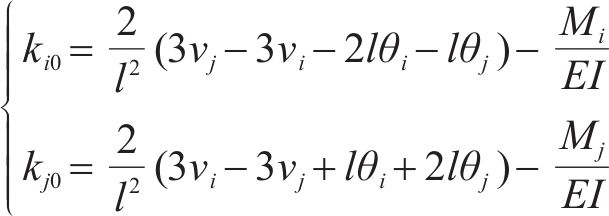
式中:l为单元的初始长度;Δl为最终状态单元的轴向变形;ui、uj分别为单元i、j端的轴向位移;vi、vj分别为单元i、j端的横向位移;θi、θj分别为单元i、j端的转角位移;Mi、Mj分别为单元i、j端的弯矩。
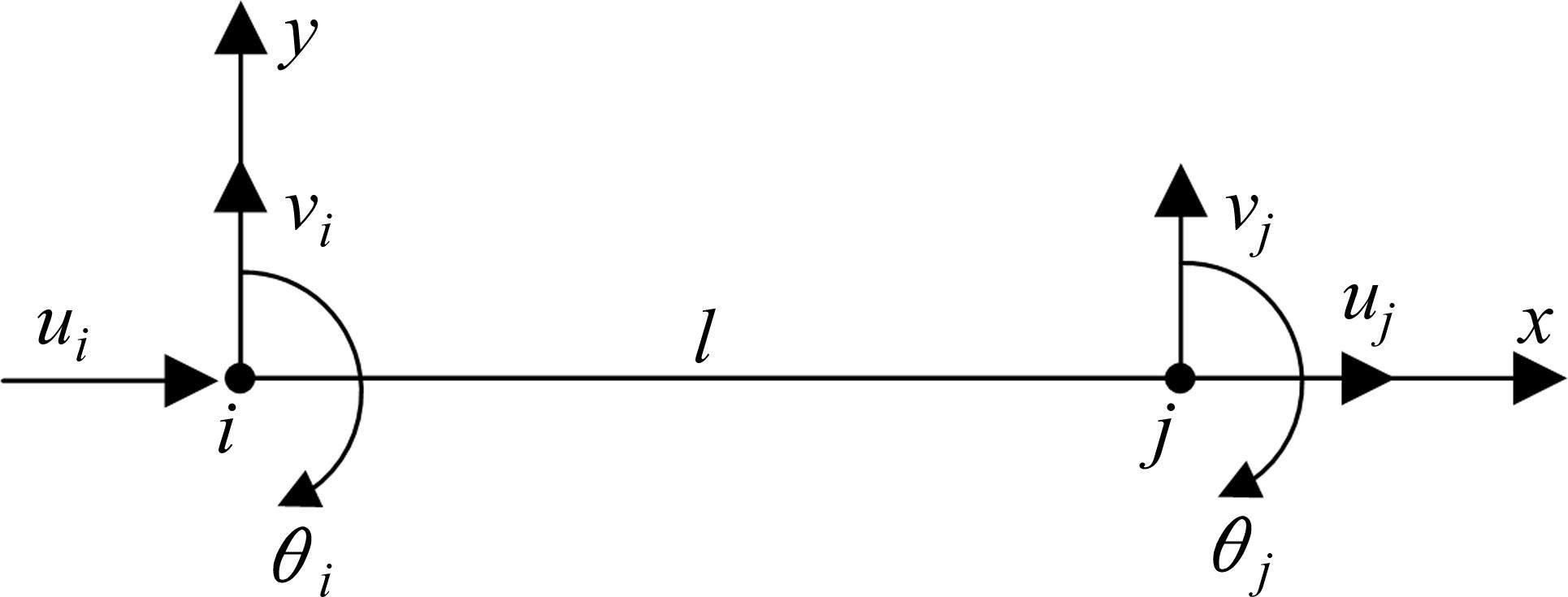
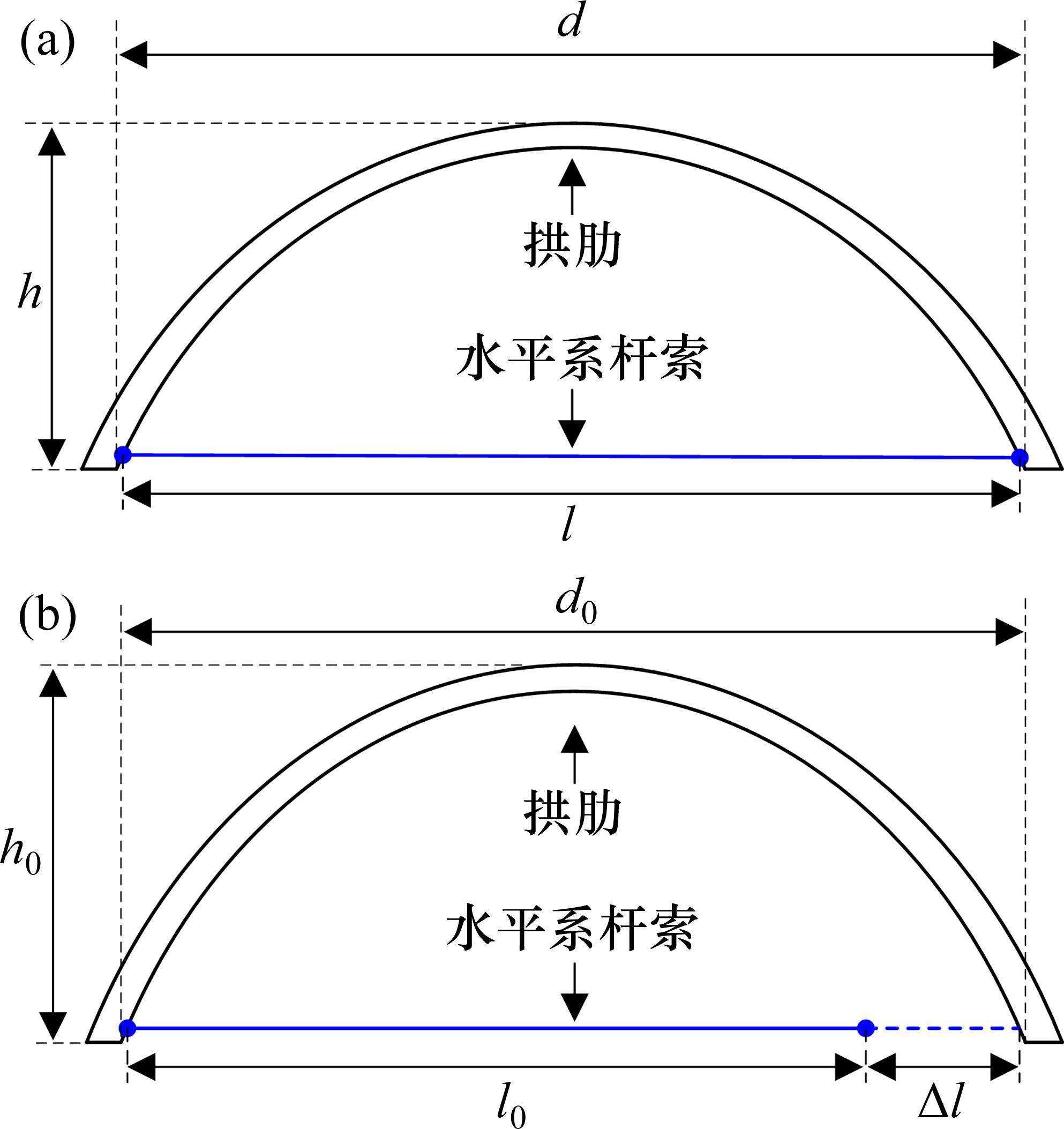
针对水平系杆索构件,假定其在荷载作用下的长度为L,弹性模量为E,截面面积为A,索力为T,则其无应力长度L0可表示为:
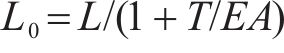
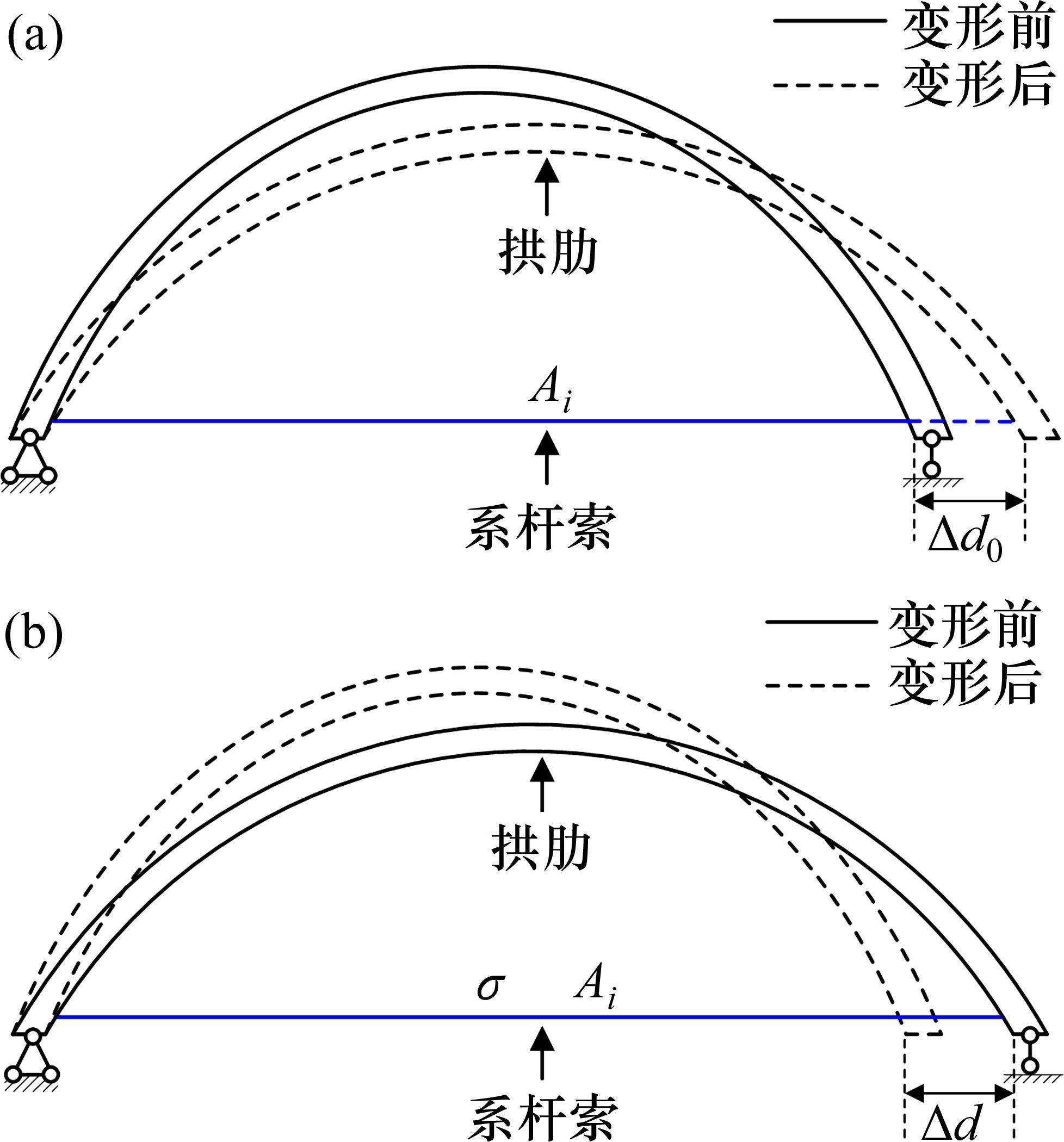
基于上述分析,对于系杆拱桥,其中成桥状态和无应力状态下主拱高度h、h0和跨度l、l0均不同,其中主拱、水平柔性索构件在2种状态下的对比如图3(a)和图3(b)所示。
值得指出的是,当成桥状态跨度与无应力状态跨度相等(d=d0)时,水平索无应力长度小于其成桥状态下长度(l0<l),二者差值∆l取决于成桥状态下系杆索力。本文针对钢桁系杆拱桥,基于其成桥状态空间位置信息,通过反演迭代计算钢桁系杆拱桥拱肋无应力状态下线形、节点空间位置以及水平系杆索成桥索力(无应力长度)。
2 无应力状态空间位置精准计算方法
2.1 成桥系杆索力
成桥状态下水平系杆索力是影响结构体系受力及无应力状态信息计算的关键因素,在拱肋-系杆体系中,柔性系杆的系杆力用来抵消拱肋承载时拱脚处产生的水平推力,让拱肋-系杆形成自锚体系[22],从而实现原地起拱。水平系杆力用于平衡恒载、1/2活载作用下拱脚处水平推力和水平位移量,基于该思路计算成桥状态下水平系杆索力值。
假定系杆拱桥处于简支状态,其在恒载、1/2活载作用下拱脚处产生的水平位移量为Δd0,如图4(a)所示;水平系杆拉力作用于拱脚时产生的反向位移量记为Δd,如图4(b)所示。令Δd=Δd0,两者相互抵消,使拱脚的最终水平位移为0。由于水平系杆均是截面形式固定的索结构,可以采用应力形式量化其受力,假定成桥状态下系杆索拉应力相等均为σ,系杆第i束索的截面面积为Ai,如图4所示。结合影响矩阵法建立水平系杆拉应力与结构在恒载、1/2活载作用下拱脚位移的对应关系如下:
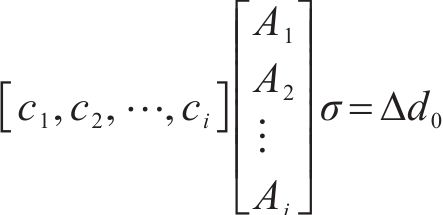
式中:ci为第i束水平系杆力变化量对拱脚水平位移的影响系数,由拱肋刚度决定。令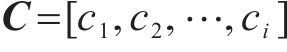
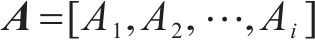
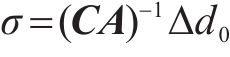
由上式可知,拱肋结构在恒载和1/2活载作用下的拱脚水平位移量Δd0决定系杆力设置值。充分考虑系杆拱桥结构几何非线性和成桥过程中可能存在的体系转换等特点,为较好地抵消拱肋结构在竖向荷载作用下的水平位移量,需对成桥状态下系杆力取值进行精准计算。
2.2 基于“双目标”控制的无应力状态空间位置迭代算法
开展钢桁系杆拱桥无应力状态几何信息迭代计算时,首先假设初始无应力状态并逐次更新,直至无应力状态经历荷载施加和变形后逼近设计成桥状态。值得指出的是,本文方法同时以变形后线形空间位置与设计位置间的差异和拱脚水平位移均趋近于0(Δd=Δd0)作为迭代计算目标,即“双目标”控制。
针对拱肋结构无应力状态空间位置和系杆索成桥应力水平(或无应力长度)进行精准迭代计算,主要步骤及思路如下。
1) 初始无应力状态信息选定,一般以设计成桥参数作初始无应力状态信息;
2) 变形量计算,依次计算“拱肋-系杆”、“拱肋-主梁-系杆”等结构体系在分级荷载作用下各节点空间变位信息和拱脚水平位移量;
3) 更新无应力状态信息,获取结构变形后空间位置信息与设计位置信息的差值,将空间信息差反向叠加至上述无应力状态位置信息,并根据拱脚位移,结合式(5)计算系杆索初始应力水平,从而实现一次无应力状态更新;
4) 以更新后的无应力状态信息为基准,重复步骤2、步骤3进行有限次数迭代计算,直至无应力状态下结构经荷载施加和变形后逼近设计成桥状态,且拱脚水平位移量趋近于0。
值得指出的是,钢桁系杆拱桥各构件从无应力状态经拼装施工至成桥状态时,荷载分阶段施加于不同结构体系上,因此系杆拱桥无应力状态下结构信息计算还需考虑实际施工工序中存在的体系转换特征。
假定设计成桥状态空间位置信息为Φ0,第i次迭代计算得到的变形后线形空间位置信息为Φi,xin和yin为第i次迭代计算得到的变形后线形中第n个节点的横坐标和纵坐标,Φ0和Φi可由节点坐标表示:
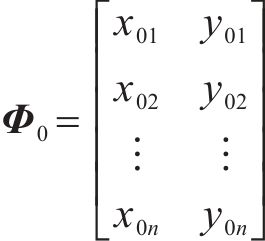
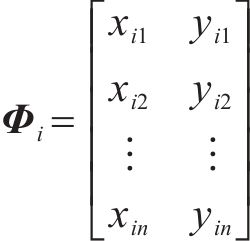
则第i次迭代计算的变形后线形与设计线形空间位置偏差ΔΦi可表示为:
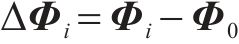
随着迭代次数的增加,无应力线形和水平柔性系杆成桥应力逐渐维持不变,同时设定荷载和系杆力共同作用下的变形后线形与设计线形空间位置偏差和拱脚水平位移均趋近于零,若空间位置偏差和位移小于容许范围则停止迭代。
假定第i次迭代计算的线形空间位置信息差的二范数为Ri,如式(8),拱脚水平位移量为di。
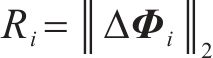
结合计算经验,当Ri<10-4 m且di<10-5 m时,停止迭代。此次计算采用的无应力线形即可作为钢桁系杆拱桥精准无应力线形,算得的成桥水平系杆力即为合理成桥系杆力。
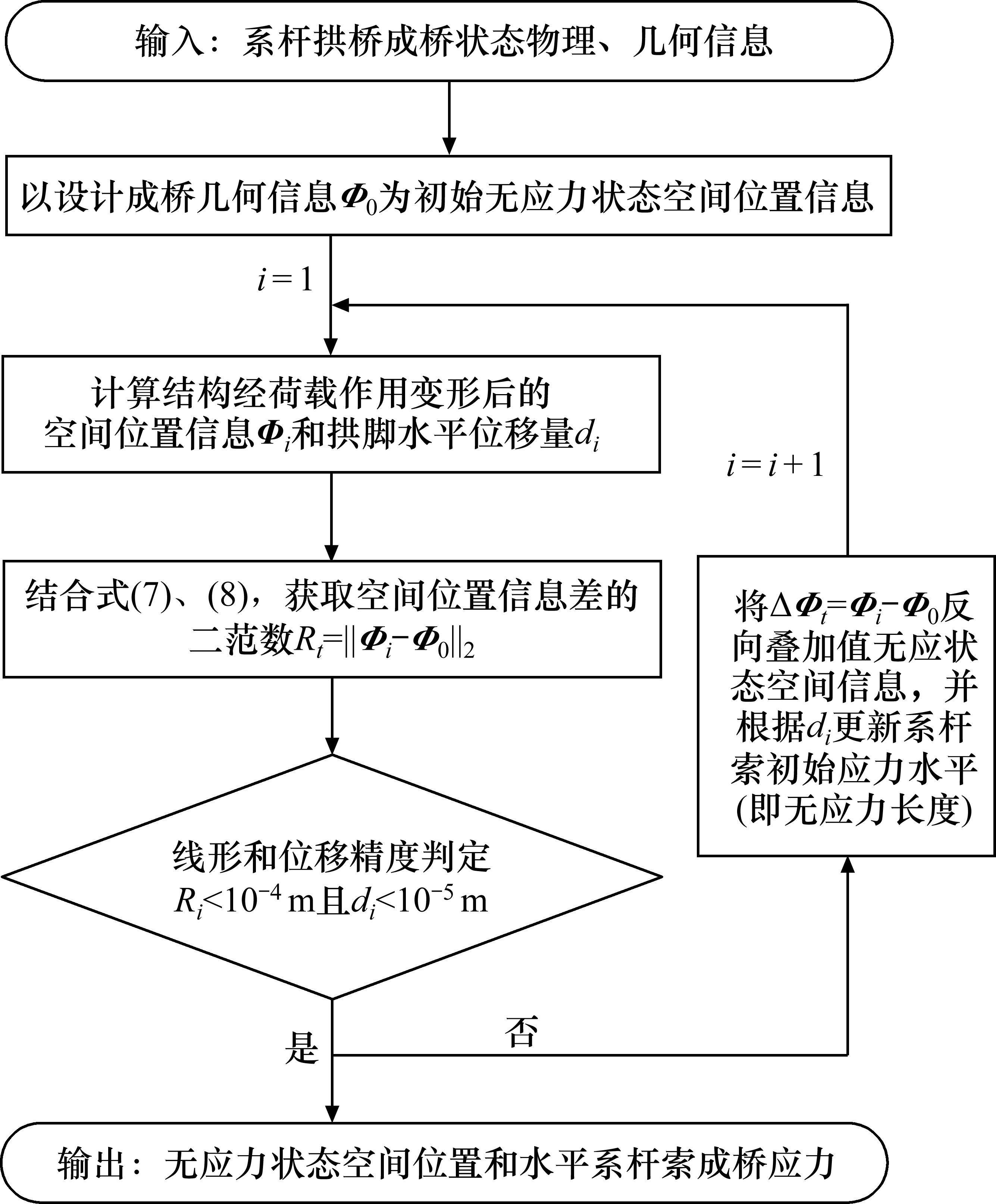
上述双目标有限迭代算法可以实现系杆拱桥无应力状态空间位置信息和合理成桥系杆力精准获取,考虑了结构几何非线性效应的影响,适用于大跨钢桁系杆拱桥。同时该方法在求解结构几何非线性不明显的中、小跨钢桁桥梁的无应力线形时,一次计算即可得到精准无应力线形,无需迭代。基于“双目标”控制的无应力状态空间位置和系杆索成桥应力水平(无应力长度)迭代计算流程如图5。
3 数值计算研究
为验证本文多目标控制的系杆拱桥无应力空间位置计算方法的正确性及可行性,结合某大跨钢桁系杆拱桥设计参数,基于Matlab数值计算平台,开展基于多目标控制的系杆拱桥无应力状态计算研究。该桥为(70+180+180+70) m四跨连续中承飞燕式钢桁拱桥,主跨2×180 m,主拱矢高36 m,主梁采用叠合梁结构,全桥横桥向采用双片钢拱架。约束体系采用四跨连续支撑体系,中墩设置固定支座,其余各墩均设置单向或多向活动支座,桥型布置如图6。

3.1 模型参数特征
出于简化计算的目的,仅采用单侧钢桁架进行有限元建模,忽略风撑、桥面纵横梁以及吊杆。建模时,上、下弦杆、腹杆以及主梁均视为梁单元,水平柔性系杆视为杆单元,全模型一共342个梁单元和2个杆单元,有限元建模流程参考文献[23]。水平系杆具体参数见表1。
水平 系杆 | 弹性模量/MPa | 截面面积/mm2 | 抗拉刚度/ 108 N |
|---|---|---|---|
| 柔性系杆X1 | 195 000 | 20 720 | 40.40 |
| 柔性系杆X2 | 195 000 | 17 360 | 33.85 |
| 主梁 | 206 000 | 210 000 | 432.6 |
该桥采用“拱梁同步”的施工方式,拱肋架设过程中,桥面钢梁同步架设,先拱肋合拢,然后安装柔性系杆、安装桥面合拢段外的混凝土桥面板,最后进行主梁和桥面系钢结构合拢。其施工工序具有明显的结构体系转换特征,如图7所示,主梁不参与平衡一期恒载作用下拱肋产生的水平推力。因此,开展无应力状态精准迭代计算时,应将荷载分阶段施加在不同的结构体系上,具体见表2。值得指出的是,吊杆、主梁自重等一期恒载,以及作用在主梁上的二期恒载和1/2活载,均被等效为吊杆力作用于拱肋对应节点上。

| 结构体系 | 拱肋-系杆 | 拱肋-主梁-系杆 |
|---|---|---|
| 荷载组合 | 一期恒载(桥梁钢结构和混凝土桥面板自重) | 二期恒载(桥面铺装和附属设施自重)和1/2活载 (汽车荷载、人群荷载和非机动车荷载) |
3.2 有限元计算结果
结合桥梁有限元模型和“双目标”控制的有限迭代算法,采用荷载分阶段施加思路,以设计状态信息为基准,计算系杆拱桥精准无应力状态。本文方法可同步获取桥梁无应力线形节点空间位置和合理成桥水平系杆力,避免传统预拱度设置方法中复杂的起拱设计,算得的右侧拱肋无应力线形及节点空间位置如图8,对应成桥状态系杆索拉应力为465 MPa。
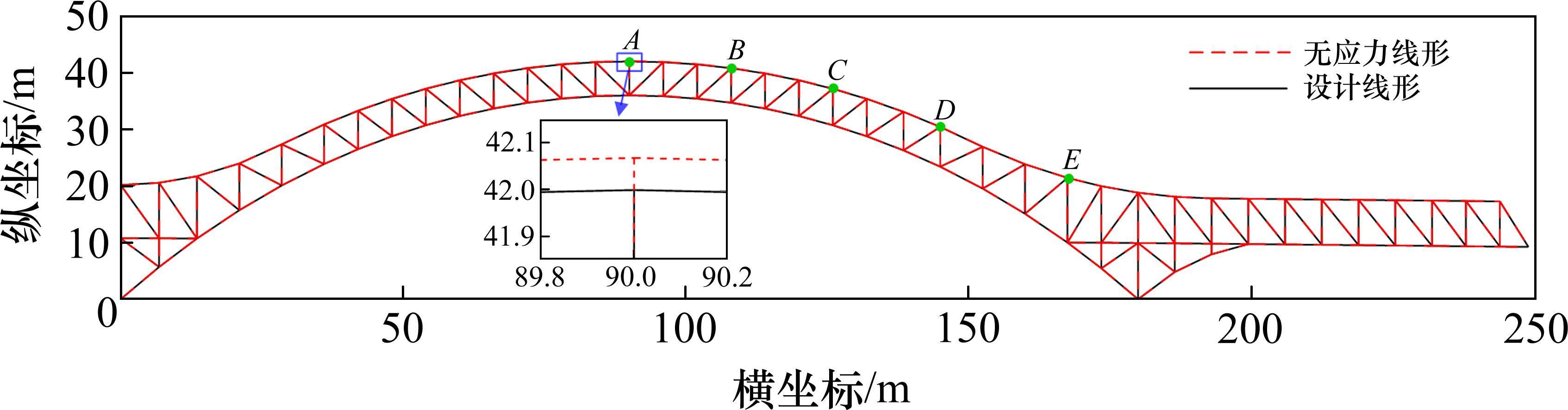
作为对比,根据设计思路进行预拱度计算,通过对当前施工阶段对应的结构体系施加本阶段的荷载(包括恒载荷载和临时荷载)计算变形量,根据施工流程更新结构体系和荷载,将所有施工工序对应的变形量叠加从而得到预拱度。以右侧主拱为例,本文上弦杆预拱度计算结果与设计采用值对比如图9所示,可以看出二者预拱度计算结果比较接近,证明本文方法的正确性。
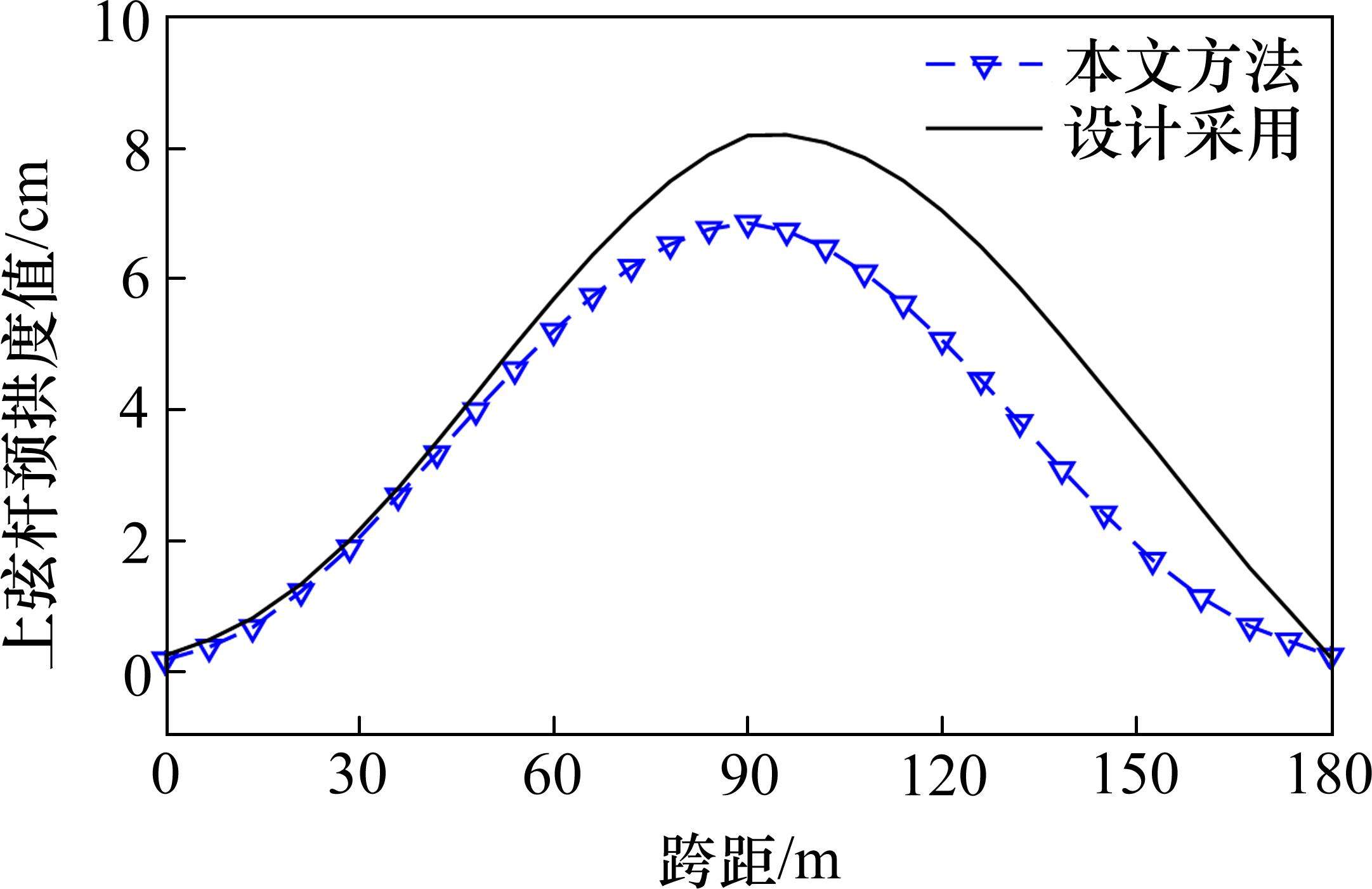
上弦杆预拱度幅值、拱脚水平位移量和成桥水平系杆力的计算结果与设计值采用值对比见表3。对比分析可知,本文方法拱脚水平位移的计算结果比设计值更优,满足原地起拱这一成桥系杆力取值目标。
| 计算结果 | 系杆X1成桥内力/kN | 系杆X2成桥内力/kN | 上弦杆预拱度峰值/cm | 拱脚水平位移量/cm |
|---|---|---|---|---|
| 本文方法 | 9 634 | 8 076 | 6.9 | 3.1×10-5 |
| 设计采用值 | 10 780 | 9 800 | 8.2 | 1.2 |
值得指出的是,设计方法根据桥跨结构的最大挠度计算值,采用经验曲线法[24]进行预拱度的分配计算,无法保证预拱度计算精度。而本文所提出的基于“双目标”控制的有限迭代方法可直接获取拱肋精准无应力空间位置信息(即全部节点预拱度),能指导拱肋构件的制造,并且得到的合理成桥水平系杆力可为系杆索张拉提供参考。
3.3 结果评价
系杆拱桥的精准无应力状态应满足:其经荷载作用后得到的最终空间位置信息与设计空间位置信息吻合,且拱脚位移为0。本文基于“双目标”控制的无应力状态迭代算法,每次迭代均更新结构无应力状态信息,逐步减小变形后线形空间位置与设计位置间的差异和拱脚位移,从而得到结构精准无应力状态。
选取桥梁右侧拱肋的若干节点,记为A、B、C、D、E,其具体位置见图8。这些节点的预拱度值以及拱脚水平位移量di随迭代次数的变化如图10所示。从图中可以看出,随着迭代次数的增加,各拱肋节点的预拱度值渐趋稳定,拱脚水平位移逐渐趋近于0,表明计算达到收敛状态。
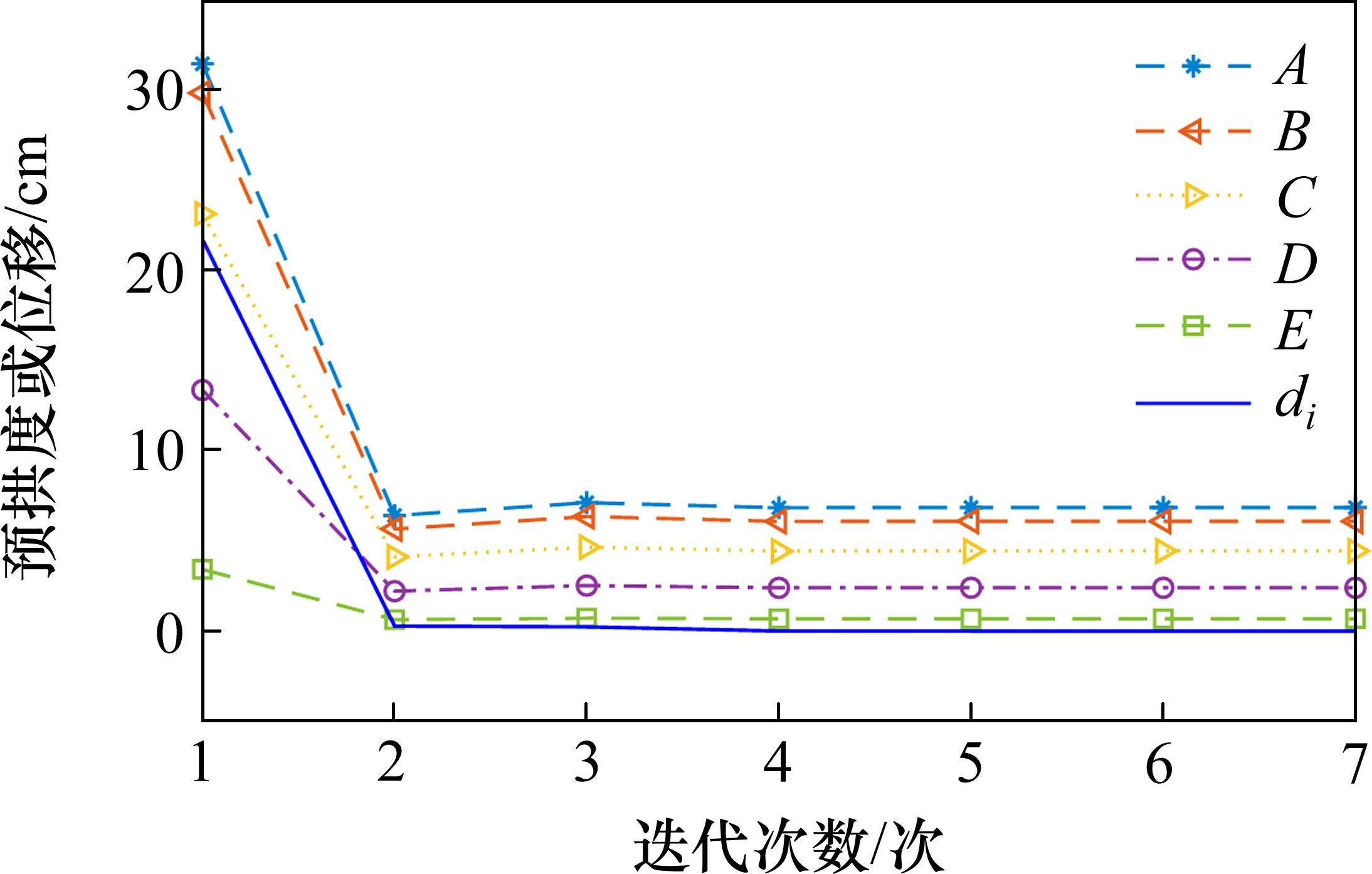
为了更直观地表示无应力空间位置信息计算精度,可将拱肋线形空间位置信息差的二范数Ri,表达式见式(8),作为无应力状态信息精准度指标,其随迭代次数的变化如图11所示。可以看出,精准度指标Ri经过数次迭代计算后趋近于0,表明本文基于双目标迭代的无应力状态计算方法的高精准性,仅需少量迭代计算即可得到大跨钢桁系杆拱桥精准无应力状态。
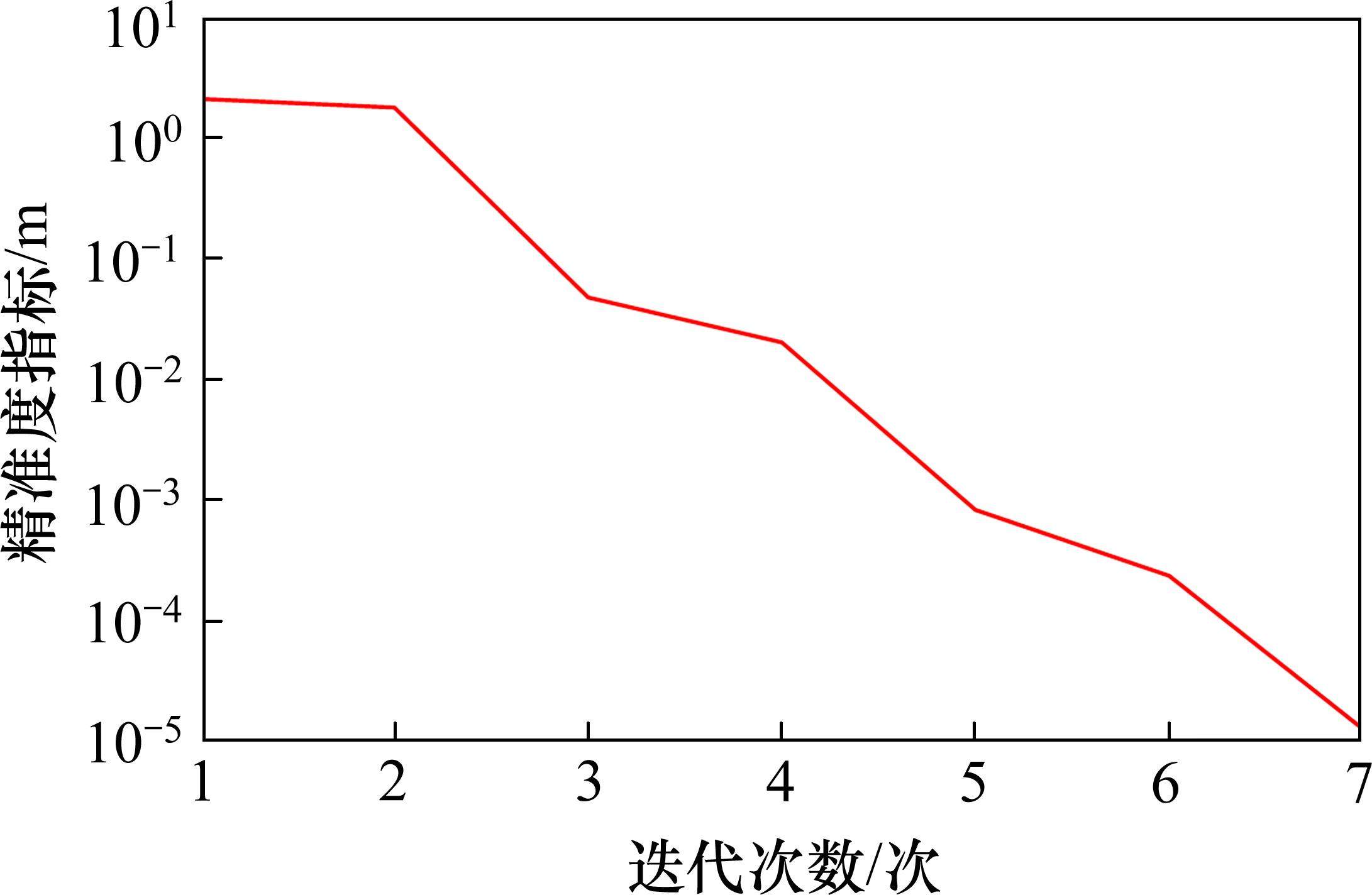
既有设计思路通常将预拱度计算和水平系杆力设定分开考虑,即:先确定钢桁系杆拱桥成桥系杆力,再计算拱肋预拱度和拱脚水平位移。由于水平系杆力取值对拱脚位移计算有较大影响,因此该思路无法确保系杆拱桥经设定荷载和系杆力共同作用变形后拱脚不产生位移。本文方法将无应力状态和成桥状态的拱脚位置一致作为目标之一,同步迭代拱肋无应力空间位置信息和系杆索初始应力(无应力长度),从而得到钢桁系杆拱桥精准无应力线形节点空间位置和合理成桥水平系杆力,确保拱脚不产生位移。
4 结论
1) 基于多目标控制的钢桁系杆拱桥无应力状态计算方法,充分考虑系杆拱桥无应力状态特征和成桥水平系杆力取值目标,经过少量迭代计算即可得到拱肋无应力状态空间位置信息和合理成桥系杆索力(无应力长度)。
2) 本文方法充分考虑结构体系转换与荷载施加特征,计算思路清晰,可直接获取无应力线形节点空间位置,得到拱肋全部节点预拱度和精准制造线形,避开了传统预拱度设置方法中的起拱设计。
3) 结合某大跨钢桁系杆拱桥设计参数进行数值计算,验证了本文基于多目标控制的系杆拱桥无应力状态计算方法的可行性与正确性。该方法在使成桥线形与设计线形精准相符的同时,保证了无应力线形和成桥线形拱脚位置基本一致。
王宁波,范治豪,常柱刚.基于多目标控制的钢桁系杆拱桥无应力状态计算研究[J].铁道科学与工程学报,2025,22(02):748-756.
WANG Ningbo,FAN Zhihao,CHANG Zhugang.Research on stress-free state calculation of steel truss tied arch bridge based on multi-objective control[J].Journal of Railway Science and Engineering,2025,22(02):748-756.

