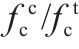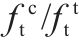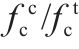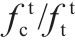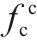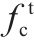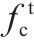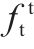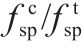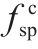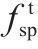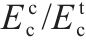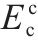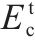地聚物混凝土是由胶凝材料、骨料和碱激发剂混合制备而成,配置地聚物混凝土的胶凝材料通常为粉煤灰、矿渣等工业固废或偏高岭土等自然矿物,由于其制备过程不需经过煅烧,大大减少了环境污染和CO2的排放,符合国家“双碳”战略,因此具有优越的发展前景[1]。国内外学者对地聚物混凝土的基本力学性能进行了大量研究,主要集中在轴心抗压强度[2-7]、劈裂抗拉强度[8-15]、弹性模量[16-22]等方面,轴心抗拉强度虽也有一定的研究,但成果较少[23-27]。CUI等[4]、VERMA等[8]分别研究了粉煤灰基地聚物混凝土、高炉矿渣和粉煤灰基地聚物混凝土的力学性能相关性,均给出了劈裂抗拉强度、弹性模量和轴心抗压强度的换算关系。MOHAMMED等[28]提出了劈裂拉伸强度、抗弯强度、弹性模量、泊松比和轴心受压峰值应变与轴心抗压强度的换算关系。CONG等[26]、TALHA等[29]对Collins提出的高强混凝土本构模型进行修正,分别提出了高炉矿渣和粉煤灰基地聚物混凝土、粉煤灰基地聚物混凝土的轴心受压本构关系。NGUYEN等[16]基于弹性理论,利用弹性模量、轴心受压应力-应变关系、泊松比及劈裂抗拉强度提出了粉煤灰基地聚物钢筋混凝土梁抗弯承载力公式,并基于普通混凝土本构关系建立了相应有限元模型,发现有限元模拟结果优于弹性理论计算结果。综上所述:1) 影响地聚物混凝土力学性能的因素较多,包括胶凝材料种类、碱激发剂种类、比例及浓度、养护温度等,导致地聚物混凝土力学性能的离散性较大,学者们基于小样本统计分析提出的基本力学性能计算公式适用性较局限;2) 现有研究成果主要集中在轴心抗压强度、劈裂抗拉强度和弹性模量统一计算公式,而对于轴心抗拉强度、轴心受压峰值应变和轴心受拉峰值应变等统一计算公式研究较少;3) 现有地聚物混凝土单轴受力本构关系的研究虽然取得了一定的成果,形成了各式各样的本构关系模型,但多数研究并未给出其三轴受力的本构关系模型,也未将本构关系应用至相应混凝土结构非线性有限元分析中。课题组前期提出了适用于多类混凝土的损伤比强度理论[30],形成了相应的约束混凝土塑性-损伤模型,并将其应用至相应结构非线性有限元分析中,但地聚物混凝土的约束三轴塑性-损伤模型尚未提出。为了便于地聚物混凝土基本力学性能计算及结构非线性有限元分析,拟开展工作如下:1) 提出地聚物混凝土的轴心抗压(拉)强度、劈裂抗拉强度、弹性模量和轴心受压(拉)峰值应变等力学性能指标统一计算公式;2) 建立地聚物混凝土单轴拉(压)应力-应变全曲线,提出地聚物混凝土损伤比强度理论,建议膨胀角、拉压子午线强度比值和二轴等压与单轴抗压强度比值等三轴参数取值,形成约束地聚物混凝土三轴塑性-损伤模型;3) 通过ABAQUS有限元软件进行基于约束地聚物混凝土塑性-损伤模型的钢筋地聚物混凝土简支梁四点弯曲加载、钢管地聚物混凝土短柱轴向压缩加载及钢筋地聚物混凝土柱拟静力加载等结构非线性分析,验证该本构模型的有效性。
1 地聚物混凝土力学性能指标
1.1 尺寸换算系数
石晓贝[31]研究表明地聚物混凝土的尺寸效应趋势不同于普通混凝土,由于地聚物混凝土会泛碱,导致地聚物试块尺寸越小,强度越小。但刘杉[21]研究表明地聚物混凝土的尺寸效应趋势和普通混凝土一致。由于现有文献中关于地聚物混凝土的尺寸效应研究较少,且存在观点相左现象,故根据现行规范GB/T-50081―2019[32]中的规定,暂时取地聚物混凝土的立方体抗压强度(fcu)和边长为100 mm的立方体抗压强度(fcu,100)的比值即fcu/fcu,100为0.95,下文参考数据中涉及尺寸效应均采用此系数。
1.2 轴心抗压强度
图1为国内外35组地聚物混凝土轴心抗压强度(fc)和相应立方体抗压强度的关系。由图1可见,地聚物混凝土的轴心抗压强度和立方体抗压强度基本呈现为线性相关。
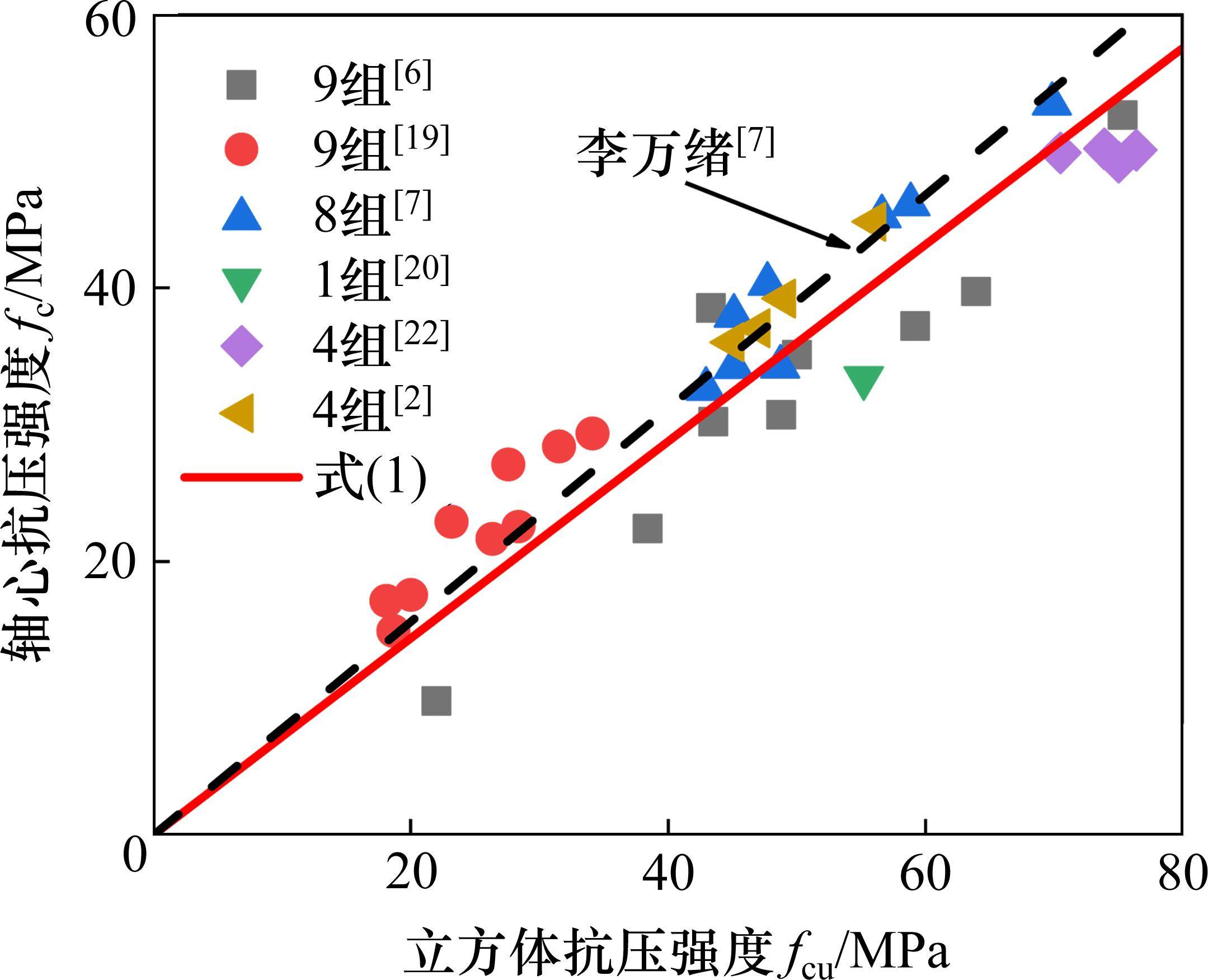
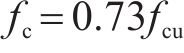
轴心抗压强度和轴心抗拉强度计算结果特征值见表1。由图1和表1可见,采用李万绪[7]公式得到的计算结果要大于实测结果,且其标准差要大于公式(1);采用公式(1)得到的计算结果更为接近轴心抗压强度实测值,且计算结果偏安全。
1.3 轴心抗拉强度
基于国内外文献实测数据分析,提出了地聚物混凝土轴心抗拉强度(ft)统一计算公式:
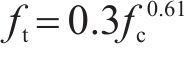
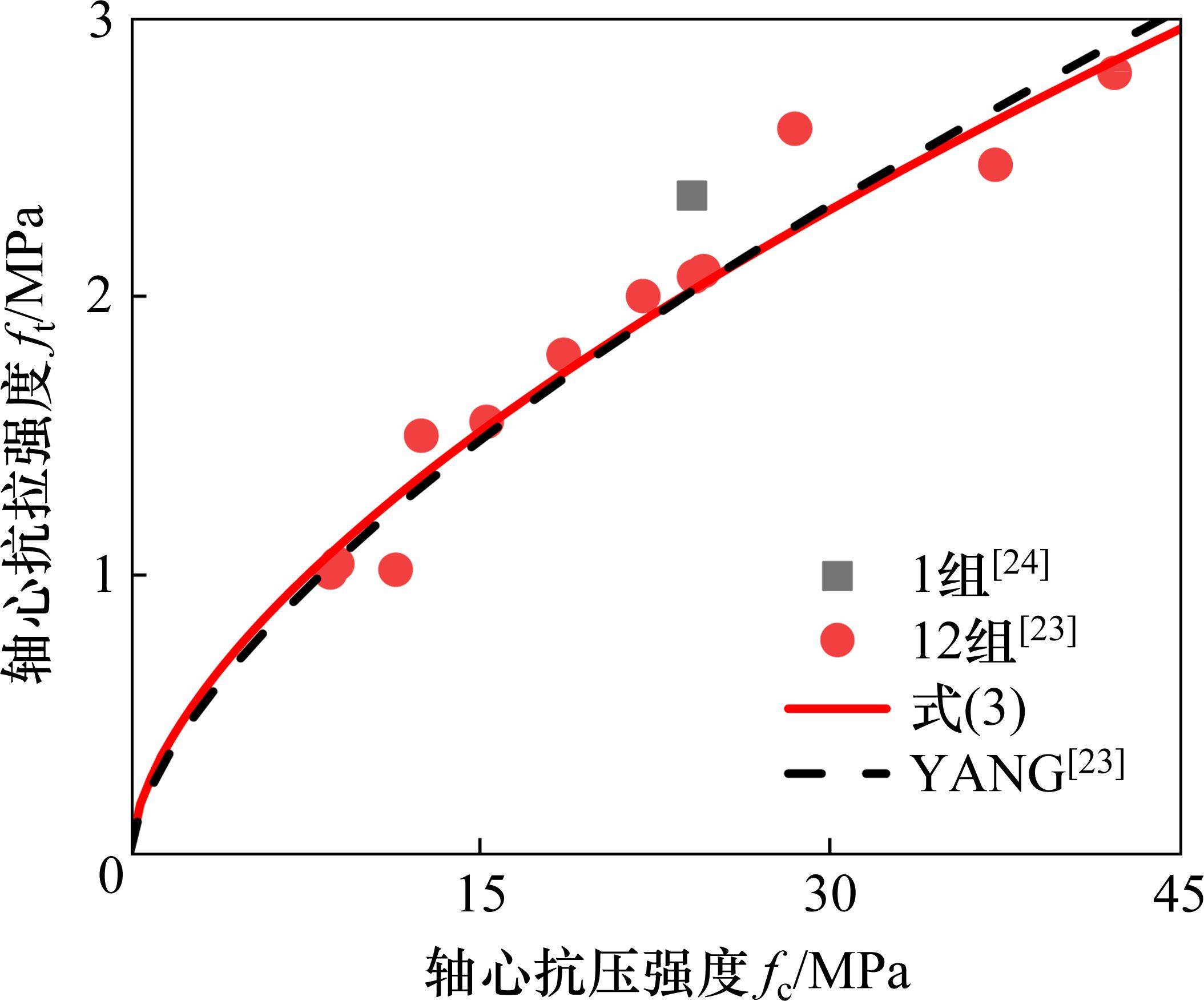
图2为地聚物混凝土轴心抗拉强度和轴心抗压强度的关系图。由图2和表1可见,本文提出的轴心抗拉强度统一计算公式计算值以及YANG等[23]的计算方法均能较好地预测地聚物混凝土的轴心抗拉强度。
将式(1)代入式(2),则地聚物混凝土轴心抗拉强度和立方体抗压强度的关系式为:
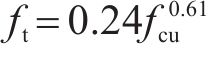
1.4 劈裂抗拉强度
地聚物混凝土劈裂抗拉强度和轴心抗压强度的关系如图3所示。基于图3所示的大量国内外文献数据分析,提出了地聚物混凝土劈裂抗拉强度统一计算公式:
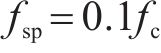
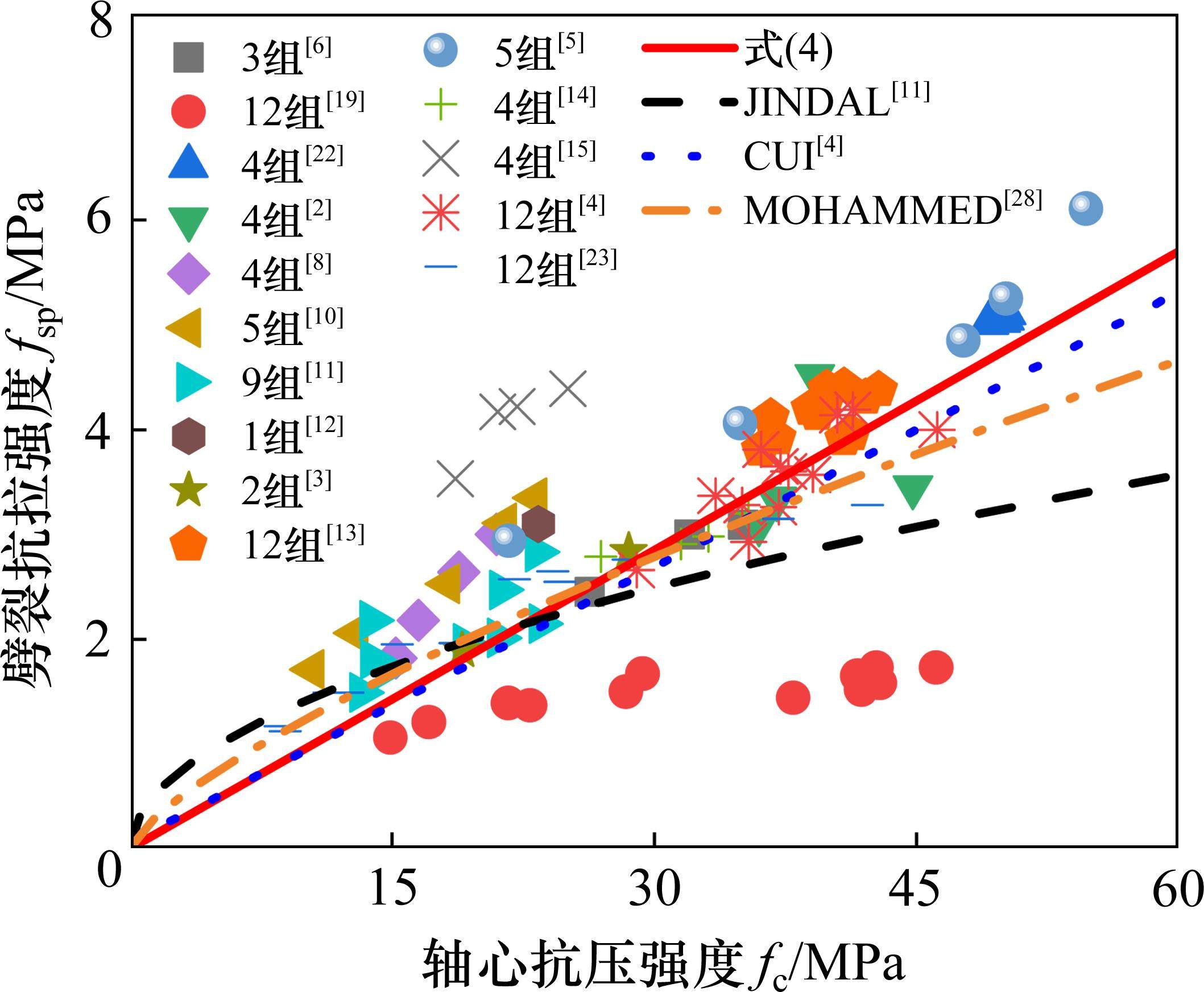
表2为劈裂抗拉强度计算结果特征值。由表2和图3可见,JINDAL等[11]的劈裂抗拉强度公式计算结果相对实测数据偏小,而CUI[4]公式、MOHAMMED[28]公式以及公式(4)的计算结果和实测数据均较为吻合,但实测数据的离散性较大。提出的劈裂抗拉强度计算公式(4)较为简洁且与公式(1)形式一致。
将式(1)代入式(4)中,得到地聚物混凝土劈裂抗拉强度和立方体抗压强度关系式:
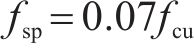
1.5 弹性模量
MOHAMMED等[28]发现地聚物混凝土的弹性模量(Ec)和轴心抗压强度相关,但通过两者拟合得到的计算公式相关性较差,而引入密度之后得到的计算公式相关性较好。图4为地聚物混凝土弹性模量与密度和轴心抗压强度的关系。基于图4文献相关实测数据,提出了地聚物混凝土弹性模量的统一计算公式:
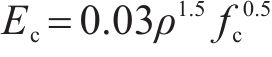
式中:Ec为地聚物混凝土弹性模量,MPa;ρ为地聚物混凝土密度,kg/m3。
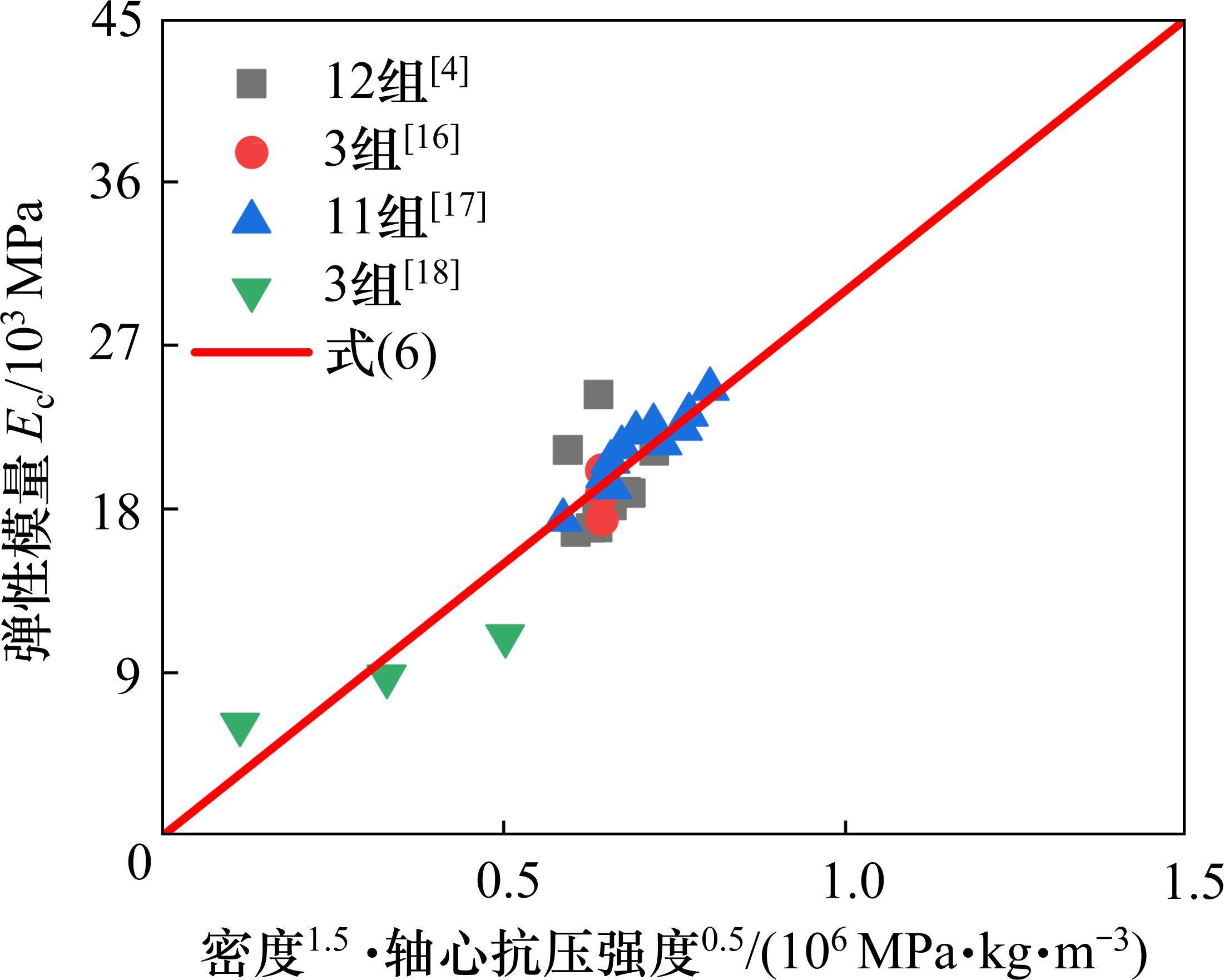
表3为地聚物混凝土弹性模量计算结果特征值。由图4和表3可见,提出的弹性模量统一计算公式结果和试验数据吻合良好;CUI[4]、NATH[17]弹性模量计算公式的计算结果和试验数据也较为吻合,但标准差和变异系数更大;MOHAMMED[28]的公式则高估了地聚物混凝土的弹性模量。
将式(1)代入式(6)得到地聚物混凝土弹性模量和立方体抗压强度的关系:
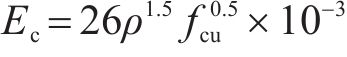
1.6 轴心受压峰值应变
图5为地聚物混凝土轴心受压峰值应变(εc)和轴心抗压强度的关系。基于国内外文献[20, 23, 25-27, 29]试验数据,提出了地聚物混凝土轴心受压峰值应变统一计算公式:
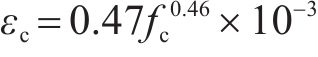
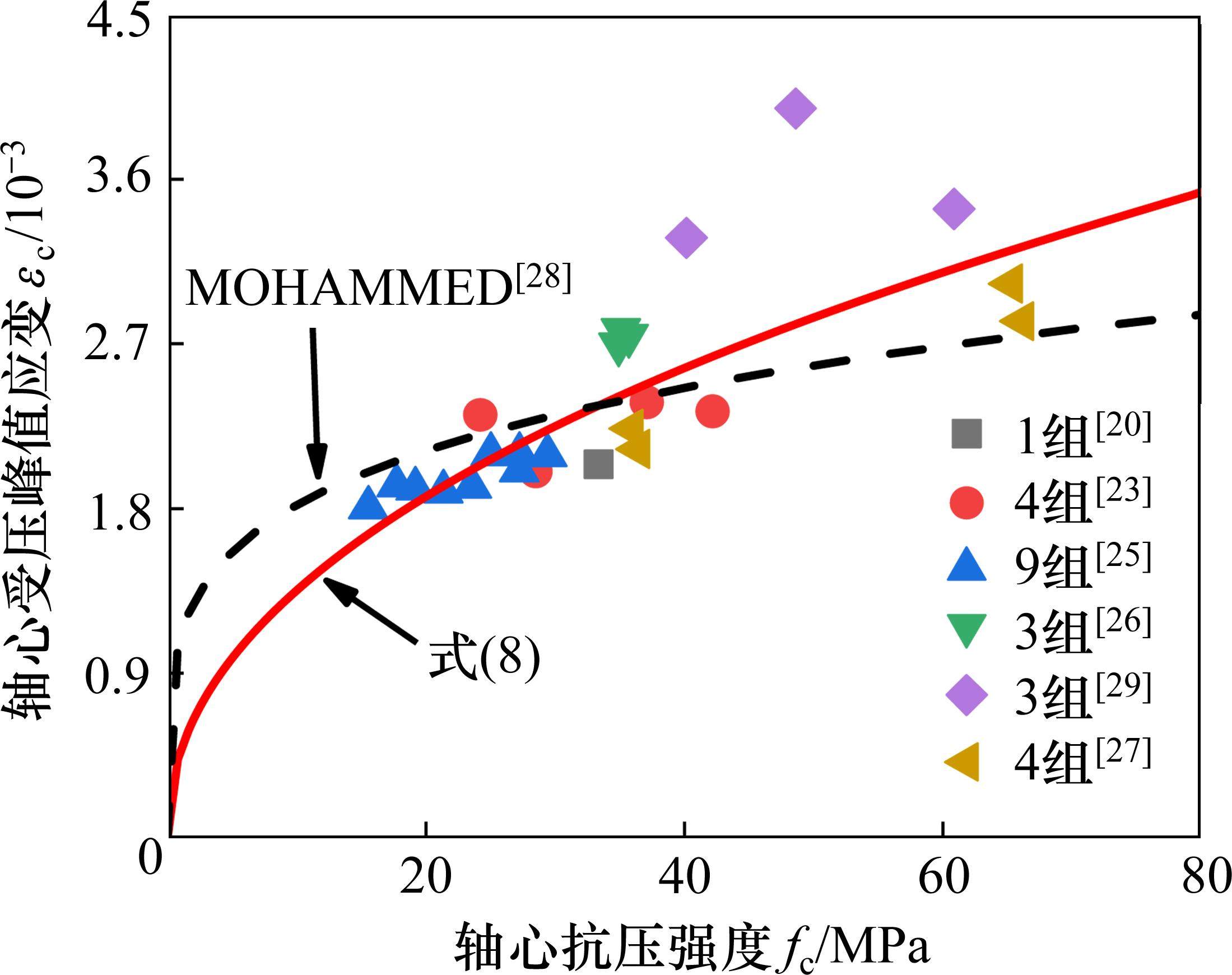
表4为轴心受压峰值应变和轴心受拉峰值应变计算结果特征值。由表4和图5可知,公式(8)、MOHAMMED[28]公式的计算结果和试验数据均吻合良好,但公式(8)的标准差和变异系数更小。
| 特征值 | 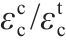 | 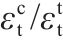 | |
|---|---|---|---|
| 式(8) | MOHAMMED[28] | 式(18) | |
| 均值 | 0.992 | 1.002 | 1.005 |
| 标准差 | 0.116 | 0.138 | 0.077 |
| 变异系数 | 0.117 | 0.138 | 0.077 |
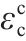
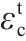
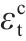
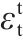
将式(1)代入式(8)中得到轴心受压峰值应变和立方体抗压强度的关系:
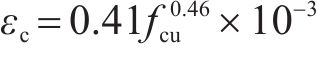
1.7 轴心受拉峰值应变
图6为地聚物混凝土轴心受拉峰值应变(εt)和fc的关系。基于图6中文献的试验数据,提出了地聚物混凝土轴心受拉峰值应变统一计算公式:
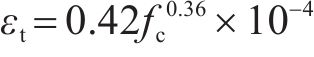
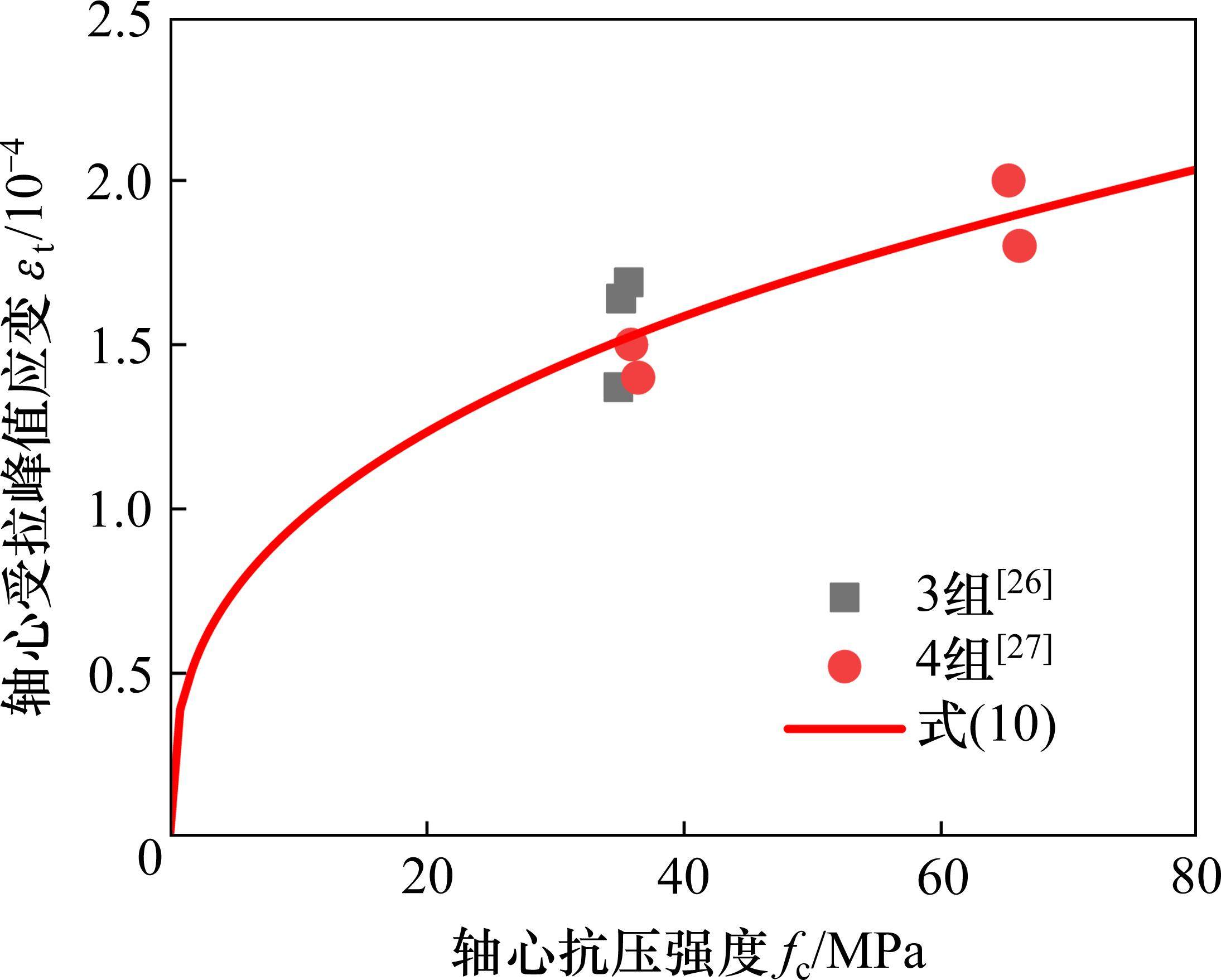
由图6和表4可见,公式(10)计算得到的结果和试验数据吻合良好,变异系数仅为0.077,且公式形式和公式(8)一致。
将式(1)代入式(10)中得到轴心受拉峰值应变和立方体抗压强度的关系式:
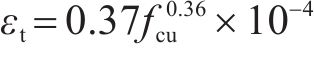
2 三轴塑性-损伤模型
2.1 单轴压(拉)应力-应变全曲线
参考DING等[33]提出的普通混凝土单轴应力-应变全曲线,同样建议地聚物混凝土单轴压(拉)应力-应变全曲线:
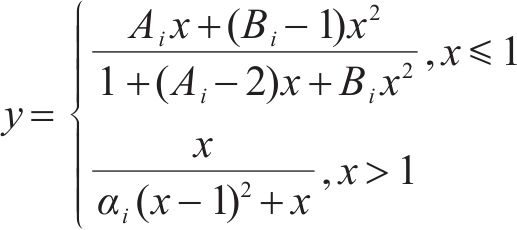
式中:Ai为弹性模量与峰值割线模量之比;Bi为应力-应变全曲线上升段弹性模量衰减程度控制系数;αi为应力-应变全曲线下降段参数。
当地聚物混凝土处于单轴受压状态时,此时i=1,式(12)中的y=σ/fc,x=ε/εc,,则根据A1的定义,代入式(1)、式(7)、式(9)可得:
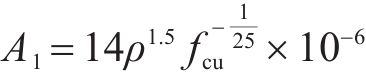
当y≤0.4时,认为地聚物混凝土处于弹性阶段,即单轴受压曲线为一条直线,则当x=0.4/A1时,y=0.4,由此可得上升段弹性模量衰减程度控制系数B1的表达式为:
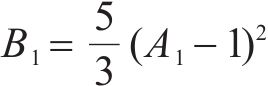
下降段参数α1由试验数据拟合得到:
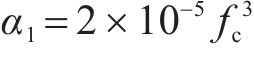
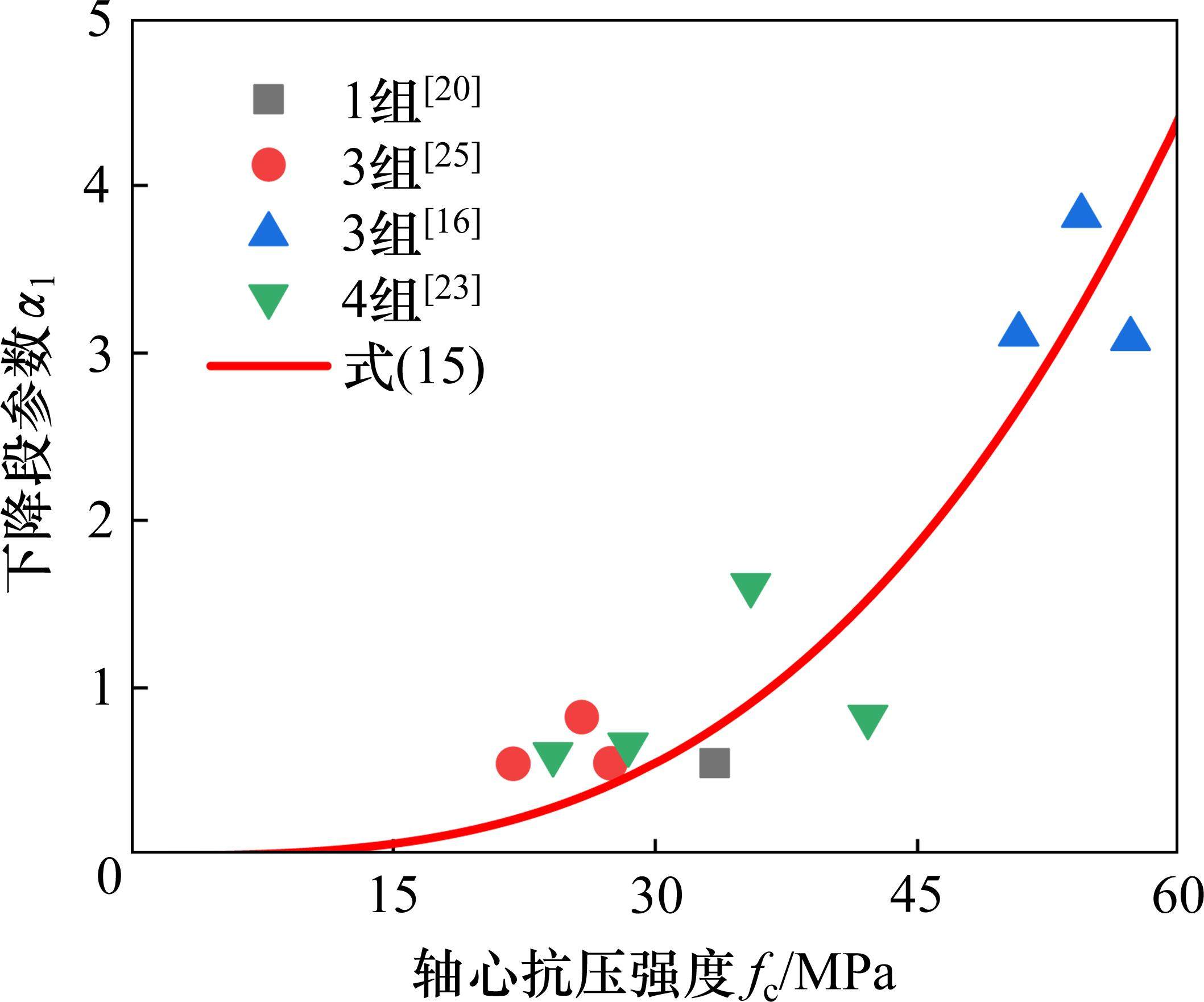
下降段参数α1和fc的关系如图7所示。由图7可见,公式(15)的计算结果和试验数据较为吻合。
将式(1)代入式(15)得到下降段参数和立方体抗压强度之间的关系:
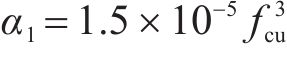
地聚物混凝土结构有限元分析中,考虑钢筋骨架或钢管对地聚物混凝土的约束作用,当地聚物混凝土构件配箍率或含钢率为2%及以上时,参考其他类型混凝土[34],取α1=0.15;当地聚物混凝土构件配箍率或含钢率在0%~2%时,α1取值在1.5×10-5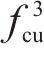
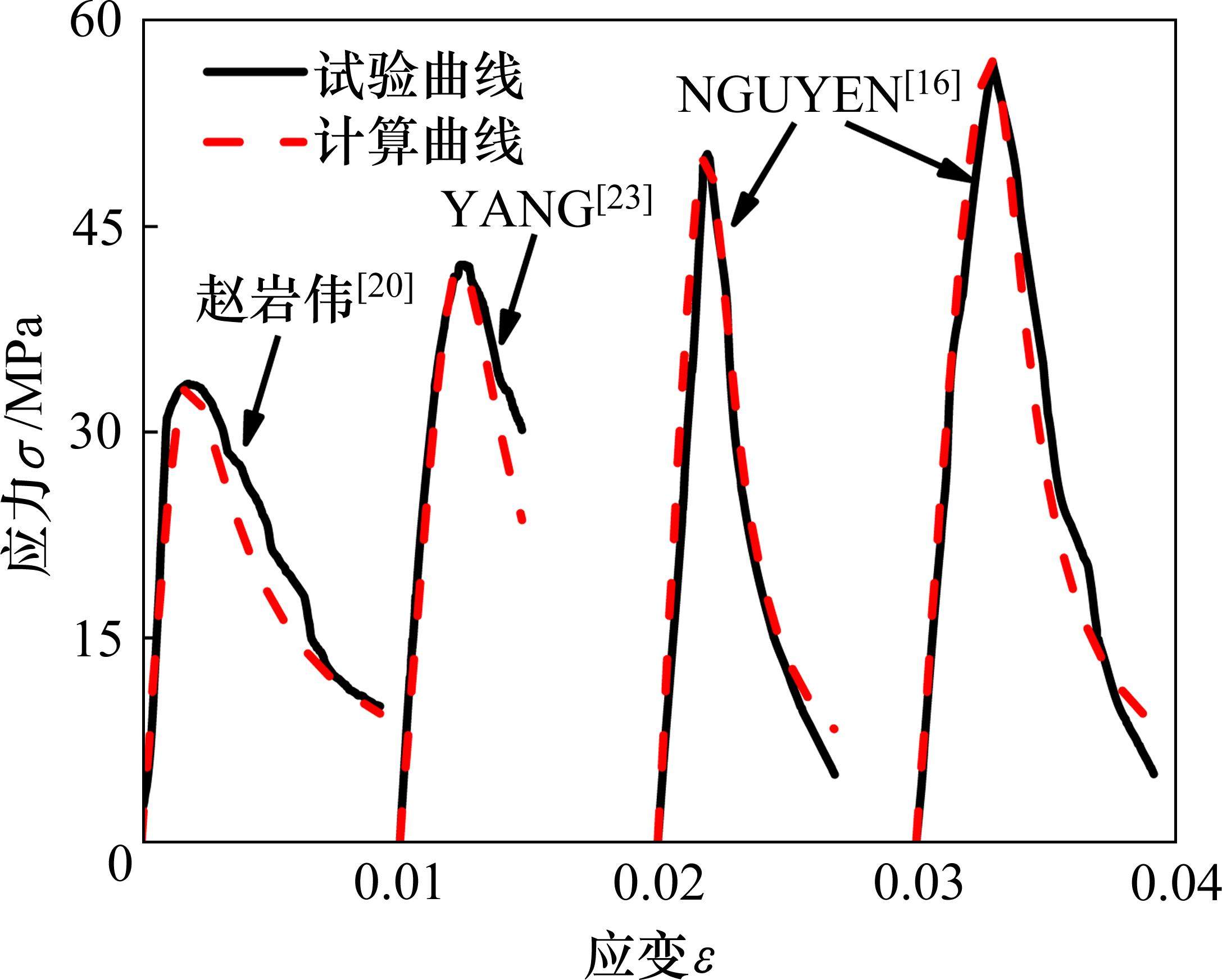
试验曲线和地聚物混凝土单轴受压应力-应变计算曲线的比较如图8所示。可见,提出的地聚物混凝土单轴受压应力-应变全曲线计算公式的上升段及下降段和试验曲线吻合良好。
当地聚物混凝土处于单轴受拉状态时,此时i=2,式(12)中的y=σ/ft,x=ε/εt,,则根据A2的定义,代入式(3)、式(7)、式(11)可得:
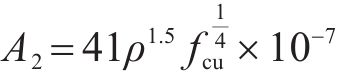
单轴受拉时的上升段弹性模量衰减程度控制系数B2同样可用类似上述受压时的条件求得:
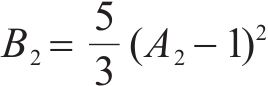
由于目前对于地聚物混凝土单轴受拉的研究较少,文献[24, 26-27]只给出了地聚物混凝土单轴受拉应力-应变曲线的上升段,并未给出下降段;YANG等[23]则未给出地聚物混凝土单轴受拉应力-应变曲线。参考普通混凝土单轴受拉应力-应变全曲线下降段参数[34],暂时将地聚物混凝土单轴受拉应力-应变全曲线下降段参数α2取为:
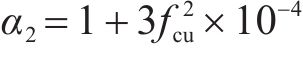
在实际工程中地聚物混凝土通常和钢筋或钢管共同工作,因此在地聚物混凝土结构有限元分析中,可以通过拉伸硬化考虑钢筋或钢管的作用,参考其他类型混凝土的取值,建议下降段参数α2取为0.8[34]。
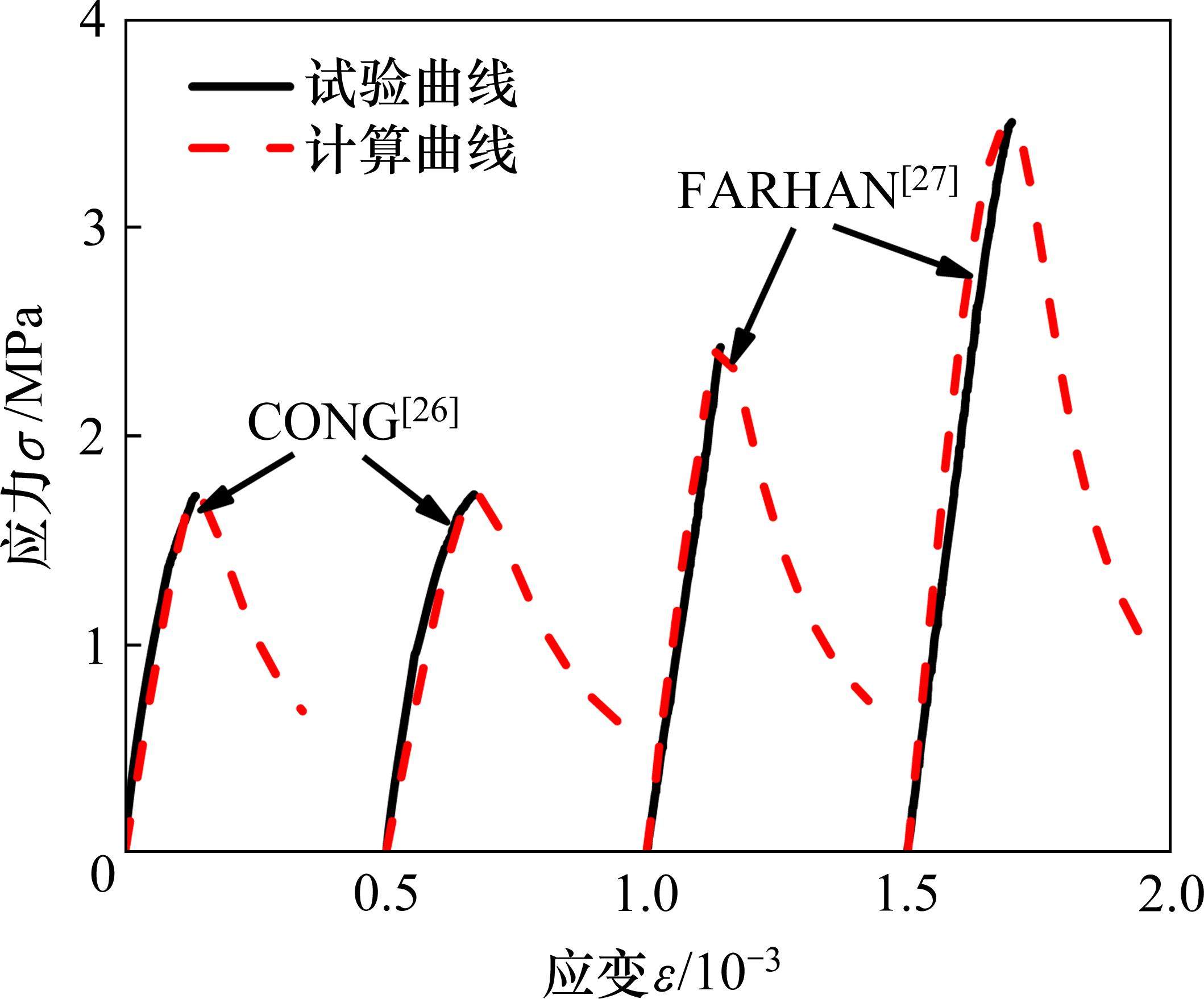
地聚物混凝土单轴受拉本构计算曲线和试验曲线的对比如图9所示。由图9可见,地聚物混凝土单轴受拉本构上升段计算曲线和试验曲线吻合良好。
地聚物混凝土弹性模量损伤表达式采用丁发兴等[30]提出的普通混凝土计算公式,具体如下:
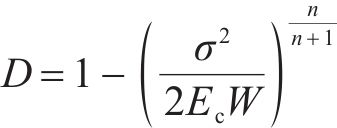
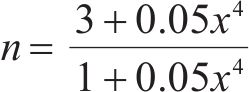
式中:D为地聚物混凝土弹性模量损伤因子,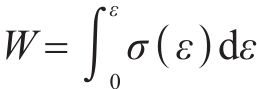
2.2 损伤比强度理论与三轴参数取值
参考普通、纤维和轻骨料等多类混凝土损伤比强度理论,丁发兴等[30]提出的通用表达式为:
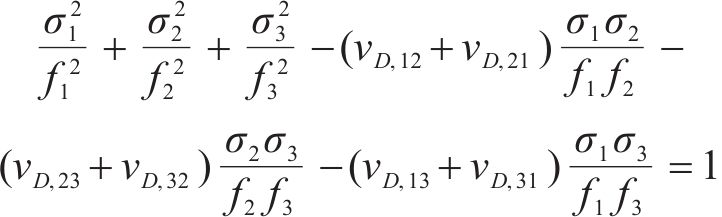
式中:fi(i=1,2,3)为混凝土单轴受力时的峰值应力,当为压应力时fi=fc,拉应力时fi=ft,fc和ft分别为单轴轴心抗压和轴心抗拉强度;νD,ij为损伤比。
损伤比参数表达式采用五经验系数表达式:
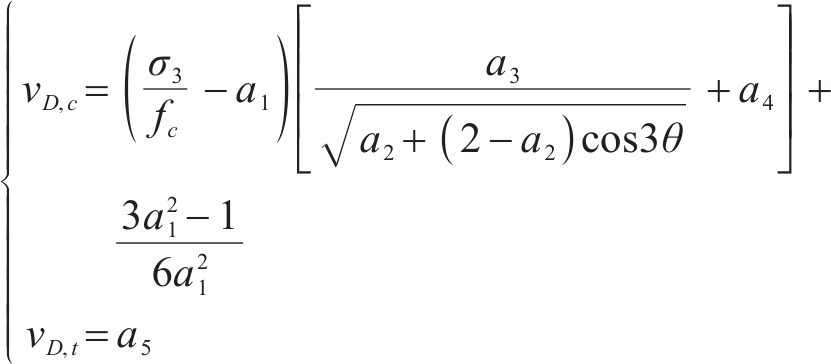
式中:νD,c为压损伤比;νD,t为拉损伤比;a1~a5为经验系数,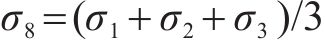
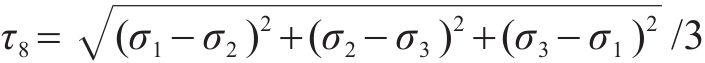
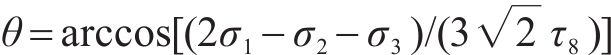
当混凝土处于围压三轴状态且围压应力水平较低时,围压三轴强度表达式可简化为线性表达式:
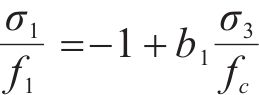
式中:b1为侧压系数。
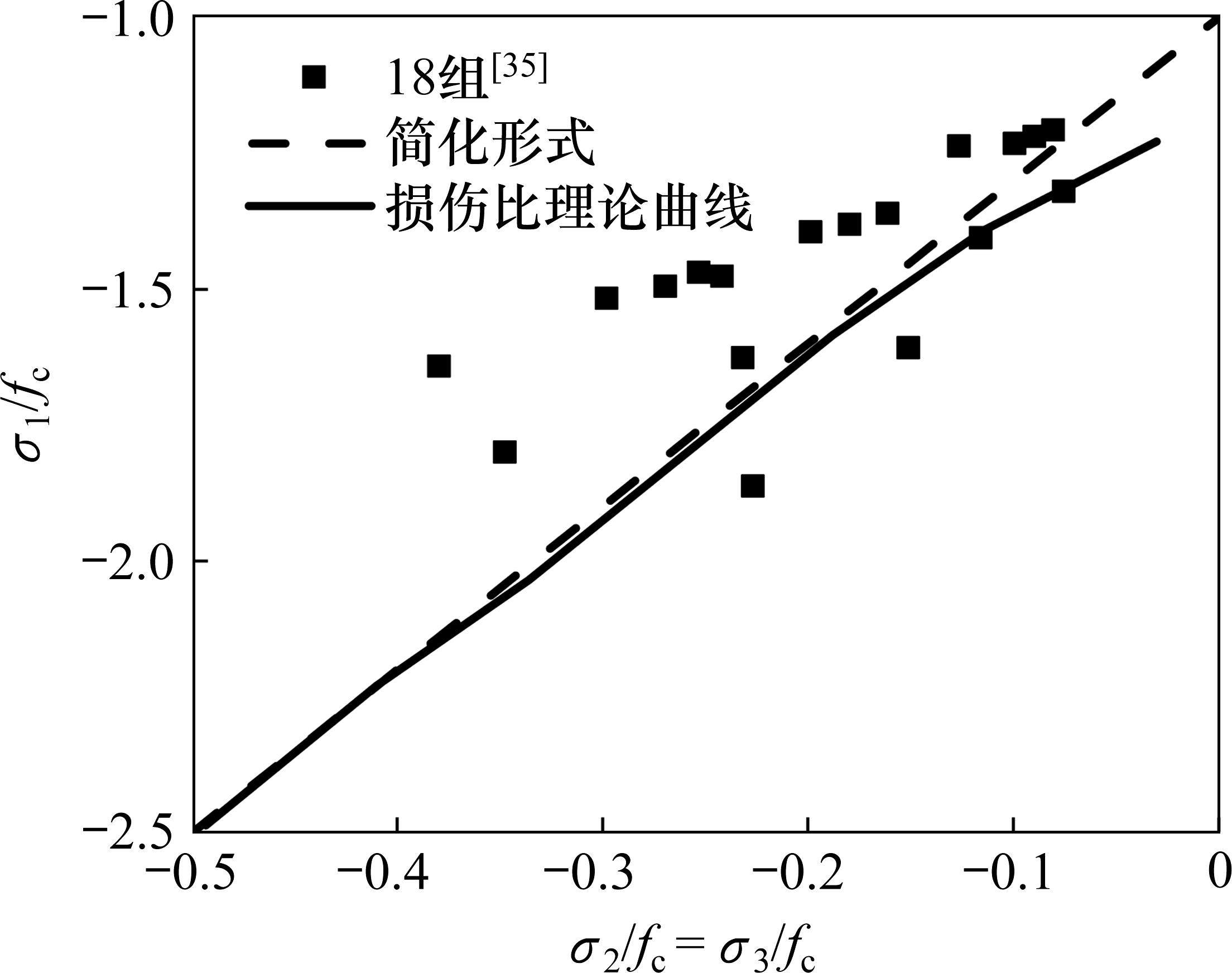
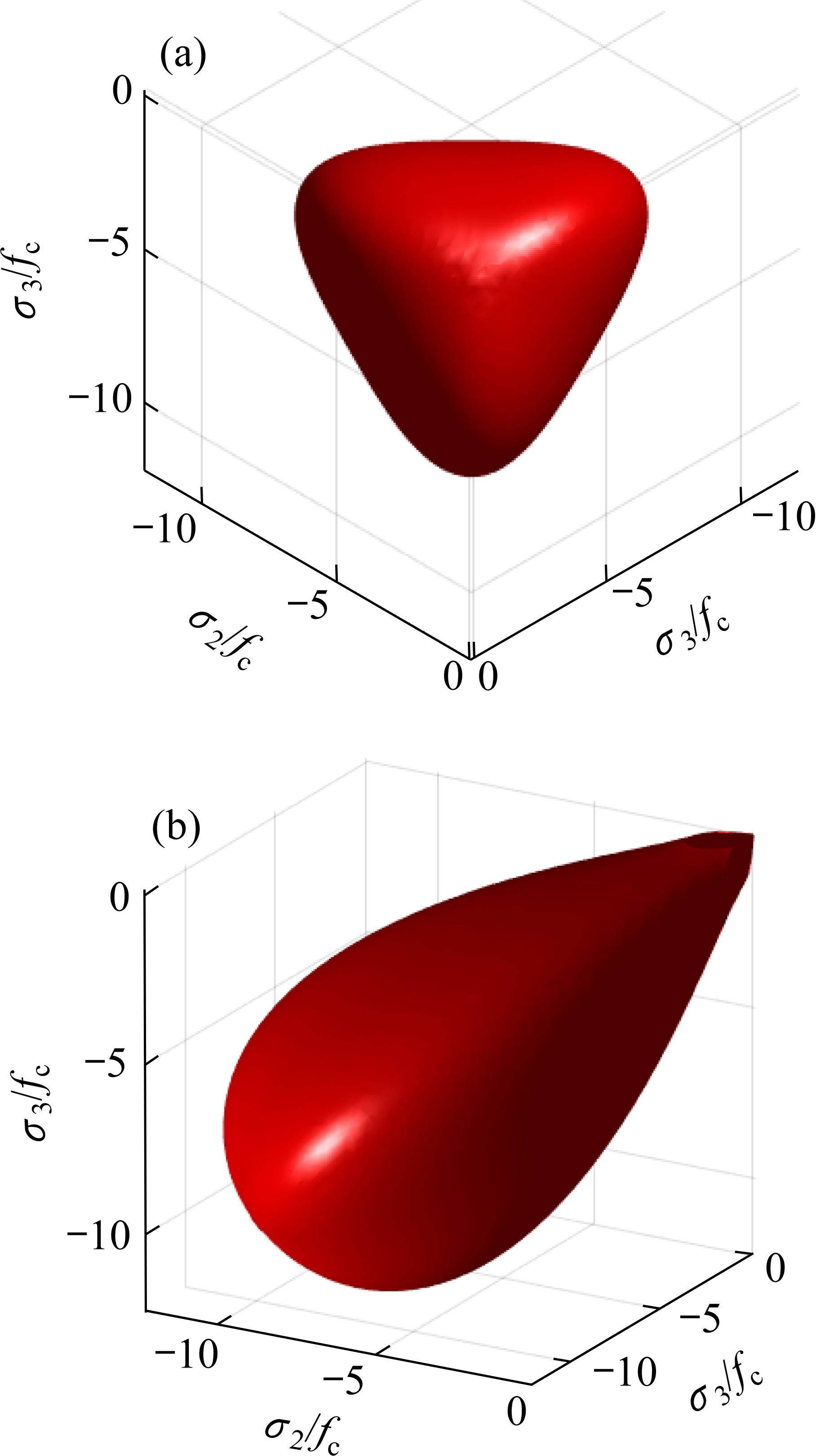
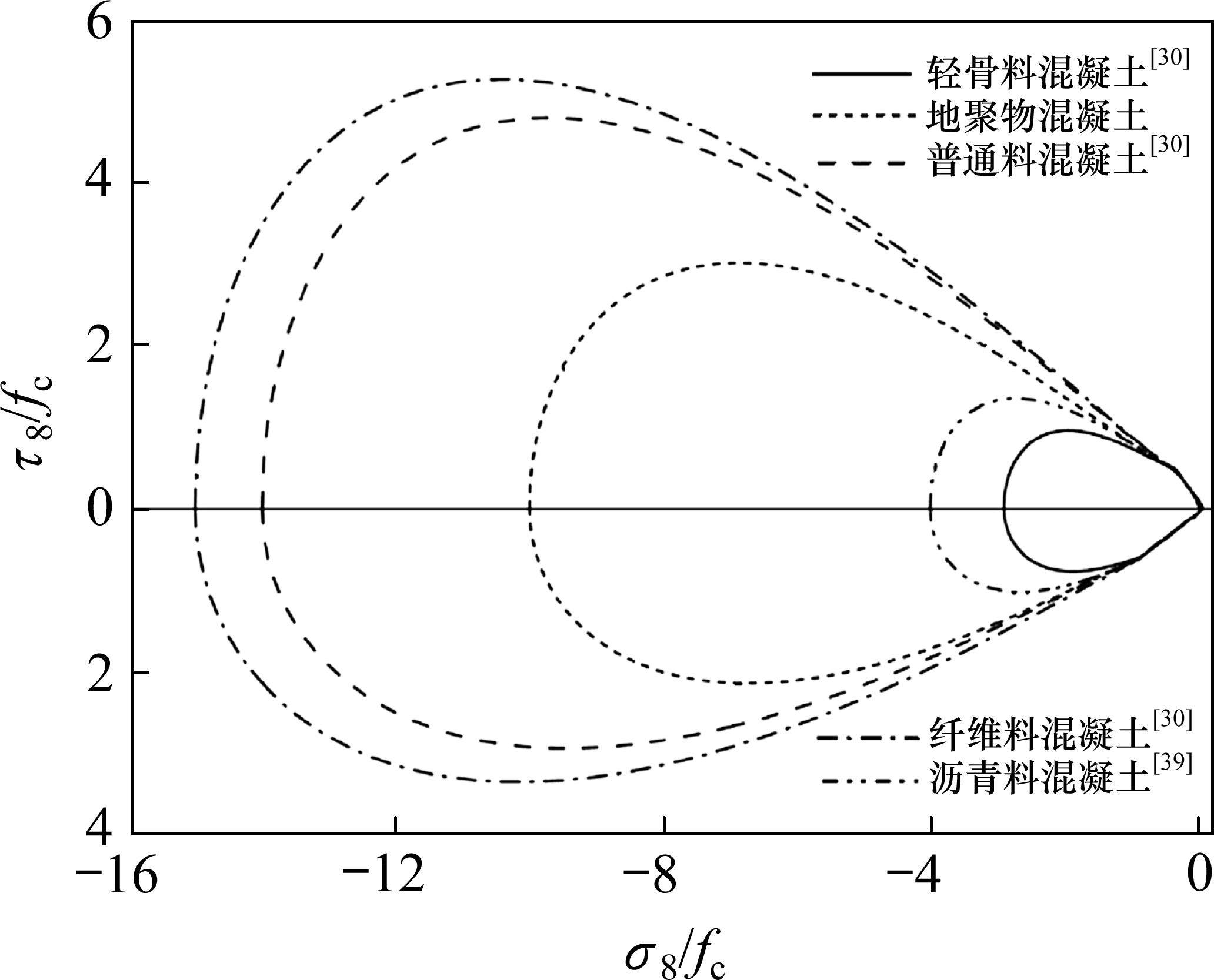
图10为地聚物混凝土围压三轴强度试验结果的规律,基于GUO等[35]的试验数据及式(24),拟合得到地聚物混凝土围压三轴强度准则的侧压系数b1=3.0。再结合普通混凝土、纤维混凝土、轻骨料混凝土和沥青混合料等多类混凝土材料多轴损伤比强度理论[30, 36-38],在有限的地聚物混凝土围压三轴强度试验结果范围内,提出地聚物混凝土损伤比强度理论如图11所示,对应的损伤比参数表达式经验系数取值为:a1=-10,a2=1.3,a3=0.044,a4=-0.007,a5=0.1。地聚物混凝土损伤比强度理论所表述的数学包络曲面与其他混凝土材料损伤比强度理论的比较如图12所示。
2.3 塑性-损伤模型三轴参数及其他参数取值
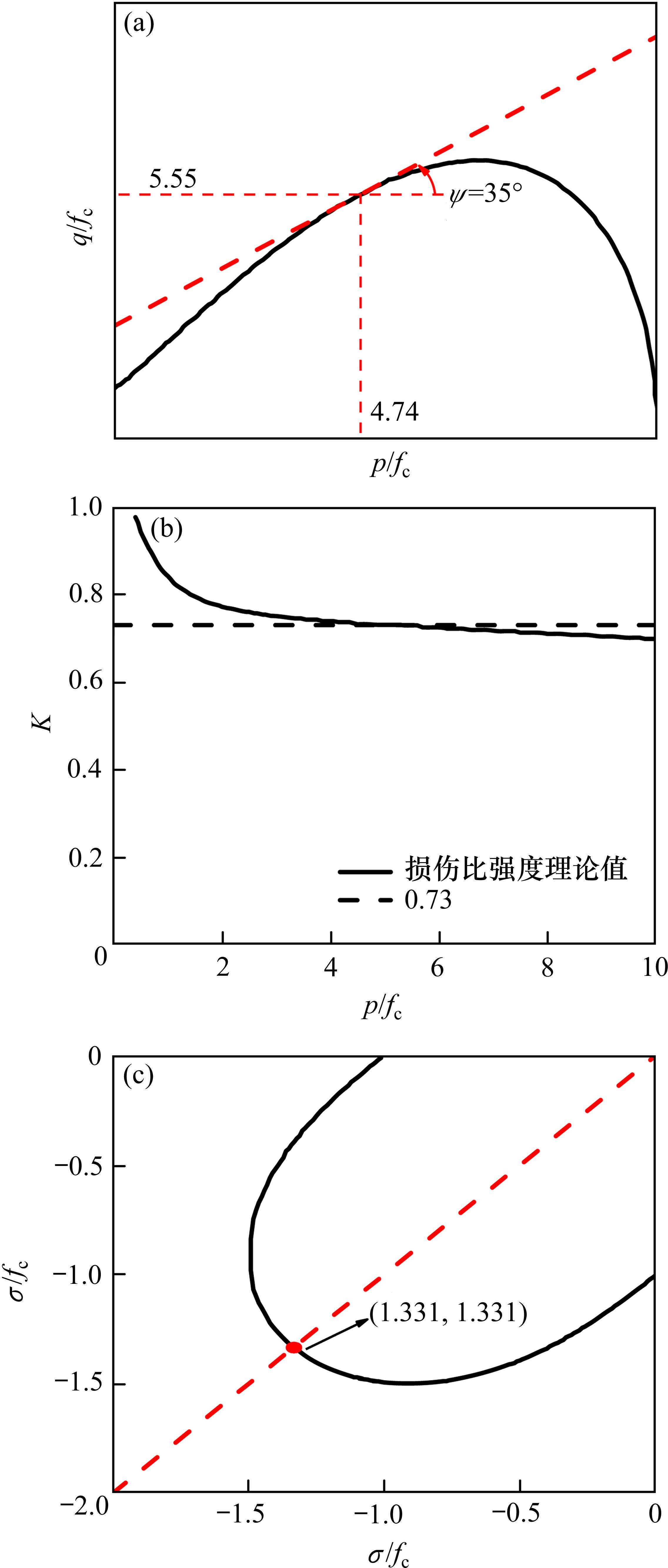
在ABAQUS有限元分析中采用混凝土塑性-损伤模型需要确定混凝土的三轴参数,即膨胀角ψ、拉压子午线强度比值K、双轴等压强度与单轴抗压强度比值fcc/fc等。膨胀角为p-q平面压子午线上高围压时的切线斜率,根据地聚物混凝土损伤比强度理论,其压子午线上高围压值p/fc=4.74时所对应的膨胀角取ψ=35°,对应的拉压子午线强度比值K=0.73,以及双轴等压强度与单轴抗压强度比值fcc/fc=1.331,如图13所示。此外,地聚物混凝土流动偏角取值为0.1,黏性系数取值为0.000 5,泊松比取值为0.2。
3 三轴塑性-损伤模型应用
3.1 试验及有限元模型简介
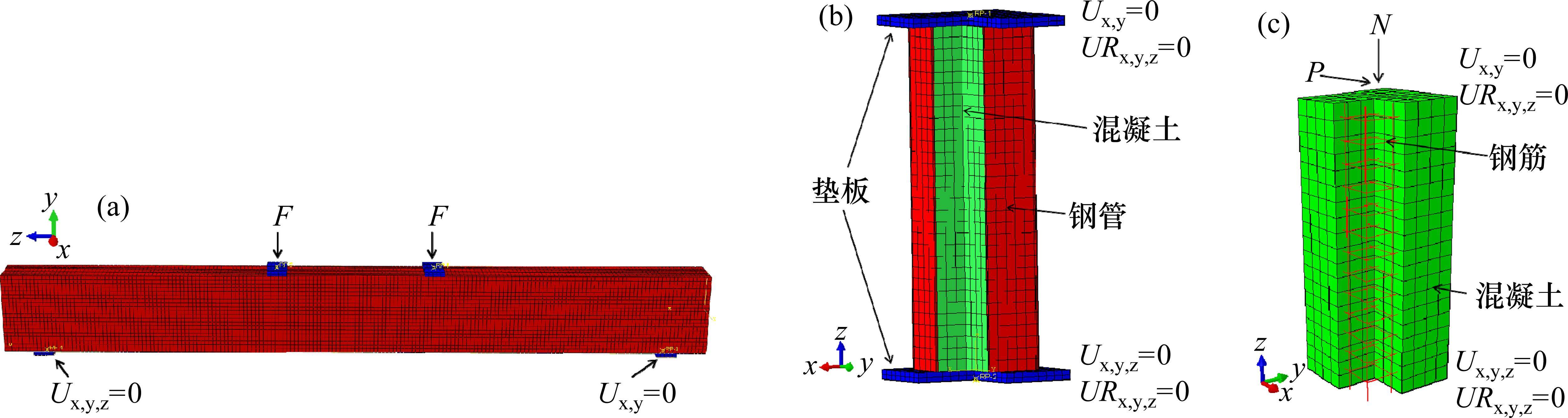
采用上述提出的地聚物混凝土塑性-损伤模型对王佳[40]制备的地聚物混凝土梁、石宵爽等[41]制备的钢管地聚物混凝土短柱及QU等[42]制备的钢筋地聚物混凝土柱进行精细化有限元建模。其中钢筋地聚物混凝土简支梁及钢管地聚物混凝土短柱采用静力加载,钢筋地聚物混凝土柱采用拟静力加载。钢筋地聚物混凝土梁、钢管地聚物混凝土柱及钢筋地聚物混凝土柱试件尺寸信息如表5所示,模型如图14所示。
| 试件种类 | 试件尺寸/mm | fcu/MPa | fc/MPa | fy/MPa |
|---|---|---|---|---|
| 钢管地聚物混凝土轴压短柱 | 200×6×750 | — | 56.0 | 467.0 |
| 钢筋地聚物混凝土简支梁 | 200×400×3 600 200×500×3 600 | 33.3 52.2 70.4 | — | 358.0(Ф10) 502.5(Ф18) 456.0(Ф20) 451.5(Ф22) |
| 钢筋地聚物混凝土悬臂柱 | 350×350×950 | 69.8 | — | 449.8(Ф16) 481.2(Ф8) |
单调加载中钢材采用丁发兴[34]提出的四折线弹塑性本构,具体表达式如下:
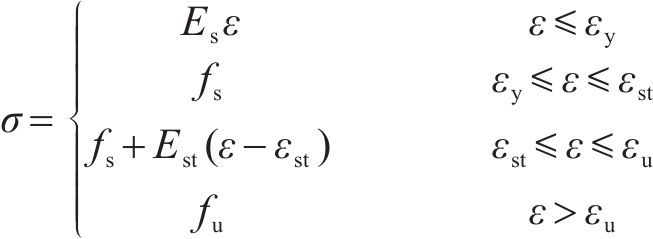
式中:σ为应力;Es为弹性模量;fy为屈服强度;fu为极限强度;εy为屈服应变;εst为强化时应变;εu为极限强度时应变;Est为钢材强化模量,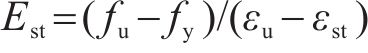
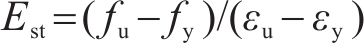
拟静力加载中钢筋采用孙浩等[43]提出的混合强化-韧性损伤模型,具体参数取值为:零塑性应变处的屈服应力和等效应力取钢材的实测屈服强度fy,随动硬化参数取750,背应力变化率取50,屈服面的最大变化取0.5fy,硬化参数取0.1。
钢管、地聚物混凝土、刚性垫板单元类型为C3D8R,钢筋单元类型为T3D2。钢筋地聚物混凝土梁中,钢筋和混凝土的接触关系为内置,刚性垫板和混凝土绑定;钢管混凝土短柱中,钢管和核心混凝土之间采用面-面接触,切向为罚函数,摩擦因数设置为0.5,法向为硬接触,刚性垫板和钢管采用绑定约束。采用位移控制加载。钢筋地聚物混凝土梁、钢管地聚物柱及钢筋地聚物混凝土柱的网格划分及边界条件如图14所示。
3.2 结果验证
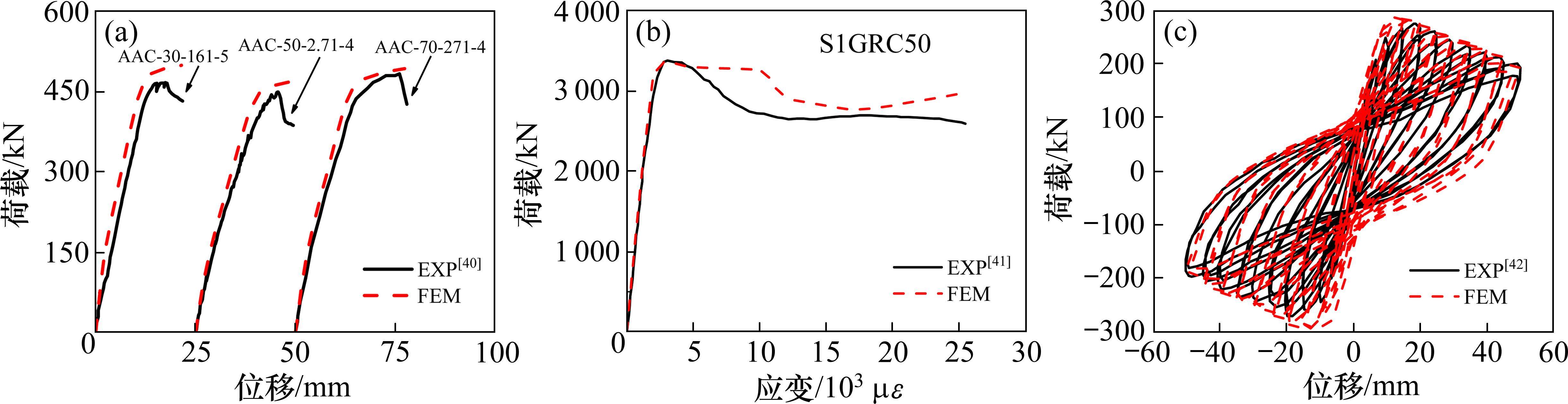
有限元模型计算结果与王佳[40]地聚物混凝土简支梁受弯试验结果、石宵爽等[41]钢管地聚物混凝土短柱轴压试验及QU等[42]钢筋地聚物混凝土柱拟静力试验结果比较如图15所示。由图15可见,钢筋地聚物混凝土梁的计算荷载-挠度曲线、钢管地聚物混凝土短柱轴压的计算荷载-应变曲线及钢筋地聚物混凝土柱滞回性能的计算荷载-位移滞回曲线和试验曲线吻合良好,表明作者提出的约束地聚物混凝土三轴塑性-损伤模型可有效应用至相应的结构有限元分析中。
4 结论
1) 建立了地聚物混凝土单轴力学性能指标统一计算公式,计算精度较高。
2) 建立了地聚物混凝土单轴拉(压)应力-应变全曲线,根据地聚物混凝土围压三轴强度试验结果,再结合普通、纤维、轻骨料等多类混凝土的损伤比强度理论,提出了地聚物混凝土损伤比强度理论,建议了膨胀角、拉压子午线强度比值和二轴等压与单轴抗压强度比值等三轴参数取值,形成了约束地聚物混凝土三轴塑性-损伤模型。
3) 基于提出的约束地聚物混凝土三轴塑性-损伤模型,进行了钢筋地聚物混凝土梁、钢管地聚物混凝土柱静力加载及钢筋地聚物混凝土柱拟静力加载等结构非线性有限元分析,计算结果与试验结果吻合程度较高。
张绍松,丁发兴,吴霞.基于损伤比强度理论的约束地聚物混凝土塑性-损伤模型及应用[J].铁道科学与工程学报,2025,22(04):1735-1746.
ZHANG Shaosong,DING Faxing,WU Xia.Plastic-damage model and application of confined geopolymer concrete based on damage ratio strength theory[J].Journal of Railway Science and Engineering,2025,22(04):1735-1746.