随着轻质高强材料的广泛使用和其他工程技术的发展,人行桥变得更轻、阻尼更小、跨度更大,导致结构频率降低,容易落入人行荷载作用的频带内,在人行荷载激励下产生过量振动的问题日益增多[1-2]。国内外已有许多学者对人-结构相互作用振动响应问题展开了研究并取得大量成果[3-5]。聂建国等[6]在进行人致结构振动分析时,指出采用我国国民的平均身体质量作为行人的质量值能更好地反映实际情况,但未深入分析行人质量对结构人致振动响应的影响。SILVA等[7]研究得出行人动力学参数与个体质量和步频有关,不能单一取值。周涛等[8]基于规范中的纯荷载理论研究了曲线连续梁人行桥的振动响应,提出一种有效的减振系统。罗晓群等[9]通过研究单斜面索拱支承曲梁人行桥,模拟计算了随机人群荷载对结构的响应。张琼等[10]通过研究人-桥竖向动力相互作用,得出考虑相互作用情况下结构阻尼比会较大幅度提高,频率会较小幅度降低。郭瑞等[11]提出了一种考虑人群同步率与行走步频随人群密度变化而改变的随机人群荷载模型。梁鸿斌等[12]研究人-结构系统问题,得出结构上静止的人会改变结构的动态特性,增加其阻尼。评估行人对结构人致振动响应时,行人的存在会改变结构的动力特性,综合考虑HSI(Human-Structure-Interaction)是预测可靠动态响应的基础,明确一个简单且合理的行走状态下的人体动力学模型至关重要[13-14]。现行部分研究多采用规范的纯荷载模型,难以考虑到人-结构相互作用中的人体模型对人桥系统的影响,此外部分研究中人体只考虑其竖向效应,并未对人体横向的动力属性进行综合考量,探索一种综合考虑个体差异、真实反映人群效应的人群模型很有必要。本文基于移动步行荷载与人体动力学模型联合施加的方式模拟人-结构相互作用,综合对比建立基于国人身体特性并考虑交通流的行人荷载模式及合理的SMD人体模型,讨论行人整体效应对人行桥动力特性及响应的影响,得到较为合理的行人模拟方式。重点分析人群对人行桥动力特性及振动响应的影响,提出考虑人群分布状况和交通流状况的人群效应模拟方式,研究人群行走下人行桥响应的影响因素以及人群-桥耦合对不同动力特性的简支人行桥动力性能的影响。
1 考虑HIS的行人效应相关理论及程序模拟
精细模拟行人效应是研究考虑HSI对人行桥振动响应的关键,本文选择单人傅里叶荷载模型及人体动力学SMD模型,基于ABAQUS有限元软件中Dload子程序进行移动行人效应的模拟。
1.1 步行荷载模型
单人荷载研究是人群荷载研究的前提和基础,可分为傅里叶级数模型、冲量模型、自激力模型和随机模型,其中使用考虑随机概率分布的傅里叶级数模型来表达单人步行荷载更符合实际[15],为人体静荷载和多阶谐波动荷载之和,如式(1)所示。
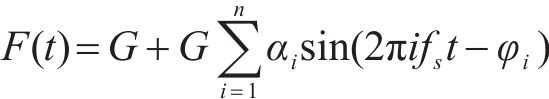
式中: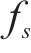
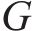
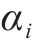
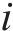
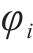
模拟人群时重点从交通流条件下人群中单个行人效应出发进行研究,更能反映实际加载情况。行人交通学领域研究的重点是行人步速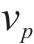
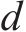
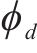
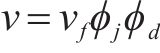
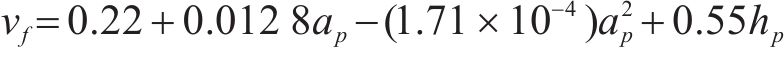
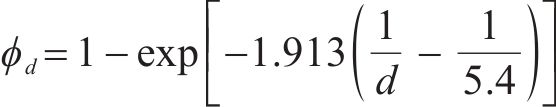
式中: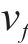
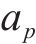
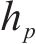
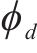
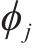
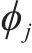
步频预期均值fp由步速v的二次函数来描述[16]。后续利用该模型的标准差0.178和步频预期均值一起定义特定步速v下步频的正态分布特性,见式(5)。
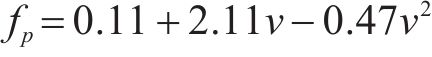
依据上述研究成果,可得到d-v-fp三者之间的关系。步速和步频呈现出正态分布规律,选定一种单人傅里叶荷载模型后,可以很好地通过随机变量的方式将模型参数随机化,再利用ABAQUS移动荷载子程序进行参数定义即可模拟出每个行人独特的步行特征。结合最新交通学领域的研究成果,在随机概率分布的单人步行荷载模型基础上,实现在特定人群密度下的具有预测性质的人群荷载模拟。具体流程如图1所示。
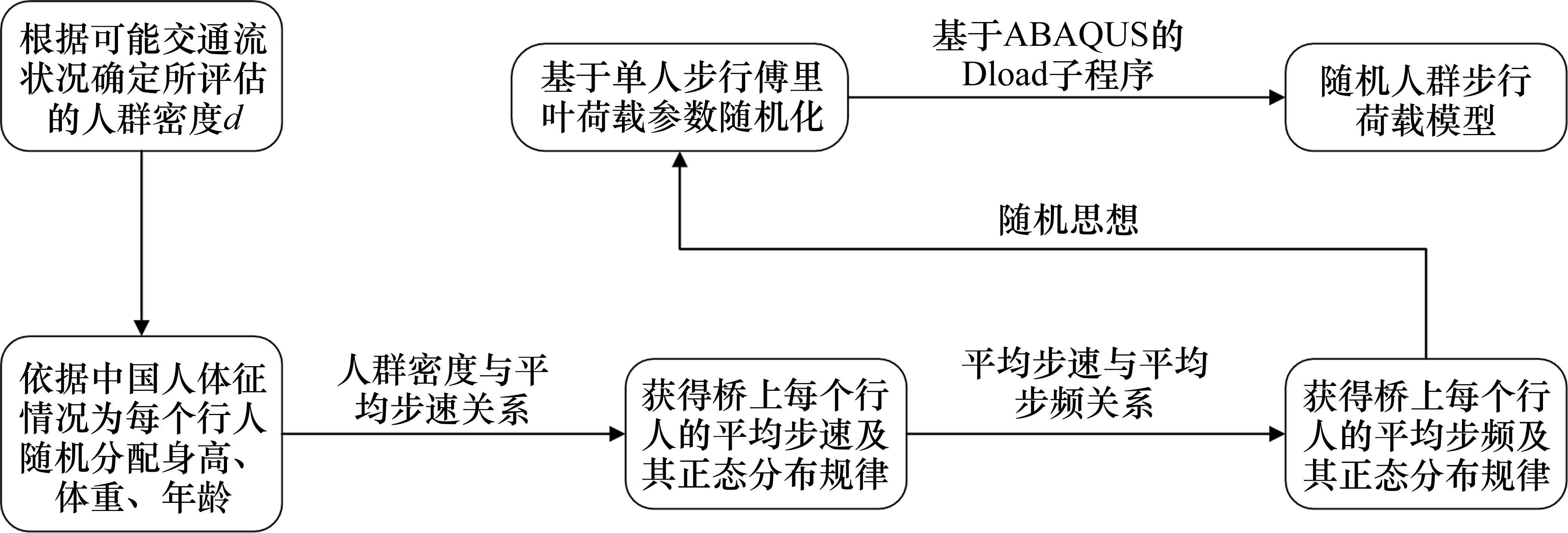
基于国人身体特性和步态特征,可得到每个行人步行荷载参数间的关联分布情况,可较为真实地预测不同人群密度工况下行人行走的状态特征分布情况,见表1。
| 关键参数 | 均值 | 标准差 |
|---|---|---|
| 体重/kg | 67.4 | 9.17 |
| 身高/cm | 168 | 5.59 |
| 年龄/岁 | 41.7 | 3.7 |
| 自由步速/(m∙s-1) | 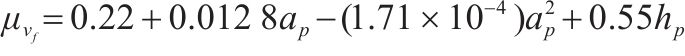 | 0.087 |
| 步速/(m∙s-1) | 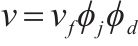 | — |
| 步频/Hz | 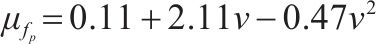 | 0.178 |
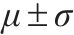
1.2 人体动力学模型
人体是一个非常复杂的非线性动力系统,人体模型对于研究人与结构相互作用必不可少,常用的人体模型有弹簧-质量-阻尼器(SMD)模型、连续体模型、倒钟摆模型、多链杆模型[18]。SMD模型是将行人模拟为具有一定刚度和阻尼的质量体,该模型考虑了行人与地面之间的相互作用,将其视为整体的单自由度模型。SMD模型相比其他模型,参数和假设更少,模拟操作性更强,该模拟方式不同于纯荷载模型只考虑人体对人行桥的强迫振动效应,将人体动力学特性纳入到结构振动计算中,很好地弥补了人-桥相互作用影响的缺失[19]。本文采用SMD模型和步行力联合模拟的方式来模拟行人整体动力效应,如图2所示。
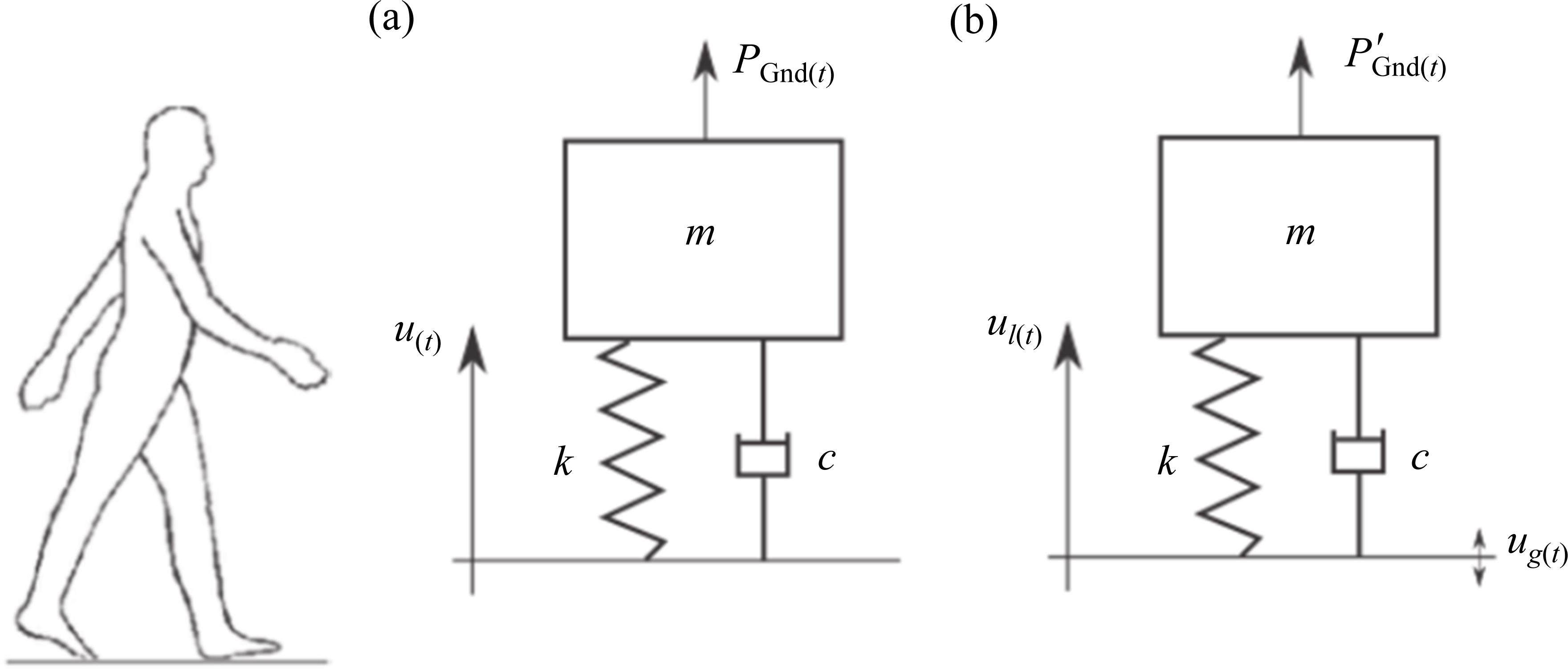
SMD模型中表示行人重心运动的方程式为:
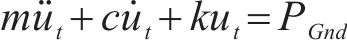
式中:ut为人体质心相对于固定面的竖向位移;PGnd为在刚性板上测获的地面反作用力;m为行人的整体质量;c和k分别代表行人在振动过程中如何耗散能量和弹性变形。
假设结构振动使人体模型的生物动力学参数保持不变,可得到行人在移动面上运动的动力学方程为:
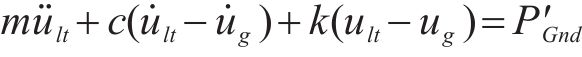
式中:ug、ult分别是支撑面和人体质心相对于固定面的位移量。
为表示2个公式的独立性,将人体相对位移量用不同符号表示。然后,基于单自由度模型的加速度频率响应函数的表达式如式(8)所示,获得人体SMD模型参数。
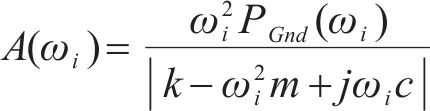
式中:j为虚数符号;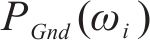
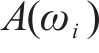
由于式(8)中存在3项未知数,为了显著性考虑,通过获取力和加速度前3阶谐波分量幅值即可建立3个非线性方程组,求解并拟合得到人体动力学参数,见式(9)。

式中:M为行人体重;m为模型质量。
1.3 基于ABAQUS子程序的移动行人效应模拟
本文采用Standard求解器模块中的Dload子程序模拟,选择动力隐式的直接积分法进行动力响应求解。用户子程序是ABAQUS分析中的一个独立的模块,Dload子程序存在于求解器的荷载定义环节上,在每个增量步中需要与主程序间进行反复调用、更新、迭代来完成最终的求解任务。图3为ABAQUS/Standard动力隐式分析流程图以及Dload子程序在当中的位置和作用。
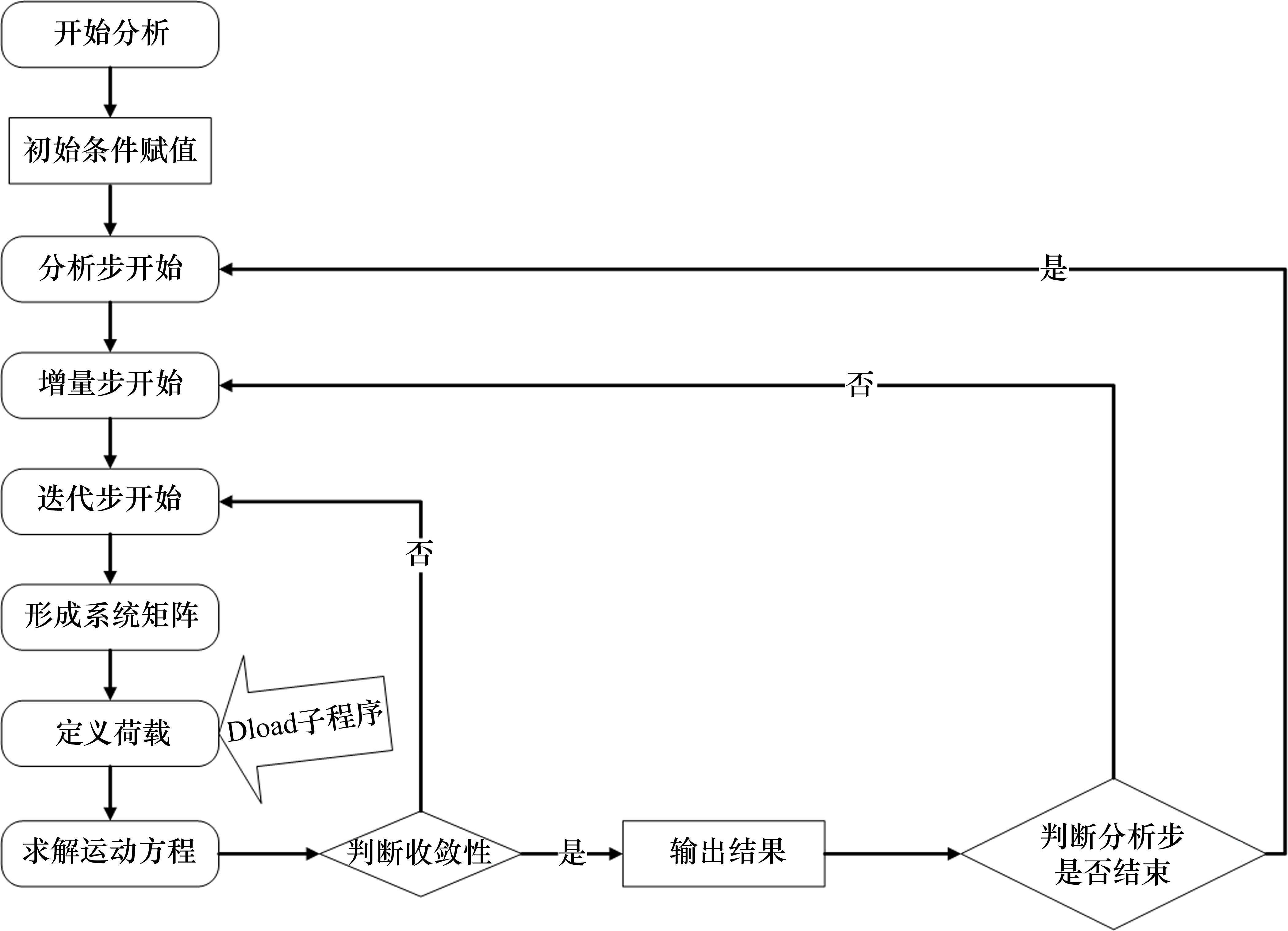
采用质量单元(MASS)和弹簧/阻尼器单元(SPRING/DASHPOTA)来联合实现,在结构加载面上以子结构的形式施加,以自由节点的形式表示行人质量的非关联节点和与结构接触的关联节点,关联节点通过绑定约束,使其与节点附近的单元积分点之间产生类似共节点的特性设置,质量单元设置在横竖向的2个非关联节点上,得到2个方向上各自模型中的质量定义,在非关联节点与关联节点间创建SPRING/DASHPOTA单元,模拟2个方向上的刚度和阻尼属性。
2 基于HSI效应下人行桥动力性能研究
2.1 工程背景及计算模型
本文计算选定的模型为SILVA等[7]所采用的缩尺模型,进行该简支人行桥考虑HIS效应下的结构动力特性及动力响应影响分析。该人行天桥的固有频率约为4 Hz,处在快走行人荷载的二阶谐波频率和慢走行人荷载的3阶谐波频率范围内。该结构由1块10 cm厚的桥面板和2根间距1.80 m的支撑梁组成,两侧支撑梁竖向高度为0.3 m,计算跨径为11.3 m,第1阶竖弯振动模态的自振频率为4.27 Hz,阻尼比平均值为1%,处在快走行人荷载的2阶谐波频率和慢走行人荷载的3阶谐波频率范围内。SILVA缩尺简支人行桥尺寸见图4。
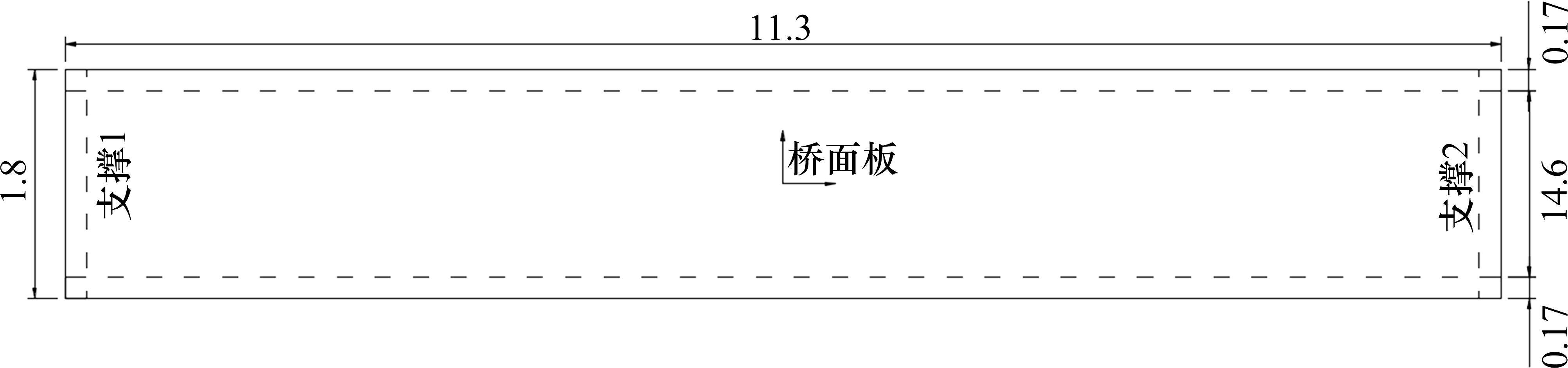
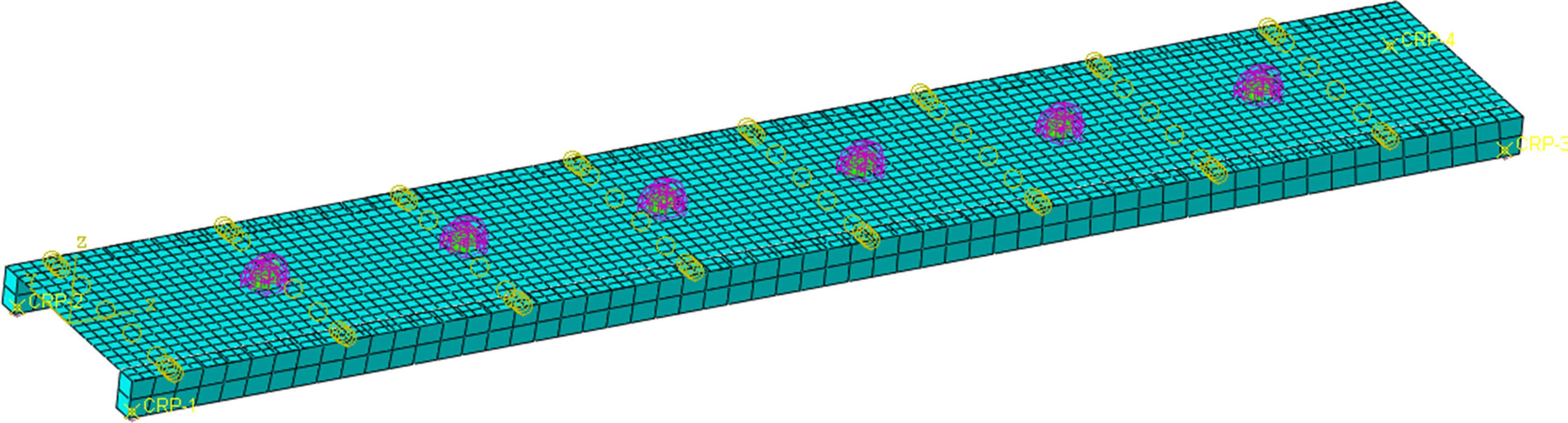
SILVA等[7]实验测试表明,结构的低频率受人体影响显著,侧重分析前3阶结构模态受人体的影响。对于SILVA所采用的缩尺模型,本研究采用ABAQUS有限元软件建立缩尺人行桥的有限元模型。两纵梁采用C3D8I六面体实体单元,桥面板则采用S4R四边形壳单元,桥面板壳单元的网格划分尺寸为0.1 m×0.1 m,实体单元的网格尺寸为0.15 m×0.15 m,纵梁与桥面板间采用绑定方式建立边界约束。简支梁的边界条件设置为:在支撑位置设置参考点,一侧约束X、Y、Z,另一侧约束Y、Z。采用动力隐式的直接积分法进行响应求解,对于该结构依据经验准则,固定增量步长取0.005 s,材料属性的瑞丽阻尼依据SILVA实验的实测值代入计算。再利用ABAQUS独有的Python脚本的形式在结构模型基础上建立人体模型,将关联节点与桥面板建立绑定约束进行模型耦合,人群-简支梁联合系统有限元模型见图5。表2为结构在空载状态下结构前3阶模态振型及频率值。
| 模态阶数 | 频率/Hz | 模态形式 |
|---|---|---|
| 1 | 4.261 6 | 一阶对称竖弯 |
| 2 | 12.608 | 一阶扭转 |
| 3 | 16.487 | 一阶反对称竖弯 |
2.2 不同行人模拟方式的影响
为了分析在不同单人行走模拟方式下人行桥的响应情况,分别采用移动力MF、SMD模型、带耦合质量的SMD模型(SMD-M)模拟行人。行人分配的相关属性参数依据表1给出的参数上下限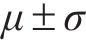
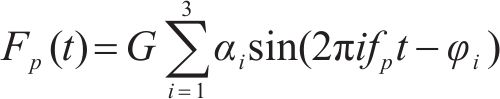
式中:G为行人重量,取700 N,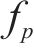
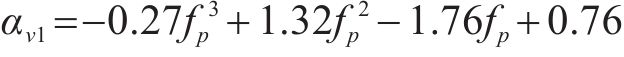
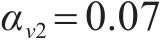
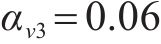
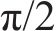
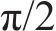
行人沿着结构中轴线行走,编写对应的Dload接口,在结构上模拟移动步行力。
采用上述荷载参数时,结构频率未在步行荷载敏感频率范围内,属于非共振情形,3种模拟方式得到的跨中竖向加速度响应如图6(a)所示,分析时长取8.7 s,图中均方根加速度为时程中0.1 s内的有效值。为与共振情形下3种模拟方式结果进行比较,选择一阶步行荷载模型,假定步频等于结构基频4.26 Hz,其余参数保持一致,其模拟得到的跨中竖向加速度响应如图6(b)所示。
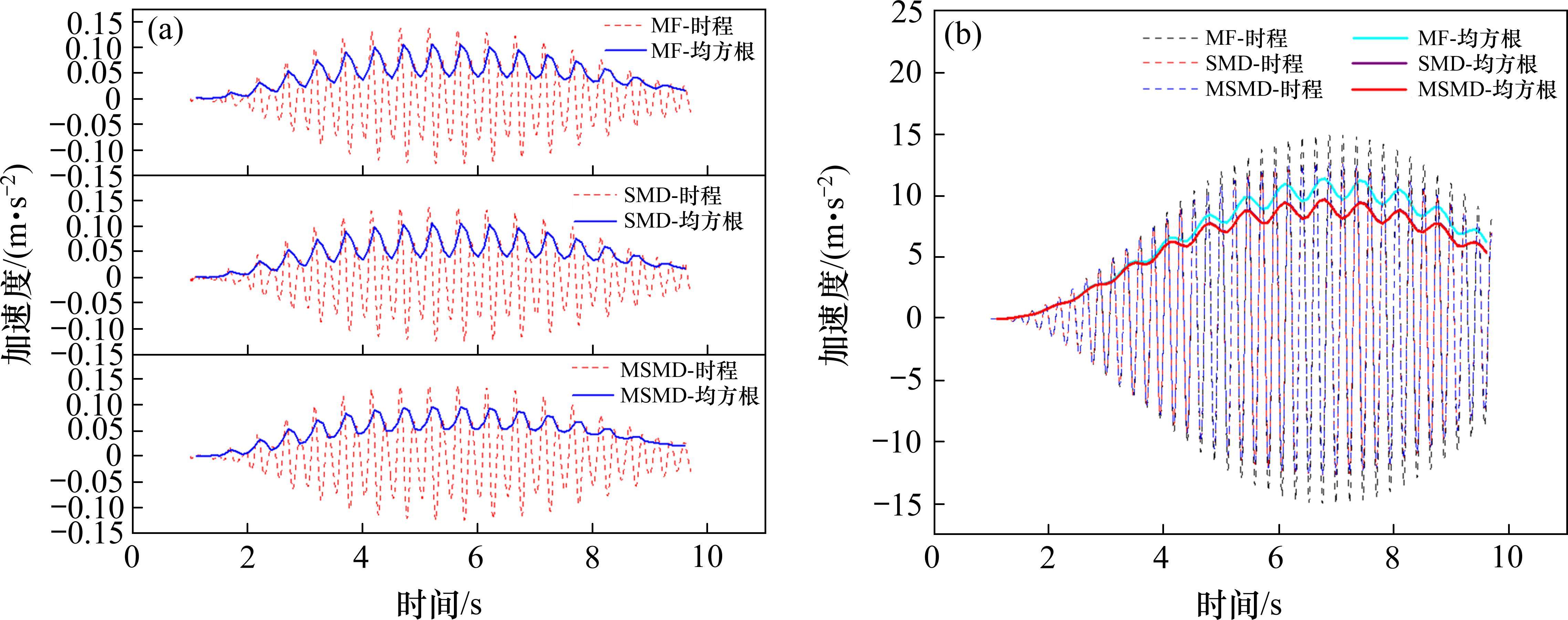
图6表明:当人行桥处于非共振状态下,此时MF模型和SMD模型模拟的结果较接近,差异率仅为0.8%,而MSMD模型与MF模型间的差异率为9.5%,说明人体模型对振动响应影响很小,在保守计算时可不考虑。但当人行桥处于共振状态时,MF模型和SMD模型模拟的结果差异显著,SMD和MSMD模型的响应值与MF模型相比均降低约15%。因此在精细化分析人致振动的最不利响应时,有必要考虑人体模型的影响。
2.3 小组人群过桥模拟分析
模拟小组工况的方法是将组内行人荷载集中化处理,本文借助Dload子程序的独特优势可进一步考虑小组内成员离散加载的情况,更细微地考虑行人所处位置的差异性,单人荷载离散化加载模式也更贴近现实荷载状态。为进一步探究单人荷载模型选取对模拟结果的影响,在离散加载方式中增加3阶傅里叶荷载模型进行对比分析,考虑以下几种工况。
工况1:简化荷载模型+集中加载;
工况2:简化荷载模型+离散加载;
工况3:基于KERR的3阶荷载模型+离散加载(3阶相位角均随机);
工况4:基于KERR的3阶荷载模型+离散加载(首阶相位角为0,高阶为随机分配);
工况5:基于KERR的3阶荷载模型+离散加载(首阶相位角为0,高阶为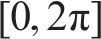
工况6:IABSE竖向荷载模型+离散加载(首阶相位角为0,高阶为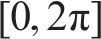
行人荷载集中化处理后,忽略实际人体位置分布,以唯一加载范围的形式模拟,如图7所示。

小组结伴而行时每个人步态大致相同,因此每个人步速设为1.3 m/s,步频取2.0 Hz,重量取700 N。对于简化荷载模型中的动载因子按KERR的首阶表达式取值,相位角服从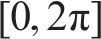
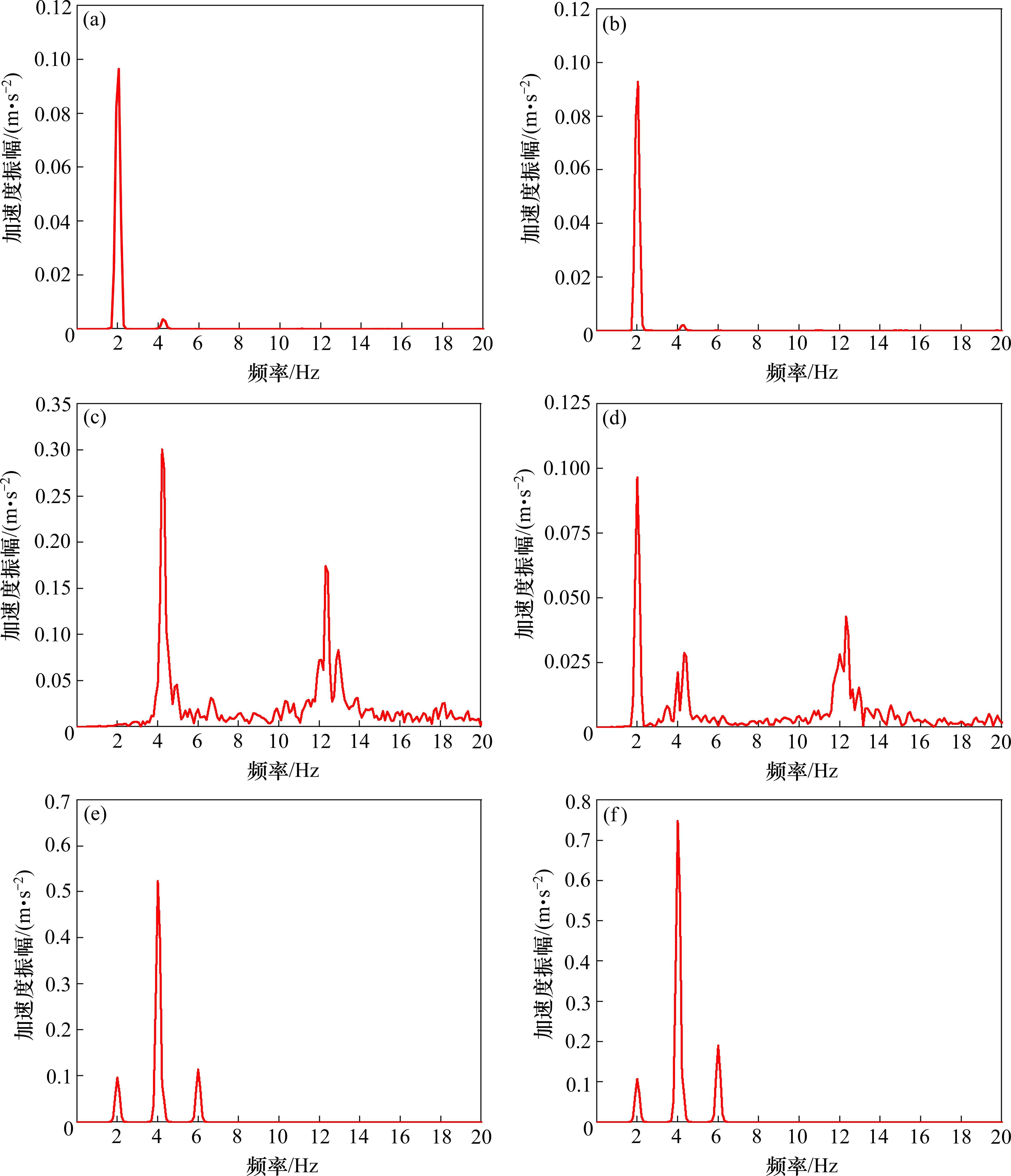
图8表明当所有行人处于完全同步状态时,集中加载和离散化模拟的结果很接近,最大偏差仅为8%,在动力可接受范围内。考虑高阶谐波的响应比简化模型有了显著增加,最小增幅为83.2%,因此高阶谐波仍然有考虑的必要。此外,相位角的选取也对响应有明显影响,相位角按照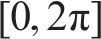
2.4 连续行人流过桥模拟分析
为了与SILVA在该桥上的实测结果进行对比,以验证利用ABAQUS子程序施加步行荷载的合理性,选取KERR动载因子进行步行荷载的模拟,人群密度选取0.3,0.7,0.9 人/m2 3种工况,对应桥上同时存在的人数为5,11,15,0.3 人/m2的密度表示在一个群体中对个人的速度和步幅的选择不受限制的情况。
人体动力学模型施加方式是移动力和固定人体动力学模型,根据给定的行人密度沿结构分布固定的人体动力学模型。为验证SILVA研究中施加随力同时移动的人体动力学模型和固定的人体动力学模型的模拟结果相近性,采用沿结构纵向均匀分布固定的人体动力模型的方式来模拟结构上人群动力学特性。为了模拟20 s的连续移动行人流,需要在子程序中设计一组队列加载位置点,下面以0.3 人/m2工况来进行说明。
1) 首先,确定加载位置点的延伸。此延长距离为等候的行人在离开结构前必须经过的距离。为了得到20 s持续行人流,通过将平均速度乘以20 s并将此结果与人行桥的跨度长度相加,获得队列行人的延伸长度。
2) 为了保持结构上行人数始终近似保持特定人群密度,延长线上放置的行人数需要计算获得。
3) 队列中每个人的加载位置点从出桥口位置反向延伸并依据平均间距均匀分布。
在固定人体动力学模型的情况下,为与文献中的ANSYS梁单元模型模拟结果对比,队列中所有行人的随机步频和质量均来源于SILVA实验中数据,详见表3,获得人体横竖向SMD模型参数。表4给出了各密度下实测和模拟分析的均方根加速度的平均值和标准差。
| 工况 | 人数 | 步频/Hz | 体重/kg | |
|---|---|---|---|---|
| 均值 | 标准差 | |||
| 人群密度0.3 人/m2 | 5 | 1.90 | 0.12 | 均值:63.82 标准差:9.88 |
| 人群密度0.7 人/m2 | 11 | 1.80 | 0.12 | |
| 人群密度0.9 人/m2 | 15 | 1.76 | 0.11 | |
| 人群密度/(人∙m-2) | 实测值/(m∙s-2) | 文献[7]中纯荷载/(m∙s-2) | 本文中纯荷载/(m∙s-2) | 力和人体动力模型/(m∙s-2) | ||||
|---|---|---|---|---|---|---|---|---|
| 均值 | 标准差 | 均值 | 标准差 | 均值 | 标准差 | 均值 | 标准差 | |
| 0.3 | 0.116 4 | 0.019 9 | 0.139 7 | 0.035 5 | 0.129 7 | 0.008 3 | 0.119 1 | 0.003 5 |
| 0.7 | 0.085 4 | 0.009 7 | 0.113 0 | 0.019 1 | 0.116 2 | 0.007 0 | 0.102 7 | 0.003 5 |
| 0.9 | 0.098 4 | 0.005 0 | 0.112 2 | 0.021 1 | 0.113 1 | 0.002 3 | 0.096 5 | 0.005 4 |
从表4可知,与纯荷载模拟相比,在荷载模拟基础上考虑人体效应的结果与测量结果更为符合,因此在获取更为精确模拟效果时,有必要采用力和人体动力学模型联合模拟来表示行人的行为。对比文献[7]在ANSYS梁单元中模拟纯移动荷载和在ABAQUS实体壳体混合单元模型中借助Dload接口施加移动步行荷载的模拟结果,均值最大误差为7%左右,利用ABAQUS的子程序施加步行荷载的合理性得到了验证。
分析0.3,0.7,0.9 人/m2 这3种人群密度在2种人群模拟方式下的跨中竖向典型加速度时程曲线及其频谱图和平均频谱图,其中0.7 人/m2的计算加速度频谱结果见图9。
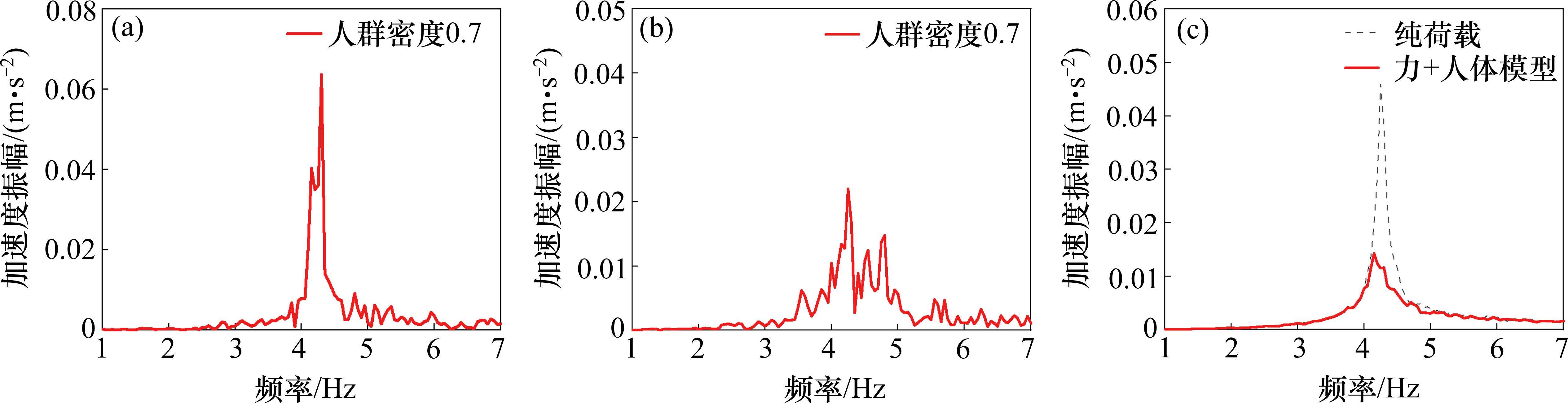
从图9可知,单纯荷载表示行人行为时结构振动能量相当集中,只有在结构基频值处出现峰值。在典型频谱图中可以看出,结构上考虑人体动力模型后,在结构空载基频周围也存在较为显著的能量贡献,与文献实测频谱图中观察到的现象较为一致。联合模拟在共振区上的峰值仅为纯荷载模拟的32%,主要由于人体模型提供了额外的阻尼。实测结果表明,随着结构上的行人数量的增加,测得的特征峰对应的频率持续降低。这在联合模拟中也发现类似的现象,而在单纯荷载模拟中无法体现这一现象。可见联合模拟方式很好体现了行人在振动表面行走的净效应。在模拟人群工况时,考虑人体动力学模型可有效避免单纯荷载模型导致的保守估计。
3 人群行走下人行桥振动影响因素分析
多人荷载的精确模拟问题较为复杂,存在行人与行人、行人与人行桥间的相互作用。针对2.1节建立的人行桥三维空间实体-壳有限元模型,基于ABAQUS子程序中较真实地模拟交通流状况的人群效应的方法,探究人群模拟方式和分布,以及考虑HSI效应对不同动力特性人行桥的动力性能的影响。
3.1 不同人群模拟方式的差异分析
在分析人群宏观模拟方式和Dload子程序所施加的微观人群荷载模拟方式差异时不考虑人体动力学效应。为涵盖主要的人群密度工况,选取0.3,0.7,1.1,1.5,1.9 人/m2的5个人群工况进行分析,对应的人数依次为6,14,22,30,38人。由于分析行人流中整体化和离散化加载的区别,需要消除荷载模型的差异,故微观加载和宏观加载均采用ISO10137的3阶竖向荷载模型。微观加载中需考虑加载位置的随机性,分析得出随机模拟15次即可获取其正态统计规律。宏观模拟采用10 s加载计算,微观采用连续20 s行人流加载计算。表5为不同人群模拟方式在各种密度下的简支梁跨中横竖向加速度响应值。
| 模拟方式 | 工况 | 人群密度/(人∙m-2) | ||||
|---|---|---|---|---|---|---|
| 0.3 | 0.7 | 1.1 | 1.5 | 1.9 | ||
| ISO10137宏观模拟 | 竖向 | 0.489 1 | 0.304 9 | 0.136 5 | 0.207 3 | 0.204 7 |
| 横向 | 0.000 4 | 0.000 2 | 0.000 1 | 0.000 2 | 0.000 2 | |
| ISO10137微观模拟 | 竖向均值 | 0.656 8 | 0.319 0 | 0.138 5 | 0.224 3 | 0.219 0 |
| 竖向标准差 | 0.034 1 | 0.012 5 | 0.006 0 | 0.009 2 | 0.008 0 | |
| 横向均值 | 0.001 5 | 0.001 4 | 0.001 3 | 0.001 3 | 0.001 0 | |
| 横向标准差 | 0.000 2 | 0.000 3 | 0.000 3 | 0.000 4 | 0.000 3 | |
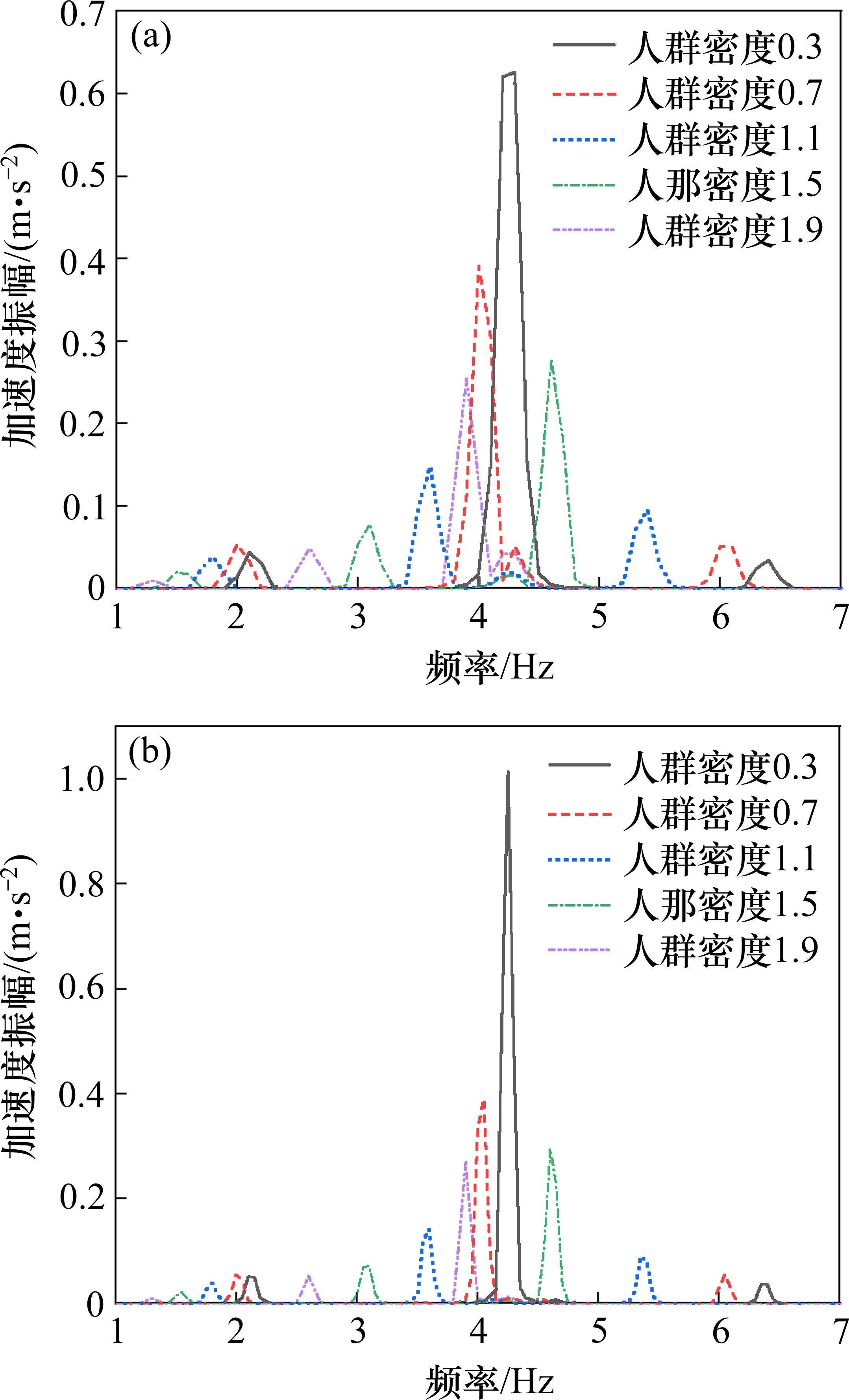
表5说明在人群密度较低时,宏观和微观模拟的响应有较大差异,差异率达到26%。而当人群密度达到0.7以上后差异率均低于10%,满足工程等效误差,可采用宏观方式进行简化。对不同人群模拟方式下的跨中竖向加速度时程进行快速FFT变换得到相应的频谱图,见图10。2种模拟方式在竖向共振频率带附近的主特征峰的振幅值及其偏差率[(微观-宏观)/微观],见表6。
| 模拟方式 | 人群密度/(人∙m-2) | ||||
|---|---|---|---|---|---|
| 0.3 | 0.7 | 1.1 | 1.5 | 1.9 | |
| 宏观 | 0.626 7 | 0.391 4 | 0.148 3 | 0.278 2 | 0.256 7 |
| 微观 | 1.015 0 | 0.390 9 | 0.141 3 | 0.295 0 | 0.271 4 |
| 偏差率/% | 38.3 | -0.1 | -5.0 | 5.7 | 5.4 |
表6说明在低密度条件下,以均布形式代替实际人群空间分布的近似方式存在一定的缺陷。随着密度增加,人群中个体间距的缩短,当密度达到0.7以上后采用均布方式替代模拟可起到合理简化的作用。
3.2 人群分布差异的影响
为探究人群行走时空间位置分布差异的影响,本文从分布状态和人群通行方向进行了分析,主要考虑4种模拟工况,工况布置见表7,分析过程中发现模拟15次结果较为稳定,可获取其正态统计规律,由于结果随机,采用15次计算的均方根加速度响应均值作为中心结果,不同工况下横竖响应随路径间距的变化计算结果见图11。
| 工况编号 | 路径 | 人数/人 | 纵向分布方式 | 上桥方向 |
|---|---|---|---|---|
| 工况1 | 双路径 | 12 | 均匀分布 | 同向 |
| 工况2 | 随机分布 | 同向 | ||
| 工况3 | 均匀分布 | 相向 | ||
| 工况4 | 随机分布 | 相向 |
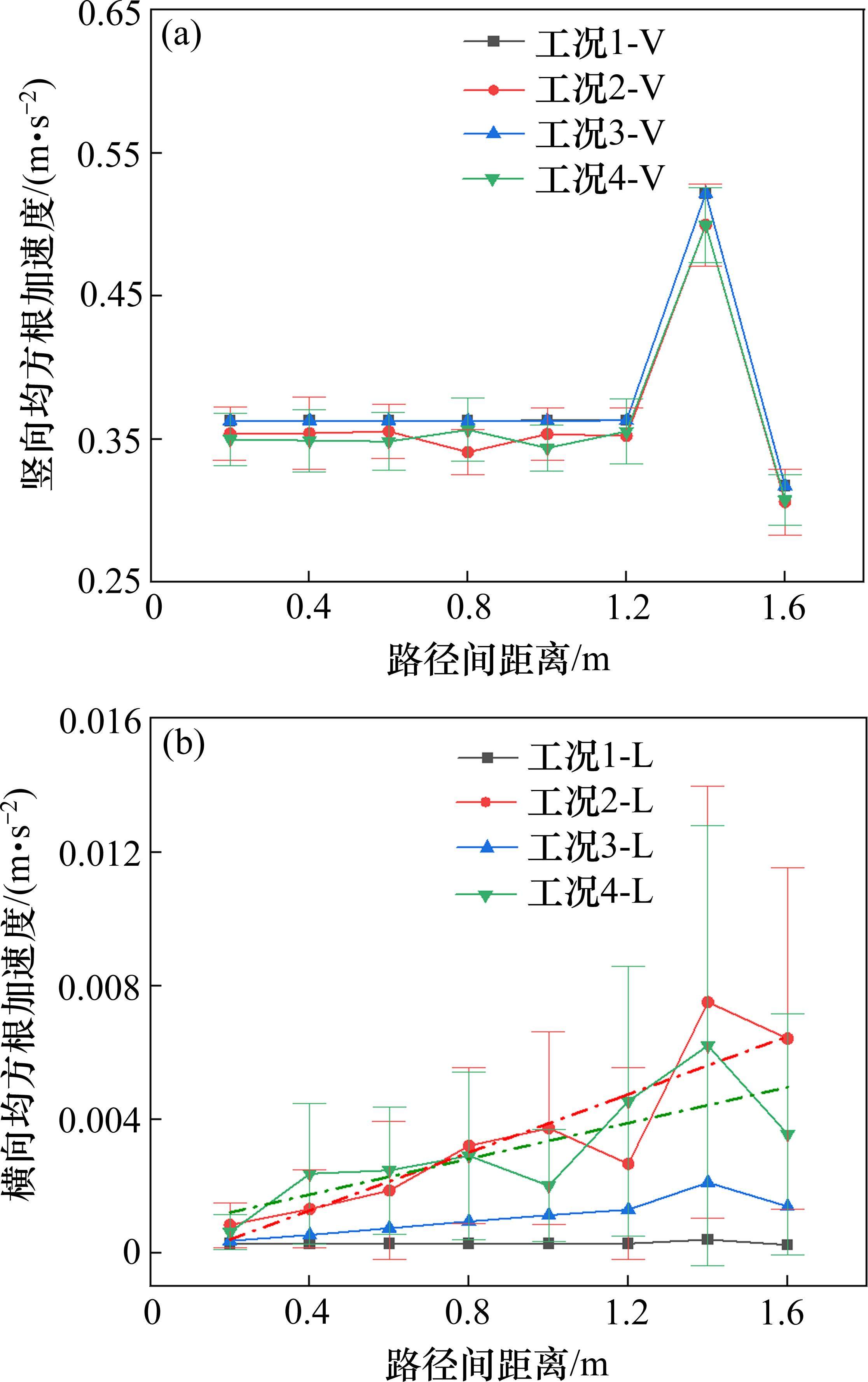
由图11可知双路径在不同纵向分布的竖向响应的最大差异率为6.1%,而横向的最小差异率为71.1%,说明行人纵向分布对横向振动响应的影响更显著。在双路径下不同行走方向的竖向响应的最大差异率为4.4%,而对应的横向响应的最小差异率为23.2%,表明路径的方向性对横向振动的影响更显著,对竖向的影响也可忽略不计,人行桥的振动响应与人群步行同步率之间存在强烈的正相关性。
3.3 人群-桥耦合对结构响应的影响
为分析人群-桥耦合状态下不同空载基频的结构上的人群对耦合系统的影响,与不考虑人群-桥耦合下的振动响应进行对比。选择人群密度0.3 人/m2作为研究工况,假设每位行人步行状态一致,设定每人质量为70 kg,步频恒为2.0 Hz,步速为1.3 m/s,同时行人沿着结构中轴线移动且人群沿结构纵向均匀分布。为保证作用在处于不同动力特性状态下的结构上的行人流荷载的一致性,采用确定的前3阶相位角,即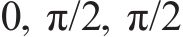
由于模拟连续行人流状态,人体模型可采用固定的方式模拟,沿结构中轴线纵向均匀布置,与人群初始移动荷载位置一致。按照人群密度0.3人/m2对应的人体动力学模型表达式建立与结构相耦合的人体生物动力学SMD模型。通过调整ABAQUS中材料属性的弹模参数,达到改变结构频率的效果。结构尺寸及材料密度均保持不变,弹性模量在2~50 GPa间取值,经ABAQUS频率求解器得到结构基频从1.1 Hz变化到5.5 Hz,大致涵盖了易出现大幅振动的人行桥的基频范围。
图12为是否考虑人-桥耦合(联合系统和空载状态)各自对应的前3阶系统频率随结构刚度的变化情况,频率及响应的变化率表示为[(联合系统-空载状态)/空载状态]。图13为不同动力特性的简支梁的跨中、1/4跨、3/4跨侧边节点上的竖向均方根加速度的变化曲线。
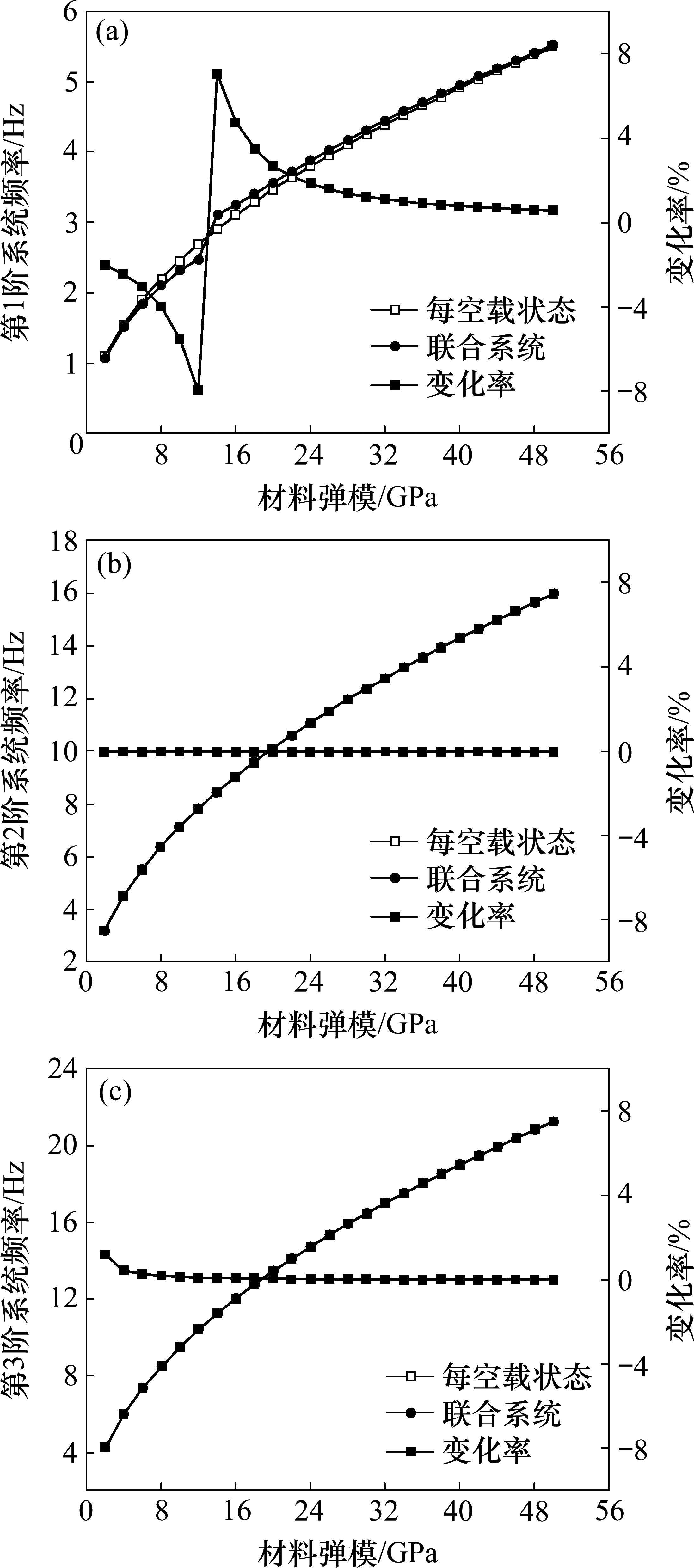
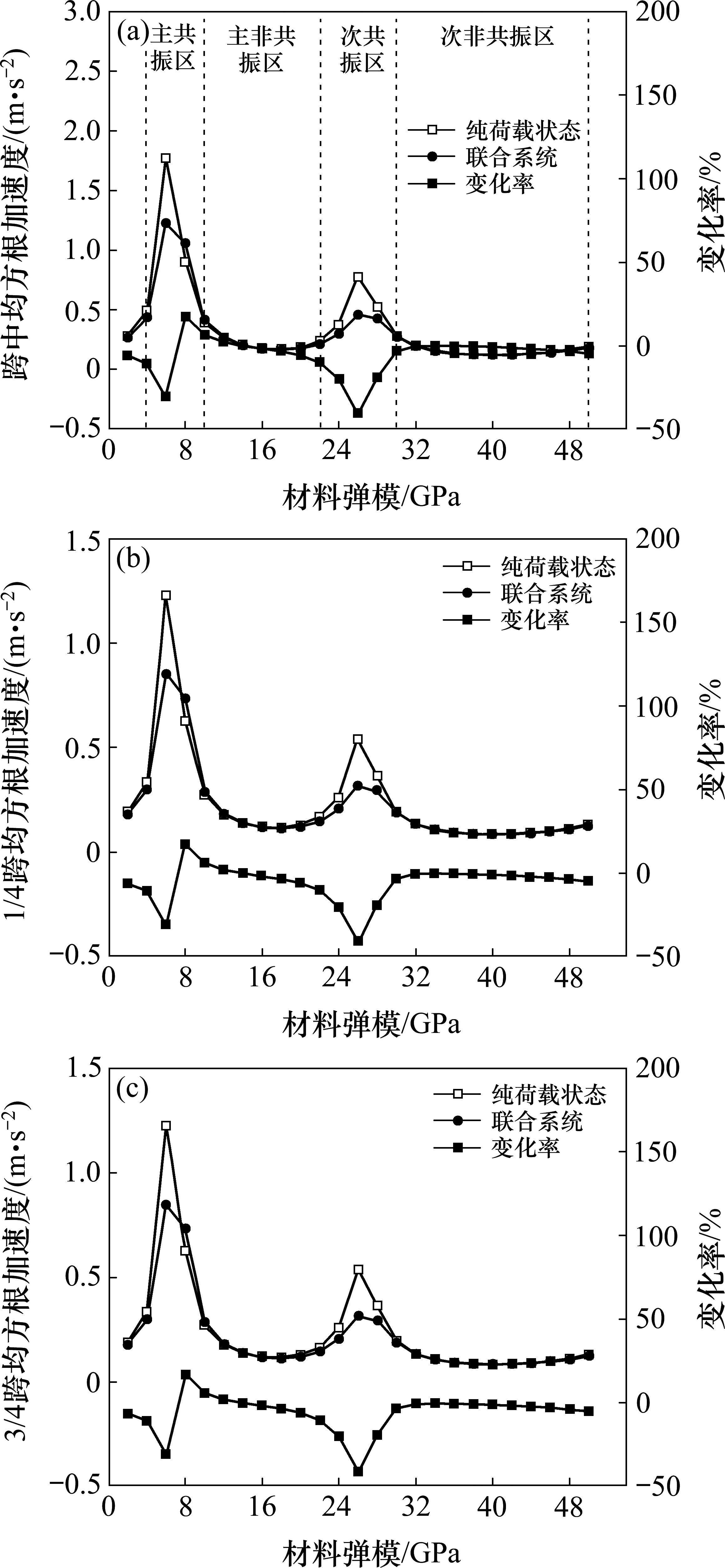
图12和图13表明人群对人行桥的动力特性的影响与空载基频和人群整体模态频率相对大小有关,当空载基频小于人群整体模态频率时会出现耦合系统基频降低的趋势,反之有增加的趋势,而当两者相接近时,所引起的变化率也越大。当人行桥基频处于人群整体步行频率及其倍频范围上时,为避免高估结构的振动响应,有必要在人行桥动力设计中考虑HSI效应对振动响应的影响。而在非共振区上,两者间的差异率普遍处于10%以下,HSI效应对响应结果影响可以忽略不计。
4 结论
1) 当人行桥处于非共振时MF模型和SMD模型的差异率仅为0.8%,此时人体模型对振动响应影响很小,但当人行桥处于共振时两模型的差异率约为15%。因此在临近共振状况下,有必要考虑人体模型的影响。
2) 分析小组和连续行人流过桥,发现考虑高阶谐波的响应比简化模型有显著增加,最小增幅约为83.2%,因此高阶谐波有考虑的必要;相位角按照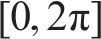
3) 行人纵向分布和路径的方向性对横向振动的影响很显著,对竖向振动的影响可忽略;人行桥振动响应与人群同步率之间存在强烈的正相关性;当人行桥基频处于人群整体步行频率及其倍频范围内时,为避免高估振动响应,有必要考虑HSI效应对振动响应的影响。在非共振区域,两者间的差异率普遍处于10%以下,HSI效应对响应结果影响可以忽略不计。
唐冕,张金龙,宋旭明等.人-结构相互作用对人行桥振动响应的影响分析[J].铁道科学与工程学报,2025,22(01):207-220.
TANG Mian,ZHANG Jinlong,SONG Xuming,et al.Influence of human-structure interaction on vibration response of footbridge[J].Journal of Railway Science and Engineering,2025,22(01):207-220.

