注浆是岩土工程加固的重要手段,在交通、水利、采矿等工程领域得到广泛应用[1-2]。研发注浆加固的新理论、新方法始终是人们关注的重要问题[3-5]。根据注浆机理,现有注浆方法主要可分为渗透注浆、裂隙充填注浆、压密注浆、劈裂注浆等类型[6-9]。中国学者于1997年提出了振动注浆方法,其核心原理是利用振动装置对饱和砂土施加扰动,使孔隙水压力升高,有效应力降低,强度随之下降,从而减小浆液在土体中的流动阻力,增强其扩散性能,最终达到提升注浆作业效率和加固效果的目的[10]。近20年来,关于振动激励对浆液在饱和砂土中扩散性能的影响受到广泛关注,不少学者采取试验、仿真模拟等方法开展相关研究。杨秀竹[11]利用沿竖向振动的模型试验装置(设3个振动支承点),对装满饱和砂土的水平放置圆管进行了振动频率为1 Hz的整体振动注浆试验(注浆孔位于圆管中部),发现浆液在饱和砂土中的扩散范围随注浆压力、振动时间的增加而增大。凌晨[12]采用小型振动台对装有饱和砂土的有机玻璃圆桶施加振动荷载使土体发生液化后进行注浆实验,结果表明在振动条件下极小的注浆压力即可驱动浆液扩散,振动作用能够显著增大浆液在饱和细砂中的扩散范围。李晓广[13]利用振动棒对饱和粉细砂开展了振动试验,发现随着振动时间延长和离振动中心距离的减小,土体表观黏度和锥尖阻力逐渐降低,在试验范围内随着振动频率增加,砂土液化效果愈加明显。马成伟等[14-15]利用水平放置的钻杆(一端连接声频振动试验台、一端伸入砂土试样)对非饱和粉细砂土施加轴向声频振动,研究了振动频率、激振力和振动持时对扩散性能的影响规律,结果发现,在轴向振动条件下,酸性水玻璃浆液扩散半径随振动持时和振动频率的增加而增大,激振力大小对浆液扩散性能影响不明显。周海林[16]围绕振动注浆问题,采用有限元方法模拟分析了振冲泵垂直振动激励作用下饱和砂土的液化特征,发现振动频率愈高,超静孔隙水压力增长愈快,随着振动时间增加,孔隙水压力逐渐上升,土体有效应力减小,刚度下降,对应力波的传播产生抑制作用,进而影响扰动范围。雷金山等[17]基于有限元方法,采用套叠屈服面模型分析了注浆孔底部和孔壁分别作用振动力情况下孔隙水压力分布特征,结果显示注浆孔中部结点残余孔压和峰值孔压最大,其次是注浆孔底部结点,注浆孔顶部结点孔压最小,振动力越大,各结点残余孔压和峰值孔压越大。总体来看,目前关于振动注浆研究虽取得了一定成果,但依然相对匮乏,离工程化应用尚有一定距离。振动注浆过程中振动激励的作用方式从原理上可分为轴向和径向加载2种。轴向方式通过对钻杆施加的轴向振动荷载,经杆体作用于杆端前方土体,对杆体径向大范围土体几乎不产生扰动效应,且由于杆端作用面较小,对轴向土体产生的扰动影响区域十分有限,目前声频振动注浆试验主要采取这种方式。径向加载方式是利用装置将径向振动作用施加于孔壁,从而引发周围径向土体的松动,但目前径向激振研究主要集中在数值模拟方面,试验研究相对较少,主要在于试验方法还不够成熟,缺乏必要的激振设备。由于实际工程中的激振荷载通常为局部振源,因此基于振动台的整体振动试验方式不足以有效反映工程现场局部振源对周围土体的空间扰动效应。采用振动棒尽管能够对土体产生径向扰动影响,但该试验方法无法调节振动频率,无法与注浆部件组合形成完备的振动注浆试验装置。鉴于此,本文研制了具有径向激振和频率可调功能的振动注浆模型试验装置,首先利用该系统开展饱和砂土振动系列试验,研究径向振动激励对饱和砂土的扰动机制,揭示不同振动频率下饱和砂土超孔隙水压力演变规律和时空分布特征,然后进行振动注浆试验,测试不同振动频率、注浆压力和注浆时间条件下水泥浆液在饱和砂土中的扩散特性,旨在为深入开展振动注浆机理研究提供一定参考。
1 试验装置及试验材料
1.1 试验装置
振动注浆模型试验装置主要包括振动注浆系统、模型箱和支架,如图1所示。

振动注浆系统主要由振动器、环形出浆孔、输浆管、隔振装置、止浆塞、传动软轴、变频器、变频电机和注浆机等构成。振动器为圆柱状,长40 cm,直径7.6 cm,位于注浆管出浆段。振动器内部设置偏心块,通过传动软轴与变频电机连接,利用变频器调节电机转速,从而使振动器产生不同频率和大小的径向激振力,其激振力计算表达式如式(1)所示:
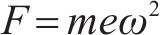
式中:ω为角速度;m=0.29 kg(偏心块质量);e= 0.012 m(偏心距);F为振动器激振力。
振动器通过柔性隔振装置、连接杆与支架连接,柔性隔振装置将振动器产生的振动能量集中作用于注浆位置,提高能量利用率;环形布置的出浆孔设置于振动器中部;连接杆下部设止浆塞,通过充气膨胀封闭杆体与土体间隙,阻断下部浆液向上部扩散。变频电机如图2(a)所示,其额定功率为3 kW,转速最高可达3 000 r/min。变频器控制电机转速,激振频率调节范围为0~50 Hz,如图2(b)所示。采用螺旋注浆机实施注浆,如图2(c)所示,最大注浆压力可达3 MPa,最大流量为20 L/min,可通过调节螺杆转速控制注浆压力和流量。

圆柱状模型箱采用1 cm厚钢板制作,高1.3 m,直径为1.2 m。支架用于承载和固定振动器、连接杆和变频电机。
1.2 试验材料
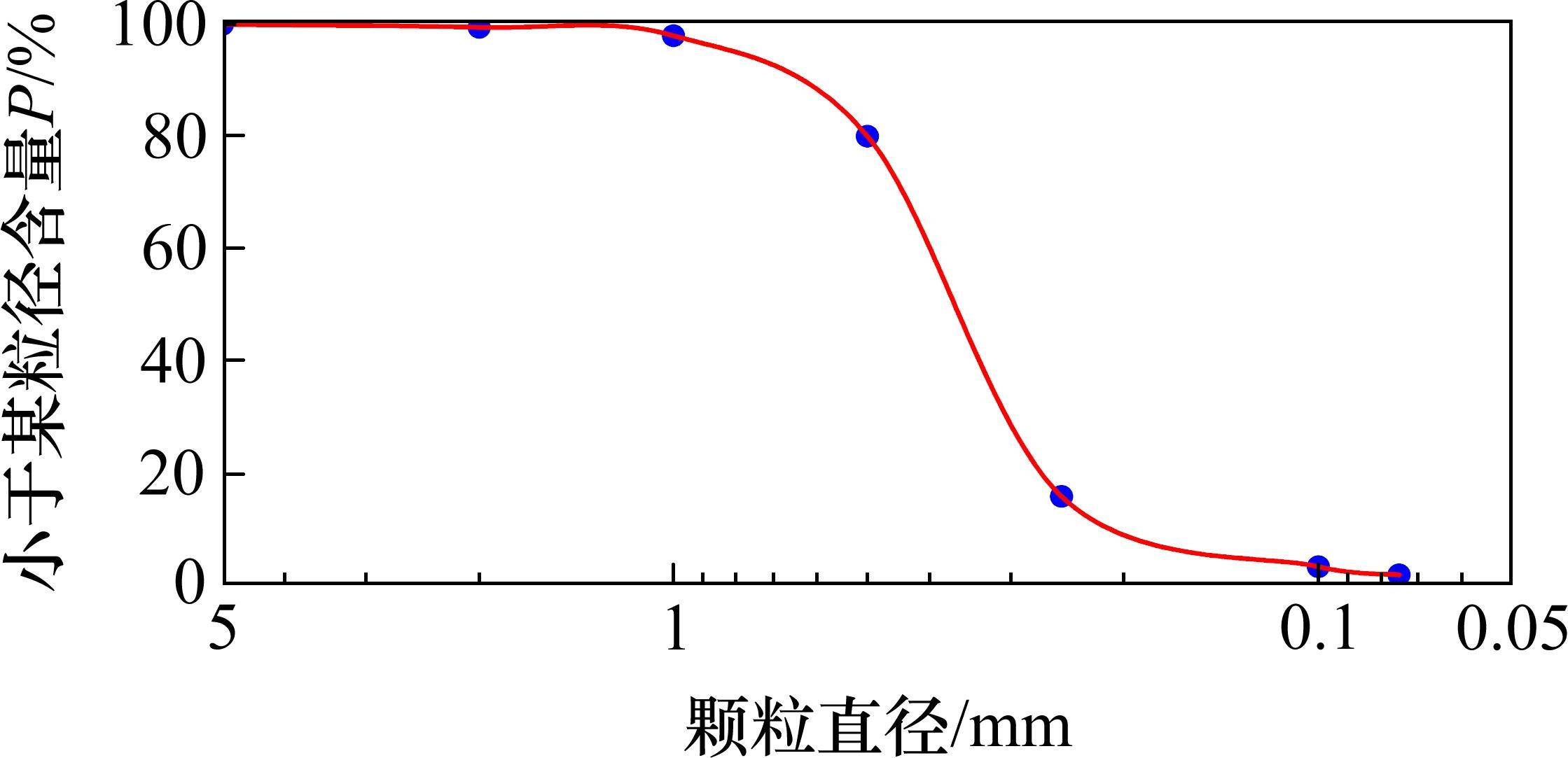
试验使用的砂样取自河南省赵口引黄灌区工地。灌区渠道施工过程中,受施工设备振动荷载作用,砂土地基出现不同程度液化现象,丧失承载能力,导致挖掘机沉陷,无法作业,为解决灌区饱和砂土液化影响施工问题,利用该地区砂土开展振动注浆模型试验研究。图3所示为试验砂土粒径级配曲线,表1列出了砂样基本物理性质。将试验砂土摊铺均匀并晾干,然后采用水沉法制备饱和砂土。
| Gs | γsat/ (kN∙m-3) | K/ (cm∙s-1) | ρdmax/( g∙cm-3) | ρdmin/ (g∙cm-3) |
|---|---|---|---|---|
| 2.70 | 19.8 | 1.69×10-2 | 1.852 | 1.396 |
注浆材料采用地聚物浆液,由水泥、粉煤灰、矿粉、微硅粉、氧化钙类、硫铝酸钙-氧化钙类、硫铝酸钙类等组分配置而成,试验中按设定水灰比0.4称取定量的水和地聚物材料,先将水倒入拌合桶,再将地聚物材料分次倒入,边加边利用电动搅拌器搅拌,将材料混合均匀后,倒入螺旋注浆机,实施注浆。浆液流动度约为12.7 s,初凝时间为180 min,终凝时间为360 min,固结体抗压强度可达34 MPa。
2 径向振动对饱和砂土扰动特征试验
2.1 试验方案设计
2.1.1 监测系统及传感器布置
设计振动频率10、30和50 Hz这3个工况,分别开展振动试验。
数据监测系统由动态孔压传感器、动态数据采集仪构成,如图4所示。动态数据采集仪选用DH5922N采集仪;孔压传感器选用CYY2型号动态水压力传感器,其量程范围为-50~50 kPa,精度可达0.5%。

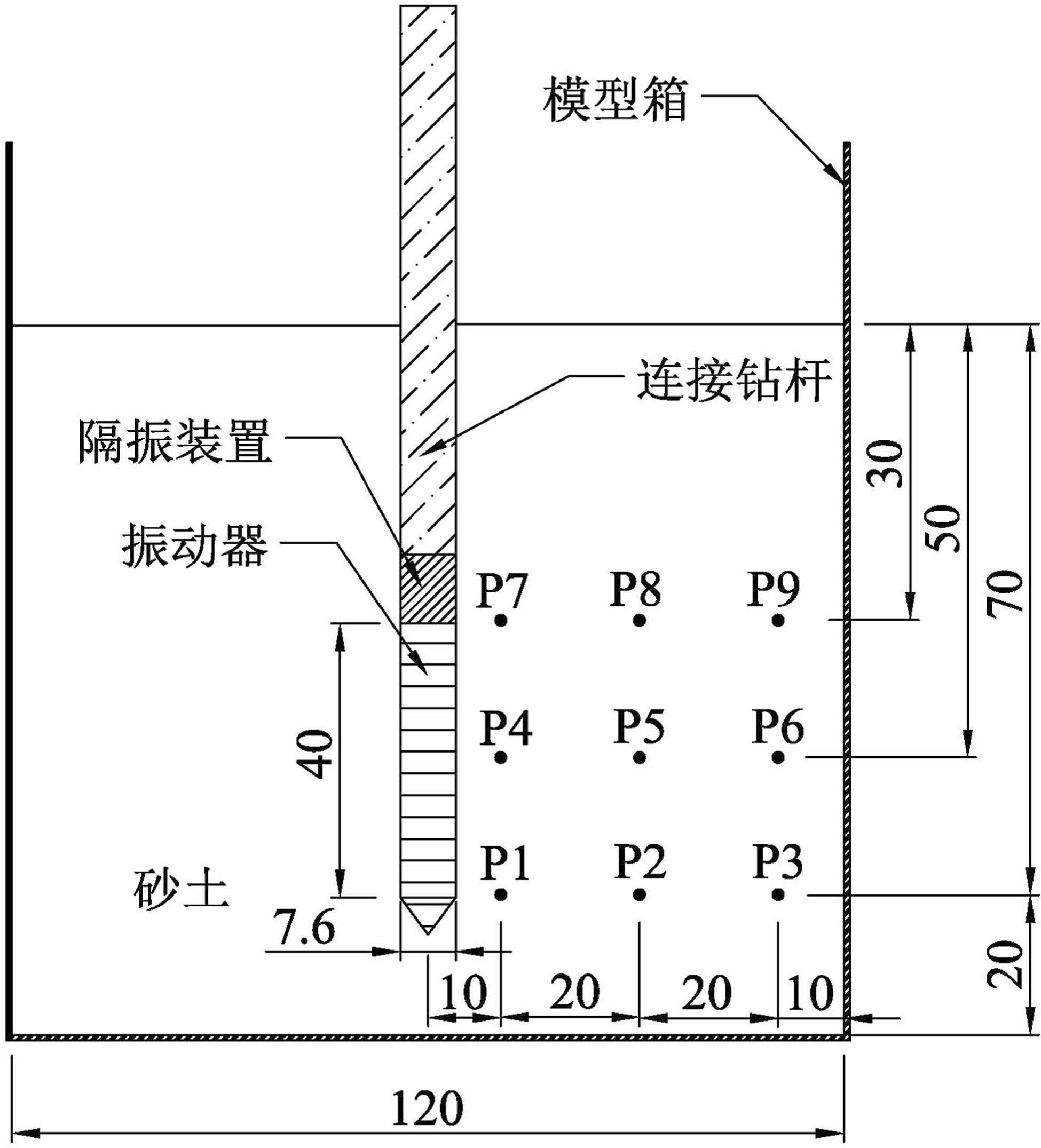
本研究中,在径向振动激励作用下,饱和砂土的受扰动状态以振动器中心轴为轴心,呈中心对称分布,因此取过振动器中心轴的剖面为监测断面,以振动器中心为基准点,以与其等高位置水平线为基准线,沿径向在距振动器中心10、30和50 cm处各设一监测点,沿竖向在与振动器顶部和底部对应位置分别布置监测点,如图5所示,以获取沿竖向特定位置和沿径向不同距离处土体的扰动数据,便于分析振动器周围土体受扰动效应的空间分布特征。
2.1.2 试验步骤
试验步骤如下。
1) 将振动器放置于设定深度;
2) 在模型箱内利用水沉法制备饱和砂土,达到孔压传感器设计深度时暂停装入砂土,随后埋设传感器,继续向模型箱内添加水和砂土至预定高度;
3) 在模型箱中制备土样并静置24 h;
4) 通过变频器设定振动频率,开启监测设备与振动器;
5) 记录孔隙水压力随时间变化数据;
6) 达到设定振动时间,停止振动。
2.2 试验结果分析
2.2.1 孔压变化特征指标
最大孔压振荡幅度ΔPmax为孔压波动过程中各循环周期内最大孔压与最小孔压差值的最大值,其计算表达式如式(2)所示:
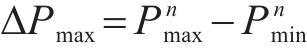
式中: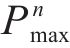
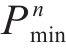
最大孔压相对振荡幅度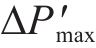
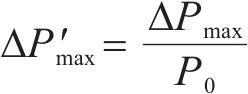
式中:P0为初始孔压。
2.2.2 振动频率的影响
由于P5测点位于监测断面中心位置,能够较好反映土体受扰动响应随振动频率变化过程,因此选取P5测点进行分析。图6为测点P5在10~50 Hz振动频率下孔压变化时程曲线,可以看出,不同频率振动作用下,饱和砂土孔压变化存在显著区别。10 Hz条件下,孔隙水压力基本无变化,超静孔压比峰值仅为0.02,未发生液化。振动频率为30 Hz时,振动开始后孔压逐渐波动上升,30 s左右时达到峰值10.2 kPa,此时超静孔压比为1.06,随后孔压缓慢下降,振动结束时回落至8.8 kPa,孔压振荡幅度也逐渐减小;振动停止后,孔压快速下降,下降速率由快变慢,最终趋近于初始孔压。50 Hz振动条件下,孔隙水压力在短时间内迅速上升至11.5 kPa,超静孔压比峰值达到1.32,孔压振荡过程中平均值大于10 kPa,且振荡幅度有逐渐增大趋势。
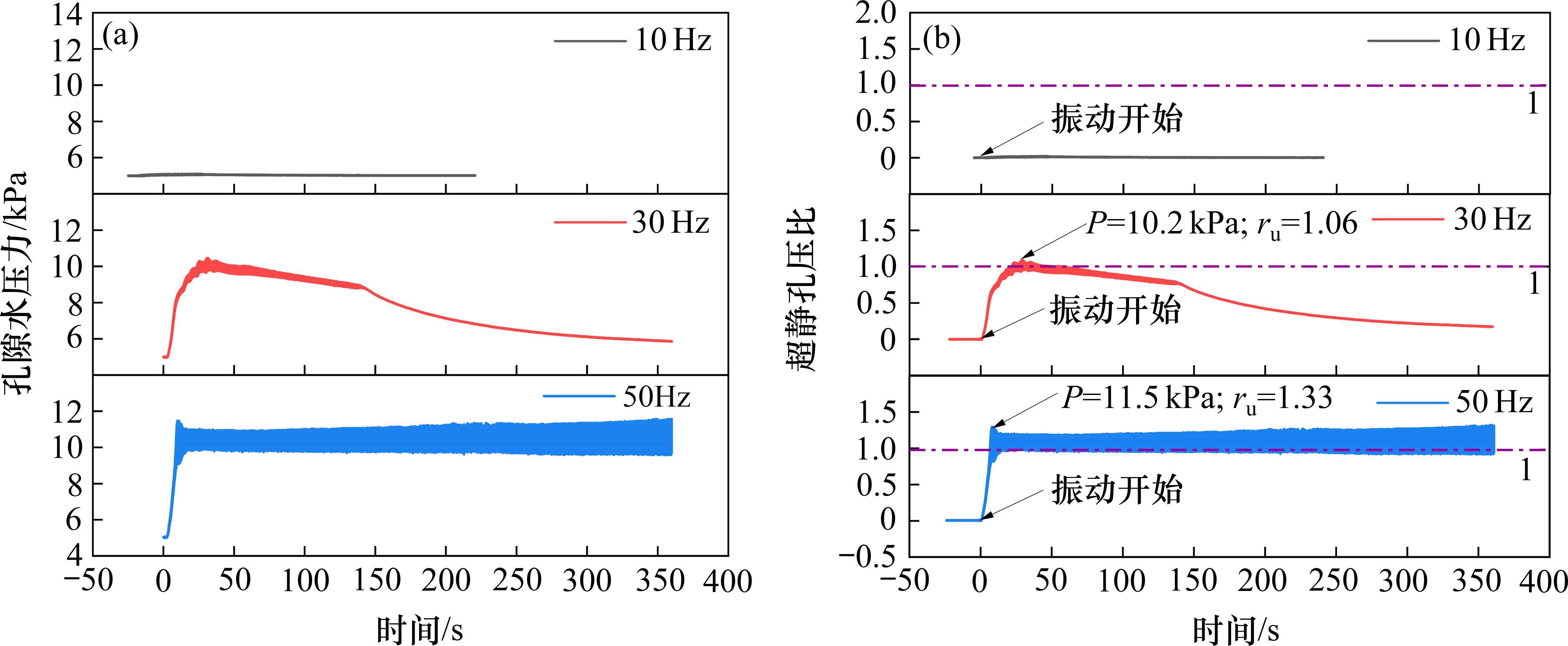
表2列出了P5测点在不同频率下的扰动参数,可以发现,随着频率增加,孔压峰值与最大孔压振荡幅度逐渐增大,超静孔压比大于1.0持续时间变长。这是由于饱和砂土在振动器正弦振动作用下趋于紧密,孔隙水来不及排出,导致孔压增大,随着振动作用的持续,孔压累积上升,直至达到峰值。根据公式(1)可知,激振力随振动频率增加迅速增大,孔压升高速度加快,振荡幅度越大,扰动范围越广。
振动频 率/Hz | 孔压峰 值/kPa | 最大孔压振 荡幅度/kPa | 超静孔压 比峰值 | 超静孔压比大于1.0持续时间/s | 超静孔压比达 到1.0时刻/s |
|---|---|---|---|---|---|
| 10 | 5.1 | 0.1 | 0.02 | 0 | — |
| 30 | 10.2 | 0.8 | 1.06 | 26 | 25 |
| 50 | 11.5 | 2.0 | 1.32 | 355 | 5 |
图7所示为不同振动频率下孔压峰值和超静孔压比峰值。可以看出,10 Hz条件下,所有监测点孔压基本无变化;f=30 Hz时,只有P1、P2、P4和P5达到液化,其余虽未达到液化状态,但其监测点超静孔压比均大于0.8,与土体液化临界值(超静孔压比1.0)较为接近;振动频率为50 Hz时,所有测点达到液化。
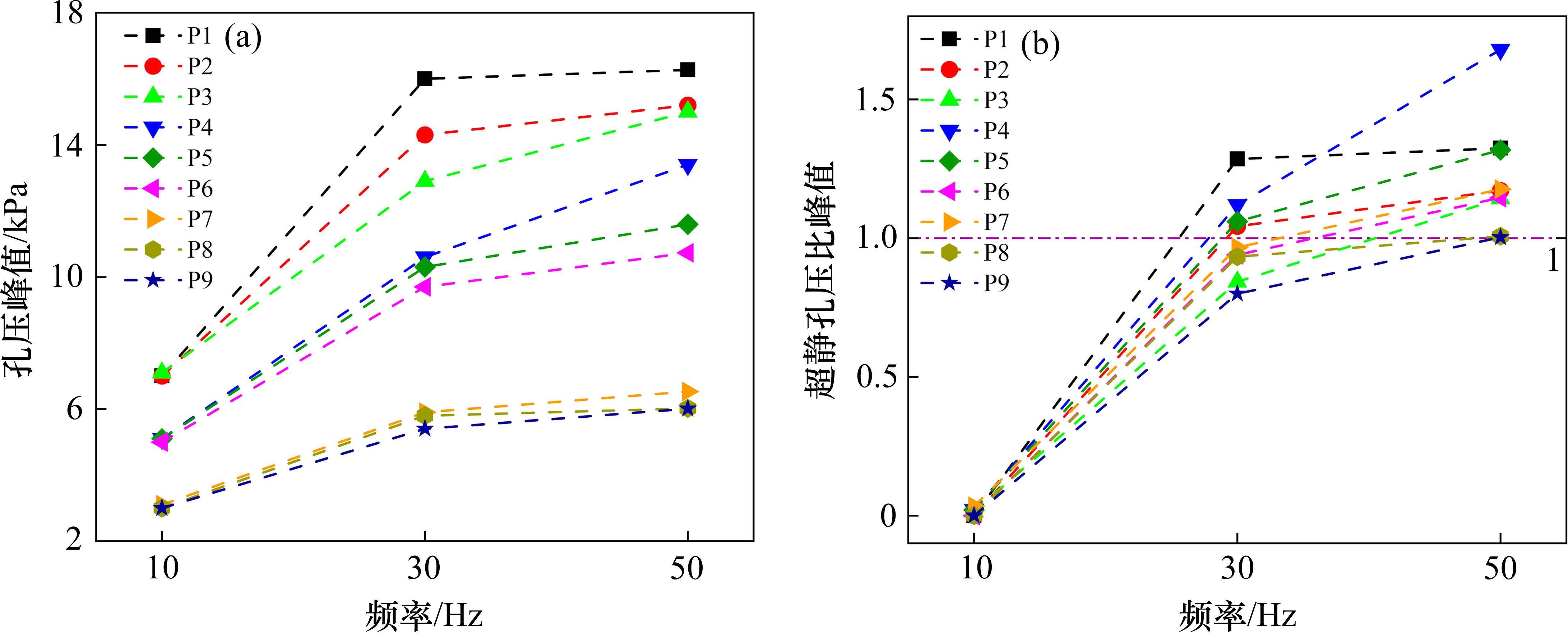
2.2.3 埋深的影响
图8为振动频率50 Hz,距离振动器中心轴10 cm的P1、P4和P7监测点(埋深分别为70、50和30 cm)孔压和超静孔压比时程曲线。可以明显看出,振动试验开始后,P1测点孔压迅速升高至16.2 kPa,然后保持稳定,150 s后孔压振荡幅度略微增大,超静孔压比大于1.0的时间从5.8 s持续至试验结束。P4测点前期孔压迅速升高到13.1 kPa,随后保持稳定振动状态,孔压振荡幅度在4.1~5.5 kPa之间,超静孔压比大于1.0的时间从6.2 s持续至试验结束。P7测点孔压前期迅速上升至6.2 kPa,然后基本保持不变直至振动结束,孔压在0.9~1.2 kPa之间波动,超静孔压比大于1.0的时间从15.8 s持续至试验结束。
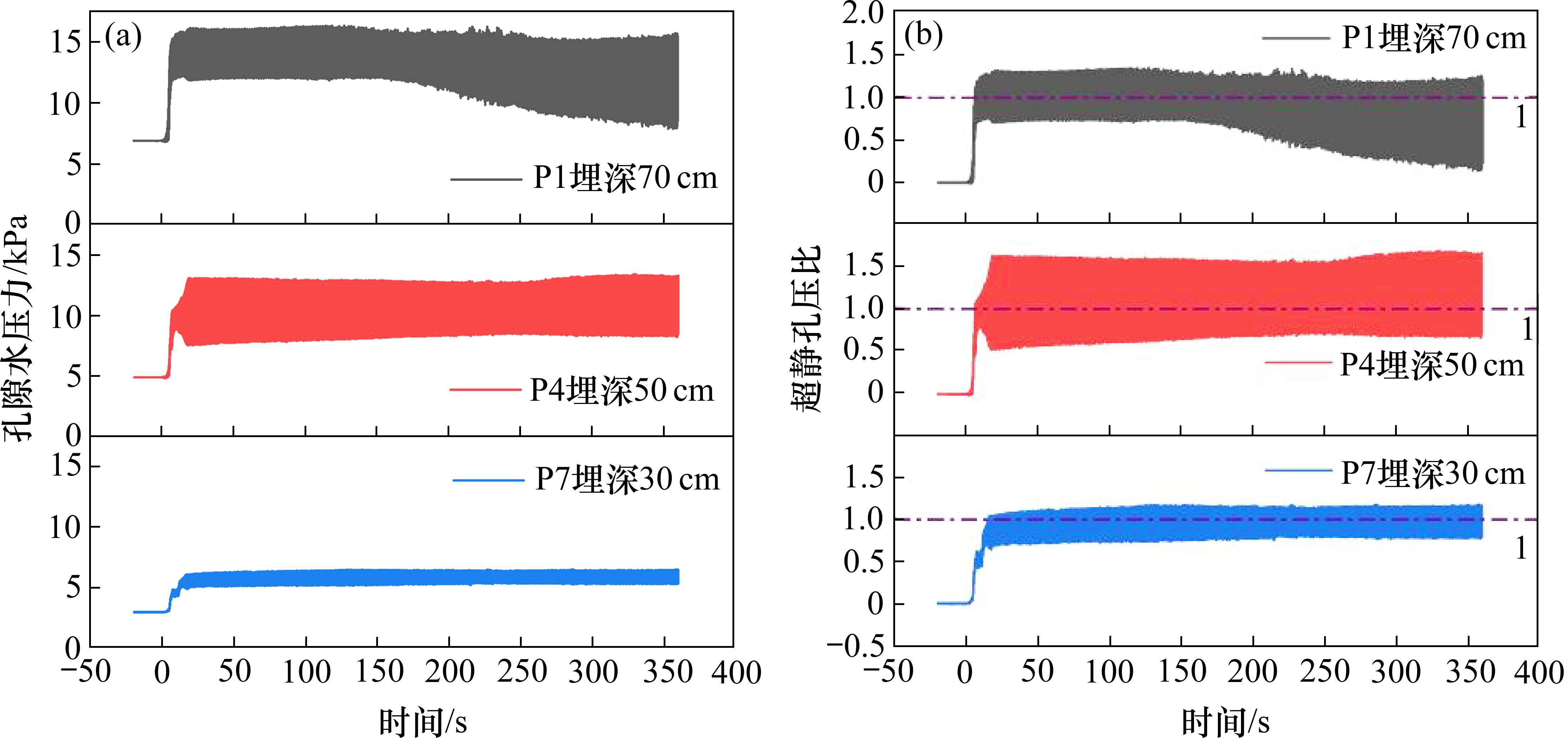
在深入分析P1、P4和P7号测点孔压变化曲线的基础上,提取关键扰动特征参数列于表3中。结果显示,埋深为50 cm的P4测点超静孔压比峰值和最大孔压相对振荡幅度均显著高于P1和P7测点。原因在于,P4测点与振动器中心等高,相较处于振动器两端水平高度的P1和P7测点,受到的振动能量更加集中,从而产生更剧烈扰动影响。因此,在后续的振动注浆试验中,把注浆孔出口设置于振动器中部,理论上有利于浆液扩散。
测点 编号 | 埋深/ cm | 超静孔压比大于1.0起始时间/s | 最大孔压振荡幅度/kPa | 最大孔压相对振荡幅度 | 最大超静孔压比 |
|---|---|---|---|---|---|
| P7 | 30 | 15.8 | 1.2 | 0.4 | 1.16 |
| P4 | 50 | 6.2 | 5.5 | 1.1 | 1.62 |
| P1 | 70 | 5.8 | 7.1 | 1.0 | 1.30 |
2.2.4 测点距振动中心距离的影响
图9为振动频率为50 Hz时,与振动器中心距离分别为10、30和50 cm的P4、P5和P6号监测点(覆土深度50 cm)孔压和超静孔压比时程曲线。可以看出,50 Hz条件下,P4、P5和P6号测点孔压曲线均呈两阶段变化特征,首先在短时间内快速升高,随后保持稳定波动状态。3个测点超静孔压峰值分别为13.1、11.4和10.5 kPa,超静孔压比大于1.0的起始时间分别为6.5、10.6和13.5 s,显然,距离振动器中心越近的土体受扰动影响越剧烈,越早发生液化。
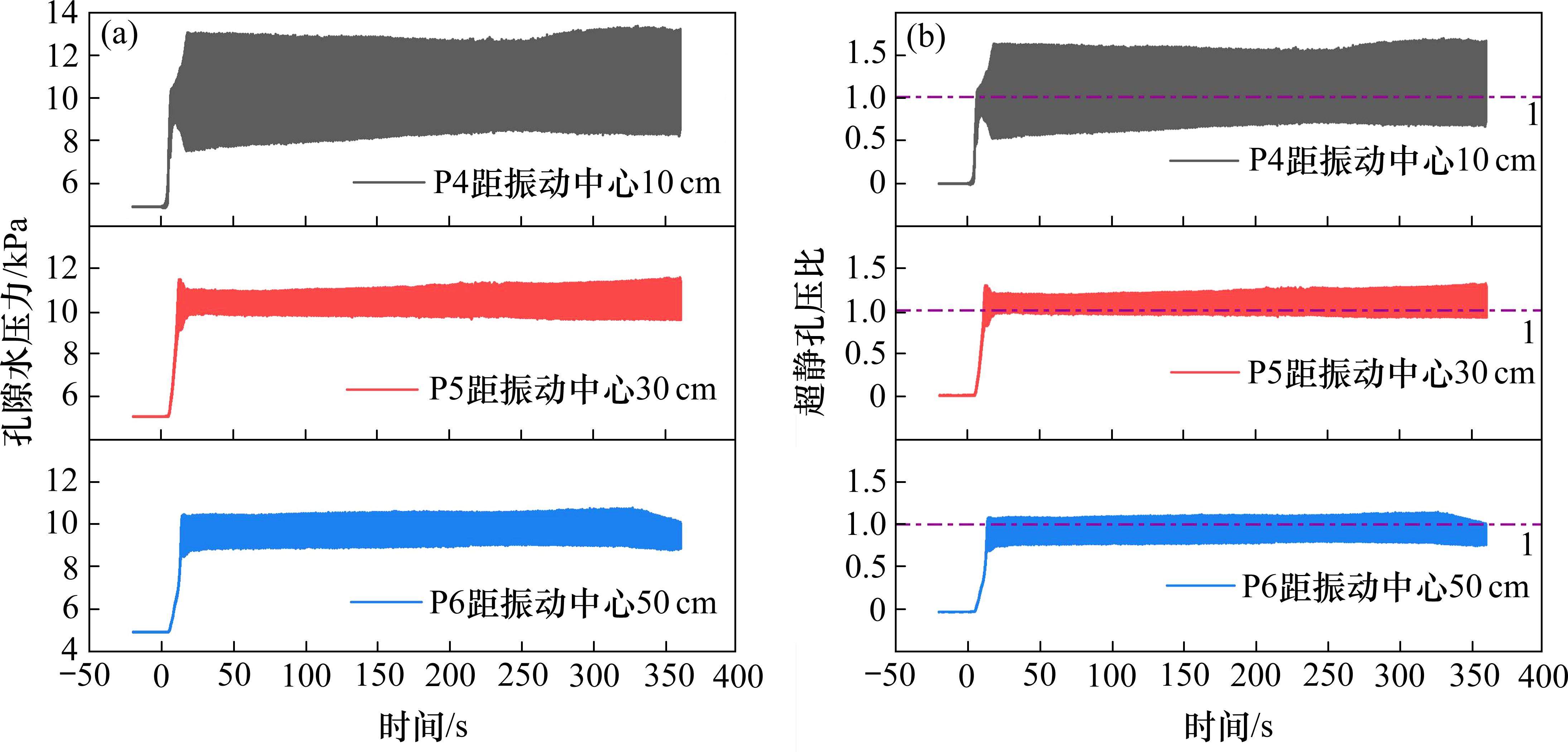
表4中列出了P4、P5和P6号测点孔压特征参数。可以发现,测点离振动器中心越近,其最大孔压振荡幅度、最大孔压相对振荡幅度、超静孔压比峰值越大,超静孔压比达到1.0时刻越早;距离中心越远,各指标变化趋势则相反。表明随着测点与振动器中心距离的增大,振动能量逐渐衰减,振动激励对土体的扰动影响随之降低。
| 测点编号 | 距振动中心距离/cm | 超静孔压比大于1.0起始时间/s | 最大孔压振荡幅度/kPa | 最大孔压相对振荡幅度 | 超静孔压比峰值 |
|---|---|---|---|---|---|
| 4 | 10 | 6.5 | 5.5 | 1.10 | 1.62 |
| 5 | 30 | 10.6 | 2.5 | 0.50 | 1.30 |
| 6 | 50 | 13.5 | 1.6 | 0.32 | 1.11 |
2.2.5 超静孔压比空间分布特征
图10所示为50 Hz条件下超孔压比峰值空间分布图。可以看出,在过振动器中心轴的竖向剖面内,与振动器中心等高的P4、P5和P6测点超静孔压比峰值均高于与振动器顶部和底部等高的对应位置测点;相同埋深处各测点超静孔压比峰值均沿径向逐渐减小。离振动器中心最近的P4测点超静孔压比峰值明显大于其他测点,超静孔压比近似呈以P4测点为中心向四周逐渐减弱的放射状分布特征。
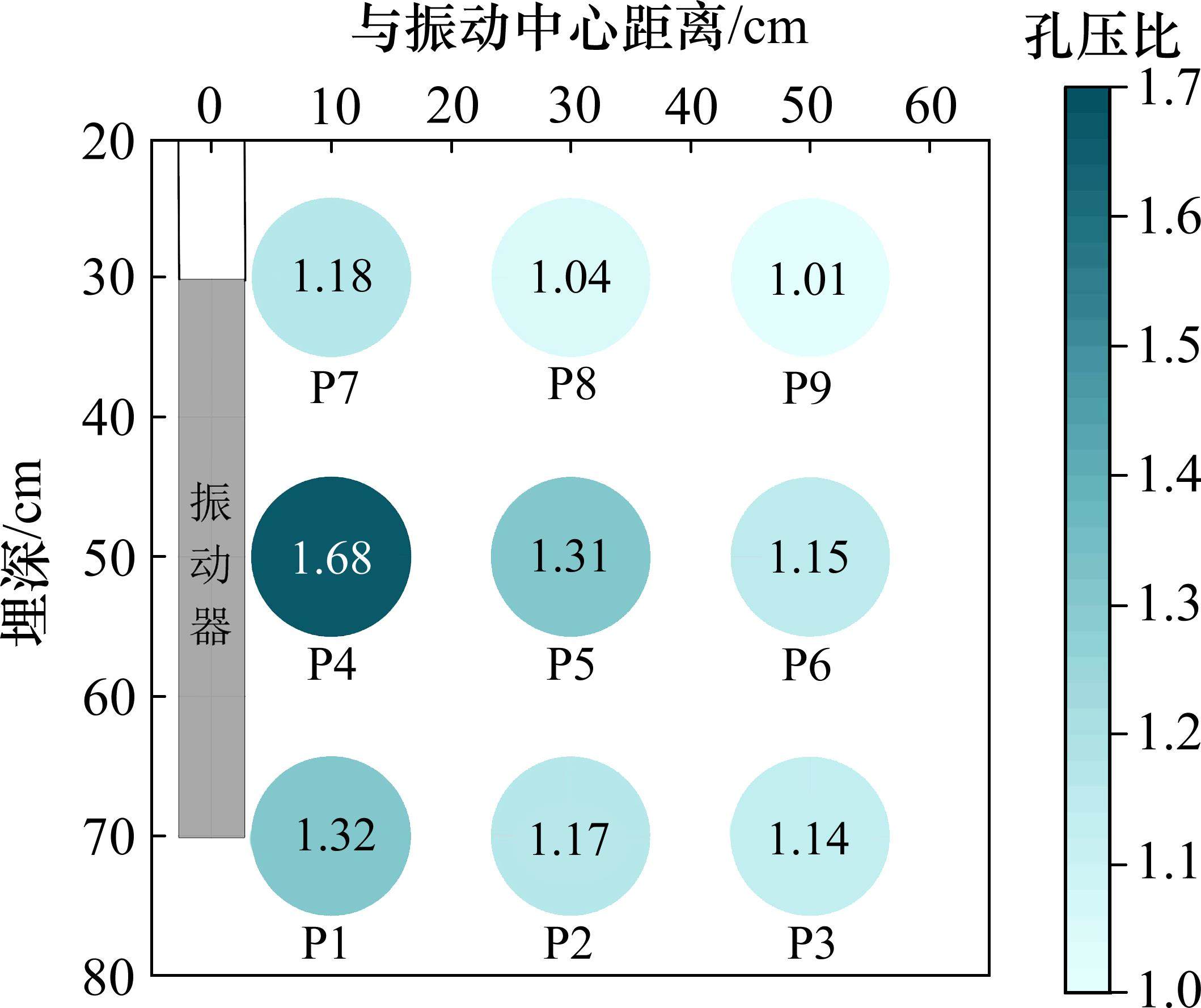
3 径向振动作用下浆液扩散特性测试
3.1 试验方案设计
基于不同条件下饱和砂土扰动特征试验结果,设置振动注浆试验工况如表5所示。试验步骤如下。
| 工况 | 振动频率/Hz | 注浆压力/kPa | 注浆时间/min |
|---|---|---|---|
| 1 | 0 | 100 | 4 |
| 2 | 10 | 100 | 4 |
| 3 | 30 | 100 | 4 |
| 4 | 50 | 100 | 4 |
| 5 | 50 | 20 | 4 |
| 6 | 50 | 60 | 4 |
| 7 | 50 | 100 | 1 |
| 8 | 50 | 100 | 2 |
| 9 | 50 | 100 | 3 |
1) 将振动注浆器放置于设定深度;
2) 采用水沉法在模型箱中制备土样并静置24 h;
3) 按照试验工况设定振动频率和注浆压力,然后开启振动器和注浆机实施注浆;
4) 注浆结束等待12 h后开挖检验。
3.2 试验结果分析
3.2.1 振动频率对浆液扩散性能的影响
图11所示为注浆持续时间4 min,注浆压力100 kPa,振动频率0、10、30和50 Hz条件下最终形成的固结体。图12为各工况固结体轮廓线图。图13为4种工况下固结体宽度和长度对比柱状图。可以看出,相同条件下,随着振动频率的增加,浆液径向扩散范围逐渐增大,但竖向扩散范围较为接近,分别为49.5、42.5、50.5和48.4 cm,平均长度比振动器长度(40 cm)长约20%。

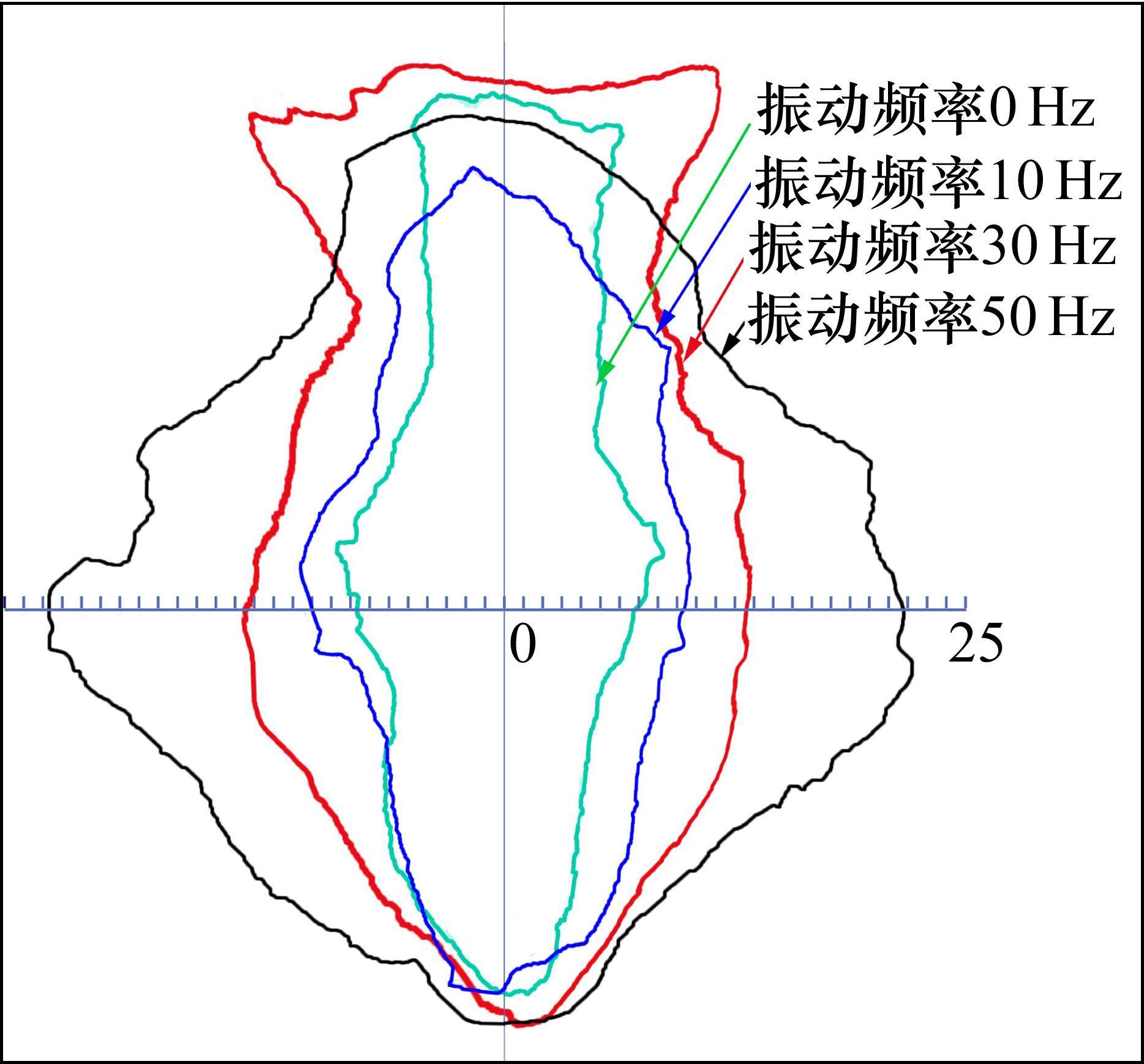
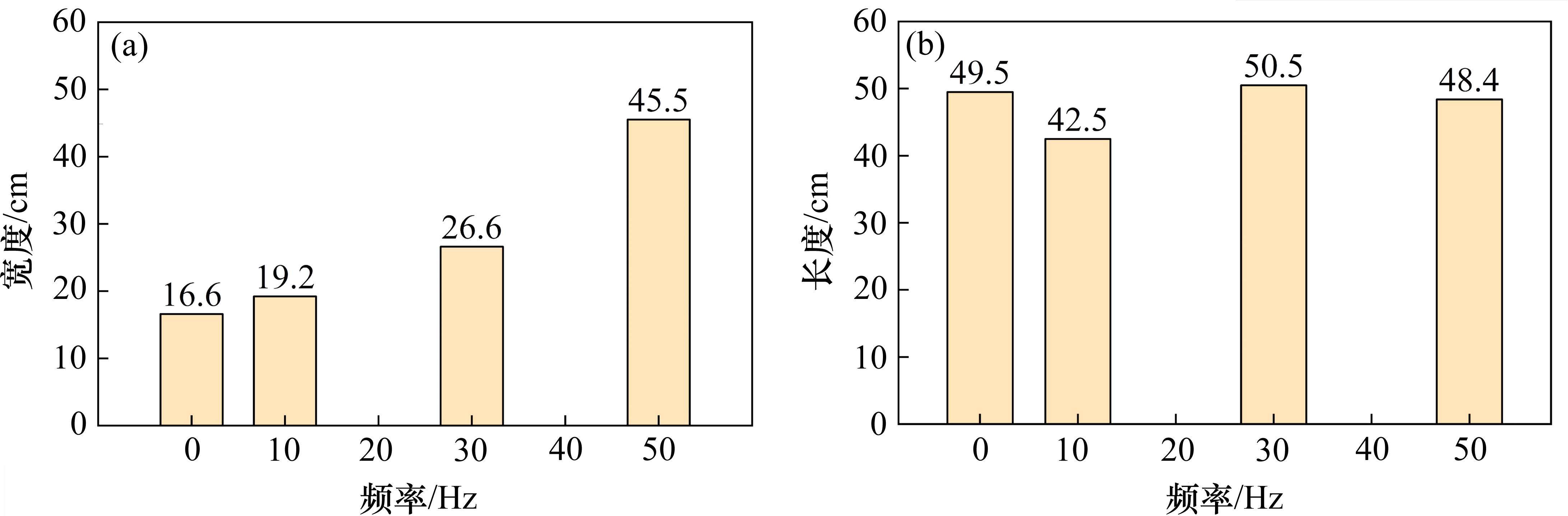
试验发现,无振动(f=0 Hz)条件下,注浆时间持续至90 s时(未达到设定的时间4 min),浆液已难以继续注入,最终形成的固结体体积较小,长度为49.5 cm,最大宽度仅为16.6 cm,形态呈中间略鼓的圆柱状(鼓出部位与出浆口位置相对应)。表明浆液主要沿振动器外表面分别向上、下两端方向扩散,沿径向的扩散范围较小。
振动频率为10 Hz时,浆液横向扩散宽度为19.2 cm,比无振动条件下扩散范围增加了15.7%。前期的振动测试结果显示,该频率下周围砂层受到的扰动较为微弱尚未达到液化状态(超孔压比峰值为0.02),因此浆液流动阻力依然较大,扩散范围相对较小。
f=30 Hz时,浆液径向扩散范围达26.6 cm,与10 Hz时相比增大7.4 cm,与无振动条件下相比增大60.2%,分析其原因在于该振动频率下,振动器附近部分土体产生液化(超孔压比峰值达到1.08),强度降低,浆液流动扩散过程中的阻力下降,使浆液径向扩散范围得到较大幅度增加。
50 Hz振动条件下,浆液径向扩散范围达到45.5 cm,比f=30 Hz时增大18.9 cm,与无振动条件下相比增大28.9 cm,增幅为174.1%,原因在于该频率下砂层受到剧烈扰动,处于深度液化状态(超孔压比峰值达到1.68),使得土体强度急剧下降,浆液流动阻力大大降低,扩散性能显著提升,径向扩散范围大幅度增加。
需要指出的是,f=30 Hz时,固结体轮廓图形态与其他频率下的固结体形态存在一定区别,其固结体上端部宽度明显高于其他频率下固结体的对应位置宽度,其原因是该工况下注浆试验结束后,将振动器提起过程中,振动器上部柔性隔振接头位置附近的孔壁土体发生失稳引起塌孔,土体掉落后坠入注浆孔中,占据注浆孔空间,导致孔内未固结浆液上涌至塌落土体位置,填充塌孔区域,固化后形成上部偏大的固结体。
总体上,从浆液固结体现场开挖照片看,在径向振动激励作用下浆液的扩散方式表现出挤密扩散特征,相对于无振动时的压密注浆,径向振动作用下浆液扩散半径显著提高,主要原因在于2个方面。一方面,在径向振动激励作用下,振动器附近的饱和砂土受到剧烈扰动,孔压升高,使得有效应力降低,强度下降,流动性增强,从而减小了浆液扩散阻力;随着振动频率的增加,土体超静孔压值与受扰动范围显著增大,进入深度液化状态,浆液流动阻力持续下降,扩散能力进一步增强。另一方面,径向振动激励对已注入的浆液产生周期性冲击作用,进一步增加了浆液扩散的驱动力,以上2个因素的叠加作用,促使浆液扩散半径显著增大,与静压注浆相比,振动注浆浆液的挤密扩散效果明显增强。
3.2.2 注浆压力对浆液扩散范围的影响
图14所示为振动频率50 Hz,注浆持续时间4 min,注浆压力20、60和100 kPa条件下最终形成的固结体开挖照片。图15为各工况固结体轮廓线。图16为3种工况下固结体宽度和长度对比柱状图。可以看出,随着注浆压力的增大,固结体轮廓线由最初的两端稍尖中部略鼓的枣核状,逐渐发展为中部鼓出形态较为饱满的洋葱状。

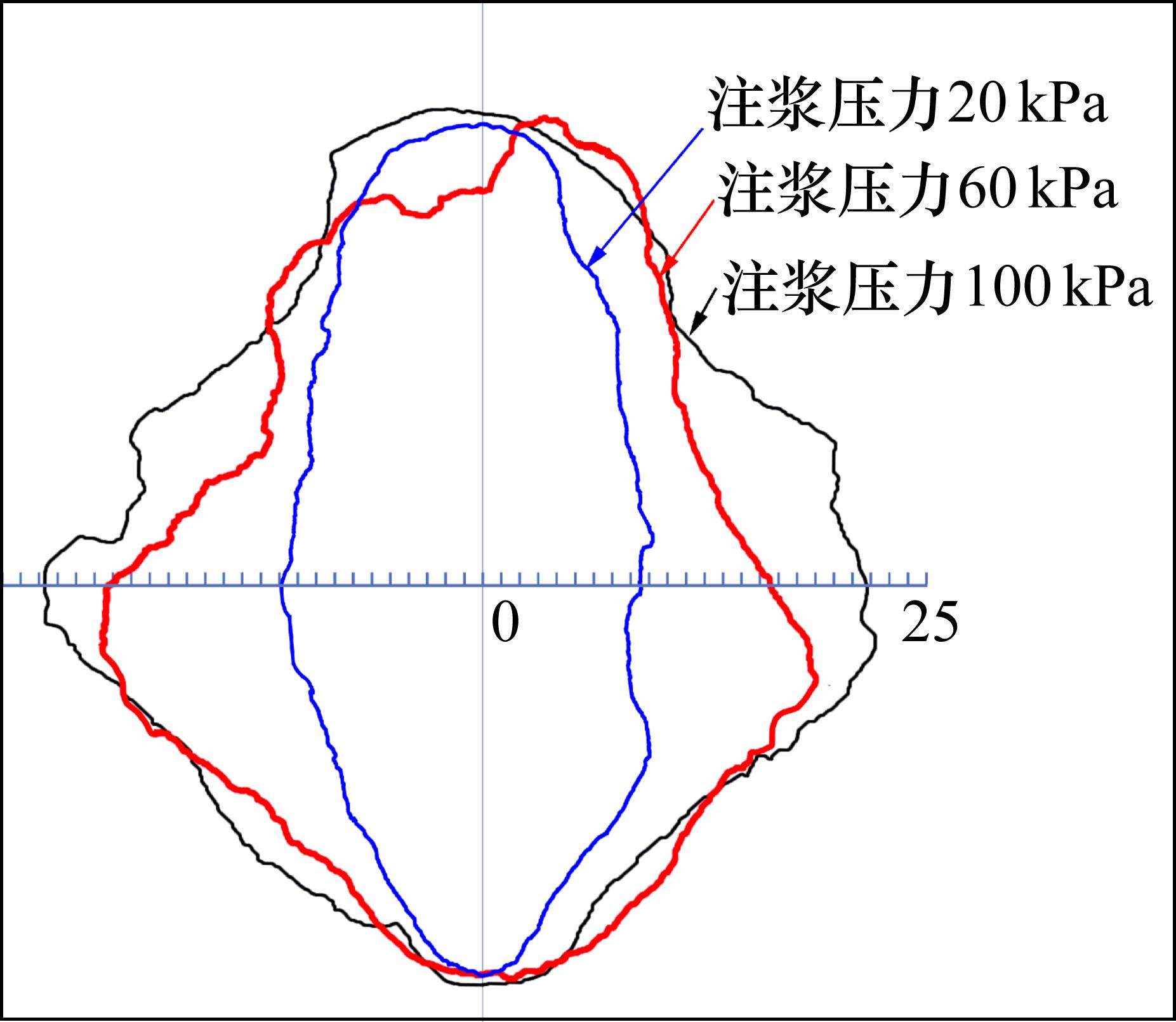
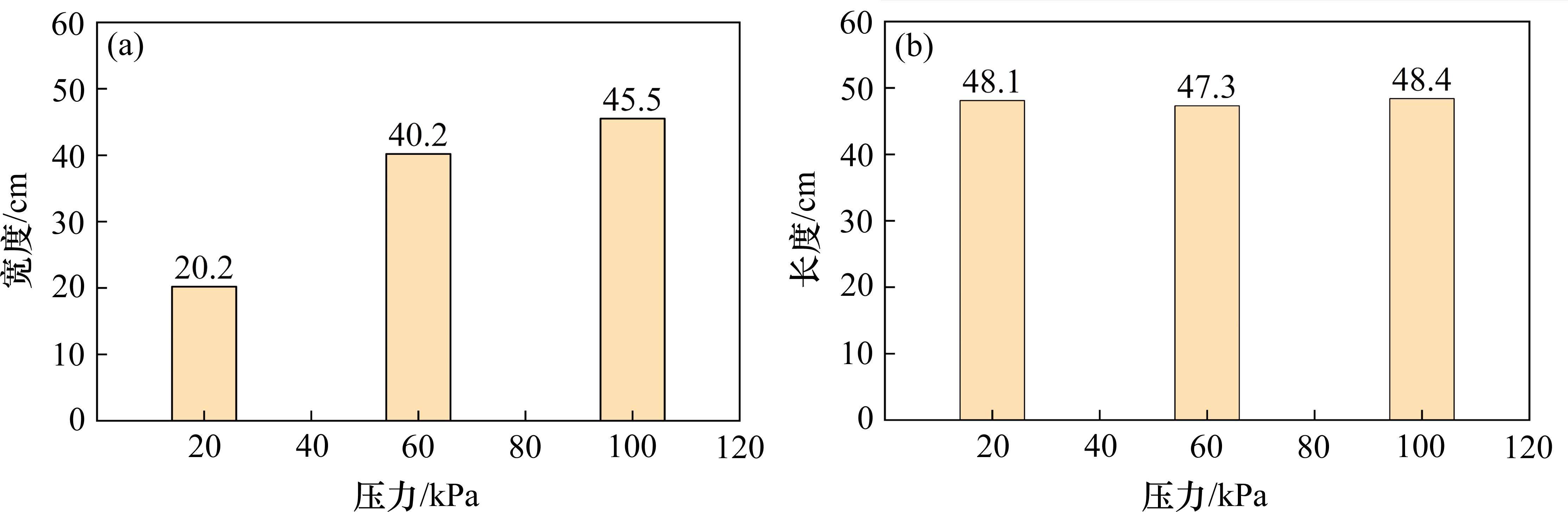
3种注浆压力条件下形成的最终固结体长度较为接近,分别为48.1、47.3和48.4 cm,比振动器长度(40 cm)大7~8 cm;固结体宽度分别为20.2、40.2和45.2 cm。总体来看,注浆压力变化对固结体宽度的影响较为显著,随着注浆压力增加,浆液横向扩散范围逐渐增大,但其增幅则呈逐渐减小趋势,与注浆压力20 kPa相比,60 kPa时的固结体宽度增幅为20 cm,而注浆压力100 kPa时的固结体宽度仅比60 kPa时增大5.3 cm。
显然,在保持振动频率不变的情况下,增加注浆压力能够提升注浆效率,扩大横向扩散范围,但注浆效率的增量随注浆压力的增大呈下降趋势,在现场施工中可以综合考虑能耗、注浆时间等因素对其实施优化确定最佳注浆压力。
3.2.3 注浆时间对浆液扩散范围的影响
图17所示为振动频率50 Hz,注浆压力100 kPa,注浆持续时间t分别为1、2、3和4 min时形成的固结体开挖图片。图18为各工况固结体轮廓线。图19为4种工况下固结体宽度和长度对比柱状图。


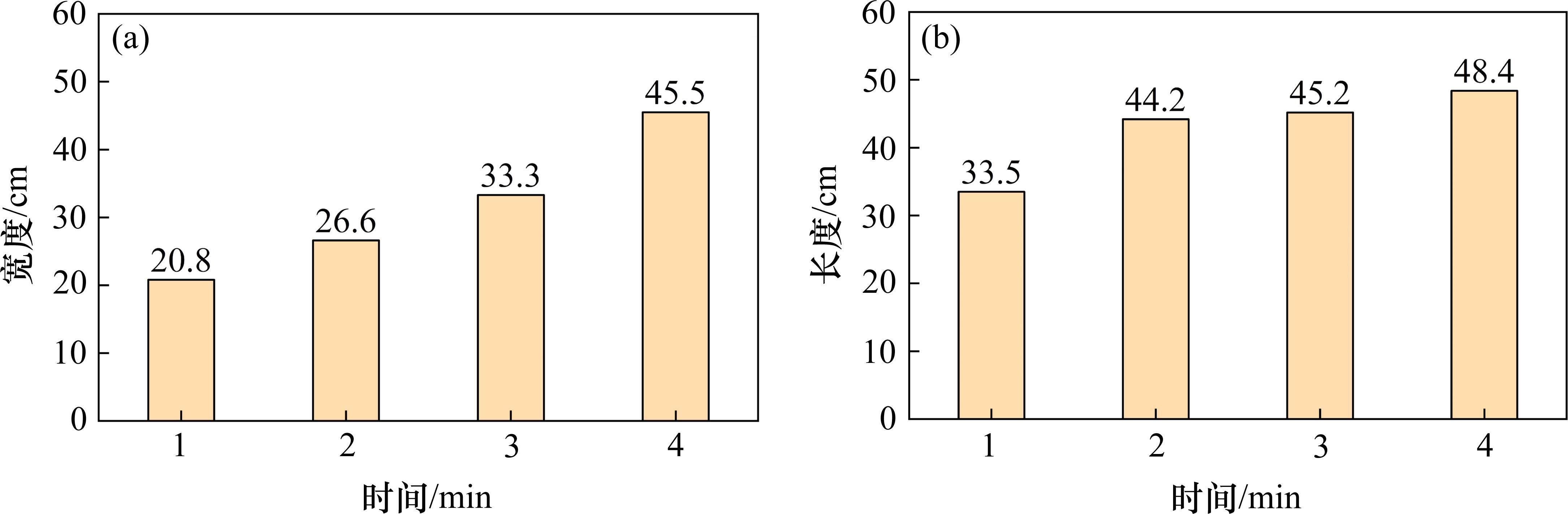
可以看出,随着注浆持续时间的增加,最终形成的固结体长度和宽度逐渐增大。4种工况下的固结体长度分别为33.5、44.2、45.2和48.4 cm,宽度分别为20.8、26.6、33.3和45.5 cm。其中t=1 min工况由于注浆持续时间较短,浆液注入量较少,其扩散范围明显小于其他3种工况,固结体长度仅为33.5 cm,小于振动器长度。t=2、3和4 min这3种工况下的结体长度较为接近,均大于振动器长度。
各工况下固结体长度均大于其宽度,两者差值分别为12.7、17.6、11.9和2.9 cm,可以发现,固结体长度与宽度的差值随注浆过程先增大然后逐渐减小,表明注浆初期浆液优先沿振动器轴向扩散,在该阶段径向扩散速度相对较慢。分析其原因在于紧邻圆柱状振动器的饱和砂土受到扰动并产生松动,同时伴随着振动器周期性振动,振动器周围壁面与土体间产生周期性瞬时脱离趋势,2个因素的叠加使得浆液沿该区域流动过程中阻力降低,因此扩散速度较快。当浆液到达振动器两端扰动区与非扰动区分界面时,受非扰动区的约束作用,浆液扩散受阻,扩散速度迅速下降,使得轴向扩散范围逐渐趋于稳定。随后浆液沿径向的扩展速度相对加快,逐渐转变为优势扩散方向,振动器中部临近区域成为优势扩散区域,原因在于该阶段振动器中部砂土受扰动程度最剧烈,其最大孔压振荡幅度和相对振荡幅度及超静孔压比峰值均高于振动器两端土体,处于深度液化状态,浆液流动阻力相对较小,大量涌入并集聚在该区域,使得振动器中部区域浆液扩散范围逐渐扩大,形成中部鼓起形态饱满的洋葱状固结体。
总的来看,与对固结体长度的影响相比,注浆持续时间对固结体宽度的影响更加显著。浆液扩散区域的最终形态与砂土受扰动程度和空间分布特点基本一致,符合扰动特征试验结果所反映的规律。
4 结论
1) 研制了一种具有径向激振和频率可调功能的振动注浆模型试验装置,振动器与上部连接杆通过柔性隔振装置连接,使振动能量集中作用于周围土体,扩大扰动范围;通过调节变频器控制振动器产生不同频率和大小的径向激振力。
2) 对饱和砂土开展了径向振动扰动模型试验,结果表明,随着振动频率增加,激振能量越大,测点孔压升高越快,各测点孔压峰值、超静孔压比和扰动范围越大;各测点孔压峰值随着埋深增加逐渐增大;与振动器中心等高的测点受扰动程度明显大于与振动器两端等高的各测点,最早达到液化状态,超静孔压比峰值高于前两者;沿径向距振动中心越近的测点,孔压上升越快,超静孔压比峰值越高,进入液化状态的时刻越早。
3) 开展振动注浆模型试验,结果显示,附加振动激励对浆液扩散性能具有显著增强作用,与无振动静压注浆相比,振动频率为10、30和50 Hz时,浆液扩散半径分别增加15.7%、60.2%和174.1%;各工况下浆液沿振动器轴向的扩散范围较为接近,相同振动频率下,浆液扩散半径随注浆压力和注浆持续时间的增大而增大;浆液固结体形态与砂土受扰动程度的空间分布特征相吻合。
李晓龙,陈永利,肖伟帆等.径向振动激励作用下饱和砂层中浆液扩散特性试验研究[J].铁道科学与工程学报,2025,22(03):1087-1099.
LI Xiaolong,CHEN Yongli,XIAO Weifan,et al.Experimental research on slurry diffusion characteristics in saturated sand under radial vibration[J].Journal of Railway Science and Engineering,2025,22(03):1087-1099.

