随着地下空间的建设和发展,交叉邻近工程已屡见不鲜。其中,在既有隧道上方开挖基坑的施工越来越多。这类工程情况复杂,基坑施工朝着“深、大”趋势发展,开挖过程中通常都需采取降水措施。因此,研究基坑开挖及降水共同作用下对既有隧道产生的不利影响,分析既有隧道的受力变形特征,保证基坑施工安全尤为重要[1-2]。目前,国内外学者对基坑开挖、降水引起下方既有隧道的受力变形进行了较多研究,其中,理论分析方法具有逻辑清晰、计算快速等特点,在初步分析隧道变形时有一定的优势。学者们常采用两阶段法分析上述施工对既有隧道的影响。第1阶段中,对于基坑开挖对既有隧道影响的研究,两阶段应力法多采用Boussinesq解、Mindlin解计算基坑坑底卸荷作用对既有隧道产生的附加应力[3-4],两阶段位移法多采用Loganathan和Poulos提出的解析解计算坑底卸荷作用引起的土体自由位移场[5],但上述研究均忽略了坑侧卸荷作用对既有隧道的影响。对于基坑降水对既有隧道影响的研究,先前学者大多采用数值模拟方法 [6-7],但数值模拟耗时较长,计算结果不易收敛。近年来也有学者进行了基坑降水对既有隧道解析解的研究,但成果仍然较少。且已有的研究中,常忽略降水的空间效应,降水引起的附加应力影响范围有较大的局限性。针对上述研究不足,也有学者基于大井法理论,提出了一种单井降水引起邻近管线变形的解析计算方法,推导了降水引起的有效应力计算公式[8-9]。总体来讲,第1阶段中,考虑基坑坑底、坑侧卸荷及降水共同作用的施工工况的理论研究尚且不多。第2阶段中,已有研究常将既有隧道视为作用于弹性地基模型上(如Winkler地基、双参数地基模型、三参数地基模型等)的梁模型(如短梁模型、Euler-Bernoulli梁模型、Timoshenko梁等模型),从而计算既有隧道在附加荷载作用下的响应规律。但上述研究中,为了简化计算,采用Kerr-Timoshenko这一模型进行的研究较少[10-11],但其仅分析了既有盾构隧道的位移和承受的弯矩,尚未进一步分析既有盾构隧道承受的剪力、接头张开量、管片错台量等指标。此外,在两阶段分析方法中,地基梁模型往往涉及到高阶非齐次微分方程,先前研究通常采用有限差分法[12-14]、通解方法[15-16]。在上述求解方法中,需要对控制方程进行矩阵变换、积分构造,从而解的形式较为复杂。仅有少量研究采用加权余量法求解了4阶微分方程近似解,求解结果形式简单,但仅采用Winkler地基模型针对基坑开挖的案例进行分析[17]。综上所述,针对基坑施工对既有盾构隧道的影响的研究,目前主要采用两阶段分析方法,该方法能够快速计算既有隧道的变形,分析土-隧相互作用。然而,上述研究仍存在以下不足之处:在基坑施工方面,较少研究综合考虑基坑坑底、坑侧卸荷及降水共同作用对既有隧道的影响。模型选取方面,采用计算精度更高的Kerr地基模型、更符合既有盾构隧道受力状态的Timoshenko梁的研究较少,且仅有的一些研究成果中,对既有盾构隧道的受力及变形研究不充分,尚未全面分析既有盾构隧道承受的剪力、接头张开量、管片错台量等指标。在两阶段分析方法的求解方面,大多研究需要对控制方程进行矩阵变换、积分构造,导致解的形式较为复杂。针对上述不足,本文的主要贡献如下:
1) 首先,第1阶段中,针对基坑施工工况分析方面,综合考虑了基坑坑底、坑侧卸荷及降水共同作用等工况,计算了上述工况施工对既有盾构隧道产生的附加应力。
2) 第2阶段中,采用计算精度更高的Kerr地基模型、更符合既有盾构隧道受力状态的Timoshenko梁模型,建立了既有盾构隧道纵向变形平衡微分方程,并在此基础上分析了既有隧道的竖向变形、管片接头张开量、管片错台量等指标。
3) 针对两阶段分析方法的求解问题,基于上述基坑开挖及降水共同作用的既有隧道纵向变形平衡微分方程,通过Galerkin方法构造出符合特定边界条件的试函数,使得计算结果易于收敛,形式简单,方便快捷。
1 基坑开挖及降水引起的附加荷载计算
1.1 基坑开挖卸载计算公式
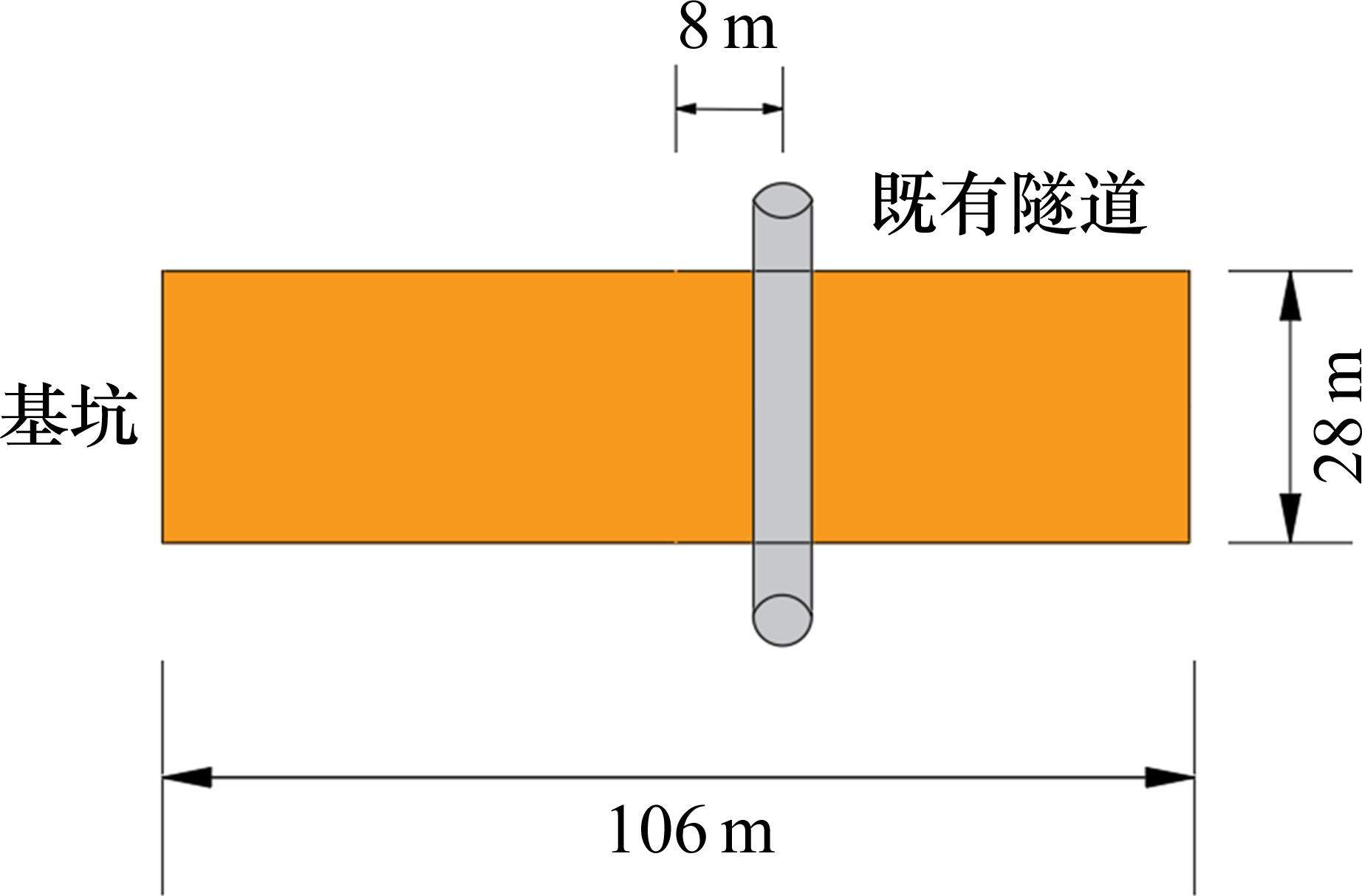
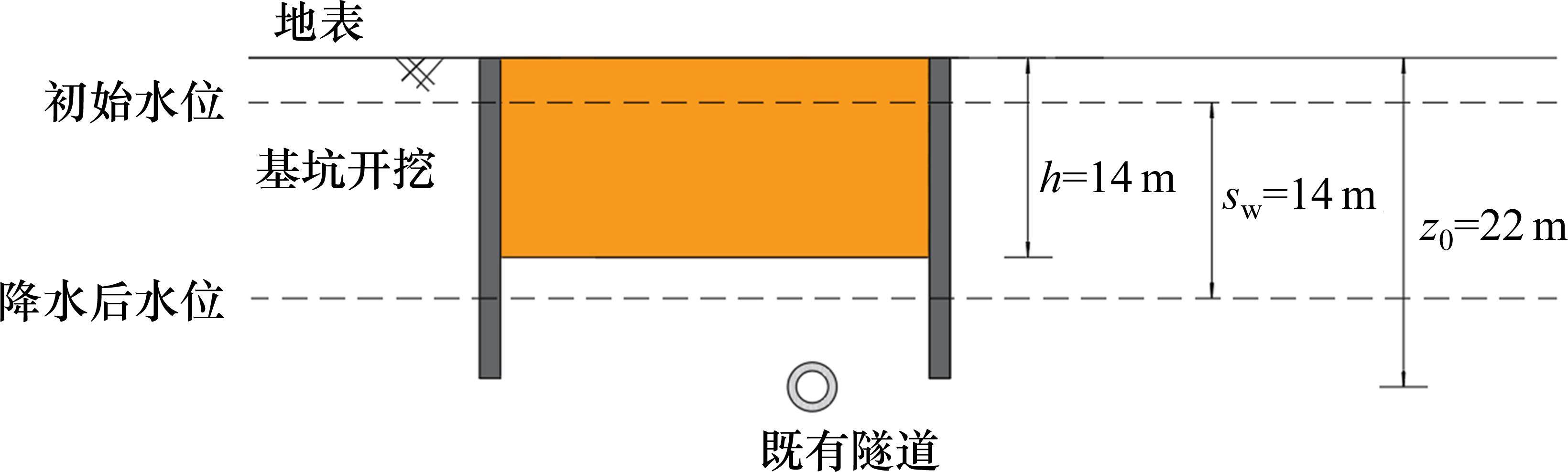
图1所示为在既有隧道上方开挖矩形基坑,图2所示为开挖基坑与既有隧道的总体相对位置。如图1所示,基坑长L,宽B,开挖深度h,下卧隧道轴线埋深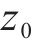
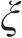
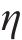
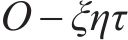

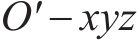
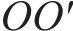
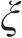

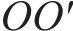
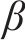
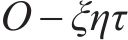
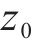
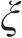
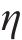

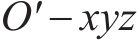
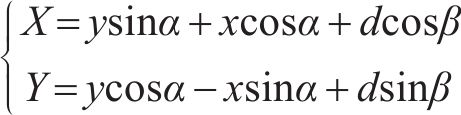
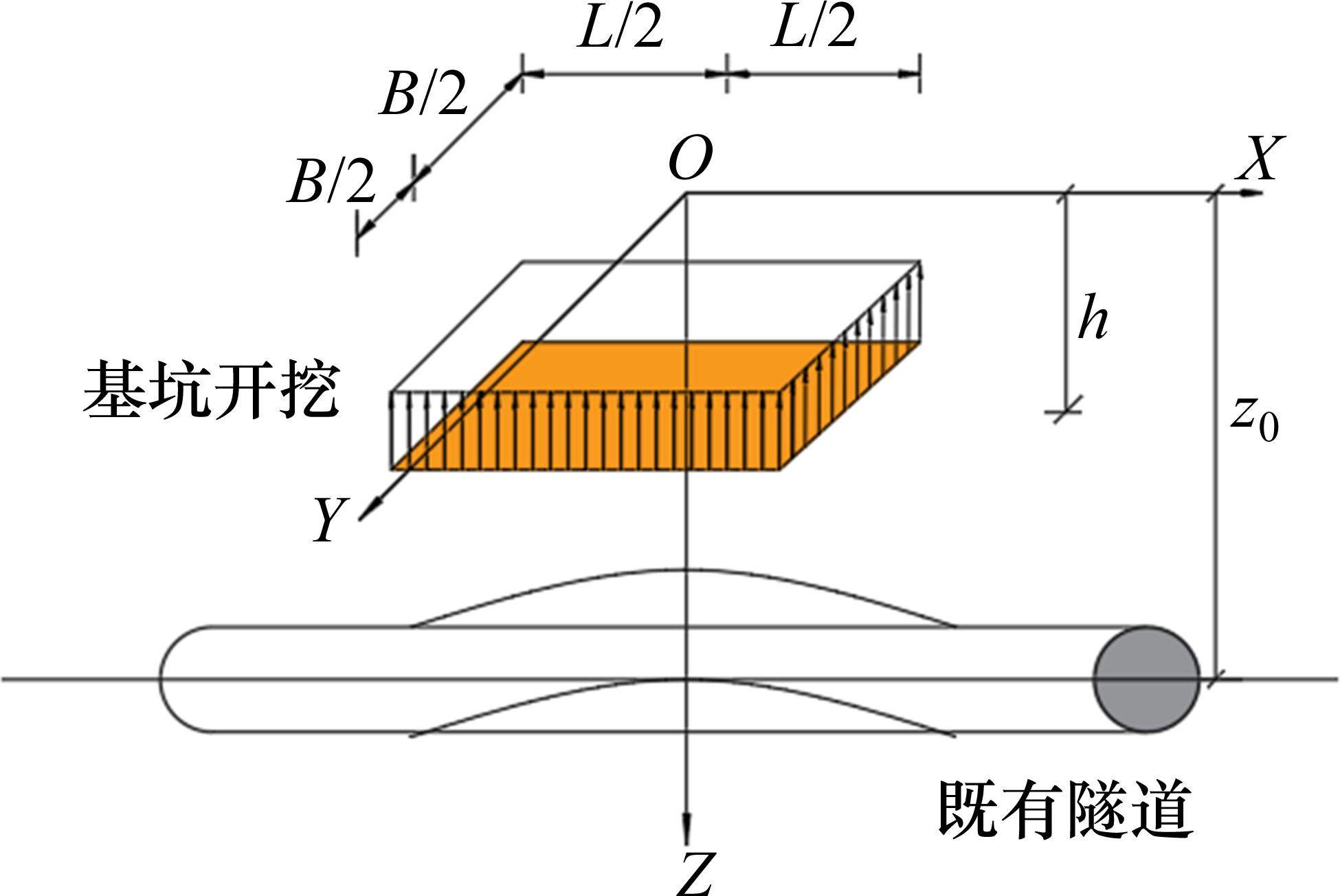
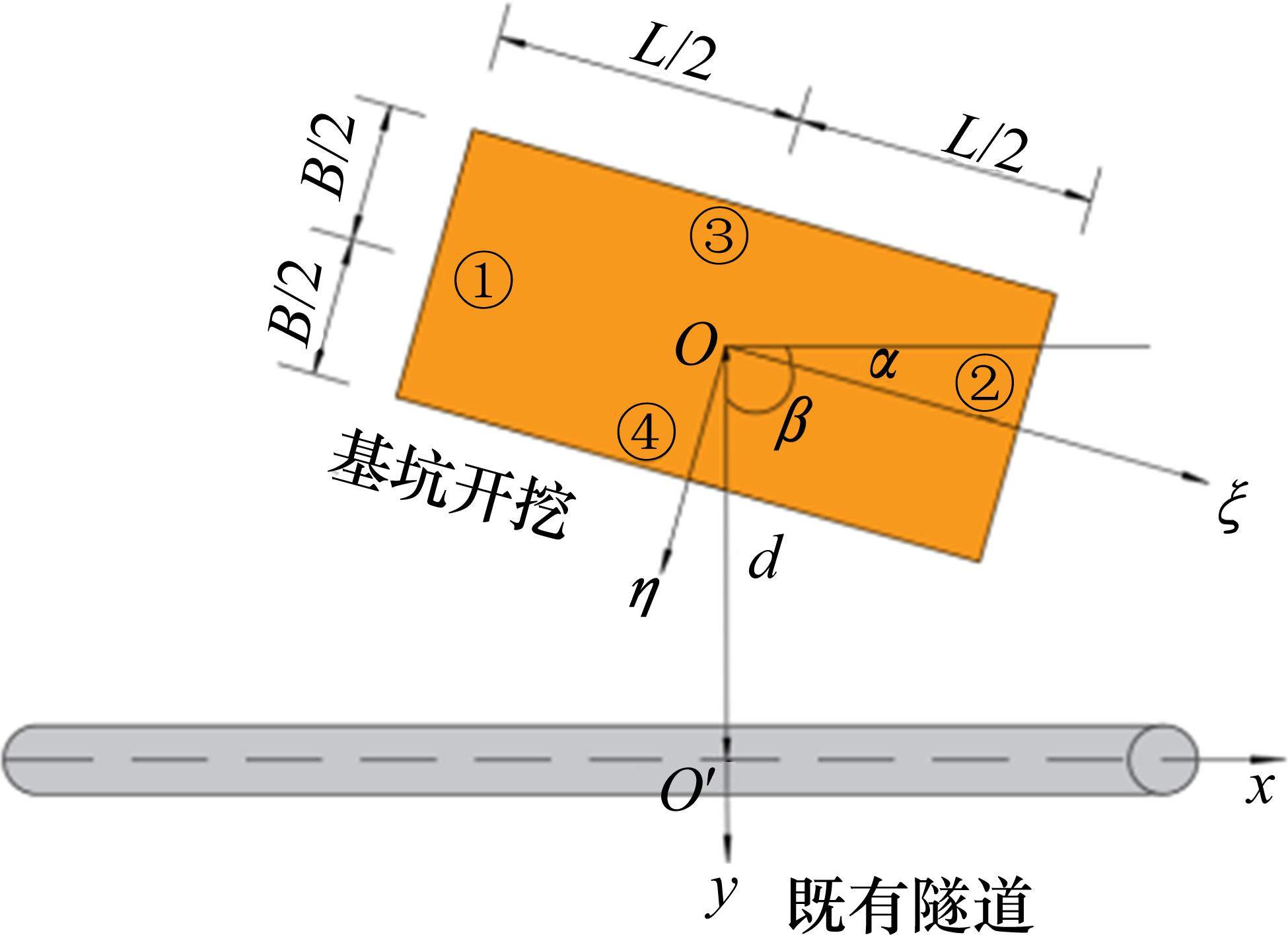
基坑开挖前,可把坑内土体对坑底的竖向作用作为均布荷载,开挖后,坑底受到竖直方向的作用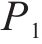
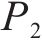
1.1.1 坑底土体开挖引起的附加荷载
由Mindlin弹性解知,坑底土体开挖引起的附加荷载为:
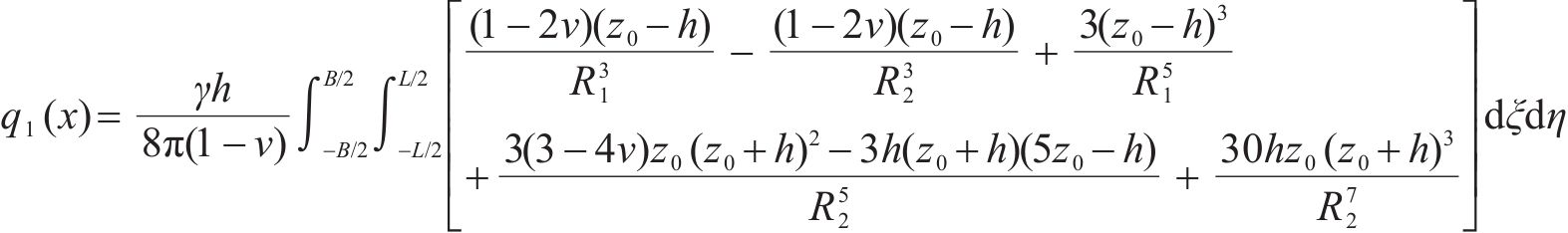
根据基坑和隧道的相互位置,记:
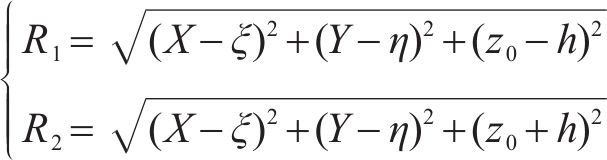
1.1.2 坑侧土体开挖引起的附加应力
考虑侧壁①卸荷作用时:记侧壁①上任一点(-L/2,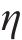

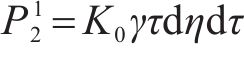
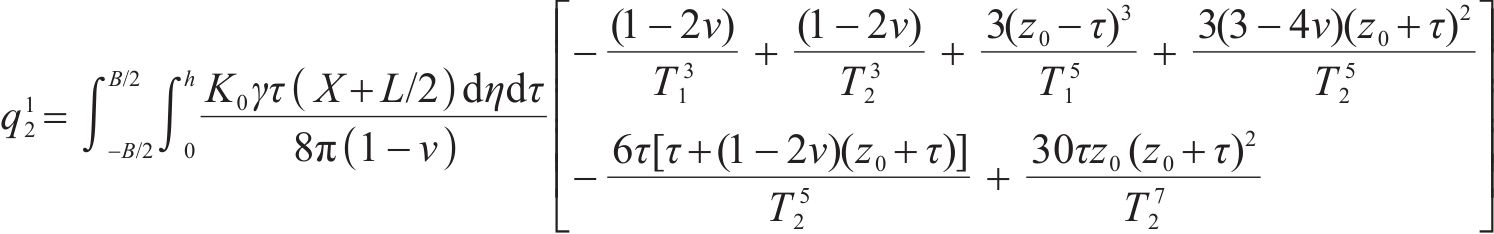
其中,
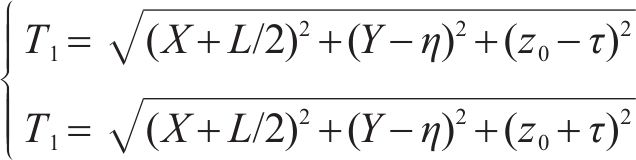
同理,可求出考虑侧壁②~④土体卸荷作用引起的附加荷载,由叠加原理知基坑开挖卸荷引起的既有隧道附加应力如式(6)所示:
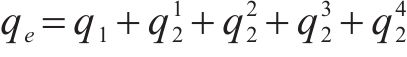
1.2 降水引起的隧道应力计算公式
文献[8]指出,合理选取参数及模型时,可选取大井法计算基坑涌水量。利用基坑降水漏斗曲线计算土体应力及地表沉降是合理的。基坑降水漏斗曲线如图3所示。基坑降水对既有隧道产生的附加应力如式(7)所示:
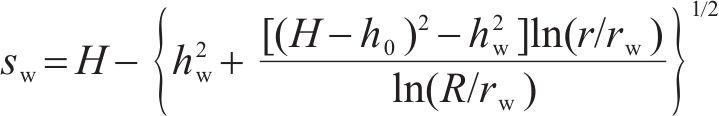
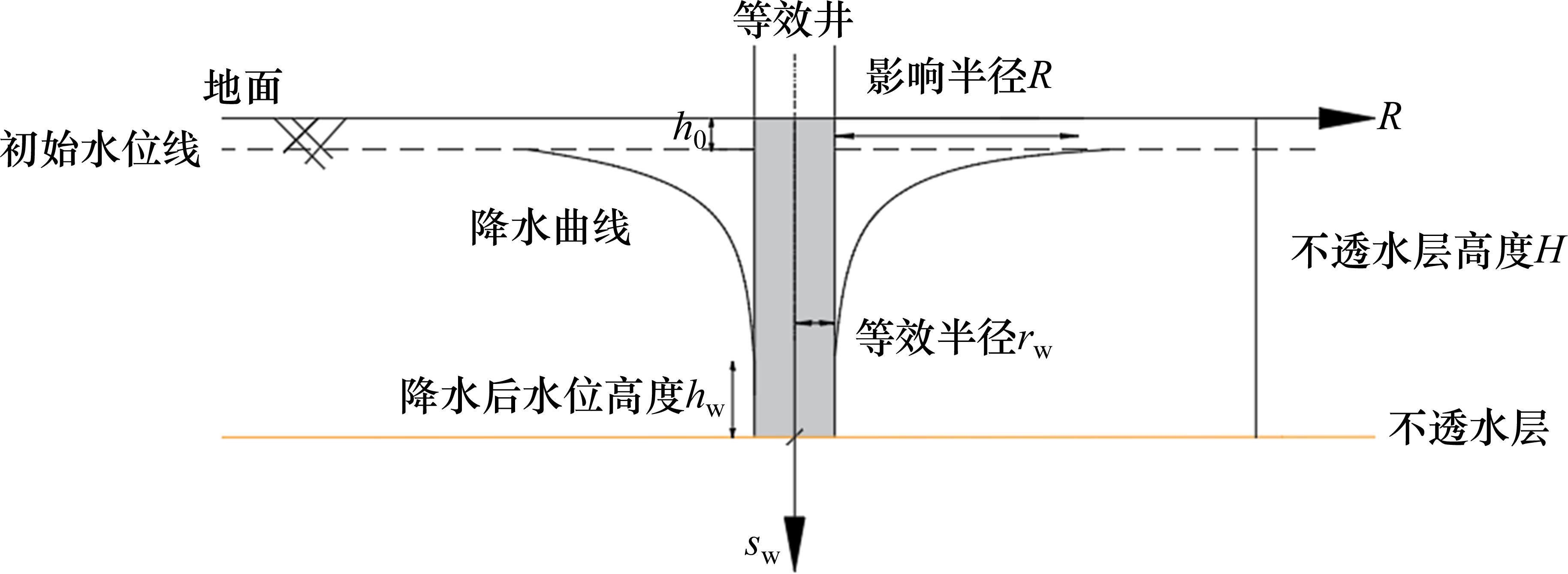
式(7)中:H为隔水底板至地表距离;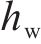
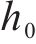
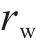
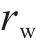
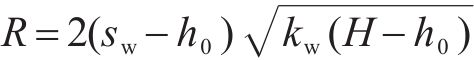
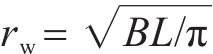
式中:kw为渗透系数。
在降水影响半径内,根据有效应力原理可知,基坑降水时,土体中孔隙水压力减小,有效应力增加。根据土体与降水后水位的相对位置关系,有效应力变化量可表示为式(10)所示:
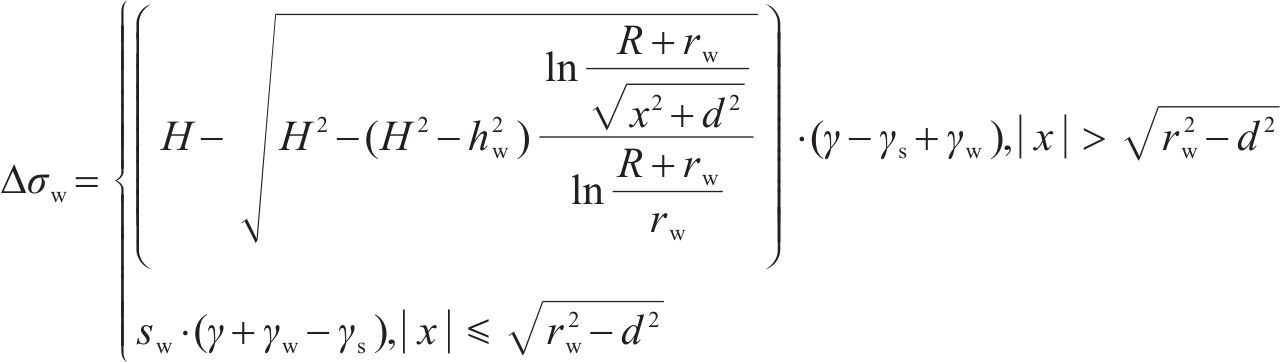
式中: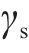
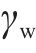
利用叠加原理,可得基坑开挖降水引起的下卧隧道轴线处附加应力为式(11)所示:
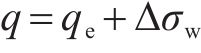
2 隧道控制方程
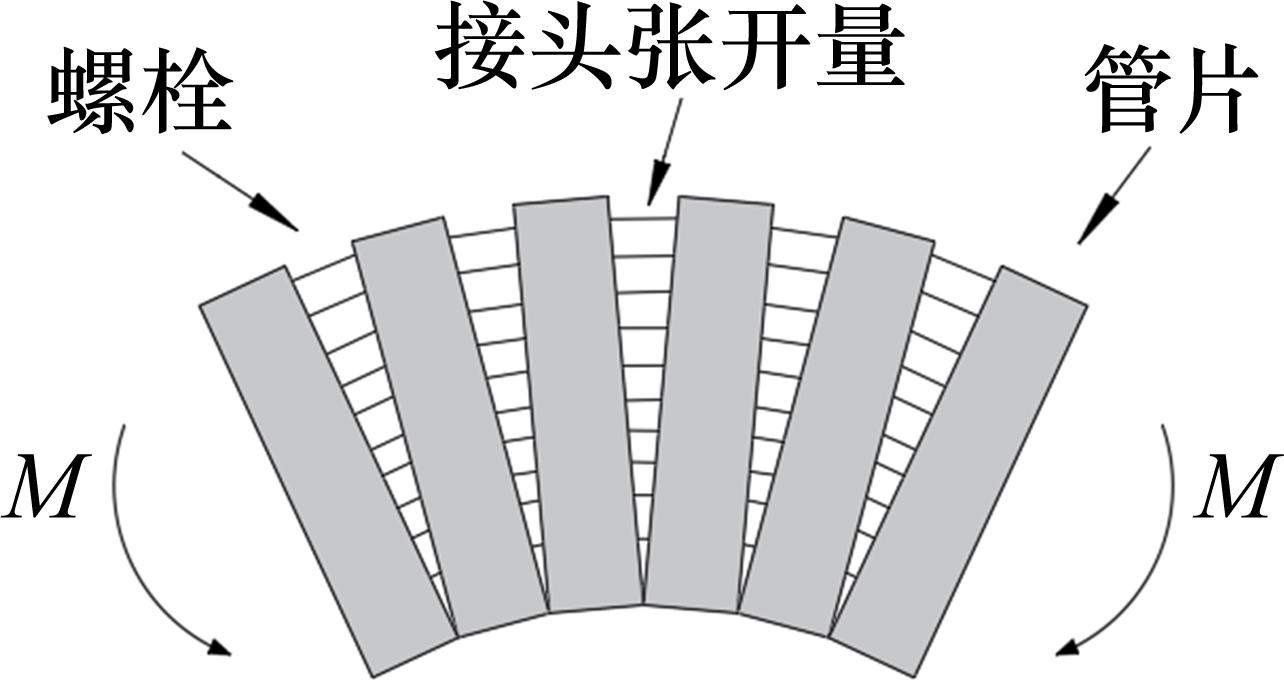
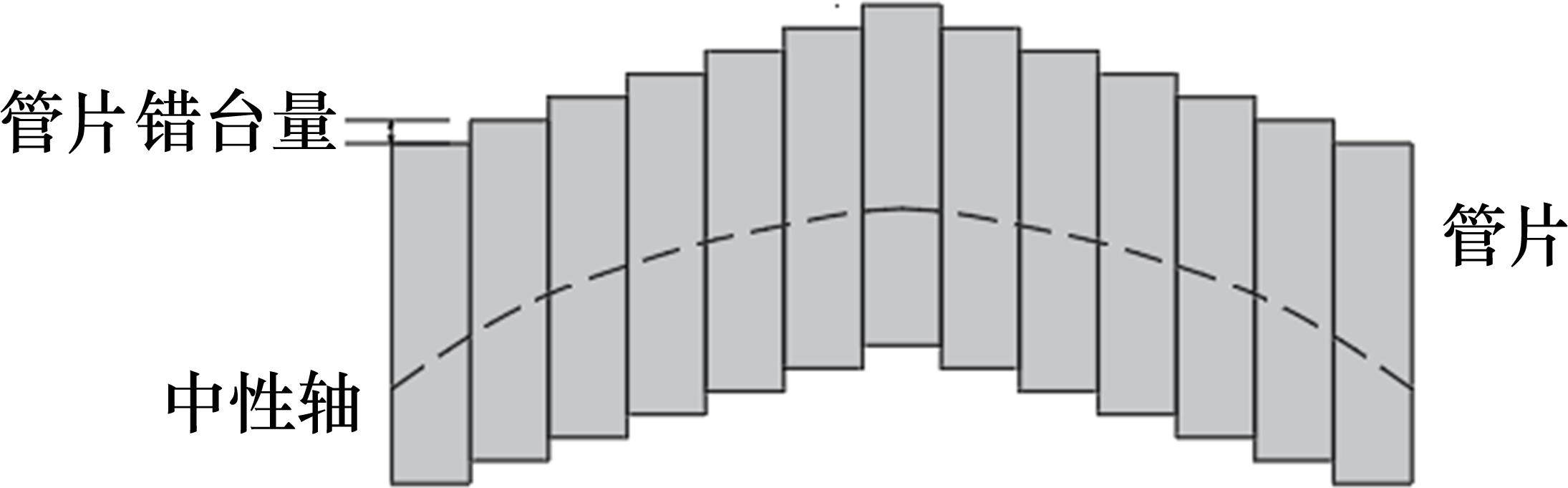
盾构隧道衬砌由预制管片通过螺栓连接而成。根据文献[3],如图4和图5所示,受盾构隧道接头的影响,外部荷载作用下,隧道产生纵向变形弯曲,且管片间会发生剪切错台变形,造成相邻管片间的接头处最易破坏。此时,将盾构隧道视为Timoshenko梁可以考虑管片接头刚度对整体刚度的削弱作用,计算接头张开量及管片错台量。
2.1 模型简化及假设
本文所述方法拟用于初步分析基坑开挖及降水影响下既有隧道的受力变形。为便于分析,作出如下假设:
1) 既有隧道视作Timoshenko梁;
2) 地基处于弹性状态,可视作Kerr弹性地基模型;
3) 各土层各向同性且隧道与各土层变形协调;
4) 开挖范围为潜水层且边界水头恒定;
5) 假定基坑内外侧存在一定的水位联系,且围护结构两侧地下水位相同;
6) 假定帷幕结构深入含水层深度较小,即忽略帷幕结构对渗流场的影响作用。
2.2 控制方程
如图6所示,根据Kerr地基模型理论,既有隧道变形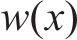
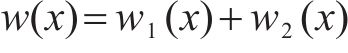
式中: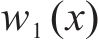
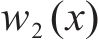
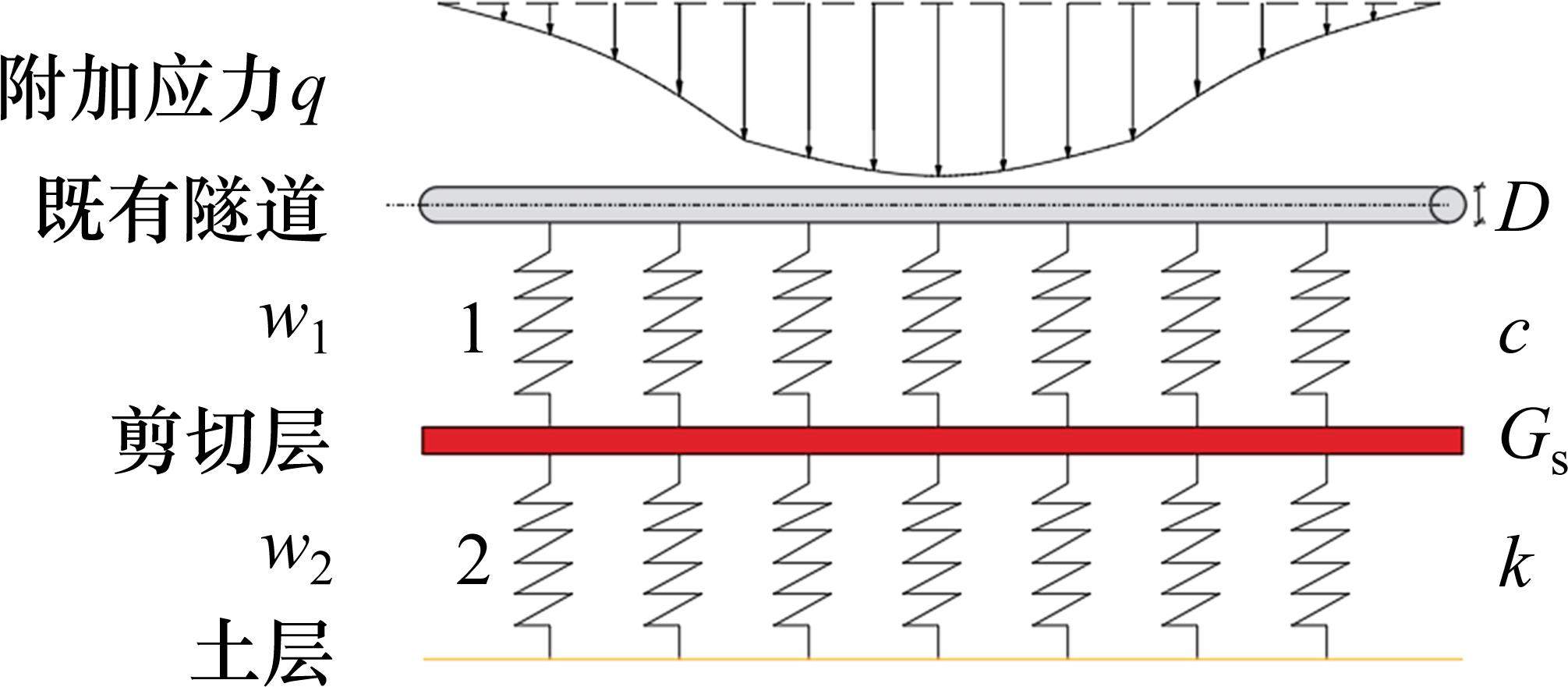
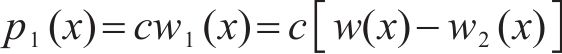
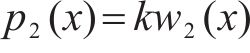
式中: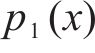
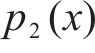
剪切层受力如式(15)所示:
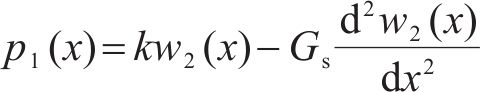
式中:Gs为剪切层刚度。
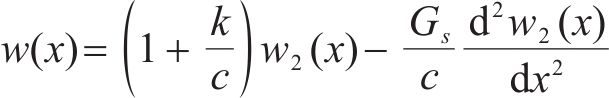
根据Timoshenko梁理论,既有隧道弯矩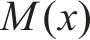
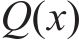
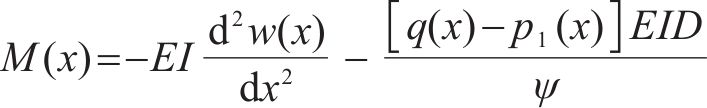
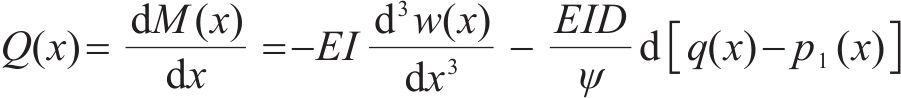
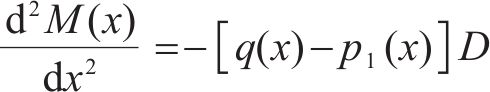
式中:E为既有隧道弹性模量;I为既有隧道惯性矩;D为既有隧道直径;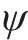
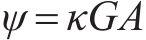
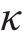
既有隧道剪切层弯矩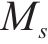
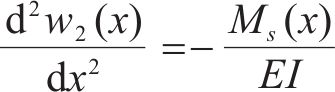
微分平衡方程如式(21)所示:
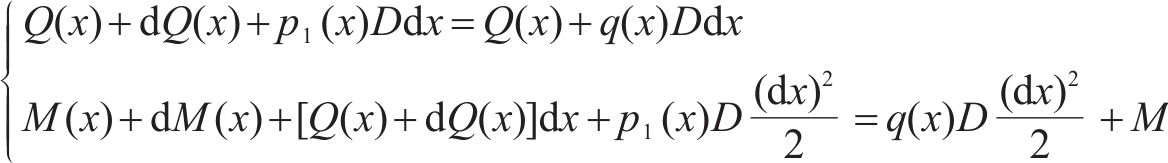
联立式(12)~式(21),得Timoshenko梁搁置在Kerr地基上的控制方程,如式(22)所示:
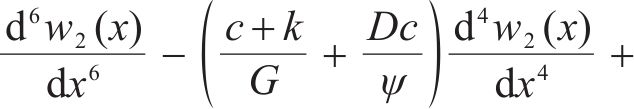
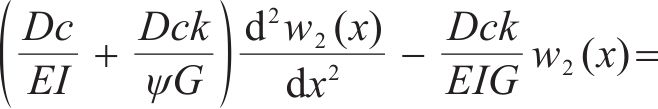
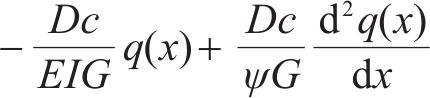
2.3 地基模型参数确定
Kerr地基模型中,地基模型参数包括2层弹簧系数c、k,剪切层刚度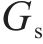
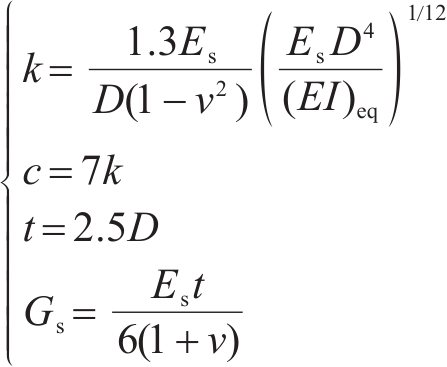
式中: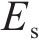
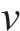
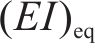
2.4 隧道模型参数确定
2.4.1 隧道等效抗弯刚度
目前,盾构隧道等效抗弯刚度的计算多采用竖向等效连续化模型[18],其等效抗弯刚度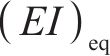
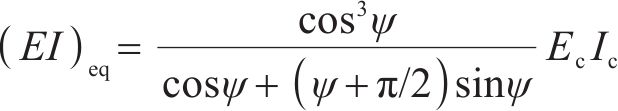
式中: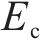
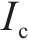
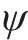
根据几何关系,管片接头张开量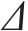
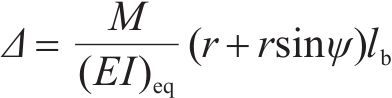
式中: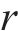
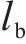
2.4.2 隧道等效抗剪强度
目前,基于Timoshenko梁理论,文献[19]提出了盾构隧道等效抗剪强度计算公式,如式(26)所示。
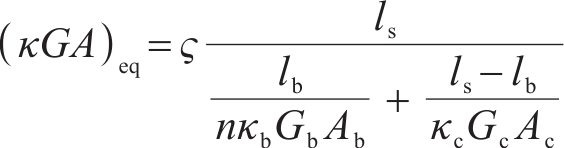
式中:
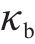
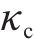
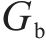
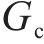
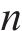
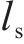
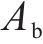
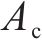
根据几何关系,管片错台量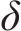
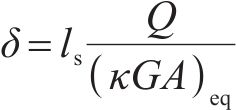
2.5 求解过程
式(22)是6阶非齐次微分方程,难以求得其解析解,本节采用Galerkin法对其求解。
根据边界条件可知,既有隧道两端弯矩和剪力为0,位于既有隧道两端的土体剪切层弯矩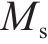
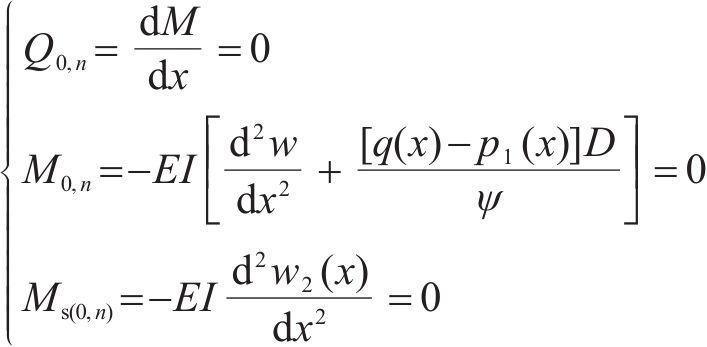
为此,引入基底函数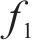
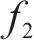
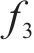
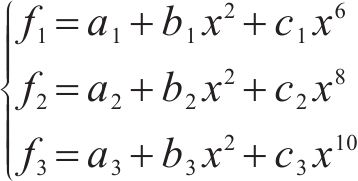
将式(11)、式(15)、式(16)代入式(28),并使式(29)满足式(28)进而可求出基底函数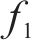
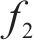
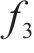
求得各基底函数后,构造试函数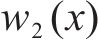
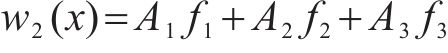
将式(30)代入式(22),即可求出线性组合系数A1、A2、A3。
将式(30)代入式(15)~(18),可得既有隧道的纵向位移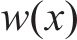
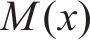
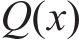
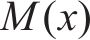
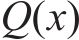
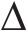
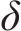
3 验证
选取文献[20]报道的某基坑工程开挖降水作用下对既有隧道变形的监测数据进行验证。如图7和图8所示,本工程开挖尺寸为106 m×28 m×14 m(长×宽×高),既有隧道位于基坑正下方,且隧道轴线距基坑中心d=8 m。隧道直径6 m,弹性模量30 MPa,等效抗弯刚度9.38×104 MN∙m2。采用潜水完整井的降水类型,初始地下水位位于地表以下2 m,降水后控制地下水位位于基坑坑底下方2 m。土层物理力学性质指标见表1。
| 土体参数 | 取值 |
|---|---|
| 土体天然重度/(kN∙m-3) | 18.2 |
| 土体饱和重度/(kN∙m-3) | 20.3 |
| 渗透系数/(cm∙s-1) | 1.6×10-4 |
| 泊松比 | 0.28 |
| 弹性模量/MPa | 83.57×106 |
| 第1层土体厚度/m | 2 |
| 第2层土体厚度/m | 12 |
| 静止土压力系数 | 0.6 |
| 初始水位高度/m | 71.7 |
图9为本文理论方法与文献[20]工程实测数据、数值模拟计算结果、不考虑降水影响下的理论方法及数值模拟计算结果的对比。从图9中可以看出,本文理论方法计算结果与实测值、数值模拟计算结果相吻合,且曲线趋势与文献[9]中采用的Kerr地基上Euler-Bernoulli模型的计算结果一致,验证了本文理论方法的可行性。坑内下方区域的既有隧道处于隆起状态,坑外区域下方的既有隧道处于沉降状态。且考虑降水作用后,既有隧道最大隆起量从10.44 mm降为4.23 mm,可见,降水可以较为显著地减少既有隧道的隆起变形,减少了59.5%,因此计算时不宜忽略降水作用对既有隧道变形的影响。经过计算,降水井等效半径为30.74 m,降水影响半径为91.83 m。在降水井等效半径范围内(x=±15 m),本文理论计算值与实测值更为接近,降水影响效果更为明显。超出这一范围,降水与否产生的影响逐渐减小,出现这种现象的综合原因为:本工程基坑开挖宽度为28 m,略小于降水井等效半径。降水井等效半径内,基坑开挖卸荷使得既有隧道产生的隆起变形与降水使得既有隧道产生的沉降相互抵消,且抵消作用较为明显,超出降水井等效半径范围,即超出开挖宽度范围时,基坑开挖产生的影响弱化,这也与工程实际相符合,进一步验证了降水计算方法的合理性。
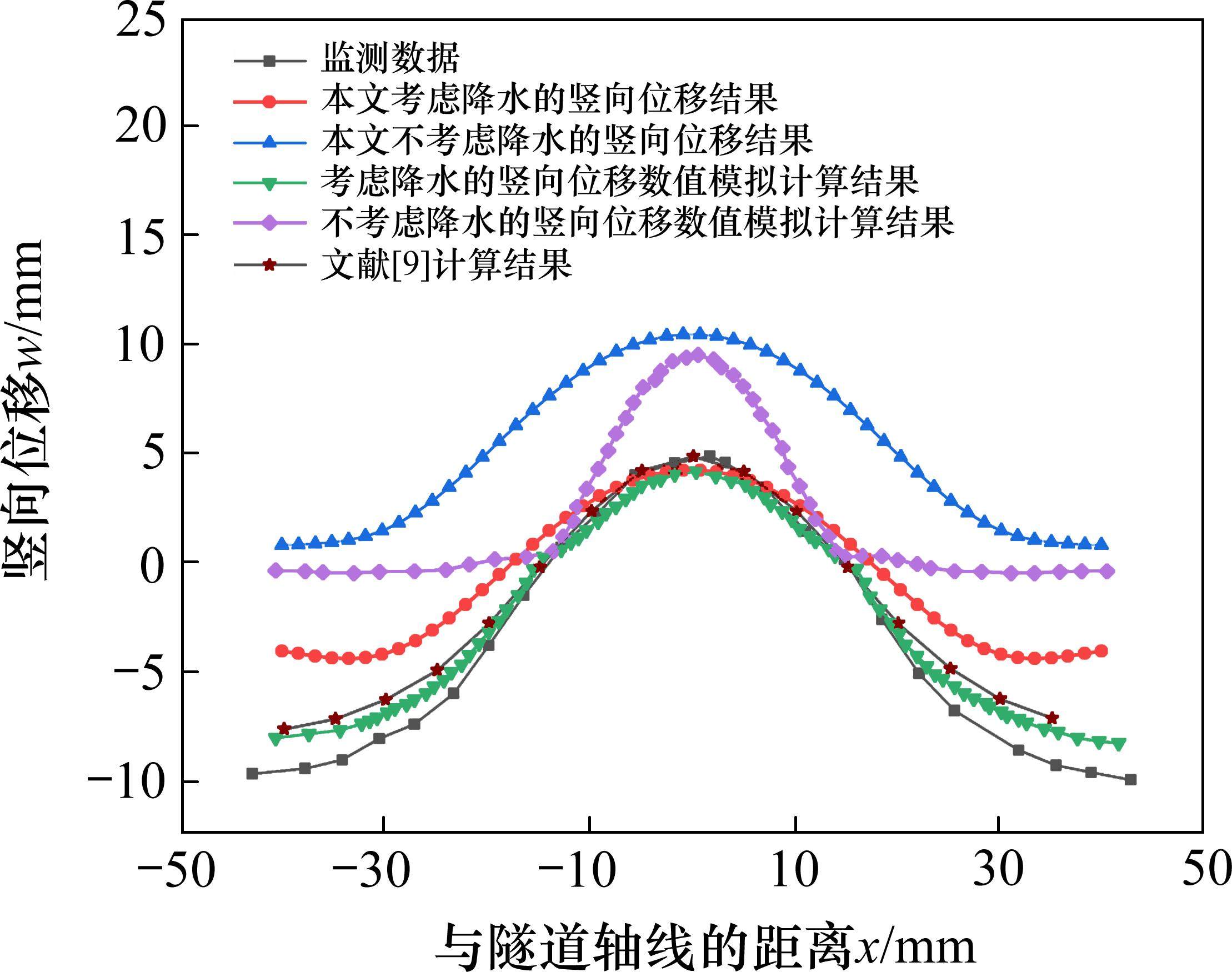
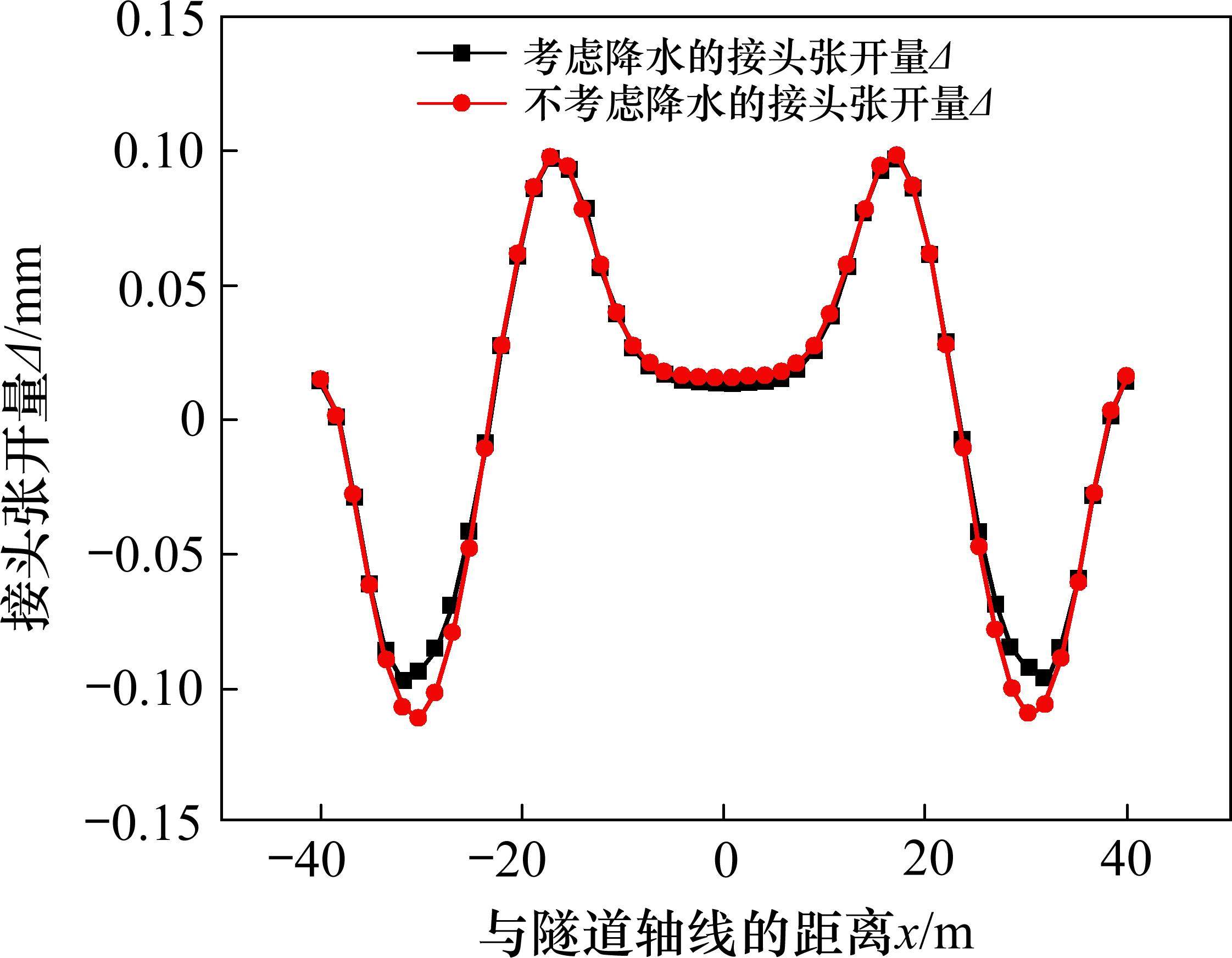
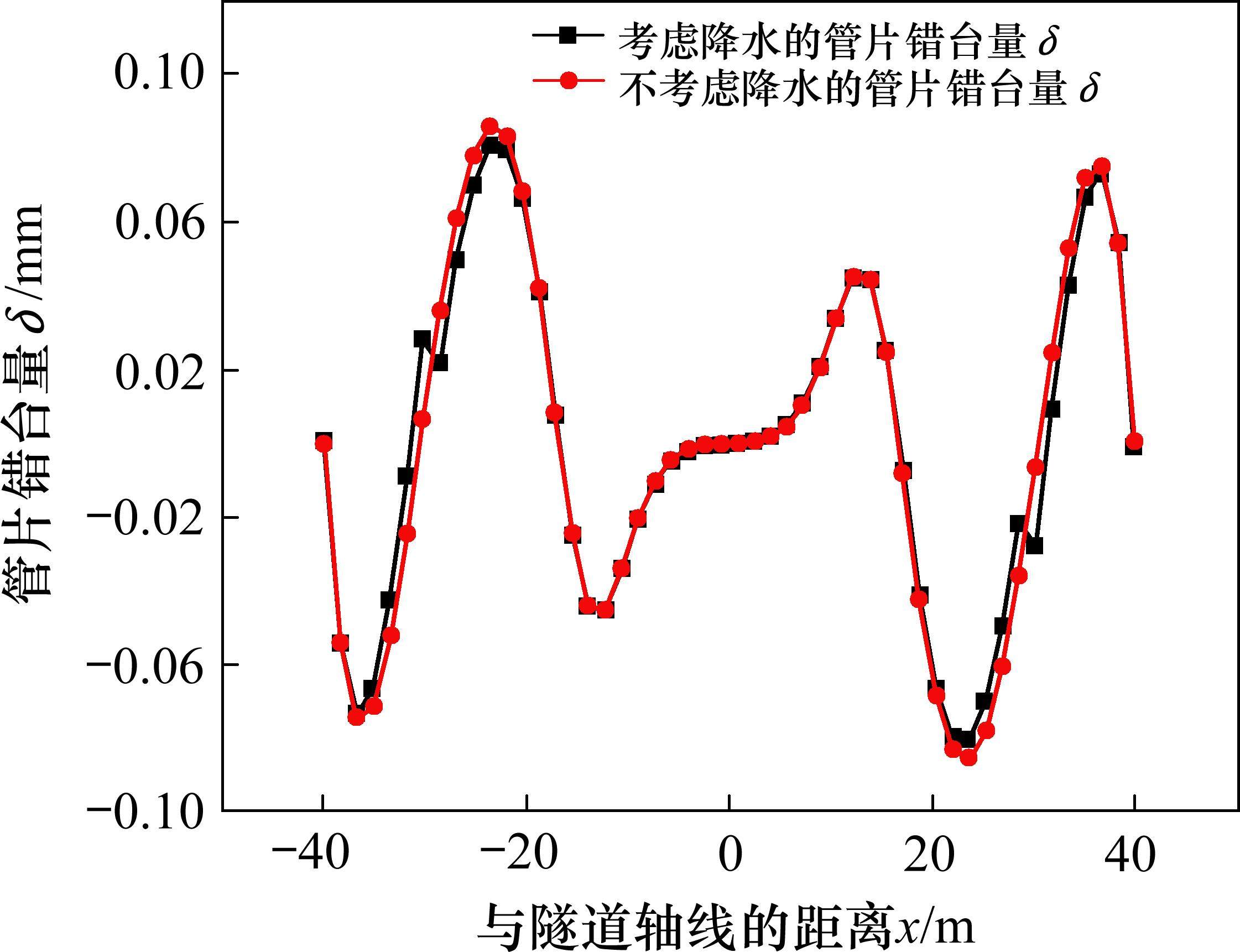
图10为计算得到的既有隧道管片张开量,图11为计算得到的既有隧道管片错台量。曲线趋势与相关文献[12, 21]中采用Pasternak地基上Timoshenko模型计算结果相似,且满足规范[22]要求,具有一定的合理性。如图10所示,盾构隧道管片接头张开量在沿着隧道纵向方向有4个峰值。不考虑降水时,在距离基坑中心17 m附近,即在基坑开挖边缘附近,管片接头张开量出现正峰值,为0.1 mm,这是因为考虑此处为坑内上覆土体开挖临界面,在基坑开挖范围内,随着开挖宽度的增加,土体挖方量逐渐增加,产生的附加应力随之逐渐增加,既有隧道在基坑侧壁附近受到的弯矩最大。超出这一临近面,既有隧道所受弯矩逐渐减小。在基坑1倍开挖宽度附近,即距基坑中心28 m附近,管片接头张开量出现负峰值,为0.12 mm。考虑到本基坑开挖长度远大于开挖宽度,基坑长度方向的侧壁卸荷作用大于基坑宽度方向的侧壁卸荷作用,在基坑开挖1倍宽度附近,使得既有隧道在此处受到较大的弯矩影响,进而管片接头张开量较大。此外,考虑降水作用时,既有隧道管片接头张开量负峰值为0.10 mm,略小于不考虑降水作用时的管片接头张开量计算值。且实际工程中,应注意基坑开挖边缘与基坑1倍开挖宽度附近的接头张开量,并可称之为管片接头张开量特征点。如图11所示,在距离基坑14 m附近,即基坑开挖边缘处,管片错台量出现峰值,为0.05 mm。有趣的是,不考虑降水影响时,最大正错台量0.09 mm(x=±22 m)和最大负错台量-0.075 mm(x=±36 m)也出现在1倍开挖宽度两侧相近对称的位置,因此此处是开挖过程中较危险的地方。
4 参数分析
为研究基坑开挖及降水共同作用引起的既有隧道沉降变形和管片接头张开量、错台量,以算例验证中的工程参数建立模型进行参数分析。参数包括基坑开挖长度、基坑开挖宽度、隧道埋深、降水深度。分析过程中采用控制变量法思想,仅改变研究对象参数,其他参数不变。
4.1 基坑开挖长度
为研究基坑开挖长度(L)对既有隧道的影响,选取5组开挖长度,即L=86,96,106,116,126 m。记隧道最大相对变形为隧道最大隆起量与最大沉降量之差,管片接头最大相对张开量为最大正张开量与最大负张开量之差,管片最大相对错台量为最大正错开量与最大负错开量之差,下同。
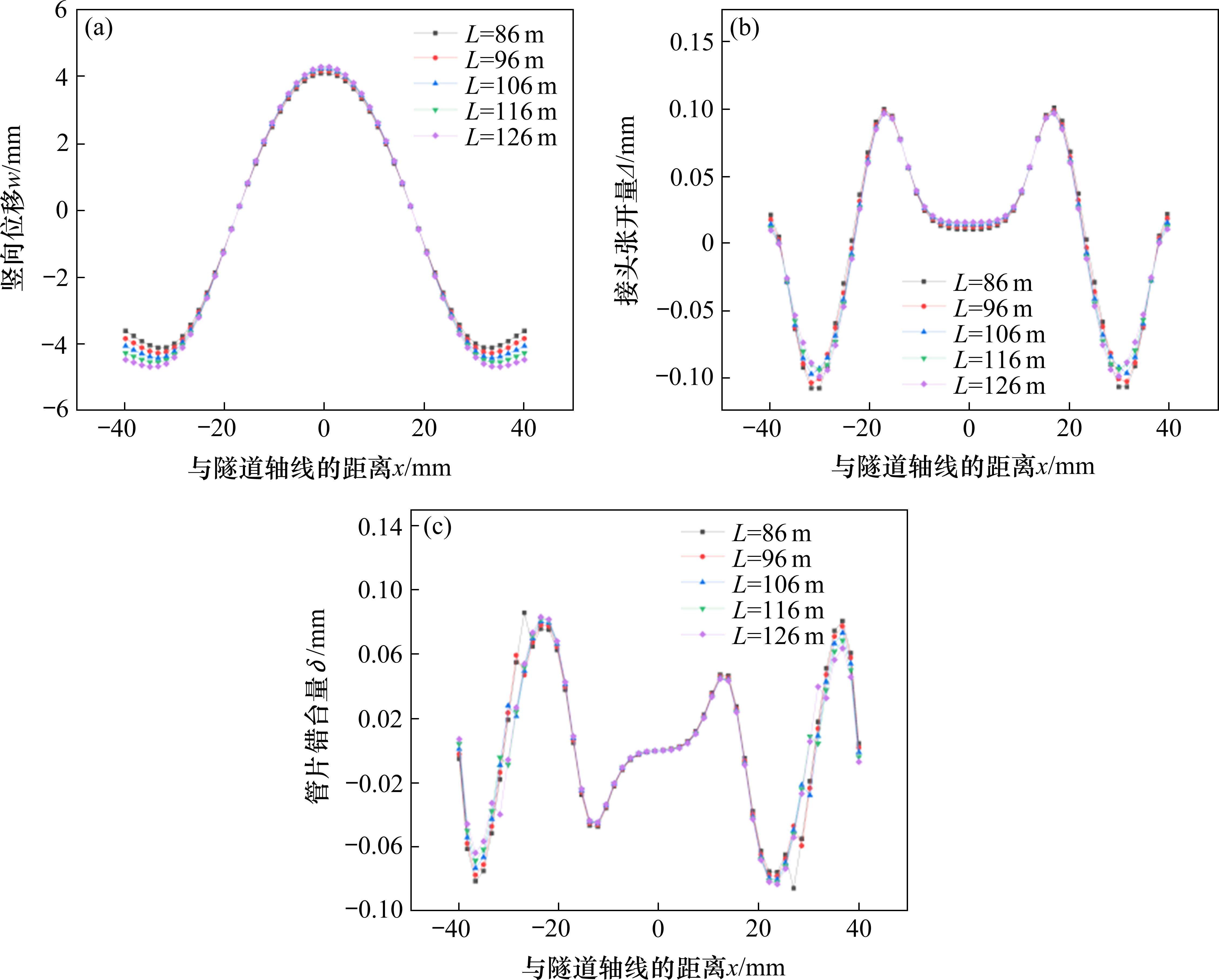
由图12(a)可知,隧道变形受基坑开挖长度的影响不显著,不同开挖长度下,隧道变形趋势相同。基坑开挖范围内,距基坑中心最近点附近,隧道为隆起状态,超出隧道开挖宽度,隧道逐渐变为沉降状态。这是因为在基坑开挖范围内,开挖卸荷和降水增荷共同作用,且两者使得隧道产生的变形量相互抵消。超出开挖范围,开挖卸荷产生的影响逐渐减小,隧道在降水增荷作用下,逐渐产生沉降。当超过降水影响半径时,降水增荷产生的影响逐渐减弱,曲线又呈现平缓趋势。由图12(b)可知,管片接头张开量受基坑开挖长度的影响不明显,不同开挖长度下,管片接头张开量变化趋势相同,管片接头张开量特征点位置大体如第3节所述。由图12(c)可知,管片错台量受基坑开挖长度影响较小,管片错台量变化趋势相对一致。但是当基坑开挖宽度为86 m时,在1倍开挖宽度附近处,管片错台量有突变现象。
4.2 基坑开挖宽度
为研究基坑开挖宽度(B)对既有隧道的影响,选取5组开挖宽度,即B=8,18,28,38,48 m。
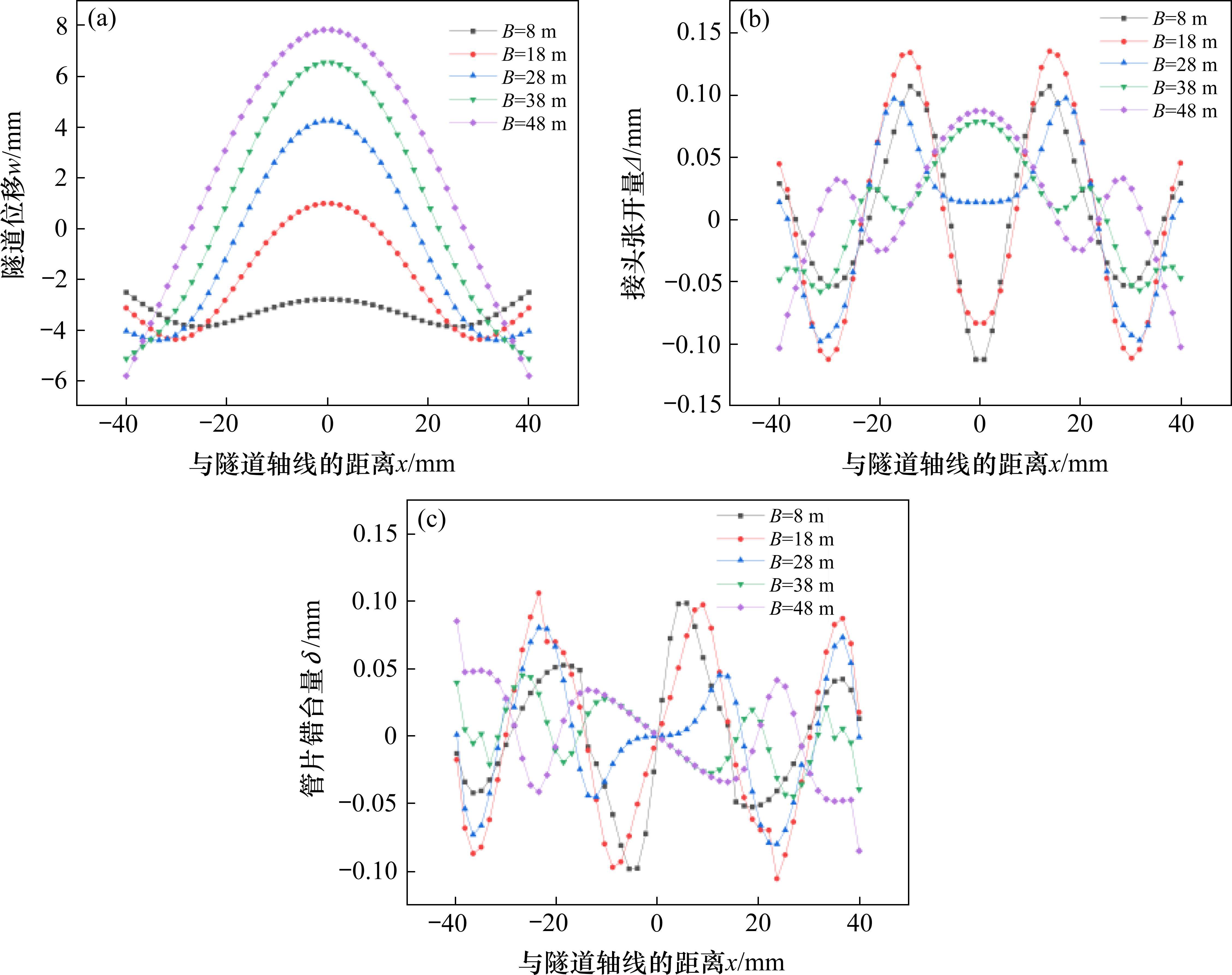
由图13(a)可知,与受开挖长度影响不同的是,隧道变形受开挖宽度的影响较大。当基坑开挖宽度从8 m增加到48 m时,隧道中心处的变形量由沉降3.1 mm变为隆起7.9 mm。沉降随着开挖宽度的增加,距基坑中心最近点附近处的隧道变形逐渐增加。且当隧道宽度较小时(B=8 m),隧道表现为沉降状态,这是因为此时基坑为狭长型基坑,基坑开挖范围小,开挖卸荷使得隧道产生的沉降量不能够抵消降水增荷产生的隆起量,且隧道开挖宽度过小时,隧道两侧变形出现翘起现象。由图15(b)可知,管片接头张开量受基坑开挖宽度的影响较大,且张开量趋势出现明显的不同。相比于工程实例中的开挖参数,即当B<28 m时,基坑中心处的隧道管片接头张开量呈“深井”状,且开挖宽度越小,深井趋势越明显。当B>28 m时,基坑中心处的隧道管片接头张开量呈“鼓包”状。由图15(c)可知,管片错台量受基坑开挖宽度的影响也较大,且错台量趋势出现明显的反转变化。当B<28 m时,错台量变化趋势与工程实例中得到的曲线变化趋势一致,当B>28 m时,错台量变化趋势发生反转。
4.3 隧道埋深
为研究隧道埋深(z0)对既有隧道的影响,选取5组隧道埋深,即z0=18,20,22,24,26 m。
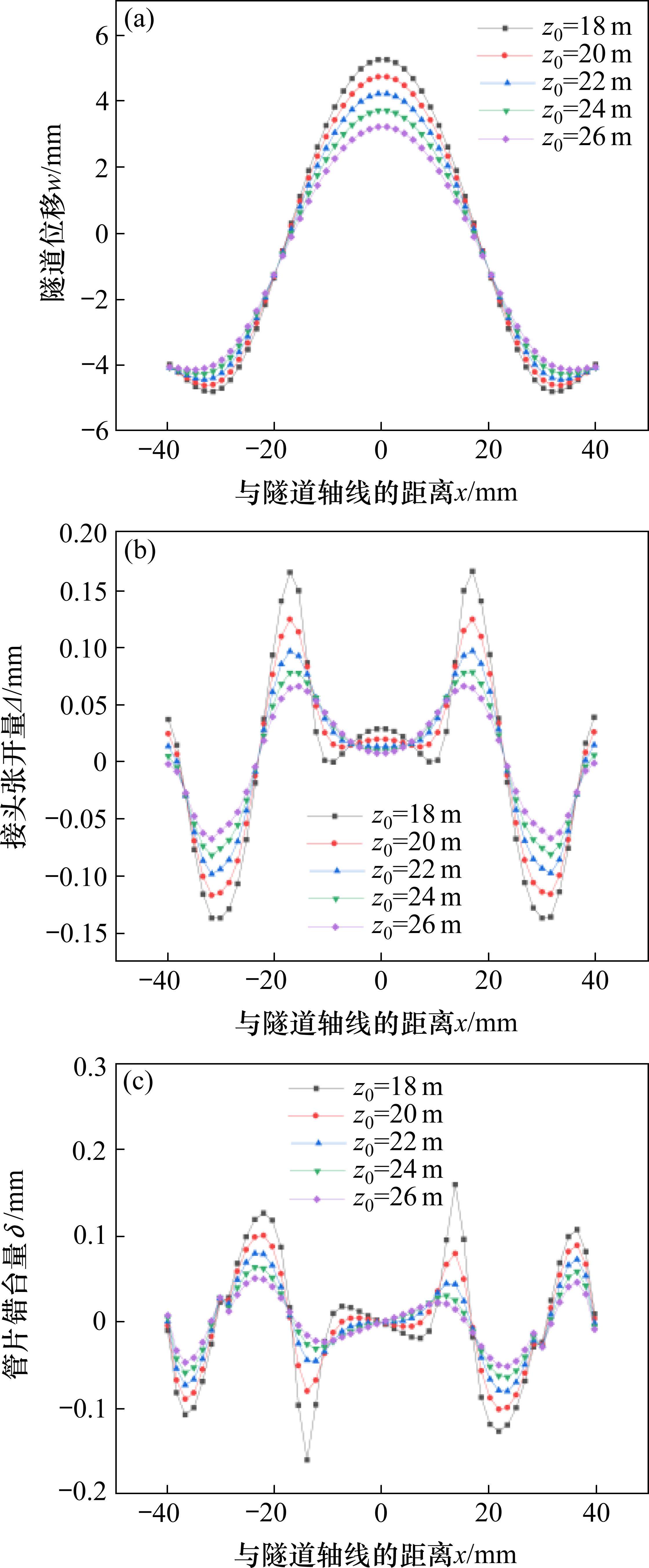
由图14(a)可知,随着隧道埋深的增加,隧道变形逐渐减小。当埋深从18 m增加到26 m时,隧道最大隆起量也从5.26 mm减小到3.23 m。一方面,开挖卸荷产生的作用力随着隧道埋深的增加而减小;另一方面,虽然降水增荷产生的作用力随着隧道埋深的增加也减小,但相较于开挖卸荷,降水增荷产生的作用力更为显著,使得随着隧道埋深的增加,隧道最大隆起值逐渐减小,降水的影响不可忽视。由图14(b)可知,隧道埋深较浅时,基坑中心处的管片接头张开量呈“鼓包”形状,且埋深越浅,“鼓包”趋势越明显。当埋深超过22 m时,基坑中心处的管片接头张开量呈“深井”形状,且埋深越浅,“深井”趋势越明显。由图14(c)可知,错台量最大值发生在x=±14 m附近处,即为降水井影响半径附近处,因此降水作用对错台量的影响不可忽视。
4.4 降水深度
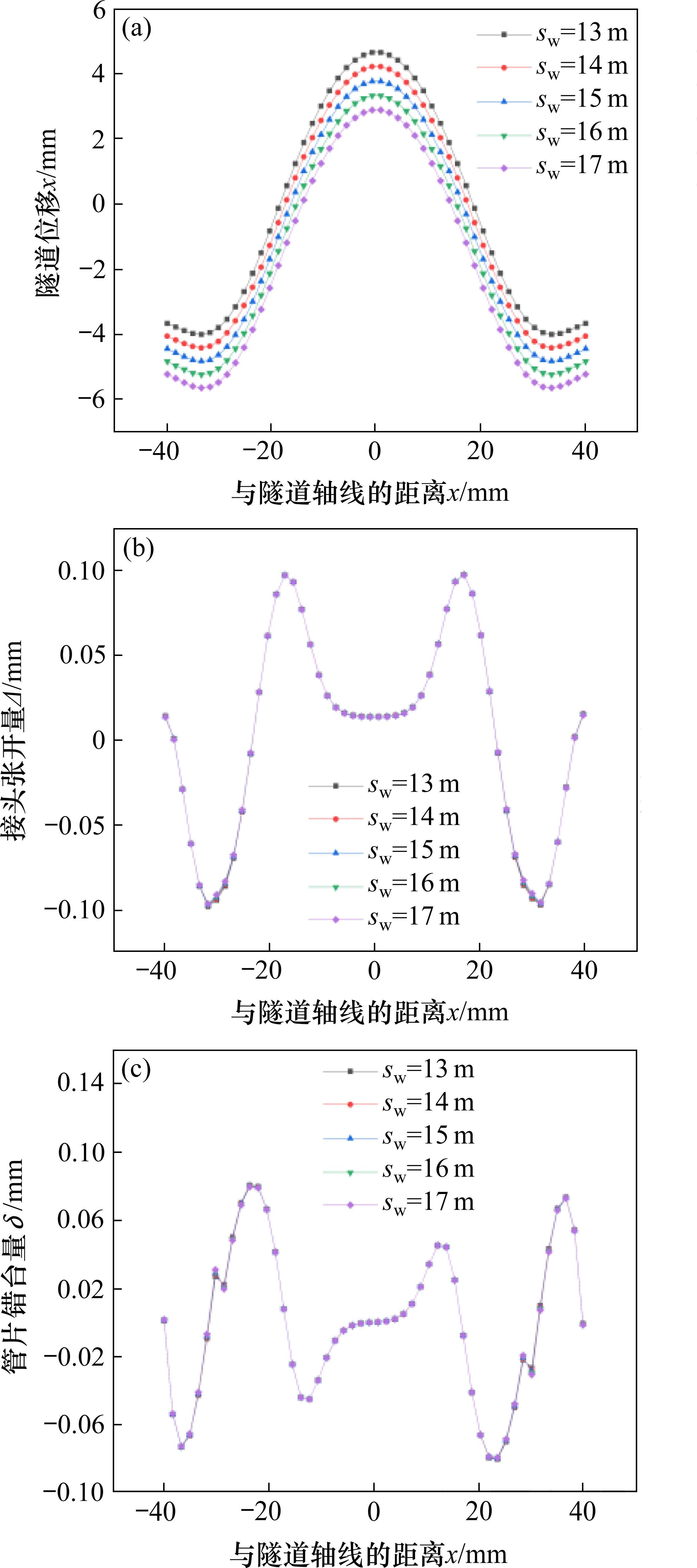
为研究降水深度(sw)对既有隧道的影响,取5组降水深度,即sw=13,14,15,16,17 m。
由图15(a)可知,隧道变形量受降水深度影响较大。降水深度改变时,隧道最大隆起值显著变化。且随着降水深度的增大,隧道最大隆起值从4.67 mm减小为2.90 mm,且整个降水影响半径范围内,相较于隧道中心点处,基坑边缘处受到降水影响的作用较小,这也验证了2.2节所述基坑降水曲线呈漏斗状的合理性。随着降水深度的增加,降水增荷作用增强,抵消了部分因基坑卸荷对既有隧道产生的附加应力。由图15(b)知,随着降水深度的增加,管片接头张开量变化平缓,最大管片接头张开量逐渐减小。由图15(c)可知,在x=±31 m附近,即1倍降水井等效半径附近,错台量有突变现象。
5 结论
1) 本文第1阶段采用Mindlin方法求解基坑坑底、坑侧卸荷及降水共同作用在既有隧道处产生的附加应力,第2阶段把既有隧道看成Kerr弹性地基上Timoshenko梁,通过Galerkin法计算既有隧道处产生的竖向变形、管片接头张开量、错台量,并与现场实测结果、数值模拟结果、不考虑降水结果进行了对比,验证了本文方法的合理性。
2) 降水作用对既有隧道的变形不可忽视。考虑降水作用后,既有隧道最大隆起量从10.44 mm降为4.23 mm,减少了59.5%,且管片接头张开量和错台量均略小。
3) 在一些隧道变形特征点处:如基坑1倍开挖宽度、1倍降水井等效半径处,管片接头张开量和错台量形状易发生突变,需要特别关注。
4) 当改变基坑开挖长度或宽度时,管片接头张开量和错台量形状发生了突变、反转现象。合理控制基坑开挖长宽比,对隧道变形有着较大的影响。
基于Kerr地基模型基坑开挖及降水引起的下卧隧道变形
[J/OL]. 工程力学, 2023: 1-12. (孟非,乔世范,陈道龙等.基坑开挖及降水引起既有盾构隧道变形分析[J].铁道科学与工程学报,2025,22(01):246-258.
MENG Fei,QIAO Shifan,CHEN Daolong,et al.Simplified analytical method for evaluating effects of excavation and dewatering of pit on shield tunnel considering shearing effect[J].Journal of Railway Science and Engineering,2025,22(01):246-258.

