在城市中心区,空间狭窄、建筑密集、人口集中、沉降控制严格等问题逐渐成为开发利用地下空间的制约。如何有效提高地下空间的利用率,高效有效地利用地下空间成为当前城市规划的重点。而传统圆形隧道空间利用率较低,修建双线隧道时往往造成大量的空间浪费。基于此,各种异形盾构隧道应运而生。类矩形作为一种合理的断面形式,因其具有空间利用率高、地表沉降控制好、双线一次成型等优点,被广泛采用[1-3]。盾壳是盾构机的重要组成部分,承担着保护施工人员安全、防止外部水土入侵的作用,对盾构机性能进行准确预测[4],可有效保证施工安全与施工效率[5-6]。盾尾作为管片拼装区域,无法加装大型隔板以及肋条等加固措施,因此刚度往往小于盾壳其余部分,在实际工程中往往由于过大的变形影响正常施工的进行,是盾壳最薄弱的位置。已有部分学者对盾尾的力学性能进行了研究。MEDEL-MORALES等[7]采用离散元模型对开挖模式下的盾构机性能进行了模拟。LIAO等[8]建立了硬岩隧道掘进机控制器设计的多系统耦合闭合动力学模型,比较了盾构机在不同岩层下的力学性能。管会生等[9]将盾尾简化为等截面圆环形梁结构,建立盾尾受力分析的简化力学模型,并以上海地铁某工程的盾构参数为基础,对盾尾的受力和强度进行验算。赵洁咏等[10]使用三维实体单元建立了圆形盾尾的数值模型,对其刚度及强度进行了校核。孙海力等[11]提出了一种有限元分析与应变检测相结合的方法,得到了盾尾应力与变形之间的本构关系。陈明江等[12]采用有限元建模和解析方法对盾尾立体结构进行仿真计算,校核了盾尾刚度。黄志影等[13]采用壳单元分段建立了切口环以及盾尾的模型,详细考虑了竖直和水平水土压力、自重、地基反力、转向力的影响,并计算了静止和掘进工况下的变形及应力。邵成猛[14]采用数值模拟方法,研究了在下方出现暗洞以及注浆压力影响等特殊工况对盾尾的应力和变形的影响。王胜勇[15]使用实体单元建立了大断面矩形顶管机切口环精细化有限元模型,分析了其在水土压力下的应力与变形,并对顶管机壳体提出了优化设计。王小盾等[16-17]采用壳单元建立类矩形盾尾的数值模型,计算了其在静止工况、直线推进工况和转向工况3种工况下的力学性能。当前在盾尾力学性能的研究中,所针对的研究对象主要以传统圆形盾尾为主,仍缺少针对类矩形盾尾力学性能的深入研究。在分析方法方面,当前研究通常将盾尾作为一个独立的薄壳结构进行分析,忽略了其余盾壳及盾尾刷等细部结构对盾尾力学性能的影响[18-20],会导致其分析结果存在一定的不确定性。在分析工况方面,当前绝大多数研究仅考虑了静止工况,尚未考虑施工掘进的影响。为此,本文基于郑州地铁8号线T061型类矩形盾构机,建立了类矩形盾尾的全盾壳数值分析模型,并考虑掘进和盾尾密封系统的影响,对盾尾的受力行为进行研究。
1 基本参数
1.1 工程地质概况
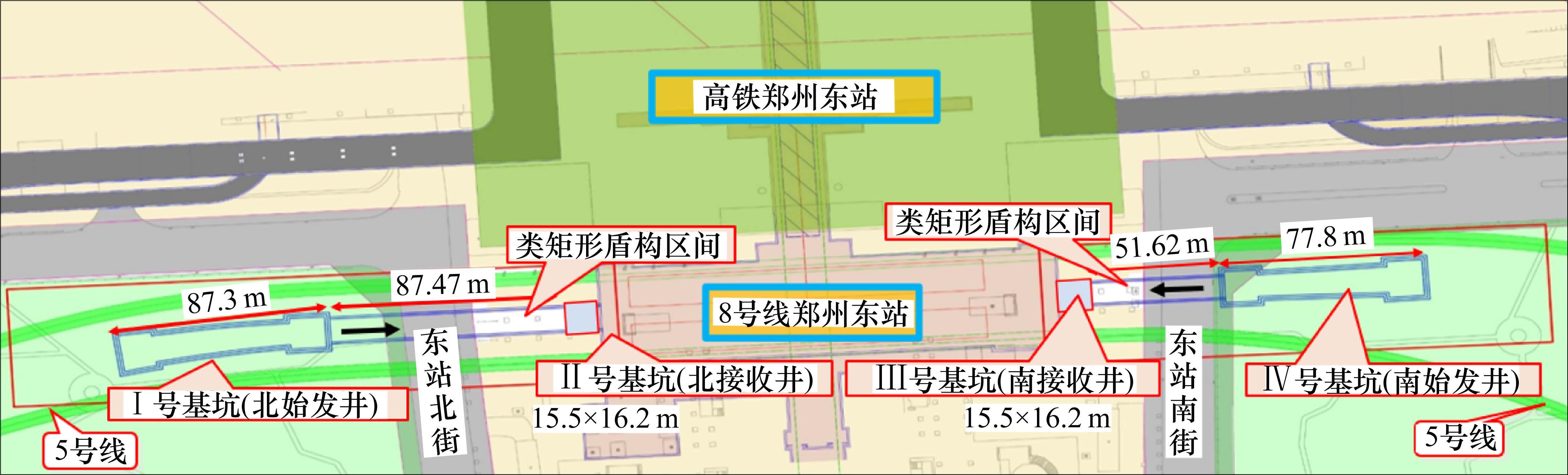
郑州地铁8号线郑州东站南~北类矩形盾构段采用一台开挖断面为11.83 m×7.27 m类矩形土压平衡盾构机进行掘进施工,从北明挖段Ⅰ号基坑(北始发井)始发,掘进至郑州东站北明挖段Ⅱ号基坑(北接收井)吊出。后转场至南明挖段Ⅳ号基坑北端头井(南始发井)始发,掘进至郑州东站南明挖段Ⅲ号基坑(南接收井)吊出。施工区间如图1所示。北段区间隧道长度为87.473 m,顶覆土埋深为16.94~18.47 m,主要穿越地层为粉砂和细砂层。北段区间隧道长度均为51.621 m。顶覆土埋深为17.49~19.38 m,主要穿越地层为粉砂、黏土地层,基本地层参数如表1所示。
| 编号 | 名称 | 天然重度γ/ (kPa∙m-1) | 黏聚力c/kPa | 内摩擦角φ/(°) |
|---|---|---|---|---|
| 1 | 黏质粉土 | 18.5 | 15 | 22.5 |
| 2 | 细砂 | 19.5 | 3 | 30 |
| 3 | 粉砂 | 20.0 | 2 | 32 |
1.2 类矩形盾构
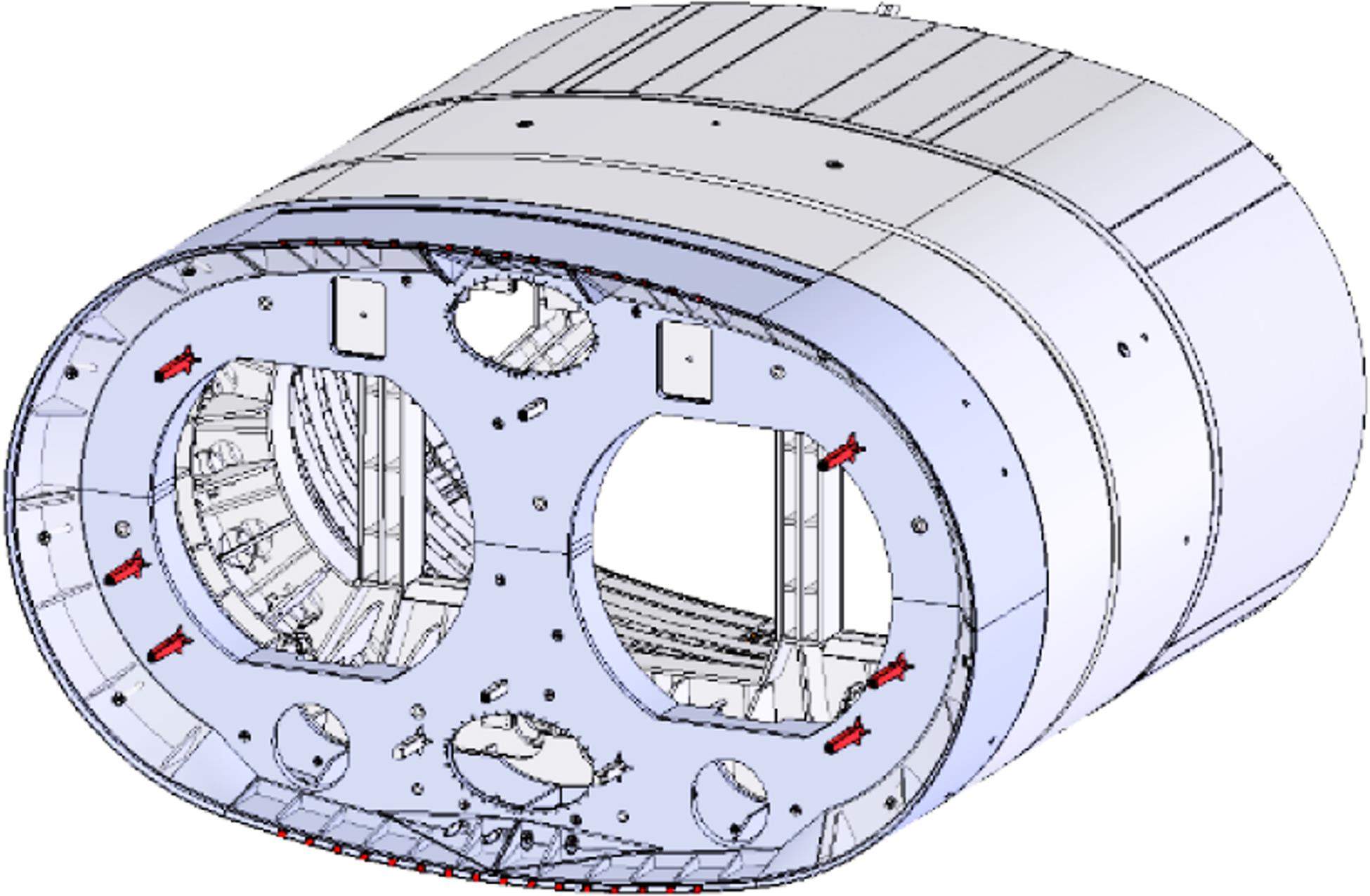
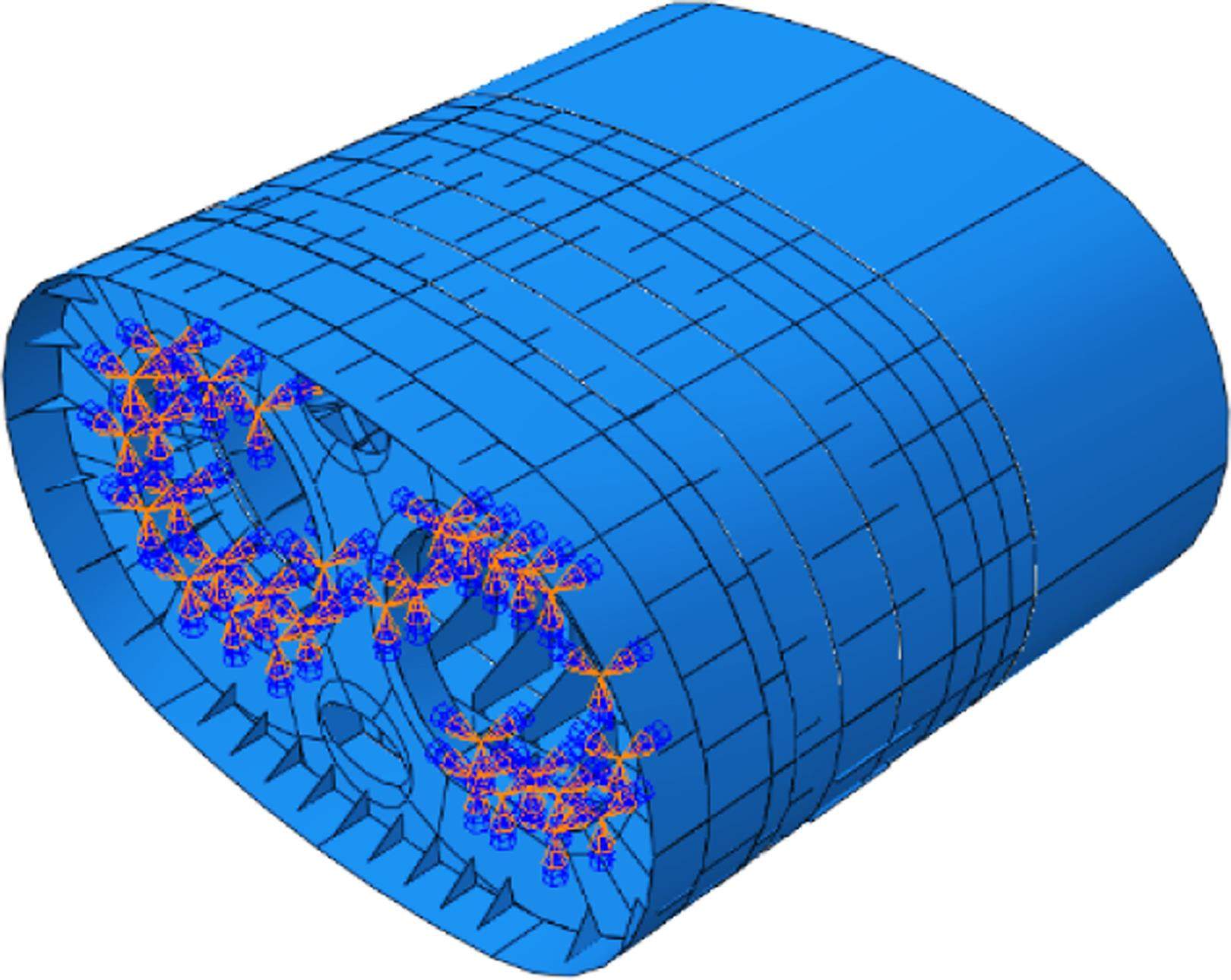
类矩形盾构壳体的钢结构是根据给定的土压、水压和在运行时所产生的负载等条件而进行设计,通过焊接成为一个整体钢结构,所有钢板屈服强度为460 MPa。所有的盾构机运行所需的连接件及连接附件均集成布置在盾壳内,盾构壳体由前壳体1、前壳体2、后壳体和盾尾组成,整体设计效果图如图2所示。
2 类矩形盾壳数值模型
2.1 几何模型
盾构壳体由前壳体1、前壳体2、后壳体和盾尾组成,前壳体1也称切口环,尺寸为11 830 mm×7 270 mm×1 880 mm,外壳体厚度80 mm。与前壳体2通过焊接连接。前壳体2和后壳体称为支撑环,前壳体2尺寸为11 830 mm×7 270 mm×1 180 mm,外壳体厚度70 mm;后壳体尺寸为11 800 mm×7 240 mm×3 480 mm,外壳体厚度70 mm。前壳体2和后壳体通过铰接油缸连接。盾尾尺寸为11 800 mm×7 240 mm×3 980 mm,外壳体厚度70 mm,与后壳体通过焊接连接。
全盾壳模型拟采用分段建模的方式对前壳体1、前壳体2、后壳体和盾尾4部分壳体进行建模。各部件模型按照实际尺寸以板壳的形式建立,主要考虑筋板、胸板及横隔板等受力部件,其余细部结构以及部分部件中的不规则空洞忽略不计。各部件为接触关系绑定连接(刚接)。
分段建模完成后,各部分盾壳按照连接关系进行组装。其中,前壳体1和前壳体2通过法兰板进行连接,模型中省略连接螺栓,将2块法兰板表面通过tie命令绑定连接(刚接)。前壳体2和后壳体通过铰接油缸进行连接,由于不考虑铰接油缸转向作用,故省略该连接部分油缸,将后壳体与前壳体2嵌套部分通过tie命令绑定连接(刚接)。后壳体和盾尾为焊接连接,使用tie命令将两外壳体边缘节点绑定连接(刚接)。网格划分采用壳单元,网格控制为四边形结构化网格,网格大小约为0.04 m2。几何模型如图3所示。

2.2 单元选择及材料参数
本文主要关注盾壳的应力及变形,且材料主要为钢结构,可以将模型材料考虑为弹性材料。参考Q460高强钢,取弹性模量206 GPa,泊松比0.3,密度7 850 kg/m3。
模型单元选择方面,考虑到盾壳的厚度远远小于其长度及宽度,在有限元分析中适用于板壳理论的假定,故选择采用壳单元进行建模。
2.3 荷载模型
模型采用荷载-结构法计算,工况考虑为18 m埋深下的直线掘进工况。荷载按照作用方向分为径向荷载和轴向荷载两部分。荷载施加模式如图4所示。
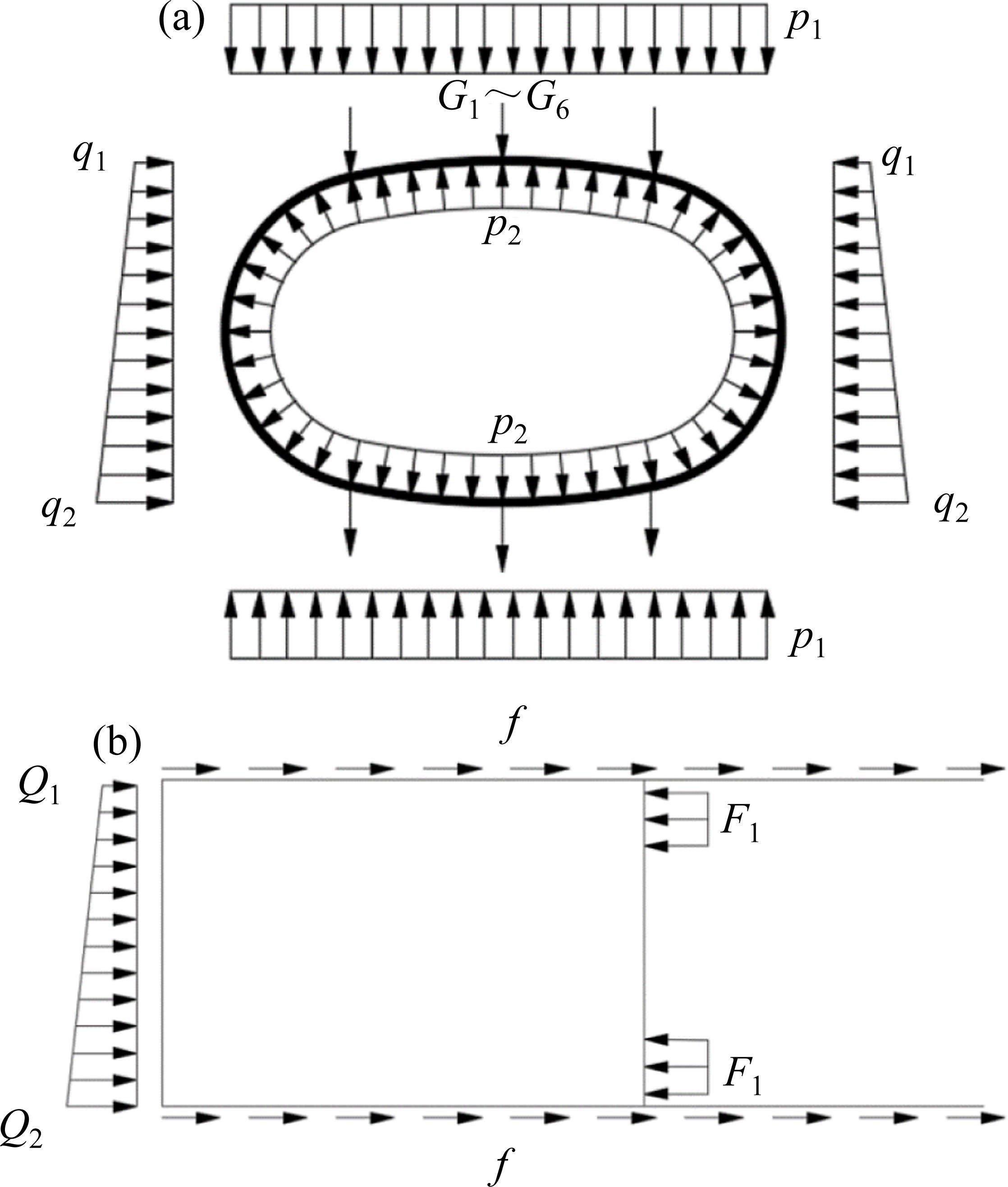
径向荷载为作用方向沿盾壳径向的荷载,考虑垂直和水平土压力、结构自重以及油脂腔压力,隧道埋深按照实际埋深18 m进行计算。参考主要地层参数将地层简化考虑为单一性质的地层。荷载计算采用全覆土理论,水土合算,侧压力系数取0.6,地层重度偏不利取20 kN/m。基床系数取20 MPa/m。自重考虑为2部分,第1部分为壳体等结构重量,该部分以竖向均布荷载的形式施加在对应外壳体内表面。第2部分为设备重量,如刀盘驱动等,直接施加在设备安装位置。实际工程中为阻挡外部水土进入盾尾,会在2道盾尾刷之间充填盾尾油脂,并使用油脂泵使其维持一定的压力,而该区域被称为油脂腔。油脂腔荷载即指这部分压力对盾壳形成的荷载。
1) 垂直水土荷载p1:
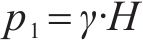
2) 水平水土荷载q1(顶部)和q2(底部):
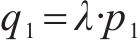
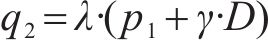
3) 自重荷载g1~g6:
g1~g4:分别为前壳体1、前壳体2、后壳体、盾尾的外壳体以及内含设备重力荷载,施加在对应壳体内表面。
g5~g6:大小刀盘驱动重力荷载,施加在前壳体1对应安装处。
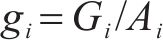
自重计算结果按表2取值。
| g1 | g2 | g3 | g4 | g5 | g6 |
|---|---|---|---|---|---|
| 41 | 30.07 | 26.14 | 17.3 | 7.3 | 3 |
4) 油脂腔荷载p2:
由于需要抵御外部水土压力,油脂仓荷载应略大于外部水土荷载,施加位置位于盾尾固定环之间,方向指向外部的均布荷载。按照工程经验,考虑取值如下:
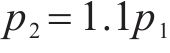
轴向荷载为作用方向沿着盾壳轴向的荷载。考虑刀盘正面水土压力、地基与盾壳间的摩阻力以及推进千斤顶的顶推力。刀盘正面水土压力与水平径向水土压力计算方法相同。盾壳与土体间的摩阻力按照工程经验取值。推进千斤顶的顶推力根据直线推进阶段施工数据,取最大顶推力平均分配在每个油缸上,荷载以小范围均布荷载的形式施加在对应位置。
轴向荷载取值如下:
5) 刀盘正面水土压力Q1(顶部)和Q2(底部):
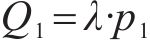
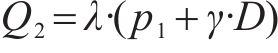
6) 盾壳与土体间的摩阻力f:
按照工程经验取值为10 kPa。
7) 推进千斤顶顶推力F1:
平均分配在32个油缸上。荷载以小范围均布荷载的形式施加在对应位置。
单个千斤顶荷载:
F1=F/a
式中:γ为土层重度;H为盾壳埋深;D为盾尾横截面短轴长度;G1~G6分别对应前壳体1、前壳体2、后壳体、盾尾、大刀盘驱动和小刀盘驱动所包含设备的重力;A1~A6分别对应G1~G6的作用面积。除自重荷载外,其余荷载按照表3取值。
| p1 | q1 | Q2 | p2 | Q1 | Q2 | f | F1 |
|---|---|---|---|---|---|---|---|
| 360 | 216 | 312 | 396 | 216 | 312 | 10 | 17 400 |
2.3 边界条件
1) 固定边界条件
考虑将盾壳相对刚度最大的位置作为固定约束,按照工程经验,考虑将大刀盘驱动安装位置作为固定约束,约束位置如图5所示。
2) 地基反力
地基反力由设置在外壳体的仅受压接地弹簧提供。外壳体单元大小为a,故单个弹簧受压劲度系数k计算如下:
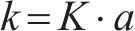
式中:K为地层基床系数;a为外壳体单个单元面积。计算得k=800 kN/m
3) 盾尾刷
为准确模拟盾尾刷性能,对盾尾刷进行了受压性能试验。试验采用万能试验机对盾尾刷进行了压缩性能试验。盾尾刷由夹具固定在万能试验机上。夹具主要由上加载板和下固定板组成,其中上加载板可滑动,如图6所示。

位移控制的方式,从盾尾刷自由状态开始加载,加载持续至盾尾刷被完全压紧结束。试验加载的作用力可看作作用于盾尾和管片的径向力。
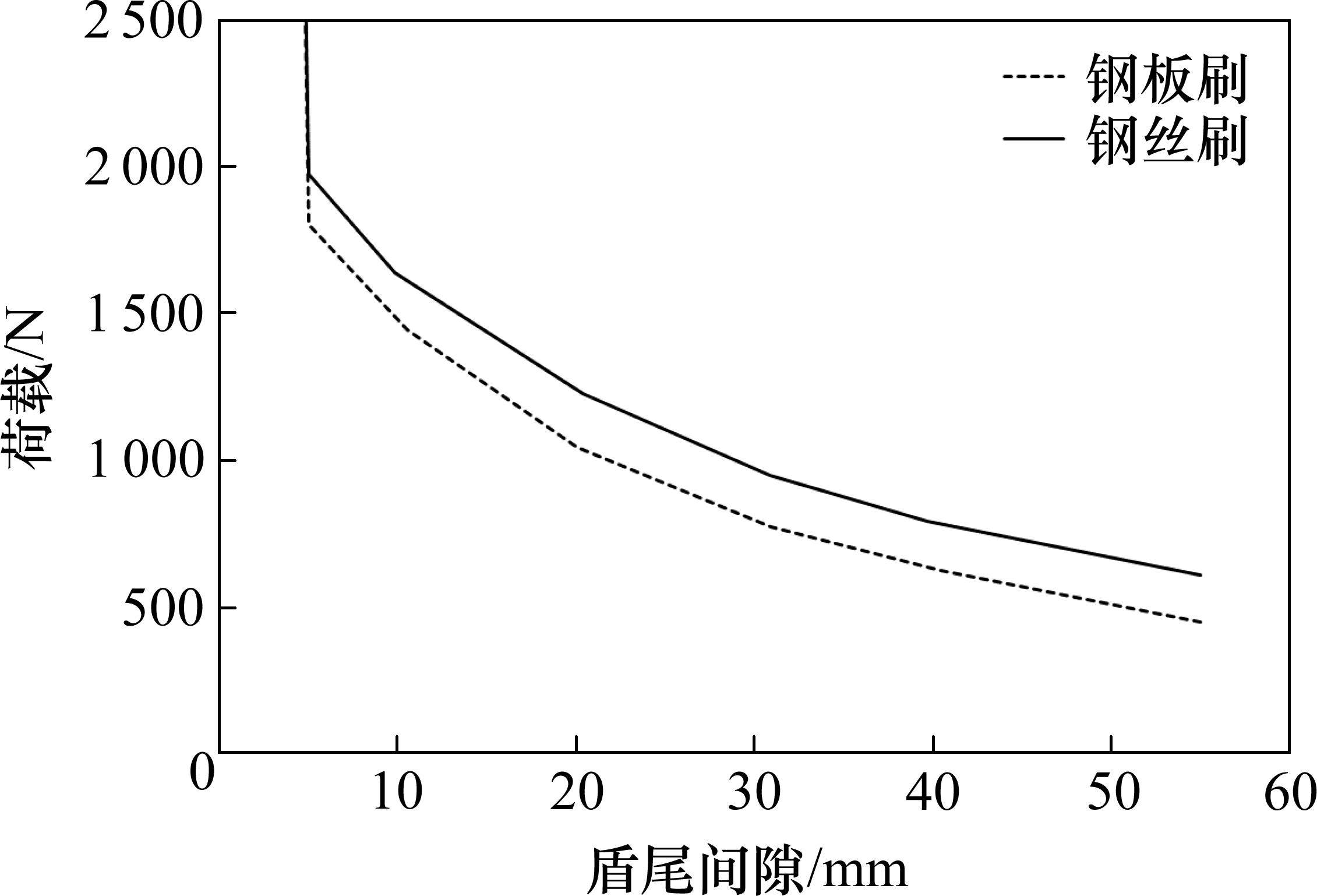
盾尾刷的模拟考虑在盾尾实际位置设置3排非线性弹簧模拟2道钢丝刷和1道钢板刷,如图7所示。单个盾尾刷连接板尺寸为200 mm*200 mm,与网格大致尺寸相似。可近似考虑为每个弹簧即对应一个盾尾刷。弹簧仅受压,劲度系数参考盾尾刷压缩性能试验结果,以折线形式拟合。考虑试验误差,将压缩试验结束时看作盾尾刷处于完全压紧状态,此时盾尾间隙视为5 mm。当盾尾间隙小于5 mm后,视为管片、盾尾刷和盾尾发生硬接触,此时弹簧刚度增大10倍。单个盾尾刷弹簧作用力与盾尾间隙的关系如图8所示。

3 计算结果与分析
3.1 盾尾受力模拟
数值模型计算结果如图9所示,限于篇幅仅展示整体和盾尾的应力与变形情况。
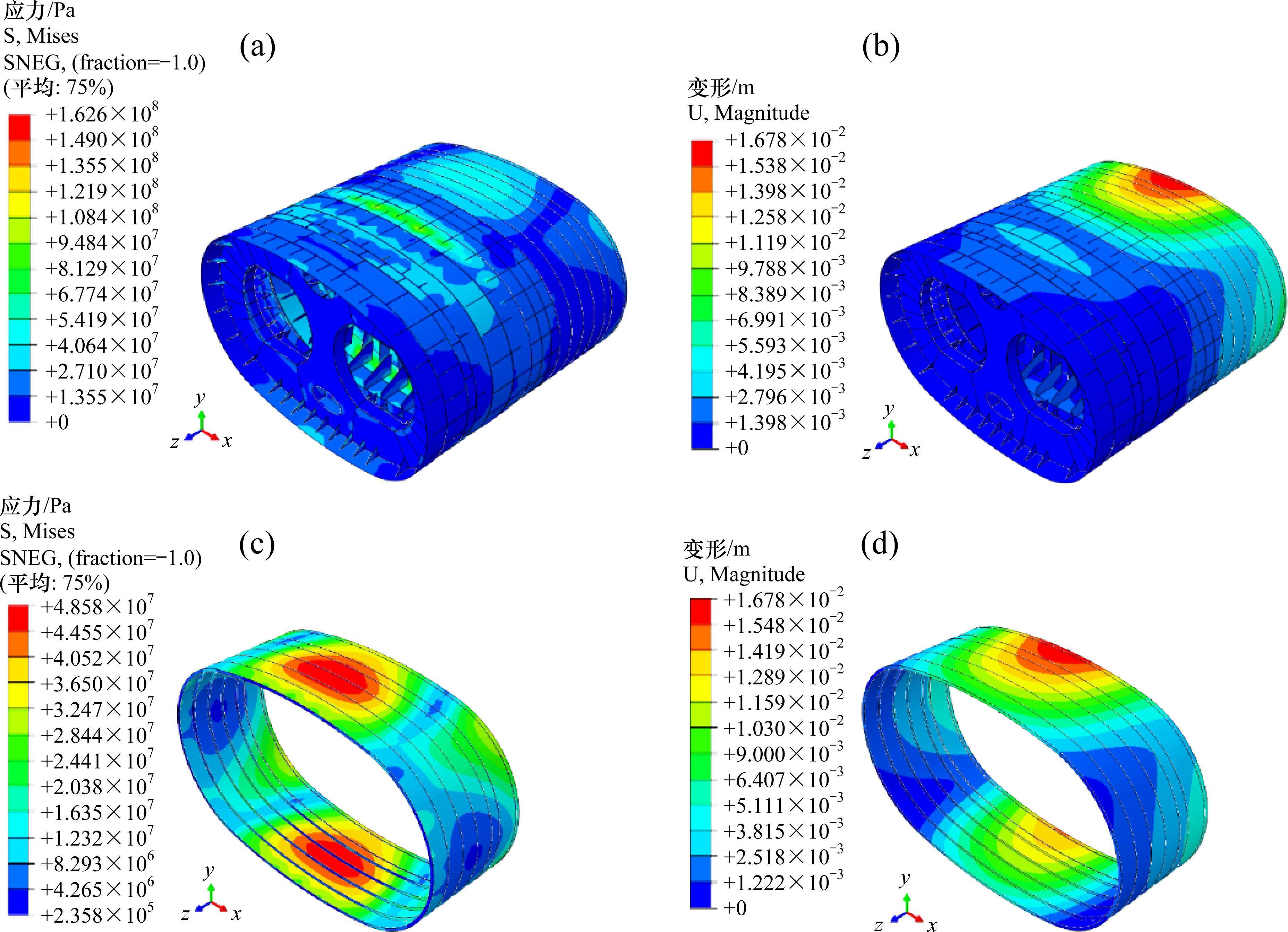
应力方面,各壳体整体应力水平相当,大部分应力水平都处于100 MPa左右。前壳体1、前壳体2和后壳体3部分都存在不同程度的应力集中,常见于倒角位置和构件连接处(截面变化处)。最大应力162.6 MPa,位于后壳体的H梁斜梁处。对于盾尾来说,盾尾应力分化明显,拱腰圆弧段应力水平远小于拱顶与仰拱圆弧段,原因是拱腰圆弧段半径较小,形成了较强的拱效应。从约束端到自由端,盾尾应力呈现先增大后减小的趋势,最大应力为48.6 MPa,位于盾尾中部拱顶位置。
变形方面,整个类矩形盾壳变形呈“蝴蝶结”形式,即拱顶拱腰向内变形,拱腰向外变形。对于盾尾来说,从横截面角度来看,盾尾2点钟和10点钟位置变形较小,拱顶(12点钟位置)、仰拱(6点钟位置)呈现明显内缩趋势而拱腰(3点钟和9点钟)处呈现部分外扩趋势,拱顶和仰拱处变形明显大于拱腰处变形。造成该现象的原因首先是顶底水土压力较腰部水土压力更大,其次拱顶和仰拱曲率半径较大,筋板密度较小,局部刚度较拱腰小。从轴向角度来看,越远离后盾连接处变形越大。造成该现象的原因是盾尾类似于平面悬臂结构,其与后壳体的焊接处类似于其约束端,因此越远离约束端则变形越大。最大水平变形为5.88 mm,位于盾尾自由端拱腰位置。最大竖向变形为16.75 mm,位于盾尾自由端拱顶位置。
盾壳各部分主要计算结果如表4所示。
| 部位 | 最大应力/MPa | 水平向变形/mm | 竖向变形/mm |
|---|---|---|---|
| 前壳体1 | 94.57 | 0.79 | 1.02 |
| 前壳体2 | 78.36 | 0.51 | 3.05 |
| 后壳体 | 162.62 | 2.74 | 7.69 |
| 盾尾 | 48.58 | 5.88 | 16.66 |
3.2 模拟结果验证
为验证全盾壳模型计算的适用性以及盾尾计算的关键控制参数,因此额外建立了计算模型与施工监测数据进行对比。由于施工现场条件限制,仅能测量到盾尾中部的收敛值,故以此为衡量指标确定各计算模型的偏差。其中全盾计算模式为按照3.1节计算模式,将盾尾考虑为盾壳的一部分参与计算。而仅盾尾计算模式为将盾尾单独进行计算,把盾尾和后壳体连接处考虑为固定约束。偏差量指各数值模型与施工数据的相对偏差百分比。所有模型计算埋深为18 m,盾壳的外壳厚度与实际相同。各模型计算参数与结算结果如表5所示。
| 模型编号 | 计算模式 | 盾尾刷 | 油脂腔荷载/MPa | 盾尾中部收敛/mm | 偏差量/% |
|---|---|---|---|---|---|
| 1 | 全盾 | 有 | 0.4 | 19.3 | 13.5 |
| 2 | 全盾 | 有 | 无 | 30.5 | 76.4 |
| 3 | 全盾 | 无 | 0.4 | 19.5 | 14.7 |
| 4 | 仅盾尾 | 有 | 0, 4 | 10.4 | -39.8 |
| 5 | 施工数据 | — | — | 17 | — |
根据计算结果可看出,使用全盾壳模型计算并考虑盾尾刷与油脂腔荷载的计算模式与实际施工监测数据最为接近,而不考虑油脂腔荷载的全盾计算模式偏差最大。值得注意的是仅考虑盾尾的计算模型得出的计算结果明显小于全盾计算模型,主要原因可能是该计算模型下盾尾与后盾连接处视为固接,连接处的转角被限制,与实际情况不符。而在全盾壳模型中,盾尾与后盾视为通过焊接连接,连接处的模拟更接近实际情况,可以产生转角。另外,从计算结果可以看出,油脂腔压力对盾尾变形影响较大,盾尾刷对盾尾变形的影响较小,其原因可能是盾尾刷本身刚度较小,不能有效限制盾尾变形,而油脂腔压力作用于盾尾自由端,可以有效抵抗外部水土压力,有利于盾尾受力。
3.3 影响参数分析
为确定影响盾尾力学性能的因素,需要对计算模型进行参数化分析。由3.2节结论,该节采用考虑盾尾刷以及油脂腔荷载的全盾壳模型进行计算。根据3.1节全盾壳模型计算结果可知,盾壳变形主要发生在盾尾位置,因此参数分析仅对盾尾部分进行,前壳体及后壳体结构参数保持不变。
3.3.1 地层性质和埋深
隧道沿线的地层性质和埋深往往会产生变化,为验证盾壳在不同地层参数时的安全储备,需要对地层性质和埋深进行参数分析以便研究其对盾尾结构应力与变形的影响。以80 mm盾尾厚度为基础,地层性质分为黏土和砂土,如表6所示。埋深参数划分为6,12,18,24,30和36 m。参数分析结果如图10所示。
| 地层 | 重度/ (kN∙m-1) | 侧压力 系数 | 地基基床系 数/(MPa∙m-1) |
|---|---|---|---|
| 黏土 | 20 | 0.5 | 20 |
| 砂土 | 19 | 0.4 | 35 |
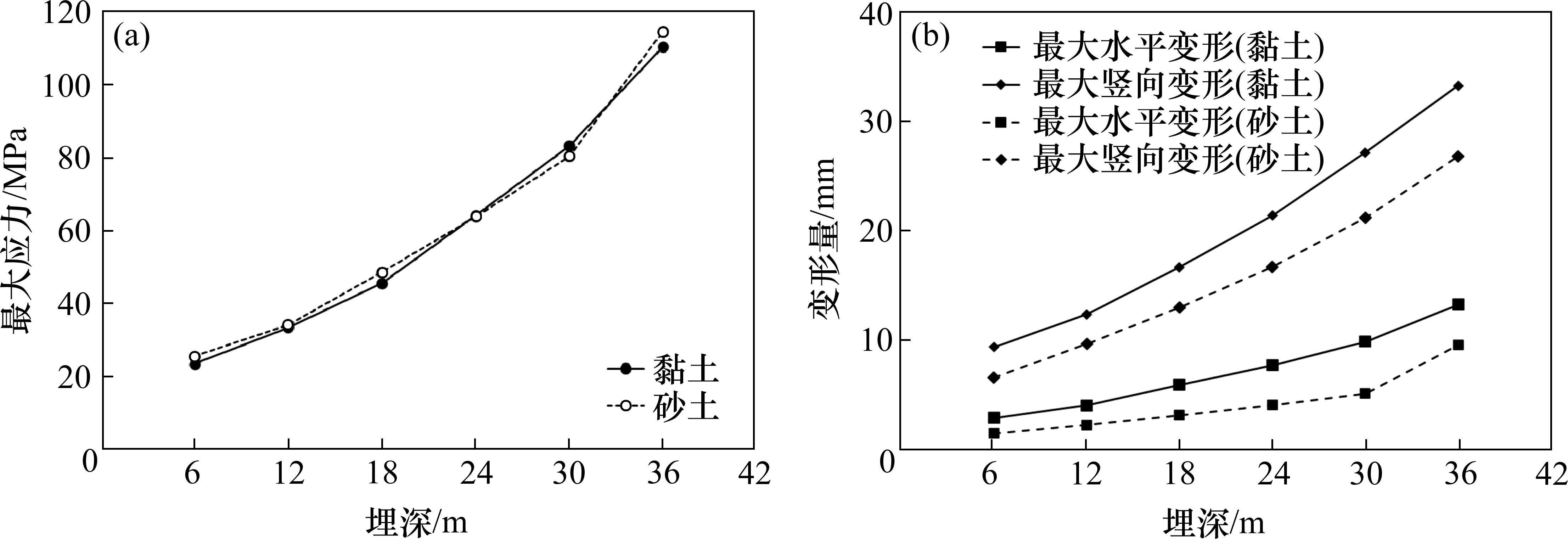
应力方面,随着覆土厚度增大,最大应力增大近似呈线性增大,覆土厚度越大,应力的增长趋势越快。在砂土和黏土2种地层情况下,各埋深应力大小相当,无明显差别。在36 m埋深下,黏土地层和砂土地层最大应力分别为114.5 MPa和110.3 MPa。从结果可知,在该埋深下所有工况最大应力都小于盾尾屈服强度,可认为盾尾具有足够的强度储备。
变形方面,随着覆土厚度增大,最大水平变形与最大竖向变形都近似呈线性增大趋势,覆土厚度越大,变形的增长趋势越快。砂土地层变形量要明显小于黏土地层,原因是砂土地层基床系数较大,对盾尾的约束能力更强。在36 m埋深下,黏土地层和砂土地层最大水平变形分别为13.22 mm和9.53 mm,最大竖向变形分别为33.23 mm和26.77 mm。
3.3.2 盾尾厚度
盾尾厚度是决定盾尾刚度和造价的关键因素,为了更好地对设计进行优化,故需要对盾尾厚度进行参数化分析。以18 m埋深的黏土地层为基础,盾尾厚度划分为60,70,80,90和100 mm,参数分析结果如图11所示。
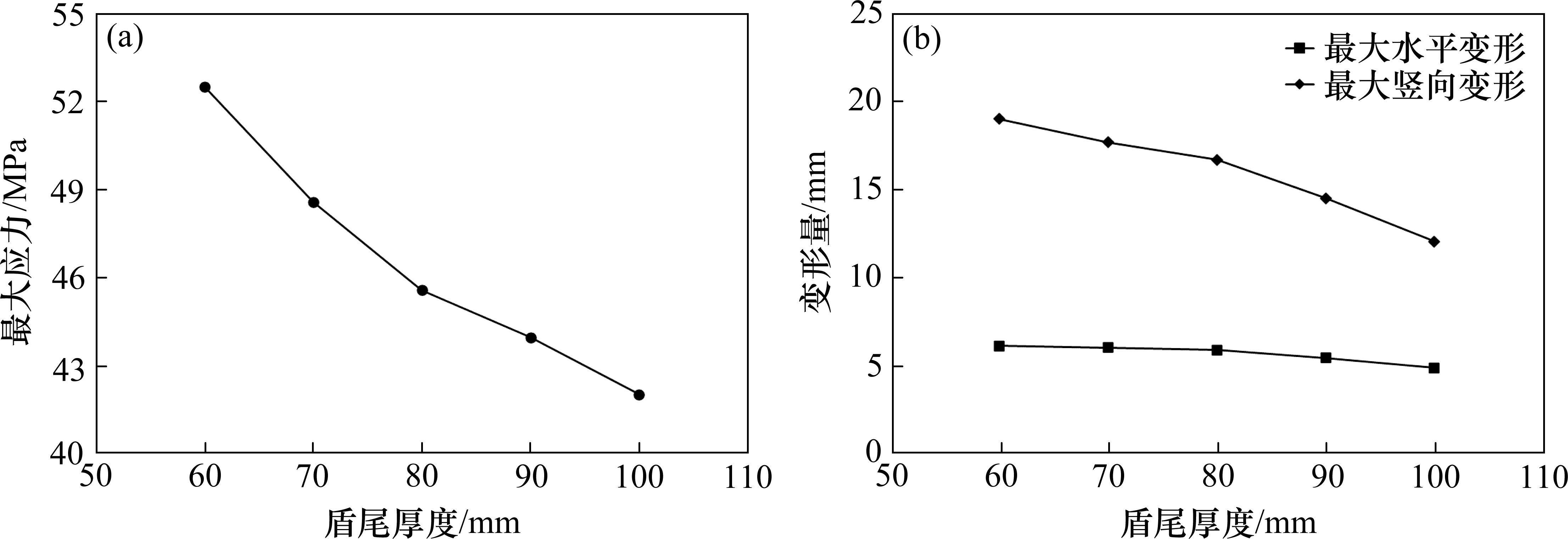
应力方面,随着盾尾厚度的增大,盾尾最大应力逐渐减小,超过80 mm后减小幅度变慢。在18 m埋深情况下,盾尾厚度60 mm对应最大应力为52.5 MPa,盾尾厚度为100 mm对应最大应力为42.03 MPa,最大应力减少了19.3%。在18 m埋深下所有厚度盾尾最大应力均小于钢板屈服应力,具有足够的强度储备。
变形方面,随着盾尾厚度增大,盾尾最大水平变形和最大竖向变形都有不同程度的减小。最大竖向变形减小趋势加快,而最大水平变形减小趋势总体较小。盾尾厚度60 mm对应最大水平变形6.12 mm,最大竖向变形18.97 mm;盾尾厚度100 mm对应最大水平变形4.88 mm,最大竖向变形12.03 mm。
3.3.3 顶推力
为确定千斤顶顶推力对盾尾力学性能的影响,因此需要对顶推力进行参数化分析。以18 m埋深的黏土地层,盾尾厚度80 mm为基础,将顶推力划分为5 000,6 000,7 000,8 000和9 000 t,参数分析结果如图12所示。
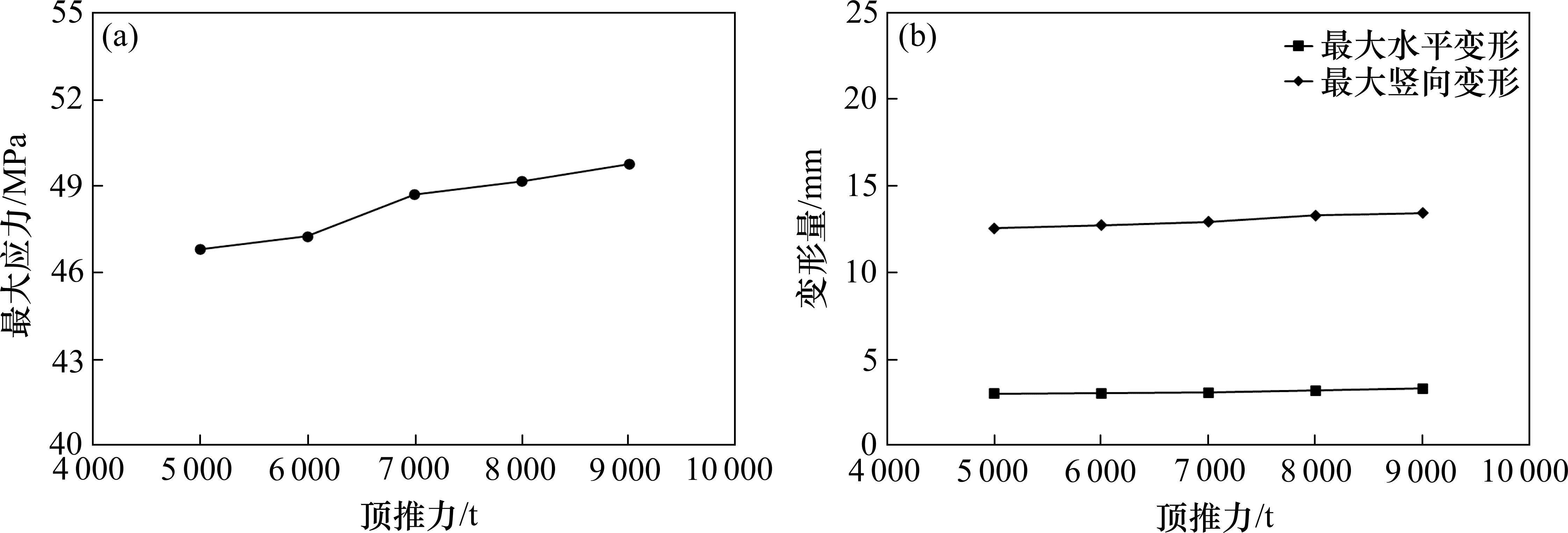
由计算结果可知,随着顶推力增大,盾尾的最大应力值和最大变形值无明显变化,原因是推进油缸作用力作用在管片和后盾上,盾尾未直接受力,因此可以认为顶推力对盾尾的力学性能无明显影响。
4 结论
1) 背景工程中,全盾壳应力分布总体较为均匀,部分位置存在应力集中现象。类矩形盾壳在实际埋深18 m情况下最大应力为162.62 MPa,出现在后壳体H梁处;最大变形16.66 mm,出现在盾尾自由端拱顶部位。盾尾变形量明显大于盾壳其他部位,是盾壳的薄弱部位。类矩形盾尾在实际埋深18 m以及最大计算埋深36 m情况下均有足够的强度与刚度储备,可靠性较高。
2) 全盾计算模型相比仅考虑盾尾的计算模型能更准确反映盾尾的变形情况。全盾壳模型盾尾与后盾连接处视为焊接,因此在盾尾受力后会产生转角,与实际情况更为接近;盾尾模型连接处为固定约束,转角被限制,与实际情况不符,导致计算出的盾尾变形明显偏小。
3) 在盾尾力学性能研究中需考虑盾尾密封系统的影响。其中,油脂腔荷载显著影响盾尾变形,在计算中不可忽略。盾尾刷本身由于刚度较小,对盾尾变形没有明显限制作用。
4) 通过对模型进行参数分析可知,随着隧道覆土厚度的增大,盾尾的应力与变形均呈近似线性增大,呈逐渐加快趋势。随着地层基床系数增大,地层对盾尾的限制能力变强,因此盾尾变形量会有一定程度地减小。随着盾尾厚度增大,盾尾的最大应力和最大变形量均减小,呈现先快后慢的趋势。由于顶推力未直接作用于盾尾,因此顶推力对盾尾力学性能无明显影响。
沈皓,潘汪洋,石元奇等.基于全盾壳模型的类矩形盾尾力学性能数值模拟研究[J].铁道科学与工程学报,2025,22(01):235-245.
SHEN Hao,PAN Wangyang,SHI Yuanqi,et al.Numerical simulation study on mechanical performance of rectangular shield tail based on full shield shell model[J].Journal of Railway Science and Engineering,2025,22(01):235-245.

