近年来,国家加大了对西部地区发展的支持,大量的隧道工程、铁路、高速公路等基础交通建设开工[1]。然而,由于我国西部地区地质构造特殊,隧道工程面临着极其复杂的地质、地形问题,特别是在断层破碎带[2],隧道穿越该地区时,地层性质和荷载会发生突变,严重影响隧道的结构稳定和运营安全。此外,我国西部地区位于环太平洋地震带和地中海-喜马拉雅地震带[3],地震灾害频发,地震作用也会对隧道造成不可逆的损害[4]。因此,开展跨断层隧道的地震响应研究,是复杂地质环境下隧道建设[5]不可忽略的问题。
隧道结构通常被认为是抗震性能优越的工程建筑[6],然而,处于断层破碎带的隧道及围岩在地震作用下会产生严重的破坏。当断层出现在隧道局部时,采取传统抗震措施[7],如注浆加固、喷锚支护和设置减震层等,即可获得较为可靠的抗震性能。但当隧道穿越断层时,传统的锚索支护材料和抗震措施难以适应围岩破坏时的瞬间大变形[8]。何满潮等[9]研发出一种具有负泊松比效应、恒阻、吸能、大变形量的NPR锚索,NPR锚索在静力拉伸过程中能保持较高的恒阻力,同时具有大变形量,对于易产生大变形破坏的破碎带围岩有很好的支护效果。
如今,NPR材料及其NPR支护体系[10]已较完善,国内外学者对此开展了大量研究。TAO等[11]通过静态拉伸、周边应变测量等多种方法,研究了NPR锚索的径向变形规律和负泊松比特性,验证了NPR锚索的负泊松比特性及其优越的吸能特性。陶志刚等[12]通过室内静力拉伸试验对微观NPR钢的力学特性进行了研究,阐明了微观NPR锚杆恒阻大变形的特性;胡杰等[13]对静力拉伸作用下NPR锚索-围岩的相互作用机理进行了分析,揭示了NPR锚索与围岩的相互作用与NPR锚索的锚固机理;孙晓明等[14]在巷道支护中运用微观NPR锚索,通过现场开展支护应用试验与监测,提出并验证了长短微观NPR钢锚索联合支护对策的良好围岩大变形控制效果。
目前,振动台试验[15]已广泛应用于大型隧道地震反应的研究,XU等[16]开展了一系列三维振动台试验,研究了山地隧道抗震措施的机理和效果,并提出了一系列提高隧道抗震性能的措施。ZHANG等[17]通过振动台试验,对1座由斜拱和曲梁组成的新型异形拱桥BIACB模型的抗震性能进行了研究,探讨了被测BIACB模型在3种典型地震激发(El-Centro波、Taft波和人工波)下的地震响应。ZHAO等[18]通过大型振动台试验研究了隧道注浆穿越非活动断层的抗震效果,并开发了优化的设计参数。试验结果表明,注浆降低了断层内隧道的加速度响应,减小了断层引起的隧道纵向加速度响应的差异。张熙等[19]通过开展振动台试验,研究了穿越断层带多破裂面隧道的地震损伤发展。
综上,针对隧道在地震作用下的动力响应[20]研究已经取得一定进展,隧道NPR支护技术[21]的相关研究也较为成熟,但针对NPR支护技术下的跨断层隧道在地震作用下的响应规律和动力学抗震特性研究较少。本文以他白依隧道实际工程为依托工程,针对NPR锚索支护下跨断层破碎带隧道在双向地震动作用下的动力响应等问题,基于模型相似理论开展振动台试验,从不同地震波波形、不同地震波幅值等方面研究模型隧道及围岩的加速度、动应力应变及锚索轴力响应等问题,以便为类似断层的抗震设计提供理论参考。
1 工程背景
他白依隧道位于云南省红河州元阳县境内,是元阳县连通建水县、个旧市的控制性工程,他白依隧道地理位置如图1所示。
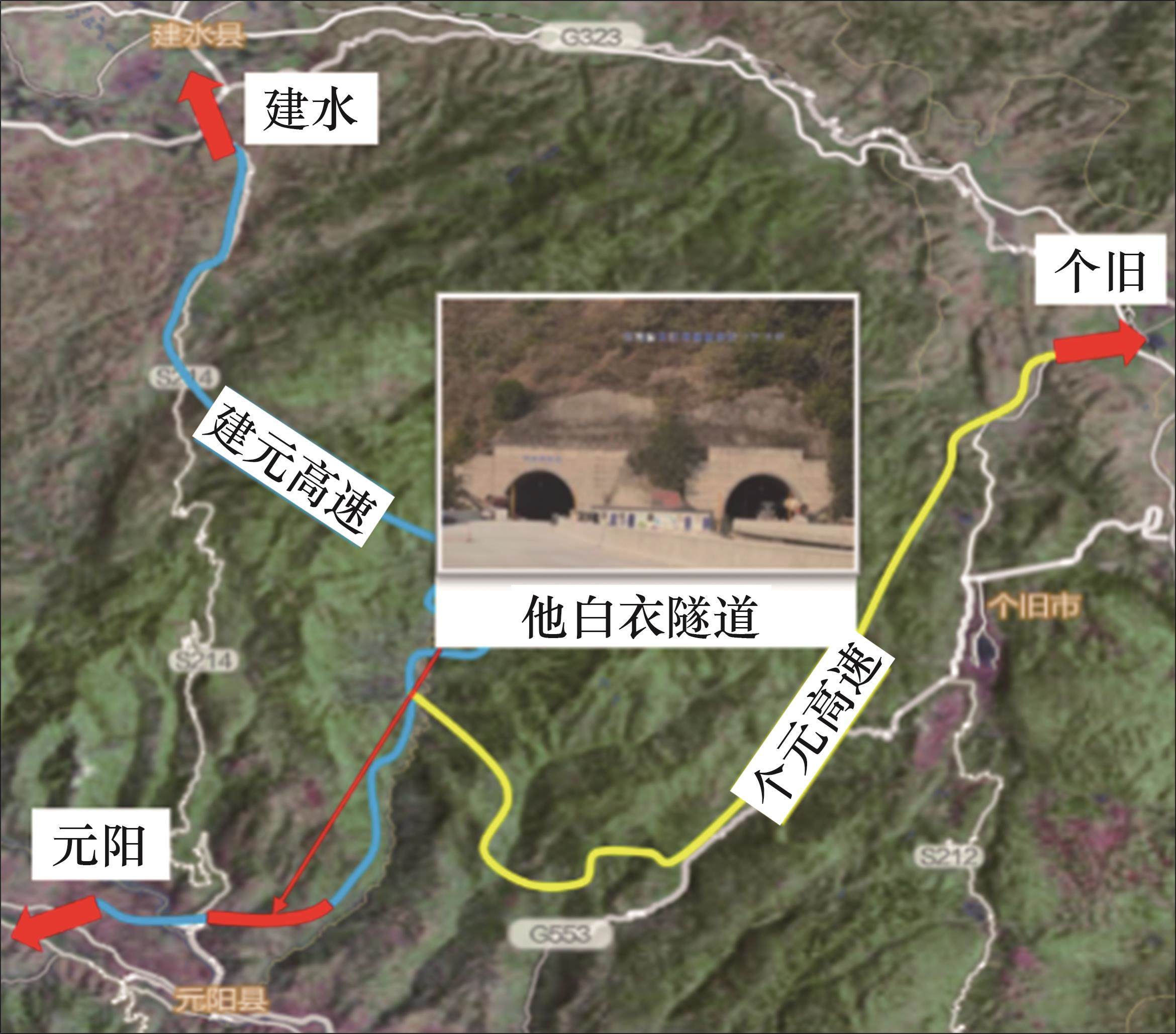
他白依隧道属建元(建水县—元阳县)高速段,建元高速公路路线起点位于鸡石高速庄子河附近,终点位于元阳县西北侧呼山公社,路线全长为73.439 km。他白依隧道为双线隧道,左线洞底设计标高为507.39 m,全长为2 613 m;右线洞底标高为570.93 m,洞底设计标高为508.45 m,全长为2 590 m。建筑限界净空(宽×高)为11.1 m×7.1 m,隧道纵坡为2.58%(单向坡)。隧道进口与轴线方向夹角为255°,隧道出口与轴线方向夹角为292°,一般埋深为100~250 m,最大埋深为297 m,属深埋长隧道。进口接他白依大桥,出口接大湾1号大桥。
根据《他白依隧道地质勘探报告》,他白依隧道穿越8条断层破碎带以及多条多级次生断层破碎带,同时断层构造带受挤压效应影响,断裂构造发育,岩层走向不一。他白依隧道围岩属软岩,主要以泥质板岩为主,其中围岩受风化程度影响严重,可将泥质板岩分为中风化和强风化2种,洞身泥质板岩强度较低且遇水极易软化崩解。在他白依隧道不同里程断面位置拣选岩石块体,制成试块进行微观矿物成分分析,其中3个试样矿物成分如表1所示。隧道围岩普通变形区为Ⅳ级与Ⅴ级围岩,破碎带为Ⅴ级围岩。他白依隧道自开工建设以来,发生了大范围的初支侵限、仰拱隆起、二衬开裂以及地表裂缝等地质灾害,初支换拱率高达70%以上,仰拱隆起段落长达334 m,发生涌水突泥4次,塌方46次,二衬开裂段落长达60 m。严重影响了隧道的工期并造成了较大的经济损失。
| 编号 | 石英 | 钾长石 | 斜长石 | 石盐 | 云母 | 黏土矿物 |
|---|---|---|---|---|---|---|
| 1 | 11.1 | 0.2 | 17.8 | 1.2 | 13.2 | 56.5 |
| 2 | 12.4 | 0.7 | 14.8 | 1.9 | 17.6 | 51.9 |
| 3 | 13.8 | 0.5 | 18.6 | 0.9 | 8.7 | 57.4 |
2 振动台物理模型试验
2.1 相似系数设计
基于J.Buckingham相似理论,模型需满足的相似条件包括材料相似和动力相似,选取几何尺寸、密度及弹性模量为控制参数,相似常数计算公式分别如下:
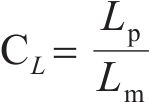
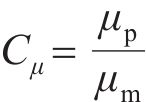
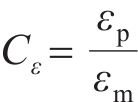
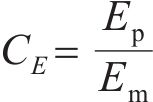
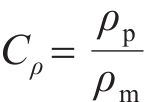
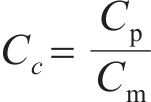
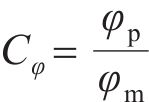
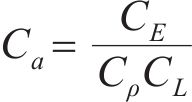
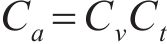
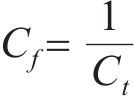
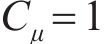
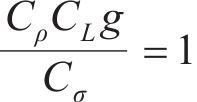
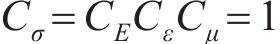
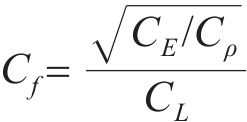
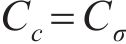
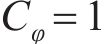
式中:Lp和Lm分别为原型物理量和模型物理量的几何尺寸;μp和μm分别为原型物理量和模型物理量的泊松比;εp和εm分别为原型物理量和模型物理量的应变;Ep和Em分别为原型物理量和模型物理量的弹性模量;ρp和ρm分别为原型物理量和模型物理量的密度;Cp和Cm分别为原型物理量和模型物理量的相似常数;φp和φm分别为原型物理量和模型物理量的内摩擦角;g为重力加速度;其他参数含义见表2。
| 特性 | 物理量 | 值 |
|---|---|---|
| 材料相似 | 几何尺寸相似常数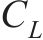 | 40 |
弹性模量相似常数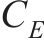 | 40 | |
密度相似常数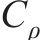 | 1 | |
黏聚力相似常数 | 40 | |
泊松比相似常数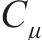 | 1 | |
内摩擦角相似常数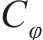 | 1 | |
| 动力相似 | 应力相似常数 | 40 |
位移相似常数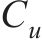 | 40 | |
应变相似常数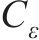 | 1 | |
时间相似常数 | 6.33 | |
频率相似常数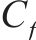 | 0.158 | |
加速度相似常数 | 1 | |
速度相似常数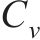 | 6.33 |
综合考虑振动台性能、施工条件以及材料试验性能等多方面因素,最终选取相似常数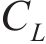

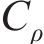
2.2 模型试验设计
模型试验依托燕郊中国地震局工程力学研究所地震模拟试验台系统,振动台台面长×宽为5 m× 5 m,最大承重为30 t,最大行程距离为0.5 m,最大输入加速度为2.0g,最大速度为1.5 m/s,最大频率为100 Hz。
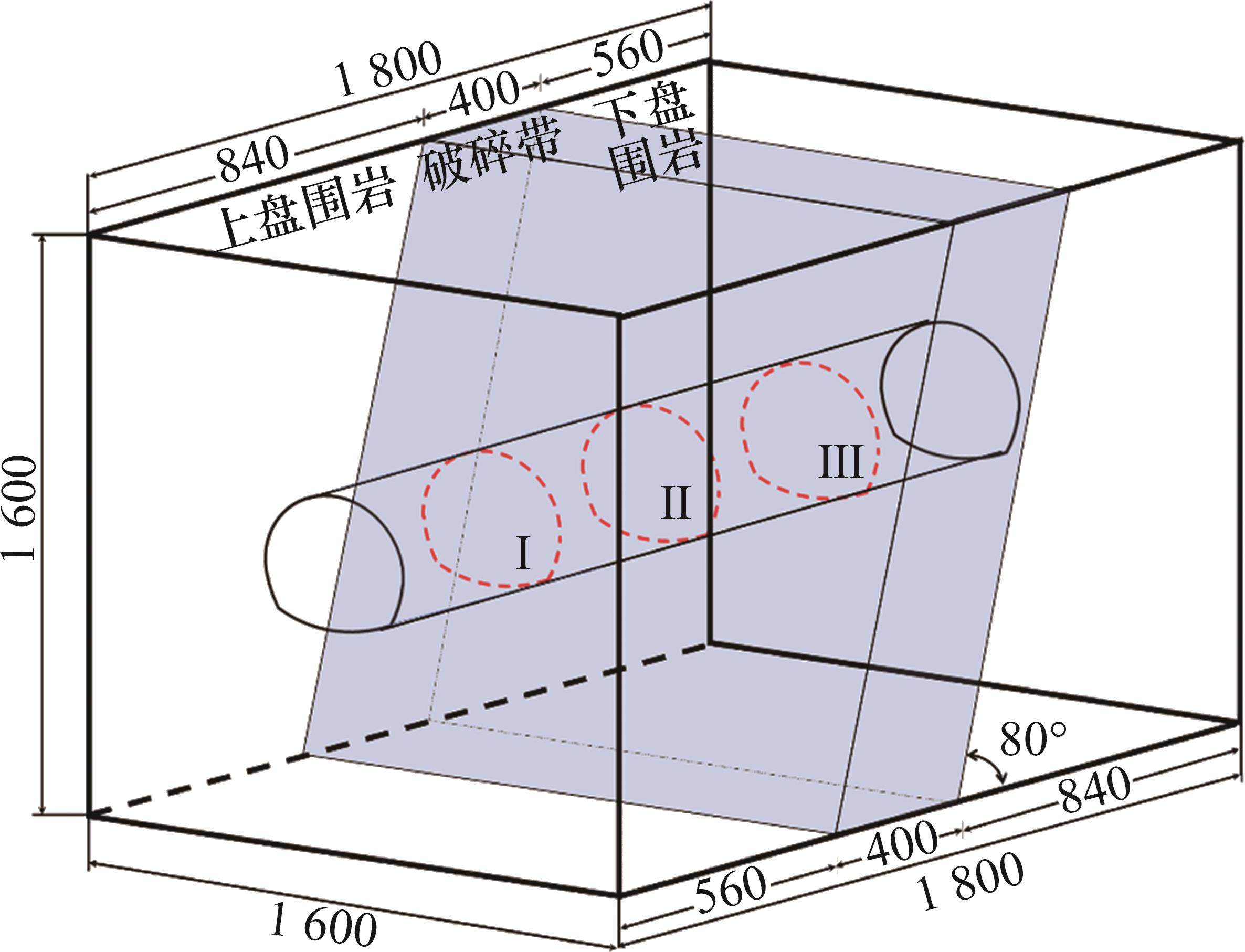
他白依隧道所在地地震活动较为频繁,由于他白依隧道所处地质条件特殊,一旦发生地震将产生重大安全事故,因此,选择其跨断裂带的一段右线隧道所处区域作为模型试验的原型,开展振动台试验。经相似比计算,模型尺寸为 X=1.6 m、Y=1.6 m、Z=1.8 m(X表示平行于隧道断面的水平方向,Y表示垂直于隧道断面的方向,Z表示竖直方向),他白依隧道右线截面为马蹄形,宽×高为13 m×9 m,模型隧道宽×高为325 mm× 225 mm,拟定破碎带与水平夹角为80°,同时于上盘围岩、破碎带、下盘围岩分别设置断面Ⅰ、Ⅱ、Ⅲ,用以布置传感器对试验数据进行检测采集,模型设计如图2所示。
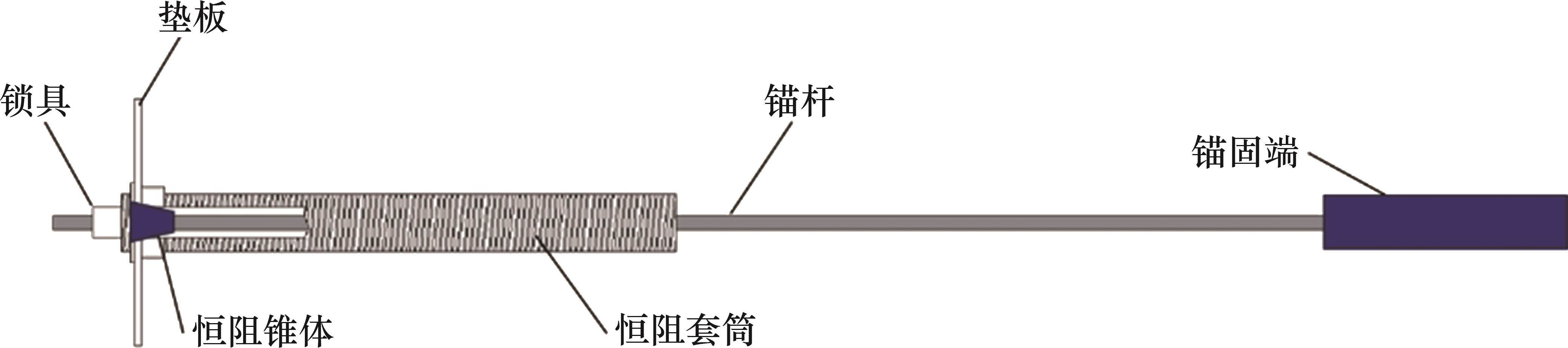
本试验隧道支护的主体为NPR锚索,其结构如图3所示。由图3可见:NPR锚索主要由恒阻装置、恒阻体、锚索和垫板组成。NPR锚索的性能释放分为2个阶段:第一阶段,当锚索承受的荷载小于或等于设定恒阻摩擦力时,通过锚索承担荷载;第二阶段,当承受的荷载超过设定恒阻摩擦力时,套筒内的恒阻体沿轴向发生摩擦滑移,利用恒阻装置的变形和恒阻体的动摩擦力来抵抗荷载,从而达到恒阻的效果。本试验支护系统选取“长/短NPR锚索+钢带+柔性网”组成的点、线、面一体化支护方案,短NPR锚索有效地提高了近层软弱岩层的整体性,长NPR锚索有效地提高了深层围岩的自承载力。此方案可较大限度地发挥NPR锚索的性能。
2.3 试验模型制作
2.3.1 围岩相似材料
围岩相似材料使用河砂、BaSO4、石膏和水制作,制作不同配比的标准圆柱体试样,通过室内单轴压缩试验,最终确定普通围岩相似材料配比,即河砂、普通围岩、重晶石粉、石膏、水质量比为 15꞉5꞉3꞉2,破碎带围岩相似材料配比,即河砂、重晶石粉、石膏、水质量比为15꞉5꞉2꞉2,见表3。
| 岩体 | 弹性模量E/GPa | 黏聚力c/MPa | 抗压强度/MPa | 内摩擦角/(°) |
|---|---|---|---|---|
| 实际围岩中的普通围岩 | 8.89 | 4.50 | 19.69 | 29 |
| 实际围岩中的破碎带围岩 | 6.14 | 3.30 | 11.90 | 25 |
| 相似围岩中的普通围岩 | 0.21 | 0.10 | 0.50 | 31 |
| 相似围岩中的破碎带围岩 | 0.16 | 0.08 | 0.29 | 24 |
2.3.2 支护相似材料
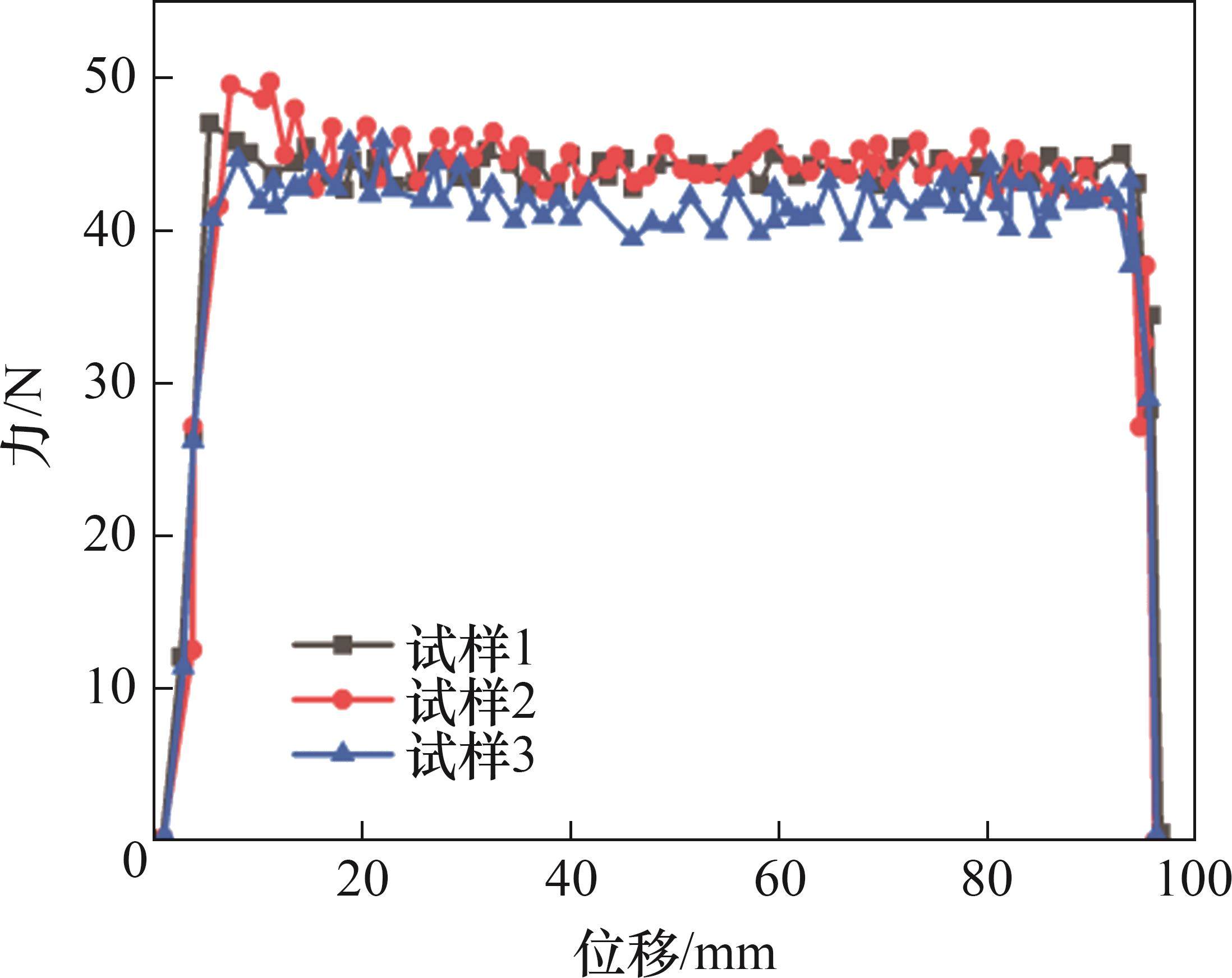
NPR锚索的相似材料采用树脂通过3D打印制作,恒阻套筒长为100 mm、内径为8 mm,恒阻体直径为8.2 mm,长、短锚索长度分别为315 mm和215 mm。通过调整恒阻套筒内径和锚索大端直径改变恒阻摩擦力,室内静力拉伸试验结果如图4所示。由图4可知:相似NPR锚索具有恒阻效应,其恒阻摩擦力为40~45 N,恒阻变形量约为90 mm。锚固圆片与钢带使用0.5 mm厚不锈钢制作,柔性网选取细铁丝纱网。支护相似材料如图5所示。

2.3.3 试验模型制作
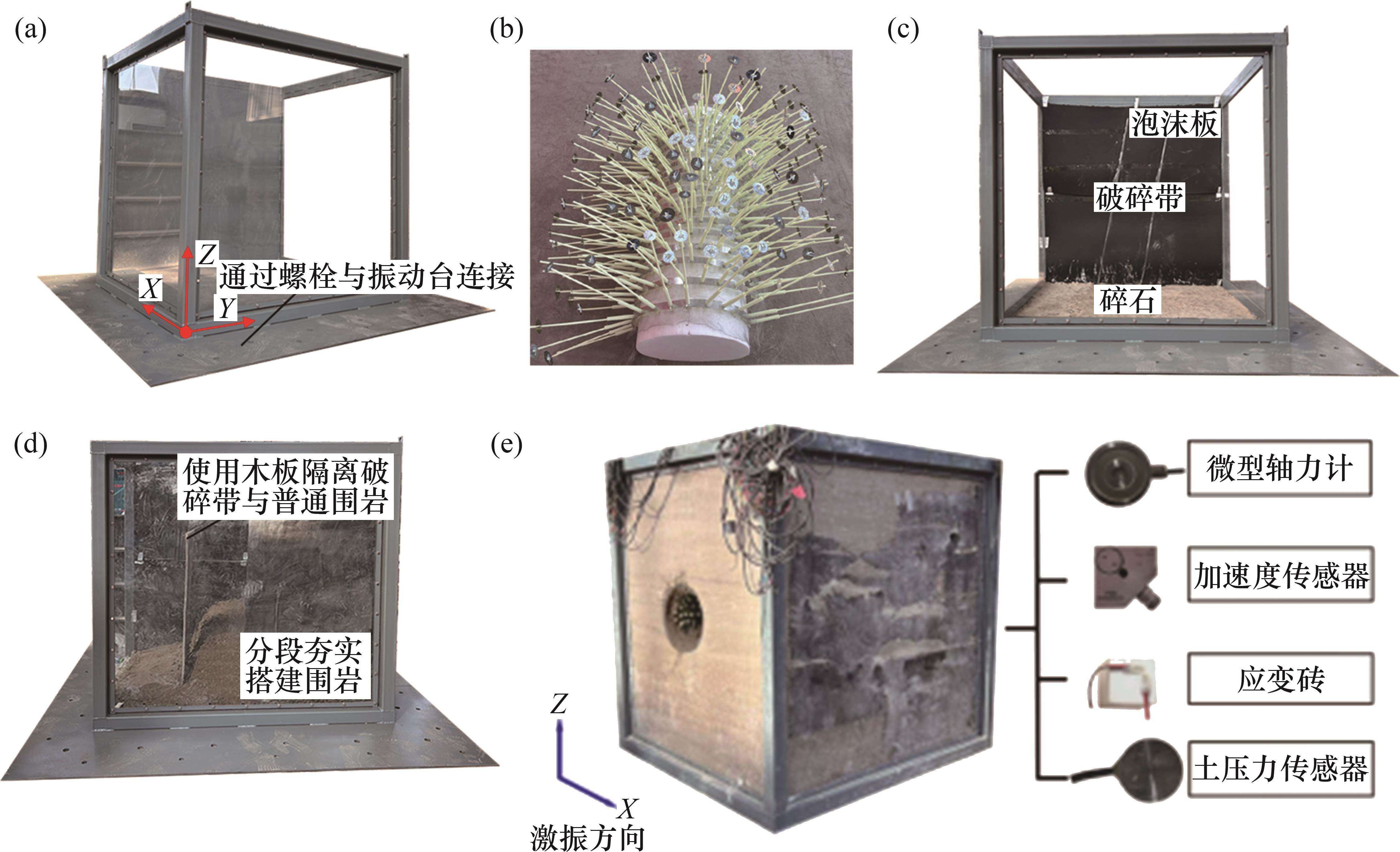
模型搭建流程如下:1) 铺设泡沫板与碎石以削弱边界效应,并划分破碎带区域;2) 分层搭建围岩并夯实,预埋传感器;3) 制作并预埋隧道支护模型;4) 挖去泡沫隧道模型。实验模型搭建流程与完成效果图如图6所示。
2.4 加载方案
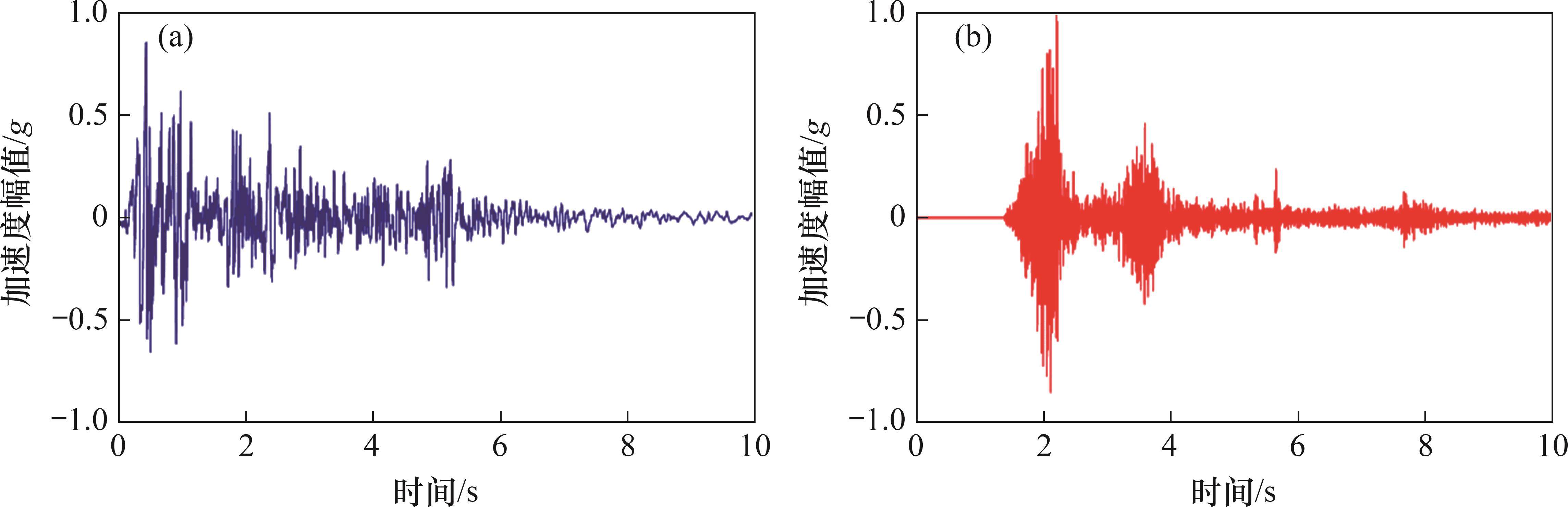
本试验输入地震波选用El-Centro波和汶川地震波。图7所示为压缩后的地震波加速度时程曲线,具体加载方案如表4所示。
| 阶段 | 工况 | 地震波波形 | 加速度幅值/g | 备注 | |
|---|---|---|---|---|---|
| X | Z | ||||
| 1 | 1 | 白噪声 | 0.05 | 0.05 | 单向 |
| 2 | EL-Centro地震波 | 0.10 | — | ||
| 3 | 汶川地震波 | 0.10 | — | ||
| 2 | 4 | 白噪声 | 0.05 | 0.05 | 双向 |
| 5 | EL-Centro地震波 | 0.10 | 0.06 | ||
| 6 | 汶川地震波 | 0.10 | 0.09 | ||
| 3 | 7 | 白噪声 | 0.05 | 0.05 | 单向 |
| 8 | EL-Centro地震波 | 0.40 | — | ||
| 9 | 汶川地震波 | 0.40 | — | ||
| 4 | 10 | 白噪声 | 0.05 | 0.05 | 双向 |
| 11 | EL-Centro地震波 | 0.40 | 0.24 | ||
| 12 | 汶川地震波 | 0.40 | 0.36 | ||
| 5 | 13 | 白噪声 | 0.05 | 0.05 | 单向 |
| 14 | EL-Centro地震波 | 0.80 | — | ||
| 15 | 汶川地震波 | 0.80 | — | ||
| 6 | 16 | 白噪声 | 0.05 | 0.05 | 双向 |
| 17 | EL-Centro地震波 | 0.80 | 0.48 | ||
| 18 | 汶川地震波 | 0.80 | 0.72 | ||
3 试验结果及分析
3.1 监测点布置
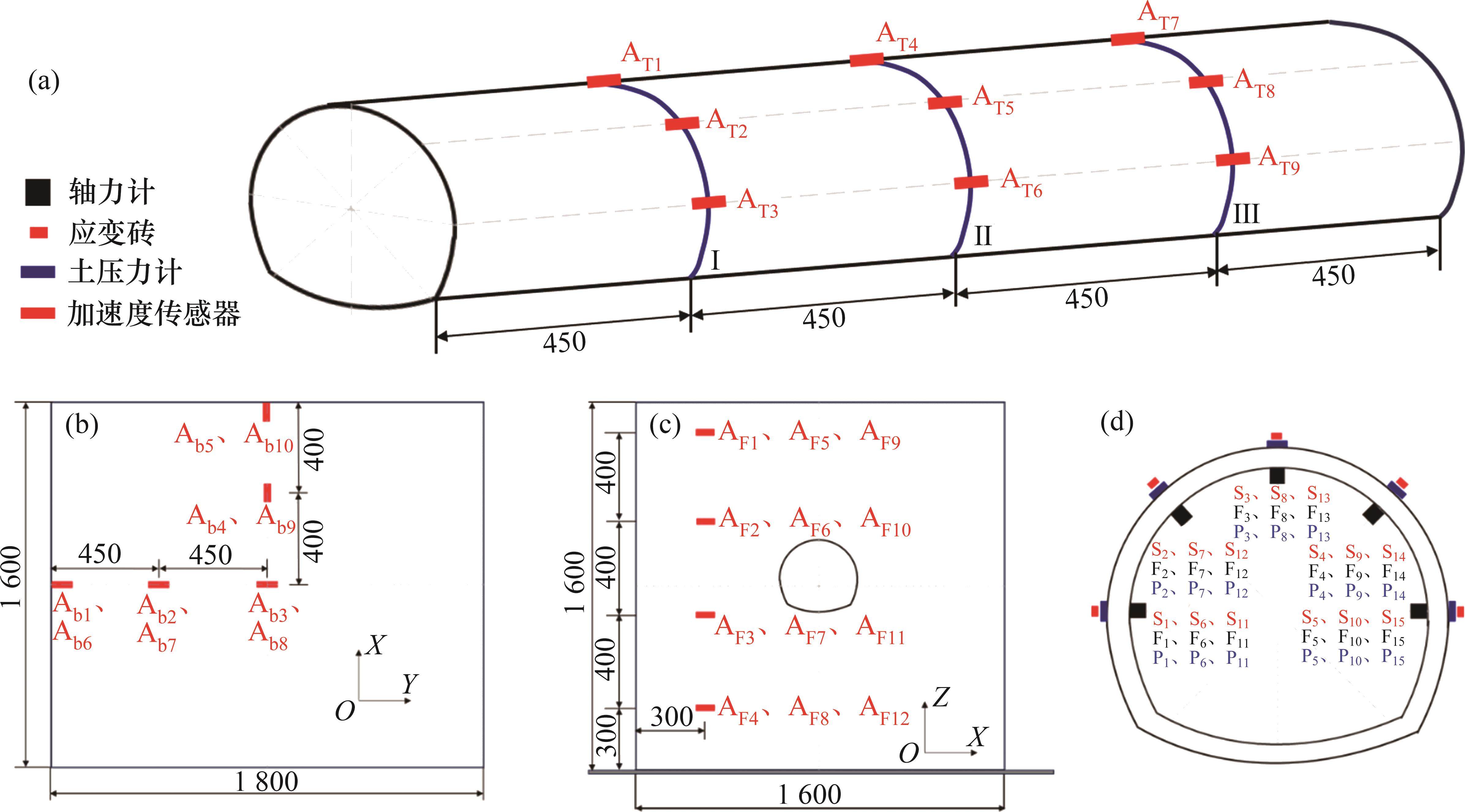
本次试验供需加速度传感器31个,锚索轴力传感器15个、土压力传感器15个和应变砖15个,其中,加速度传感器Ab1~Ab5布置于地基土表面,Ab6~Ab10布置于地基土深处,以分析设计模型对边界的减弱效果;加速度传感器AF1~AF4布置于监测断面Ⅰ,AF5~AF8布置于监测断面Ⅱ,AF9~AF12布置于监测断面Ⅲ,以监测不同埋深处地基的加速度响应;选取三断面拱顶、拱肩和拱腰3个位置布置传感器(包括加速度传感器AT1~AT9、土压力传感器P1~P15、应变片S1~S15以及轴力计F1~F15)以分析不同隧道关键位置动力响应规律。传感器具体布置方案如图8所示。
3.2 模型地基加速度反应分析
选取工况5、11、17分析模型地基加速度的变化特性。如图9所示。从图9可以看出:随地震动幅值增大,加速度响应逐渐增大;随埋深增加,加速度响应逐渐降低,这反映了由深到浅地基土对加速度的放大效应。且对比各断面可以发现,破碎带处隧道加速度峰值远比普通段隧道加速度峰值大,说明破碎带围岩加剧了地震作用下隧道的动力响应,破碎带处地震幅值放大效应明显比普通洞身段的放大效应大。同时可发现,断面Ⅲ加速度响应比断面Ⅰ的大,下盘加速度峰值比上盘加速度峰值大,这是由于在地震作用下,上盘围岩相对上升,下盘围岩相对下降,形成逆断层,加剧了围岩的变形。当输入地震波幅值为0.8g时,各个断面的加速度峰值远比前面的加载工况的加速度峰值大,且Ⅲ断面的加速度急剧增大,呈明显非线性,可认为在输入加速度幅值为0.8g时隧道Ⅲ断面部分发生较大变形。
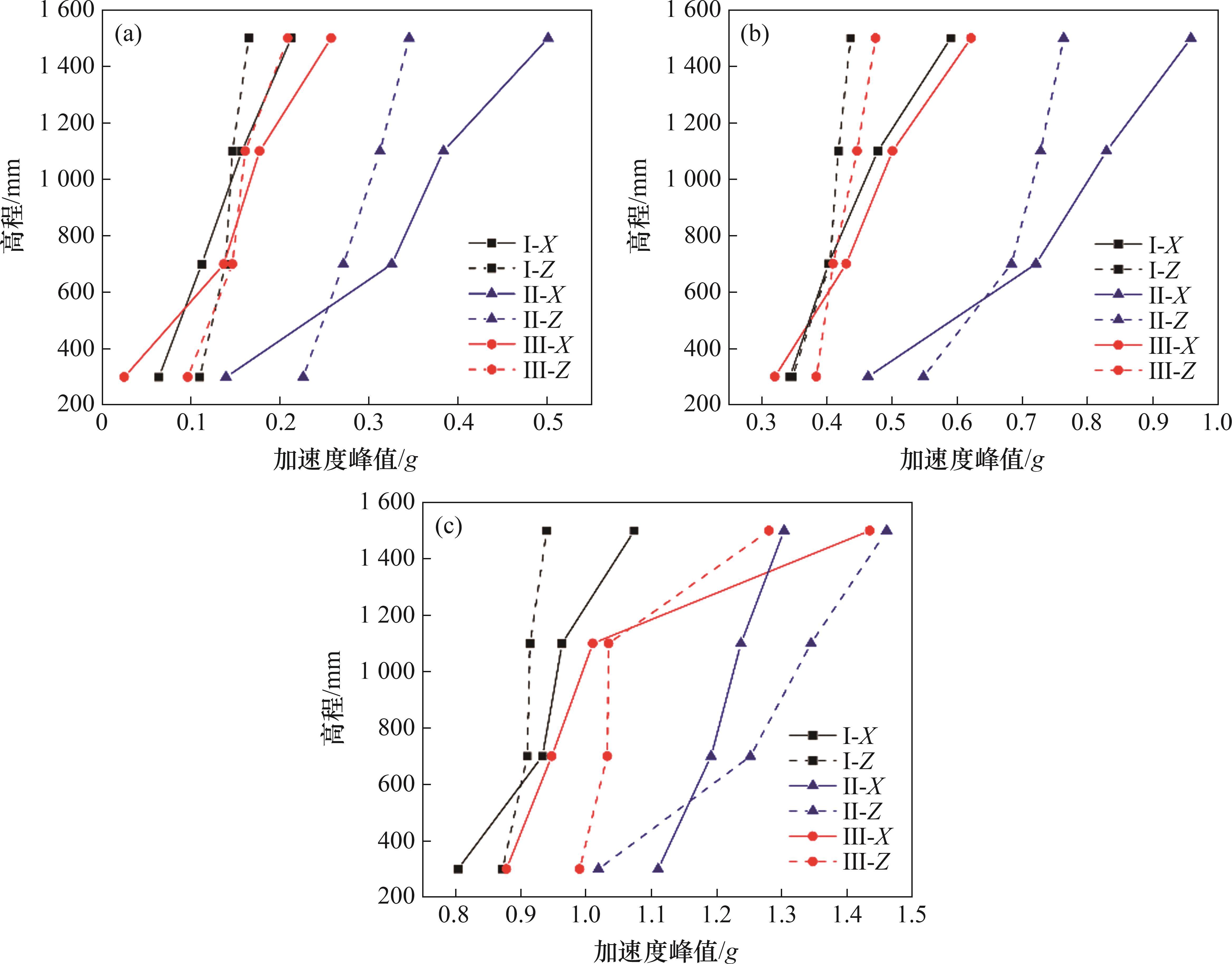
对比不同方向地震加速度响应可知,在高程为1 500 mm处,X方向围岩的加速度响应比Z方向的大,在高程为300 mm处,Z方向围岩的加速度响应比X方向的大,这说明在同一工况下,Z方向围岩的加速度响应比X方向的大,在地基深处以Z方向地震波为主导,在地基表层以X方向地震波为主导。在汶川地震波的振动测试下也得到了相似的结果。
3.3 模型边界效应分析
本试验通过在模型箱边界布设泡沫板,底部铺设碎石以减弱边界效应,采用2-范数偏差方法对对模型箱边界效应消除效果进行评估,2-范数偏差用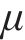
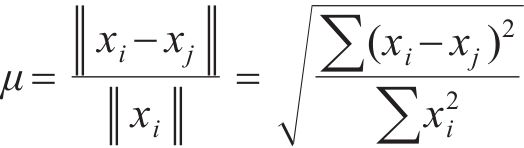
式中: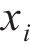
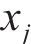
选取工况5、11和17分析双向El-Centro地震波作用下边界效应消除效果,选取工况6、12和18分析双向汶川地震波作用下边界效应消除效果。由于地基表面加速度响应比地基深处的响应大,因此,若地基表面处模型箱对边界效应的消除效果满足要求,则地基深处同样满足要求。对各工况下加速度时程进行傅里叶变化,Ab1~Ab5的加速度频谱相对于基准信号Ab3的2-范数偏差如图10所示。
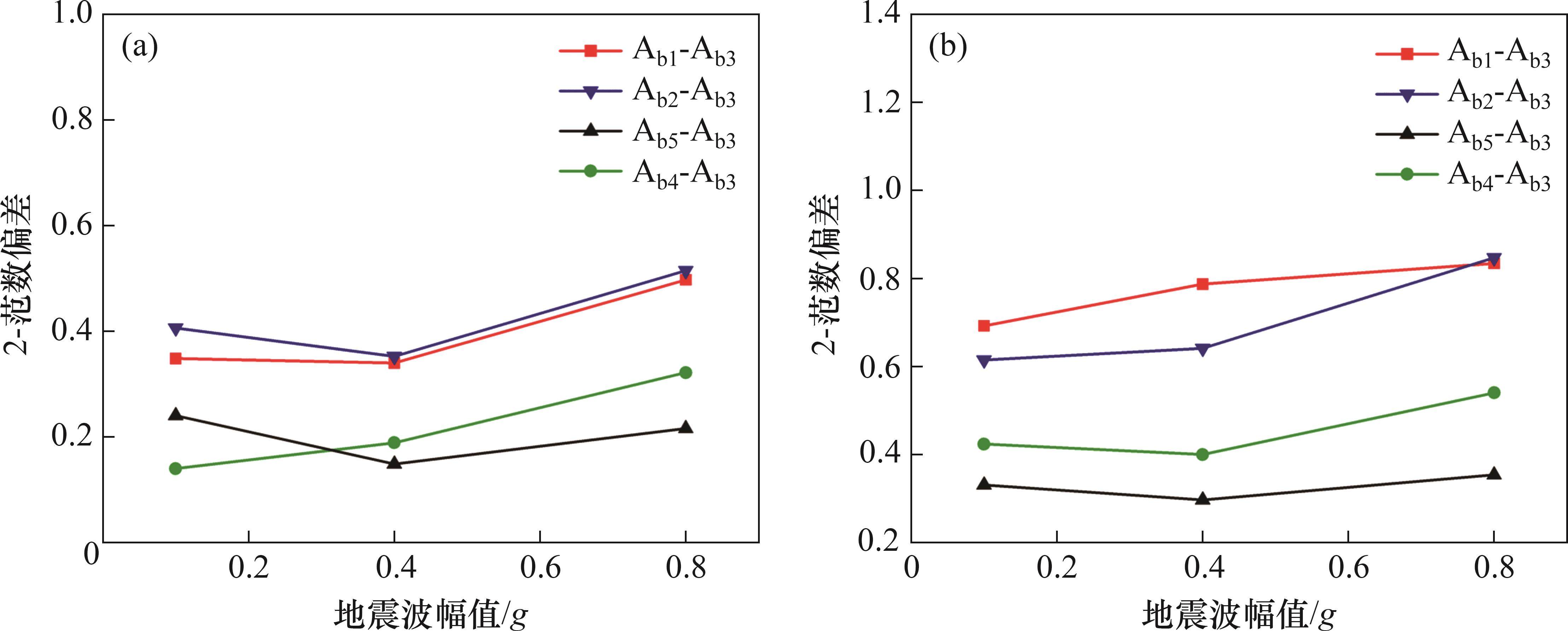
2-范数偏差越小,说明边界效应减弱效果越好。由图10可知:Ab3~Ab1和Ab3~Ab5的2-范数偏差较大,这是由于本试验模型箱为刚性模型箱,边界效应不可完全消除,但边界并不属于隧道检测断面,故不影响实验结果。其余各监测点的2-范数偏差均在0.5左右,因此,本试验减弱边界效应的响应措施具有较好的效果,同时,El-Centro波的减弱效果比汶川波的减弱效果好。
3.4 模型结构加速度反应分析
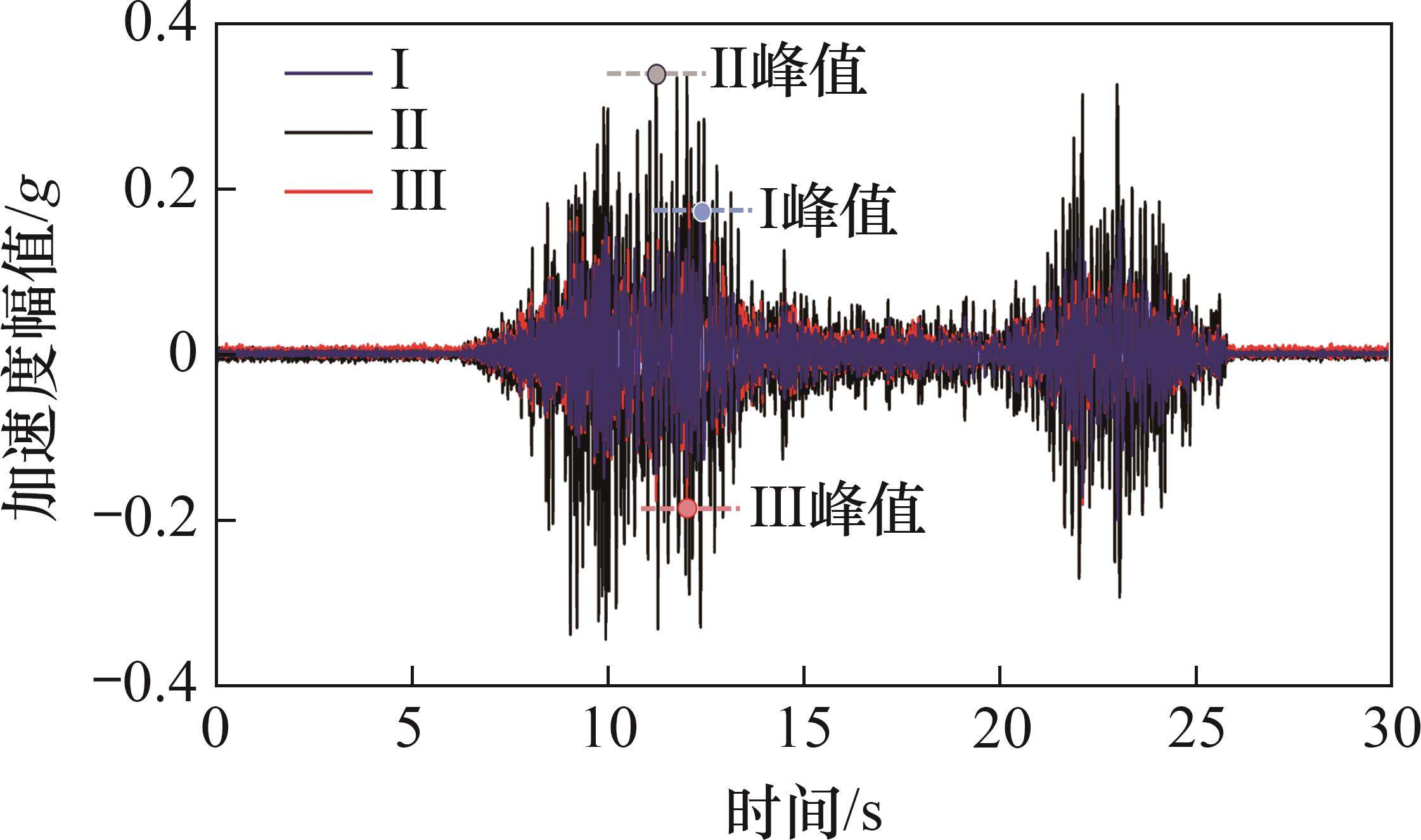
选择工况12,对拱顶、拱肩和拱腰3处加速度取平均,分析隧道整体加速度响应。如图11所示。由图11可见:3个断面的加速度时程曲线变化规律与原始输入地震波的加速度时程曲线变化规律相同,且都在12 s左右达到了加速度峰值,同时,位于断层破碎带的监测断面Ⅱ的整体加速度振幅明显比其他断面的大,这是由于断层破碎带的设置,监测断面的整体加速度峰值出现了放大效应。3个断面的加速度峰值依次为0.17g、0.36g、0.19g,最大峰值是最小峰值的2.12倍,由此可知破碎带放大效应显著。
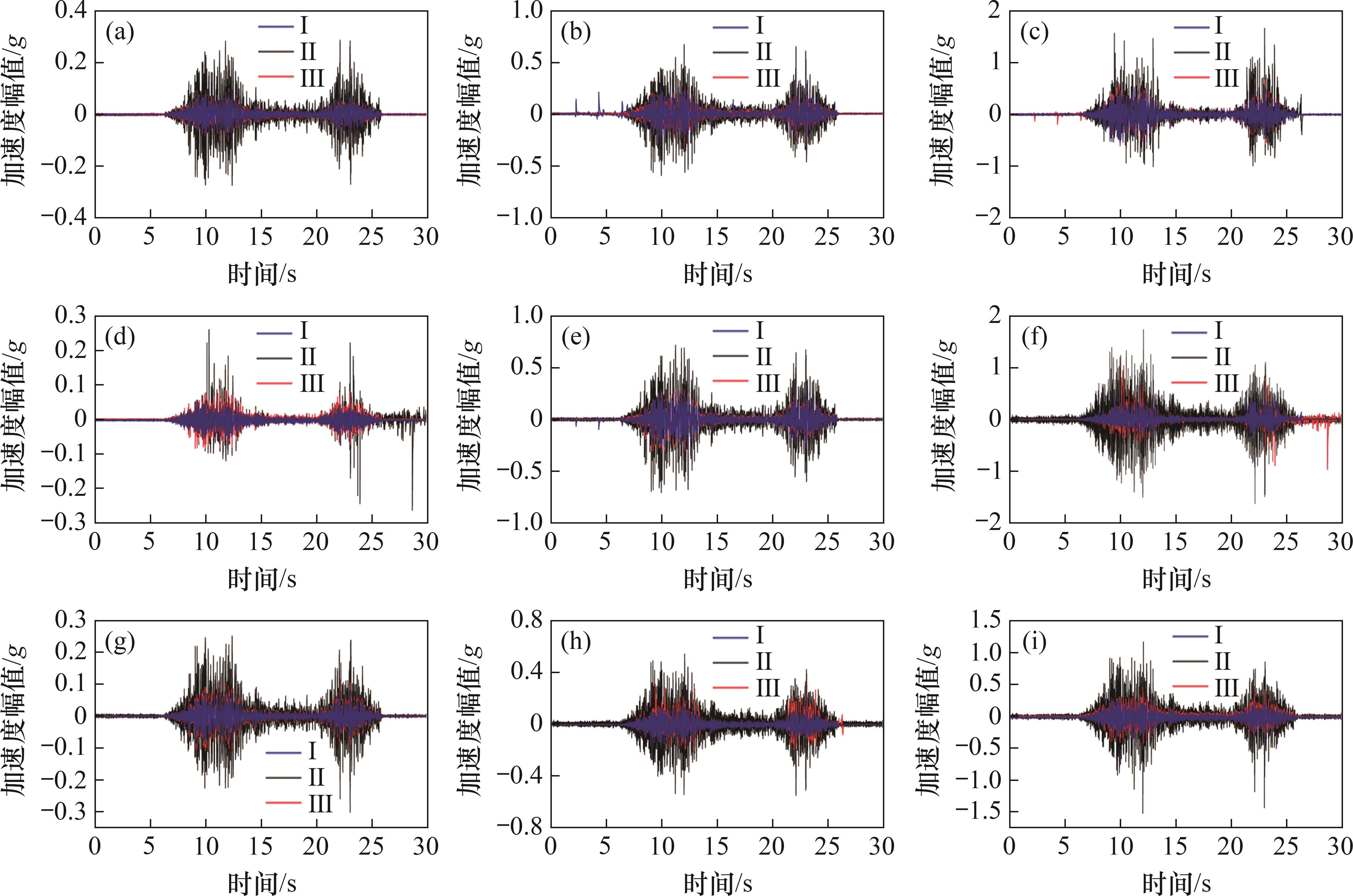
选择工况6、12和18对隧道关键位置(拱顶,拱肩和拱腰)进行分析,结果如图12所示。由图12可见:对于同一幅值下的地震波激励,拱肩处受地震波影响最大,拱腰处次之,而拱顶处动力响应最小。以断面Ⅱ为例,当输入幅值为0.1g时,隧道拱顶、拱肩和拱腰的加速度峰值分别为0.24g、0.28g、0.25g;当输入幅值为0.4g时,峰值分别为0.7g、0.8g、0.73g;当输入幅值为0.8g时,峰值分别为1.3g、1.6g、1.4g,在其他断面也得到了类似的结果。这是由于拱顶主要受Z向地震作用影响,拱腰主要受X向地震作用影响,拱肩处于隧道顶部和侧部的过渡位置,受双向地震作用力的影响,地震波能量在此聚集较大,受力较为复杂,承担荷载作用最大,因此,拱肩加速度响应最大。在实际地震作用中,X向地震占比较大,本试验输入地震荷载也符合此规律,故拱腰加速度响应比拱顶加速度响应大。
3.5 模型结构应变反应分析
选取工况5、11和17,对各断面不同位置的应变极值进行分析,应变极值如表5所示。由表5可知:应变极值由大到小的断面依次为断面Ⅱ、断面Ⅰ和断面Ⅲ,应变极值由大到小的部位依次为拱肩、拱腰和拱顶。地震波幅值增大,隧道拱肩处应变显著增大,且该现象在断面Ⅱ处更加明显。在地震波加载过程中,隧道承受循环拉压作用,应变的变化规律与各部位在地震作用下的受力情况和动力响应呈正相关,动力响应越大,其所承受荷载变化更大,进而产生的变形更大。同时,由于拱肩处的曲率较小,当地震波通过结构时,拱肩处的曲率变化相对较小,根据结构动力学,曲率变化小的地方,结构的位移相对较大,从而导致拱肩处的变形较显著。
| 工况 | 检测位置 | 应变极值/(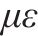 | ||
|---|---|---|---|---|
| 断面Ⅰ | 断面Ⅱ | 断面Ⅲ | ||
| 5 | 拱顶 | 65.31 | 142.41 | 41.42 |
| 左拱肩 | 92.38 | 202.62 | 78.32 | |
| 右拱肩 | 99.68 | 183.54 | 81.63 | |
| 左拱腰 | 44.55 | 115.26 | 30.17 | |
| 右拱腰 | 51.59 | 124.32 | 31.30 | |
| 11 | 拱顶 | 266.32 | 323.62 | 252.36 |
| 左拱肩 | 389.31 | 467.32 | 320.55 | |
| 右拱肩 | 405.32 | 477.91 | 334.21 | |
| 左拱腰 | 200.88 | 247.32 | 198.22 | |
| 右拱腰 | 213.46 | 251.67 | 201.48 | |
| 17 | 拱顶 | 420.40 | 612.66 | 501.59 |
| 左拱肩 | 698.37 | 910.37 | 834.62 | |
| 右拱肩 | 721.54 | 886.45 | 851.22 | |
| 左拱腰 | 346.35 | 579.82 | 396.53 | |
| 右拱腰 | 352.37 | 574.98 | 389.72 | |
3.6 动土压力反应分析
图13所示为各循环下土压力峰值曲线。由图13可知:断层破碎带处隧道的动土压力峰值明显比普通洞身的动土压力峰值大,这是由于断层破碎带处围岩较松散,强度较低,在同等地震作用下会产生更大的变形,从而产生更大的土压力;断面Ⅲ处土压力峰值比Ⅰ断面的稍大,这是由于在地震挤压作用下,断面Ⅲ处的下盘围岩向下滑动,形成反向断层,产生大于上盘围岩的变形,从而导致上盘围岩土压力较大。
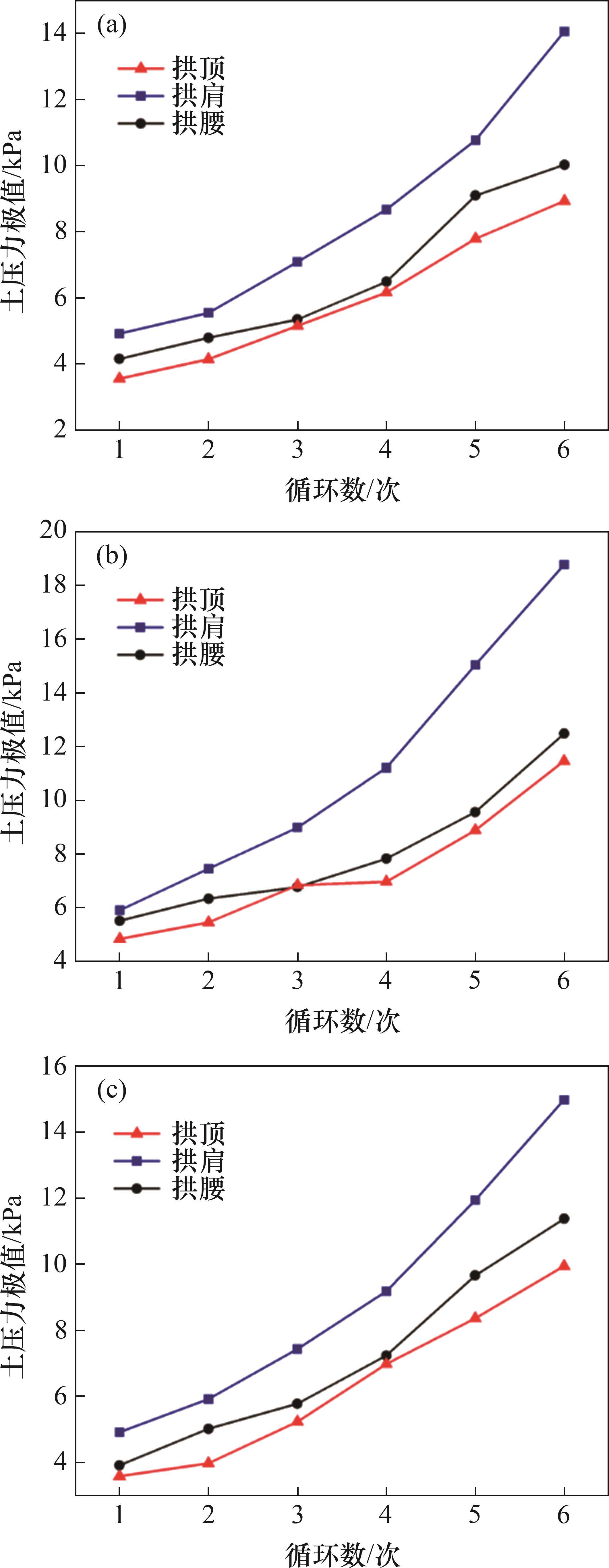
三断面表现出相同的趋势。以图13(a)为例,分析拱顶、拱肩与拱腰处动图压力相应规律。由图13(a)可知,隧道动土压力峰值由大至小的部位依次为拱肩、拱腰、拱顶,且随输入地震波幅值增大,这一现象会更加显著。在地震作用下,隧道结构所承受的土压力包括围岩自重压力、地震作用力。围岩自重压力由埋深决定,这部分力由大至小的部位依次为拱腰、拱肩、拱顶;对于地震作用力,土压力的响应规律与加速度反应呈正相关,拱顶处土压力增量受Z向地震作用主导,X向地震主对拱顶处土压力变化影响较小,X向地震对围岩施加剪切力,导致拱顶围岩结构趋于松散,进而使该部位的土压力增加;拱腰处同理。因为输入双向荷载中X向地震波占比较大,因此,拱腰处动土压力响应比拱顶处动土压力响应大。
3.7 地震作用下NPR锚索轴力响应分析
通过全程监测的NPR锚索轴力曲线,分析处于不同关键位置的NPR锚索在地震作用下的力学响应,锚索轴力曲线如图14所示。由图14可见:锚索轴力呈现出随输入地震波强度增大而增大的趋势,且轴力曲线增大趋势与输入地震波幅值的变化基本吻合。锚索轴力曲线的变化大致可分为3个阶段。
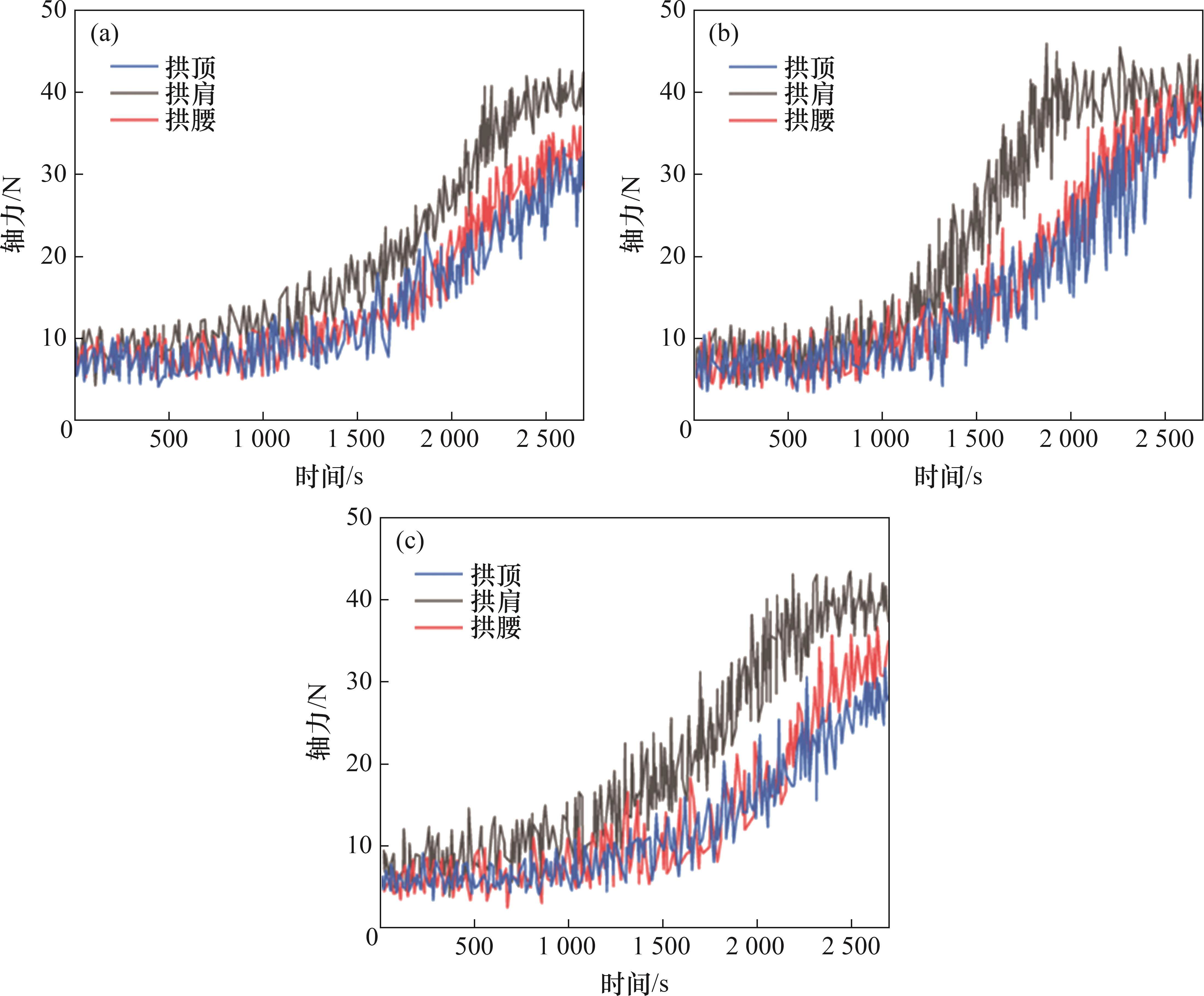
1) 试验加载前期([0,900] s,工况1~6),输入地震波幅值较小,地震对围岩影响很小,锚索轴力变化较稳定,峰值增长缓慢,三断面各处轴力峰值为10~15 N。
2) 试验加载中期((900,1 800] s,工况7~12),锚索轴力变化趋势增大,锚索轴力变化趋势及峰值由大至小的断面依次为断面Ⅱ、断面Ⅲ、断面Ⅰ,峰值依次为46 N、32 N、29 N。同一断面不同部位处,拱肩锚索轴力峰值最大,拱腰的锚索轴力峰值次之,拱顶的锚索轴力峰值比拱腰的略小。
3) 试验加载后期((1 800,2 700] s,工况13~18),输入地震波能量较大,断面Ⅰ拱肩处锚索于
2 400 s、断面Ⅱ拱肩处锚索于1 900 s、断面Ⅲ拱肩处锚索于2 250 s表现出恒阻现象。这3个断面拱腰与拱顶处并未出现恒阻现象,按拱肩、拱腰、拱顶的顺序,断面Ⅰ的锚索轴力峰值分别为43、35、33 N,断面Ⅱ的锚索轴力峰值分别为46、40、39 N,断面Ⅲ的锚索轴力峰值分别为44、36、32 N。
综上可知,断面Ⅱ处锚索轴力最大是因为其处于破碎带,软弱的围岩对地震波有更大的放大作用,锚索在破碎带中将承受更多的地震波能量,表现为破碎带处围岩变形较大,轴力变化比正常洞身处的变化大。断面Ⅲ轴力峰值比断面Ⅰ的峰值大,是因为断面Ⅲ所处下盘围岩在地震作用下形成反向断层,下盘围岩变形量比上盘围岩的变形量大,因此,断面Ⅲ轴力峰值比断面Ⅰ的大。且锚索轴力由大到小依次为拱肩轴力、拱腰轴力、拱顶轴力,这是由于在XZ双向地震作用下,拱顶处锚索轴力主要受Z向地震波影响,拱腰处主要受X向地震波影响,拱肩处受XZ双向地震影响,同时,输入地震波中X向地震波占比较大,因此,表现出拱肩轴力最大、拱腰轴力次之、拱顶轴力最小的现象。同时可观察到,振动台试验中锚索轴力峰值比锚索静力拉伸试验峰值略小,这是由于周期作用的地震作用力使NPR锚索恒阻装置产生疲劳效应,故使其恒阻摩擦力下降。
3.8 隧道结构震害分析
对试验前后的隧道结构进行拍摄记录,选取部分典型破坏部位进行对比分析,如图15所示。由图15可知:在地震作用下,不同围岩条件下的隧道结构具有相似的破坏模式,均表现出随着输入地震波幅值增加,以拱肩、拱腰、拱顶的顺序相继出现变形,直至隧道结构产生破坏的趋势。隧道结构的变形与应力应变响应基本对应。各部变形情况表现为:拱顶、拱腰处变形较小,部分围岩碎屑脱落,锚索恒阻端仅发生收紧,并未发生滑移,未产生严重变形;拱肩处锚索滑移,产生较大变形,部分区域锚网破裂,围岩隆起、脱落,已产生影响隧道安全的大变形,但并未发生坍塌。地震的挤压作用使上、下盘围岩发生错动,因此,下盘围岩处变形较大,上盘围岩变形最小。综合分析隧道结构变形情况可知,拱肩处产生变形最大,需重点在拱肩处加固支护设计。

4 结论
1) 断层破碎带对地震波具有放大效应。在同等地震波作用下,破碎带的动力响应更加强烈,并且围岩条件越差,对地震波的放大效应越显著。因此,在实际工程中,应对破碎带等软弱围岩进行重点加固设计。
2) 在双向地震作用下,模型地基的加速度随输入地震波幅值增大而增大,随地基土高程增加而逐渐增大,且在地基深处,Z向地震波加速度响应显著,在地基浅层,X向地震波加速度响应显著。
3) 在双向地震作用下,隧道拱顶主要受Z向地震波影响,拱腰主要受X向地震波影响,拱肩受XZ双向地震波影响,且双向地震中X向地震波占比较大,因此,隧道结构的加速度、应力、应变与轴力响应由大至小的部位依次为拱肩、拱腰、拱顶,且随输入地震波幅值增大而更加显著。
4) 在地震作用下,隧道结构模型的变形主要发生在拱肩处,拱肩处NPR部分锚索恒阻端出现滑移现象,部分区域隧道结构隆起,产生大变形,部分锚网破裂,土体脱落,但隧道结构并未发生坍塌,从侧面说明了NPR锚索起到了吸能作用。因此,拱肩属于隧道结构薄弱位置,在实际工程中应对该位置加强支护。
陶志刚, 赵易, 丰于翔, 等. 双向地震作用下跨断层破碎带隧道地震响应动力学试验研究[J]. 中南大学学报(自然科学版), 2025, 56(2): 637-650.
TAO Zhigang, ZHAO Yi, FENG Yuxiang, et al. Dynamic experimental study on seismic response of cross fault fractured zone tunnels under bidirectional seismic action[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 637-650.

