随着地下轨道交通系统在全球范围内的迅速发展,地铁车站作为其重要组成部分,在城市交通网络中发挥着不可替代的作用。然而,地震作为一种不可预测的自然灾害,对地铁车站的安全运行构成了严峻挑战。1995年1月17日发生的阪神大地震中,位于神户市中心的地下车站(大开站)在地震中遭到了严重破坏。地震导致大开站靠近长田高速公路一侧的25根中柱受损,尤其是5号至11号中柱受损最为严重,因此,开展地铁车站地震响应的研究,对于确保公共安全和城市交通的可持续发展具有重要意义。近年来,学者们对地铁车站的抗震问题开展了一系列的研究并取得了一些成果。苏健等[1]采用数值模拟方法,对十字换乘地铁车站的地震响应进行研究;张广宇等[2-5]通过数值模拟的方法对地铁车站的减隔震性能进行研究;王建宁等[6-8]采用数值模拟的方法对异跨地铁车站的抗震性能进行研究;YUE等[9]对采用加强中柱的车站结构进行了振动台试验研究;MA等[10]通过数值模拟的方法分析了土体力学参数对地下结构抗震性能的影响;CHEN等[11]通过振动台试验对多层地铁车站的地震响应做了相关研究,得知地铁车站除了水平剪切变形之外,还存在旋转振动的情况;包小华等[12]对多个地下结构的相互作用进行了数值模拟研究,得到桩基和上部结构对车站结构中柱剪力有明显的影响;李明等[13]针对上盖一体化地铁车站结构的抗震设计,提出振型分解法与反应加速度法相结合的简化分析方法,通过与传统的抗震计算方法对比,证明该简化方法的计算结果偏于安全;韩学川等[14-15]采用振动台试验与数值模拟的方法,对地上及地下一体化结构的地震响应进行分析;LI等[16]采用振动台试验分析了隧道与邻近地上结构的相互作用规律;YAO等[17]采用振动台试验的方法研究了层状液化场地中管廊隧道的地震响应及液化机理;TAO等[18-19]对整体现浇地铁车站与预制装配式地铁车站的地震响应开展了振动台试验对比研究;CHEN等[20]通过数值模拟与振动台试验,对地铁车站与隧道连接处的抗震性能展开研究;ZHANG等[21]通过振动台试验对比了中庭式地铁车站与框架地铁车站地震响应的异同。综上所述,学者们的研究内容主要包括装配式地铁车站、中庭式地铁车站、上盖一体化地铁车站、异跨地铁车站以及框架地铁车站的地震响应研究,地下管廊的地震响应研究,隧道与邻近地上结构的动力相互作用等。同时,主要采用数值模拟和振动台试验2种研究方法。其中,数值模拟具有安全性、经济性、数据丰富性等优点,但是其计算结果需要进行试验验证,如果缺乏相应的试验支持,数值模拟结果的可靠性可能受到质疑。振动台试验能够提供真实的动态加载,同时还可以精确地控制试验条件(振动频率、振幅、持续时间),直观地观察模型的破坏模式。地震具有突发性、复杂性和严重性等特点。对于地震的突发性,无法预知下一次地震是什么样,只能从已经发生过的地震记录来推断现有的结构是否满足抗震要求;对于地震的复杂性,地震波本身的频谱组成特别复杂,无法预知下一次地震波的频谱特性是什么样;对于地震的严重性,地震波强度无法预测,也不知道下一次地震波的幅值是多少。基于地震的特性,本文设计了地下一体化车站地震响应的振动台试验,旨在研究不同主频率、不同峰值加速度(PGA)的地震波对地下一体化车站地震响应的影响,评估地铁车站在极端地震作用下的安全性能,并提出相应的建议。
1 试验准备
1.1 试验背景
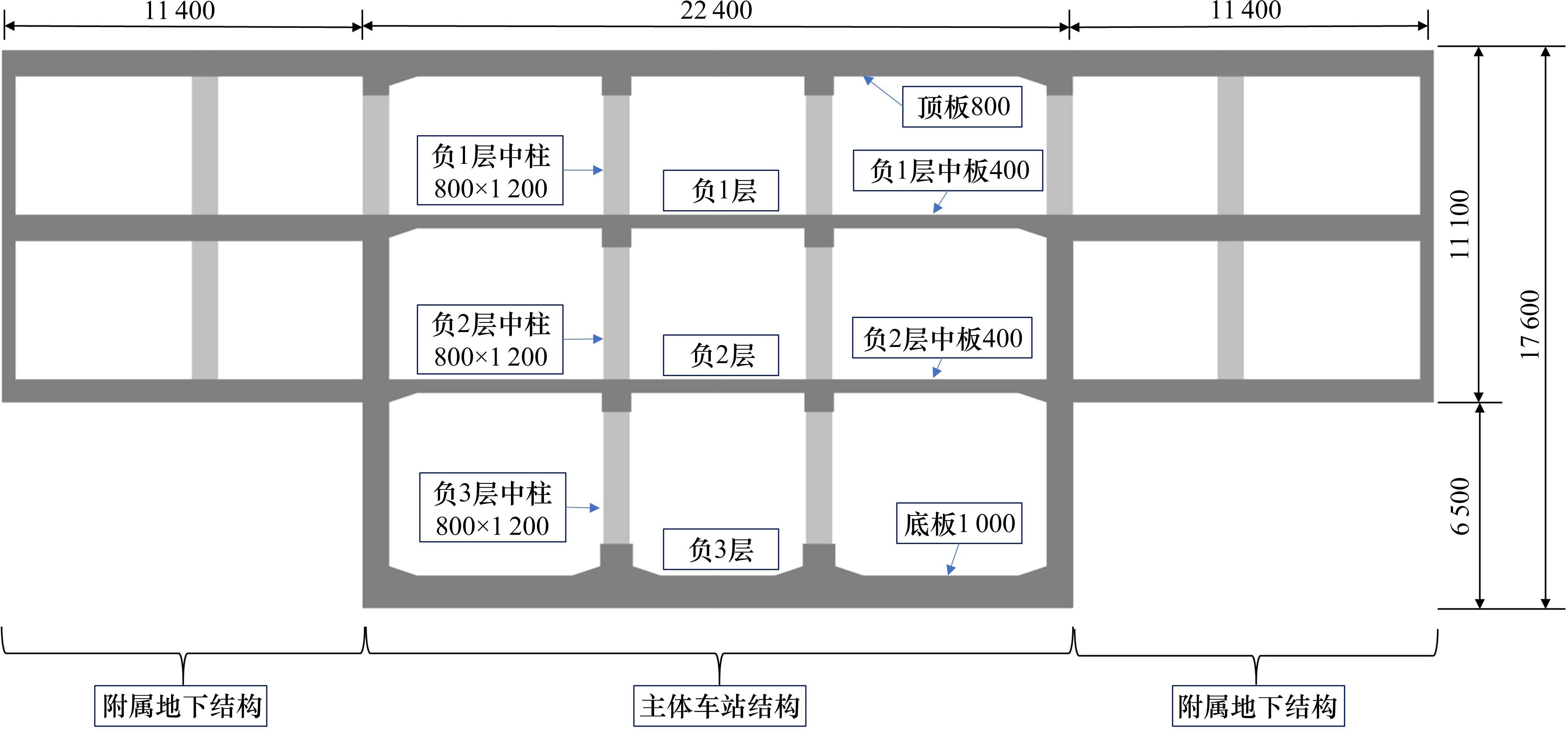
试验以北京市通州区某地下一体化地铁车站为背景。该地下一体化地铁车站是由主体车站结构与两侧的附属地下结构组成,其中,主体车站结构是3层3跨的标准地铁车站结构,两侧的附属地下结构是2层2跨的结构。主体车站结构与两侧的附属地下结构在负1层互联互通。一体化地铁车站结构形式如图1所示。
1.2 试验设备及相似关系
试验采用的振动台与模型箱如图2所示。振动台的技术参数见表1。模型箱为层状剪切模型箱[22],其长度为2.5 m,宽度为1.2 m,高度为1.2 m,由14层框架组成。

| 名称 | 取值 | 名称 | 取值 |
|---|---|---|---|
| 平面尺寸/m | 3×3 | 加速度/g | ±1 |
| 载重/t | 10 | 频率/Hz | 0.5~50 |
| 自重/t | 6 | 振动方向 | X单向 |
| 位移/mm | ±127 |
根据Bukinghan π定理,选取长度、弹性模量、加速度为模型结构相似关系设计的基本物理量。考虑到模型的尺寸以及传感器布置的便利性,得到各物理量的相似关系,见表2。
| 类型 | 物理量 | 相似关系 | 取值 |
|---|---|---|---|
| 几何特征 | 长度l | Sl | 1/40 |
| 惯性矩I | SI= Sl4 | 3.9×10-7 | |
| 材料特征 | 密度ρ | Sρ | 1 |
| 弹性模量E | SE | 0.25 | |
| 土的剪切波速v | Sv | — | |
| 动力特性 | 力F | SF=SρSl3Sa | 1.6×10-5 |
| 输入加速度a | Sa | 1 | |
| 振动持时t | St=(Sl/Sa)0.5 | 0.158 | |
| 动力响应应力σ | Sσ=SlSaSρ | 0.025 |
1.3 模型结构制作
采用微粒混凝土模拟地下结构的混凝土,用2.5~5.0 mm的粗砂代替混凝土中的粗骨料,0.15~1.0 mm的细砂代替混凝土中的细骨料。采用镀锌钢丝模拟地下结构中的钢筋,主筋为φ1.4 mm,箍筋为φ0.8 mm,分布钢筋为φ0.8 mm@20。由于车站结构较为复杂且断面不规则,所以采用自下而上分批浇筑的方式,通过支模、绑扎钢筋、浇筑微粒混凝土和试件养护等步骤制作模型结构。制作流程如图3所示。

浇筑模型的同时预留6组边长为70.7 mm×70.7 mm×70.7 mm微粒混凝土试块,对其进行抗压强度试验(如图4所示),得到试块的立方体抗压强度的平均值为7 MPa。

1.4 模型土的制备
振动台试验所用的砂土取自北京市通州区某地下工程现场。采用分层填筑,分层夯实的方法将砂填筑到模型箱中。模型土制备过程如下(如图5所示)。

1) 将进入试验场地的砂土进行晾晒以及筛分。
2) 在模型箱内壁上粘贴软尺,以便在装土时可以随时控制土量。
3) 将加速度传感器用鱼线悬挂到设计位置。
4) 进行砂土填筑工作,使用起重机搭配漏斗将砂土均匀铺撒至模型箱内,随后利用平头铁锹大致将砂土表面调平。控制每一层砂土的自由放置高度约为25 cm。接下来,通过手持夯锤进行人工压实作业,同时在选定的位置进行取样,并执行相对密度的测定,确保砂土达到预定的密实度。在压实过程中,严格计数夯击的次数,以确保各层砂土的压实度相一致,避免出现显著差异。每填充完一层砂土并完成压实后,对表层进行粗糙化处理(即拉毛),以增强连续层间的结合力,之后才进行下一层的填筑工作,确保砂土层间具有良好的结合性与整体性。
5) 当砂土填筑到预定高度后(即结构底板位置),将结构吊装就位,然后向模型箱中继续分层装入砂土直至到达模型表面。
6) 砂土装填完毕后,将砂土表面抹平,用水平尺校核表面的平整度,然后覆盖塑料布防止水分流失,并在重力条件下固结24 h。
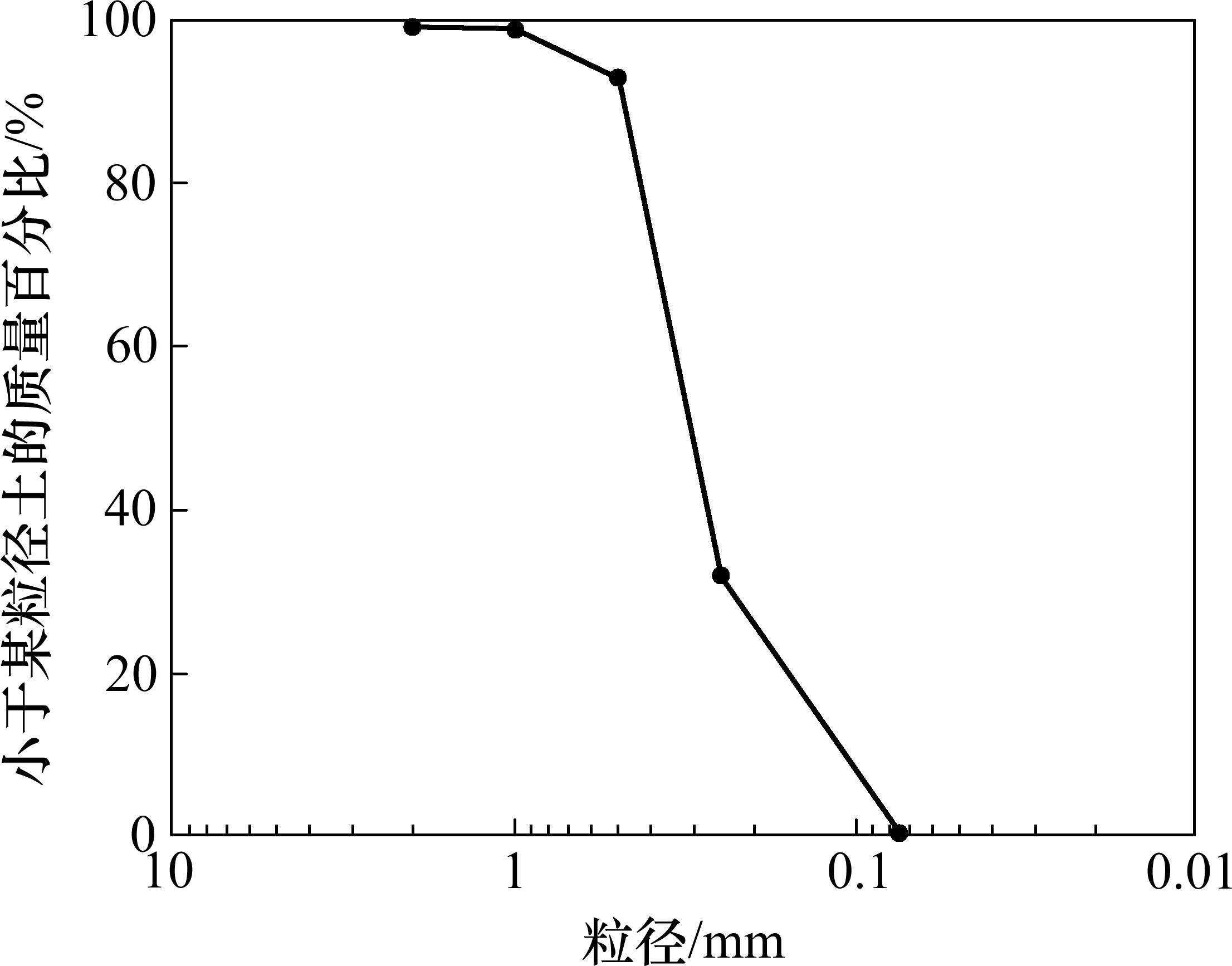
依据《土工试验方法标准》[23],测得的砂土含水率ω=18%,湿密度ρ=1.88 g/cm3,干密度ρd=1.59 g/cm3,最小干密度ρdmin=1.44 g/cm3,最大干密度ρdmax=1.91g/cm3(如图6(a)所示)。由此计算得到的砂土相对密度Dr=38.33%,依据李广信等[24]用相对密实度Dr判定土体密实度标准的描述,本次试验所采用的砂土为中密砂土。由砂土的级配分析(如图6(b)所示)得到粒径级配曲线(如图7所示)。由此可知砂土的不均匀系数Cu<5,曲率系数Cc介于1~3之间。

1.5 传感器的布置
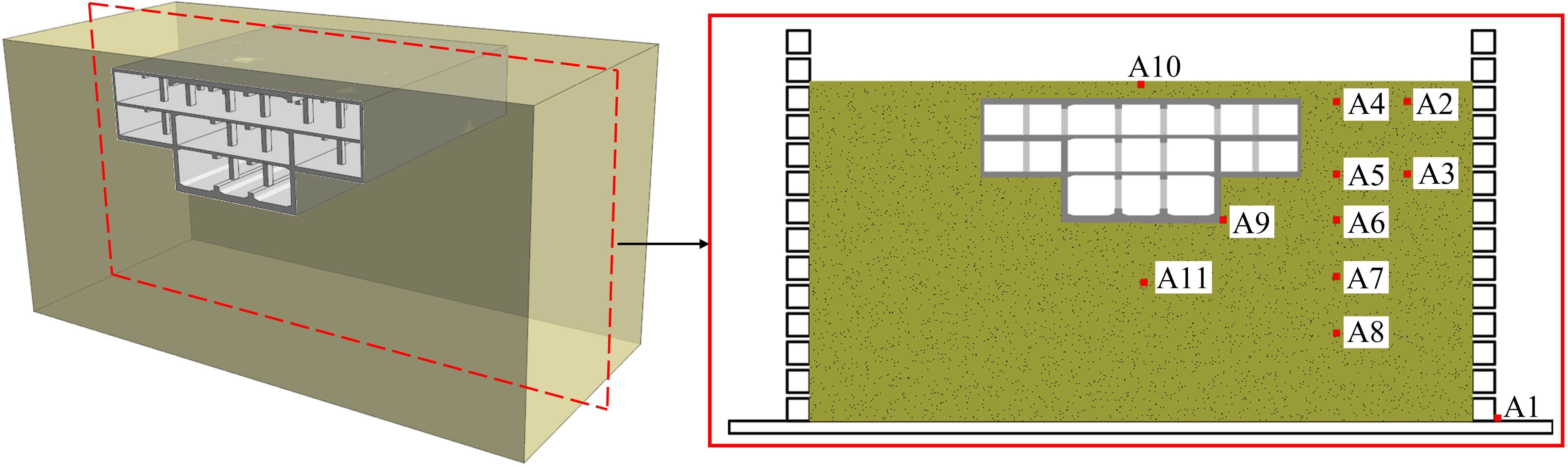
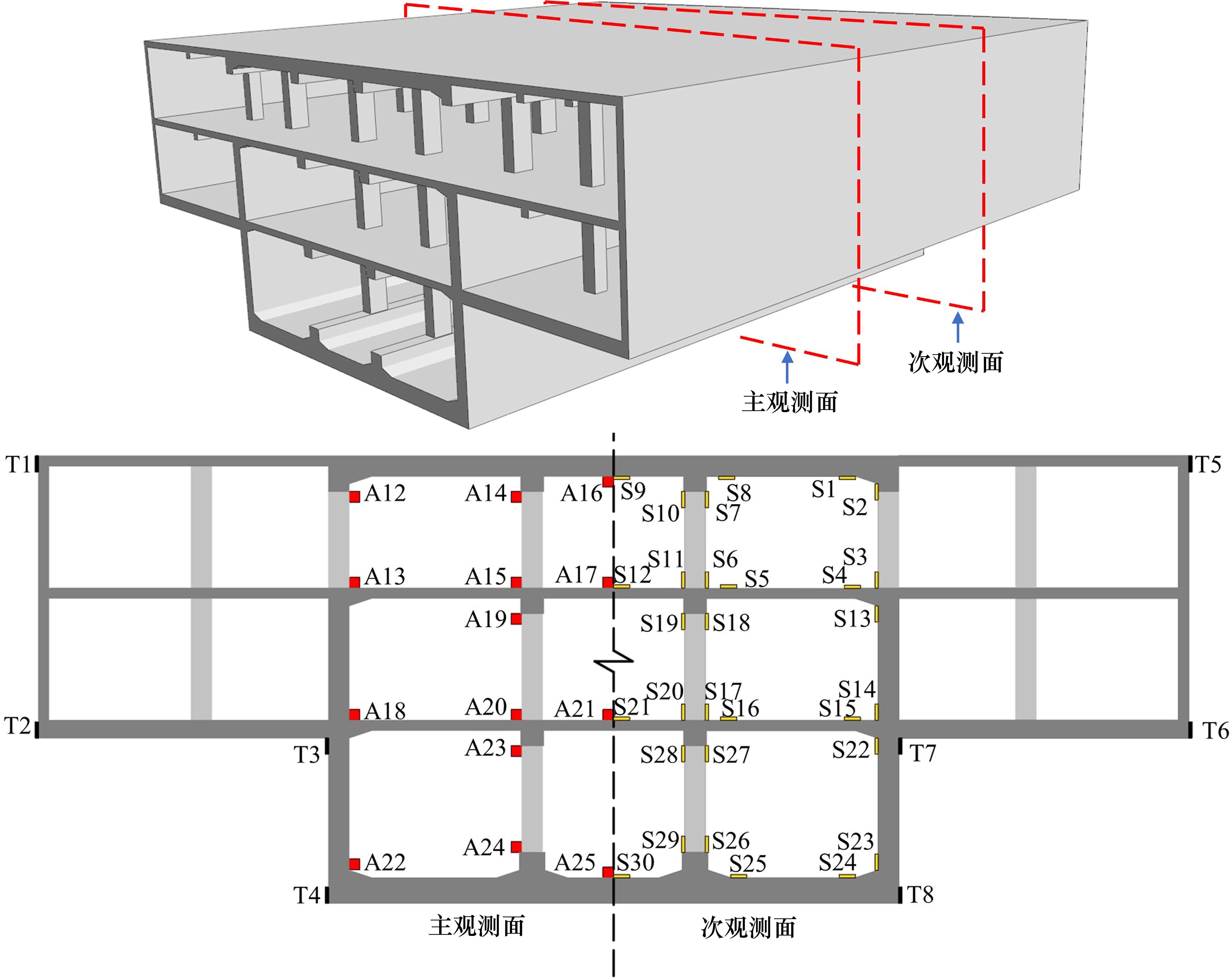
振动台试验中需要监测2部分内容,一部分是模型土的地震响应,另一部分是地下结构的地震响应。模型土中,布置加速度传感器得到土体的加速度响应;地下结构中,布置加速度传感器得到结构的加速度响应,布置应变片得到结构的应变规律,布置土压力传感器得到土体与结构的相互作用。模型土中的传感器布置如图8所示,车站结构中的传感器布置如图9所示,其中,A表示加速度传感器,S表示应变片,T表示土压力传感器。
1.6 选择地震波及加载工况设置
地下结构在地震作用下的行为研究越来越受到重视,地铁车站结构的形式越来越丰富,但是我国的地铁结构遭遇的地震灾害的案例很少,所以,振动台试验通过施加实际地震记录或合成地震波来模拟地震作用,以此来评价地下结构的抗震性能是一种有效的手段。从我国的地震记录角度看,汶川地震作为一个典型的地震灾害,发生了大量隧道结构损坏的案例[25-26]。唐山地震虽然发生的时间较早,但是其离北京较近,当时北京地区的房屋也出现了不同程度的损伤。近些年,北京地区虽未监测到明显的地震活动,但在地下结构设计过程中,必须经过抗震评估,人工波是依据建筑物所在的场地类别及地层特性,通过数学模型模拟自然地震波而产生的。从试验目的的角度看,本次试验是分析不同特性的地震波对地下一体化车站结构地震响应的影响,因此要选择特性(频率、幅值、持时)不同的地震波。
总之,对现有的地铁车站结构,通过输入已经发生的地震记录和人工合成地震波,可以全面评估地铁车站结构的抗震性能,增强建筑物抵抗未来潜在地震的能力。所以,本次试验选择的地震波分别为名山波、唐山地震北京饭店波和人工波。其中,名山波为2008年汶川地震中所记录,震中距103 km,原始峰值加速度为0.16g,持时100 s,主频15.9 Hz;唐山地震北京饭店波为1978年唐山地震中所记录,震中距157 km,原始峰值加速度为0.39g,持时50 s,主频0.7 Hz;人工波取自北京通州区某工程的地震安评报告,峰值加速度为0.26g,持时40 s,主频5.2 Hz。地震波加速度时程曲线以及傅里叶谱如图10所示。
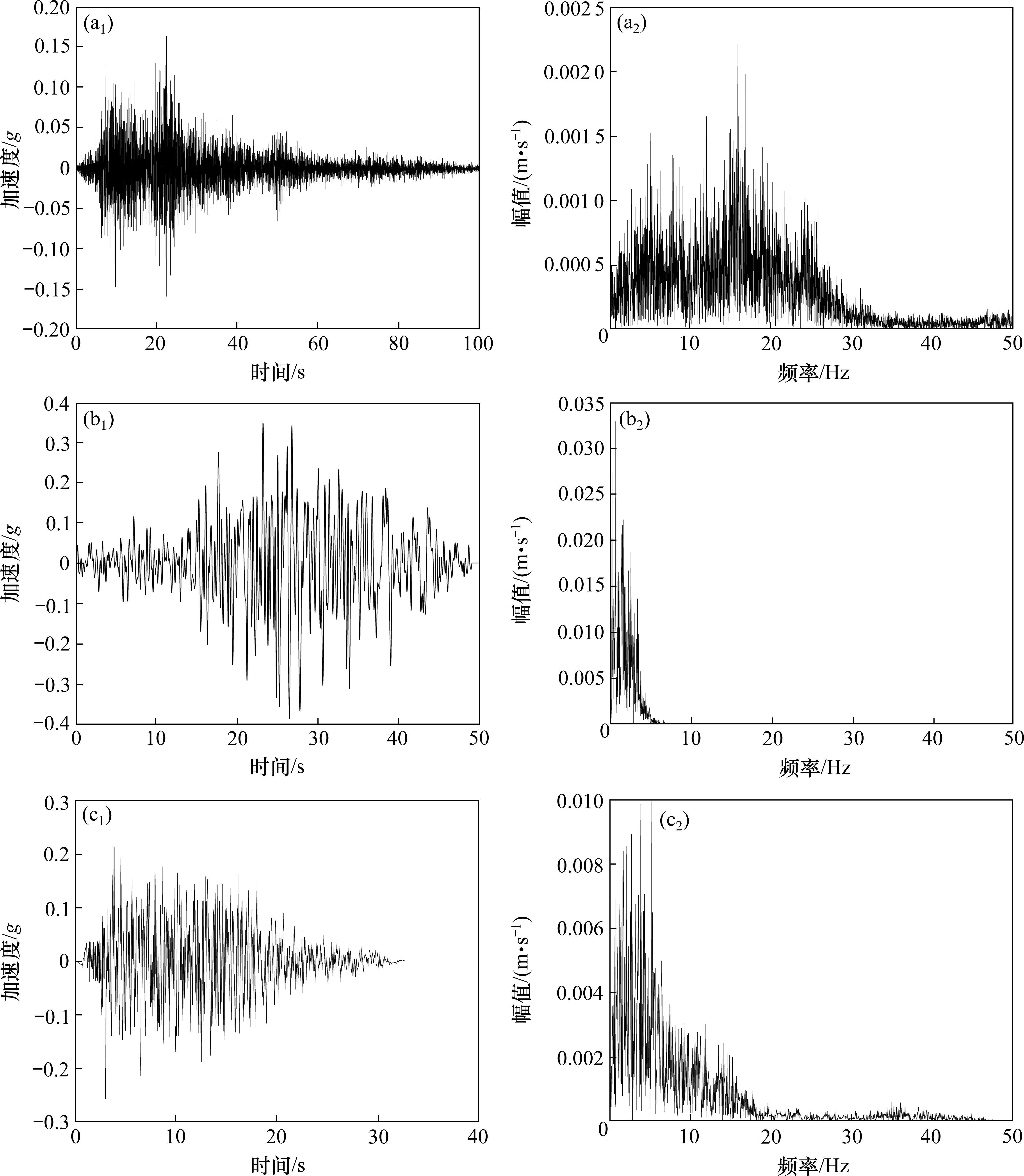
对地震波进行基线校正、归一化处理。采用逐级加载的方式施加地震波。地震波加载方案见表3。
| 输入地震波 | 工况代号 | 峰值加速度/g |
|---|---|---|
| 白噪声 | B-1 | 0.1 |
| 名山波 | MS-1 | 0.1 |
| 北京饭店波 | FD-1 | 0.1 |
| 人工波 | RG-1 | 0.1 |
| 白噪声 | B-2 | 0.1 |
| 名山波 | MS-2 | 0.2 |
| 北京饭店波 | FD-2 | 0.2 |
| 人工波 | RG-2 | 0.2 |
| 白噪声 | B-3 | 0.1 |
| 名山波 | MS-3 | 0.3 |
| 北京饭店波 | FD-3 | 0.3 |
| 人工波 | RG-3 | 0.3 |
| 白噪声 | B-4 | 0.1 |
| 名山波 | MS-4 | 0.4 |
| 北京饭店波 | FD-4 | 0.4 |
| 人工波 | RG-4 | 0.4 |
| 白噪声 | B-5 | 0.1 |
| 名山波 | MS-5 | 0.5 |
| 北京饭店波 | FD-5 | 0.5 |
| 人工波 | RG-5 | 0.5 |
| 白噪声 | B-6 | 0.1 |
2 试验结果分析
2.1 模型箱的基频
在模型箱外侧设置加速度传感器,在对应位置模型土的边界处设置加速度传感器,其中,自由场(ZY)测点A2位于地表下60 mm处,与模型箱(KX)测点A7对应;自由场(ZY)测点A3位于地表下337 mm处,与模型箱(KX)测点A5对应。通过输入0.1g的白噪声,分别对模型箱及自由场进行扫描,得到各测点的加速度时程曲线,通过傅里叶变换得到各测点的傅氏谱(如图11所示),进而得到测点的频率特性。对比自由场和空箱的频率特性,就可看出模型箱的自振特性是否对试验结果产生影响。
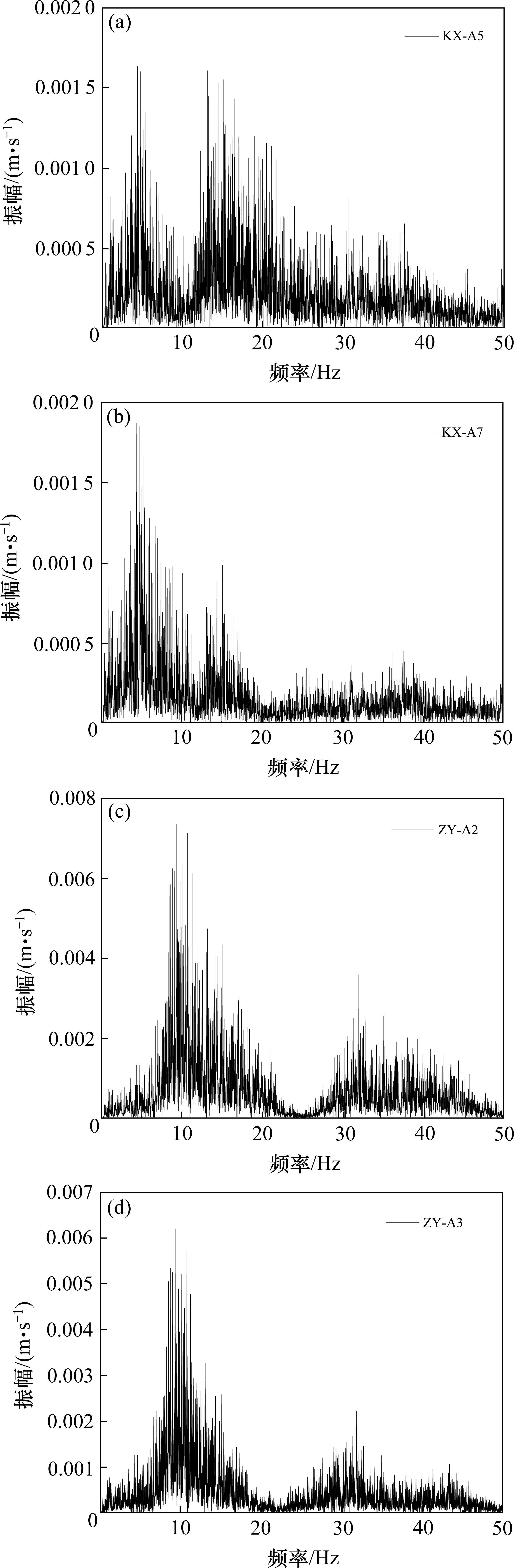
模型箱测点A5、A7的基频都为4.389 Hz,2阶频率为13.098 Hz、15.096 Hz;自由场测点A2、A3的基频都为9.394 Hz,2阶频率都为31.833 Hz。由此可知,模型箱的固有频率与自由场土层的固有频率相差很远,说明在试验过程中,模型箱与模型土不会发生共振现象,模型箱的自振特性对试验结果不会产生影响。
2.2 模型土的加速度响应
不同地震波以及不同峰值加速度(PGA)作用下,模型土峰值加速度的分布情况如图12所示。当PGA≤0.2g时,模型土中测点A4~A8的加速度响应规律为人工波>名山波>北京饭店波;当PGA=0.3g时,模型土中测点A5~A8的加速度响应规律为人工波>北京饭店波>名山波;当PGA>0.4g时,测点A4、A5的加速度响应规律为人工波>北京饭店波>名山波,而测点A6~A8的加速度响应规律为北京饭店波>人工波>名山波。
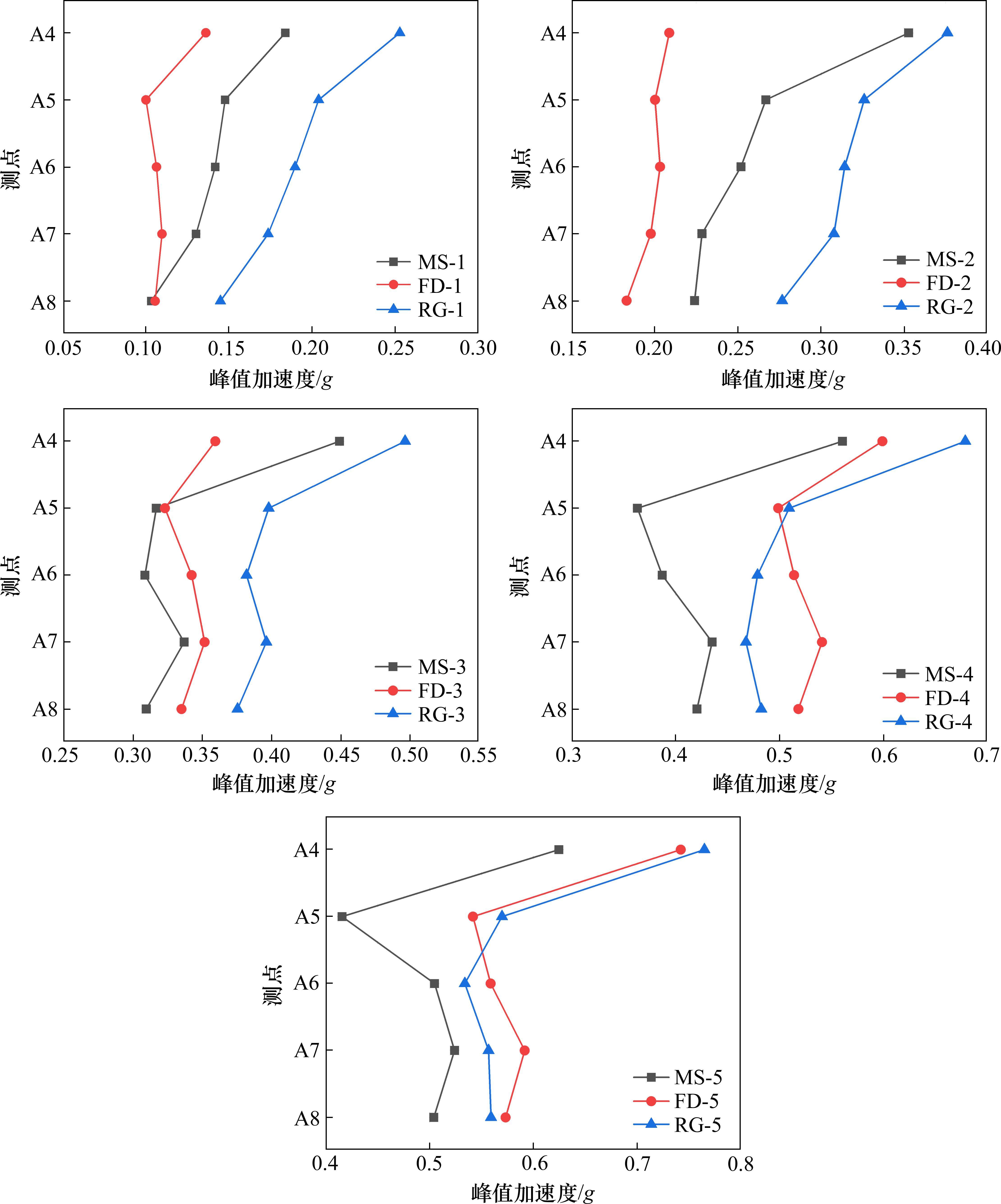
名山波属于高频波,且频带宽;人工波属于中频波,且频带适中;北京饭店波属于低频波,且频带窄。当PGA较小时,土层的加速度响应对中高频的地震波比较敏感,而低频波对土层扰动程度较小;随着PGA的增大,低频波作用下的土层加速度响应逐渐超越了高频波作用下的土层加速度响应,与中频波作用下的土层加速度响应相差不大,这是由于低频波能够在土层中传播更远的距离,因为它们受到的衰减较少,而高频波通常在土层中传播的距离较短,因为它们更快地被土层中的摩擦和非弹性变形所衰减。
2.3 中柱的加速度响应
不同地震波以及不同峰值加速度(PGA)作用下,负1层中柱的峰值加速度如图13所示。其中,测点A14位于负1层中柱顶端,测点A15位于负1层中柱底端。当PGA≤0.3g时,测点A14、A15的加速度响应规律为人工波>名山波>北京饭店波;当PGA>0.3g时,测点A14、A15的加速度响应规律为人工波>北京饭店波>名山波。
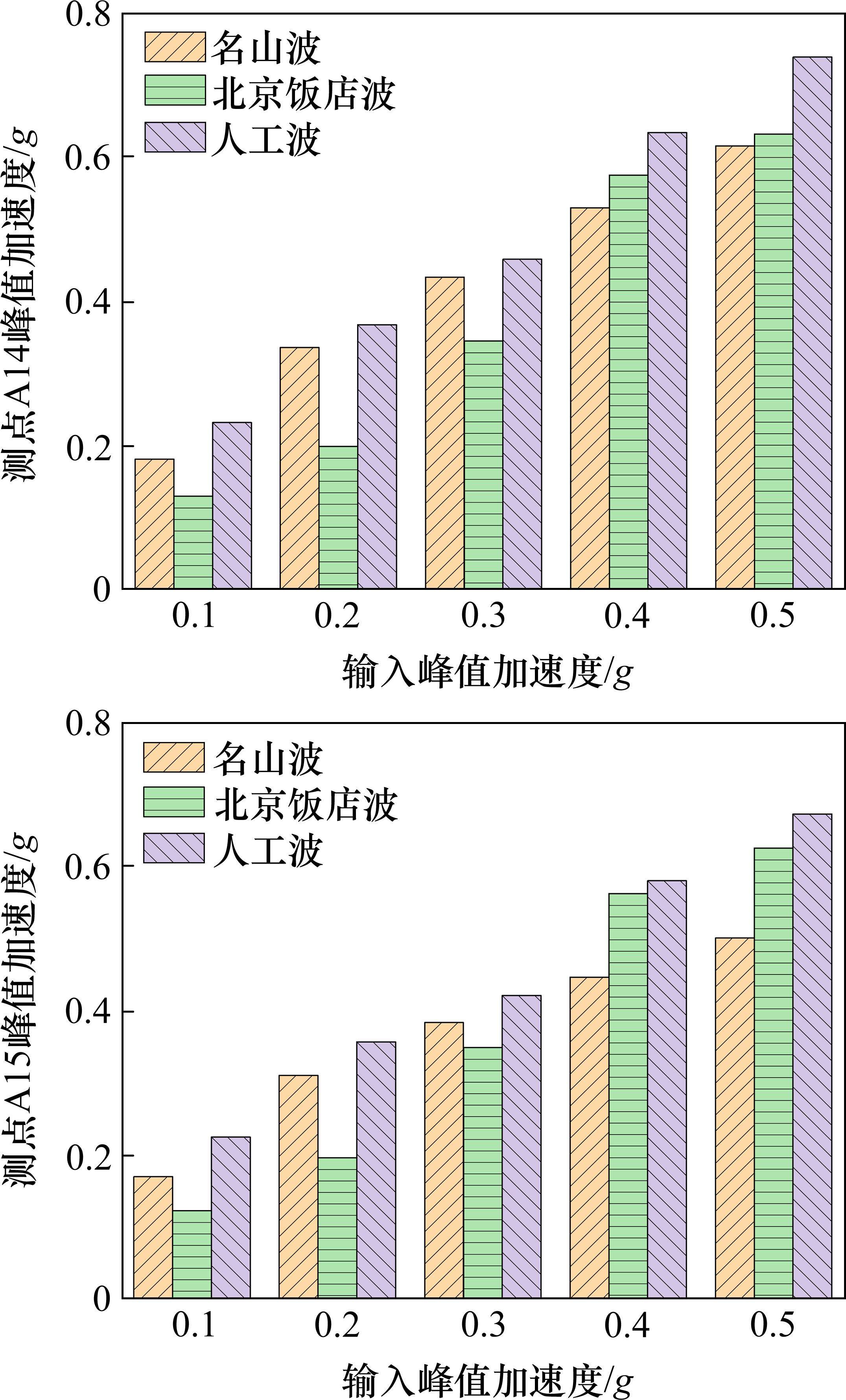
无论地震波强度如何,人工波作用下负1层中柱的加速度响应总是大于名山波以及北京饭店波作用下的。当PGA>0.3g时,北京饭店波作用下负1层中柱的加速度响应大于名山波作用下的。
不同地震波以及不同峰值加速度(PGA)作用下,负2层中柱的峰值加速度如图14所示。其中,测点A19位于负2层中柱顶端,测点A20位于负2层中柱底端。当PGA<0.3g时,测点A19、A20的加速度响应规律为人工波>名山波>北京饭店波;当PGA=0.3g时,测点A19的加速度响应规律为人工波>名山波>北京饭店波,而测点A20的加速度响应规律为人工波>北京饭店波>名山波;当PGA>0.3g时,测点A19的加速度响应规律为人工波>北京饭店波>名山波,而测点A20的加速度响应规律为北京饭店波>人工波>名山波。
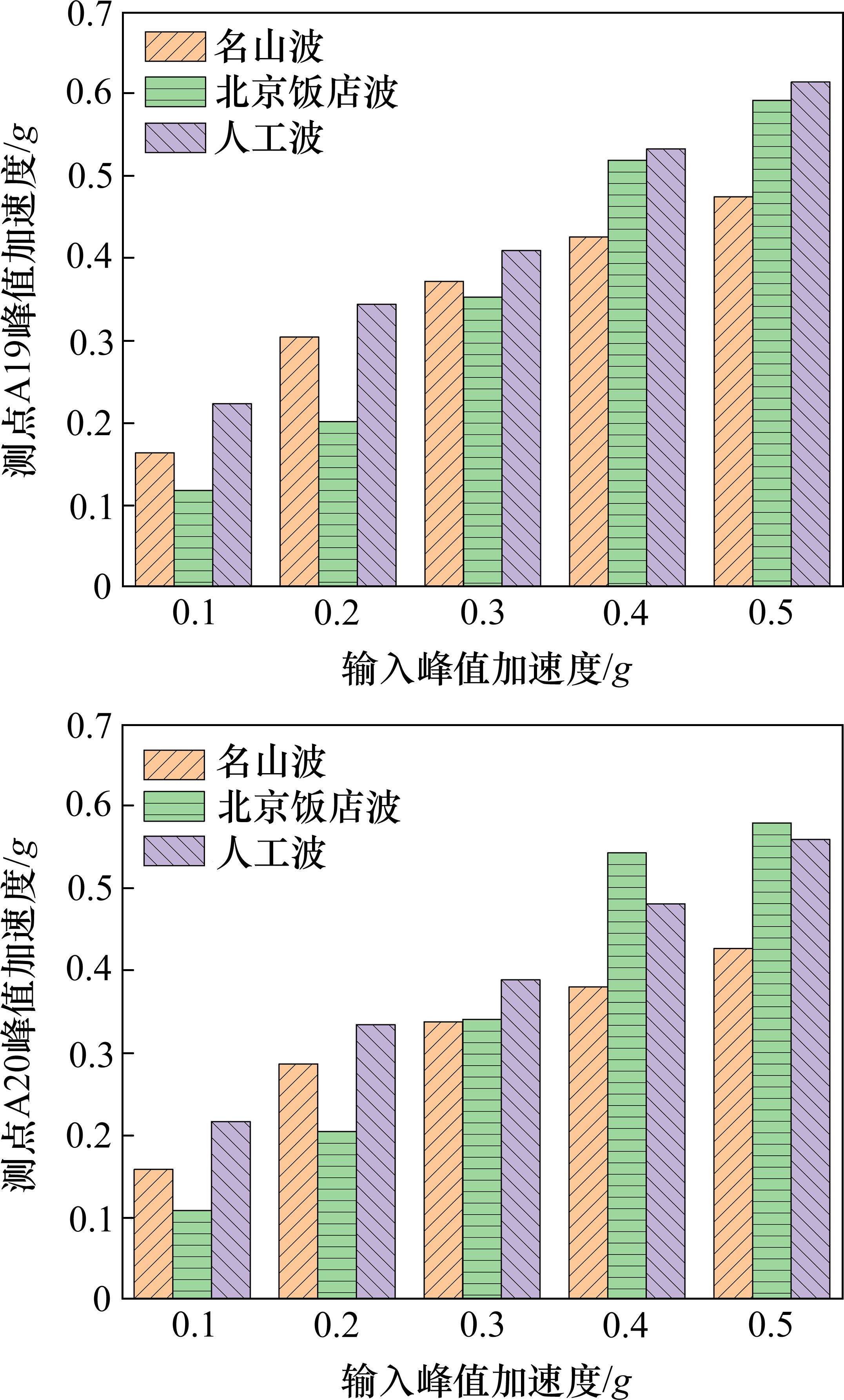
由负2层中柱的加速度响应规律可以看出,其顶端的加速度响应规律与负1层中柱的加速度响应规律大致相同,其底端的加速度响应规律与负3层中柱的加速度响应规律大致相同。
不同地震波以及不同峰值加速度(PGA)作用下,负3层中柱的峰值加速度如图15所示。其中,测点A23位于负3层中柱顶端,测点A24位于负3层中柱底端。当PGA<0.3g时,测点A23、A24的加速度响应规律为人工波>名山波>北京饭店波;当PGA=0.3g时,测点A23、A24的加速度响应规律为人工波>北京饭店波>名山波;当PGA>0.3g时,测点A23、A24的加速度响应规律为北京饭店波>人工波>名山波。
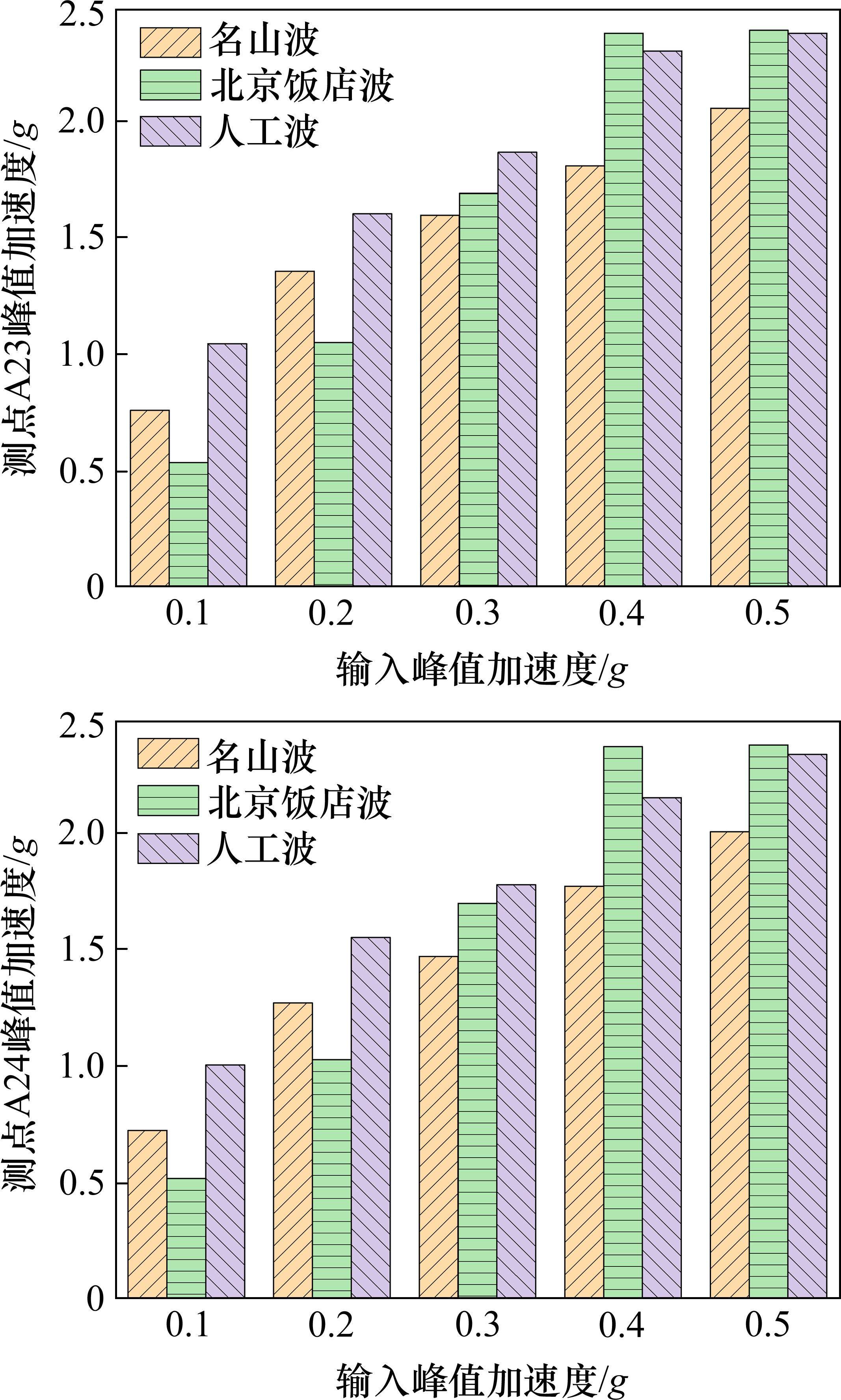
无论地震波强度如何,人工波作用下负3层中柱的加速度响应总是大于名山波作用下。当PGA<0.3g时,北京饭店波作用下负3层中柱的加速度响应最小;当PGA=0.3g时,北京饭店波作用下负3层中柱的加速度响应小于人工波作用下,但大于名山波作用下;当PGA>0.3g时,北京饭店波作用下负3层中柱的加速度响应最大。
可以看出,测点A14、A15和A19的加速度响应趋势基本一致,测点A20、A23和A24的加速度响应趋势基本一致,这说明,负2层中柱柱顶的加速度响应主要受负1层的影响,而负2层中柱柱底的加速度响应主要受负3层的影响。当地震波强度较小时,负1层中柱的加速度对中高频波比较敏感,低频波对其影响较小,随着地震波强度的增大,低频波作用下负1层中柱的加速度响应超越了高频波作用下的,逐渐接近中频波作用下的。当地震波强度较小时,负3层中柱的加速度对中高频波比较敏感,低频波对其影响较小,随着地震波强度的增大,低频波作用下负3层中柱的加速度响应逐渐超越了中频波、高频波作用下的中柱加速度响应。
2.4 结构板的加速度响应
不同地震波以及不同峰值加速度(PGA)作用下,板的峰值加速度如图16所示。其中,测点A16位于顶板,测点A17位于负1层中板,测点A21位于负2层中板,测点A25位于底板。当PGA<0.3g时,测点A16、A17、A21、A25的加速度响应规律为人工波>名山波>北京饭店波;当PGA=0.3g时,测点A16、A17的加速度响应规律为人工波>名山波>北京饭店波,而测点A21、A25的加速度响应规律为人工波>北京饭店波>名山波;当PGA>0.3g时,测点A16、A17的加速度响应规律为人工波>北京饭店波>名山波,而测点A21、A25的加速度响应规律为北京饭店波>人工波>名山波。
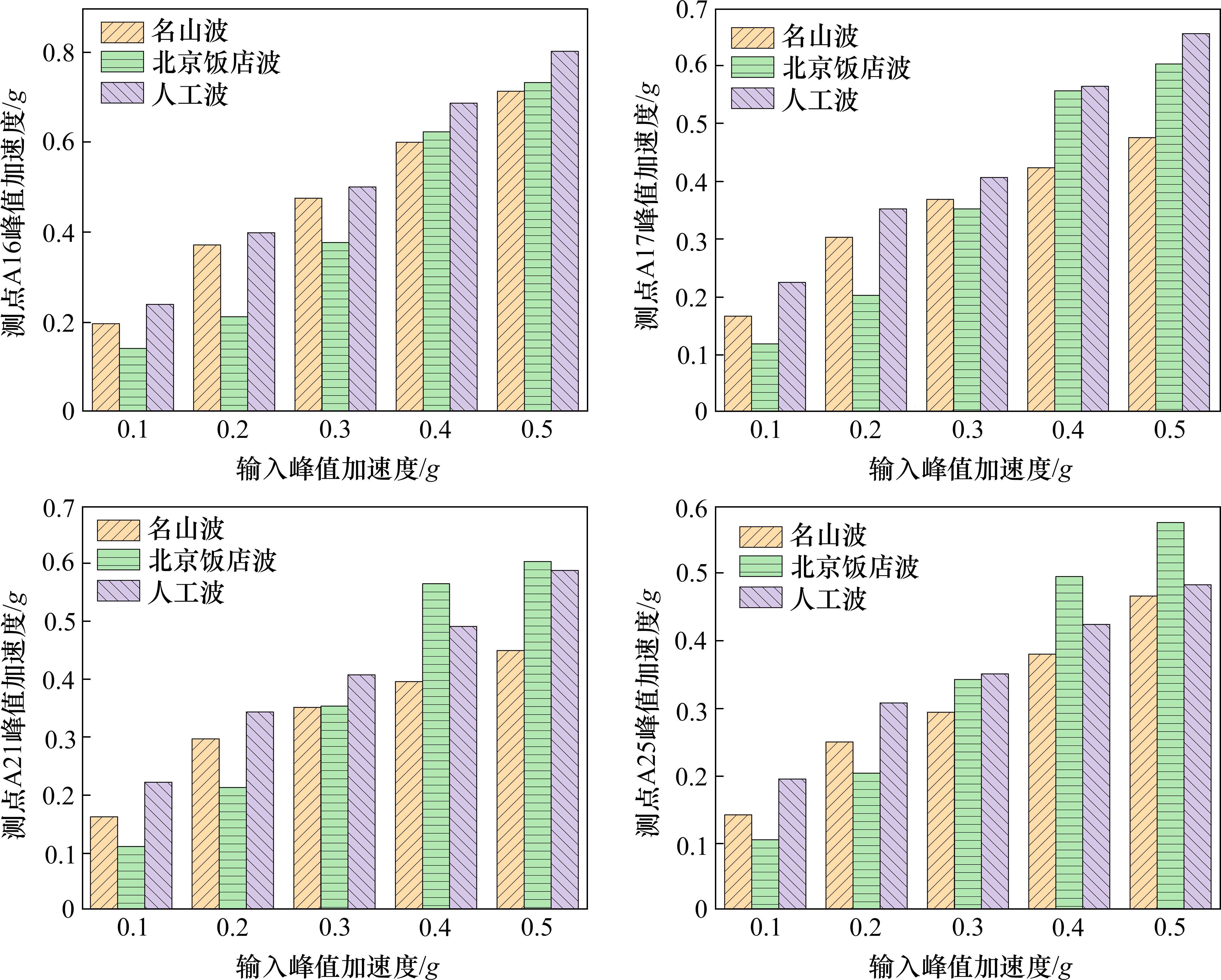
由此可以看出,顶板、负1层中板的加速度响应规律与负1层中柱的加速度响应规律基本一致;负2层中板、底板的加速度响应规律与负3层中柱的加速度响应规律基本一致。
2.5 中柱应变分析
以PGA=0.5 g为例,不同地震波作用下中柱的应变幅值见表4。测点S10、S11、S19和S28的应变幅值响应规律为人工波>北京饭店波>名山波;测点S20、S29的应变幅值响应规律为北京饭店波>人工波>名山波。
| 位置 | 测点 | 工况 | ||
|---|---|---|---|---|
| MS-5 | FD-5 | RG-5 | ||
| 负1层中柱 | S10 | 37.23 | 65.92 | 73.25 |
| S11 | 23.19 | 30.52 | 40.90 | |
| 负2层中柱 | S19 | 8.55 | 25.64 | 35.40 |
| S20 | 61.65 | 115.36 | 111.70 | |
| 负3层中柱 | S28 | 6.10 | 18.92 | 32.35 |
| S29 | 217.91 | 369.90 | 356.47 | |
北京饭店波作用下负2层中柱底端、负3层中柱底端的应变增量略大于人工波。负1层中柱、负2层中柱顶端、负3层中柱顶端的应变增量响应规律为人工波>北京饭店波>名山波。这说明,在北京饭店波、人工波作用下,中柱的应变响应较大;在名山波作用下,中柱的应变响应较小。
由此可以看出,在地震动强度较大的情况下,低频、中频地震波对车站结构中柱应变响应的影响比较接近,而且都大于高频波的影响。从结构断面形式来看,由于负1层、负2层两侧有一体化建设的地下结构,导致负1层、负2层的横向刚度远大于负3层的,所以负3层中柱柱底应变响应最大。
2.6 试验宏观现象
试验得到的宏观现象如图17所示。试验会造成地表开裂,形成沿结构两侧贯通的裂缝,如图17(a)所示;裂缝宽度为5 mm,如图17(b)所示;试验会造成紧邻结构两侧的土体发生破坏,破坏范围为60 mm,如图17(c)所示;试验会造成结构两侧的土体发生沉陷,沉陷高度为13 mm,如图17(d)所示。地铁车站结构通常由钢筋混凝土等材料构成,具有高刚性和强度,而土层则是由颗粒物质构成,具有较大的变形能力。这导致它们在地震动中以不同的频率和振幅响应,从而在它们的接触界面上产生相对位移,引起裂缝。此外,地震还可能引起砂土震密,这会导致土体沉陷,在地铁结构于土层接触界面处产生裂缝。

本次试验旨在深入探究地震波对地下一体化车站结构的影响,重点分析地震波激发下的地震动响应特性。为了确保试验结果的一致性与可比性,试验中采用了标准化的方法,包括使用相同种类的砂土、构建一致的结构模型,进而保证土-结接触模式相同。这种标准化的做法使得试验结果呈现出相同破坏模式趋势。
尽管试验中施加的地震波类型不尽相同,地震强度也有所差异,但是,无论是高频、中频还是低频地震波,它们在土层中引起的加速度响应趋势表现出了一定的一致性。这意味着,地震波的频率特征虽然对结构的地震响应带来影响,但不同频率的地震波最终导致的加速度响应趋势并未发生根本性的改变。换言之,地震波的不同频率特性造成了不同级别的影响,但在宏观层面上,即使是频率特性不同的地震波,也都遵循了相似的动力响应规律。因此,通过对不同频率的地震波引起的响应进行对比,可以更全面地理解结构在地震作用下的动力行为,为地下结构的抗震设计提供更为科学的依据。
3 结论
1) 车站结构的抗震性能与地震波的频率密切相关。低频地震波导致的结构响应较大。名山波的频率较高,对中柱和结构板的加速度响应的影响比较小;人工波的频率较低,对中柱和结构板的加速度响应的影响比较大;北京饭店波的频率非常低,当PGA>0.3g时,对中柱和结构板的加速度响应的影响突然增大,尤其是对负3层的中柱和结构板加速度响应的影响达到最大。
2) 不同幅值的地震波对地铁车站的影响差异显著。在小幅值地震波作用下,车站结构表现出良好的弹性行为,而在大幅值地震波作用下,结构会表现出非弹性行为和永久变形,要求在设计时应考虑到大震作用的潜在风险。
3) 地下一体化地铁车站的重要性质之一是其“一体化”设计,使得结构在地震波作用下的能量分散有一个较好的效果。所以,由于车站结构两侧有附属地下结构,导致车站结构负1层、负2层的横向刚度大于负3层,从而使得车站结构负1层、负2层的中柱加速度响应远小于负3层中柱加速度响应。因此,在实际工程应用中,需要通过详细的动态分析来优化结构设计,减少刚度差异对结构抗震性能的负面影响。
总之,不同地震波以及不同峰值加速度(PGA)作用下,地铁车站结构的动力响应表现不同。首先,不同的地震波具有不同的频率成分,地铁车站结构对不同频率的地震波有不同的敏感性,尤其是当地震波的主频与结构的自然频率接近时,会发生共振现象,从而导致结构响应的显著放大;其次,地震波的振幅是决定结构响应强度的关键因素之一,峰值加速度(PGA)较大的地震波将产生较大的剪切力,导致结构响应更为剧烈。
史明,陶连金,王志岗.不同地震波作用一体化地铁车站地震响应分析[J].铁道科学与工程学报,2024,21(11):4637-4652.
SHI Ming,TAO Lianjin,WANG Zhigang.Seismic response analysis of metro stations integrated with different seismic wave actions[J].Journal of Railway Science and Engineering,2024,21(11):4637-4652.

