路基是铁路轨道的重要基础结构。研究路基土的动力特性对轨道及其下部结构的动力分析和设计至关重要。阻尼比和耗散能能反映试样应力与应变的滞回特性、试样内部颗粒位置调整、摩擦和体积胀缩等导致的能量损失,是研究土体动力性能的重要内容之一。因此,研究动荷载作用下的土体阻尼比和能量耗散特性是十分必要的。目前,国内外许多学者通过动三轴试验和共振柱试验来研究土体的滞回曲线形态特性和阻尼比,分析含水率、围压和温度等因素的影响,并建立了预估模型和经验公式。罗飞等[1]开展分级加载方式下的低温状态下三轴试验,分析青海地区冻土和甘肃地区黄土的滞回曲线形态特征,并总结出围压、加载频率对滞回曲线的影响。郭林等[2]通过对软黏土的动三轴试验,发现在其它条件一定的情况下,随着围压的增大,土体的内部结构逐渐破坏,滞回圈的面积不断增大。梁珂等[3-4]对南沙珊瑚砂、长江漫滩相软土的动力特性进行研究,给出动剪切模量与阻尼比的经验公式和相关参数。庄心善等[5]利用滞回曲线的各种属性(包括封闭面积S、主轴斜率k、相邻滞回曲线中心的距离d以及未封闭的程度εp)对重组弱胀土的滞回曲线进行了定量分析,并分析了动应力幅值、围压、频率以及固结应力比对滞回曲线的形状的影响。KUMAR等[6]对在大范围剪应变下砂土的动力特性进行了研究,从围压和相对密实度的角度分析了试验样本滞回曲线的演变规律,并计算了阻尼比。KALLIOGLOU等[7]研究在大应变和小应变2个状态下,对土体阻尼比的变化规律进行了探讨,发现其应变状态与阻尼比的关系最为紧密,孔隙比和初始偏应力等因素也会影响阻尼比。阻尼比经验公式主要分为2类,一类是建立阻尼比和动模量的关系,比如HARDIN等[8]总结出直线关系,BORDIN等[9]总结出多项式关系,蔡袁强等[10]总结出指数函数关系。另一类建立阻尼比与动应变的关系,如马德翠等[11]提出将阻尼比与动应变之间用对数模型来拟合。上述研究成果主要是考虑地震荷载或连续循环荷载的作用,鲜有考虑到车辆或列车之间追踪时间间隔的影响。事实上,列车运行之间的时间间歇对路基土的累积塑性应变、回弹模量、弹性应变等都有显著的影响[12-13],在此基础上重点分析考虑列车追踪时间间隔的循环动荷载作用下的粉土填料的阻尼比和耗散能特性。以朔黄重载铁路基床层填料为研究对象,研究不同含水率、围压、动应力条件下连续加载、间歇加载下试样的动力特性,分析围压、含水率、动应力幅值对能量耗散及阻尼比的影响,揭示荷载间歇对路基稳定性的积极作用。结合试样累积塑性应变研究成果,对试样耗散能边界进行划分,提出从能量耗散的角度判断路基动力稳定性的方法。
1 土样制备和试验方案
1.1 试验土样
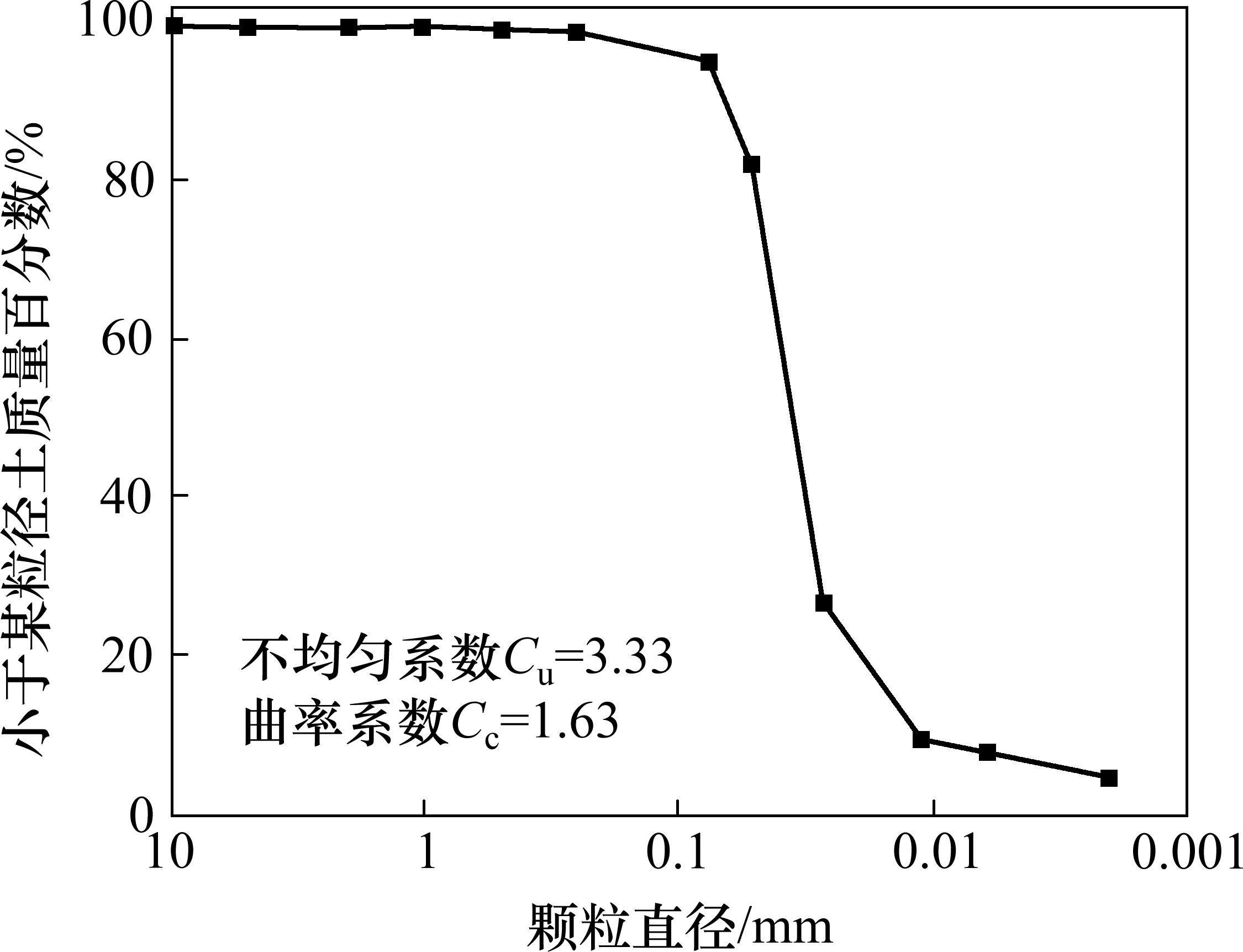
试验土取样于朔黄铁路路基基床表层,其基本物理性质指标和级配曲线见表1和图1。根据《铁路路基设计规范》(TB 10001—2016),该填料为低液限粉土。为考虑路基土不同含水状态对其力学性能的影响,试验过程中试样考虑3种含水状态,即最优含水率状态(11.80%),饱和含水率状态(19.75%)和天然含水率状态(15.00%)。土样的压实系数K设定为0.95。试样尺寸为直径39.1 mm,高80 mm,制备时分5层击实完成,每层进行刮毛处理。
| 物理性质指标 | 数值 |
|---|---|
| 颗粒相对密度Gs | 2.71 |
| 最大干密度ρdmax/(g∙cm-3) | 1.96 |
| 最优含水率wopt/% | 11.8 |
| 饱和含水率wsat/% | 19.8 |
| 液限wL/% | 26.0 |
| 塑限wP/% | 18.2 |
| 塑性指数IP | 7.8 |
| 渗透系数k/(cm·s-1) | 1.238×10-7(K=0.95) |
1.2 试验仪器
动三轴试验在中南大学岩土工程实验室DDS-70微机控制的动三轴试验仪上进行。该动三轴试验仪由围压系统(空气压缩机和加压系统)、轴向加载系统、数据调节系统以及测控系统构成。仪器允许施加最大轴向动荷载为1 372 N,最大允许轴向位移为20 mm,荷载频率为1~10 Hz。
1.3 试验参数
为模拟路基面以下不同深度处的侧压环境,动三轴试验中围压设置为σ3=30 kPa、60 kPa、90 kPa。根据现场实测,朔黄重载列车对路基的加载频率在1.39 Hz至1.85 Hz的范围内,考虑设备参数设置和加载时长等因素,本研究试验加载频率设为2 Hz。根据大量的实测结果,有意扩大动应力幅值的范围,将动应力幅值设为σd=60~360 kPa。
由于土样的渗透系数小(k=1.238×10-7 cm/s),且在每一次循环振动下,动荷载作用时长太短(0.5 s),路基土中的水无法及时排出,因此在循环荷载加载阶段,试样不排水。当列车经过之后,循环动荷载停止加载,试样发生回弹变形,超孔压逐渐消散。为模拟孔隙水压的消散过程,在间歇阶段打开排水阀门,对试样进行排水。
1.4 试验方案
铁路路基不仅承受列车行驶通过时产生的动荷载作用,还受到道砟和钢轨等产生的静偏应力作用,根据MEI等[14]的研究成果,重载铁路的静偏应力应取15 kPa。通过现场调研,在自动闭塞的线路上,同一方向追踪运行的2列列车间存在时间间隔。因此铁路路基承受的列车动荷载作用由列车通过时产生的周期性振动和无列车通过时的加载间歇组合而成。为对比分析间歇荷载对试样阻尼比和耗散能特性的影响,试验设置了间歇加载与连续加载2种动力加载方案。
1) 连续循环加载试验,最大振动次数10 000次。加载波形图如图2(a)所示。
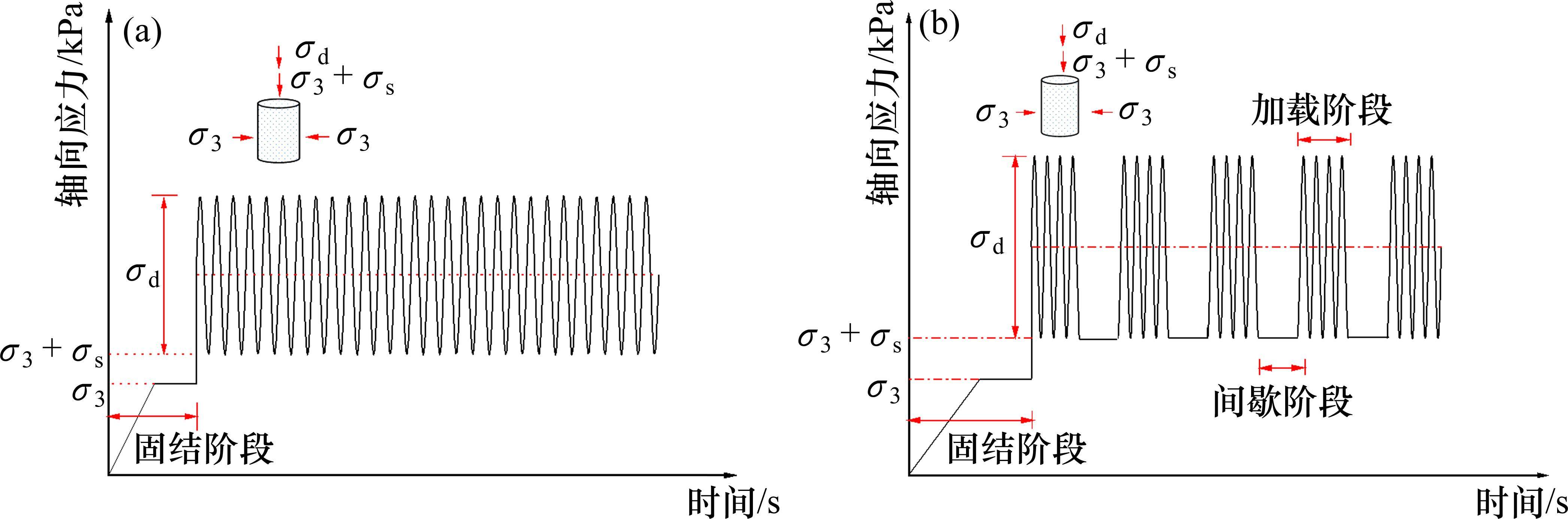
2) 考虑追踪列车的间隔时间,进行间歇循环载荷试验,载荷波形如图2(b)所示。针对朔黄铁路的运行线路进行最短追踪列车间隔时间的调查,结果如下:普通列车的间隔时间为8 min,万吨列车的间隔时间为11 min,而2万吨列车的间隔时间则为15 min。随着列车运货吨位的增加,追踪列车间隔时间拉长。15 min即900 s,因此,试验中确定加载时间间隔为1 000 s,是一个比较接近现有重载列车实际运营工况的时间间隔。在本次试验中,将每一次的循环加载次数定为2 000次,需要进行5轮的加载步骤。试验需完成5次循环的动荷载及4次时间间隔。
加载的详细步骤如下:首先,对试样施加围压σ3以便进行等压固结。接下来,关闭排水阀门,并施加偏应力σs=15 kPa,模拟上层结构所施加的静荷载。稳定后,施加循环动荷载进行加载。在连续加载测试中,试验结束以最大振次为10 000次或试样轴向应变达到10%的破坏标准时结束。在间歇加载测试中,每个1 000 s阶段施加2 000次循环动荷载,间歇时间为1 000 s。在振动停止阶段,维持σs=15 kPa,在加载总次数同样为10 000次,或试样达到破坏标准即轴向应变达到10%时结束。试验共开展了47组,具体试验方案如表2所示。
| 试验序列 | 含水率 | 试验类型 | 试样围压σ3/kPa | 动应力幅值σd/kPa |
|---|---|---|---|---|
| 1 | wopt=11.80% | 连续加载 | 30 | 240 |
| 2 | 60 | 240,300,360 | ||
| 3 | 间歇1 000 s加载 | 30 | 60,120,180,240,300 | |
| 4 | 60 | 120,180,240,300,360 | ||
| 5 | 90 | 120,180,240,300,360 | ||
| 6 | wins=15.00% | 间歇1 000 s加载 | 30 | 60,120,180,240,300 |
| 7 | 60 | 60,120,180,240,300 | ||
| 8 | 90 | 120,180,240,300,360 | ||
| 9 | wsat=19.75% | 连续加载 | 60 | 120 |
| 10 | 间歇1 000 s加载 | 30 | 60,90,120,180 | |
| 11 | 60 | 60,120,180,240 | ||
| 12 | 90 | 120,180,240,300 |
2 试验结果与分析
2.1 应力应变曲线
图3为间歇1 000 s加载情况下试样稳定和破坏2类典型的动应力-动应变关系曲线。图3(a)为稳定型试样(wins=15.00%,σ3=90 kPa,σd=180 kPa)的滞回曲线,在第1加载阶段初期,滞回圈疏松,相邻2个滞回圈间距较大,反映试样塑性应变大,累积塑性应变迅速增加。随着循环振次增加,滞回圈逐渐重叠,试样塑性应变逐渐减小,累积塑性应变速率逐渐减小。从图中还可以看出,随着加载阶段数的增加,每个加载阶段累积的塑性应变减小,表明累积塑性应变速率逐渐降低,试样变形逐渐稳定,进入稳定状态,这类试样表现出来的特性为稳定型试样。
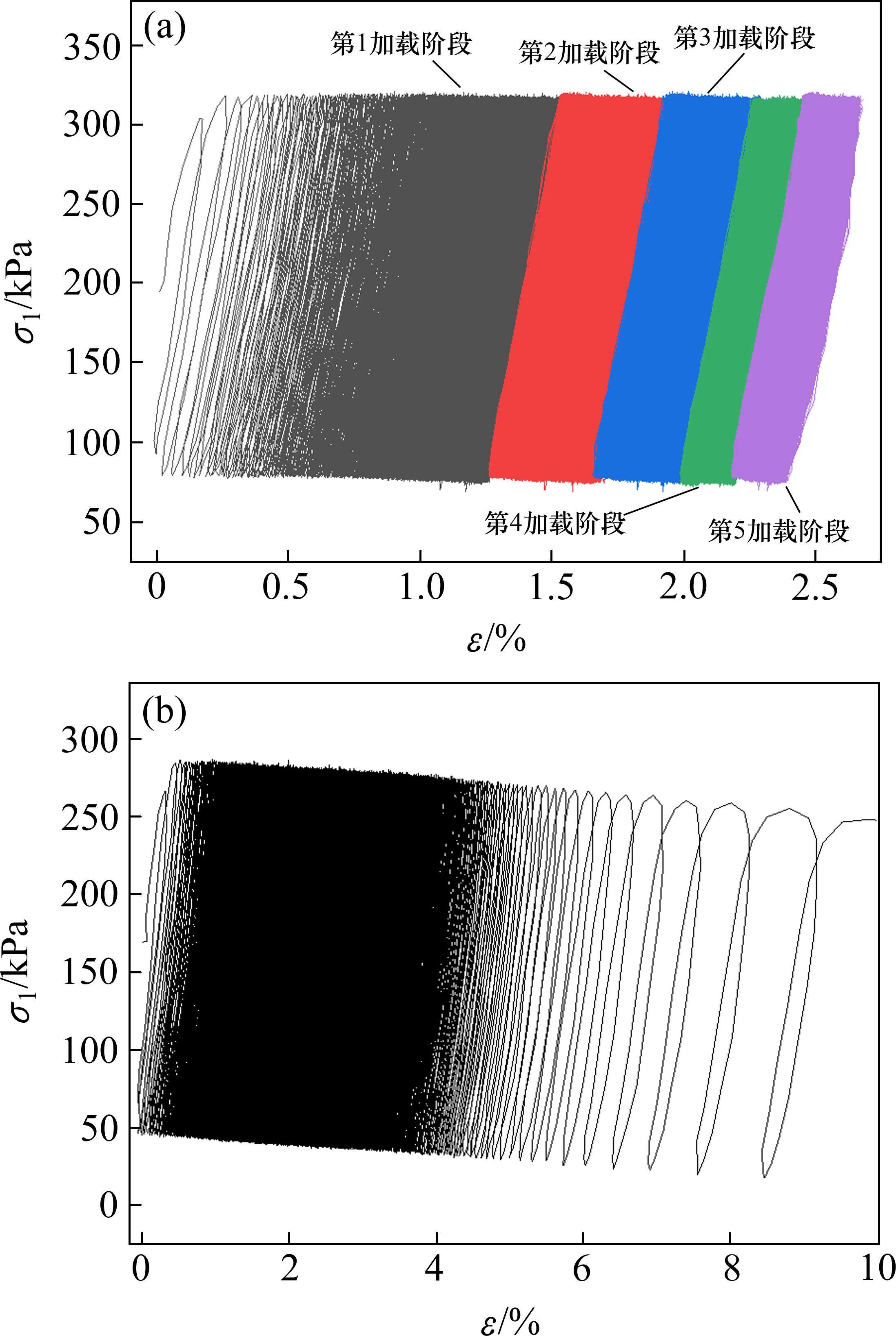
图3(b)为破坏型试样(wopt=11.80%,σ3=30 kPa,σd=180 kPa)的滞回曲线。滞回圈在加载初期逐渐致密,而随着振次的增加,后期的滞回圈又逐渐疏松。表明在动荷载作用下,试样的塑性应变经历过增大-减小-增大的过程。由于施加的动荷载过大,试样在第1加载阶段后期,相邻2个滞回圈的间距越来越大,塑性应变增加得越来越快,累积塑性应变速率也逐步增大,最终试样破坏。
2.2 耗散能与阻尼比的确定
土体在动力荷载作用下表现出显著的黏滞阻尼,会产生应变滞于应力的滞回曲线。图4中为含水率15.00%、围压30 kPa、动应力幅值180 kPa在间歇加载第2阶段第10次循环加载形成的滞回曲线。按照陈伟等[15]提出的方法,将滞回曲线的起始与末端接连,计算滞回圈的面积ΔW。ΔW表示当应力和应变循环一周时耗掉的能量。将应力最小点A与应力最大点B用直线相连,并过2点分别作水平线和竖直线相交于O点,三角形AOB的面积反映了每次循环加载时弹性应变能的最大值。土体的阻尼特性可以用等效滞回阻尼比λ来表示,计算公式如下:
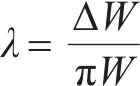
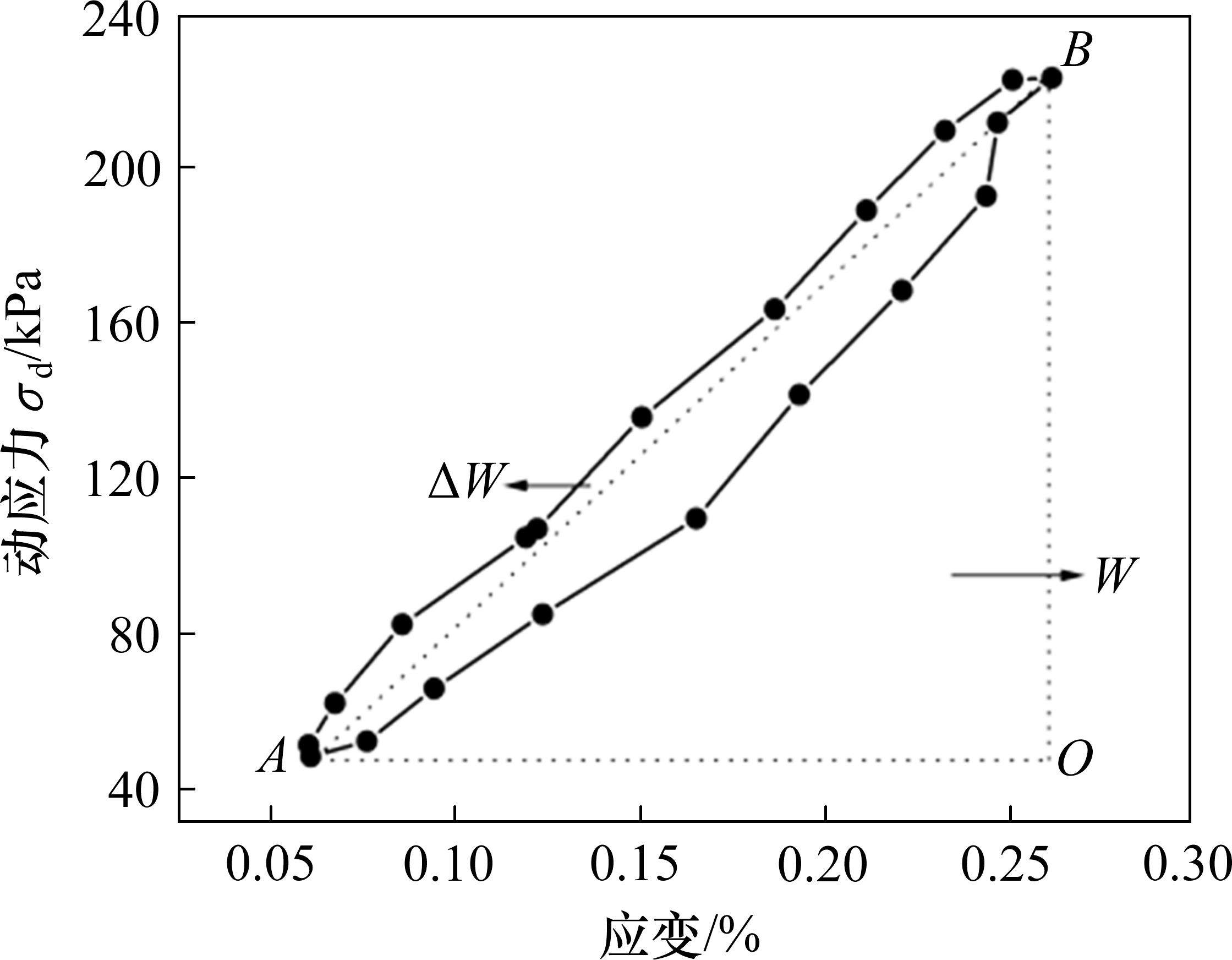
2.3 荷载间歇对试样阻尼比的影响
图5为试样在间歇1 000 s加载与连续加载条件下阻尼比随振次的变化曲线。试样在间歇加载条件下均没有达到破坏标准。在连续加载条件下,图5(a)中试样在加载8 200振次左右破坏,图5(b)中试样在加载7 000振次左右破坏。
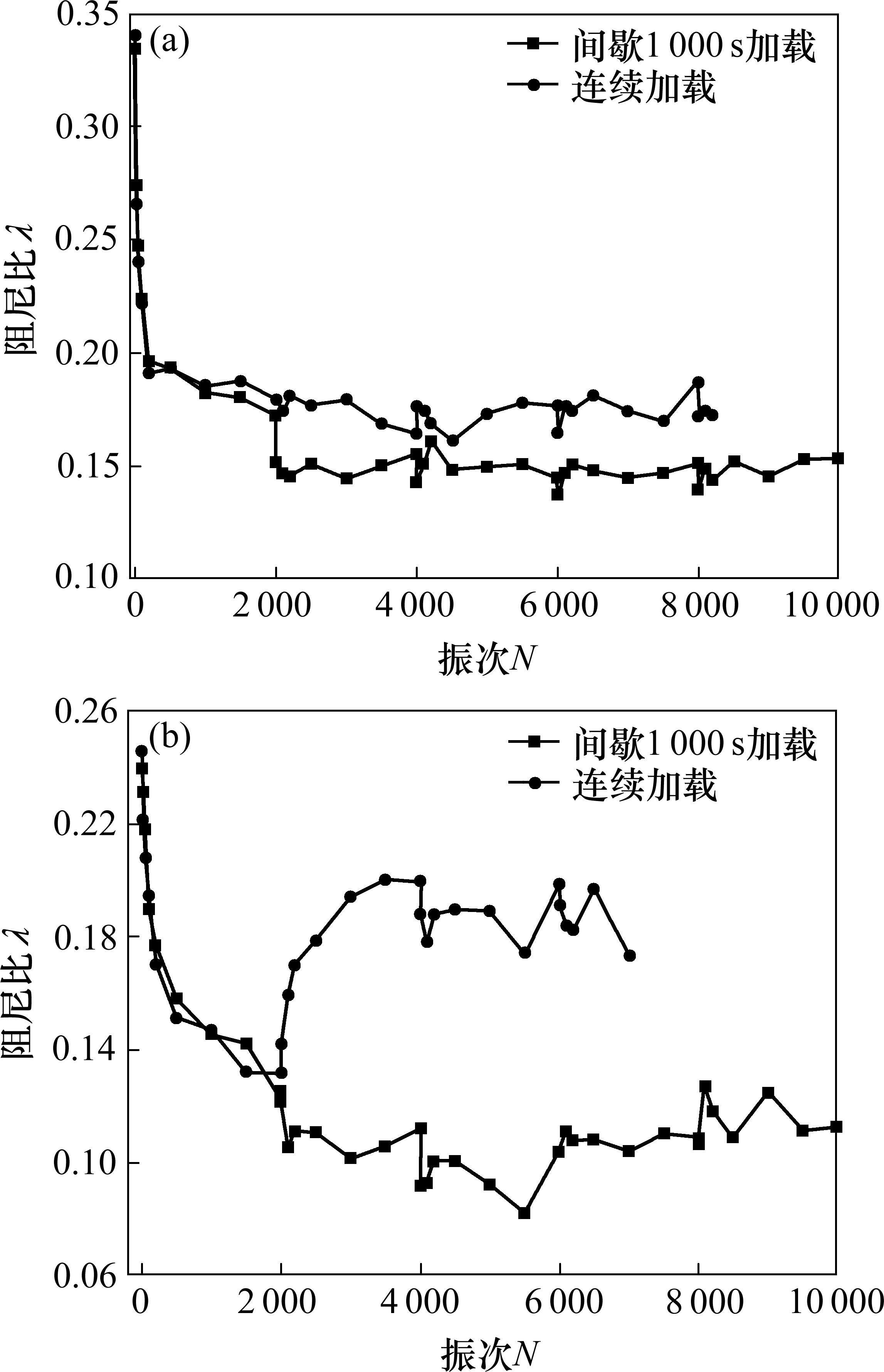
从图5中还可以看出,相同动应力幅值、含水率、围压条件下,荷载间歇有效地阻止了试样的破坏。主要原因有:1) 在持续加载下,土样中的颗粒不断转动、滚动和摩擦。这导致短小裂纹的扩大和新裂纹的出现,从而降低了土体的刚性。然而,通过增加荷载间歇,试样变形速度逐渐减小并趋于稳定,因此阻尼比也在加载间歇期间呈现下降趋势。CHEN等[16]研究了间歇荷载的粉土填料回弹模量变化情况,发现荷载间歇效应能有效提高试样的回弹模量和抵抗破坏的能力。2) 对于连续加载试样,随着循环荷载的施加,阻尼比有增大的现象,这是由于试样在加载一段时间后,土体变得较为密实,土体的孔隙率进一步减小,但此时荷载的施加并没有停止,土样颗粒间可能发生重新排列的趋势,进而导致土体克服阻尼所损耗的能量增大,进一步加快了试样的破坏趋势。3) 对于饱和试样,连续循环荷载作用下试样内部会产生超孔隙水压,且超孔隙水压随循环振次的增加逐渐累积,致使试样内部颗粒间的接触压力减小,有效应力降低,试样抵抗变形和破坏的能力降低。而间歇加载条件下,在间歇期打开了排水阀门允许试样自由排水,在每一阶段累积的超孔隙水压会在间歇期消散。在超孔压消散过程中,会使土体内部颗粒及结构发生调整,试样抵抗能力得到提高。本试验具体超孔压结果可以参见文献[17]。对非饱和试样,由于DDS-70型动三轴仪不能测试试样的基质吸力,基质吸力对连续加载和间歇加载条件下试样回弹模量的影响不能确定。
2.4 试样阻尼比随间歇加载阶段的变化
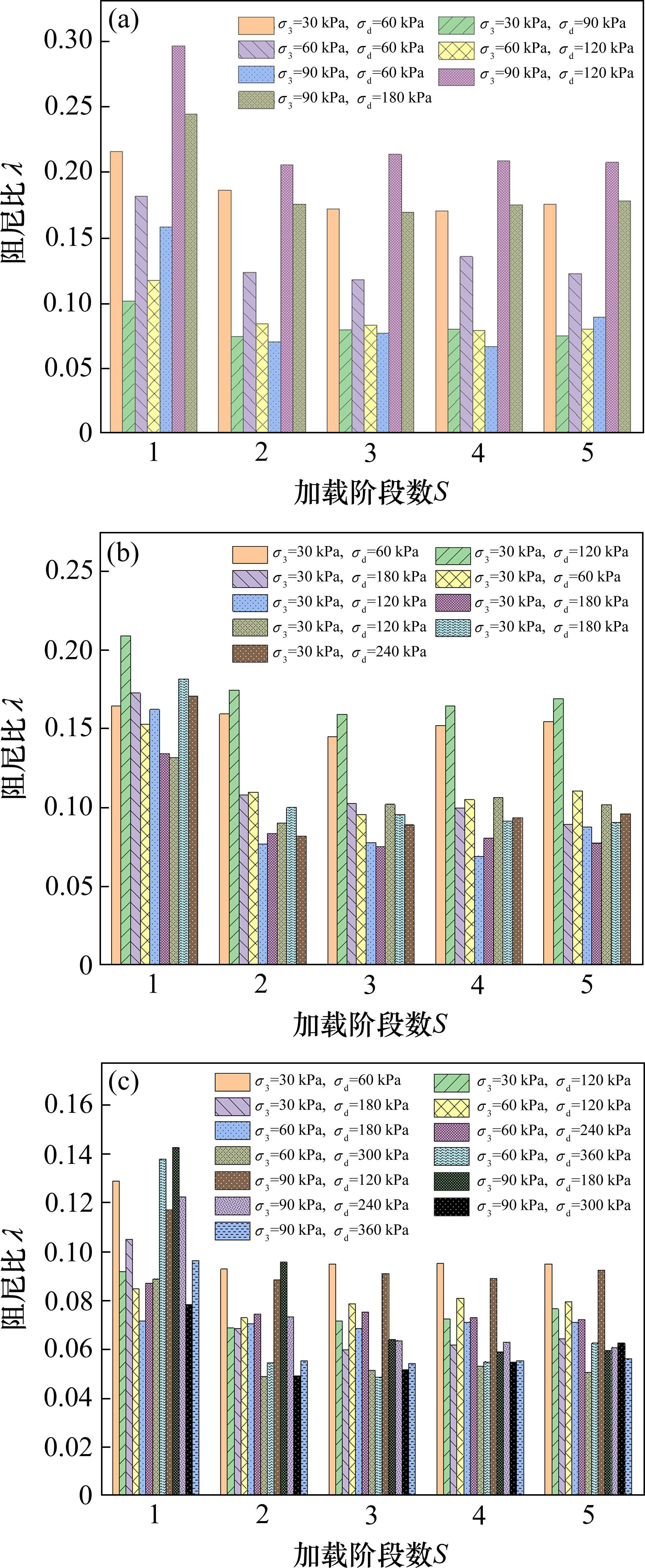
对于未破坏的试样,取各个阶段的平均阻尼比来分析试样阻尼比随间歇加载阶S的变化情况(如图6)。可以看出,3种含水率状态下试样阻尼从第1阶段到第2阶段有一个非常明显的下降,饱和含水率、天然含水率和最优含水率状态下的试样阻尼比在经过第1次间歇荷载后,下降幅度分别为13.7%~55.46%、3.1%~51.93%和1.53%~60.38%。而第4加载阶段试样平均阻尼比较第3阶段变化幅度分别为-14.83%~13.07%、-9.81%~11.48%、-12.7%~8.1%,降低的幅度大为减小。表明随着加载阶段数的增加,荷载间歇效应对减小试样阻尼的效果有所减弱。
2.5 含水率对阻尼比的影响
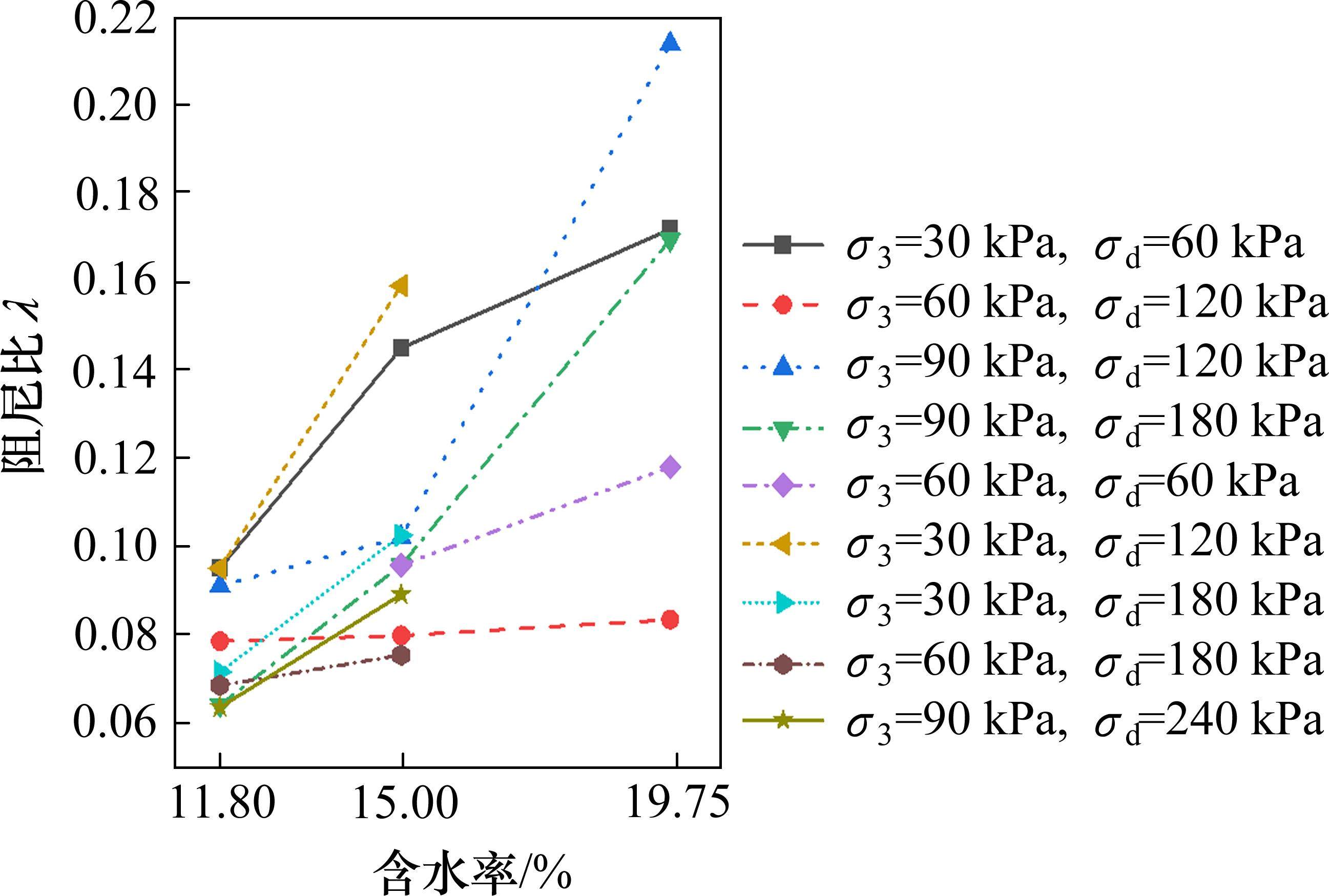
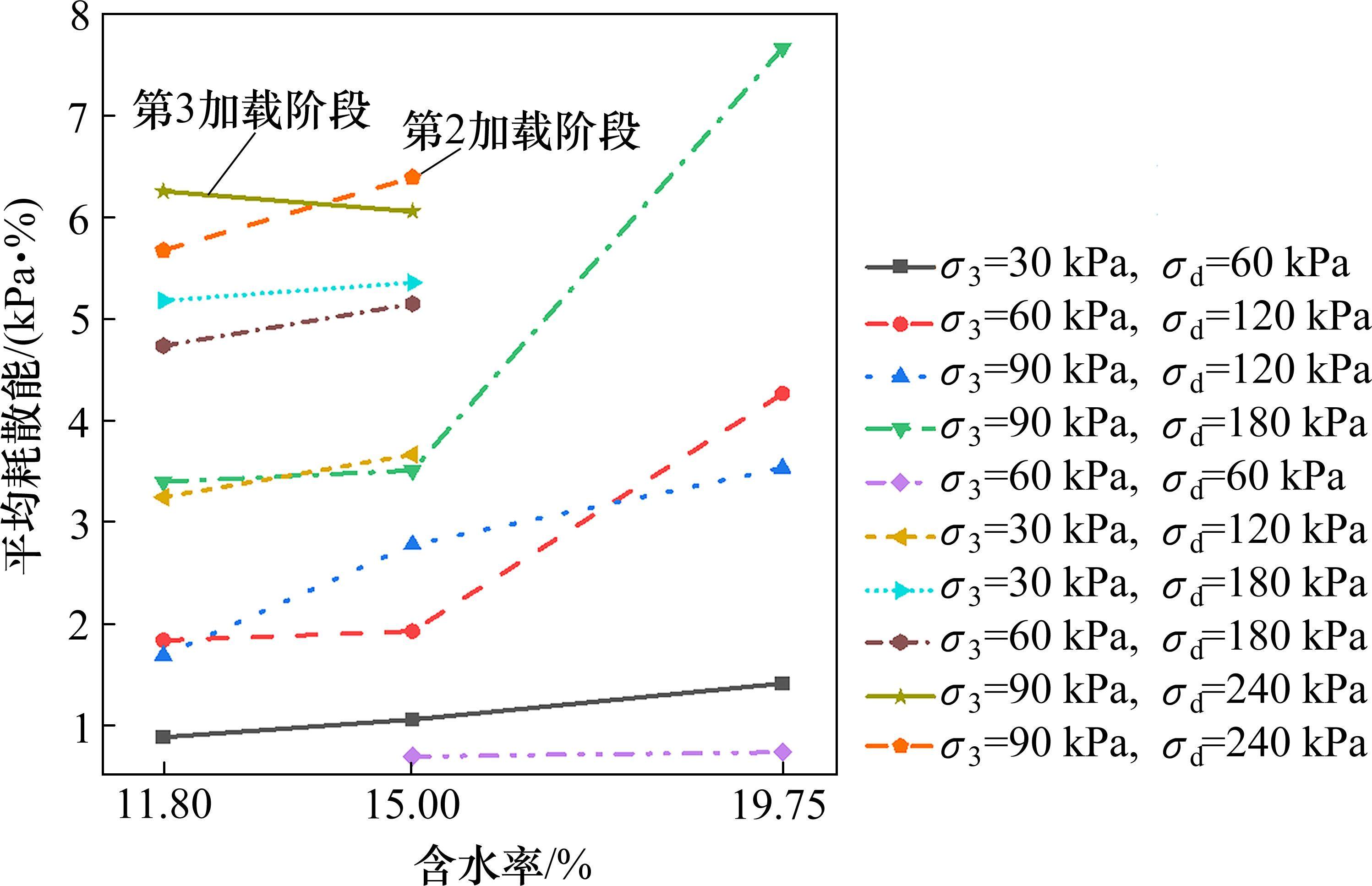
为更好地反映含水率对试样阻尼比的影响,将第3加载阶段的平均阻尼比随含水率的变化情况绘制于图7,试样含水率从11.80%增加到15.00%时,其第3加载阶段的平均阻尼比值增大幅度为1.65%~67.19%,而试样含水率从15.00%增加到19.75%时,其增大幅值为4.5%~98.55%,表明试样阻尼比随着含水率的增大而增大。
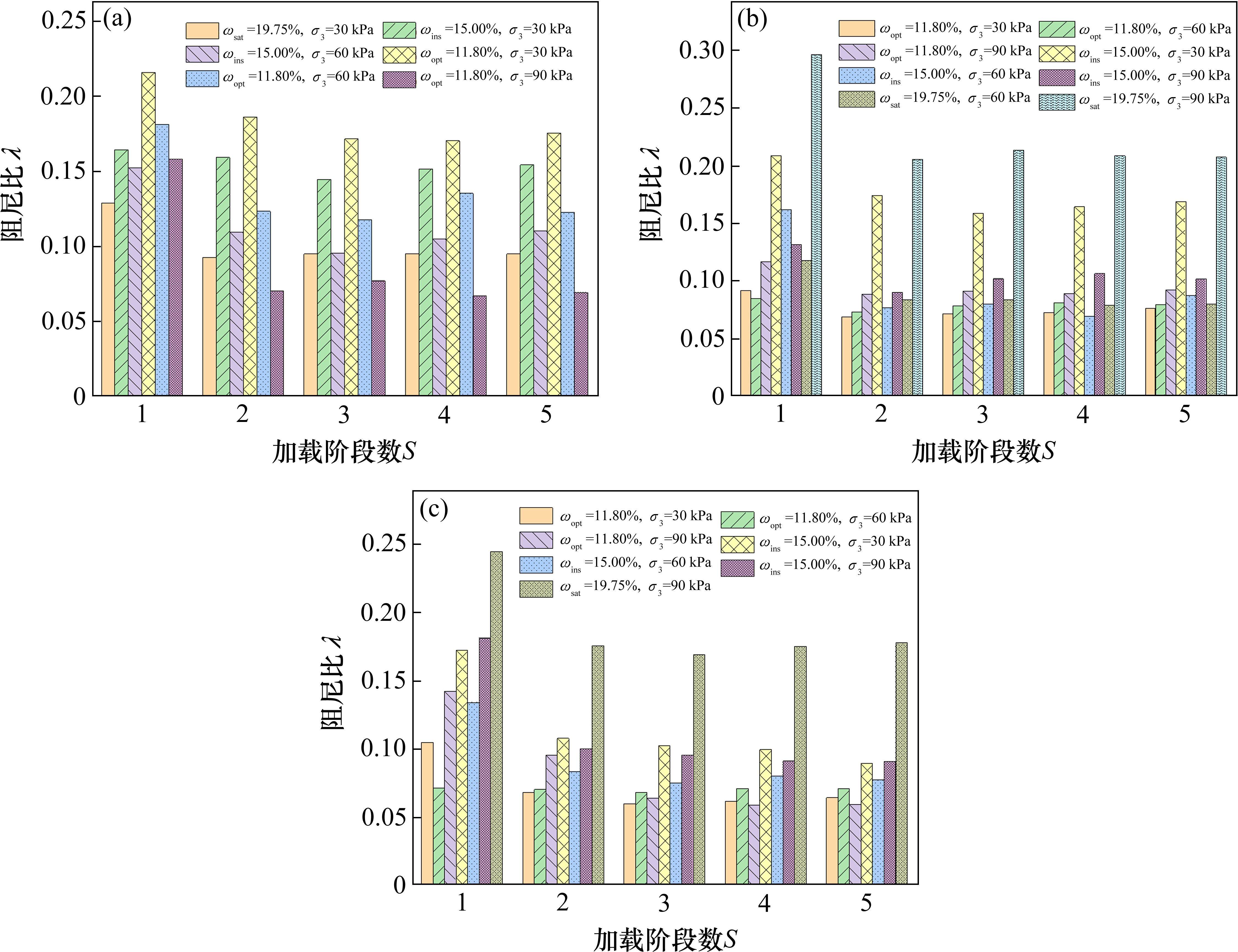
2.6 围压对阻尼比的影响
图8反映了未破坏粉土试样在不同围压下试样平均阻尼比随加载阶段数变化的整体趋势。从图中可以看出,随着围压的增大,粉土试样的阻尼比变化幅度有所收窄。30 kPa围压下粉土阻尼比变化范围为0.06~0.22,60 kPa围压下粉土阻尼比变化范围为0.049~0.18,90 kPa围压下大部分粉土试样阻尼比变化范围为0.06~0.175。
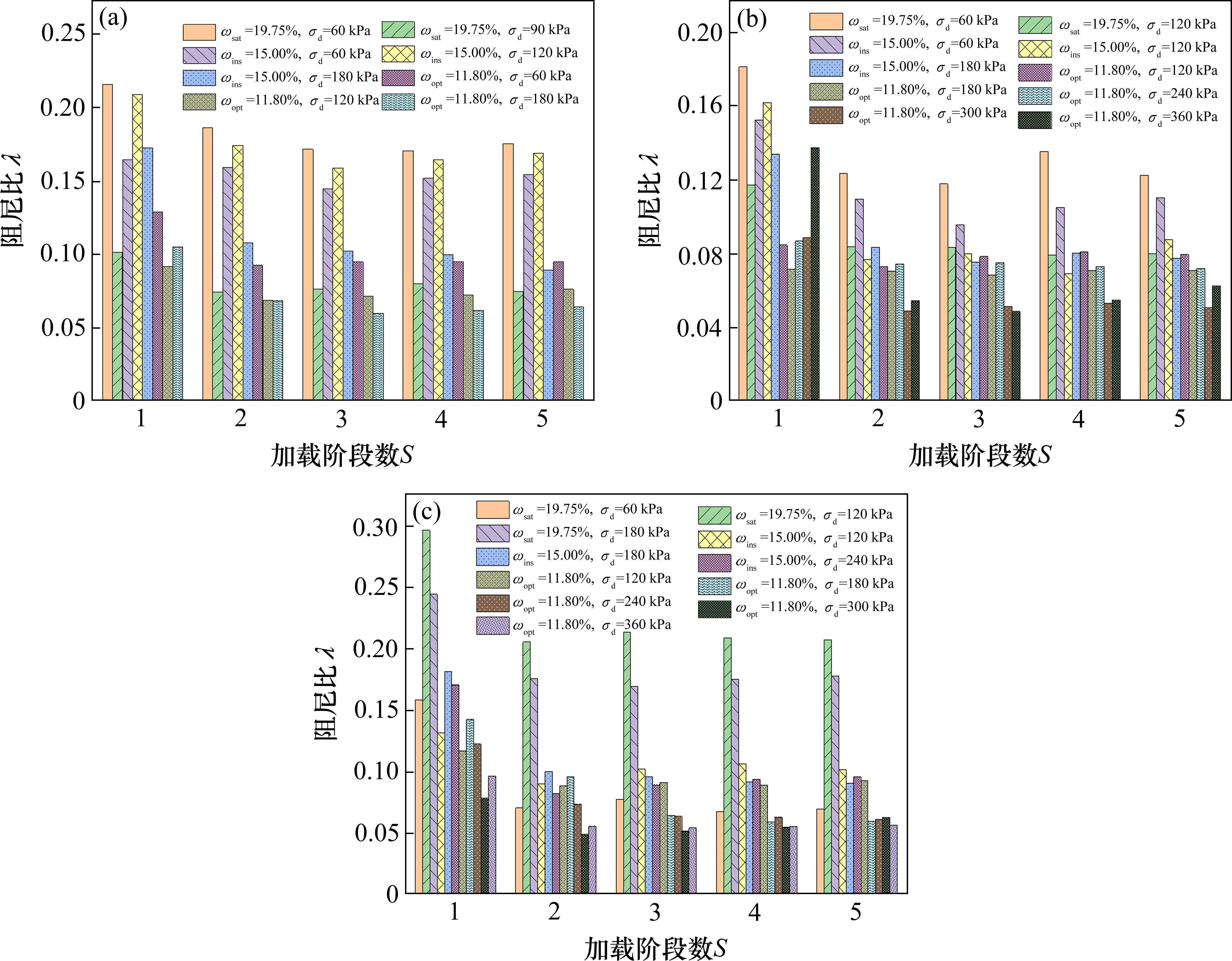
2.7 动应力幅值对阻尼比的影响
图9反映未破坏粉土试样在不同动应力幅值下试样平均阻尼比随加载阶段数变化的整体趋势。试样阻尼比没有随着动应力幅值的变化而呈现出明显的增大或减小的规律,其原因可能在于阻尼比值由耗散能与弹性应变共同决定。黄茂桐等[18]研究发现间歇作用下粉土填料试样弹性应变随着动应力幅值的增大而增大,在3.3节中,试样耗散能亦随着动应力幅值的增大而增大,但两者的相对应的变化速率不同。
3 耗散能
3.1 间歇作用对试样耗散能的影响
图10为间歇加载与连续加载下试样耗散能随振次的变化情况,图中试样在间歇加载情况下均没有发生破坏,在连续加载条件下,图10(a)中试样在加载8 200振次左右破坏,图10(b)中试样在加载7 000振次左右破坏。
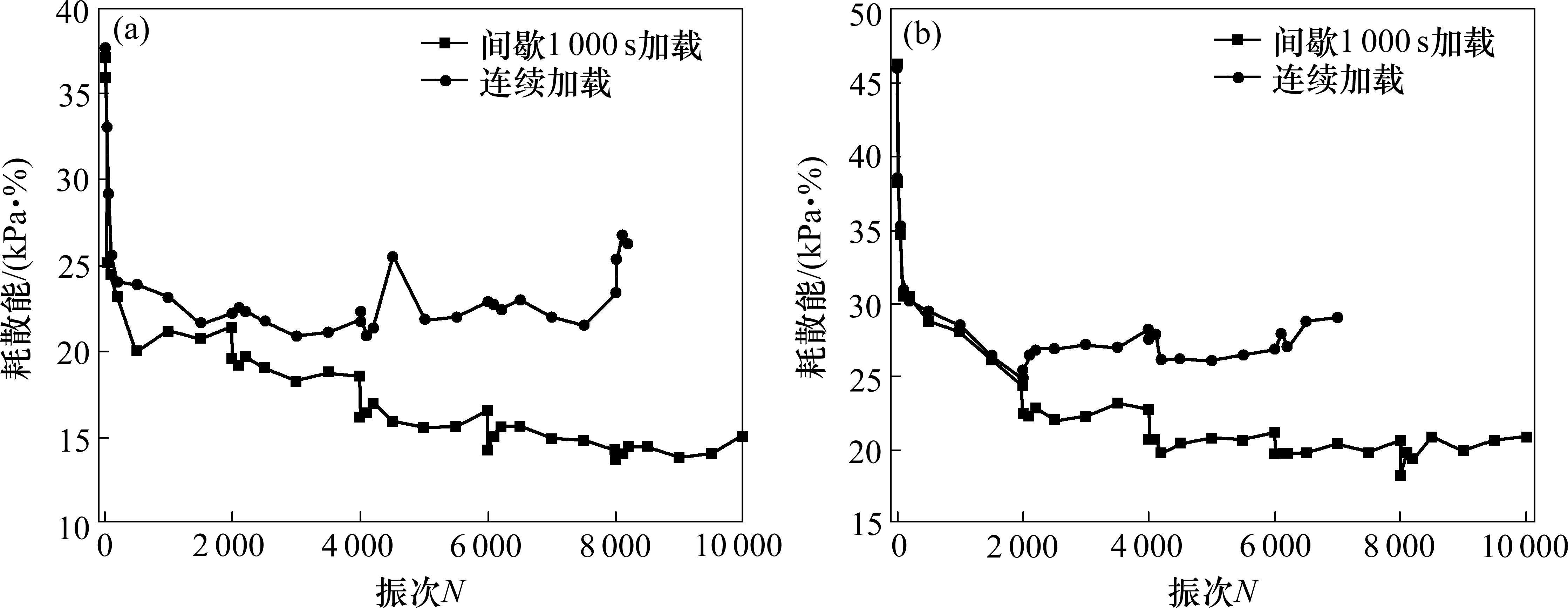
连续加载试样与间歇加载试样在第1阶段重合度比较高,说明试样的一致性比较好。在加载第1阶段的前200振次,耗散能的大小发生陡降。而在后面加载的几个阶段,2种情况下的滞回圈面积逐渐发生分离,对于间歇加载试样,在第1阶段结束后,间歇时期对试样进行排水。在开始第2阶段加载时,耗散能明显下降。这是因为在间歇阶段试样得以持续密实,进而加强了粒子间的咬合和摩擦力,同时,也减少了粒子间错动和重排列发生的几率。而连续加载试样作为对比,耗散能随着加载振次的增加,有逐渐变大的趋势,在发生破坏的最后一个阶段,出现了明显的上升趋势。
3.2 试样耗散能随间歇加载阶段的变化
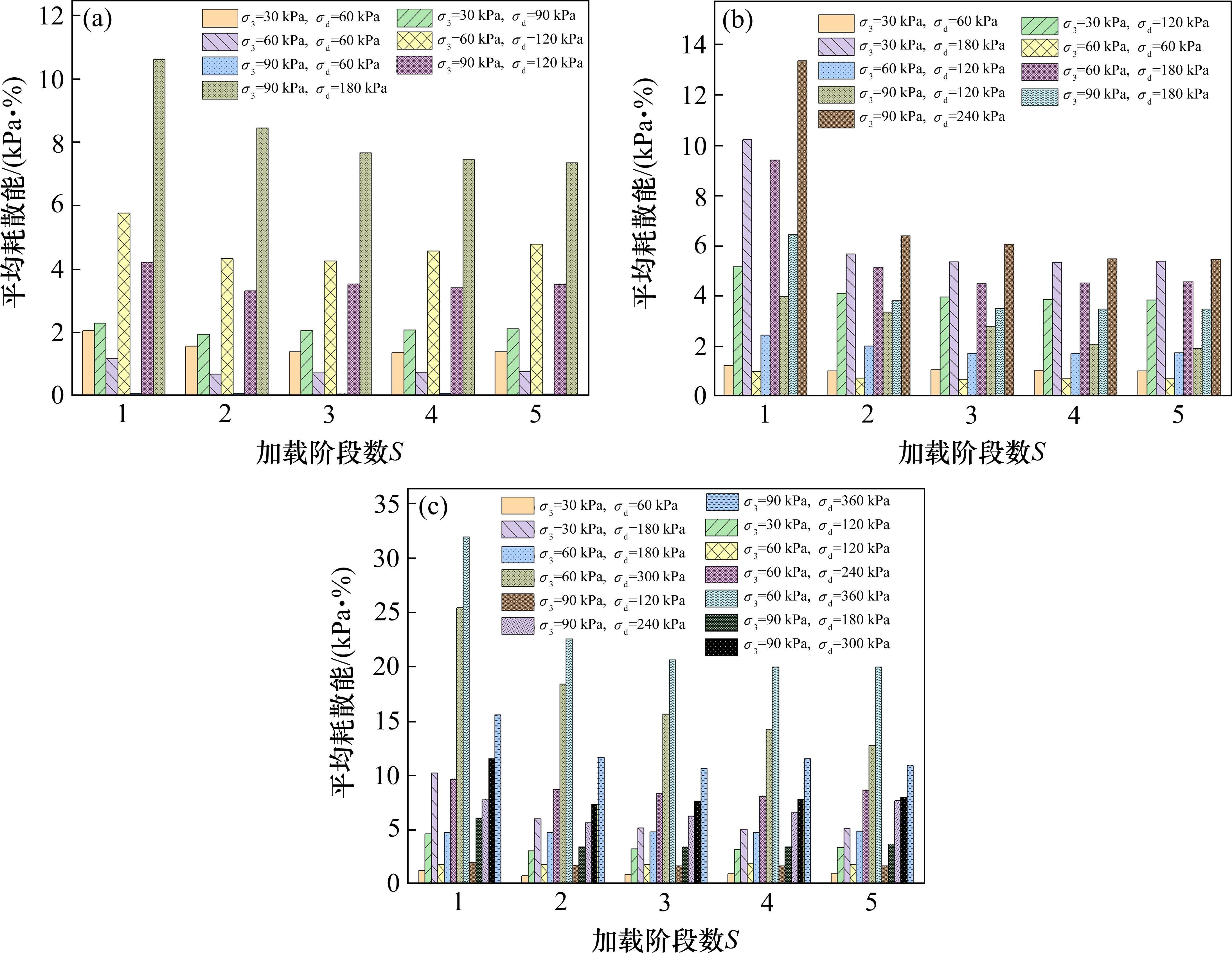
对于未破坏的试样,取各个阶段的平均耗散能来分析试样耗散能随间歇加载阶段的变化情况(如图11)。可以看出,3种含水率状态下试样耗散能从第1阶段到第2阶段有一个非常明显的下降,试样耗散能在经过第1次间歇荷载后,下降幅度分别为10.8%~20.36%、16.73%~52.12%和14.35%~29.36%。而第4加载阶段试样平均耗散能较第3阶段变化幅度分别为-7.28%~2.9%、0.58%~25%、-8.48%~8.89%,降低的幅度大为减小,而且部分工况下的耗散能随着加载阶段的增加而增大。
3.3 含水率对试样耗散能的影响
图12反映粉土试样(没有破坏的试样)在间歇加载条件下第3阶段平均耗散能随含水率的变化情况。从图中可以看出,试样含水率从11.80%增加到15.00%时,平均耗散能值增大幅度为5.93%~64.86%。其中σ3=90 kPa,σd=240 kPa试样第2加载阶段平均耗散能随含水率的增大而增大,第3加载阶段平均耗散能随含水率的增大而减小。而试样含水率从15.00%增加到19.75%时,其平均耗散能值增大幅值为6.11%~118.54%,总的来说,试样耗散能随着含水率的增大而增大。
3.4 围压对试样耗散能的影响
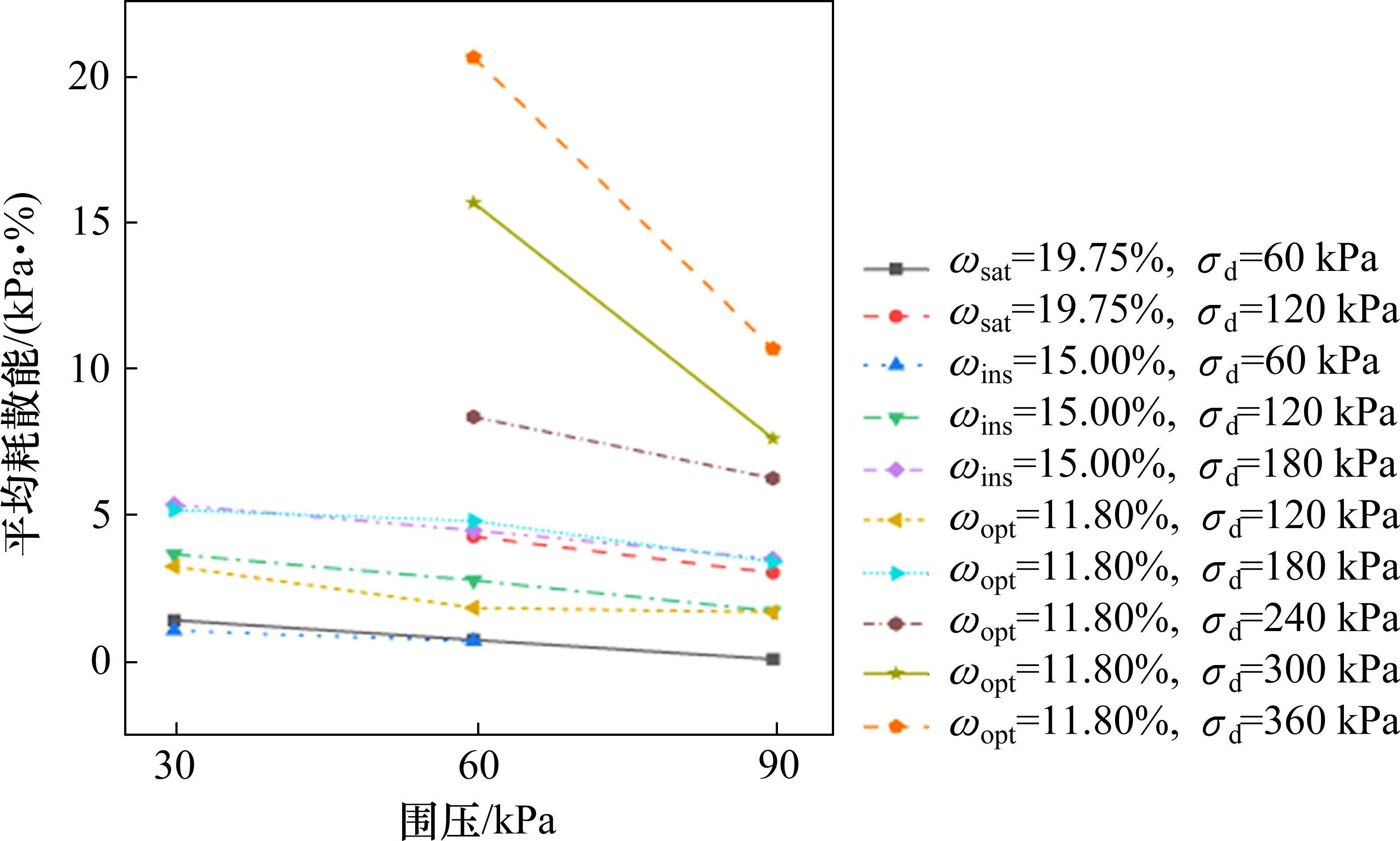
图13反映了未破坏粉土试样在第3加载阶段平均耗散能随围压的变化情况,同一含水率、动应力幅值的粉土试样循环加载时的围压从30 kPa增加到60 kPa时,其平均耗散能变化幅度为-24.3%~-19.96%;围压从60 kPa增加到90 kPa时,平均耗散能变化幅度为-8.11%~48.25%。原因可能是在固结阶段,所施加的围压越大,试样土体颗粒排列更加密实,降低了土体颗粒的可恢复旋转和滑移,因此,在加载过程中损失的能量越少。
3.5 动应力幅值对试样耗散能的影响
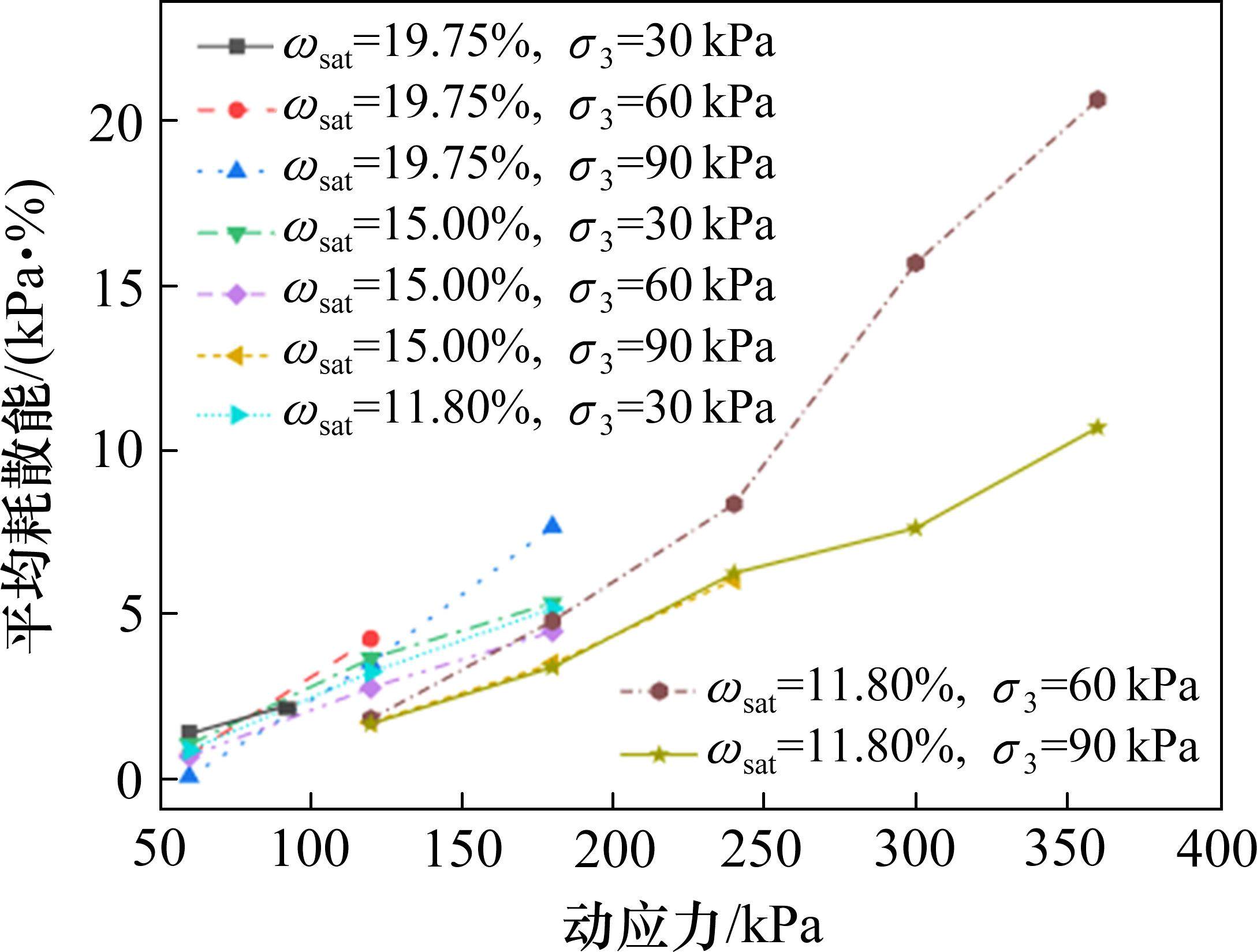
图14反映未破坏粉土试样在第3加载阶段平均耗散能随动应力幅值的变化情况,从图中可以看出,试样平均耗散能随着动应力幅值的增大而增大,动应力幅值从60 kPa增加到360 kPa时,平均耗散能变化幅度平均值为59.62%。
3.6 耗散能状态边界的划分
滞回曲线面积反映土体的能量耗散能力,能为铁路路基土体的动力分析提供参考依据。图15为不同的动应力幅值下试样的耗散能随着振动次数的变化曲线。在循环加载的初步阶段,试样耗散能急速减小,前200次的循环荷载下耗散能的下降值大约占到整个循环荷载过程下降值的70%。随后耗散能变化的幅度逐渐减小,中后期趋于稳定[19]。
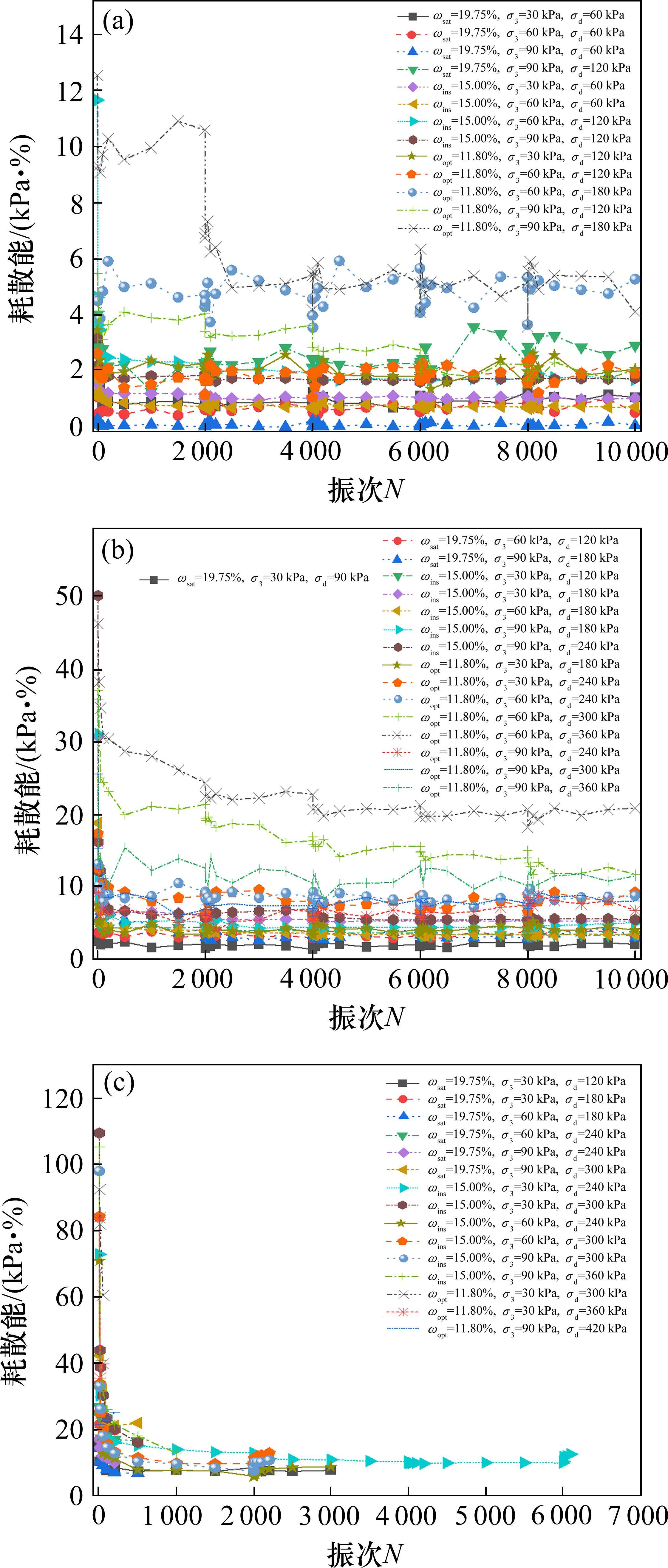
根据聂如松等[20-21]的研究,将间歇荷载作用下试样的累积塑性变形分3种情况:稳定型、临界型和破坏型。对于稳定型试样(图15(a)),在加载的第1阶段,已经进入到稳定状态,其耗散能一直保持一个比较稳定的状态,并且间歇对其造成的影响也比较微弱,说明在动应力较小的时候,土体的能量损耗为一个常量。对于临界型试样(图15(b)),间歇排水对耗散能影响比较突出,在第1阶段结束后,排水后孔隙水压力降低,土体同时也变得更加密实,在第2阶段开始加载时,土体克服阻尼损失的能量变小,耗散能同时也相应减小。对于破坏性试样(图15(c)),在加载前期,试样耗散能先是迅速减小,然后保持一个比较平稳的阶段;在试样破坏的最后阶段,由于土体应变突然增大,动应力克服土体阻尼所损失的能量也呈现出明显的增长趋势。
3.7 以能量耗散的角度来判定路基动力稳定性
路基的长期稳定性是铁路运行的重要安全保障,也是铁路路基设计关注的主要问题。在3.6节中,对试样耗散能状态边界面进行了划分,发现在同一含水率、围压条件下试样耗散能随动应力幅值有着明显的边界面,试样在超出某一动应力幅值后,会在较短振次内发生破坏。根据相对耗散能特征值XL[22]来判定路基的动力稳定性。将破坏型试样的耗散能平均值定义为Xs,即土样在循环动荷载作用下的极限耗散能,试样在进入到稳定阶段后,耗散能也会出现少量的随机性波动。为减小随机性带来的误差,取稳定阶段试样耗散能的平均值作为Xd,
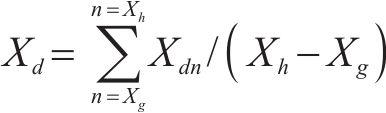
式中:Xg为试样开始稳定时的振次;Xh为试验加载设置的总振次。
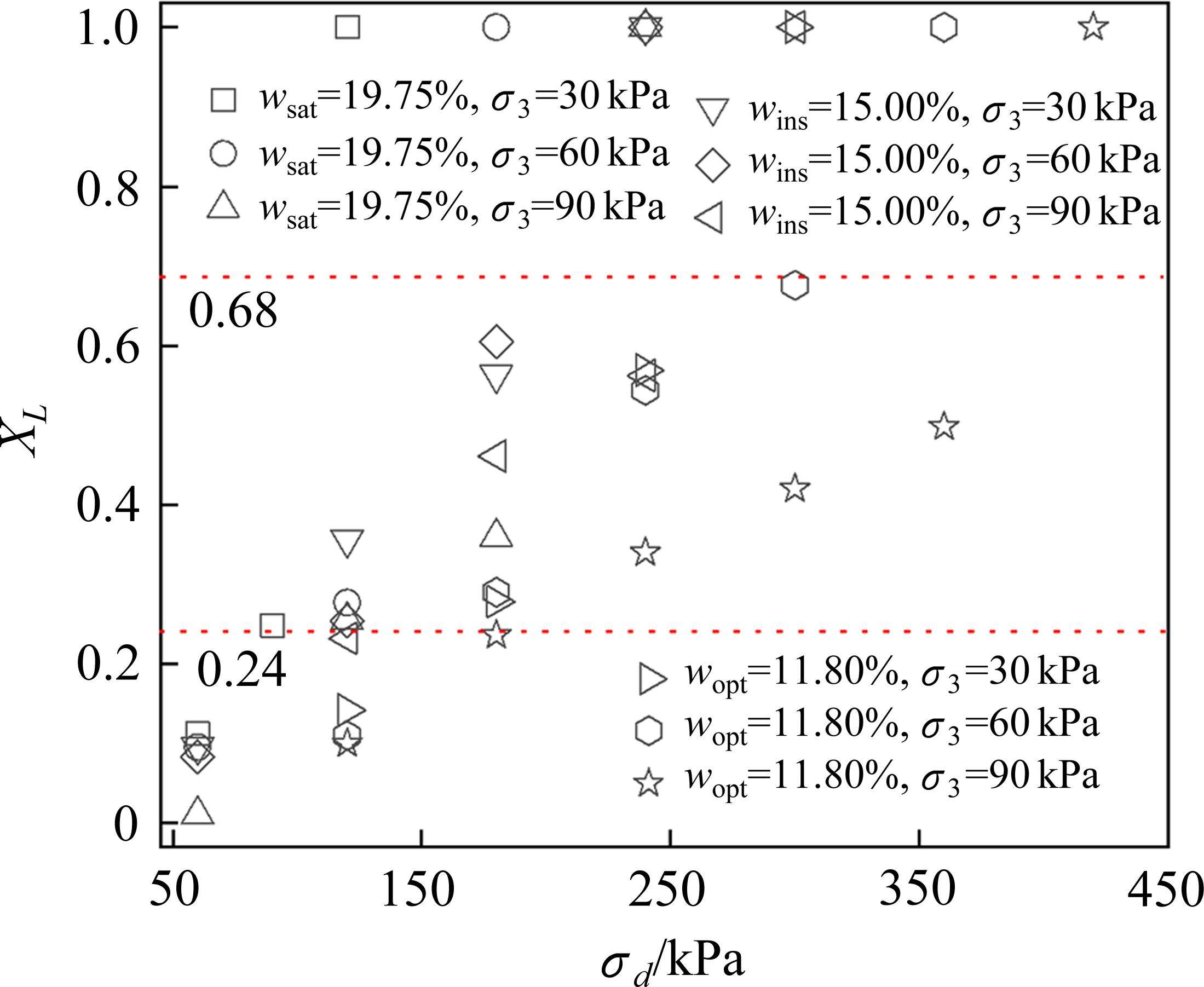
图16反映不同围压、不同含水率下粉土试样相对耗散能特征值XL随动应力的变化规律,称稳定型试样所处的相对耗散能区间为稳定区,临界型试样所处的相对耗散能区间为可接受区,破坏型试样所处的相对耗散能区间为不可接受区。当粉土填料相对耗散能特征值XL<0.24,其处于稳定状态,在重载铁路路基采用细粒土填料进行设计时,应尽量使动应力水平作用下的能量耗散水平处于该区域。当粉土填料相对耗散能特征值0.24<XL<0.68,其处于临界状态,路基稳定性对动应力的变化比较敏感,动应力的微小增加都会导致填料变形处于不稳定状态。路基设计时,应根据路基的设计使用年限和允许变形,结合能态边界面上相应的累积变形和应变速率,确定临界状态是否可接受。当所施加的动应力引起的相对耗散能特征值XL>0.68时,粉土填料处于失稳状态,相对能量水平处于不可接受区,该范围内的填料在试验中经历较少的振次中发生了破坏,在实际运营中可能在较短的年限中产生过大的路基变形,进而影响到实际的安全运行。
4 结论
1) 间歇荷载下试样的每个加载阶段累积塑性应变随着加载阶段数的增加而减小,累积塑性应变速率随之降低。而连续加载下的试样滞回圈在加载初期逐渐致密,随着振次的增加,后期的滞回圈又逐渐疏松。
2) 粉土填料阻尼比随着含水率的增大而增大,荷载间歇效应会减小试样阻尼。粉土填料耗散能随着围压的增大而减小,随着动应力幅值和含水率的增大而增大。
3) 结合试样累积塑性应变研究成果,对试样耗散能边界进行划分,提出从能量耗散的角度判断路基动力稳定性的方法。当相对耗散能特征值低于24%,试样处于动力稳定状态;当相对耗散能特征值位于24%~68%,试样处于临界状态;相对耗散能特征值大于68%时,试样处于失稳状态。研究成果为铁路路基动力稳定性评估与维护提供参考。
聂如松,周徐海,赵春彦等.间歇循环荷载作用下粉土填料阻尼比与耗散能特性试验研究[J].铁道科学与工程学报,2024,21(12):5057-5070.
NIE Rusong,ZHOU Xuhai,ZHAO Chunyan,et al.Experimental study on damping ratio and dissipated energy characteristics of silt under intermittent cyclic loading[J].Journal of Railway Science and Engineering,2024,21(12):5057-5070.

