目前,高铁路基服役期的静动变形安全标准达毫米级,故对表层的填筑质量控制提出更高更严的要求,而路基的填筑质量主要取决于填料的优选和充分合理的压实[1]。因此,路基表层常由具有良好强度、变形和渗透特性的级配碎石压实而成[2]。另外,压实度K是高铁路基压实质量控制的关键指标,是现场干密度与室内试验所得填料最大干密度的比值,因此确定填料压实的最大干密度对路基填筑质量控制具有重要意义。室内平板振动压实试验是与现场碾压机理最相似的压实方法,目前学者大多采用该方法确定填料的最大干密度和最优压实状态[3],选择合理的振动压实参数可以使填料得到充分合理的压实,进而使填料达到最优压实状态。然而,目前对最优振动压实参数的研究较少,难以快速准确地得到最优压实参数。故提出合理有效的振动压实参数确定方法,对实现其智能预测具有重要意义。现有研究表明振动压实参数的选取对粗粒土填料的最优压实状态起到关键的影响作用:王萌等[4-6]通过理论模型与现场试验发现,振动压实频率的改变可以显著影响填料的干密度,进而影响填料的压实质量;彭勃等[7-8]通过试验研究表明,当含水率到达某一值后,填料干密度随着含水率的增加而增加,当含水率偏大将对填料的压实产生不利影响。但已有研究大多基于单个振动压实参数开展试验,而且有关振动压实参数确定方法的研究大多依据压实物理指标干密度开展,较少考虑压实力学指标。因此,提出合理有效的振动压实参数确定方法对路基压实质量控制具有重要意义。在此基础上,谢康等[9]提出基于共振作用下的最优压实参数确定方法,综合压实物理和力学指标得到级配碎石填料最优压实状态下的振动压实参数,其中,最优频率fop和最优含水率wop需要通过室内试验标定得到,故确定fop和wop是设置最优振动压实参数的核心问题。随着智能压实技术的发展,振动压实参数的高精度预测也成为路基智能施工关键的一部分。目前不少学者采用线性回归模型建立fop和wop与填料特征的关系[10],但fop和wop具有复杂的非线性特征,预测结果准确性仍有待商榷。近年来,由于机器学习(Machine Learning, ML)具有强大的非线性映射能力,为振动压实各项参数的非线性预测提供了有效的手段,例如:BP神经网络(BackpropagationNeural Network, BPNN)[11]、支持向量机回归(Support Vector Regression, SVR)[12]、随机森林(Random Forest, RF)[13]。然而,采用基础的ML算法预测振动压实参数,可能存在模型稳定性差、泛化能力低的问题,而AdaBoost集成算法可以重新分配模型训练样本权重进行训练,进而提升模型的预测精度,且具有强大的兼容性[14],故将其与基础的ML模型结合来预测fop和wop理论上是可行的。同时,既有研究仅从预测精度和误差角度对模型进行评估优选[13],当单一评估指标数值相近时难以优选预测模型,因此提出一套多层次的预测性能综合评价方法尤为重要。为解决上述问题,智能快速地得到高铁路基级配碎石填料的最优压实参数,首先,基于共振作用确定振动压实试验的最优压实参数,开展试验研究,并综合级配碎石填料的物理指标干密度ρd和力学指标动刚度Krb确定最优频率fop和最优含水率wop;其次,在试验数据基础上建立级配碎石填料特征与fop和wop的关系,并明确影响fop和wop的主控特征;最后,建立预测fop和wop的PSO-ML-AdaBoost模型,结合三层次预测模型评价体系确定最优预测模型,并基于消融分析进一步验证模型的可靠性。研究成果可为振动碾压过程对高铁级配碎石的压实质量科学调控提供参数依据。
1 级配碎石最优压实参数的确定方法
1.1 共振下振动压实参数确定方法
压实度K(现场干密度与室内干密度的比值)是高铁路基压实质量控制的关键指标,确定填料压实的最大干密度对路基填筑质量控制具有重要意义。现有研究表明振动压实参数的选取对粗粒土填料的干密度起到关键的影响[5],其中,如图1所示,谢康等[9]基于共振作用提出了一种振动压实参数确定方法,为推动振动压实试验参数的标准化提供新的思路。该方法包括以下3点。
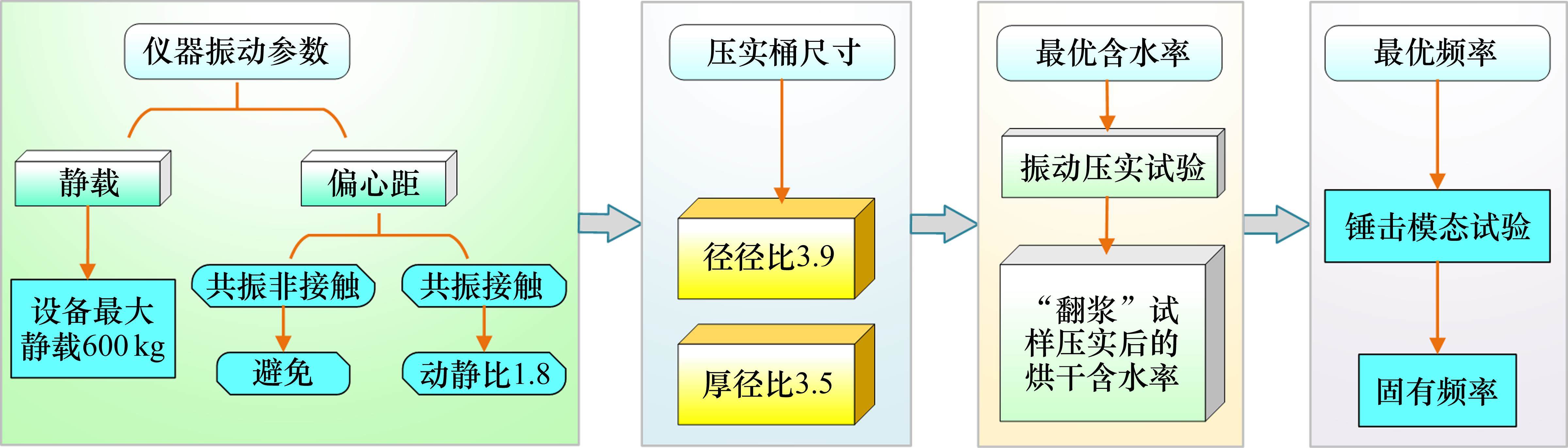
1) 通过调整参振质量Mc、振动频率f和偏心距re这3个振动参数使得激振力F0/Mc<1.9,振动压实仪达到共振状态,此时压实设备工作稳定,颗粒破碎较低,可使填料达到压实状态最优。2) 为避免“尺寸效应”的影响,确定压实筒的尺寸参数:径径比(压实筒内径Dd/dmax)为3.9,厚径比(摊铺厚度H0/dmax)为3.5。3) 通过室内试验标定得到最优含水率wop和最优频率fop。
1.2 振动压实下最优含水率确定原则
现有的研究中均通过重锤击实法得到粗粒土填料的wop,但相关文献研究成果表明[15],将击实法获得的wop运用于振动压实试验,产生“冒浆”和“起皮”现象,导致试样难以成型。为揭示振动压实前后粗粒土填料含水率的差异,如图2所示,通过“烘干法”测试出振动压实后的含水率,得到2种结果:1) 当含水率较低时,振动压实前后的试样含水率一致;2) 当含水率大于某一值后,压实过程中产生“翻浆”,部分水流失,使得压实后含水率降低,但压实后的含水率基本稳定,因此,将稳定后的含水率定义为临界含水率wv。

为验证wv为试样振动压实试验wop的正确性,开展不同含水率试样的振动压实试验,从填料压实状态的力学指标动刚度Krb层面分析不同含水率对压实特性的影响。结果表明,含水率为wv时填料压实的力学性能最优。故取wv为级配碎石填料振动压实试验的wop,可使填料压实状态最优。
1.3 振动压实下最优振动频率确定原则
现有研究基于“试错法”确定粗粒土填料的fop,选取不同频率反复开展振动压实试验,浪费大量试验资源。依据文献研究[16],填料的固有频率f0和fop存在密切联系,并且f0可以通过锤击模态试验得到,试验步骤如图3所示:
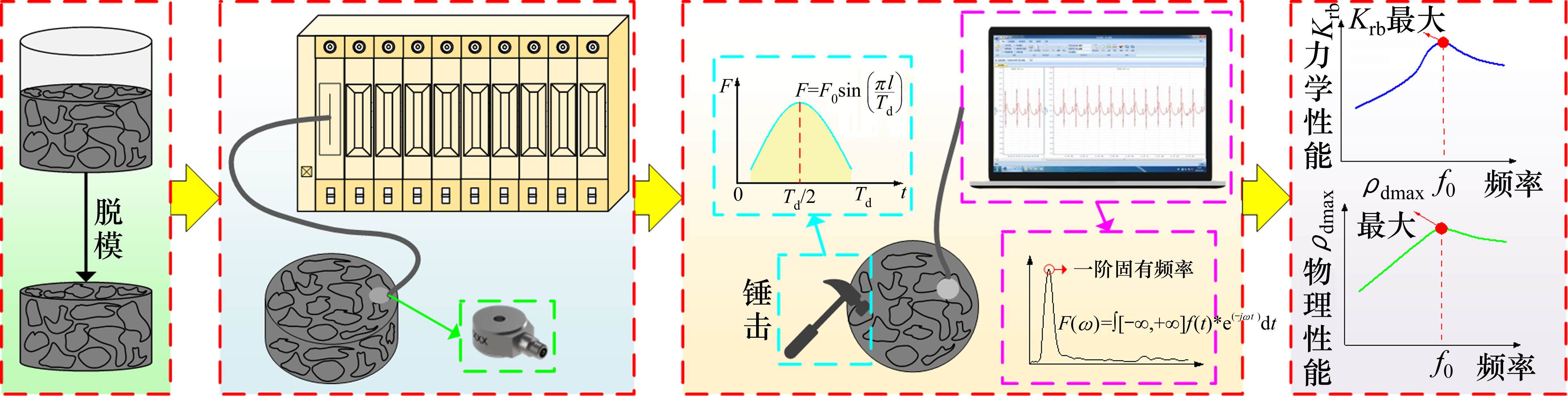
1) 使用脱模机获取完整的压实后级配碎石填料;2) 将三向加速度传感器安装在填料顶部,并将其与DH5922D动态信号采集仪连接;3) 使用橡皮锤锤击填料顶部,并实时记录填料在锤击过程中的加速度信号,确定填料不同压实度下稳定f0作为fop;4) 为验证f0为试样振动压实试验fop的正确性,开展不同频率的振动压实试验,从最大干密度ρdmax和动刚度Krb层面分析频率对压实特性的影响,结果表明,频率为f0时填料压实的物理和力学性能均最优。故取f0为级配碎石填料振动压实试验的fop,可使填料压实状态最优。
2 基于PSO-ML-AdaBoost模型的fop和wop预测
2.1 基于GRA的fop和wop主控特征分析
根据《铁路工程土工试验规程》(TB 10102―2013)深入探究路基填料性能与最佳压实参数之间的内在联系,主要包括Cu、Cc、dmax 3种典型粒径(d≤0.5 mm、d=0.5~1.7 mm、d≥1.7 mm),洛杉矶磨耗(Laa)、粗骨料(d≥1.7 mm)细长比(Ei)、粗骨料(d≥1.7 mm)吸水率(Wac)、细集料(d≤1.7mm)吸水率(Waf)和细集料(d≤0.5 mm)塑液限(Pl、Ll)12个特征指标。其中,Cu、Cc、dmax这3种典型粒径共同描述填料的级配,计算过程繁琐且对级配描述都较为简略,故参考朱俊高等[17]提出的级配方程,如式(1)所示,采用级配参数b,m和dmax表征级配。最后,如图4所示,基于《公路工程集料试验规程》[18](JTG E42―2005)对上述路基填料性能进行测试。
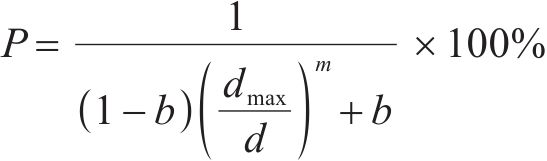
式中:b、m和dmax为级配特征参数;d为自变量,代表填料粒径。
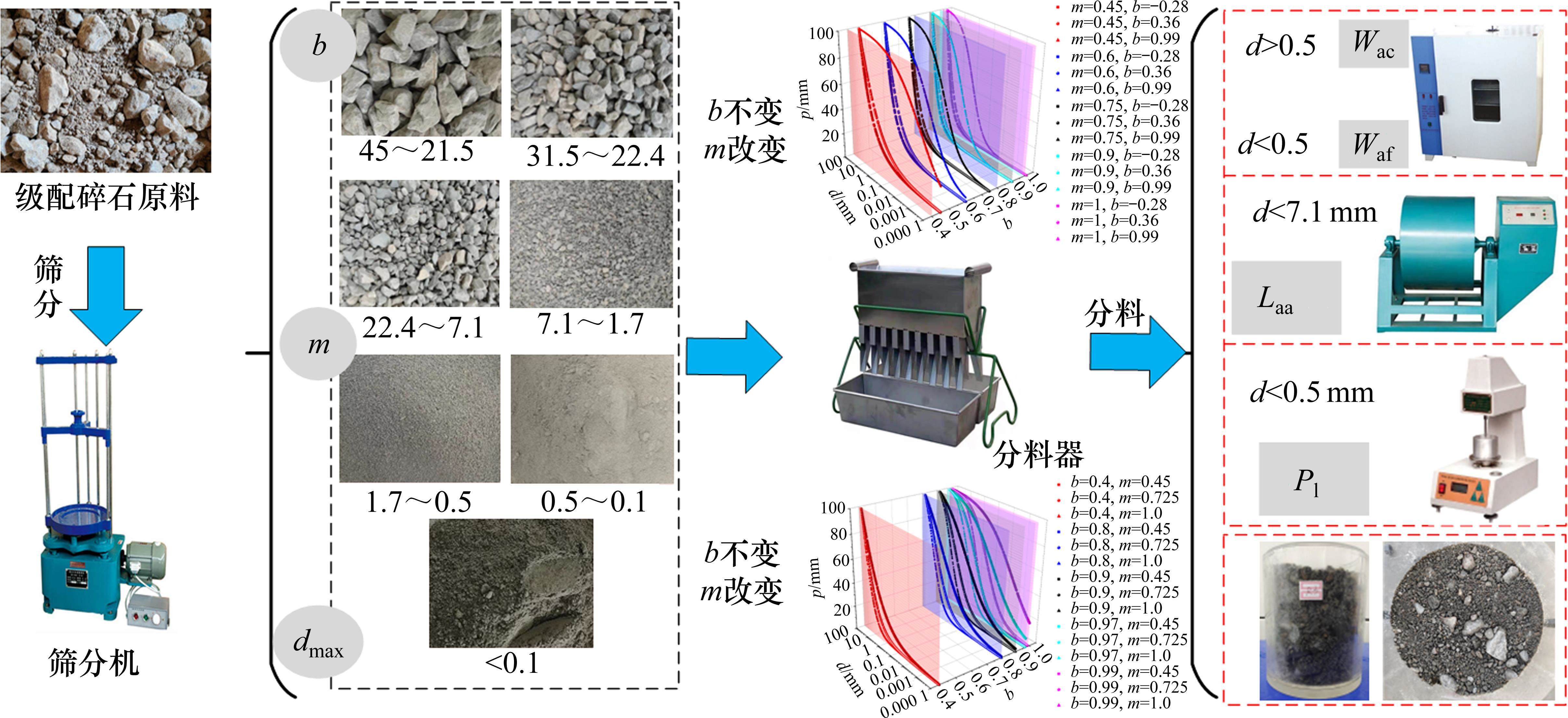
目前对上述路基填料性能与fop和wop的关系尚不清晰。若将影响fop和wop的众多参数特征输入到预测模型中,可能会掩盖主控特征参数的作用,并增加模型训练难度[12]。因此,有必要筛选出fop和wop的主控特征作为预测模型的输入特征,提高模型预测性能,进一步提高预测精度。灰色关联度分析(Grey relational analysis, GRA)[19]是通过数据序列曲线几何形状的相似程度来判断序列联系是否紧密的一种相关性分析方法,其紧密程度用关联度R量化,相应序列的关联度越大,表明序列曲线越接近。若R大于0.4则特征呈强相关,该特征可取为主控特征。因此,可基于GRA确定影响fop和wop的主控特征,计算流程如图5所示。
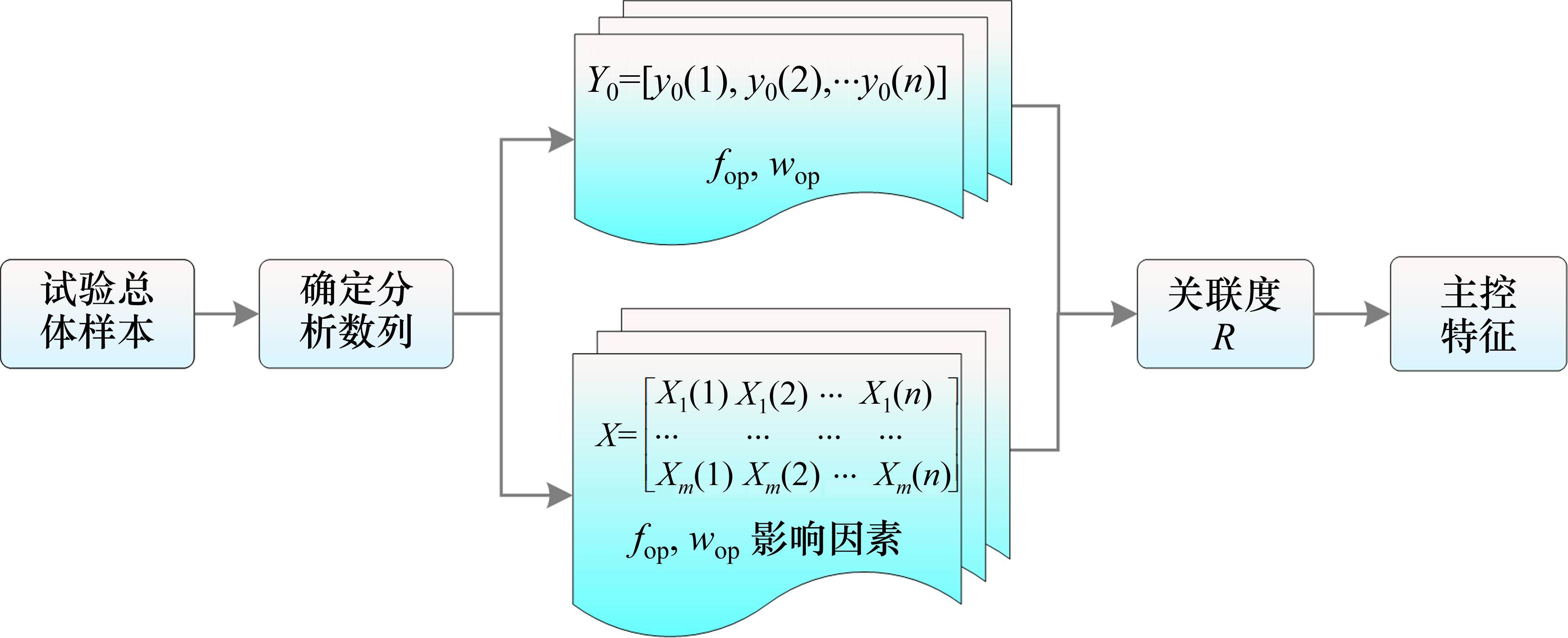
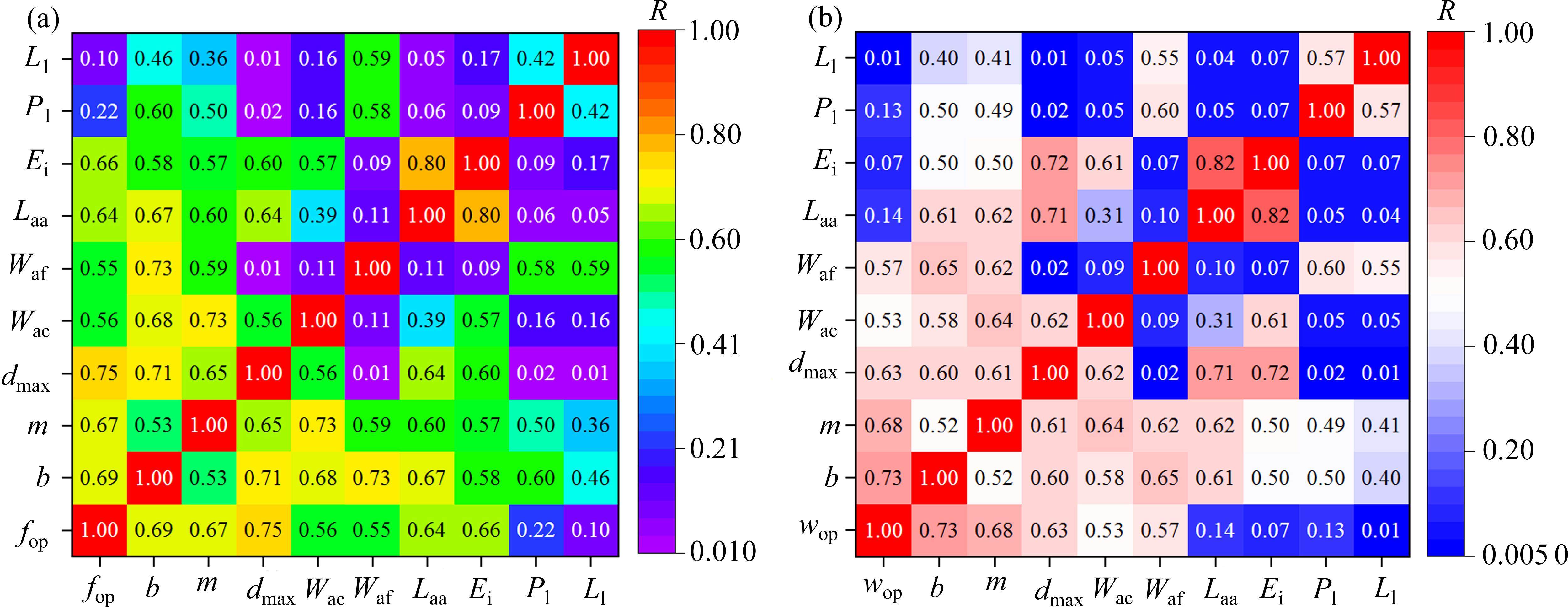
基于GRA算法确定fop和wop主控特征的结果如图6所示。由图6(a)可知,基于GRA算法计算各特征参数与fop之间的关联度R,依次为:dmax(0.75)、b(0.69)、m(0.67)、Ei(0.66)、Laa(0.64)、Wac(0.56)、Waf(0.55)、Pl(0.22)、Ll(0.10)。R>0.4时认为该特征为强相关特征,因此,与fop呈强相关的特征为:dmax、b、m、Ei、Laa、Wac和Waf。同样可以得到wop的主控特征为b、m、dmax、Waf和Wac。
2.2 基于主控特征的数据集建立
基于GRA对fop和wop的主控特征分析结果发现:级配碎石的级配特征(dmax、b和m)、形状特征(Ei)、破碎特征(Laa)、吸水率(Wac、Waf)是影响fop和wop的主控特征。根据fop和wop的7个主控特征参数和300多组不同类型级配碎石填料的测试数据,进一步构建预测模型数据集D={(xi,yi)}
2.3 PSO-ML-AdaBoost模型建立
如图8所示,采用BPNN[11]、SVR[12]和RF[13]这3种典型的ML预测算法,开展fop和wop的预估分析。其中,BPNN具有强大的逼近能力、自适应性强以及并行处理能力,SVR具有强大的处理非线性关系以及适应小样本数据的能力,RF具有强大的鲁棒性以及高效处理不平衡数据集的能力,均广泛应用于各种不同的工程类型预测。以BPNN为例建立PSO-ML-AdaBoost模型。
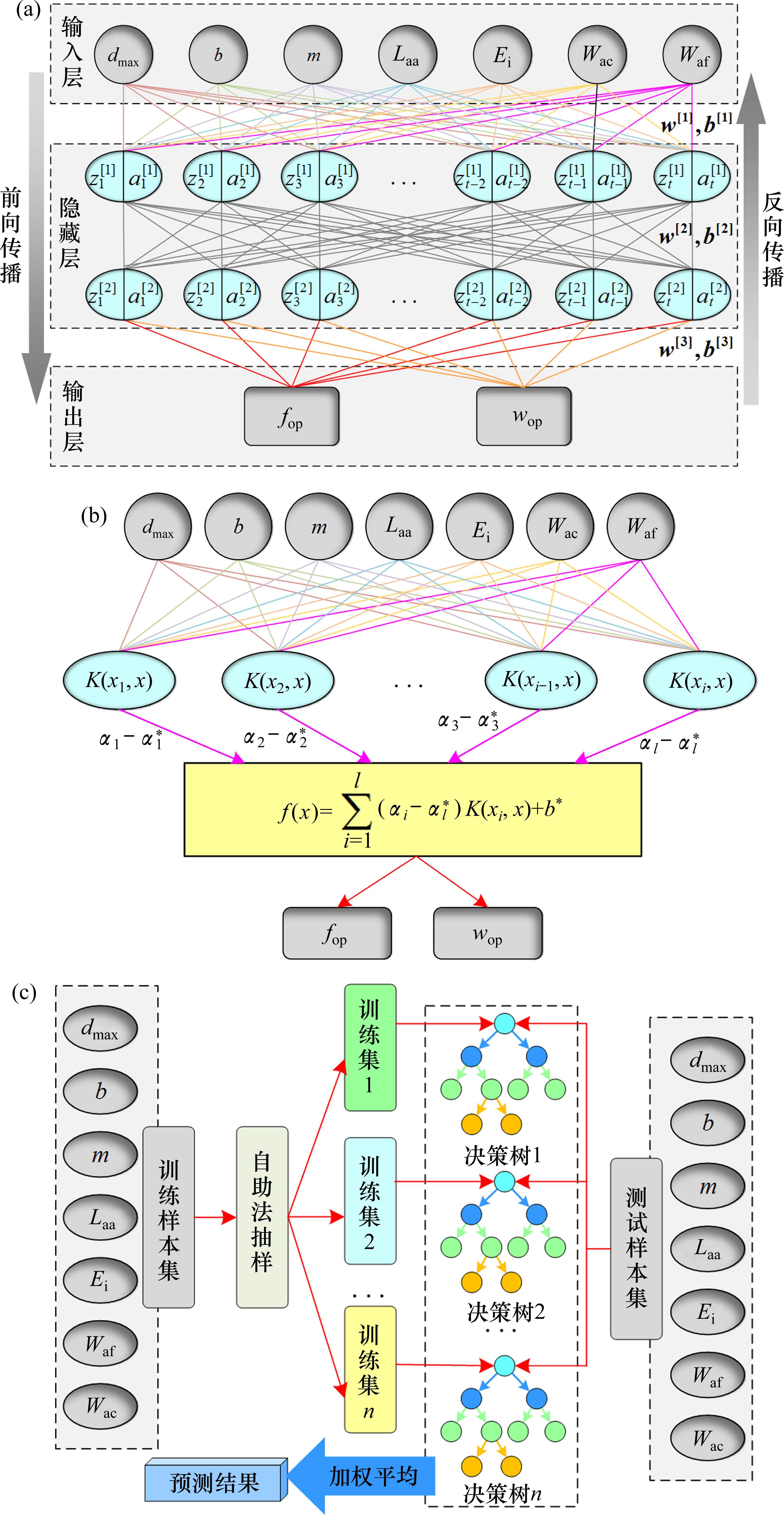
BPNN的计算流程如图8(a)所示,分为前向传播和反向传播2个阶段,由输入层、隐藏层和输出层组成。在BPNN学习过程中,误差通过网络反向传播,以调整连接和阈值的权重,从而使输出层中的均方误差(MSE)之和最小化[11],如式(2)所示:
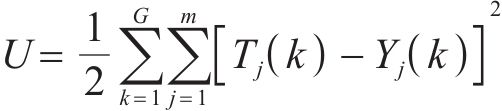
式中:U是均方误差之和;m是输出节点的数量;G是训练样本的数量;Tj(k)是期望输出;Yj(k)是实际输出。
但传统的BPNN自身收敛速度慢、稳定性差以及极易陷入局部极小点。故引入粒子群优化算法(Particle Swarm Optimiztion, PSO)[12]优化BPNN的初始网络连接权值和网络节点阈值,如图9所示形成PSO-BPNN模型,进而不断提高BPNN的性能,减少网络迭代次数。优化过程中,以平均绝对误差Mae作为目标函数计算粒子适应度(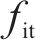
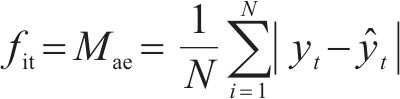
式中: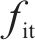
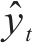
然而PSO-BPNN模型仍存在过拟合以及初始权重和参数选择的不稳定性问题,需要进一步提高预测模型的泛化和稳定性性能。因此,如图10所示,引入AdaBoost集成算法[14]对PSO-BPNN模型进行优化。所建立的PSO-BPNN-AdaBoost模型,融合了PSO全局优化和BPNN的局部寻优的特点,同时AdaBoost强预测器通过给弱预测器赋予不同的权重,实现了AdaBoost强预测器“优中选优”的目的,最大程度提高了预测精度。同理,采用相同流程分别建立PSO-SVR-AdaBoost、PSO-RF-AdaBoost模型。
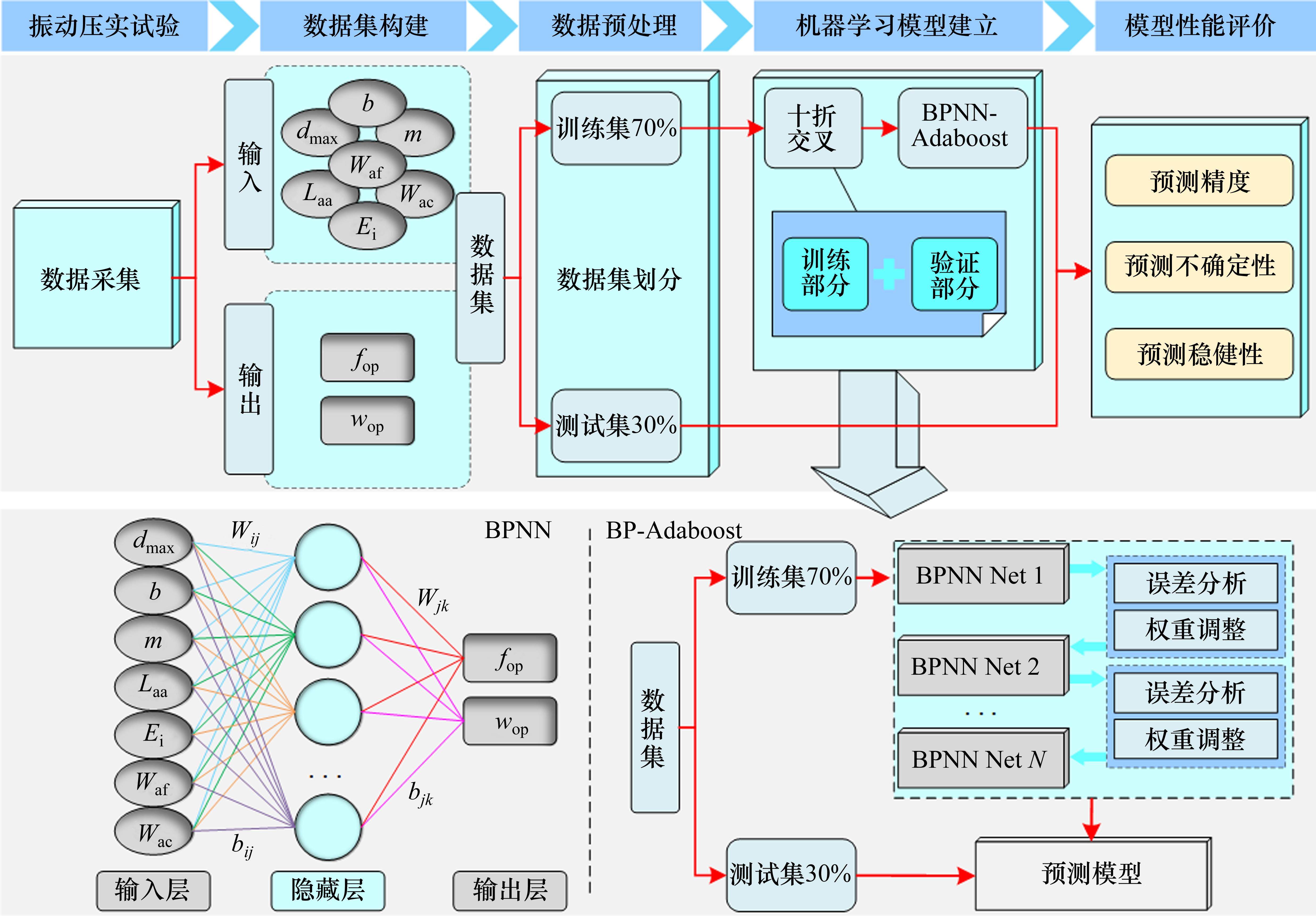
2.4 最优预测模型确定方法
采用上述PSO-BPNN-AdaBoost、PSO-SVR-AdaBoost和PSO-RF-AdaBoost模型,开展fop和wop的预估分析。基于PSO-ML-AdaBoost模型的fop和wop预测模型建立流程如图11所示,主要分为数据集的划分、基于训练集的PSO-ML-AdaBoost模型建立和基于测试集的三层次PSO-ML-AdaBoost模型优选3部分。
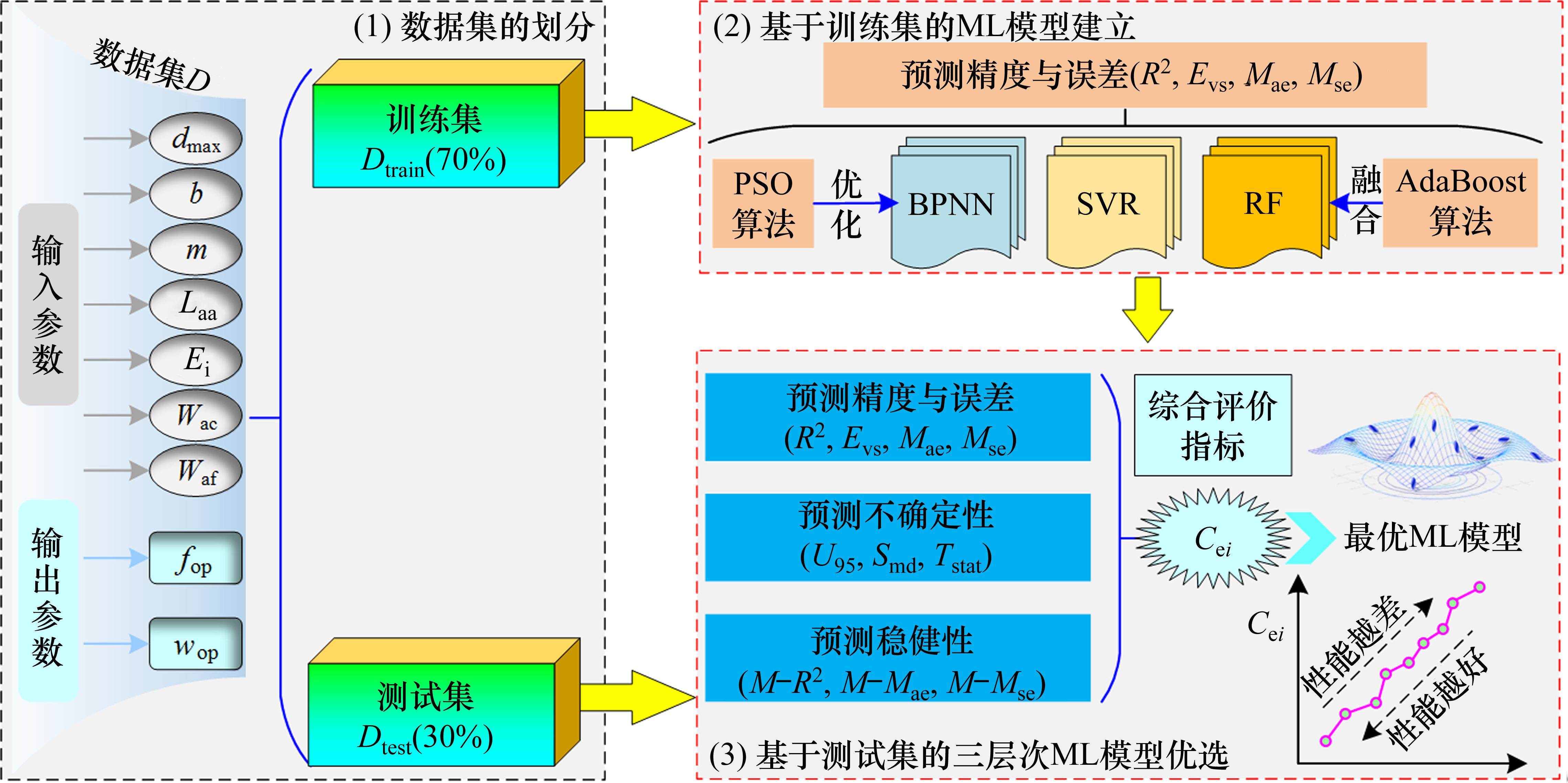
步骤1:数据集的划分
将数据集D按照7∶3的比例划分为训练集和测试集,其中训练集用于建立PSO-ML-AdaBoost模型,测试集用于测试PSO-ML-AdaBoost模型的性能。
步骤2:基于训练集的PSO-ML-AdaBoost模型建立
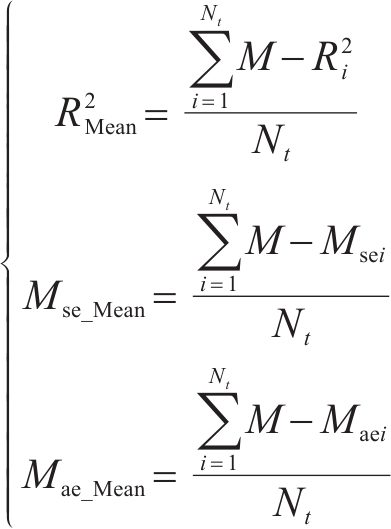
采用上述3种典型PSO-ML-AdaBoost算法预测fop和wop。运算结束后将训练集输入融合模型,并采用拟合优度R2、解释模型方差得分Evs、均方误差Mse和平均绝对误差Mae来评估各模型的拟合能力,各指标具体解释见表1。
| 名称 | 计算公式 | 特征 |
|---|---|---|
| 拟合优度(R2) | 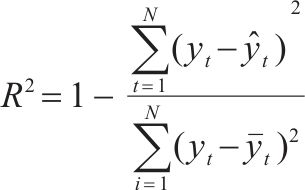 | 范围在0~1之间,值越接近1精度越高 |
| 解释模型方差得分(Evs) | 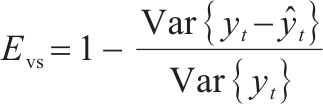 | 范围在0~1之间,值越接近1精度越高 |
| 平均绝对误差(Mae) | 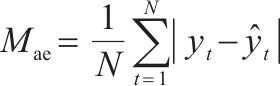 | 大于0,值越接近0误差越小 |
| 均方误差(Mse) | 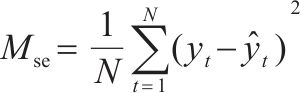 | 大于0,值越接近0误差越小 |
步骤3:基于测试集的三层次PSO-ML-AdaBoost模型优选
各PSO-ML-AdaBoost模型建立后,输入测试集进行预测fop和wop。为衡量预测模型的泛化能力,建立三层次预测模型评价体系,并进一步基于加权分析法,提出综合评价指标(Comprehensive evaluation indicators, Cei)以优选最佳PSO-ML-AdaBoost模型,具体为:
1) 预测精度与误差评估:相关评价指标同上述评价训练集上拟合效果的4个指标。
2) 预测结果不确定性分析:基于扩展不确定性U95、t统计检验Tstat和标准化平均差Smd这3个指标,从预测结果偏离中心程度、预测结果的显著性等角度对各PSO-ML-AdaBoost模型预测结果的不确定性进行分析,各指标具体解释见表2。
| 名称 | 计算公式 | 特征 |
|---|---|---|
| 扩展不确定性(U95) | 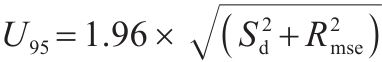 | 大于0,值越接近0不确定性越小 |
| t统计检验(Tstat) | 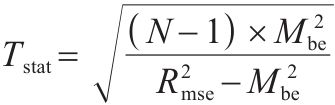 | 大于0,值越接近0预测模型的显著性越小 |
| 标准化平均差(Smd) | 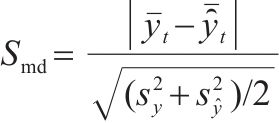 | 大于0,越接近0预测模型的偏差越小 |
3) 预测模型稳健性分析:基于蒙特卡罗方法[19],PSO-ML-AdaBoost模型输入数据的随机波动可以在输出解上传播,输出解的概率分布定量分析可表征PSO-ML-AdaBoost模型的稳健性。为更加全面地比较各PSO-ML-AdaBoost模型的性能,采用蒙特卡罗方法模拟R2、Mae和Mse的概率分布,分析PSO-ML-AdaBoost模型的稳健性,并采用R2、Mae和Mse概率分布的均值和区间宽度进行统计分析,相关公式见式(4)和式(5):
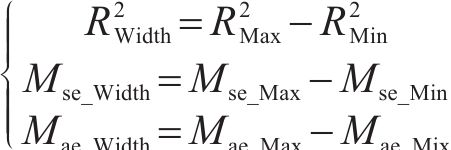
式中: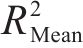
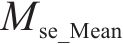
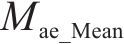
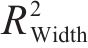
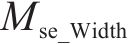
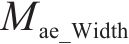
4) 预测性能综合评价:为综合以上3个层次的评价结果,提出一个综合评价指标Cei。该指标综合考虑了3个相互独立层次的主要评价信息,从预测精度与误差评估层次选择Mse和Mae这2个指标,从预测结果不确定性分析层次选择U95和Smd这2个指标,从预测模型稳健性分析层次选择Mse和Mae的均值(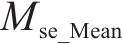
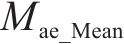
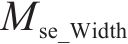
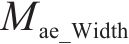
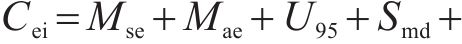
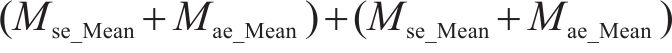
3 结果分析
3.1 模型评估结果
3.1.1 预测精度误差层次
从预测精度与误差角度评价PSO-ML-AdaBoost模型在训练集和测试集上的性能如表3所示。在训练集上,各模型的R2、Evs均高于0.9,展示了很好的拟合精度。进一步分析可知,训练集上的预测结果仅表示PSO-ML-AdaBoost模型的建模过程中的能力,尚不能展示模型的泛化能力,应利用测试集上的预测性能指标来判定。在测试集上,整体而言各模型的预测性能较好,其中PSO-BPNN-AdaBoost的预测精度指标R2、Evs为0.979 3/0.967 7、0.979 7/0.967 9,在3种预测模型中最大,误差指标Mae和Mse在3种预测模型中最小。故基于第1层次,PSO-BPNN-AdaBoost模型展示了最高的预测精度和最低的预测误差。
| 数据集 | 模型种类 | R2(fop/wop) | Evs(fop/wop) | Mae(fop/wop) | Mse(fop/wop) |
|---|---|---|---|---|---|
| 训练集 | PSO-BPNN-AdaBoost | 0.980 1/0.973 7 | 0.981 3/0.973 8 | 0.703 4/0.178 5 | 0.998 3/0.053 8 |
| PSO-SVR-AdaBoost | 0.954 5/0.941 0 | 0.956 5/0.941 8 | 1.106 0/0.262 5 | 2.047 0/0.120 7 | |
| PSO-RF-AdaBoost | 0.937 4/0.905 3 | 0.941 1/0.906 2 | 1.319 2/0.360 1 | 2.816 3/0.193 5 | |
| 测试集 | PSO-BPNN-AdaBoost | 0.979 3/0.967 7 | 0.979 7/0.967 9 | 0.657 5/0.216 5 | 0.965 0/0.081 7 |
| PSO-SVR-AdaBoost | 0.943 1/0.920 8 | 0.950 0/0.920 8 | 1.114 8/0.326 6 | 2.647 0/0.200 1 | |
| PSO-RF-AdaBoost | 0.921 7/0.886 2 | 0.926 0/0.886 4 | 1.397 1/0.428 9 | 3.645 8/0.287 4 |
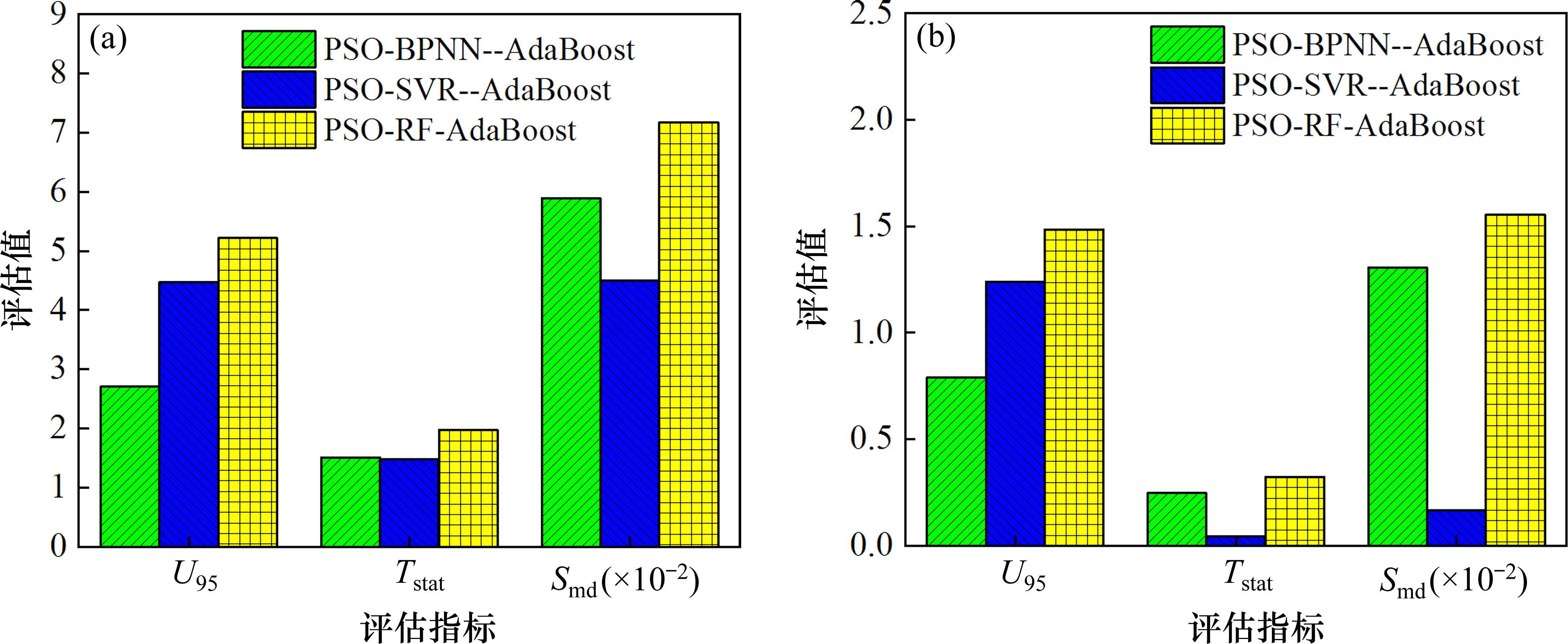
3.1.2 预测不确定性层次
图12展示了预测模型的不确定性分析结果。由图12可知,3种预测模型在不确定性层面呈现出不同的趋势,在fop和wop测试集上,PSO-BPNN-AdaBoost模型的U95指标均较优,展示了较低的不确定性。而PSO-SVR-AdaBoost模型的Tstat指标和Smd指标较优,远低于其他2种模型,说明PSO-SVR-AdaBoost具有较低的显著性和偏差性。故基于第2层次,无法判定3种模型的预测性能。
3.1.3 预测稳健性层次
设置蒙特卡罗模拟次数Nt为300[19],运算得到结果如图13和图14所示。由图13(a)可知,在fop测试集上,PSO-BPNN-AdaBoost模型的R2均值最大,达到了0.954 8。由图13(b)可知,PSO-SVR-AdaBoost模型的Mse分布区间宽度最窄,仅为3.016 7。由图13(c)可知,Mae分布结果跟均方误差Mse基本一致。综合上述分析结果,PSO-BPNN-AdaBoost模型和PSO-SVR-AdaBoost模型的稳健性能突出。前者主要体现在各项指标的均值上,后者主要体现在各项指标的分布区间宽度上。类似地,在wop的测试集上,3种预测模型的预测稳健性呈现相同规律。故基于第3层次,仍无法综合判定3种模型的预测性能。
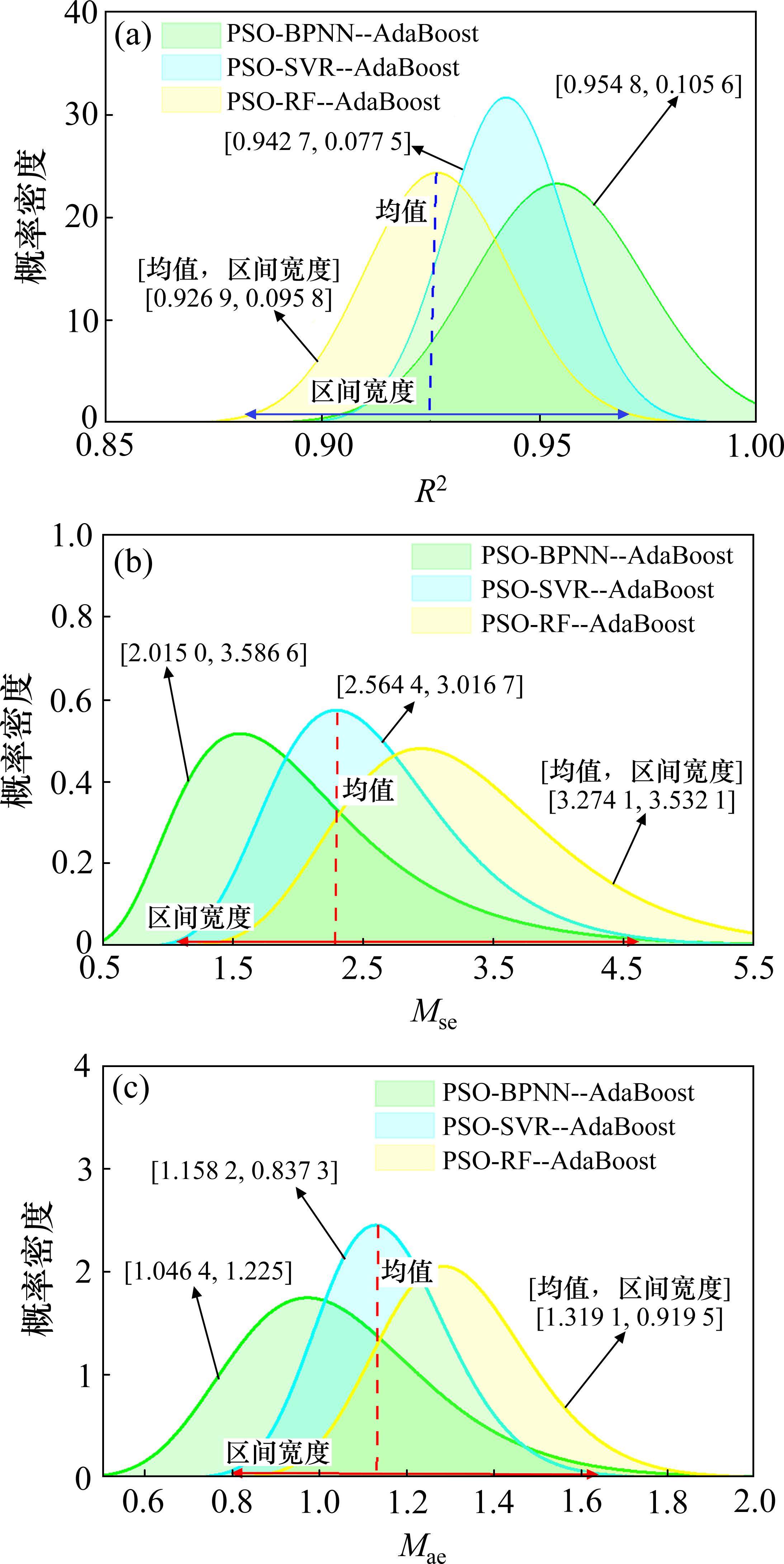
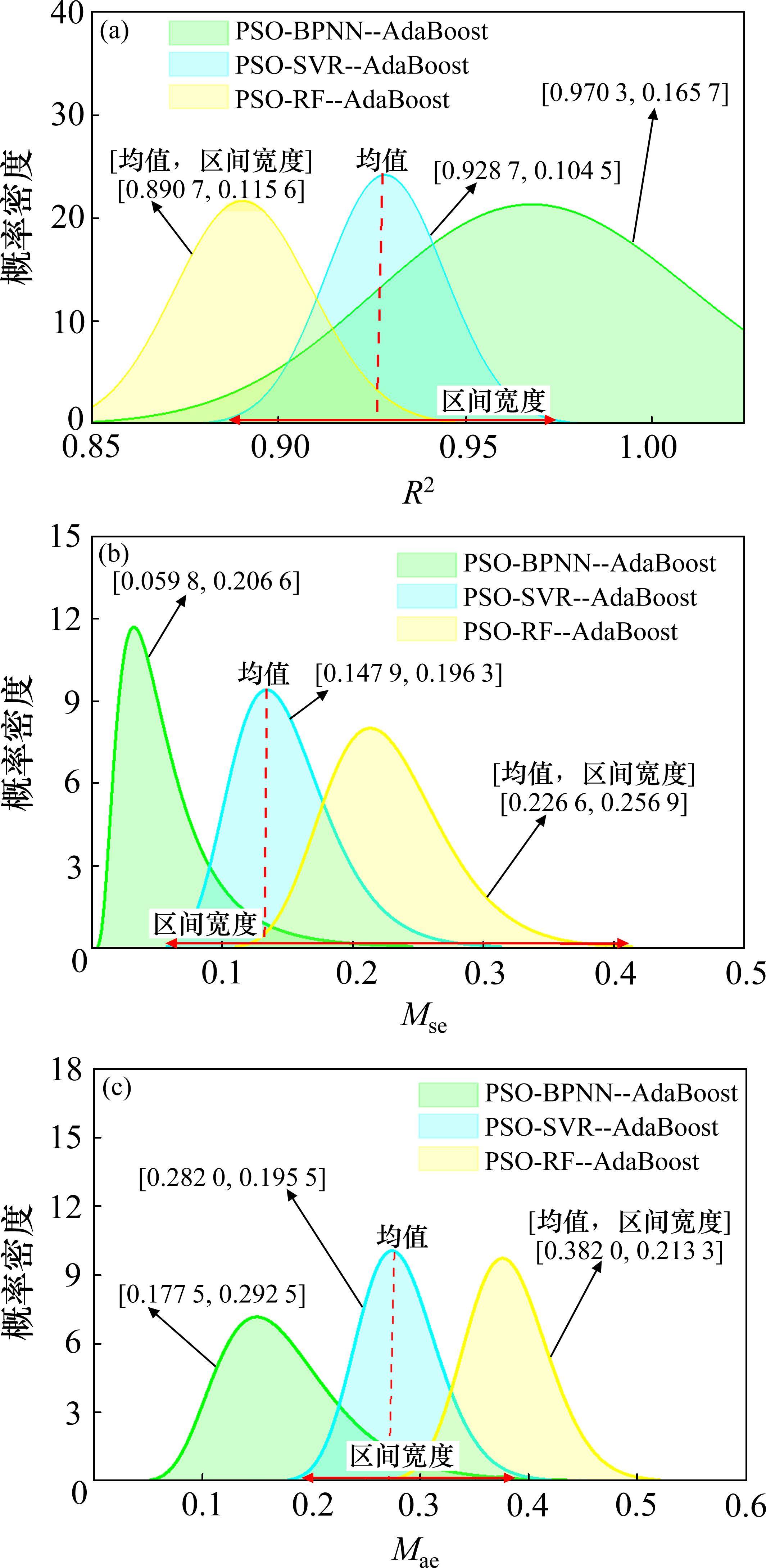
综合上述3个层次在测试集上的评价结果,计算各模型的综合评价指标Cei(fop/wop)分别为:PSO-BPNN-AdaBoost模型(12.264 5/1.838 2)<PSO-SVR-AdaBoost模型(16.228 4/2.589 9)<PSO-BPNN-AdaBoost(19.377 1/3.295 9)。最终,确定PSO-BPNN-AdaBoost模型为最优预测模型,在后续的模型消融分析中,以该模型为对象进行可解释性分析。
3.2 最优预测模型验证
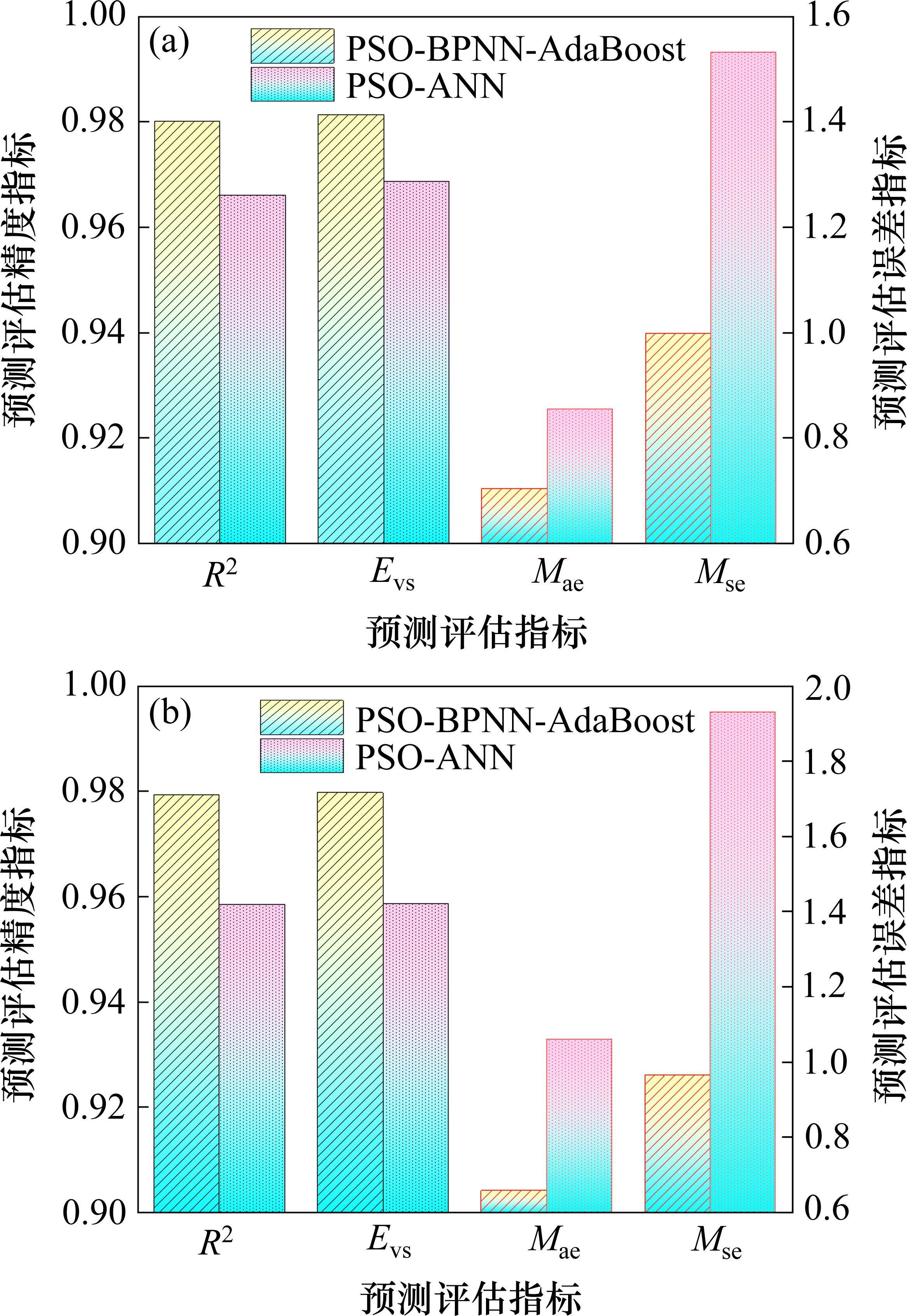
为验证PSO-BPNN-AdaBoost模型预测结果的精确性,以fop预测为例,从预测精度与误差角度对PSO-BPNN-AdaBoost模型的fop预测结果与XIAO等[20]通过PSO-ANN模型的fop预测结果进行评价并对比分析,得到结果如图15所示。由图15(a)可知,在训练集上,PSO-BPNN-AdaBoost和PSO-ANN模型的R2、Evs均高于0.9,展示了很好的拟合精度,但PSO-BPNN-AdaBoost模型的误差指标Mae和Mse明显低于PSO-ANN模型,表明了PSO-BPNN-AdaBoost模型在预测精度方面的优越性。由图15(b)可知,在测试集上,PSO-BPNN-AdaBoost模型对于R2、Evs分别为0.979 3、0.979 7,而PSO-ANN模型均小于0.96。同时,PSO-BPNN-AdaBoost模型的误差指标Mae和Mse的值分别为0.657 5、0.965,远低于PSO-ANN模型,进一步验证了PSO-BPNN-AdaBoost模型预测结果的高精确性和可靠性,并表明了AdaBoost算法与ML模型融合的可行性和必要性。
3.3 最优预测模型消融分析
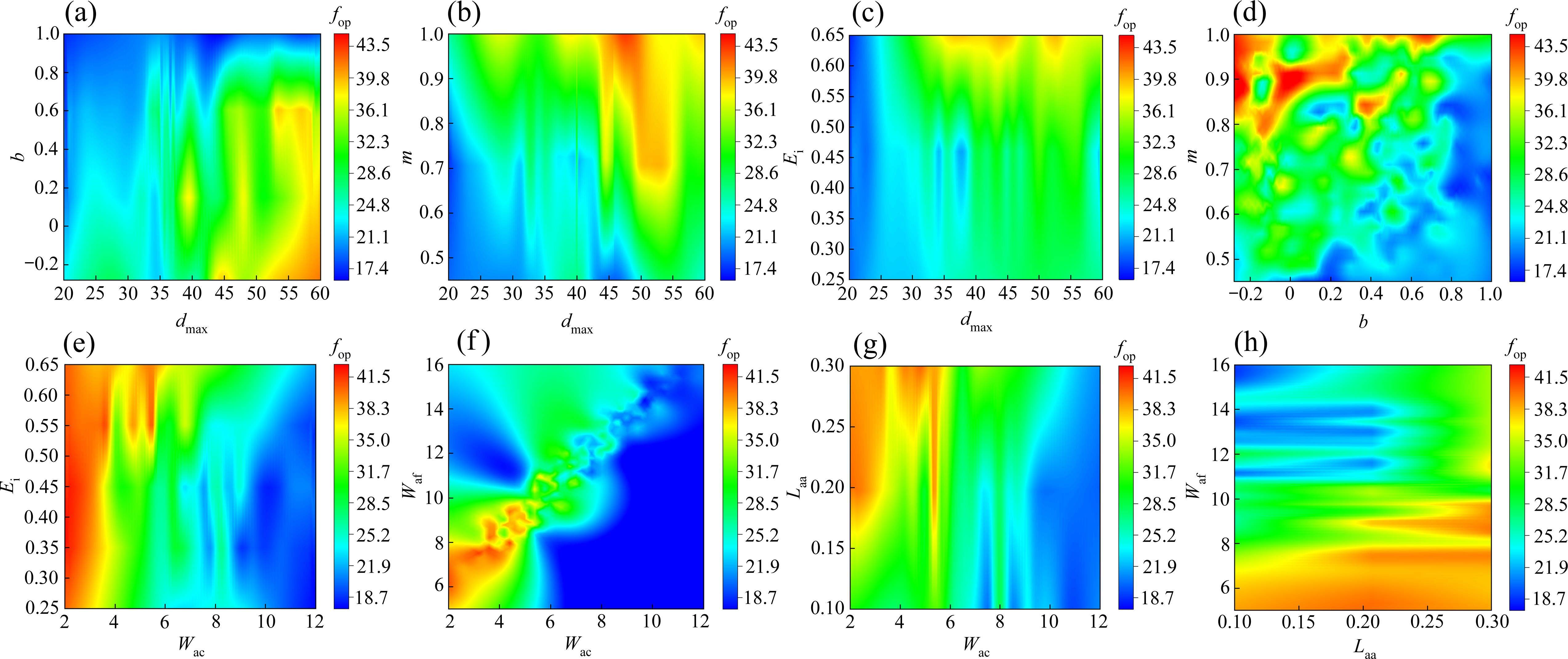
机器学习消融分析可用于理解和评估模型,旨在揭示模型的不同输入参数对预测模型整体性能的贡献[21]。消融分析主要包括:选择消融的参数、建立基准模型、重新训练模型、评估性能、重复试验以及解释结果。分别在输入参数中逐渐消去主控特征参数,重新训练模型,得到fop和wop预测的评估结果如图16所示。
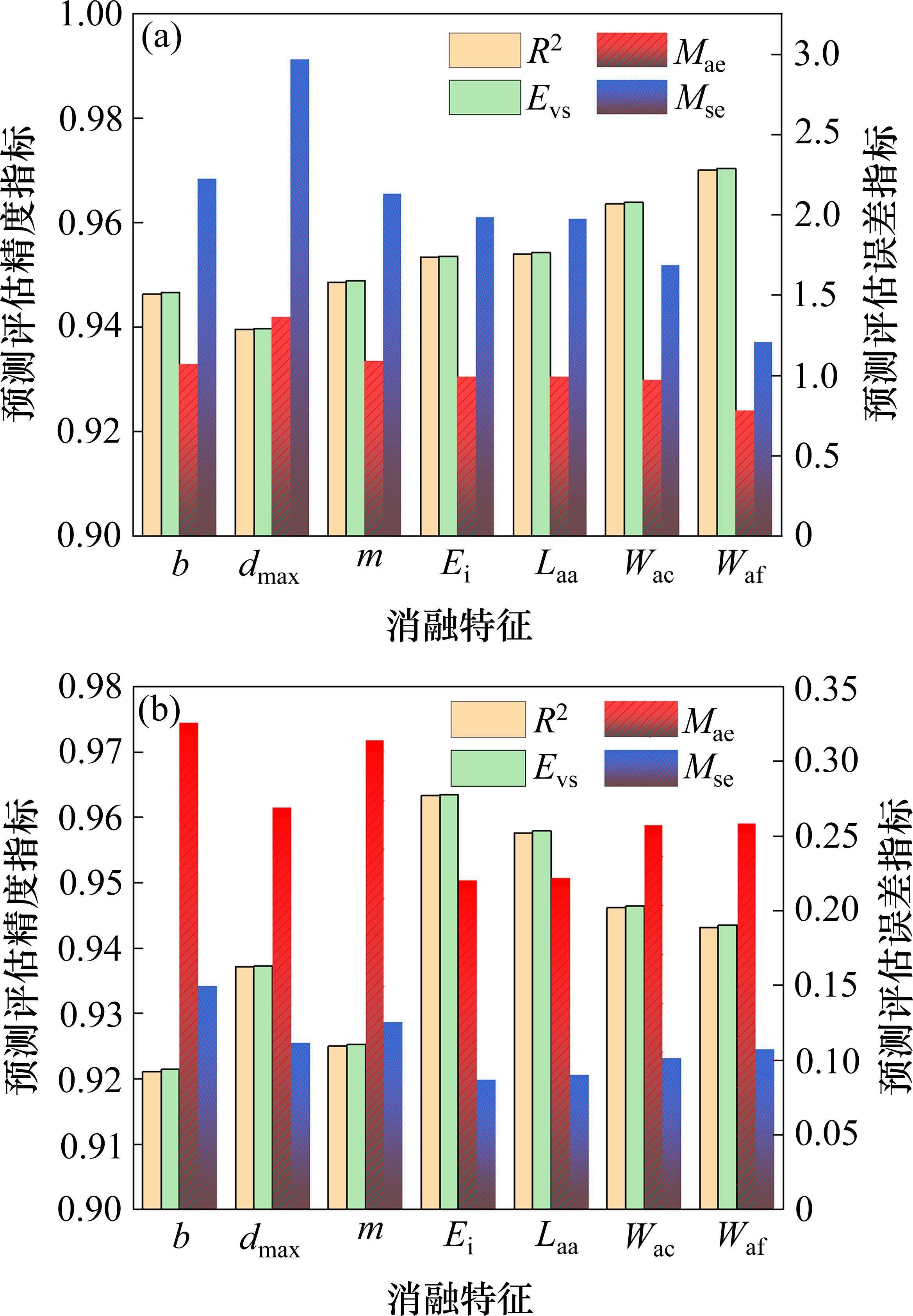
由图16(a)可知,在预测fop过程中,消融特征对PSO-BPNN-AdaBoost的影响程度排序如下:dmax>b>m>Ei>Laa>Wac>Waf,与上述主控输入参数与fop的关联程度保持一致,进一步说明了模型预测的结果可靠性。由图16(b)可知,在预测wop过程中,消融特征对PSO-BPNN-AdaBoost的影响程度排序如下:b>m>dmax>Waf>Wac>Laa>Ei,类似的,也可以说明wop模型预测结果的可靠性。同时,发现级配特征参数dmax、b、m对fop和wop预测结果影响最大,在室内外压实试验中,对不同级配类型填料需重点关注。
综合最优预测模型消融分析结果,可提升模型的可理解性,并证明该模型的预测结果是合理、可靠的。在实际应用中,只需获得现场粗粒土填料的主控特征参数,将其作为模型的输入特征,通过模型智能输出填料的fop和wop,并应用于室内振动压实试验中获得粗粒土填料的最大干密度,从而实现现场路基压实质量的评估。该方法不仅适用于级配碎石填料,也可应用于多种粗粒土填料,如对我国西南地区广泛分布的红层软岩填料同样适用。
4 结论
1) 振动压实中,取最优含水率为临界含水率,最优振动频率为填料的固有频率,可获得级配碎石填料压实状态最优的试样。
2) 基于灰色关联度分析算法得到影响fop和wop的主控特征为最大粒径dmax,级配参数b、m,粗骨料细长比Ei,洛杉矶磨耗Laa,吸水率Wac、Waf这7个特征,并优选其作为后续预测模型的输入特征。
3) 综合测试集的三层次ML预测模型优选结果,得到PSO-BPNN-Adaboost模型的综合评价指标Cei(fop/wop)值为12.264 5/1.838 2,低于PSO-SVR-AdaBoost模型(16.228 4/2.589 9)和PSO-RF-AdaBoost模型(19.377 1/3.295 9),确定PSO-BPNN-Adaboost模型为最优预测模型。
4) 基于消融分析发现,PSO-BPNN-Adaboost模型的输入参数对于fop和wop预测结果的影响程度分别为:dmax>b>m>Ei>Laa>Wac>Waf和b>m>dmax>Waf>Wac>Laa>Ei,与灰色关联度分析算法所得结果相一致,进一步说明了最优预测模型预测结果的可靠性。
陈晓斌,郝哲睿,谢康等.基于PSO-ML-AdaBoost模型的级配碎石最优压实参数智能预测研究[J].铁道科学与工程学报,2024,21(12):5042-5056.
CHEN Xiaobin,HAO Zherui,XIE Kang,et al.Research on intelligent prediction of optimal compaction parameters for graded gravel based on PSO-ML-AdaBoost model[J].Journal of Railway Science and Engineering,2024,21(12):5042-5056.

