随着“CR450”科技创新工程的推进[1],高速铁路建设向更高速度迈进,对路基的结构强度和稳定性要求也更为严苛。高铁基床表层作为承受列车动力作用的关键部位,其压实质量控制不足易引发运营期间路基产生一系列病害[2],严重威胁高铁运营安全[3]。因此,高铁路基压实质量控制是保障其长期服役性能的关键。压实度K是高铁路基压实质量的主要控制指标[4],基于不确定性理论实现路基全断面压实度快速可靠的评估,对提高高速铁路路基服役性能具有重要指导意义。压实度K由现场干密度ρd与室内最大干密度ρdmax比值得到,快速准确地确定ρdmax对于路基压实质量的评估至关重要。目前,学者大多采用与现场碾压机理最相似的室内平板振动压实试验确定填料ρdmax[5],其中振动压实时间是确定ρdmax的重要因素。王萌等[6-8]通过试验、数学模型确定ρdmax的最佳振动压实时间,但仍没有达成共识,且均未考虑压实过程中填料的力学性能变化。因此,有必要结合填料的力学指标确定最佳振动压实时间从而得到ρdmax。同时,仅通过室内振动压实试验确定ρdmax的方法仍存在效率低下的问题。近年来,机器学习(Machine Learning,ML)强大的非线性映射能力为振动压实各项参数的非线性预测提供了有效的手段,例如:XIAO等[9]采用人工神经网络(Artificial Neural Network,ANN)算法预测振动压实的最优频率;BENBOURAS等[10]利用随机森林(Random Forest,RF)、支持向量回归(Support Vector Regression,SVR)等多种ML算法预测振动压实参数。上述研究均基于ML算法对振动压实参数进行预测分析,但基础ML算法的稳健性和泛化能力可能得不到有效保障。陈晓斌等[11]提出PSO-ML-AdaBoost(PBA)模型对振动压实最优含水率wop和最优频率fop进行预测,较好地完善了基础ML算法的不足。同时,填料的ρdmax预测与wop、fop预测同属于数据驱动型问题,理论上PBA模型同样适用于振动压实中填料ρdmax的预测。然而,PBA模型只能提供ρdmax的点预测结果,不能有效量化预测过程中误差引起的结果不确定性,导致基于有误差的ρdmax预测结果得出的压实度评估结果与实际情况存在偏差。随着人们对预测模型不确定性的日益关注,通过构造预测区间来量化点预测中的不确定性的区间预测方法在多个领域得到了成功的应用。WANG等[12]基于高斯过程回归(Gaussian Process Regression,GPR)方法预测股价区间;LEE等[13]通过Bayesian提高了传感器预测不确定性的可靠性。Bootstrap方法[14]是一种基于重采样的非参数统计方法,其优点是只依赖于原始的观测数据。考虑到Bootstrap方法的独特优势,可用于振动压实中有限数据的统计分布建模。因此,引入Bootstrap方法修正PBA模型,通过区间形式量化ρdmax预测值的不确定性,对于实现路基压实度的智能可靠评估尤为重要。为解决上述问题,实现高速铁路路基压实质量快速可靠的评价。首先,建立PSO-BPNN-AdaBoost(PBA)模型,通过ρdmax的主控特征(料源参数):级配参数b和m、填料最大粒径dmax、洛杉矶磨耗LAA、粗骨料(d≥1.7 mm)细长比EI、粗骨料(d≥1.7 mm)吸水率Wac、细集料(d≤1.7 mm)吸水率Waf预测最大干密度ρdmax;最后,基于现场试坑试验和克里金插值(Kriging)算法实现路基全断面压实度区间评估,并将该方法应用于西南地区某站场路基施工最优摊铺厚度的确定。研究成果可为高铁级配碎石的振动压实质量快速可靠地评估提供理论依据。
1 路基全断面压实度区间评估方法
1.1 基于ML的最大干密度预测模型
1.1.1 基于动刚度确定级配碎石最大干密度
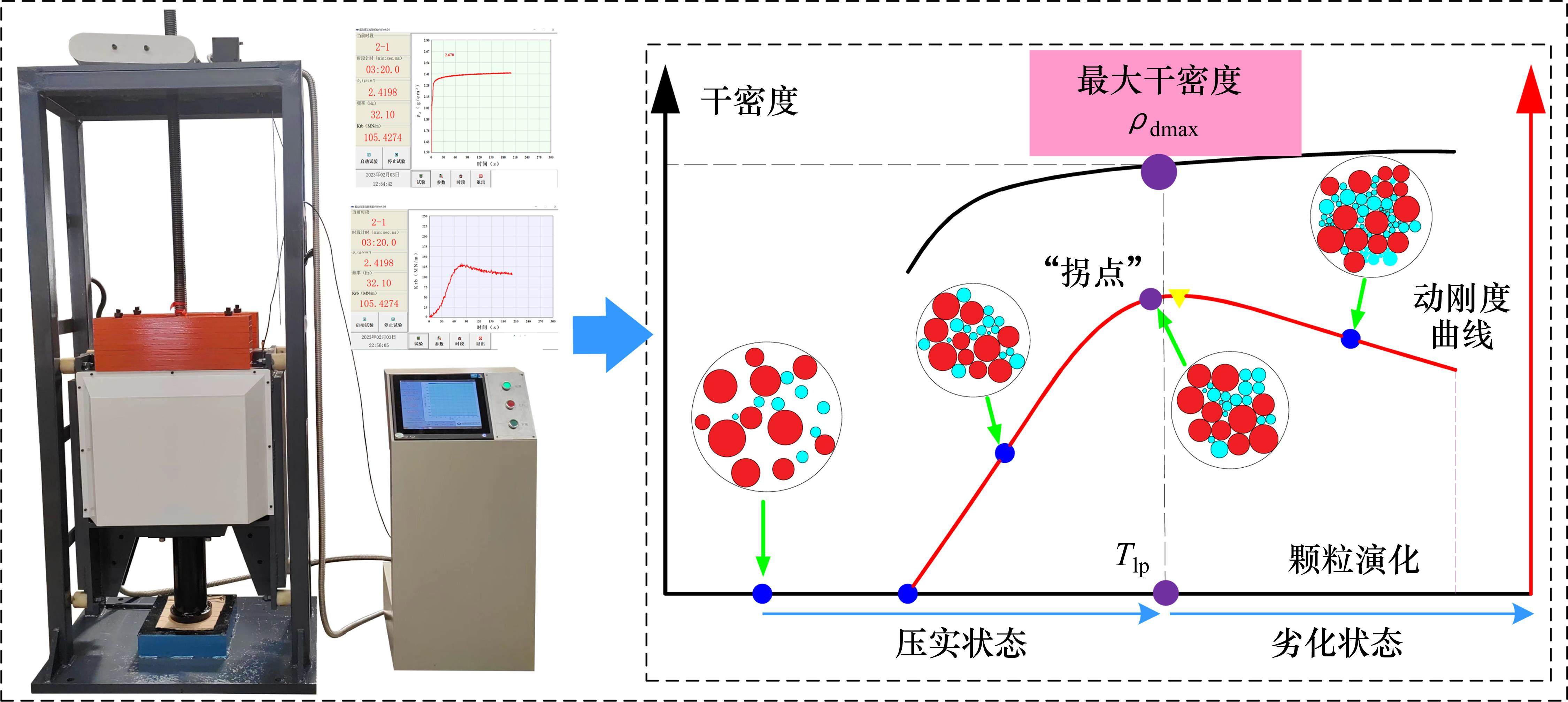
现有研究通过确定填料的最佳振动压实时间来确定填料的最大干密度ρdmax,缺乏在力学性能层面上评价路基填料压实质量的指标,XIE等[15]针对高铁路基粗粒土填料室内振动压实试验,提出了一种基于动刚度Krb曲线“拐点”确定ρdmax的新方法。如图1所示,XIE等[15]通过自研设备开展级配碎石振动压实试验,得到不同级配的级配碎石填料物理指标ρd与力学指标Krb随时间的演化曲线,ρd曲线呈现出“迅速增加-缓慢增加”的趋势,Krb曲线呈现出“迅速增加-缓慢减小”的趋势,即Krb曲线存在“拐点”,将其对应的振动时间定义为Tlp,Tlp对应的干密度为ρdmax。
1.1.2 基于PBA模型预测最大干密度
陈晓斌等[11]研究表明PSO-BPNN-AdaBoost(PBA)模型适用于振动压实中最优含水率wop和最优频率fop的预测问题。其核心思想是通过PSO算法优化BPNN的初始网络连接权值和网络节点阈值,改善传统BPNN算法自身收敛速度慢、稳定性差以及极易陷入局部极小点的问题;并引入AdaBoost算法实现预测器“优中选优”的目的,最大程度提高了模型的预测精度,解决了PSO-BPNN模型仍存的过拟合以及初始权重和参数选择的不稳定性问题。类似的,级配碎石填料的ρdmax预测与wop、fop预测同属于数据驱动型问题,因此同样可以采用PBA模型预测ρdmax。具体流程主要是数据集的建立与划分、基于训练集的PBA模型建立和基于测试集的PBA模型精度评价。
步骤1:基于ρdmax主控特征的数据集建立与划分
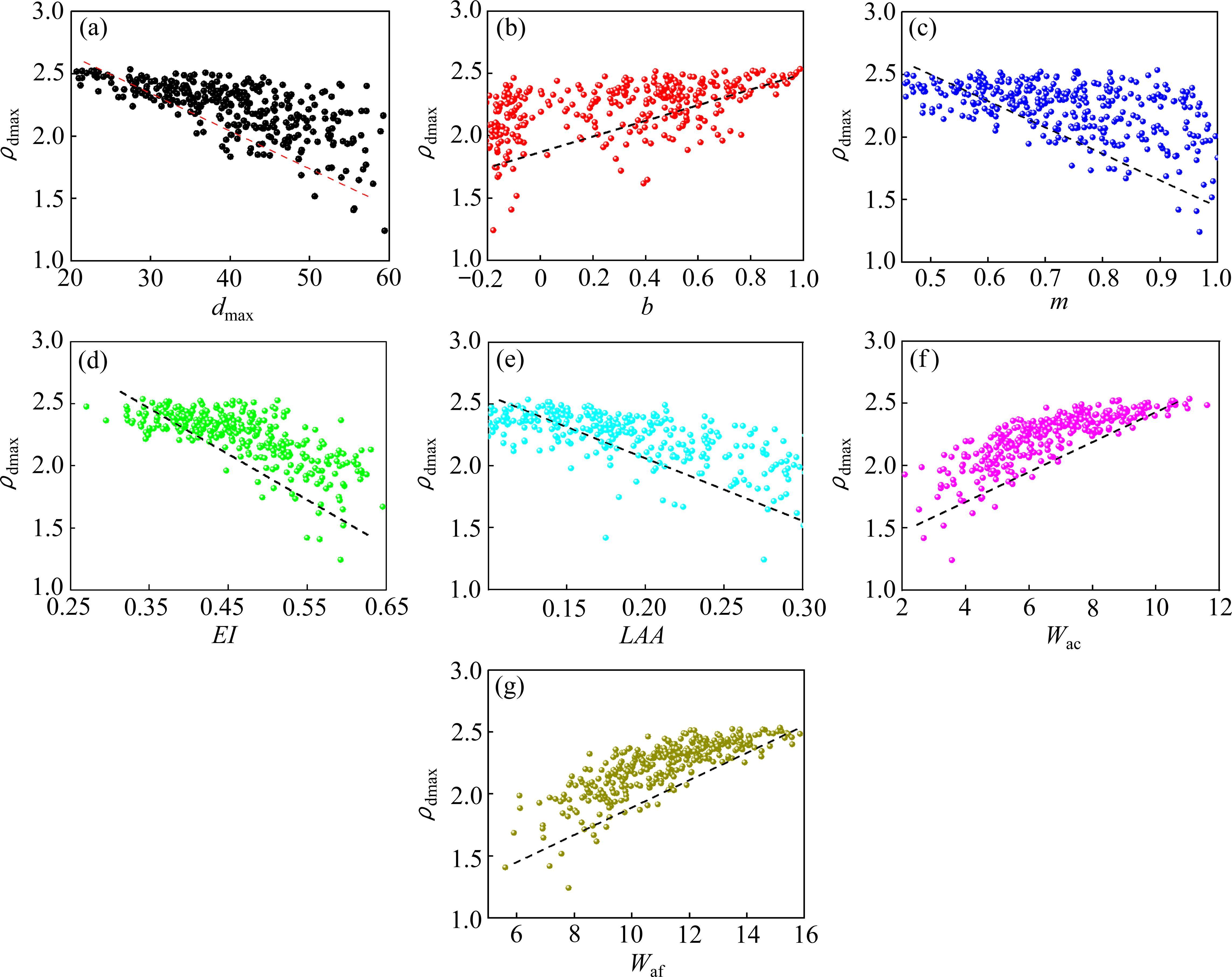
高速铁路级配碎石的性能特征主要包括级配(dmax、b、m),洛杉矶磨耗(LAA)、粗骨料(d≥1.7 mm)细长比(EI)、粗骨料(d≥1.7 mm)吸水率(Wac)、细集料(d≤1.7 mm)吸水率(Waf)和细集料(d≤0.5 mm)塑液限(PL、LL)[11]。开展316组振动压实[15]和填料性能测试[11]试验,获取不同级配填料ρdmax以及相对应的填料性能特征,并基于GRA[16]算法明确影响ρdmax的主控特征为dmax、b、m、EI、LAA、Wac和Waf。
根据ρdmax的主控特征和316组不同级配填料的试验数据,如图2所示。构建PBA模型数据集T={(xn,(ρdmax)n)}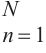
步骤2:基于训练集的PBA模型训练
采用PBA模型预测ρdmax,将训练集输入融合模型,并采用拟合优度R2[9]、解释模型方差得分Evs[10]、均方误差Mse[12]和平均绝对误差Mae[13]来评估PBA模型的拟合能力。
步骤3:基于测试集的PBA模型精度评价
将测试集输入训练后的PBA模型中,评估PBA模型预测ρdmax的泛化能力。
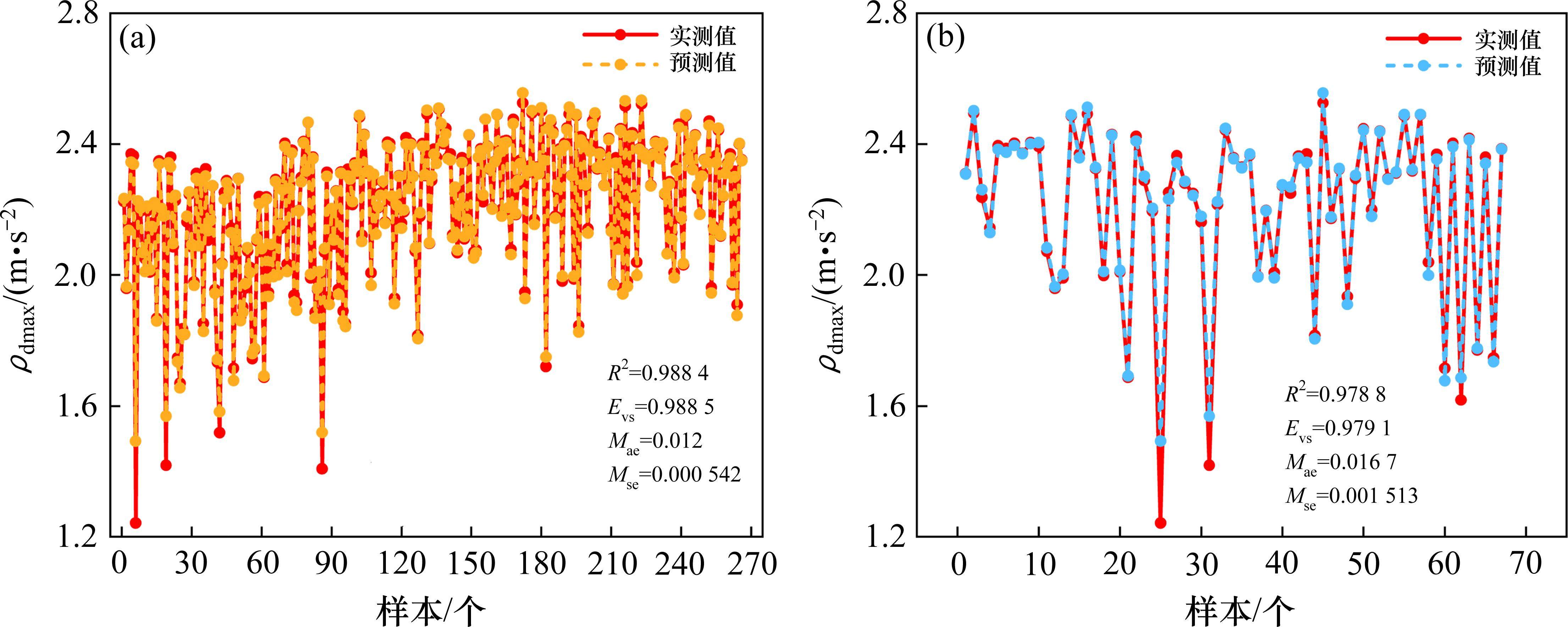
PBA模型在训练集和测试集上的预测结果如图3所示。由图3可知,训练集和测试集的预测精度均较高,R2和Evs均接近于1,且预测误差较低,Mse和Mae均接近0。可见,所建立的PBA融合模型在训练集和测试集上的预测结果均为理想,进一步说明PBA模型适用于ρdmax预测。
1.2 基于PBA模型预测的不确定性
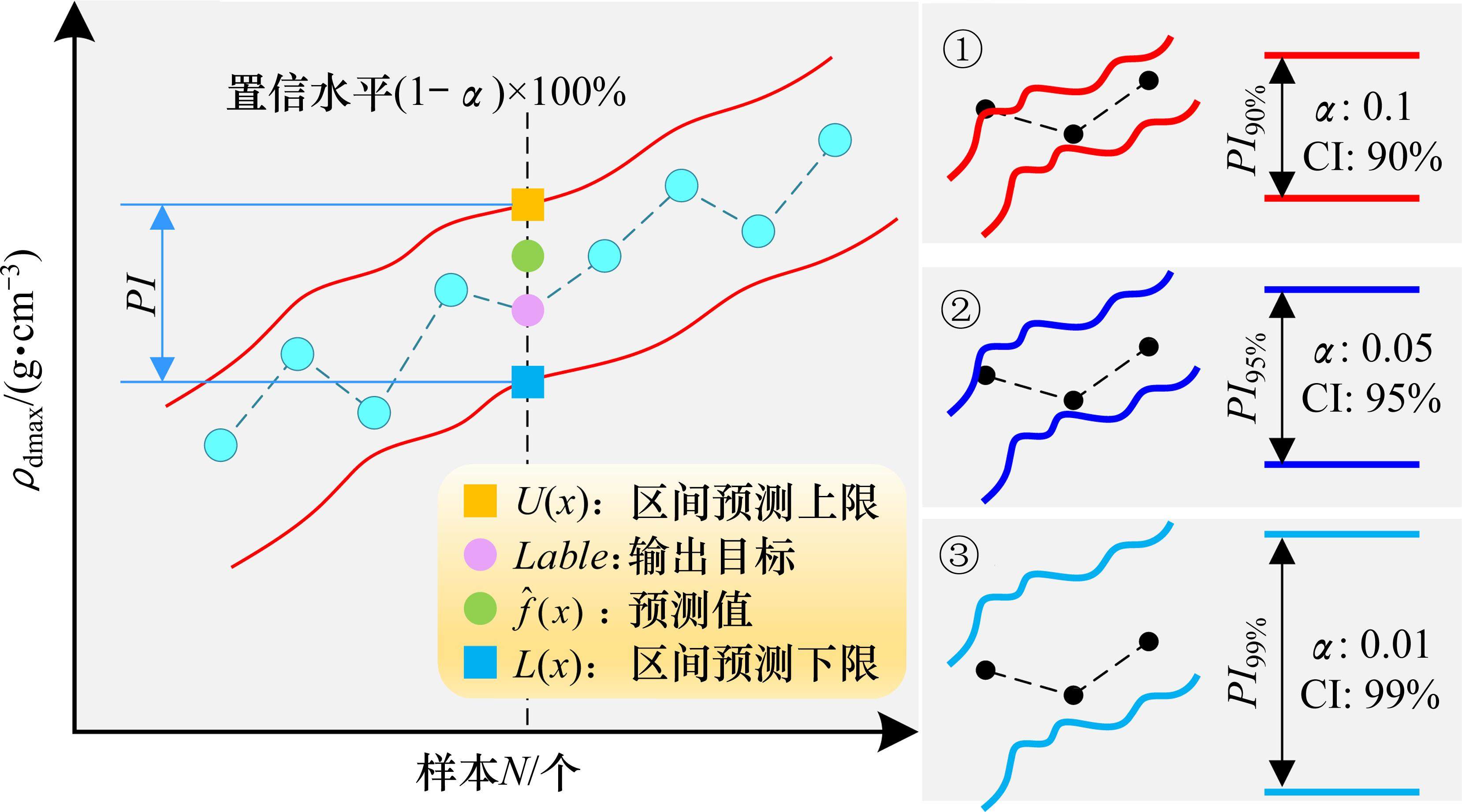
然而,PBA模型在预测ρdmax时不能考虑预测过程中不确定性带来的误差,显著影响了ρdmax预测结果的可靠性和准确性。如图4所示,基于不确定性理论[14],ρdmax预测中的不确定性如下。
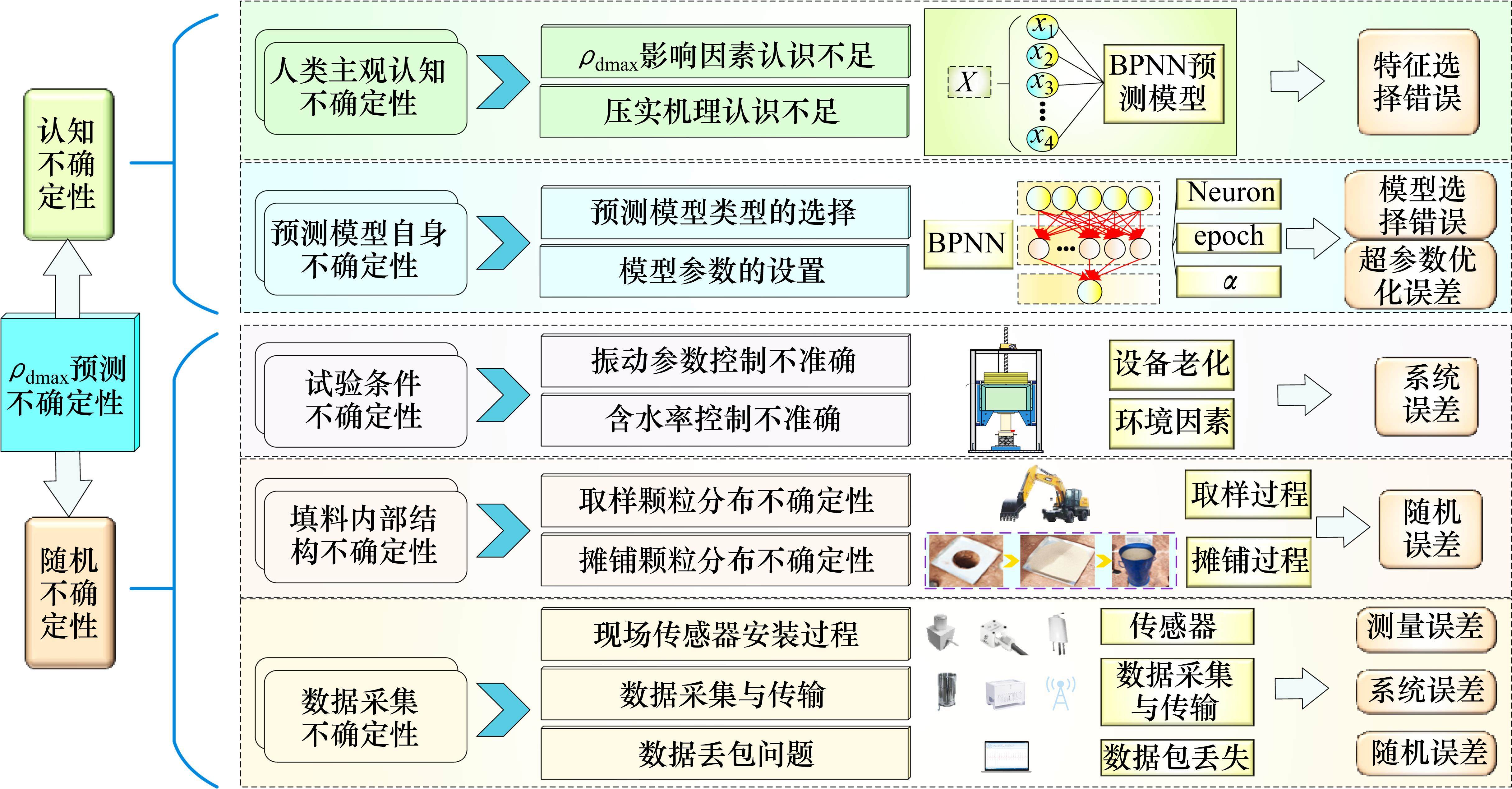
1) 认知不确定性
主要受到个体主观认知水平以及所采用的预测模型的综合影响,这些因素共同决定了认知不确定性的程度,包括:① 填料ρdmax影响因素或压实机理认识的不足,可能在预测中忽略部分影响因素或者输入参数的数据库未充分展示,导致PBA模型的输入特征不足,增加预测结果的不确定性;② PBA模型自身误差和模型参数的设置显著影响预测结果的不确定性。
2) 随机不确定性
主要是试验噪音数据集中,受试验条件、填料内部结构和数据采集过程的影响:① 振动压实设备及外界条件导致试验过程存在的不确定性;② 填料在取样和摊铺过程中颗粒分布的不确定性;③ 现场数据采集与传输过程中受到条件干扰存在的不确定性。
综上,与ρdmax预测相关的不确定性无法完全避免,显著影响了ρdmax预测结果的可靠性,使得预测结果的准确性得不到有效的保障。鉴于此,为提升预测结果的可靠性与应用价值,引入不确定性理论,运用概率手段量化ρdmax预测过程中的不确定性。
1.3 考虑ρdmax预测不确定性的全断面压实度区间计算
压实度K是现场灌砂法实测干密度ρd与室内试验最大干密度ρdmax的比值,如式(1)所示:
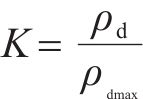
在路基试验段中开展现场试坑试验,通过灌砂法测试不同试坑点位填料的ρd,并开展不同试坑的填料特性测试试验,获得料源参数dmax、b、m、LAA、EI、Wac和Waf,将其作为PBA模型的输入参数即可预测不同试坑对应的ρdmax。进一步,基于克里金插值(Kriging)[17]算法将离散的稀疏试坑数据(料源参数、实测ρd)转换为连续试坑数据,从而得到试验段全断面数据,为全断面压实度评估提供数据支撑。
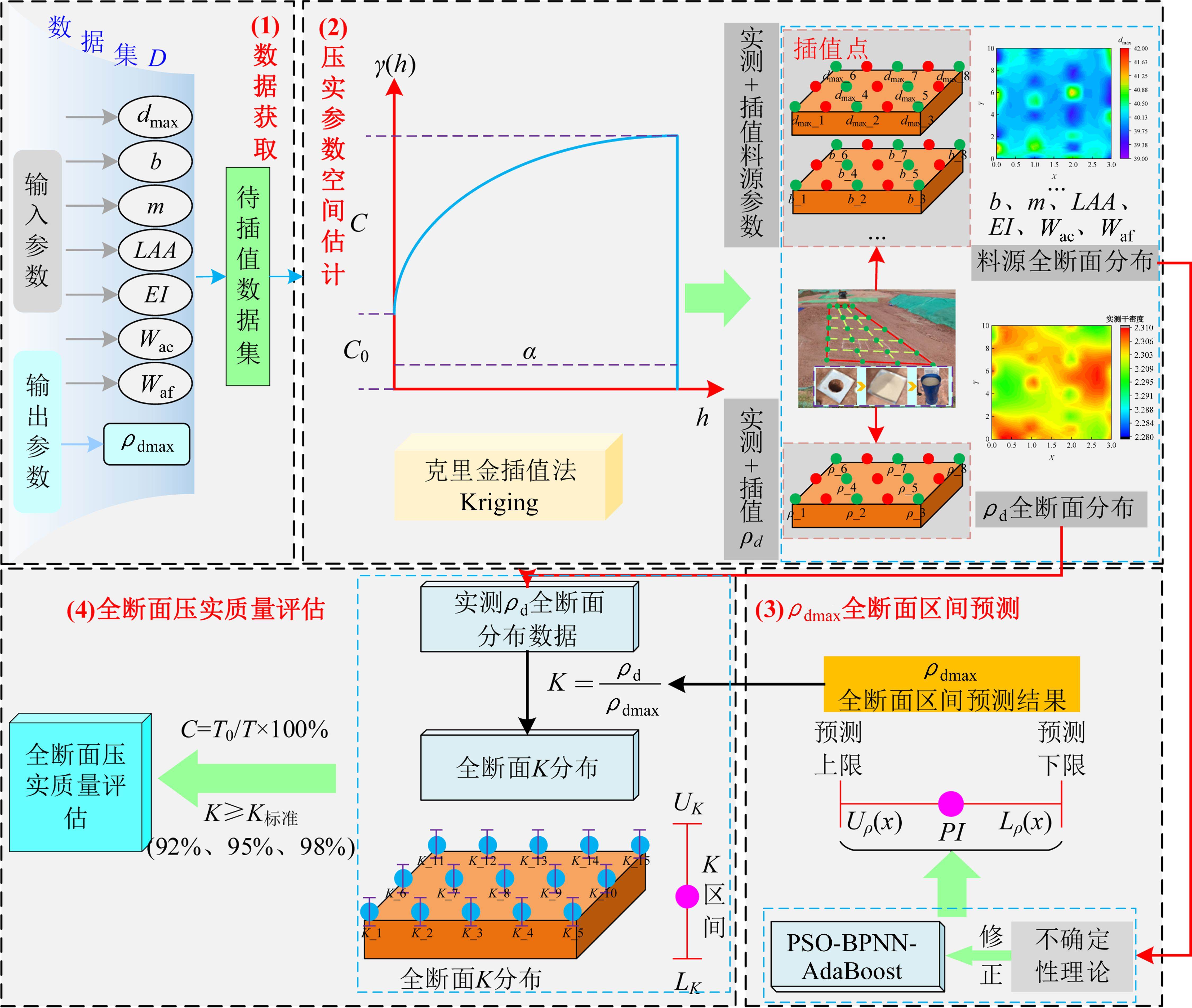
然而,由于PBA模型预测填料ρdmax存在不确定性,影响了压实度结果的可靠性和准确性。因此,如图5所示,引入不确定性理论方法修正现有压实度获取方法的不足,充分、全面、精确地计算路基试验段全断面的填料压实度,具体流程为:1) 通过试验段原位试坑试验获得料源参数、ρd数据;2) 基于试坑料源参数和ρd,通过Kriging算法计算出试验段全断面的料源参数和ρd;3) 将试验段全断面料源参数输入PBA模型中,并基于不确定方法修正PBA模型,得到试验段全断面的ρdmax区间预测结果;4) 结合公式(1)获得试验段全断面的压实度区间分布结果。
2 基于PBA模型预测最大干密度的预测不确定性计算
基于1.2节内容,PBA模型在预测ρdmax时不能有效量化误差引起的结果不确定性,影响了ρdmax预测结果的可靠性。针对这一问题,引入不确定理论,通过Bootstrap区间预测算法从原始数据中抽取多个样本,构建多个自助样本集。随后,对于每个自助样本集进行预测并记录预测结果。通过对多个预测结果进行排序,得到置信区间的上界和下界。提出基于Bootstrap[14]修正PBA模型的ρdmax区间预测方法,通过区间形式量化ρdmax预测值的不确定性[18]。
2.1 PBA模型最大干密度预测不确定性量化
根据1.1节得到ρdmax数据集为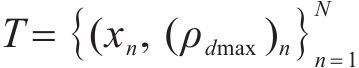
1) 确定输出目标的表达式
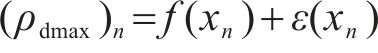
式中:f(xn)为真实的回归值;ε(xn)为随机噪音,由于ε(xn)表示的是随机因素综合作用的效果,故ε(xn)既有可能是正向影响,也有可能是负向影响。
2) ρdmax预测误差表示
预测总误差δ(xn)可表示为:
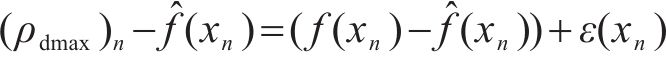
式中: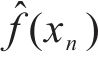
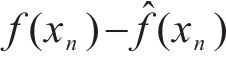
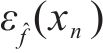
3) ρdmax预测总误差的方差计算
总误差的方差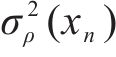
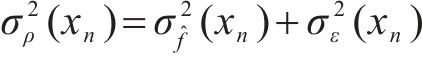
式中: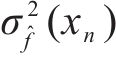
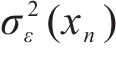
4) ρdmax预测区间构造
基于Bootstrap的预测不确定性量化方法,在给定显著性水平α的条件下,ρdmax的预测区间PIS可以通过公式(5)和公式(6)进行构造:
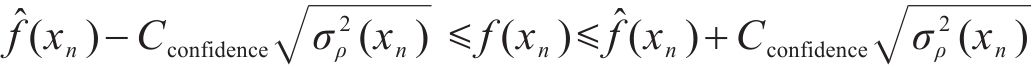
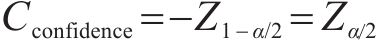
式中:Cconfidence为ρdmax预测区间的置信度,其值由置信水平(1-α)*100%决定,当置信水平分别取90%、95%、99%时,Cconfidence分别为1.65、1.96、2.58,具体求解可查阅标准正态分布的分位数表。
由公式(5)可进一步得到ρdmax预测区间PIS的预测上限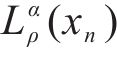
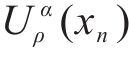
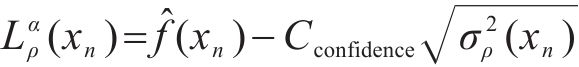
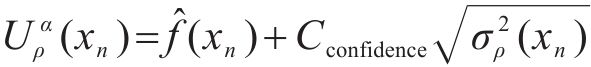
2.2 基于Bootstrap方法的最大干密度区间计算
基于ρdmax预测中不确定性的量化方法,Bootstrap-PBA-ANN模型的ρdmax不确定性预测模型建立主要包括5步,具体流程如图7所示。
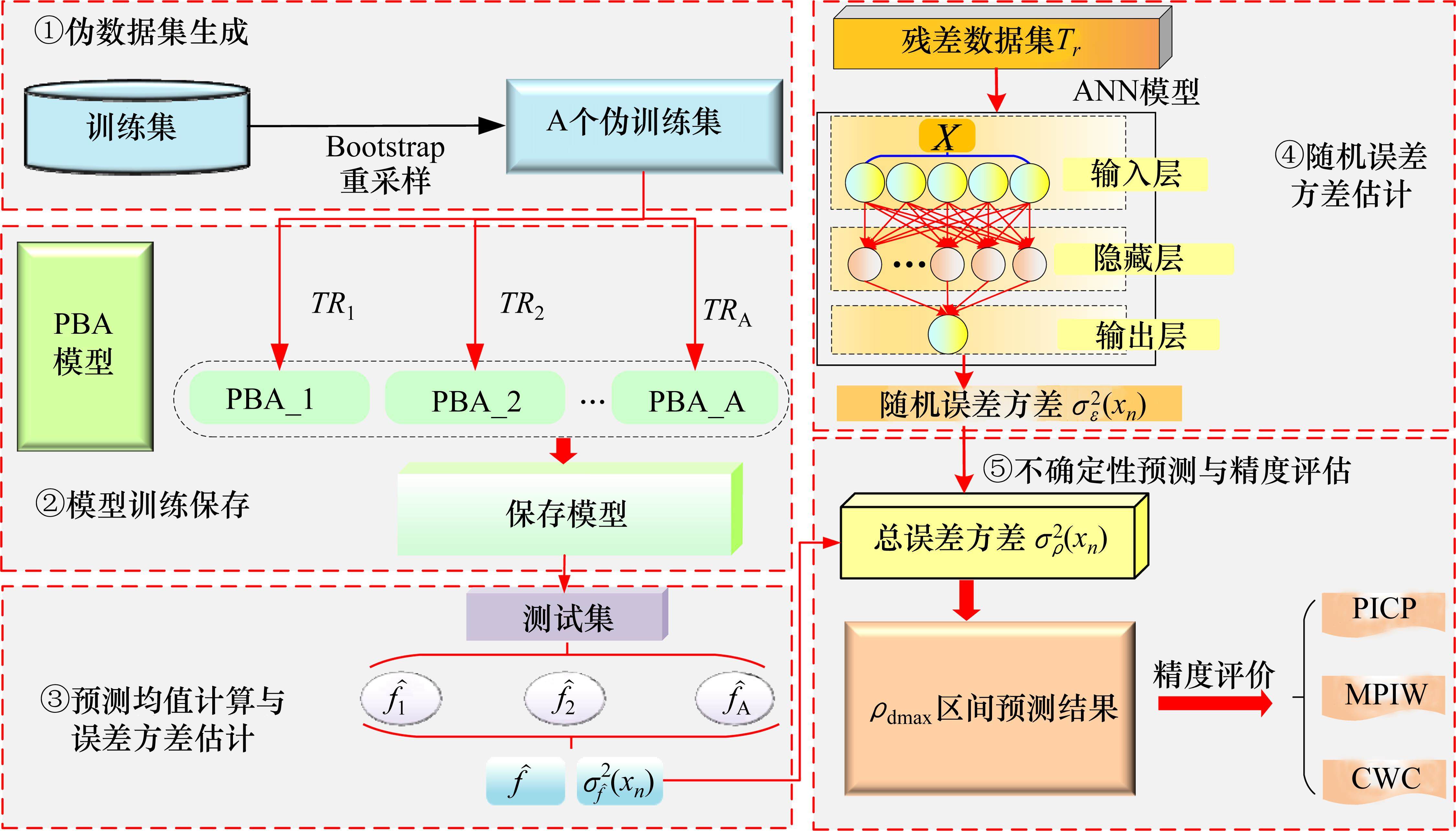
1) Bootstrap下伪数据集的生成
运用Bootstrap算法对训练集执行Ntrain次有放回的重采样步骤,其中Ntrain代表训练集内样本的总数。每次重采样操作后均生成一个伪训练集TR1。随后,通过重复上述流程A次,成功构建A个不同的伪训练集,完成伪训练集TR*的生成,为后续的深入分析提供充足且多样的数据集。
2) Bootstrap-PBA模型训练与保存
将伪训练集TR*输入到PBA模型中,保持PBA模型的超参数和结构不变,执行模型训练,得到A个训练好的PBA模型。
3) 预测均值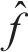
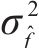
①预测均值计算
基于Ttest得到A个ρdmax预测结果:
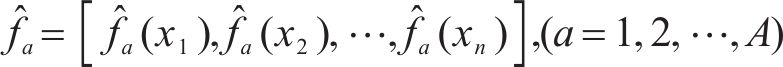
式中: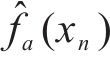
为确保预测结果的准确性和可靠性,通过计算A个预测值的均值,以逼近真实ρdmax回归值:
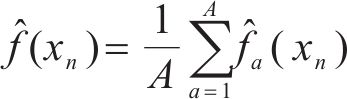
式中: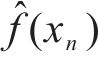
② 认知误差方差估计
在假设PBA模型的ρdmax预测值无偏的前提下,利用A个预测值的方差估算认知误差的方差:
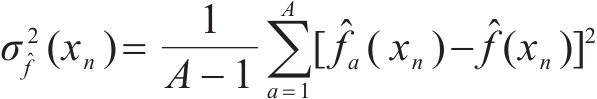
4) 基于ANN的随机误差方差估计
① 确定随机误差方差
由式(4)可知,随机误差的方差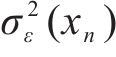
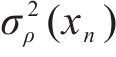
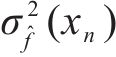
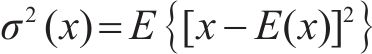
式中:σ2(x)代表随机变量x的方差;E(x)为随机变量x的数学期望。
进一步,将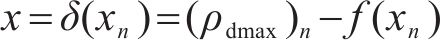
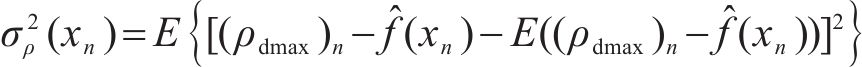
式中: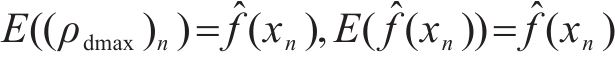
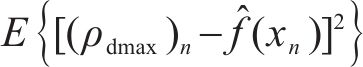
结合式(4)可得到随机误差的方差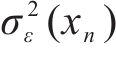
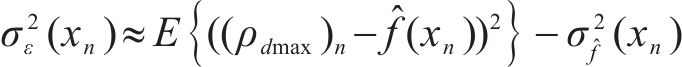
② 构建平方残差数据集
为更好地估计σ2ε(xn),基于式(14)构建一组平方残差序列拟合σ2ε(xn):
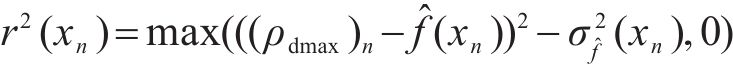
式中: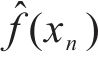
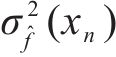
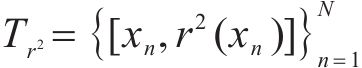
③ ANN模型损失函数改进及σ2ε(xn)预测
基于平方残差训练集Tr2_train训练ANN模型以预测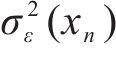
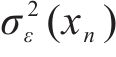
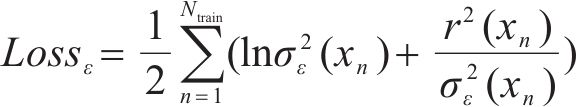
为了确保ANN模型的预测输出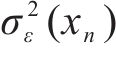
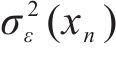
5) 不确定性预测与精度评估
在预测模型的性能评估中,预测区间覆盖率(Prediction Interval Coverage Probability, Pi)、平均预测区间宽度(Mean Prediction Interval Width, Mp)[19]和覆盖宽度综合指标(Coverage Width-based Criterion, Cw)[20]是评价预测区间可靠性与清晰度的关键指标,可用于综合评估模型的区间预测结果。计算Cw过程中的惩罚参数η设置为50[21]。
2.3 最大干密度区间预测结果
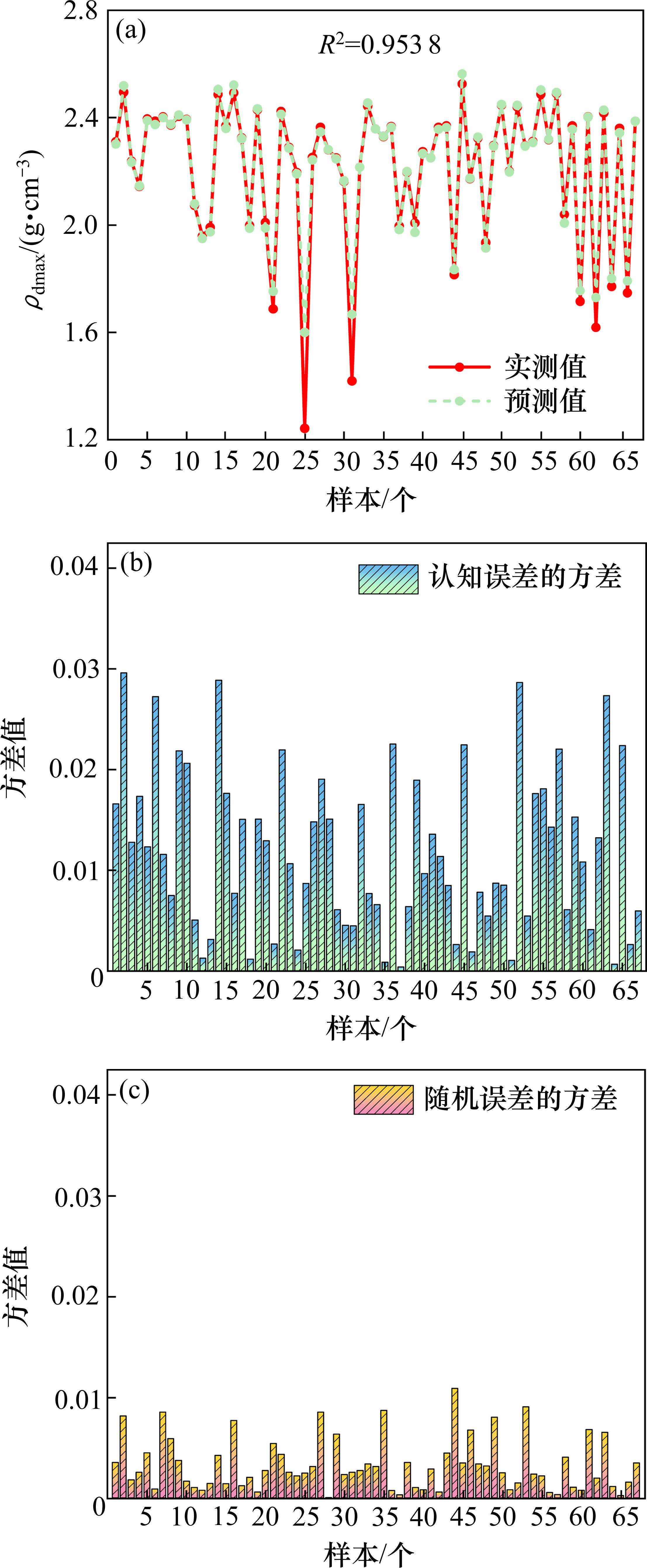
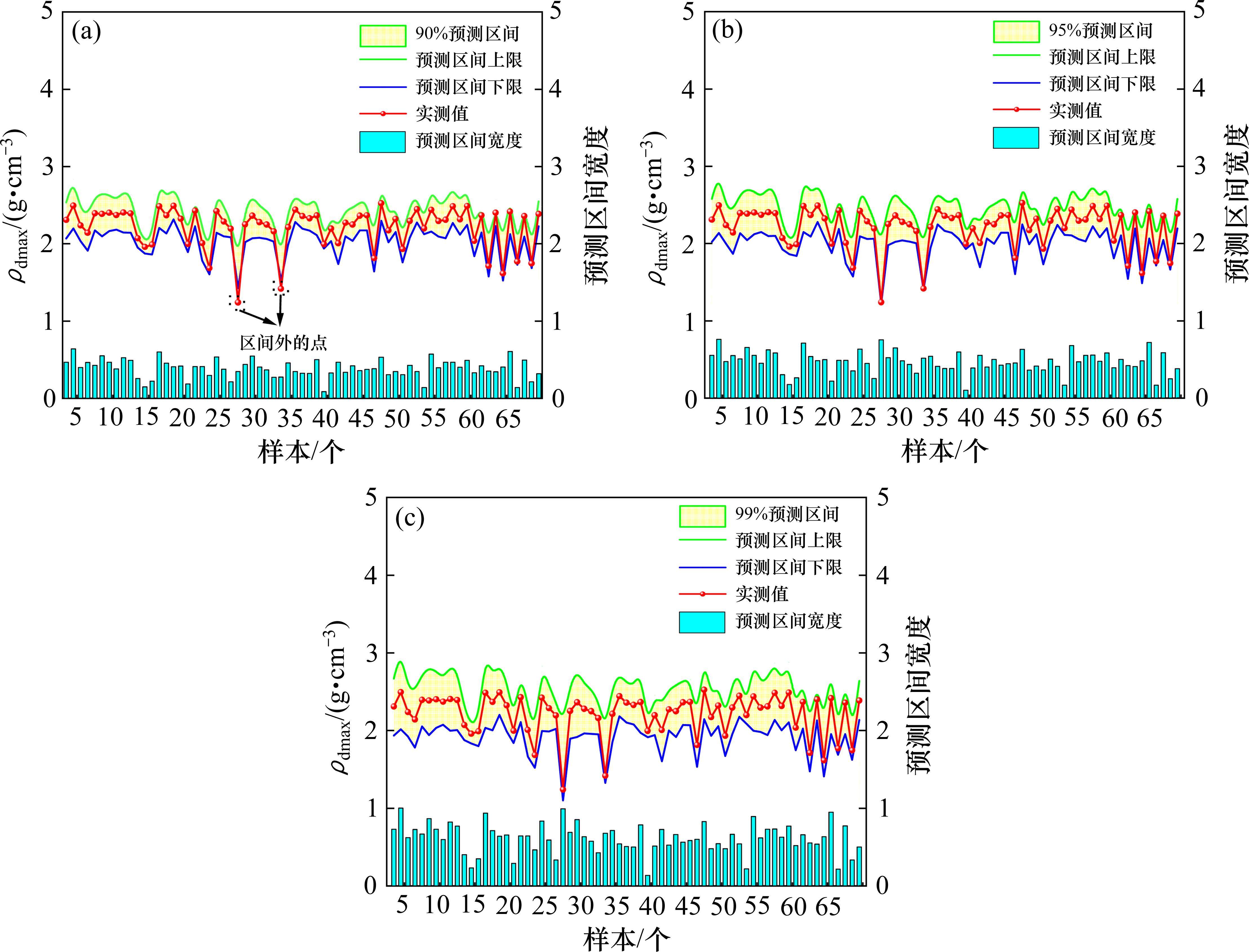
基于Bootstrap-PBA-ANN的ρdmax样本均值、认知误差和随机误差分布如图8所示,所得的区间预测结果如图9所示,不同置信度的区间预测精度评估结果如表1所示。随着置信度的提高,Pi、Mp和Cw均呈现出增加趋势,同时Pi均高于对应的置信水平,且均超过97%,进一步说明所建立的PBA最大干密度预测模型在预测性能方面表现优异。Pi越大、Mp和Cw越小,代表不确定性预测精度越高,结果越可靠[19]。因此,可选取置信度95%的参数构建级配碎石填料ρdmax预测区间,其Pi、Mp和Cw分别为100%、0.469 0 g/cm3和0.469 0 g/cm3。从预测区间的表现来看,预测区间可较好地覆盖级配碎石填料ρdmax实测曲线,且实测的ρdmax值基本上落在预测区间的中部,充分证明了区间预测结果的高度可靠性。
| 置信度/% | Pi/% | Mp/(g∙cm-3) | Cw/(g∙cm-3) |
|---|---|---|---|
| 90 | 97.01 | 0.388 2 | 0.388 2 |
| 95 | 100.00 | 0.469 0 | 0.469 0 |
| 99 | 100.00 | 0.617 4 | 0.617 4 |
3 案例应用-最优摊铺厚度的确定
3.1 现场数据准备
在大规模摊铺和碾压作业之前,开展试验段是必不可少的环节,其目的在于优化施工工艺参数,尤其是最优摊铺厚度的确定,对于提高施工效果以及实现压实质量的精确控制至关重要。以西南地区某站场碾压试验段为例,验证基于Bootstrap的全断面压实度区间评估方法的优越性。在试验段选取3个典型试验场地(长10 m,宽3 m),均使用同一批次的出厂填料,通过摊铺机铺设不同厚度的试验层,包括低厚度(40~50 cm)、中厚度(50~60 cm)和高厚度(60~70 cm),如图10所示。
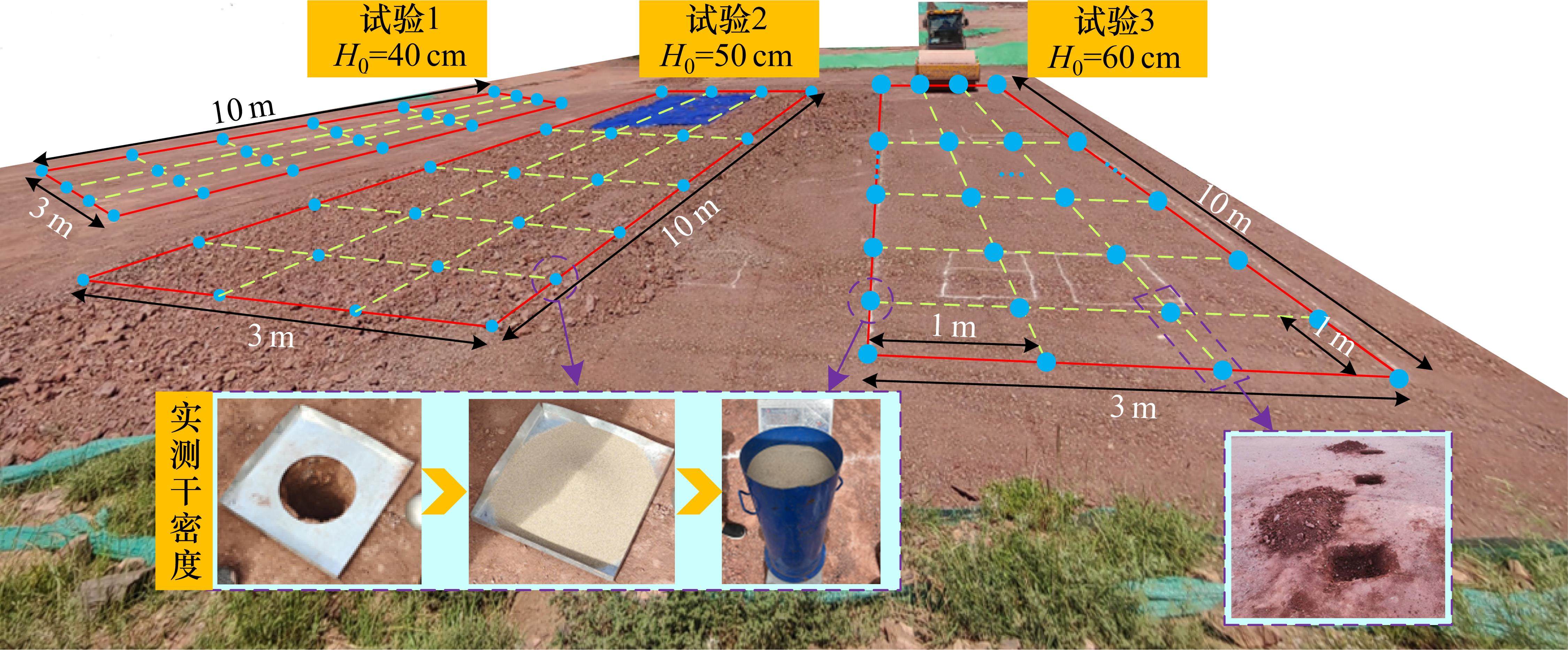
试验中采用的振动压路机型号为徐工-223型,其振动压实工艺参数经精确设定:自重为23 t,工作宽度为2.15 m,振动频率为32 Hz,振动幅值为1.03 mm。经过4~5遍的碾压后,各试验段表面沉降趋于稳定,在各试验场地每隔1 m选取试坑点,对料源参数和实测干密度ρd进行详细的测试与分析。
3.2 全断面数据插值结果
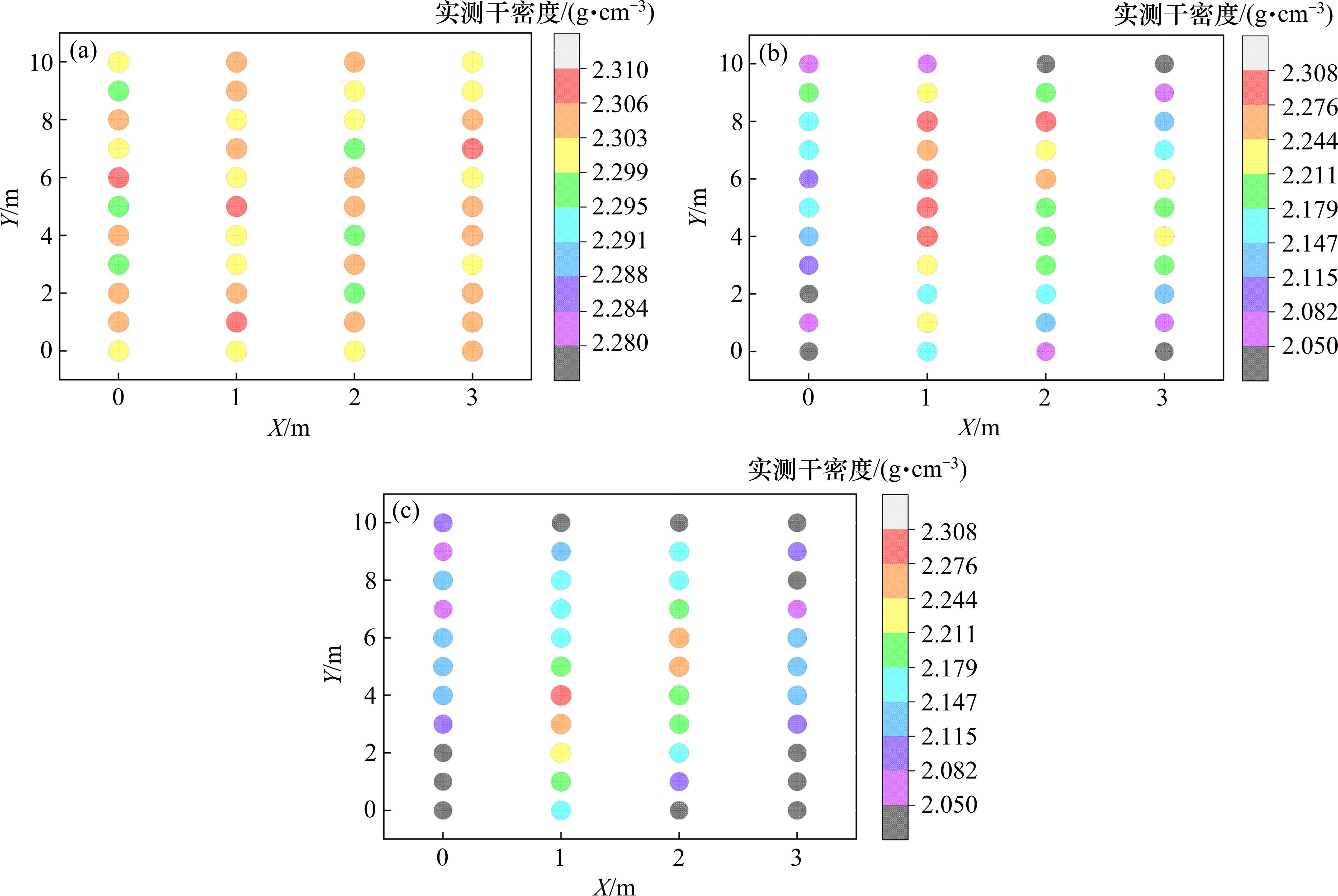
在各试验段表面沉降趋于稳定后,开展灌砂试验,获取各测点干密度ρd,结果如图11所示。在相同的试验条件下,摊铺厚度为40~50 cm试验段的ρd分布最均匀,而随着摊铺厚度的增加,ρd呈现降低趋势,且分布逐渐离散,均匀性降低,另外,试验段边缘的ρd显著小于中心区域。因此,在现场检测压实质量时,需严格控制碾压边缘“薄弱”区域。
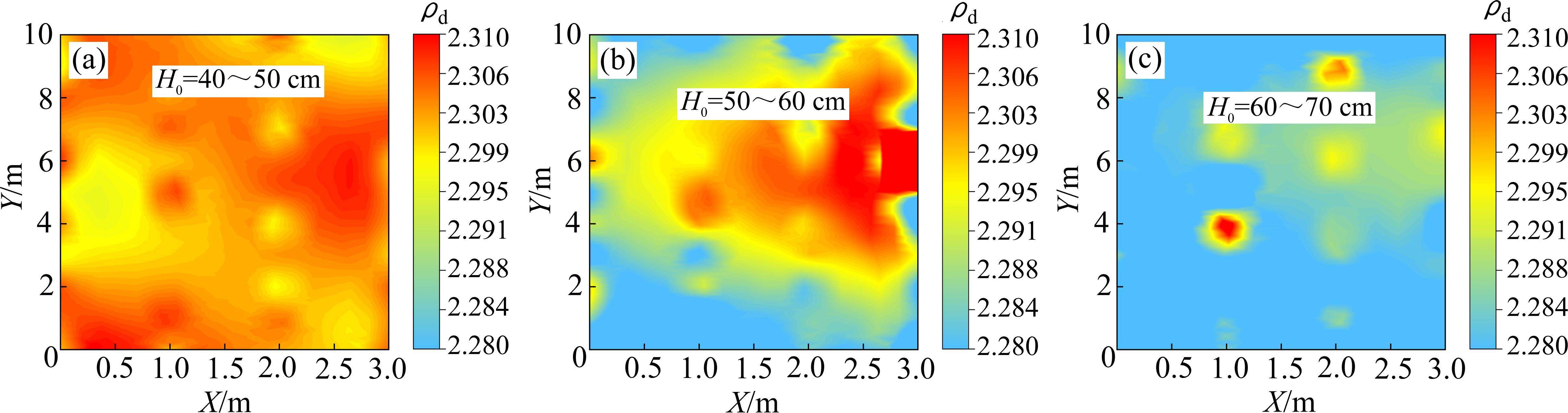
基于Kriging算法将离散的稀疏数据转换为连续数据,得到不同摊铺厚度下试验段的ρd全断面分布结果,如图12所示。由图12可知,ρd随着摊铺厚度的增加显著降低,且边缘压实“薄弱”现象愈发明显,与测点ρd分布结果类似,进一步证明插值结果的合理性。
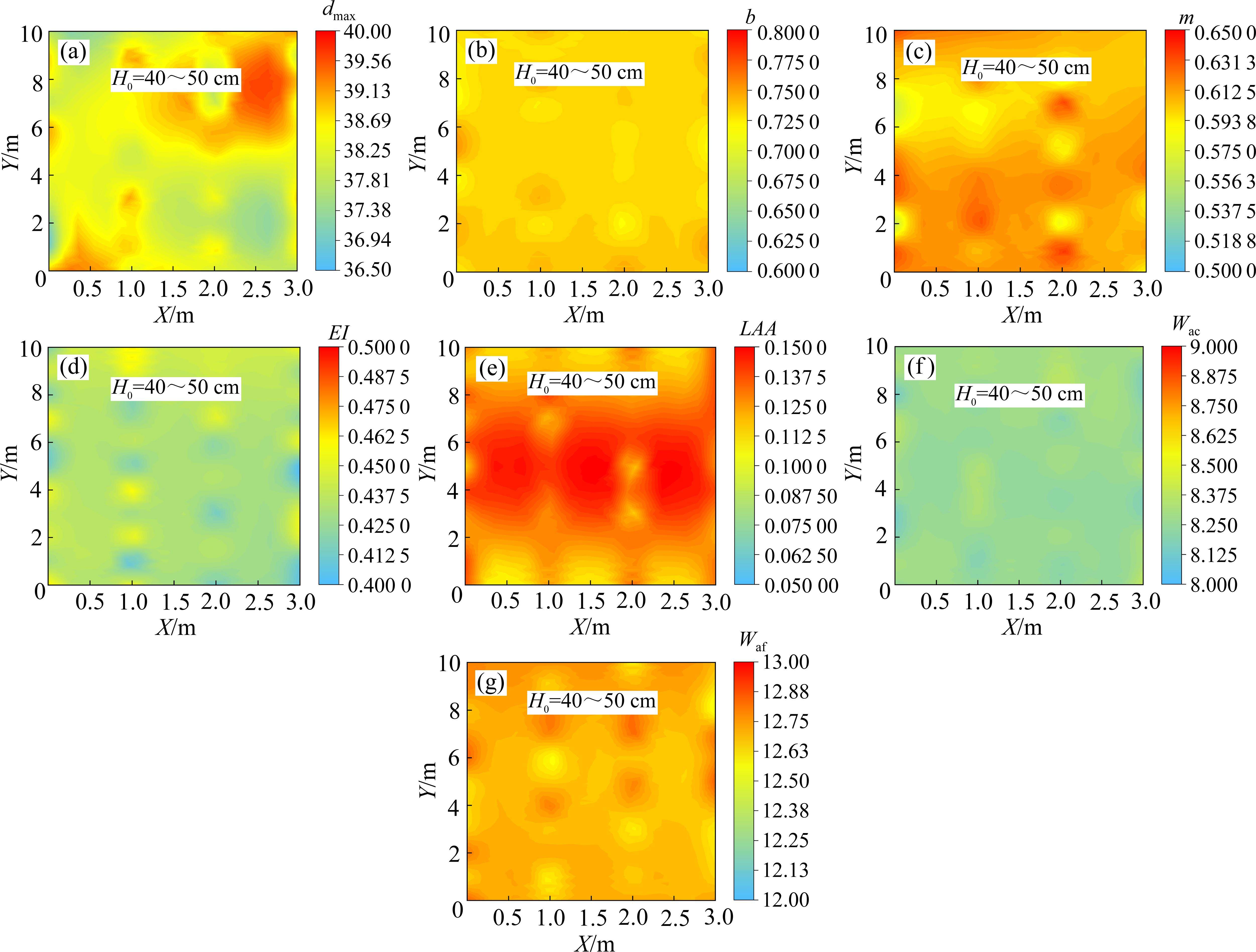
类似的,选取试坑中的料源样本(8 kg),开展填料性能测试试验,获取测点的料源参数(dmax、b、m、Wac、Waf、EI和LAA)数据,随后采用Kriging算法得到各试验段的料源参数全断面分布结果,以摊铺厚度40~50 cm为例,结果如图13所示。
3.3 全断面压实度区间评估结果
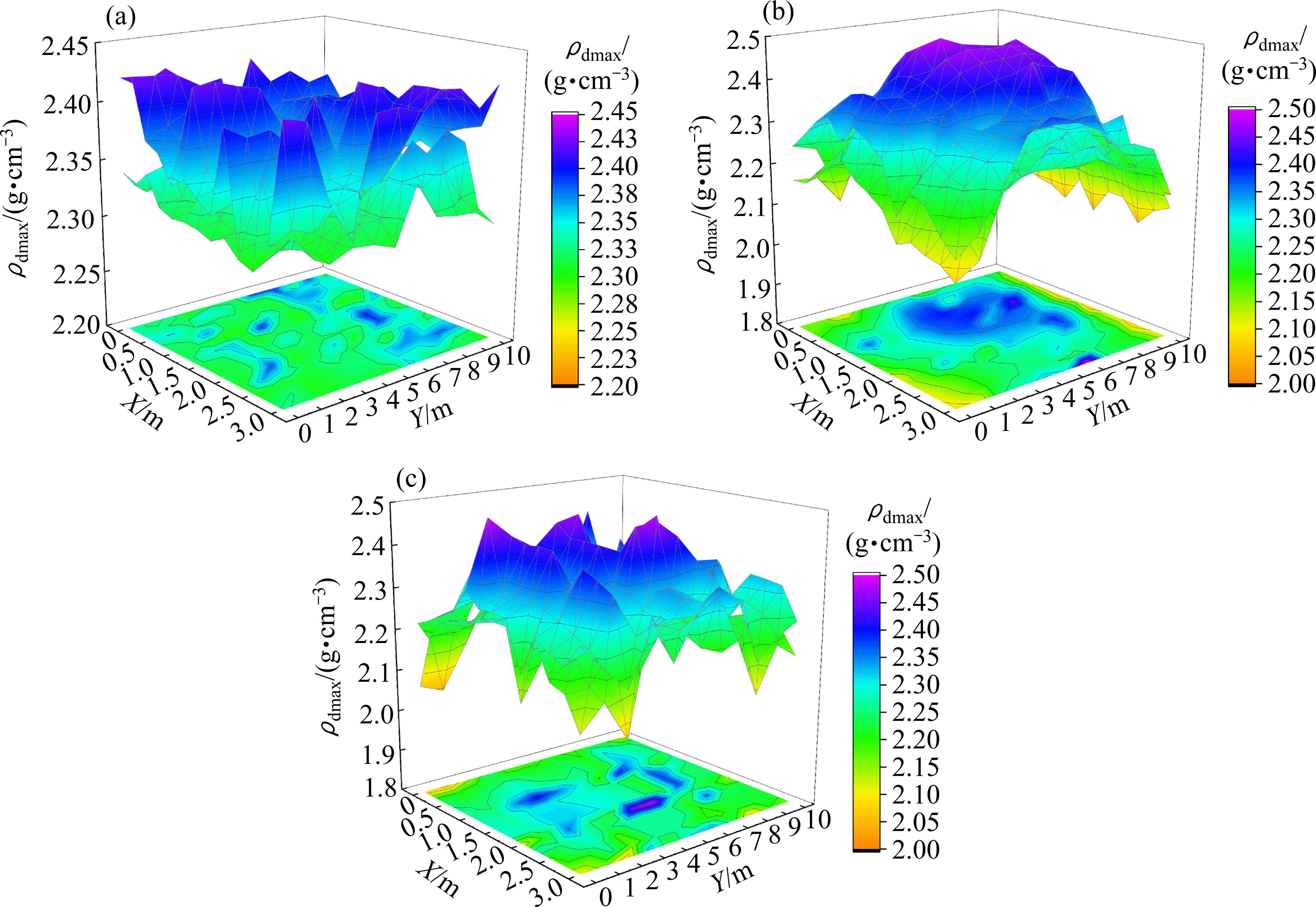
将试验段的全断面料源参数输入2.2节建立的ρdmax区间预测模型中,得到不同试验段的ρdmax全断面区间分布结果,如图14所示。由图14可知,不同摊铺厚度的试验段中,ρdmax上限均介于2.30~2.45 g/cm3。然而,随着填料摊铺厚度的增加,压实均匀性难以控制,导致摊铺厚度较大时填料级配参数与设计标准相差较大,ρdmax下限偏小。摊铺厚度为40~50 cm试验段的ρdmax下限介于2.2~2.3 g/cm3,而50~60 cm和60~70 cm的试验段ρdmax下限介于2.0~2.3 g/cm3。
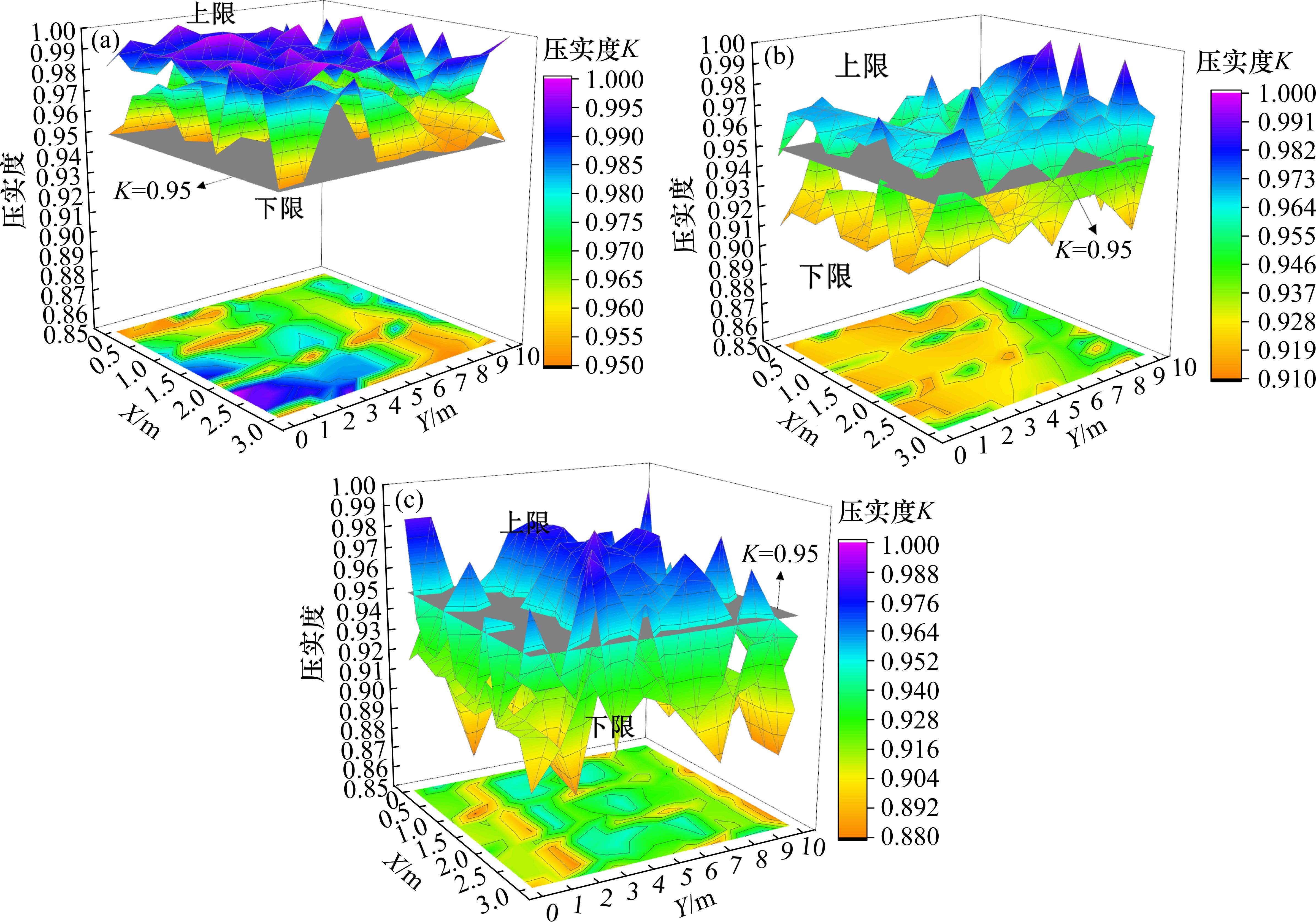
由公式(1)计算得到不同摊铺厚度试验段的全断面压实度区间分布结果,如图15所示。摊铺厚度为40~50 cm的试验段全断面压实度上下限均大于95%的压实质量标准,表明在现场碾压过程中,选取摊铺厚度在40~50 cm,可使路基结构压实质量满足规范要求。然而,当摊铺厚度为50~60 cm时,压实度下限不满足95%的压实质量标准,表明在此厚度下试验段部分区域存在碾压不充分的情况,无法保证路基结构的压实质量;当选取摊铺厚度大于60 cm时,压实度上限不满足95%的压实质量标准,说明此厚度的试验段存在大量未充分碾压区域,难以保证路基压实质量。因此,本段路基施工中,建议采用40~50 cm的摊铺厚度,可获得压实充分的路基填筑段,为保证路基服役性能奠定基础。
4 结论
1) PBA模型在训练集和测试集上预测精度较高,R2和Evs均接近1,分别为0.988 4/0.978 8、0.988 5/0.979 1,且预测误差较低,Mae和Mse均接近0,分别为0.001 2/0.016 7、0.000 542/0.001 513,表明PBA模型适用于预测ρdmax。
2) 基于不确定性理论将ρdmax预测中的不确定性分为认知不确定性和随机不确定性,计算认知误差的方差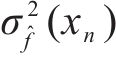
3) 基于Bootstrap-PBA-ANN模型不同置信度的ρdmax区间预测结果,选取置信度95%的参数构建填料ρdmax预测区间,此时Pi、Mp和Cw分别为100%、0.469 0 g/cm3和0.469 0 g/cm3,且预测区间可较好地覆盖填料ρdmax实测曲线。
4) 不同摊铺厚度的全断面压实度区间评估结果表明,随着填料摊铺厚度的增加,路基压实不均匀性愈发显著。在现场碾压过程中,摊铺厚度为40~50 cm的试验段压实度上下限均大于95%的压实质量标准,此时路基结构压实质量满足规范要求。
郝哲睿,陈晓斌,肖宪普等.基于ML-不确定性理论的路基全断面压实度评估方法[J].铁道科学与工程学报,2025,22(02):649-663.
HAO Zherui,CHEN Xiaobin,XIAO Xianpu,et al.A Method for full-section assessment of subgrade compaction degree based on ML-uncertainty theory[J].Journal of Railway Science and Engineering,2025,22(02):649-663.

