“十四五”时期,我国进入加快建设交通强国的新阶段,铁路作为交通运输骨干,其智能化升级改造是推动高速铁路高质量建设和发展的必由途径[1-2]。随着“车载中心化”需求日趋强烈,减少对地面设备的依赖,降低运营与维护成本,对于推进下一代列控系统、智能行车调度指挥系统应用具有重要意义[3]。全球卫星导航系统(global navigation satellite system, GNSS)与惯性导航系统(inertial navigation system, INS)组合定位模式在卫星完好时对列车状态感知具有一定优势[4],然而当列车经过隧道时,卫星信号完全失效,此时组合定位系统仅依赖惯性导航实现列车状态感知,由于缺少卫星信号的量测校正,惯性器件航位推算会受到加速度计和陀螺仪器件的累积误差影响而快速发散[5-6],从而使得列车运行状态感知能力难以保持。目前针对GNSS信号失效场景,众多研究通常采用里程计(odometer, ODO)与INS融合进而约束INS误差累计[7]。然而此类方法精度非常依赖惯性器件精度,因此多数使用高精度、高成本的光纤陀螺惯性导航进行分析。此外,部分学者采用视觉传感器约束惯性误差累积[8],但是此类方法需要大量数据在线运算以及视觉传感器受环境影响巨大,视觉信息一旦失效,惯性依旧会发散迅速。综上,传统组合系统仅考虑从位速角度进行惯性导航航位校正,然而,捷联惯性导航航位推算模式是以姿态信息为底层进行的位速更新,因此引起列车定位结果发散的根本性原因是惯性导航系统的姿态解算模型精准性不高[9],但目前在铁路导航领域,关于此姿态解算并未有过多描述和建模,其精度往往依赖于惯性器件的性能水平。因此,有必要针对列车隧道运行场景研究列车姿态底层解算方法,实现列车姿态精度保持,进而有效抑制组合定位系统在卫星信号拒止时的误差发散。为从姿态解算层面解决惯性导航系统精度保持这一问题,国内外学者提出了多种姿态求解方法以及滤波架构,目前多以基于惯性器件的加速度计和陀螺仪的动态特性,融合多传感器信息的方法为主[10-11],常用方法包括频域互补滤波架构、Madgwick模型、状态空间递归模型等。MAHONY等[12]提出频域互补滤波架构,利用惯性器件频率高低互补特性,将加速度计和陀螺仪的测量值在频域里进行融合,通过建模消除相关噪声,实现载体姿态估计。然而此类方法易受外部噪声影响,同时互补滤波器的权重无法精准设置,过大会存在滞后效应,过小会导致滤波失衡。MADGWICK等[13-14]通过引入磁力计并融合加速度计数据优化误差函数来更新四元数的估计值,从而解决陀螺仪漂移问题,实现载体姿态的准确估计。状态空间递归模型通常以卡尔曼滤波算法为底层框架,将加速度计、磁力计等传感器作为测量值进行状态空间校正[15-16]。然而Madgwick模型和空间递归模型对于载体姿态感知精度主要依赖磁力计完成,但铁路列车运行场景的磁场环境相对复杂且波动较大,对依靠地磁传感器辅助解算姿态的性能提出了极大考验,给系统姿态的精准解算也带来了极大挑战。除此之外,基于微机械(micro electromechanical system, MEMS)传感器的惯性器件由于低廉的价格得到了广泛应用[17],惯性导航技术在高精度、低成本定位领域正处于快速发展阶段[18],在MEMS传感器相关姿态精准解算研究较少的情况下,低成本惯性器件姿态补偿模型的应用研究对实现“车载中心化”的列车定位性能保持至关重要。基于上述国内外研究现状分析,研究基于惯性四元数建模的载体测姿精度保持方法意义重大。目前针对铁路列车隧道运行场景的姿态解算及精度保持方法的研究尚少,因此,本文构建运动载体加速度辅助惯性列车姿态四元数的反馈补偿解算模型(accelerometer-assisted inertial quaternions model, AAIQM),实现无卫星条件下的以惯性为中心的姿态信息稳态输出。同时,针对MEMS级惯性导航独立工作时位置、速度及姿态解算鲁棒性受限难题,提出基于AAIQM增强的INS/ODO组合定位模型,最大限度保障卫星失效时惯性精度。
1 基于INS/ODO组合定位系统
列车正常运行过程中,垂直轨道方向速度可认为0,因此在卫星完全失效时,可以采取INS/ODO组合定位系统继续获得列车实时的状态信息。将ODO解算的位、速信息与INS惯导递推的位、速信息作为卡尔曼滤波器的输入信息,经过卡尔曼滤波模型计算得到INS各项参数的校正量,完成对INS的位置、速度及姿态信息的校正,实现载体状态感知。
卡尔曼滤波组合导航系统的状态向量为:
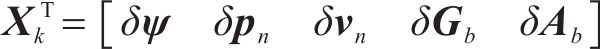
式中: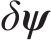
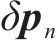
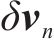
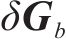
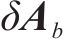
利用离散卡尔曼滤波进行计算时的状态方程以及量测方程表示方式如下:
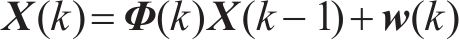
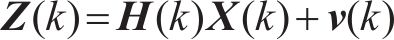
式中: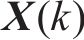
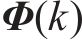
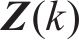
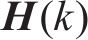
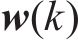
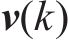
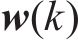
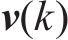
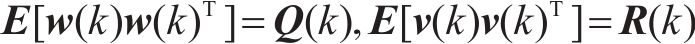
离散卡尔曼滤波模型的更新步骤如下:
步骤1:状态预测
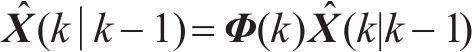
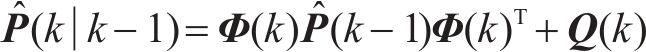
步骤2:滤波增益更新
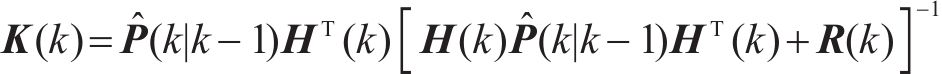
步骤3:状态估计更新
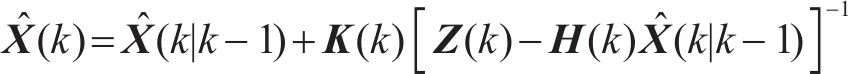
步骤4:状态协方差矩阵更新
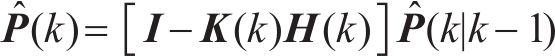
式中:
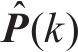
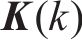
卡尔曼滤波组合导航系统的观测矩阵为:
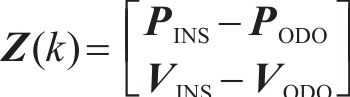
式中: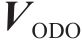
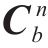



方向余弦矩阵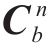
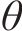
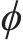
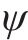
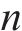
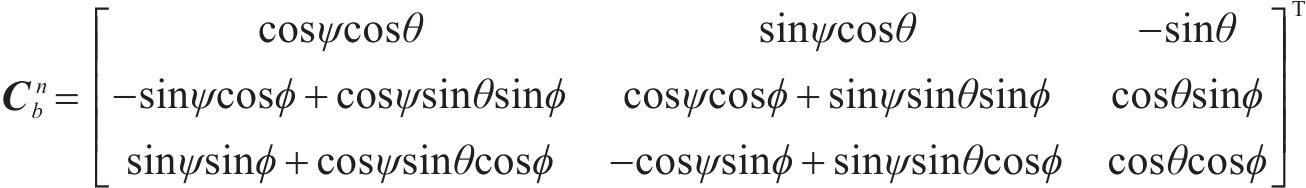
进一步,状态更新矩阵利用捷联惯导误差模型构建,其误差模型有:
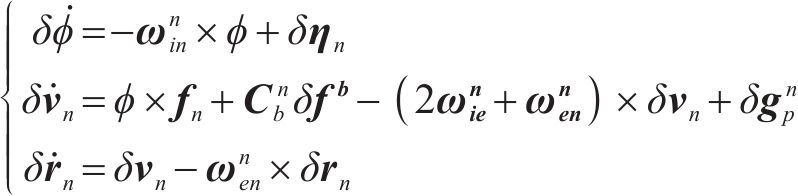
式中: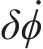
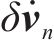
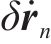
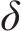
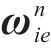
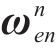
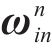
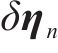
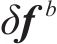
依据观测矢量与状态矢量关系,本文所用的观测矩阵的表示方式如下:
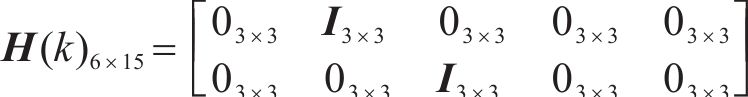
2 基于惯性四元数建模增强的列车定位精度保持方法
上述基于INS/ODO列车定位方法仅考虑位置和速度进行惯性模型校正,缺少针对轨道交通列车运行模式的惯性四元数建模的列车姿态解算方法研究,显然无法从惯性器件机械编排角度解决惯性发散问题,并未具有很好的铁路应用价值。因此,本文提出基于AAIQM的列车姿态精度保持方法,并在此基础上,提出基于AAIQM增强的INS/ODO组合定位系统。在卫星完全失效时最大限度保证以惯性为中心的列车空间解算精度。
2.1 基于AAIQM的列车姿态精度保持方法
2.1.1 列车姿态表述及推算
本文采用四元数方法来表示载体的姿态,直角坐标系空间转换关系可以通过围绕导航坐标系中定义的向量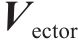
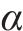
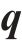
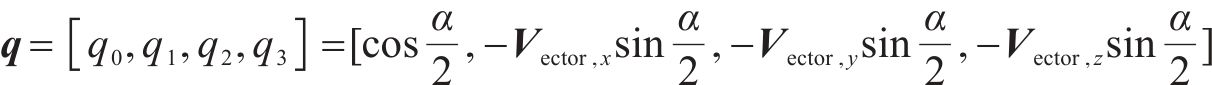
式中:四元数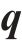
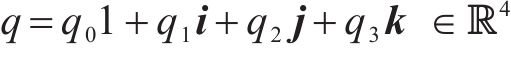
式中:分量1为四元数的实部,保持普通标量的性质,与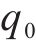
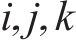
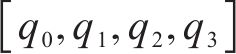
因此,式(11)的方向余弦矩阵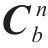
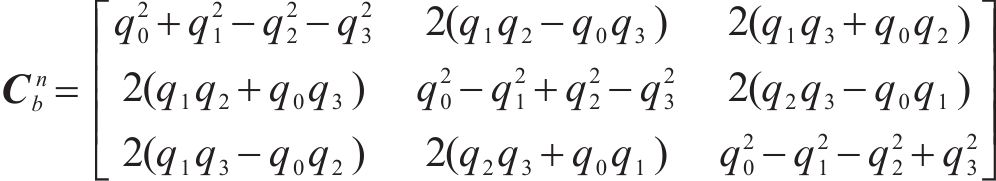
通过方向余弦阵计算出俯仰角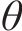
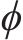
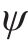
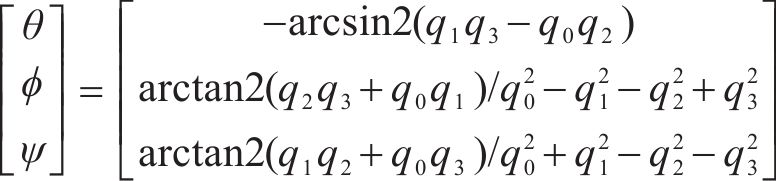
进一步,载体的姿态矩阵可通过四元数进行更新,其微分方程表示如下:
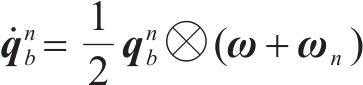
式中:上述
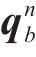
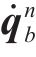

2.1.2 AAIQM模型描述
本文提出基于扩展卡尔曼滤波的惯性器件数据融合方法,总体框架如图1所示。首先,通过研究惯性器件耦合关系,挖掘陀螺仪原始观测数据及空间旋转机制,通过构建扩展卡尔曼滤波器,建立四元数空间旋转模型,即卡尔曼滤波状态观测方程;其次,将加速度计原始测量信息作为姿态解算模型的输入,通过加速度计传感器测量值映射到姿态状态空间完成陀螺仪的滤波校正,实现四元数的精确估计;最后,在滤波模型基础上,对陀螺仪零偏进行建模,完善惯性姿态保持方法,建立基于符合列车运动模式的加速度计辅助的列车姿态解算机制。

1) 状态方程建立系统状态方程选取7维状态量,其中由三轴陀螺仪输出的角速率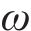
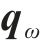
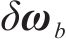
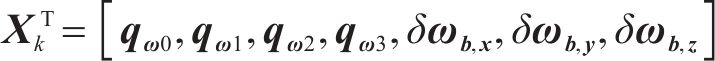
2) 量测方程建立当列车载体以恒定速度移动并处于固定方向时,加速度计仅测量重力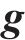
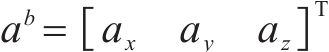
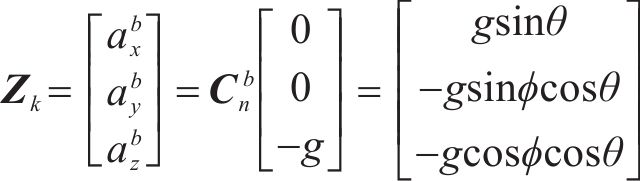
然而列车在运行过程中,会存在加速、制动过程,式(20)的建模过程会存在一定误差,但由于惯导采样频率200 Hz,此误差对模型精度的影响可以降低,由卡尔曼滤波量测噪声R表示,见式(34)。
3) 卡尔曼滤波模型建立在进行四元数微分计算时,由于惯性器件高频率特性,可假设角速度偏差从一个采样样本到下一个采样样本变化不大[19]。因此,对离散时间下姿态四元数的预测,需要对四元数的导数进行数值积分[20],有:
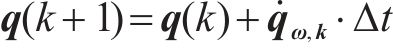
式中: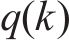
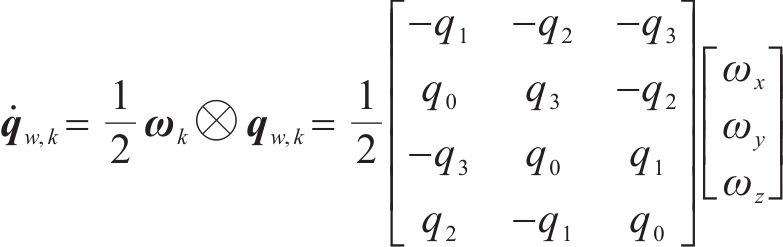
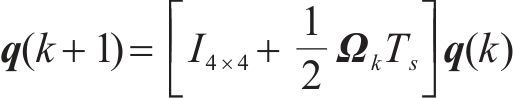
式中: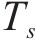
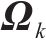
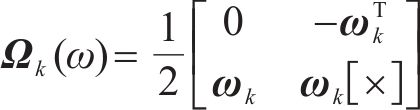
式中: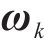
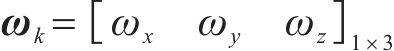
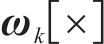
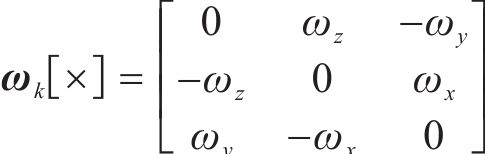
因此,综合上式,可完成状态转移矩阵构建,如下所示:
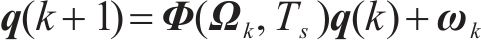
式中: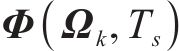
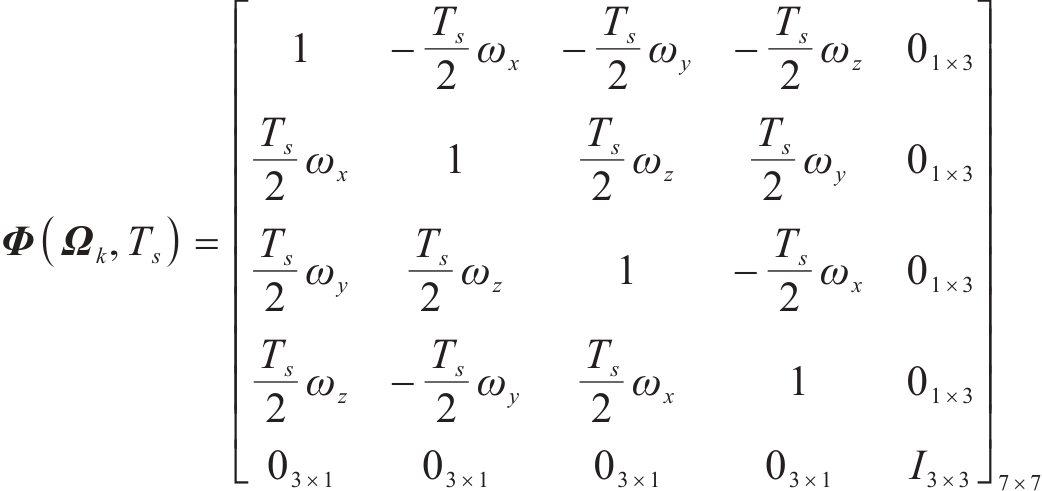
卡尔曼滤波预测过程中的系统噪声主要来自陀螺仪器件,因此可由式(18)利用四元数推算出噪声矩阵。首先利用四元数乘法规则对式(22)整理为:
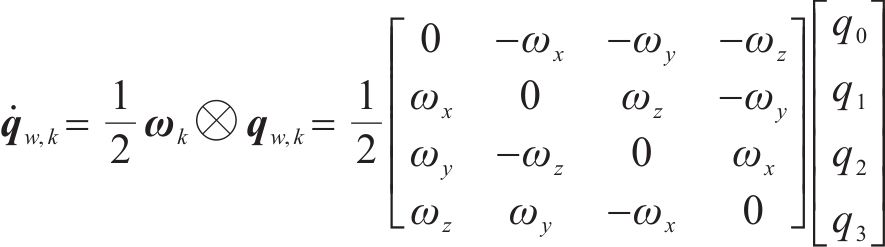
陀螺仪的测量输出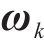
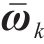
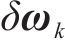
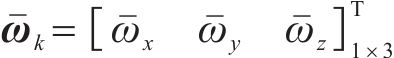
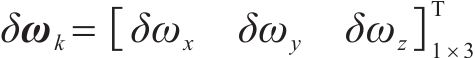
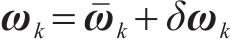
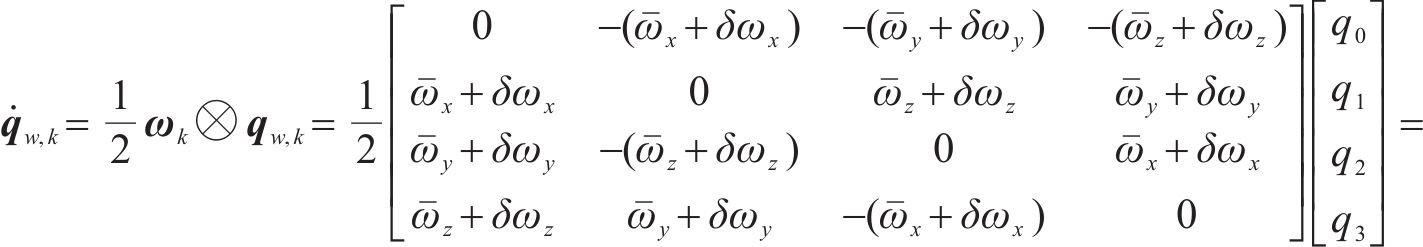
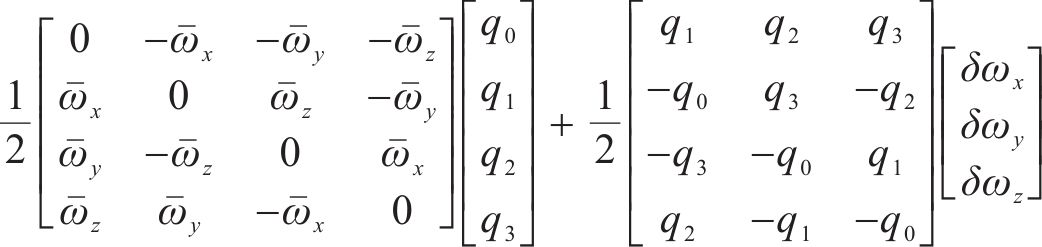
进一步,通过式(29)的噪声项,可以构建噪声转移矩阵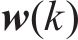
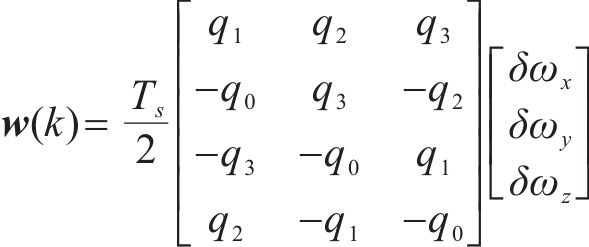
因过程噪声符合正态分布高斯白噪声,因此,可通过式(4)构建过程协方差矩阵
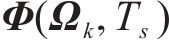
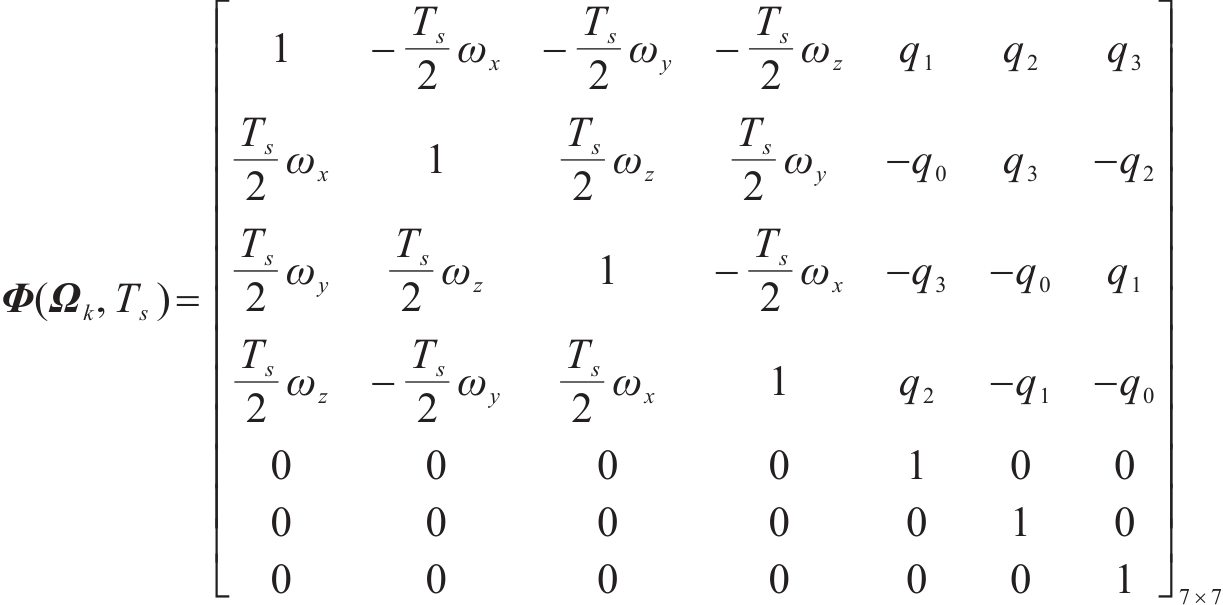
结合四元数方向余弦矩阵及式(20),量测方程可以更新为:
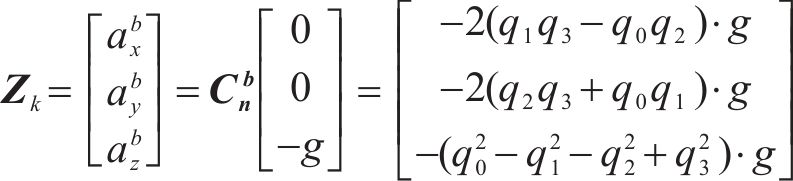
进一步可得量测转移矩阵
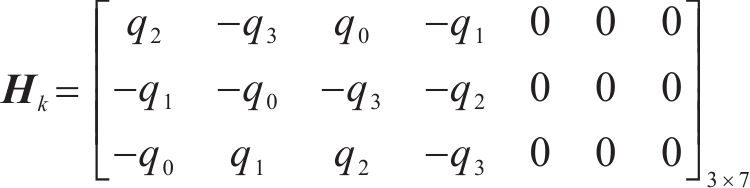
依据加速度计观测作为AAIQM的量测输入,经过参考惯性器件加速度计零偏稳定性、随机游走噪声密度等参数,以及采用后处理方式多次对现场采集的列车数据进行滤波估计、参数调整和标定实验测定,AAIQM测量噪声协方差设置如下:
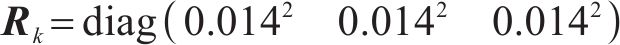
式中:参数值表示加速度计零偏不稳定性协方差,单位g。
因此,AAIQM离散卡尔曼滤波模型的总体更新框架可描述为:
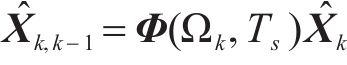
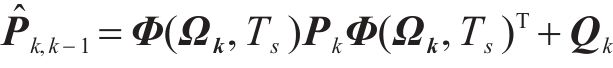
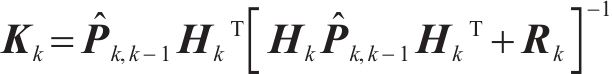
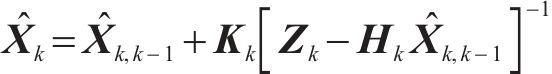
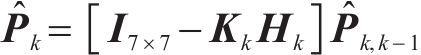
式中:k表示第k时刻,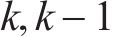
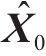
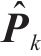
综上,式(35)和式(36)完成状态空间投影并计算式(19)状态先验状态估计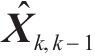
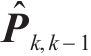

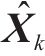
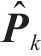
2.2 AAIQM增强的INS/ODO组合定位系统
在卫星完全失效的场景下,传统INS/ODO组合定位系统的观测信息依赖ODO解算的位、速信息实现对INS的信息进行校正,然而其观测信息是依赖INS解算的姿态信息进行反向融合,因此观测解算精度会伴随INS惯性解算姿态误差累计而迅速发散,导致组合定位系统误差发散严重。为此,本文提出基于AAIQM增强的列车状态感知系统,最大限度保障卫星失效时列车惯性解算精度。具体框架见图2。
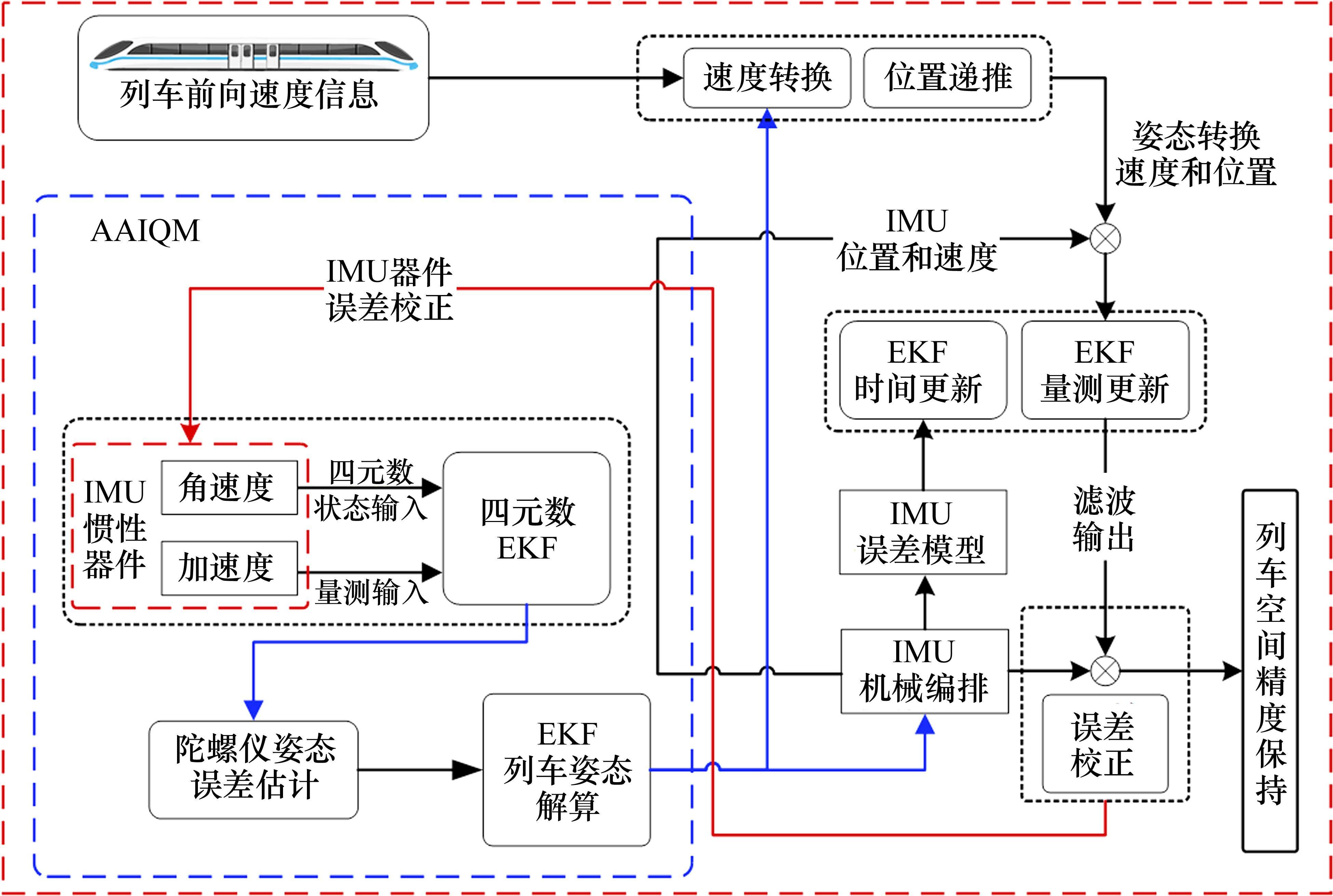
卫星失效时,基于式(12)惯性误差传递规律进行位、速、姿建模,列车前向速度信息通过AAIQM得到可信姿态信息,进而转换将速度转换为n系下三轴速度、三轴位置信息。
因此,基于AAIQM增强的INS/ODO组合定位系统的观测矩阵将式(10)更新为:
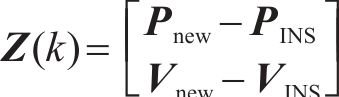
式中: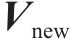

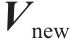


经过多次对现场采集的列车数据进行滤波估计、参数调整和标定实验测定,本文中测量噪声协方差设置如下:

式中:1~3维向量参数量表示位置噪声协方差,单位是m2,4~6维表示速度噪声协方差,单位是(m/s)2。
进一步将其作用值与惯性递推值映射到外层状态空间,通过式(5)~式(9)完成系统的滤波校正,将卡尔曼滤波计算的姿态误差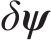
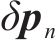
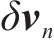
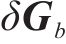
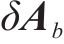
3 实验设备及性能验证
3.1 实验描述
3.1.1 实验室环境下实验描述
为验证基于AAIQM列车姿态精度保持方案,首先,在实验室环境下搭建仿真平台,将MEMS级SBG-ELLIPSE2惯导放置在高精度双轴位置速率转台JDZT-220中心位置,惯导输出频率200 Hz,通过转台静态和动态对模型进行算法模型初步验证,设备图如图3所示,SBG-ELLIPSE2惯性单元参数见表1。

| 加速度计 | 陀螺仪 | |
|---|---|---|
| 零偏稳定性 | ±14 mg | ±0.4(°)/s |
| 随机游走噪声密度 | ±57 µg/√Hz | ±0.18 (°)/√hr |
3.1.2 铁路实际环境下实验描述
为验证基于AAIQM列车姿态精度保持模型以及基于AAIQM增强的INS/ODO组合定位系统在实际铁路的解算性能,选取实验室团队于2023年9月采集的青藏铁路线实际行车数据进行验证,两颗卫星天线安装于车头正上方顶端并平行于车身排列,高精度光纤陀螺惯导SPAN-FSAS、MEMS级SBG-Ellipse-D惯导固定于车厢内部,惯导输出频率为200 Hz。高精度惯性组合系统NovAtel-SPAN的实时高精度紧组合INSPVA结果和SBG-Ellipse-D惯导双天线自滤波作为定位性能评估的参考真值。实验车辆设备如图4所示,SBG-Ellipse-D惯性单元参数见表2。

| 加速度计 | 陀螺仪 | |
|---|---|---|
| 零偏稳定性 | ±5 mg | ±0.4 (°)/s |
| 随机游走噪声密度 | ±57 µg/√Hz | ±0.18 (°)/√hr |
3.2 基于AAIQM列车姿态解算精度分析
3.2.1 实验室环境下模型可行性验证
在不使用磁力计的情况下,室内环境无法获得准确的航向初值,因此,只要通过分析横滚角及俯仰角运动规律来验证方案可行性。分别采用静态实验和动态实验进行AAIQM可行性分析。
AAIQM静态性能测试步骤为:惯导放置在转台中心,上电开始记录,全程转台保持静置,测试结果如图5(a)所示;AAIQM动态性能测试步骤为:惯导放置在转台中心,上电后,转台以顺时针方向6 (°)/s速度进行旋转、横滚角Roll和俯仰角Pitch保持静态,测试结果如图5(b)所示。
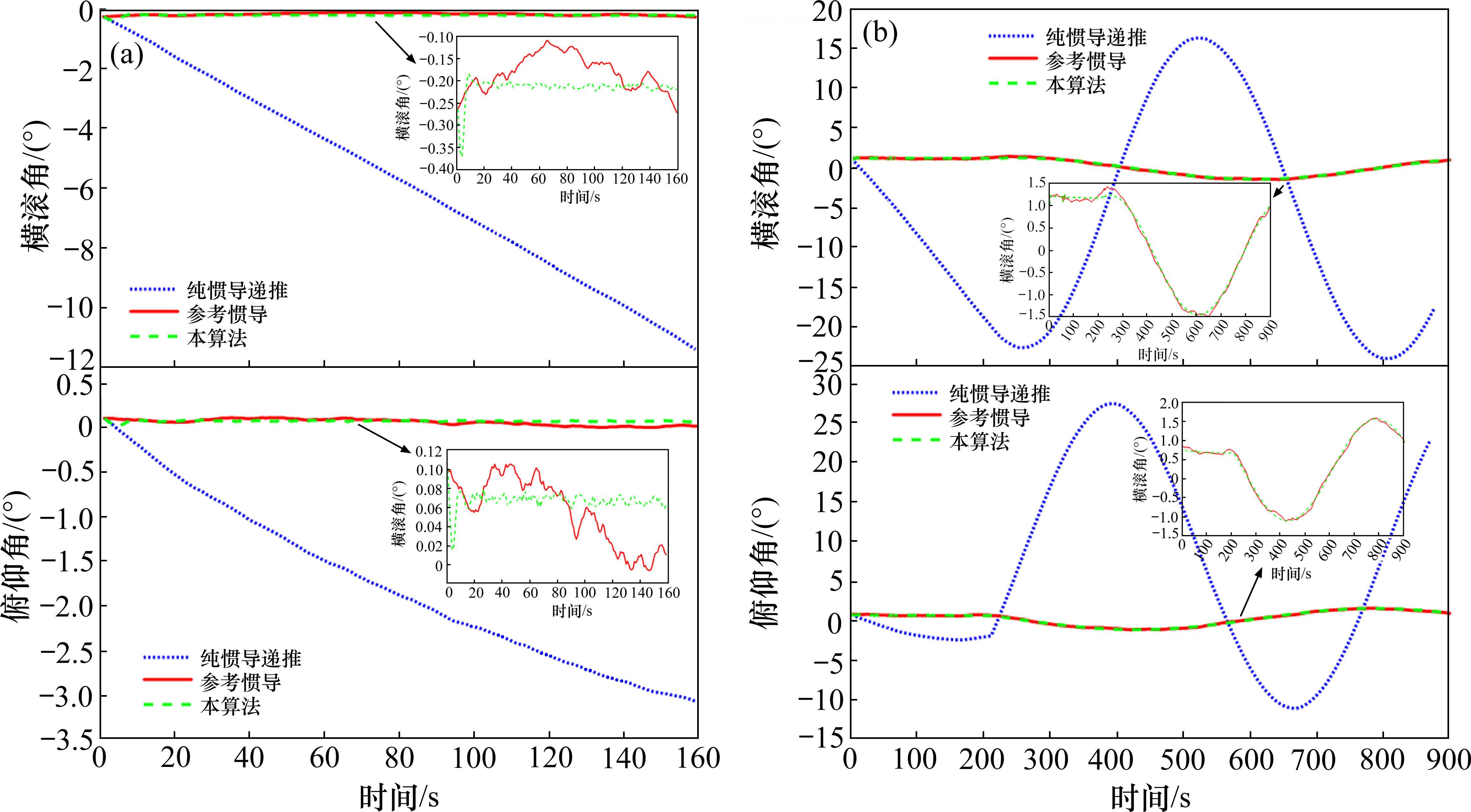
由图5(a)可知,静态AAIQM结果较优,上电启动后,纯惯性器件递推无可用姿态信息进行校准,导致姿态线性快速发散。而本文提出的基于AAIQM惯性姿态解算模型结果较优,通过加速度计的自校准,横滚角Roll、俯仰角Pitch均未出现明显波动,与参考惯导SBG自滤波结果一致,符合预估设计以及精度要求;动态结果由图5(b)可知,基于AAIQM的惯性姿态解算的横滚角Roll和俯仰角Pitch姿态解算均与SBG滤波结果保持一致,而未建模的惯性器件姿态横滚角最高发散至15°、俯仰角发散至25°。
表3是上述测试结果的定量分析,其中,误差精度分析采用静态实验均方根误差(smooth root mean square error, SRMSE)及动态实验均方根误差(dynamic root mean square error, DRMSE),IMU代表惯导纯依靠陀螺仪计算模式,AAIQM为本文提出的姿态解算模式,参考均为SBG自滤波结果。由表3可知,AAIQM算法横滚角和俯仰角静态均方根误差为0.039°和0.043°,动态均方根误差为0.067°、0.073°。测姿精度明显优于纯惯导递推。
| 横滚角 | 俯仰角 | |||
|---|---|---|---|---|
| IMU | AAIQM | IMU | AAIQM | |
| SRMSE/(°) | 2.113 | 0.039 | 6.935 | 0.043 |
| DRMSE/(°) | 65.195 | 0.067 | 72.344 | 0.073 |
综上,实验室环境下仿真结果充分验证了基于AAIQM的列车姿态精度模型的可行性。
3.2.2 铁路实际环境下模型性能验证
姿态初始信息由SBG接入双天线测得,测试过程中列车由西北方向运行至东南方向,测试时间为30 min,本算法全程仅依赖惯性器件,未接入卫星校正信息。列车运行线路如图6所示。
为验证基于AAIQM列车姿态精度保持模型的实际列车解算精度保持性能,选择与捷联惯导机械编排为底层驱动的惯性器件递推模型做结果对比,结果如图7所示。
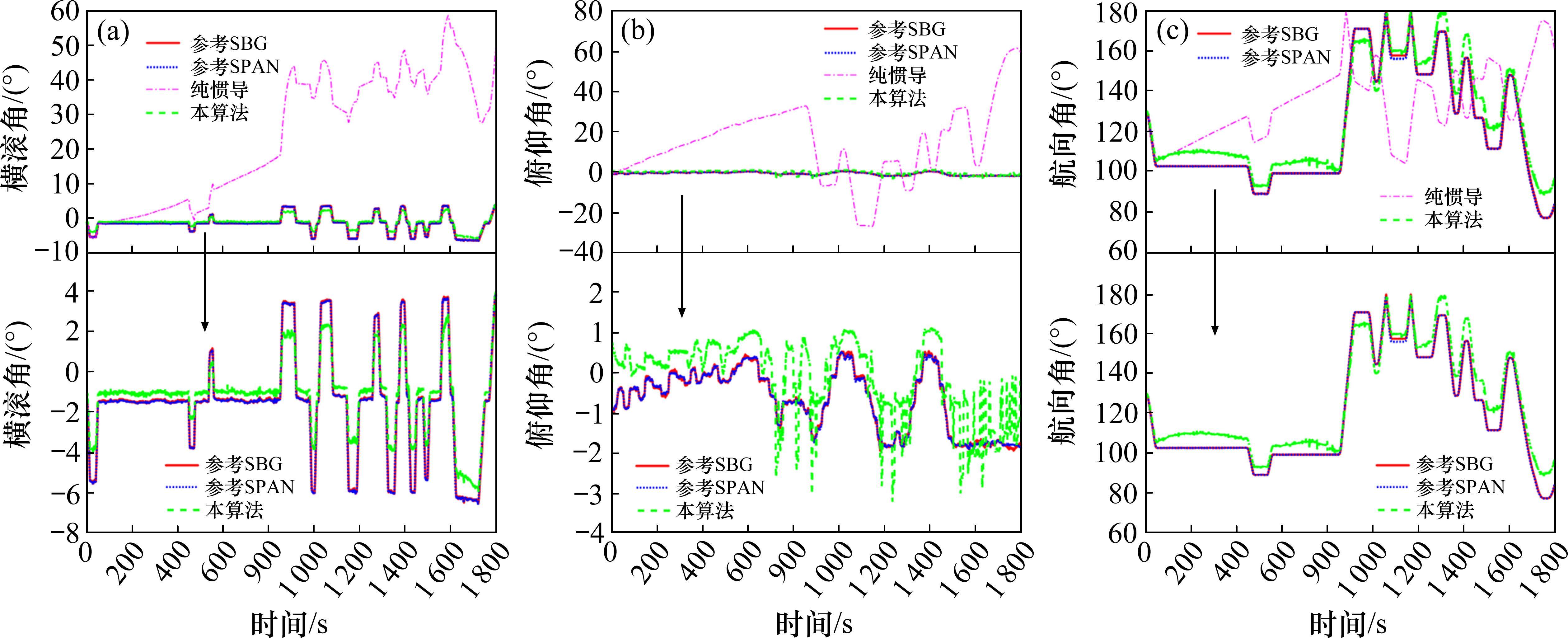
由模型解算结果可知,从宏观层面分析,图7(a)横滚角解算结果、图7(b)俯仰角解算结果、图7(c)航向角解算结果中,纯惯导递推模式均出现发散状态,本文提出的基于AAIQM惯性姿态解算精度显著优于纯惯导解算精度,因此充分证明在卫星失效时,通过本算法可以维持惯导解算精度。
进一步,通过上述分析可知SBG接入双天线解算结果与SPAN接入天线及DTU差分信号解算INSPVA的姿态结果近似,因此为方便分析,全程采用SBG接入双天线测得姿态参考结果,误差结果如图8所示。
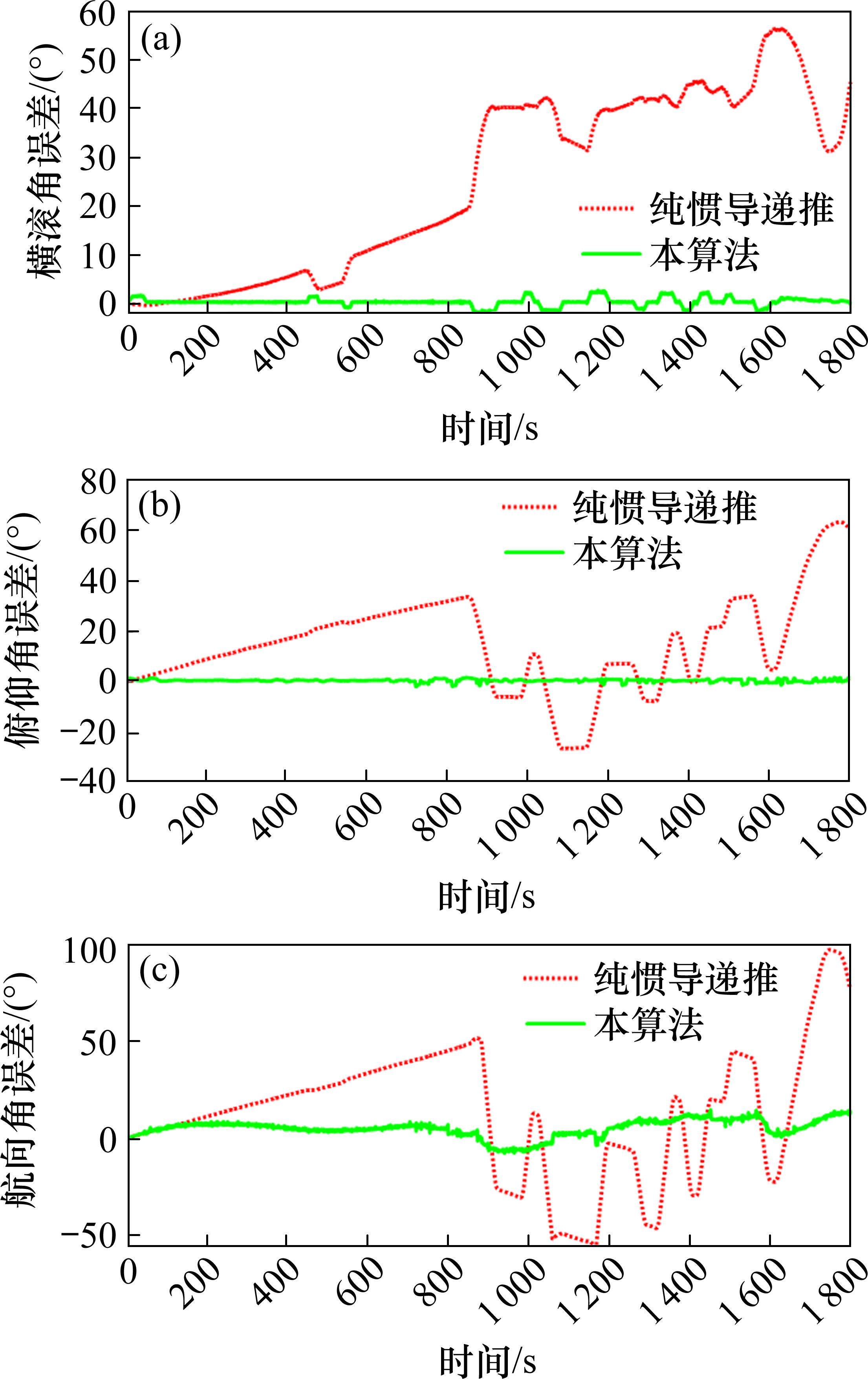
表4是上述测试结果的定量分析,其中,采用均方根误差(root mean square error, RMSE)进行性能分析。IMU为纯惯导计算模式,AAIQM为本文提出的姿态解算模式,通过结果可知,本算法解算的横滚角、俯仰角、航向角均方根误差为0.801°、0.513°和4.494°,测姿精度明显优于纯惯导递推。
| 横滚角RMSE/(°) | 俯仰角RMSE/(°) | 航向角RMSE/(°) | |||
|---|---|---|---|---|---|
| IMU | AAIQM | IMU | AAIQM | IMU | AAIQM |
| 18.317 | 0.801 | 18.557 | 0.513 | 33.653 | 4.494 |
综上,实车采集模式下测试结果充分验证基于AAIQM模型的姿态解算性能及精度。
3.3 基于AAIQM增强的INS/ODO组合定位系统精度分析
测试环境、测试数据与测试设备同前一节,为验证基于AAIQM增强的INS/ODO组合定位系统的模型性能,列车前向速度为采用卫星单点定位测得的速度,频率为1Hz,单点定位速度曲线与精度见图9。模型精度分析选择与INS/ODO松组合的定位结果进行比较,测试时间为15 min,2种定位方法的位置误差、测速误差、测姿误差见图10。
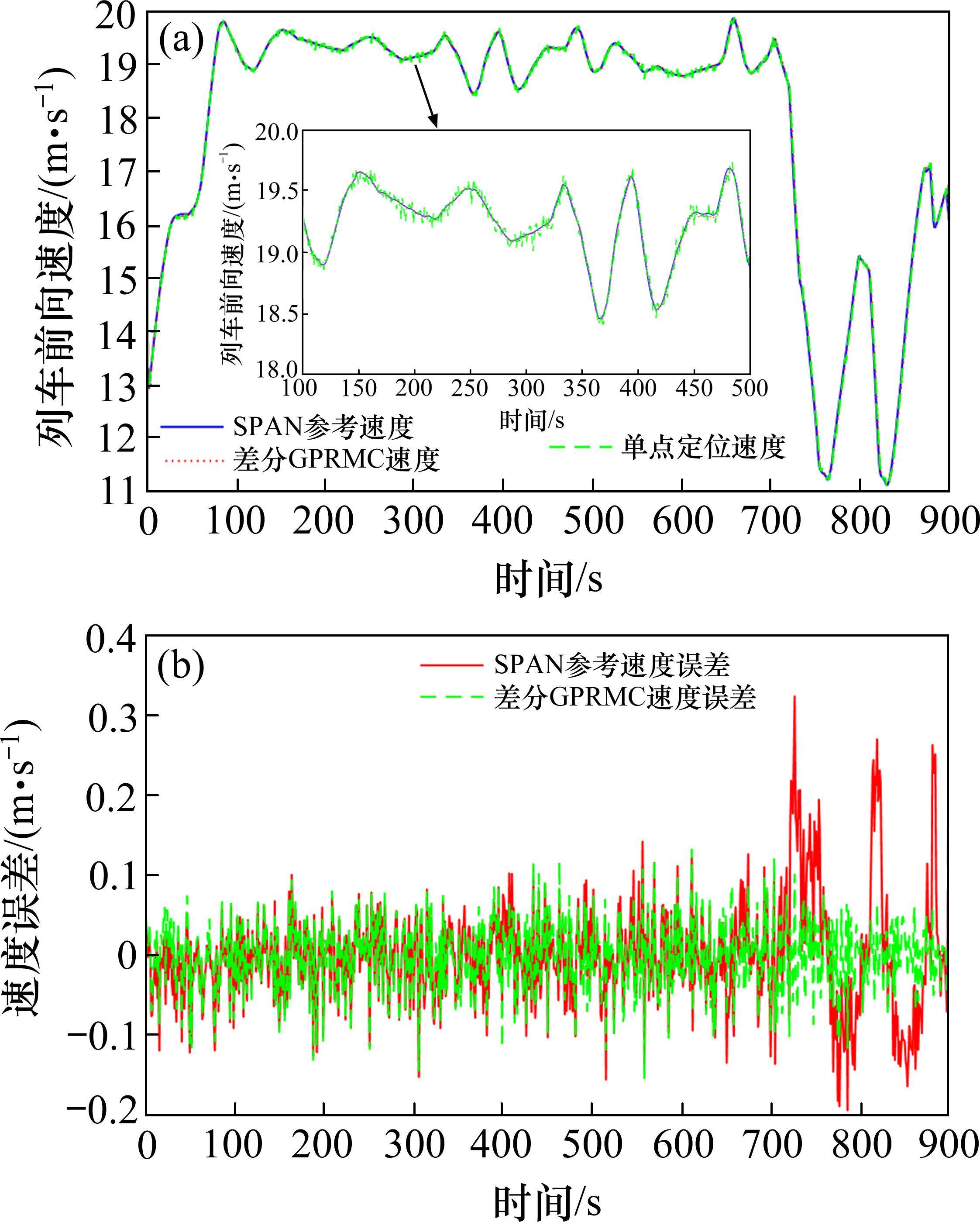
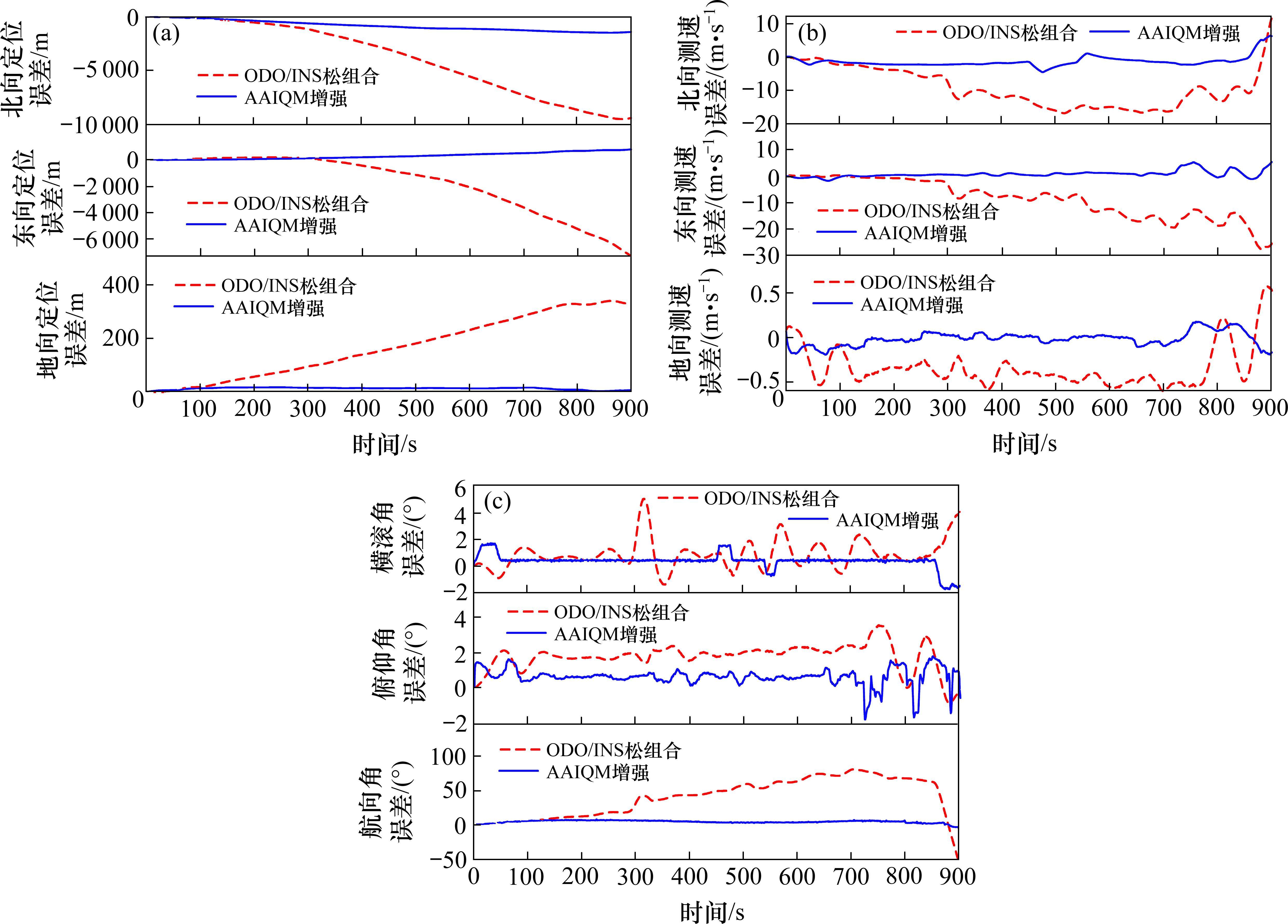
定位性能由图10(a)可知,相较INS/ODO松组合模式,15 min AAIQM定位误差明显发散速度减弱,精度明显提升;测速性能由图10(b)可知,相较INS/ODO松组合模式,虽然15 min末AAIQM测速误差有一定上升趋势,但由于测姿与定位模型的辅助校正,发散程度明显优于INS/ODO松组合模式,列车运行全程精度明显提升;测姿性能由图10(c)可知,相较INS/ODO松组合模式,15 min AAIQM测姿精度保持性能稳定,充分验证本算法测姿性能。
为更加准确地量化评估2种方法的定位、测速、测姿精度,分别采用均方根误差对2种方法进行分析,统计结果见表5。
| 定位误差/m | 测速误差/(m∙s-1) | 测姿误差/(°) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 北 | 东 | 地 | 北 | 东 | 地 | 横滚角 | 俯仰角 | 航向角 | |
INS/ODO 松组合 | 3 267.079 | 2 199.590 | 112.753 | 5.829 | 7.296 | 0.230 | 1.073 | 0.752 | 27.595 |
AAIQM 模型 | 464.151 | 246.114 | 4.035 | 1.565 | 1.227 | 0.078 | 0.526 | 0.493 | 1.904 |
由表5可知,定位方面,AAIQM模型在北向、东向、地向的定位RMSE分别为:464.151、246.114、4.035 m,相较INS/ODO松组合三向定位精度分别提高85.79%、90.17%、96.42%;测速方面,AAIQM模型在北向、东向、地向的测速RMSE分别为:1.565、1.227、0.078 m/s,相较INS/ODO松组合三向测速精度分别提高73.15%、83.18%、66.09%;测姿方面,AAIQM模型横滚角、俯仰角、航向角的测姿RMSE分别为:0.526°、0.493°、1.904°,相较INS/ODO松组合三向测姿精度分别提高50.98%、34.44%、93.10%;综上,充分验证基于AAIQM增强的INS/ODO组合定位系统的位、速、姿惯性解算性能。
4 结论
1) 本算法在真实列车行车环境且无卫星校正情况下,解算的横滚角、俯仰角、航向角30 min均方根误差可达到0.801°、0.513°和4.494°,相较于惯性结果精度显著提升。
2) 为进一步解决单一驱动模式下航位推算的可控性受限问题,基于AAIQM增强的INS/ODO组合导航系统在卫星失效15 min的水平定位精度提升86.66%、水平测速精度提升78.70%;横滚角、俯仰角、航向角测姿精度分别提升50.98%、34.44%、93.10%。
3) 充分证明长时间无卫星信息时,AAIQM模型可以最大限度保证列车空间精度,扩展MEMS惯性导航系统在铁路实际应用中的精度保持能力,提升卫星失效场景下列车以惯性为中心的状态感知精度。
姜维,郝鹏琪,王剑等.基于惯性四元数建模的列车姿态精度保持方法研究[J].铁道科学与工程学报,2025,22(04):1492-1505.
JIANG Wei,HAO Pengqi,WANG Jian,et al.Research on train attitude accuracy maintenance method based on inertial quaternion modelling[J].Journal of Railway Science and Engineering,2025,22(04):1492-1505.

