高速列车在高速运行过程中,由于不同的轨道路段及周围复杂的空气流场,对车体本身造成的振动、冲击以及气动效应尤为复杂[1-2]。外风挡系统作为高速列车车端连接处的关键组成部分,其主要功能在于有效隔离外部气动压力与车内压力,同时减少外部振动噪声与气动噪声,并承担着在列车通过曲率线路时受到拉伸和挤压力的重要职责。近年来,对于高速列车外风挡的研究日益增多。在气动特性方面,学者们针对头尾车外形、转向架、风挡等关键部位的气动性能进行了大量研究[3-5]。随着列车行驶速度的增加,外风挡面临着更大的气动载荷,导致橡胶外风挡内侧产生由内向外的压差,压差的增大会引起风挡连接处的胶囊外翻,从而导致外风挡损坏[6]。同时,由于空气流场作用,气动载荷会导致车辆在高速运行时风挡产生剧烈振动,出现橡胶外风挡结构变形,安装底部出现裂纹、龟裂、脱漆或破坏等现象[7-8]。YAMAZAKI等[9]通过实车测试研究了风挡结构对列车在隧道和明线运行期间产生噪声的影响,确定风挡连接部位是气动噪声的主要来源之一,并提出措施以减少风挡位置的噪声辐射。MIZUSHIMA等[10]通过在高速列车实际运行时进行了气动噪声数据采集,分析了不同风挡结构对高速列车气动噪声的影响特性。SHIRAISHI等[11-12]利用低噪声风洞试验分析了风挡连接部位的气动噪声特性,并研究了不同外风挡形式对列车气动噪声的影响。唐明赞等[13]利用湍流模型研究了外风挡安装间距对风挡气动特性的影响,研究结果表明安装间距对于风挡受侧向力影响较大,尤其是橡胶弧顶与来流相对的外风挡所受侧向力与安装间距成二次函数关系,这一发现为外风挡结构强度与优化设计,以及安装位置精度要求提供了指导。史永达等[14]通过流固耦合的数值模拟方法,分析了高速列车在不同横风风速条件下外风挡的气动性能,研究结果表明外风挡在迎风侧的尾流区域产生最大位移和应力,且随横风风速的提高而增大。蒋文杰等[15]利用50通道球形声阵列系统,研究了风挡区域车内噪声的分布特征,发现风挡底部为主要声源,基于车内噪声频谱特征,制定相应减振措施,为高速列车风挡区域的减振降噪提供依据。盖杰等[16]针对不同形式的外风挡结构进行流体仿真与压力测试试验分析,通过对比分析不同结构外风挡处的气动载荷及压力的变化,为外风挡的结构设计提供指导依据。张坤等[17]对于外风挡的类型、研制与生产现状进行了阐述,提出了存在外风挡变形、龟裂、脱漆及变黄等问题,同时提出了针对性的解决方案,对后续外风挡的优化设计具有一定的指导意义。高军等[18]对高速动车组的外风挡结构进行探讨,从外风挡的结构形式、材料选择、减阻效果、气动噪声与隔声效果等方面综合考虑,为外风挡结构的优化设计提供方式方法。蔡鉴明等[19]对U型橡胶外风挡进行了模态试验与有限元模态分析,并研究了网格数量与模态结果的相关性,为U型橡胶外风挡结构设计提供参考。综上所述,外风挡的振动与噪声息息相关,对高速列车运行、乘客的舒适性有着较大影响。本文聚焦于橡胶外风挡的振动特性研究,旨在提高其减振降噪的性能。设计并提出6种方案,从橡胶截面形状、橡胶硬度以及橡胶肩部开口宽度3个方面进行优化分析。考虑了列车经过不同过弯半径时外风挡之间产生的压缩量,并对各方案进行了模态分析,研究不同压缩量下各方案固有频率的变化趋势。随后,通过模态试验,将试验数据与理论计算数据进行对比,验证理论计算的准确性,以确定最终的优化方案。
1 橡胶外风挡原方案有限元模态分析
1.1 原方案185橡胶截面模态分析
模态分析包含自由模态和约束模态2种,其中自由模态适用于更为复杂的结构,无需定义边界条件,且前6阶计算结果通常接近于0,不具备实际的意义。因此,结合本文实际情况考虑,采用约束模态的Direct求解法进行模态分析。
1.1.1 模型建立、材料参数及边界条件设定
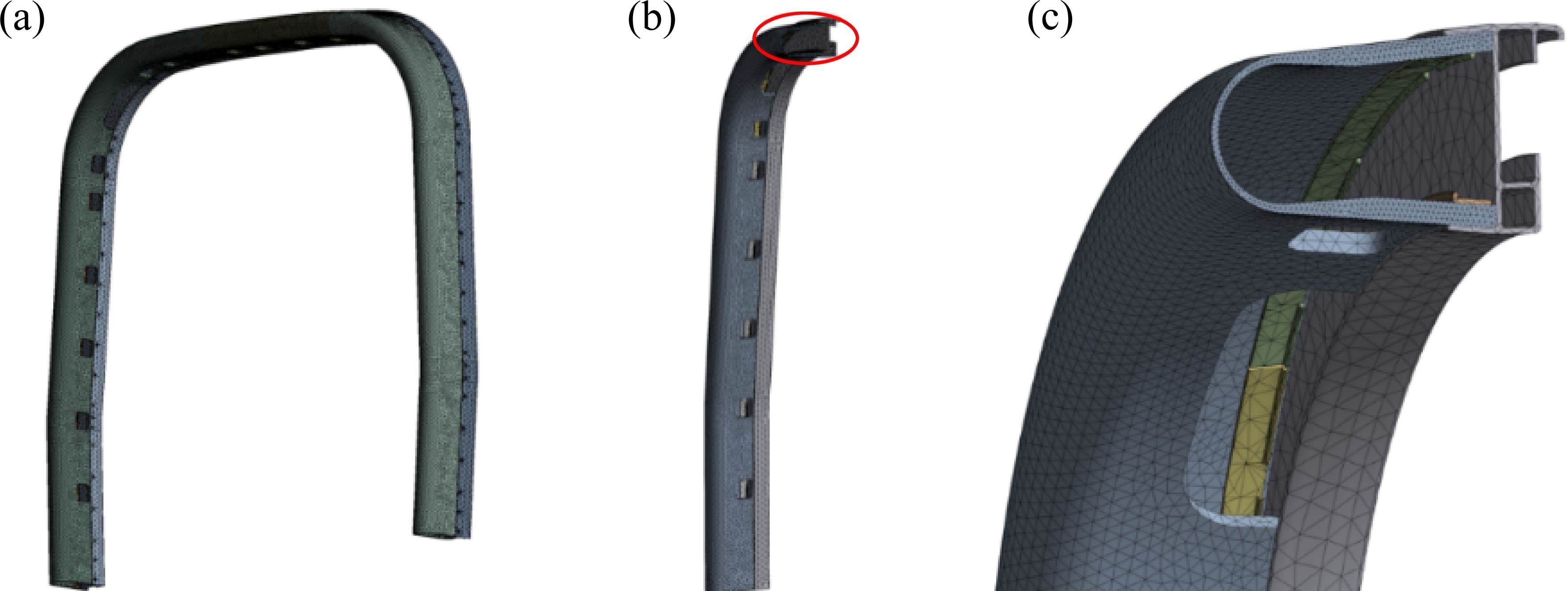
以高速列车橡胶外风挡三维模型作为原方案模型,其整体模型如图1(a)所示,橡胶截面与肩部开口的具体参数分别如图1(b)和图1(c)所示。其中,橡胶宽度185 mm,整体高度330 mm,肩部开口宽度140 mm。铝合金部件选用6063-T5系铝合金材料参数,弹性模量71 GPa,密度2.77 g/cm3,泊松比0.3。橡胶则使用Mooney-Rivlin超弹性本构模型,具体参数为C10=139 95,C01=979 864,C11=-1.8111。为了更加真实地模拟实际状态,在Ansys中采用了非线性分析方法,与橡胶接触的铝型材和螺栓的接触面设定为摩擦接触,而其他接触面则设定为绑定接触。由于铝型材与橡胶通过螺栓进行紧固连接,两者之间存在较大的摩擦效应,因此摩擦因数设定为0.5。同时,鉴于单元的位移和形变可能导致刚度矩阵的变化,启用了大变形求解器。外风挡整体模型与侧部模型的网格划分模型如图2所示。为了确保计算结果的准确性和效率,首先进行了网格无关性验证。通过对比橡胶的整体网格在不同尺寸(10、15、20、25 mm)下的仿真结果(如表1所示),发现当网格尺寸小于20 mm时,各阶模态频率趋于稳定,表明网格细化对结果影响有限。综合考虑计算精度与效率以及1.3节中模拟压缩量变化时网格大小对收敛速度的影响,最终橡胶整体网格尺寸确定为15 mm,橡胶截面网格细化至5 mm,而铝合金部件作为非重点研究对象,其网格尺寸则设定为30 mm。整个模型采用四面体实体网格进行离散,共计355 507个单元和685 769个节点。

| 橡胶网格大小/mm | f1/Hz | f2/Hz | f3/Hz | f4/Hz | f5/Hz | f6/Hz |
|---|---|---|---|---|---|---|
| 25 | 20.677 | 23.049 | 25.885 | 28.358 | 32.948 | 34.099 |
| 20 | 20.002 | 22.442 | 25.438 | 27.833 | 32.456 | 33.638 |
| 15 | 19.531 | 22.116 | 25.257 | 27.710 | 32.443 | 33.408 |
| 10 | 19.236 | 22.139 | 25.181 | 27.642 | 32.229 | 33.294 |
鉴于外风挡结构的主要特性集中于侧面,且整体结构具备对称性,选取了一段具有代表性的侧部模型(如图2(c)所示)进行深入对比分析,该侧部模型包含128 979个单元和245 697个节点。
1.1.2 原方案185橡胶截面模态结果分析
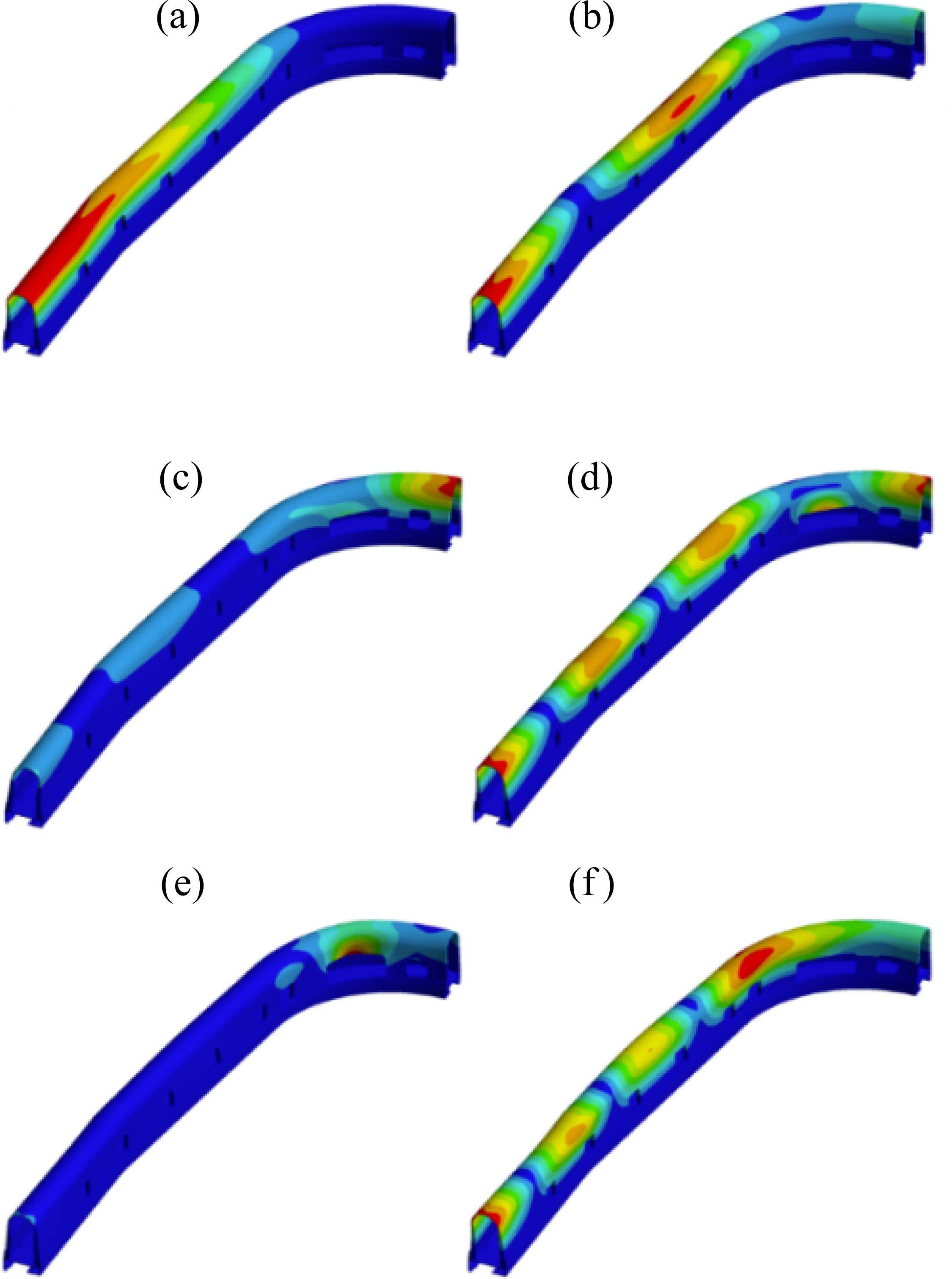
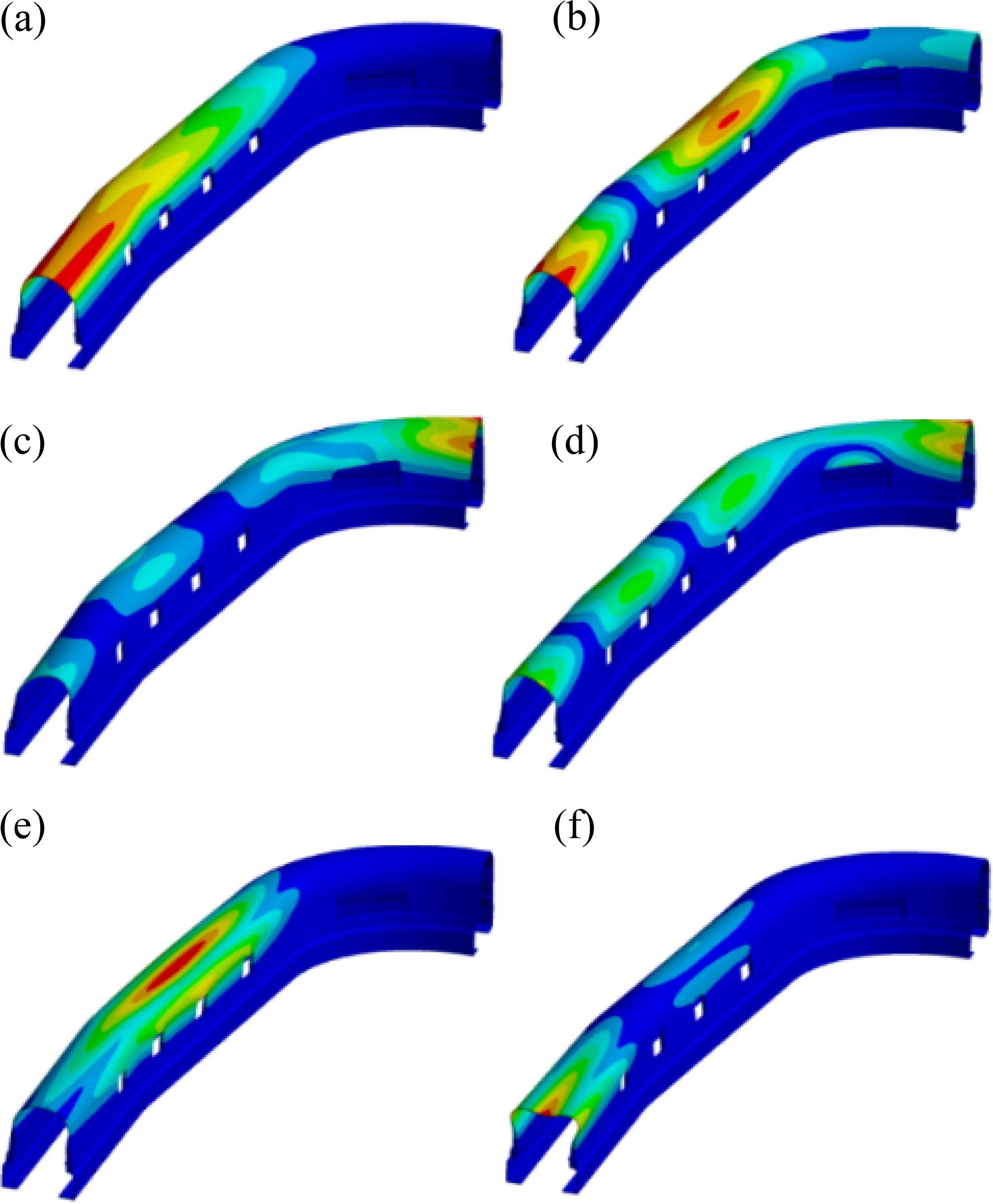
图3和图4分别为整体外风挡结构与侧部外风挡结构的前6阶模态振型图例。表2则系统地列出了这2种结构在各自前6阶模态下的变形量大小。通过对比可知,整体外风挡与侧部外风挡结构在形变量上基本一致,同时两者的振型特征也基本吻合。具体而言,1阶与3阶模态均表现为单一的最大形变区域;而2阶、4阶以及6阶模态则均展现出多个最大形变点,且这些形变点均集中在外风挡结构的圆弧部分顶部;另外,5阶模态的最大形变位置则位于橡胶肩部开口处。

| 模态 | 整体外风挡结构 形变/mm | 侧部外风挡结构 形变/mm |
|---|---|---|
| 1阶 | 18.325 | 18.423 |
| 2阶 | 15.741 | 16.431 |
| 3阶 | 18.268 | 18.792 |
| 4阶 | 14.734 | 15.432 |
| 5阶 | 44.983 | 46.524 |
| 6阶 | 24.858 | 25.772 |
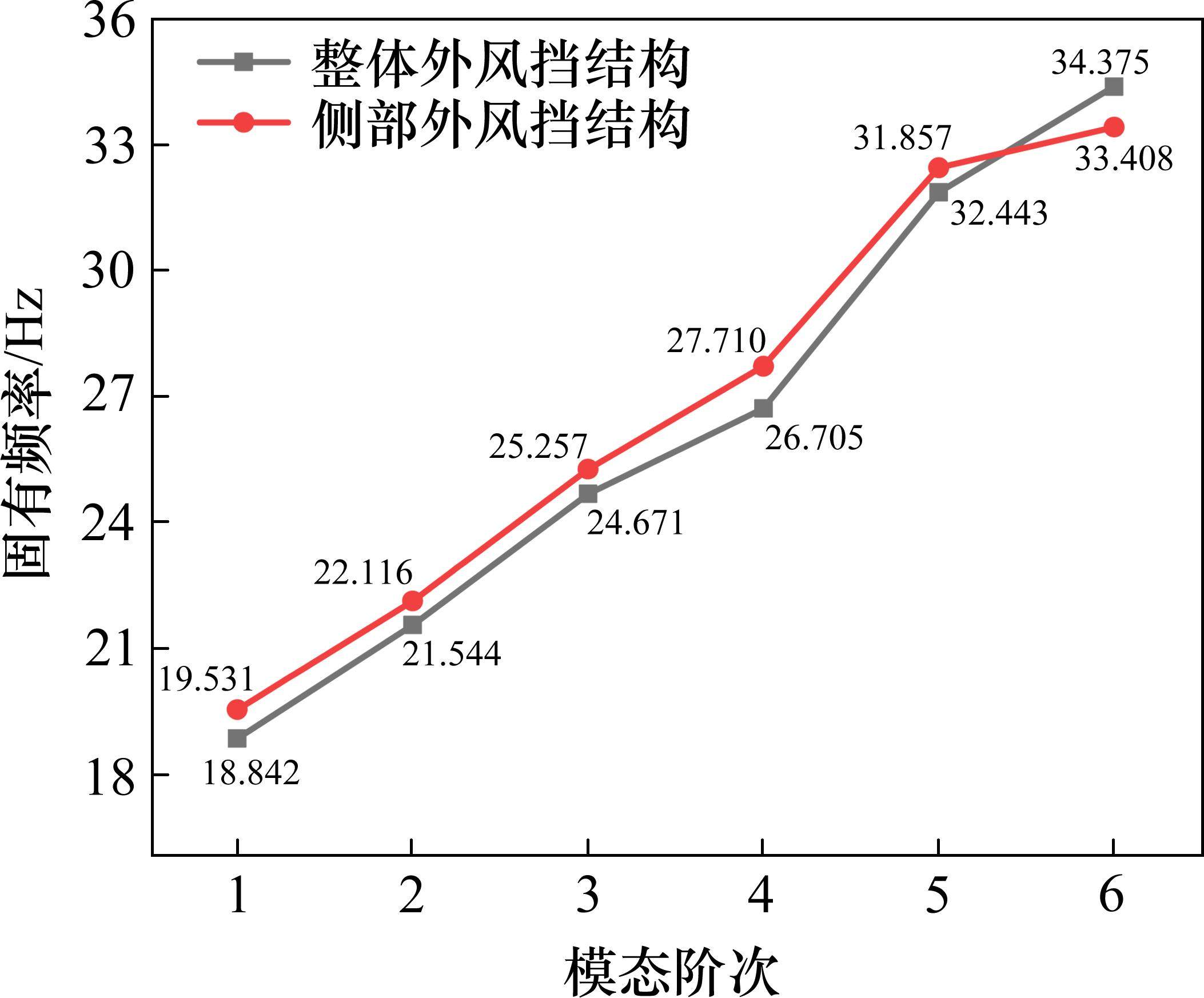
图5为整体外风挡结构与侧部外风挡结构的频率汇总对比,结果显示两者频率值基本相近。因此,可合理采用局部代替整体的方法,以提高后续的计算效率。进一步观察整体趋势,外风挡结构的前6阶固有频率展现出随振动阶次递增而逐渐升高的特性,并且侧部外风挡的最低频率达到19.531 Hz,而最高频率则不超过33.408 Hz,说明橡胶作为一种柔性材料,其特性倾向于更易激发低阶模态振型。
1.2 橡胶外风挡不同结构方案在无压缩量下的模态分析
图6(a)、图6(b)和图6(c)分别为外风挡结构的主要特征以及145和280这2种不同橡胶截面方案的示意图。
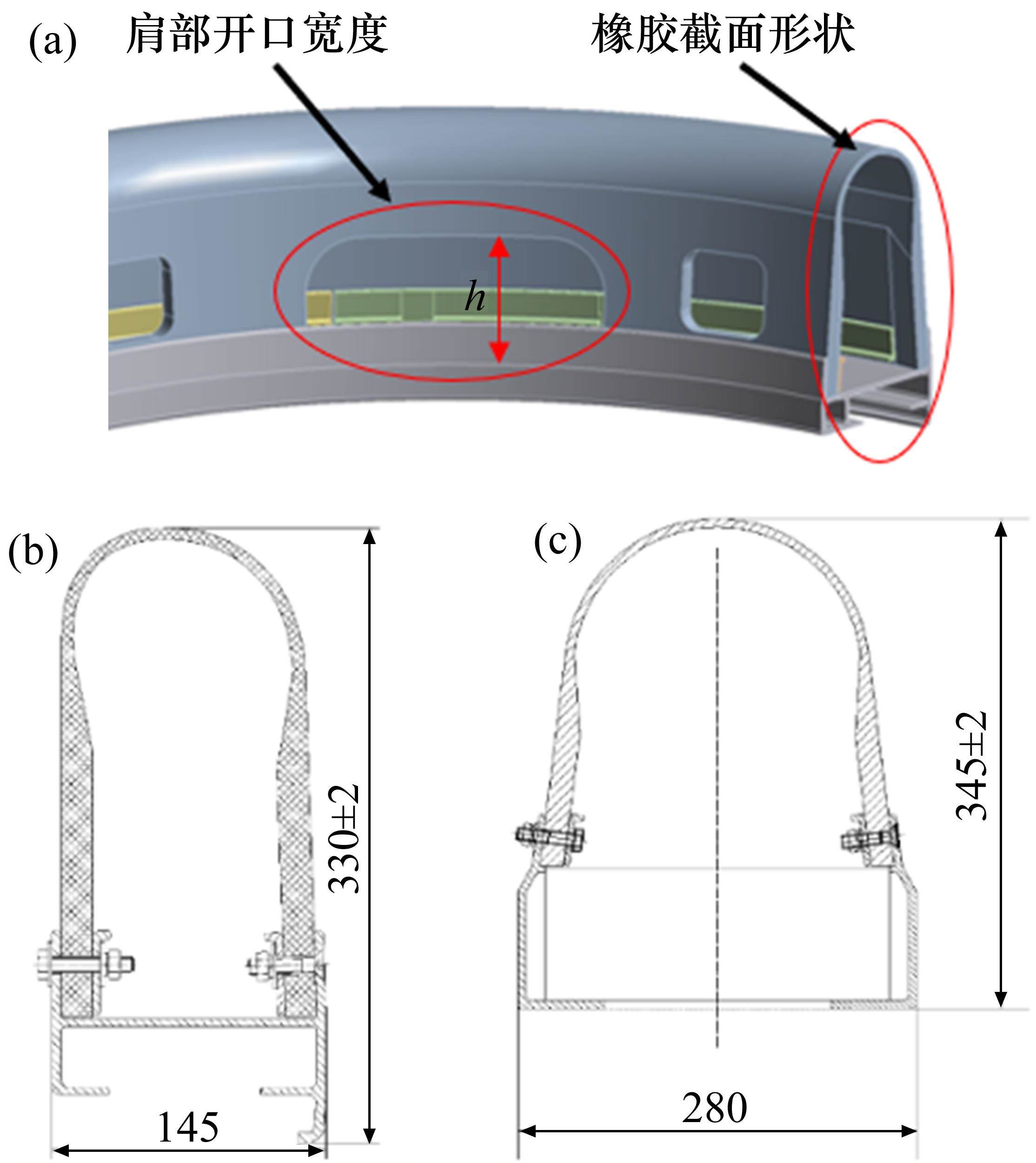
为了对比外风挡的橡胶截面形状、材料硬度与肩部开口宽度等关键结构参数对振动频率的影响,选取了如表3所示的外风挡方案参数。其中,方案1、方案2为在原方案基础上改变截面形状,使其截面过渡更加平缓;方案2、方案3、方案4通过改变材料硬度来调控外风挡的刚度,进而分析刚度变化对振动特性的影响;方案2、方案5、方案6通过改变肩部开口宽度,研究不同肩部开口宽度对振动频率的影响。
| 方案 | 截面 | 材料硬度 | 肩部开口宽度/mm |
|---|---|---|---|
| 原方案 | 185 | 70 | 140 |
| 1 | 145 | 70 | 140 |
| 2 | 280 | 70 | 140 |
| 3 | 280 | 66 | 140 |
| 4 | 280 | 62 | 140 |
| 5 | 280 | 70 | 125 |
| 6 | 280 | 70 | 110 |
图7(a)为原方案与方案1、方案2的前6阶固有频率对比。从图中可以明显观察到,尽管3种橡胶截面方案在频率变化趋势上大体保持一致,但具体数值上存在差异。具体而言,145橡胶截面方案相对于原方案,其频率最高降低了12%;而280橡胶截面方案最高降低达17.86%,且2种方案的前6阶固有频率均低于原方案。进一步分析,整体而言,280橡胶截面在降低外风挡振动频率方面优于145橡胶截面,说明调整橡胶截面设计能够有效降低外风挡的振动频率。图7(b)为方案2、方案3和方案4中材料硬度变化对固有频率的影响。从图中可以看出,随着材料硬度的逐渐降低,外风挡的固有频率也相应下降,这也与力学理论相吻合,即材料硬度的降低直接导致了橡胶刚性的减弱,进而有效降低了外风挡的振动频率。图7(c)则呈现了不同肩部开口宽度方案(110~140 mm范围内)的前6阶固有频率对比情况。可以发现这3种方案的频率变化曲线高度重合,表明在此范围内的肩部开口宽度变化并未对外风挡结构的固有频率产生显著影响。从而可以推断,对于当前设计的外风挡而言,110~140 mm的肩部开口宽度对外风挡结构频率基本无影响。
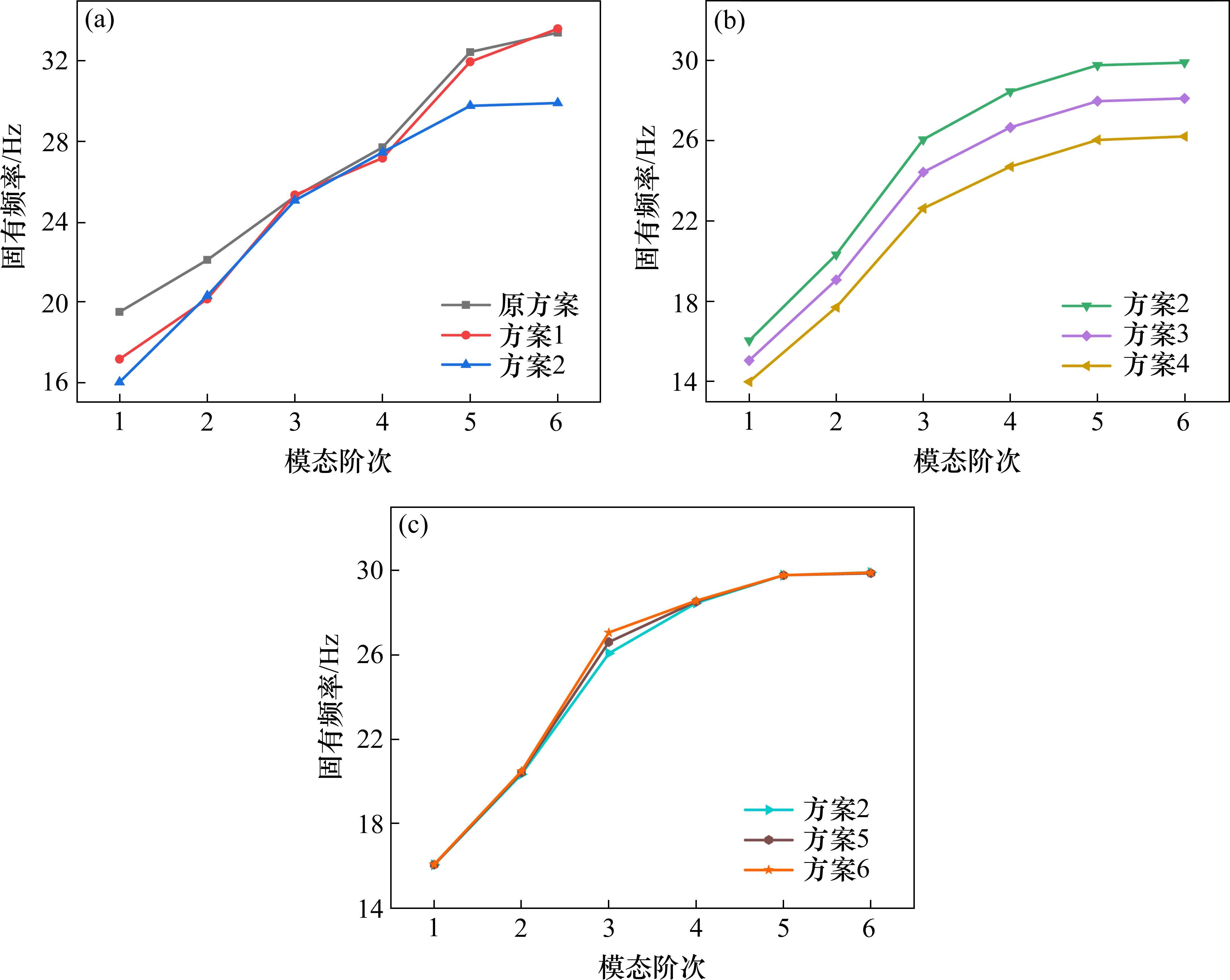
综合对比图7中所示的各个方案的前6阶固有频率,还可以发现,方案4在所有这些阶次上的固有频率均呈现为最低值。进一步观察方案4的外风挡模态振型图(如图8所示),可以发现在各阶模态下,主要的形变区域均集中在橡胶顶部,这一特点在多个振动模态中保持一致。
1.3 橡胶外风挡不同结构方案在不同压缩量下的模态分析
列车的外风挡设计通常采取两两相对的安装方式,固定于车厢的两端,其间预设了一定的预压缩量以确保密封与稳定性。当列车行驶至具有不同过弯半径的路段时,这种预压缩量会随之发生动态变化:内侧风挡被进一步压缩,而外侧风挡的压缩量随之减小。为进一步研究此过程中压缩量变化对外风挡模态振型及其固有频率的具体影响,进行了外风挡之间不同压缩量的模态分析。依据《机车车辆风挡》(TB/T 3094―2022)标准,在外风挡预压缩量20 mm,过弯半径R400 m时,内侧风挡压缩量约为130 mm。为模拟不同过弯半径时外风挡的压缩量大小,选取了如表4所示的6种工况。
| 工况 | 压缩量/mm | 工况 | 压缩量/mm |
|---|---|---|---|
| 1 | 20 | 4 | 100 |
| 2 | 40 | 5 | 120 |
| 3 | 80 | 6 | 140 |
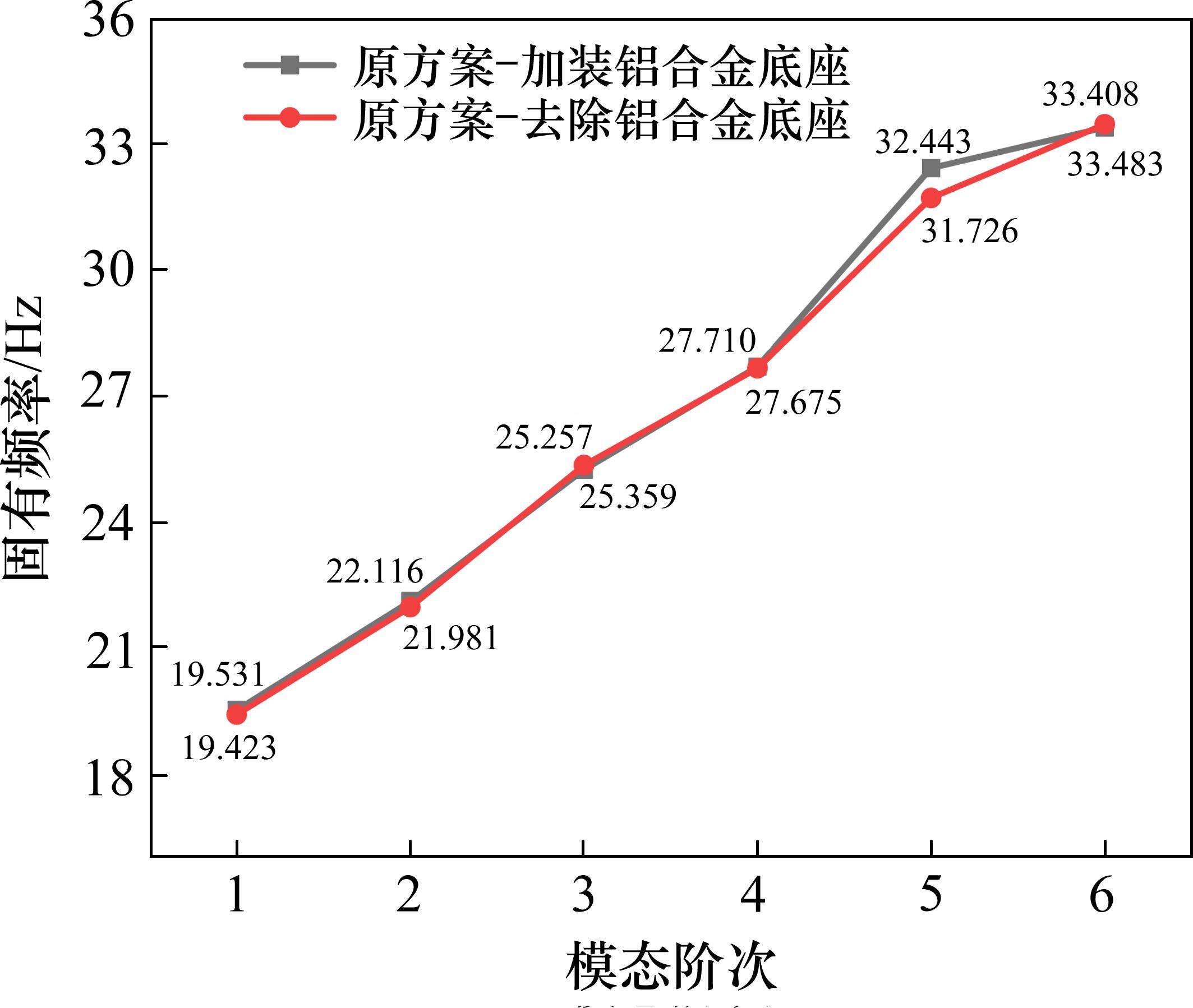
为了优化计算模型,进一步提升计算效率,拟去除铝型材底座,仅针对一对橡胶风挡结构进行仿真分析。图9展示了加装与去除铝合金底座2种情况下,各模态频率的对比结果。从图中可以看出,两者频率值基本接近,说明采用无铝合金底座的简化模型来替代原复杂模型进行计算的可行性。
针对原方案的装配模型,采取了特定的预处理措施:在下侧橡胶的底部设定分割面,施加固定约束,以确保模拟过程中的稳定性;同时,在上部橡胶的底面施加位移载荷,如图10(a)与图10(b)所示。图10(c)展示了模型的网格划分情况,采用四面体实体单元,在保证整体求解精度的前提下,对关键区域进行了网格加密处理。此外,橡胶与橡胶顶部之间的接触界面采用摩擦接触模型,设定摩擦因数0.7,以模拟真实条件下的相互作用。在计算过程中,启用大变形求解器,以确保橡胶材料的刚度矩阵能够在每一步计算中都得到及时更新,从而更加准确地反映材料在变形过程中的力学行为。

鉴于本次分析涉及复杂的几何非线性和接触非线性计算,为提升计算过程的收敛性与结果的准确性,设定每压缩10 mm作为一个主要载荷步,并在每个主载荷步内细分出100个子载荷步,以逐步递增的方式施加载荷。并且实际计算过程中,随着模型结构可能发生的变化,分析步的具体设定也会灵活调整,以适应实际情况。
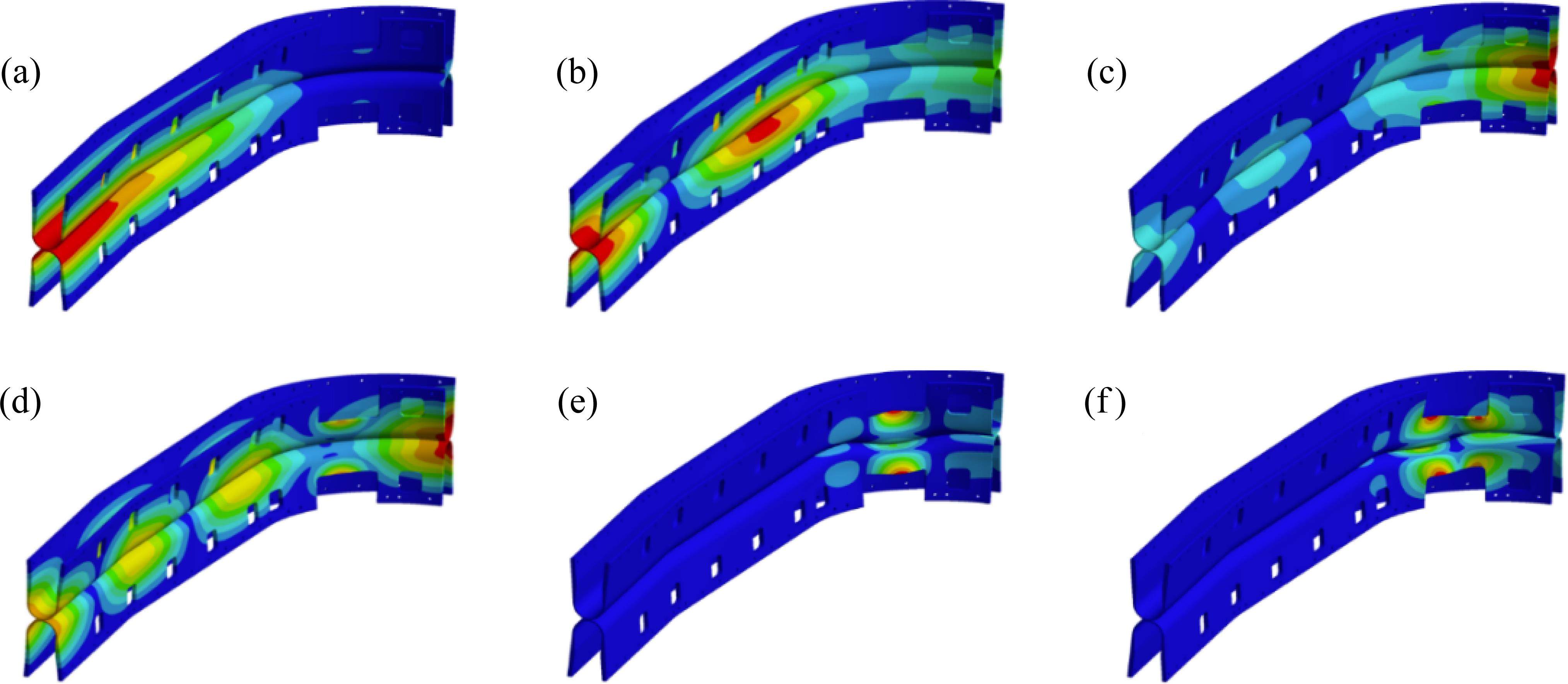
以原方案在40 mm压缩量条件时为例,通过计算得到相应的固有频率及振型,如图11所示。从图中可以发现,在外风挡的1阶和2阶模态下,振动形态主要表现为显著的左右方向扭转形变;而进入3阶和4阶模态时,振动模式转变为以内外扭转形变为主;至于5阶和6阶模态,振动则高度集中在肩部开口处,形成局部扭转形变。
进一步分析,图12展示了各方案在不同压缩量条件下固有频率的变化趋势。观察发现,随着外风挡之间压缩量的逐渐增大,结构的固有频率普遍呈现出下降的趋势。具体地,在压缩量为20 mm时,方案1的固有频率均大于原方案;方案2、方案5和方案6的固有频率接近,且它们的前3阶固有频率均大于原方案;方案3的前3阶固有频率与原方案接近,而方案4仅2阶固有频率大于原方案,这表明在20 mm压缩量下,方案4相较于其余5种方案更优。
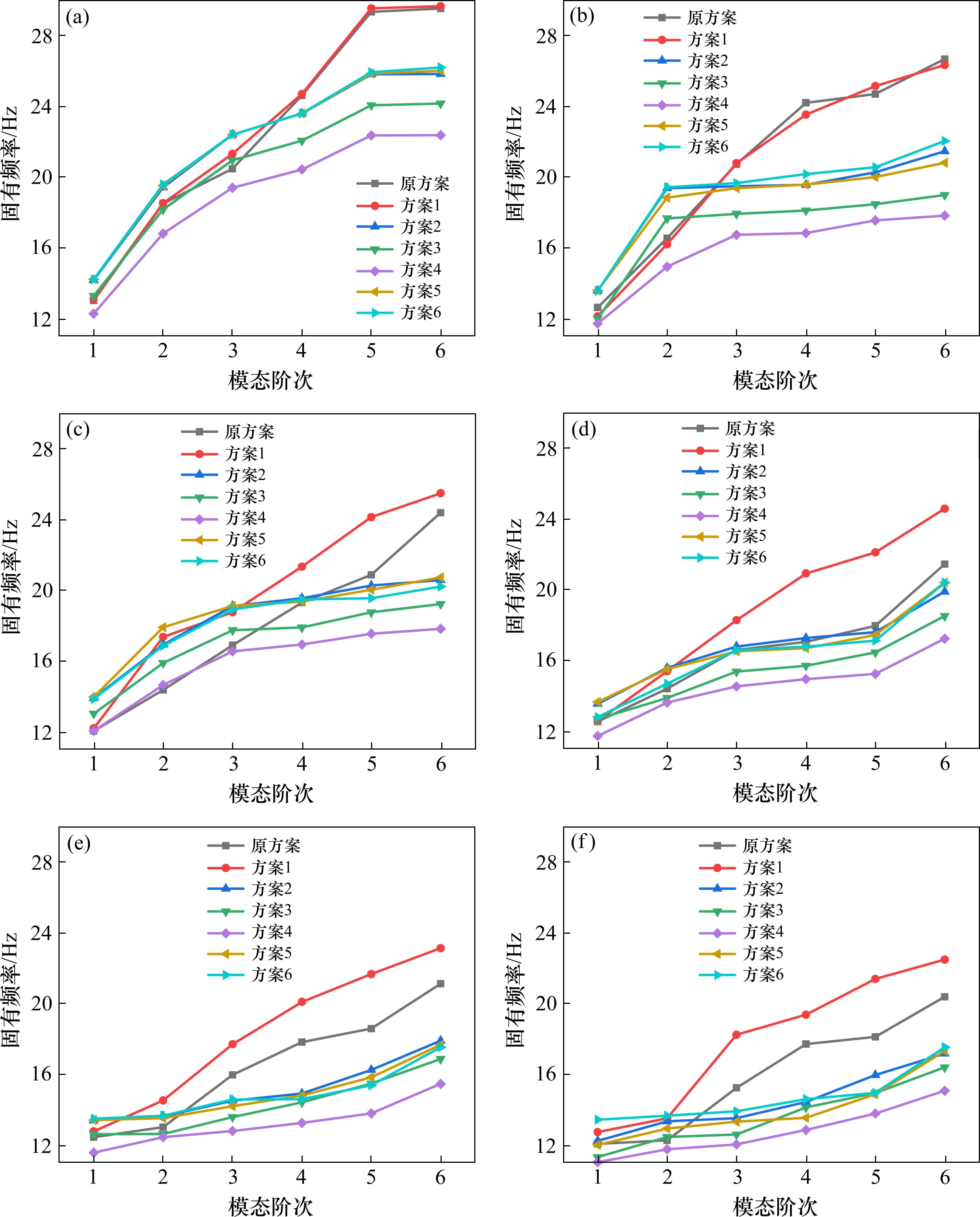
当压缩量增加至40 mm时,趋势依然清晰:方案1的固有频率依旧大于原方案;方案2、方案5和方案6的固有频率仍然接近,且前2阶固有频率大于原方案;方案3仅在2阶固有频率上略大于原方案;而方案4依然优于其余5种方案。
后续的分析结果延续了这一趋势,具体细节不再一一赘述,整体而言,方案4结构的外风挡在各个压缩量条件下均展现出了最低的固有频率,这有力地说明了方案4的外风挡结构设计在这几种结构方案中为最佳。
2 模态试验分析
为了对有限元模态计算结果进行验证,采用模态试验的方法对4种方案的振动特性进行研究。
2.1 试验设备及测点布置
本试验根据《振动与冲击 机械导纳的试验确定 第3部分:冲击激励法》(GB/T 11348.3—2006)标准,采用锤击法作为激励手段,通过力传感器(力锤)和加速度传感器(测点)采集信号,数据采集用B&K的智能信号数据采集系统和PULSE Lapshop (MTC Hammer模块),模态分析和数据处理则是采用B&K公司的Reflex分析软件。鉴于橡胶材料的制作成本较为高昂,仅对原方案以及方案2、方案4和方案6中的外风挡结构进行试验。试验聚焦于外风挡侧部结构的模态特性,故在外风挡的侧面布置了共计15个测点,测点分布如图13所示。

2.2 模态试验过程
具体测试流程如下:1) 精确布置每个测点,并测量每个测点的几何位置;2) 安装加速度传感器至预定位置,与数据采集系统连接,并连接力锤通道;3) 利用B&K Pulse MTC Hammer模态测试模块,根据测点位置信息,构建外风挡测点的几何模型;4) 对测试系统进行调试并进行关键参数的设置,包括采样频率、测量谱线数、信号源激振力选择、频响函数检验等;5) 数据处理与分析,采用B&K公司的 Reflex分析软件模块,对采集的数据进行模态提取。该软件首先运用互相关技术,计算各采集通道相对于参考通道的互相关值,以此消除噪声信号的干扰;随后,基于这些互相关信号,构建脉冲响应函数矩阵,并进一步通过变换构成频响函数矩阵;接着,利用相关算法进行模态分析,从中选取频率、阻尼值和振型向量均保持稳定的模态作为最终确定的模态频率;最后,提取各阶模态对应的振型,并进行模态置信准则(Modal Assurance Criterion, MAC)计算,以确保各模态间的相关度保持在10%以内。
2.3 外风挡侧部结构模态测试结果
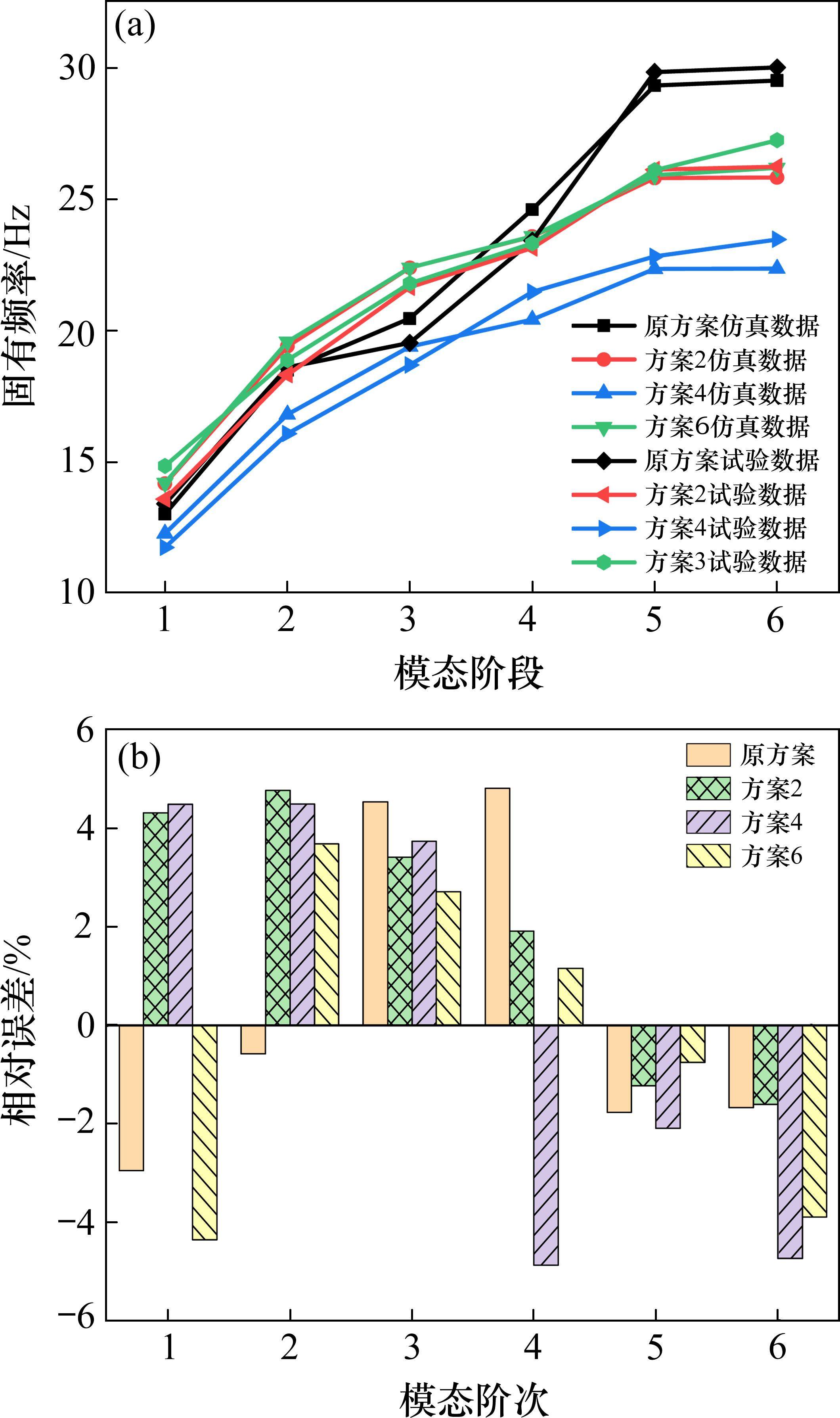
在压缩量为20 mm的条件下,对4种外风挡结构方案进行了试验测试,得到前6阶模态频率如表5所示。通过分析可得:方案2与方案6的试验结果基本接近,而方案4在性能上显著优于其余2种方案,尤为突出的是其5阶模态频率的显著降低,相较于原方案减少了23.5%。
| 模态 | 1阶 | 2阶 | 3阶 | 4阶 | 5阶 | 6阶 |
|---|---|---|---|---|---|---|
| 原方案 | 13.41 | 18.6 | 19.53 | 23.42 | 29.84 | 30.01 |
| 方案2 | 13.59 | 18.32 | 21.65 | 23.14 | 26.12 | 26.24 |
| 方案4 | 11.75 | 16.08 | 18.69 | 21.47 | 22.82 | 23.47 |
| 方案6 | 14.85 | 18.88 | 21.8 | 23.32 | 26.11 | 27.25 |
图14(a)直观展示了有限元仿真数据与试验数据的对比情况,4种方案的固有频率比较分析结果与第1.4节中的分析结果基本吻合,验证了有限元模型的准确性。进一步地,图14(b)展示了4种结构方案下外风挡前6阶模态的理论值与试验值之间的误差分析。结果显示,各方案的误差基本上均在±5%的较小范围内。误差最大值为方案4的第6阶固有频率,达到4.95%,但这仍属于可接受范围。造成此误差的主要原因可能在于:首先,试验中的边界条件相较于有限元模拟更为复杂,如螺栓等附加约束在仿真中进行了简化处理;其次,试验过程中不可避免的噪声干扰对数据的精确性造成了一定影响;最后,模型理论上的均匀性假设与实际情况中的材质不均匀性、表面凹凸不平等因素之间的差异也会对计算结果造成影响。工程应用中通常允许的误差范围不超过10%,所以,当前仿真与实验直接产生的误差在合理设计范围之内。
3 结论
1) 提出6种优化方案分别进行了模态分析,发现通过调整截面形状与降低材料硬度可以有效降低外风挡结构固有频率,对减振降噪的实现具有显著的积极作用,而改变肩部开口宽度的操作对于外风挡结构的振动特性影响并不显著。
2) 通过模态振型研究,发现在不同固有频率下,风挡结构呈现出不同的振型状态。具体而言,1阶与3阶模态下,风挡结构均呈现出单一的最大形变区域;而2阶、4阶和6阶模态出现多个最大形变点,且均处于外风挡圆弧部分顶部区域;而5阶模态最大形变区域则位于橡胶肩部开口处。
3) 研究了各方案在不同压缩量下频率的变化,随着压缩量的不断增加,各方案的固有频率整体上呈现降低的趋势,通过比较,方案4的固有频率最低,优化效果最佳。针对理论计算中的4种方案,进行了模态试验,验证了理论仿真结果的正确性。
俞成涛,顾铖,潘澳等.高速列车橡胶外风挡结构设计及压缩量对其振动特性影响研究[J].铁道科学与工程学报,2025,22(04):1468-1479.
YU Chengtao,GU Cheng,PAN Ao,et al.Research on the impact of structural design and compression of rubber exterior windshields of high-speed train on vibration characteristics[J].Journal of Railway Science and Engineering,2025,22(04):1468-1479.

