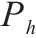铁路牵引供电领域的飞速发展带来了日益严峻的能耗和碳排放问题,在“双碳”目标背景下,牵引供电系统就近消纳光伏是未来的发展方向[1-3]。由于光伏发电的波动性和牵引负荷的间歇性,需引入储能平抑源-荷之间的供需不平衡,储能还可对再生制动能量进行回收利用,实现牵引供电系统节支降耗。随着铁路功率调节器(Railway Power Conditioner, RPC)的发展,许多学者研究了以RPC为并网变流器的光伏储能接入铁路牵引供电系统方案[4-14],目前在铁路牵引供电领域已实现RPC接入工程应用的储能技术有:钛酸锂电池[12]、飞轮[13]、超级电容、磷酸铁锂电池。飞轮和超级电容属于功率型储能,难以适应牵引负荷能量高的特点,磷酸铁锂属于能量型储能,难以满足牵引负荷功率大的特点。钛酸锂电池凭借较高的能量密度、宽温度范围、长循环寿命、高安全可靠性,已在城市轨道交通中推广应用,也适合于铁路牵引供电系统再生制动能量的回收利用。电气化铁路采用两部制电价计费政策,主要包括基本电费和电度电费,基本电费可按变压器容量和负荷最大需量2种方式计算,电度电费由铁路实际耗电量决定[14]。储能系统的容量配置方案决定其投资成本和经济效益,能量管理策略影响其最大需量削减效果和再生制动能量利用率,进而影响牵引变电所电费支出。为实现储能在铁路牵引领域的经济运行,国内外学者开展了储能接入铁路牵引供电系统配置与能量管理策略协同优化的研究。目前,针对单一储能的研究集中于固定阈值的能量管理策略,储能介质选用磷酸铁锂、超级电容或飞轮,通过设置充放电启动阈值优化储能出力,实现牵引负荷削峰填谷;以系统全寿命周期净收益为目标,对储能系统能量管理和容量配置参数进行协同优化[15-17],该方法简单可行,但无法兼顾最大需量削减和再生制动能量利用,对储能系统运行经济性提升有限。为解决上述问题,部分学者基于混合储能采用多阈值[14]和分配比例[18]的能量管理策略优化储能出力,以全寿命周期净收益为目标对混合储能配置和能量管理参数进行优化。该方法中混合储能一般选用磷酸铁锂为能量型储能对最大需量进行削减,超级电容为功率型储能对再生制动能量进行充分回收利用,可获得较好的经济效益,但在实际应用中混合储能存在初始投资成本高、控制复杂、无法在线优化等问题。还有部分学者为提升储能系统的经济性、延长储能使用寿命研究了基于动态阈值的能量管理策略[19],但并未进行容量配置优化。此外,目前大部分研究以净收益最大为目标进行容量优化[14, 16-17],在实际工程应用中会存在初始投资成本高、投资回收期长等问题。综上所述,储能接入铁路牵引供电系统的能量管理策略及容量配置方法有待改善,其运行效果和经济效益需要进一步提高。针对上述问题,选择基于RPC的钛酸锂接入方案,将混合储能的多阈值能量管理策略应用于单一储能,并提出一种基于FLC自适应多阈值能量管理策略:基于行车运行图将日牵引负荷分为高需量时段和其他时段,不同时段储能设定不同的充放电阈值,以兼顾再生制动能量利用率、最大需量削减,并从储能荷电状态(State of Charge, SOC)和牵引负荷出发,采用FLC对放电阈值自适应调整,延长储能使用寿命;然后,建立光伏储能接入铁路牵引供电系统配置与能量管理协同优化模型,以净收益和内部收益率为优化目标,能量管理策略和容量配置参数为优化变量进行求解;最后以实测牵引负荷为仿真算例,对比了自适应多阈值和固定阈值能量管理策略下储能系统的运行效果,并对不同储能方案进行经济性对比,验证了本文方法的有效性。
1 光伏储能接入铁路牵引供电系统拓扑结构
光伏储能接入铁路牵引供电系统的拓扑结构是优化配置的基础,以RPC为并网变流器的光伏储能接入铁路牵引供电系统方案发展成熟,已有工程示范案例,其拓扑结构如图1所示。
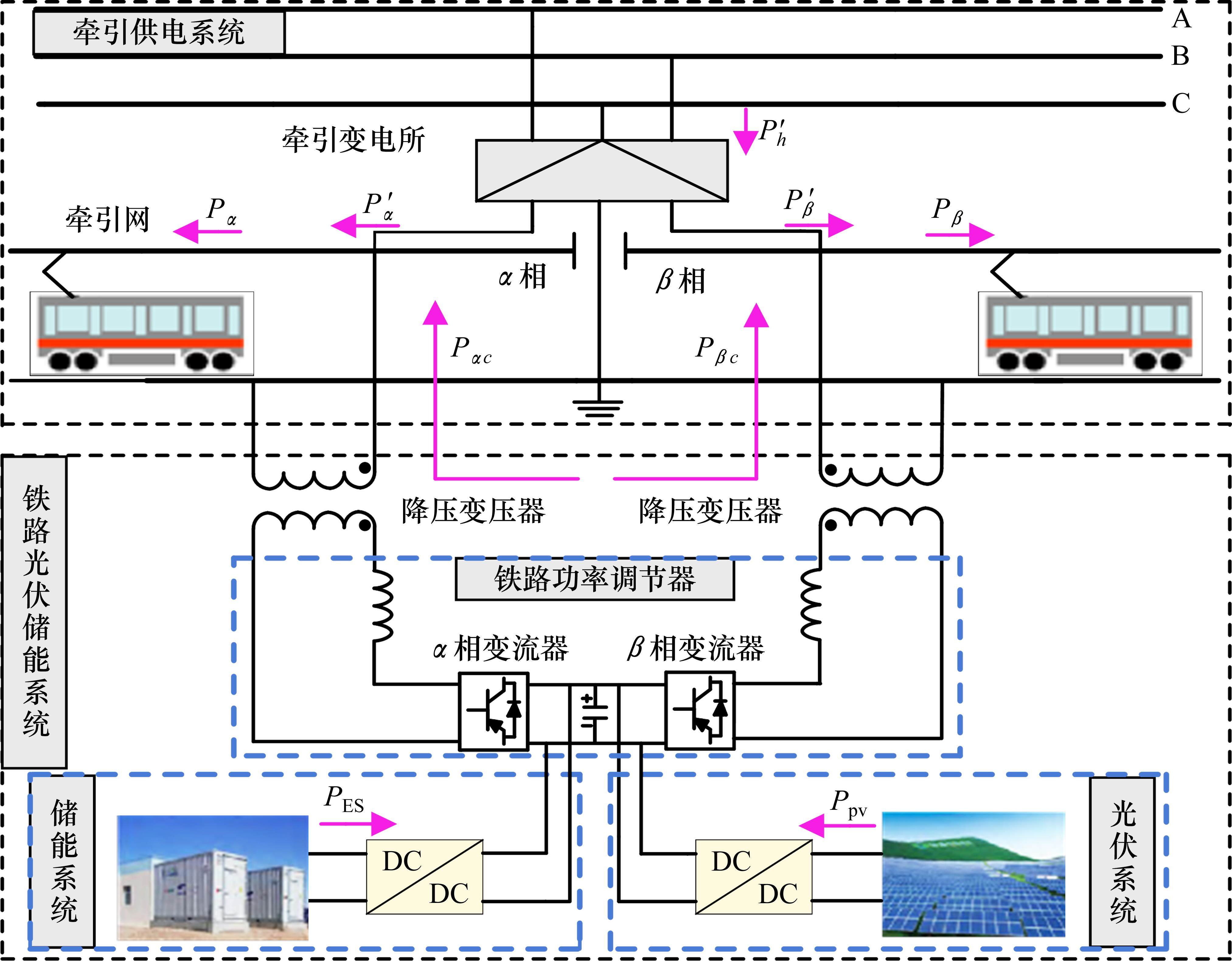
从图1可以看出,该系统在传统牵引供电系统上增设接口装置、光伏系统及储能系统构成。接口装置包括RPC和2台降压变压器,跨接在牵引变电所两侧供电臂上,可实现两侧供电臂能量转移。储能系统由双向DC-DC和钛酸锂电池构成,光伏系统由光伏电池和DC-DC构成,DC-DC与RPC的中间直流环节相连,可根据牵引负荷的运行工况,控制光伏和储能的工作状态,实现光伏电能的输出和储能的充放电。
2 光伏储能接入铁路牵引供电系统能量管理策略
储能能量管理策略主要解决储能与铁路牵引供电系统不同工况下的能量协调交互问题,优化储能出力,尽可能削减最大需量、提升再生制动能量利用率,充分发挥储能系统的运行效果。
2.1 多阈值能量管理策略
针对固定阈值能量管理策略难以兼顾最大需量削减和再生制动能量利用的缺点,将混合储能的多阈值能量管理策略应用于单一储能介质。混合储能系统一般选用磷酸铁锂和超级电容,其中磷酸铁锂设定较高的充放电启动阈值,对牵引负荷削峰填谷实现最大需量削减,超级电容一般不设置阈值,对再生制动能量进行高效回收与利用。
钛酸锂相较于超级电容具备较高的能量密度,可用于牵引负荷最大需量削减,相较于磷酸铁锂具备较高的功率密度和循环寿命,也适用于再生制动能量的回收利用。故钛酸锂可以在不同时段分别设定功率型和能量型储能的放电启动阈值,以兼顾再生制动能量利用和最大需量削减。
我国铁路电力机车根据运行图行驶,负荷曲线在运行图不变的情况下会具备极强的周期性。牵引负荷最大需量指在规定的周期或结算周期内,15 min内功率的最大平均值,与牵引供电系统的电费支出直接相关。牵引负荷的需量过滤了牵引负荷的短时剧烈波动,相较于实时牵引功率更平稳,其曲线呈现出和运行图类似的周期性。图2展示了某牵引变电所多日内的实测牵引功率及需量曲线,可以看出,不同日的牵引负荷需量曲线均在12:00―13:00间出现需量峰值,本文将此时段定义为高需量时段t1~t2,仅需利用储能系统在此段时间进行削峰即可实现最大需量削减。故储能系统的能量管理策略为:在高需量时段设定充放电启动阈值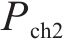
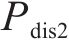
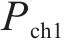
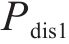
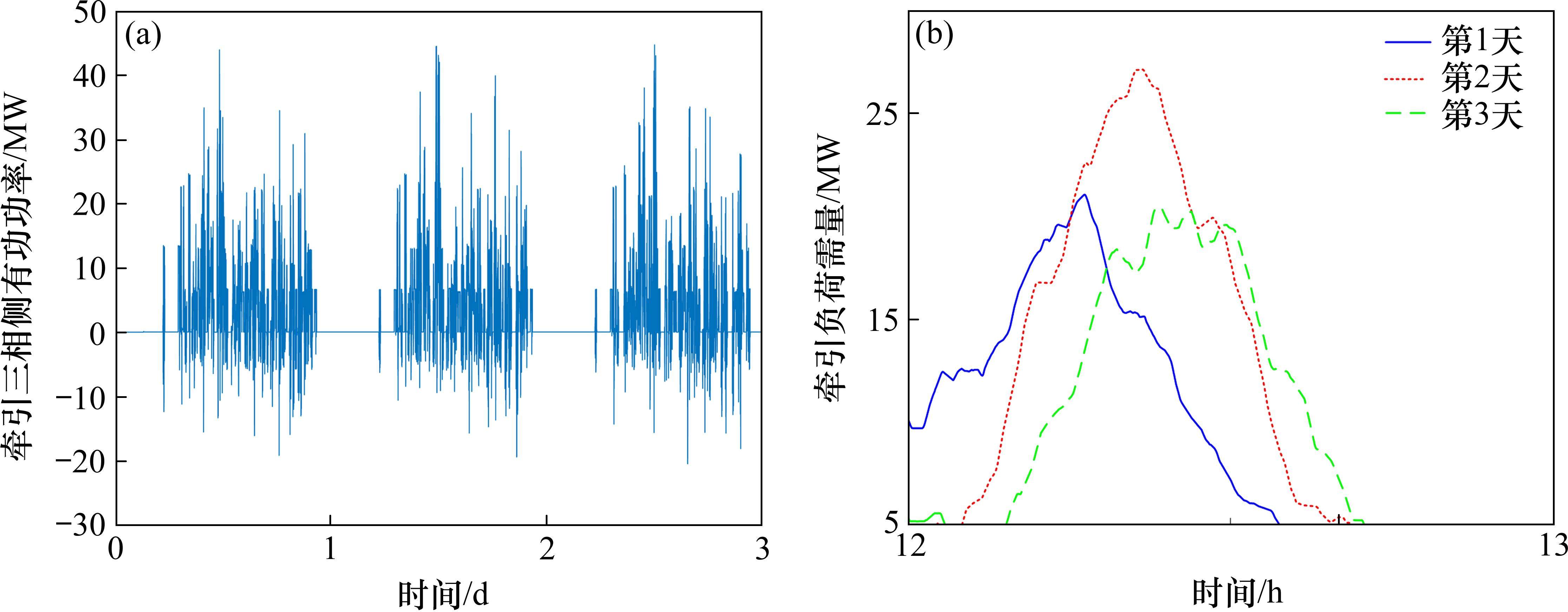
图3为多阈值能量管理策略下储能系统的分区工作情况,图中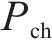
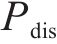
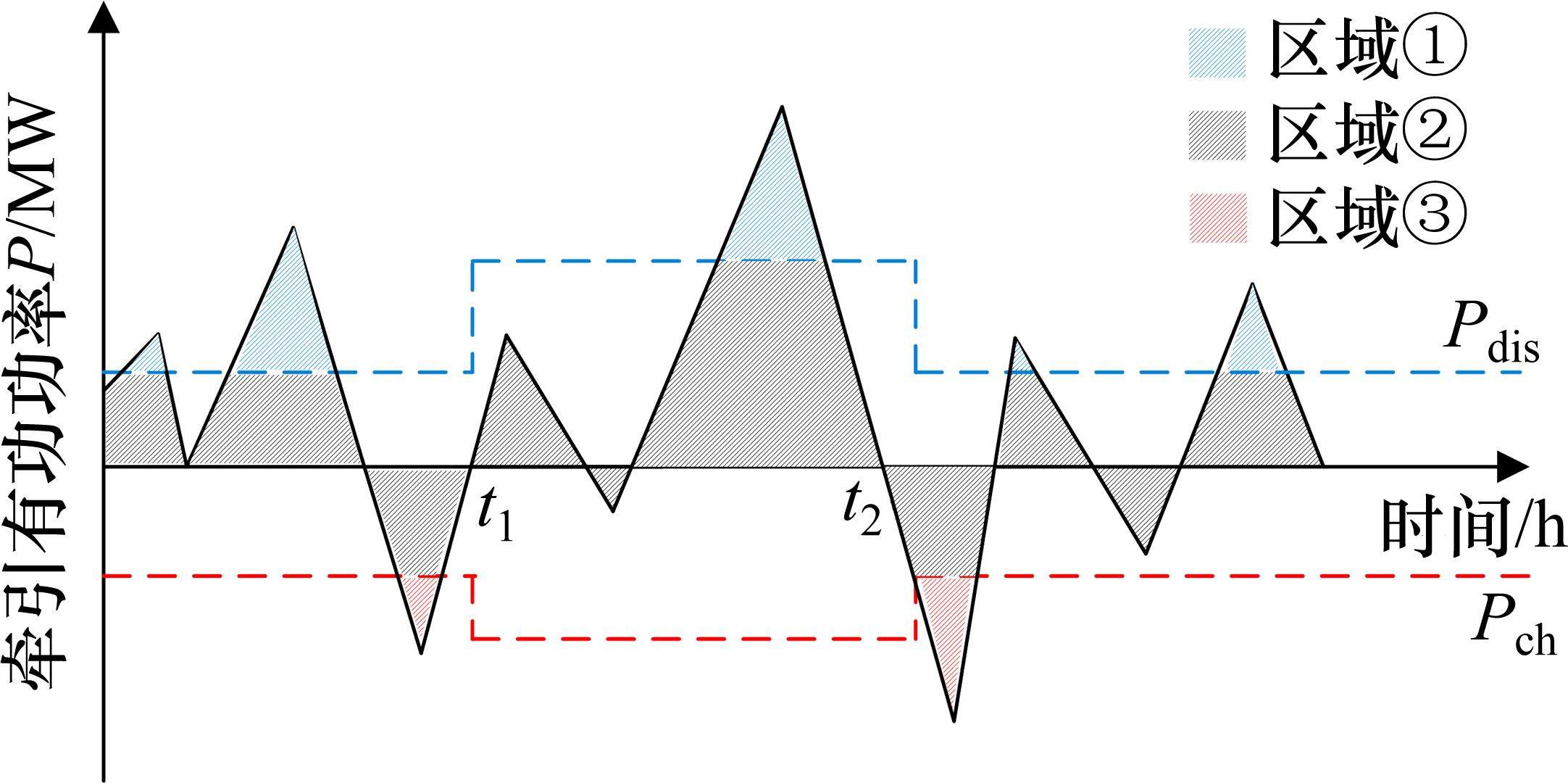
当牵引功率分别处于3个不同区域时,光伏储能工作情况如下。
1) 区域①:牵引负功率大于储能放电启动阈值,优先利用光伏电能,再由储能结合功率、容量约束进行放电。
2) 区域②:牵引功率未达到储能充、放电启动阈值,由光伏对此区域中功率进行响应,储能结合功率、容量约束对剩余光伏电能加以利用。
3) 区域③:牵引功率小于储能充电启动阈值,储能结合功率、容量约束进行充电,优先对再生制动能量进行利用,再对光伏电能进行利用。
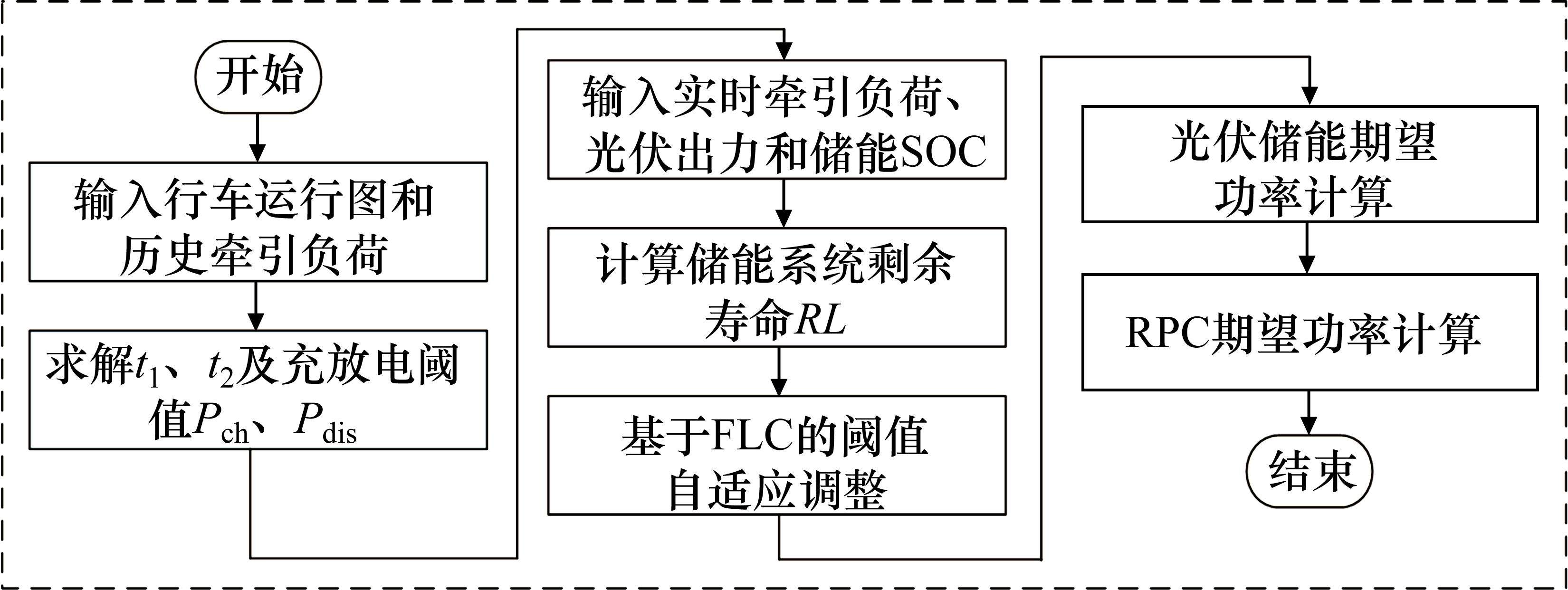
综上所述,储能期望功率的计算流程如图4所示。
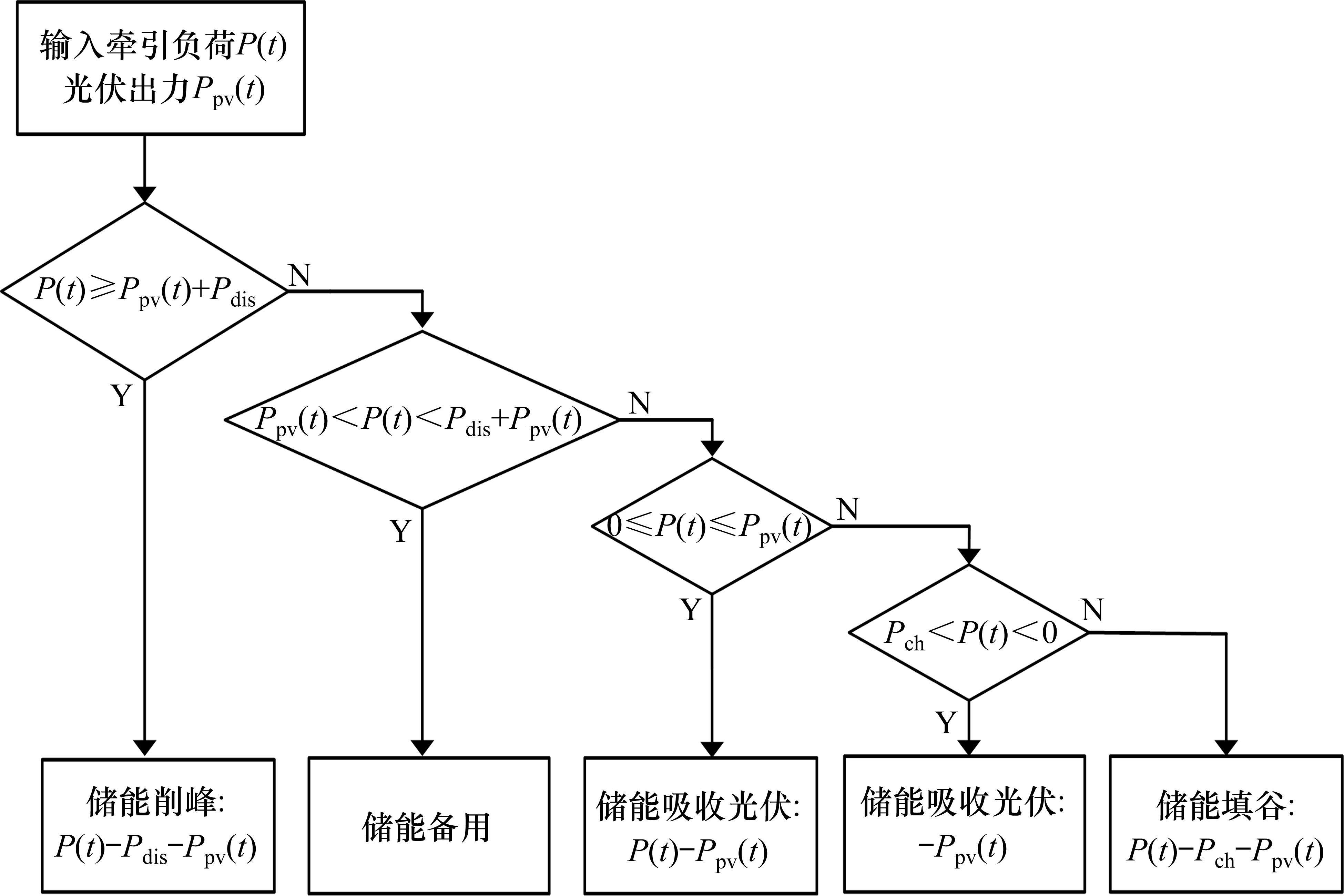
2.2 基于FLC的自适应多阈值能量管理策略
尽管列车按照运行图行驶,但在实际运行中牵引功率实时波动,动态阈值管理策略相较于固定阈值能够有效提升能量回馈效率与再生制动能量储存效率,降低储能系统的平均放电深度[20]。故本文在2.1的基础上进行改进,提出基于FLC的自适应多阈值能量管理策略,该策略以牵引功率和储能SOC为判据,在线优化储能系统放电阈值。
首先对牵引功率和SOC进行模糊化处理,输入量SOC、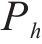
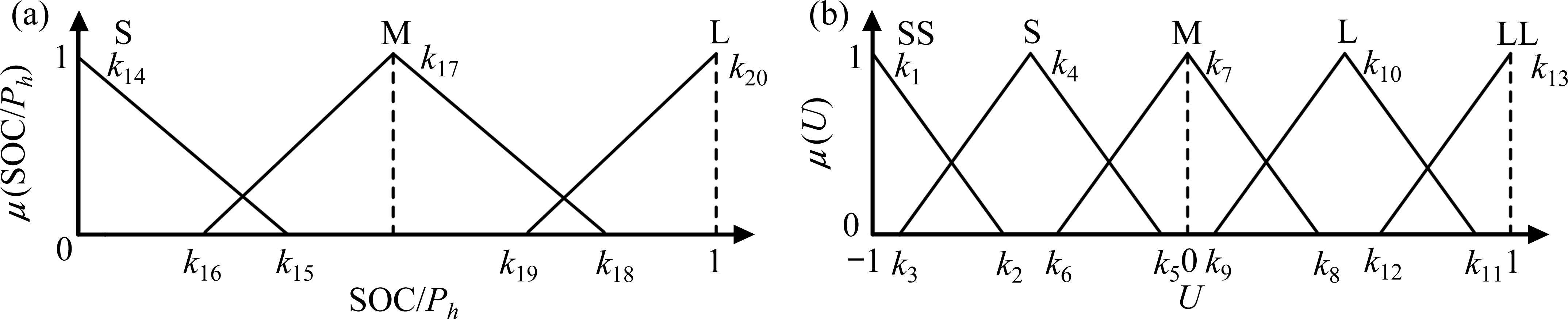
为便于模糊描述,将牵引功率归一化映射到[0,1]区间:
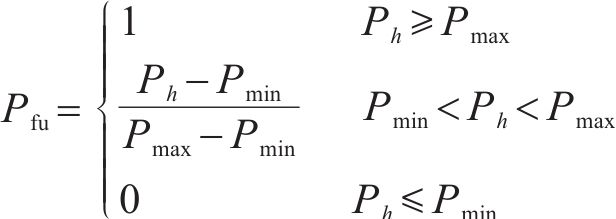
式中: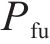
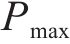
模糊规则根据牵引负荷和储能SOC变化时与阈值调整参数的对应关系来制定。牵引负荷大、储能SOC低时,储能系统放电量需要降低,此时放电阈值需要上调;牵引负荷小、储能SOC高时,储能系统放电量需要增加,此时放电阈值需要下调。模糊规则如表1所示。
| 阈值调整参数U | 储能系统SOC | |||
|---|---|---|---|---|
| S | M | L | ||
牵引 功率
| S | M | M | SS |
| M | L | M | S | |
| L | LL | L | M | |
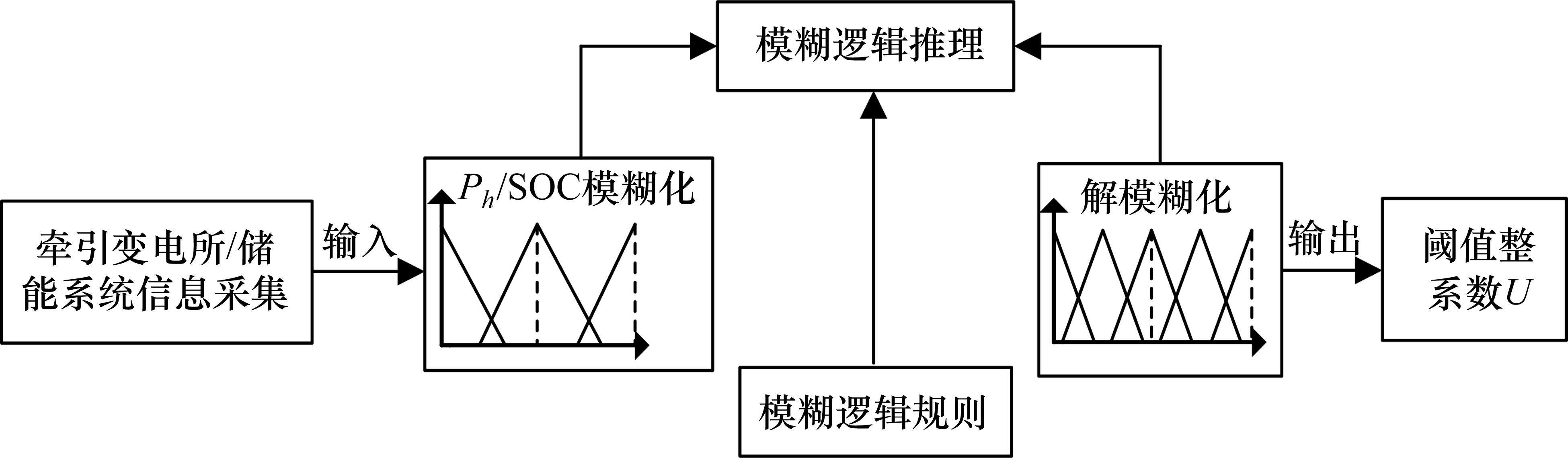
基于FLC的自适应多阈值调整策略如图6所示,通过牵引变电所和储能系统采集模糊控制中所需的信息,每个周期计算一次输入量对应的隶属度;通过模糊规则库求解输出量,并通过解模糊化确定放电阈值调整参数,修正放电阈值。
最终动态阈值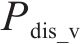
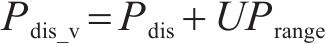
式中: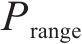
综上,本文能量管理策略流程如图7所示。
3 光伏储能接入铁路牵引供电系统配置与能量管理协同优化模型
光伏储能接入铁路牵引供电系统的容量配置方案决定其投资成本,储能能量管理策略影响其最大需量削减效果和再生制动能量利用率,进而影响牵引变电所电费支出。因此,为实现光伏储能系统的经济运行,充分发挥储能系统运行效果,对系统配置与能量管理策略进行协同优化。
3.1 目标函数
为避免系统初始投资成本过大,以光伏储能接入铁路牵引供电系统全寿命周期净收益和内部收益率(Internal Rate of Return, IRR)为优化目标。
1) 全寿命周期净收益F1
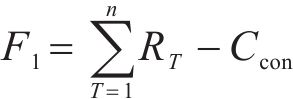
式中:T为年份;n为项目寿命周期;RT为年净收益;Ccon为初始投资成本。
初始投资成本Ccon包括设备购置成本C1、安装调试成本C2和占地成本C3:
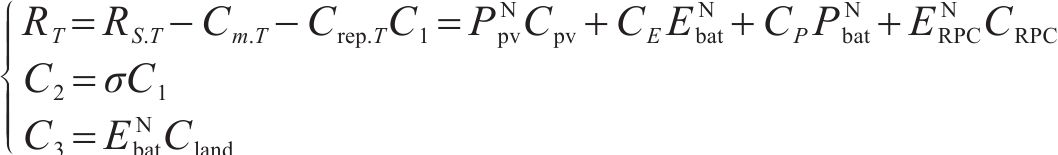
式中: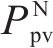
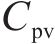
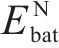
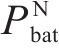


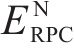
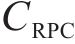
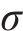
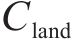
年净收益RT为年节约电费减去年运维费用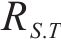
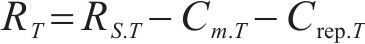
年节约电费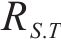

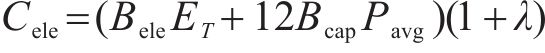
式中: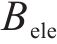
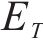
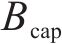
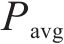

新增设备年运维费用Cm.T可以表示为年运维系数与设备购置成本相乘:
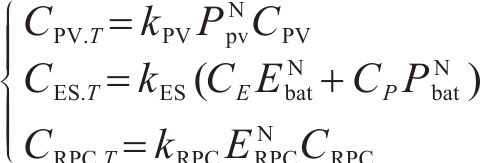
式中: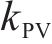
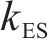

年换电成本Crep.T为:
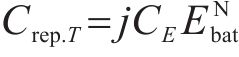
式中: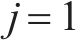
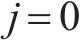
2) 内部收益率IRR
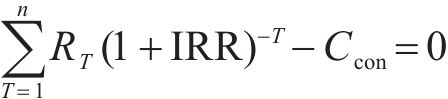
对光伏储能接入铁路牵引供电系统容量配置与能量管理参数协同优化,能量管理策略优化参数包括:储能系统充放电启动阈值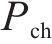
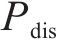
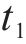
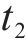
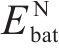
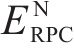
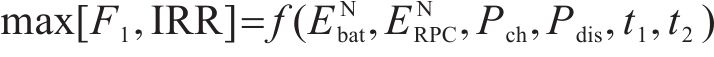
3.2 约束条件
1) 储能装机容量约束
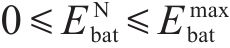
式中: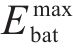
2) 运行功率约束
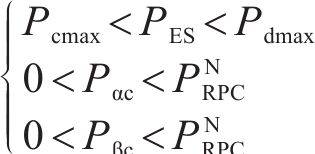
式中: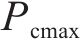
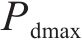
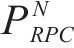
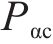
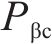
3) 功率平衡约束
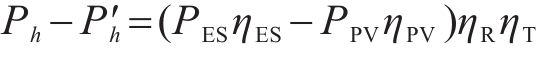
式中:
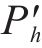
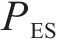
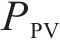
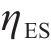
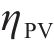
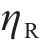
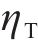
4) 储能荷电状态约束
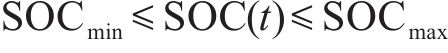
式中: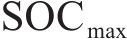
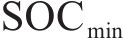
3.3 协同优化模型求解框架
协同优化模型属于混合非线性多目标优化问题,传统的多目标求解方法是将其转化为单目标问题,但不同目标的权重难以确定。NSGA-II算法通过引入和运用快速非支配排序法、拥挤距离和拥挤度算子及精英策略,可最大限度保持各优化目标之间的独立性,有效求解这一问题。通过NSGA-II算法求出Pareto 解集后,以模糊决策法求取折中解。配置与能量管理协同优化模型求解框架如图8所示。
4 算例分析
4.1 参数设置
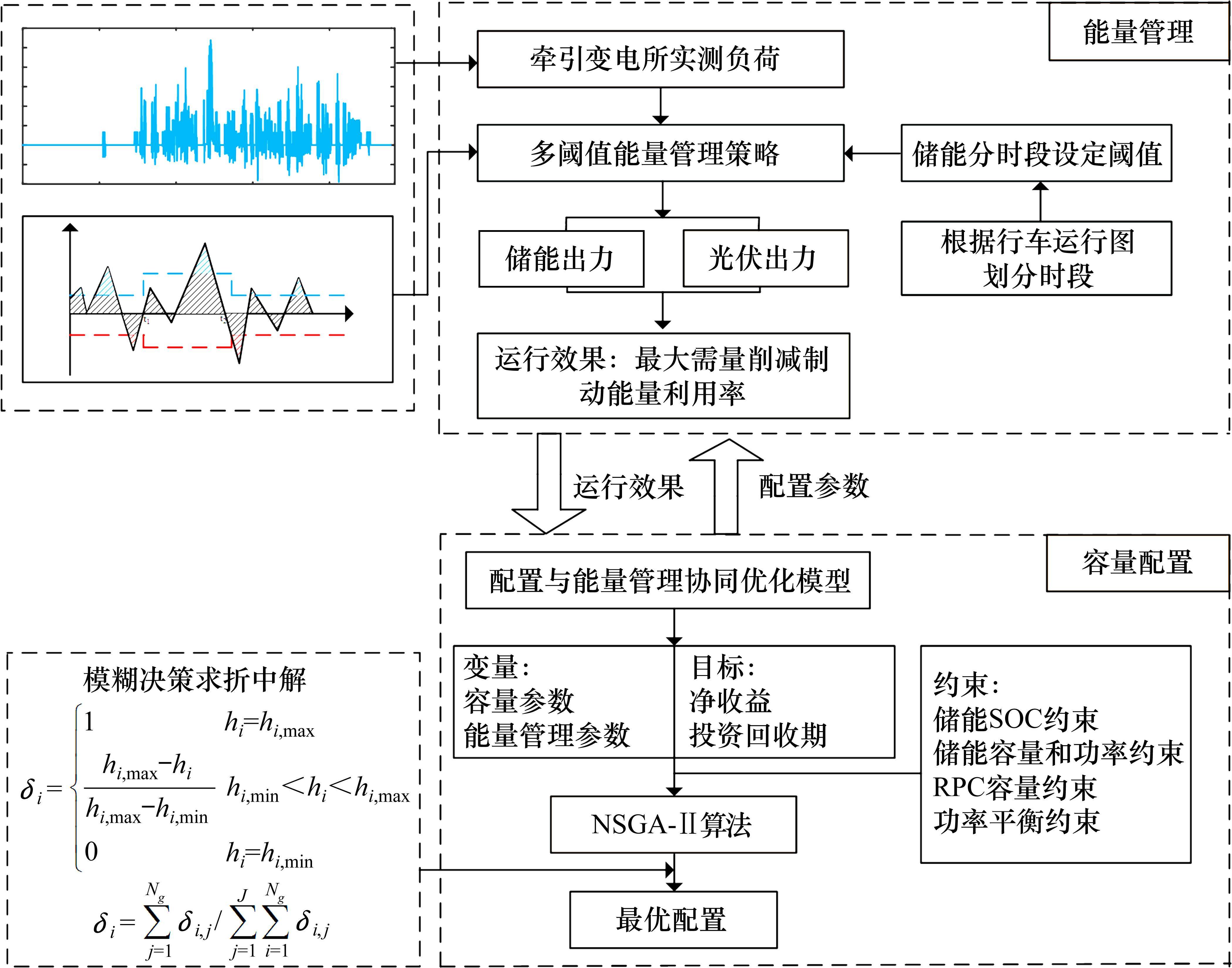
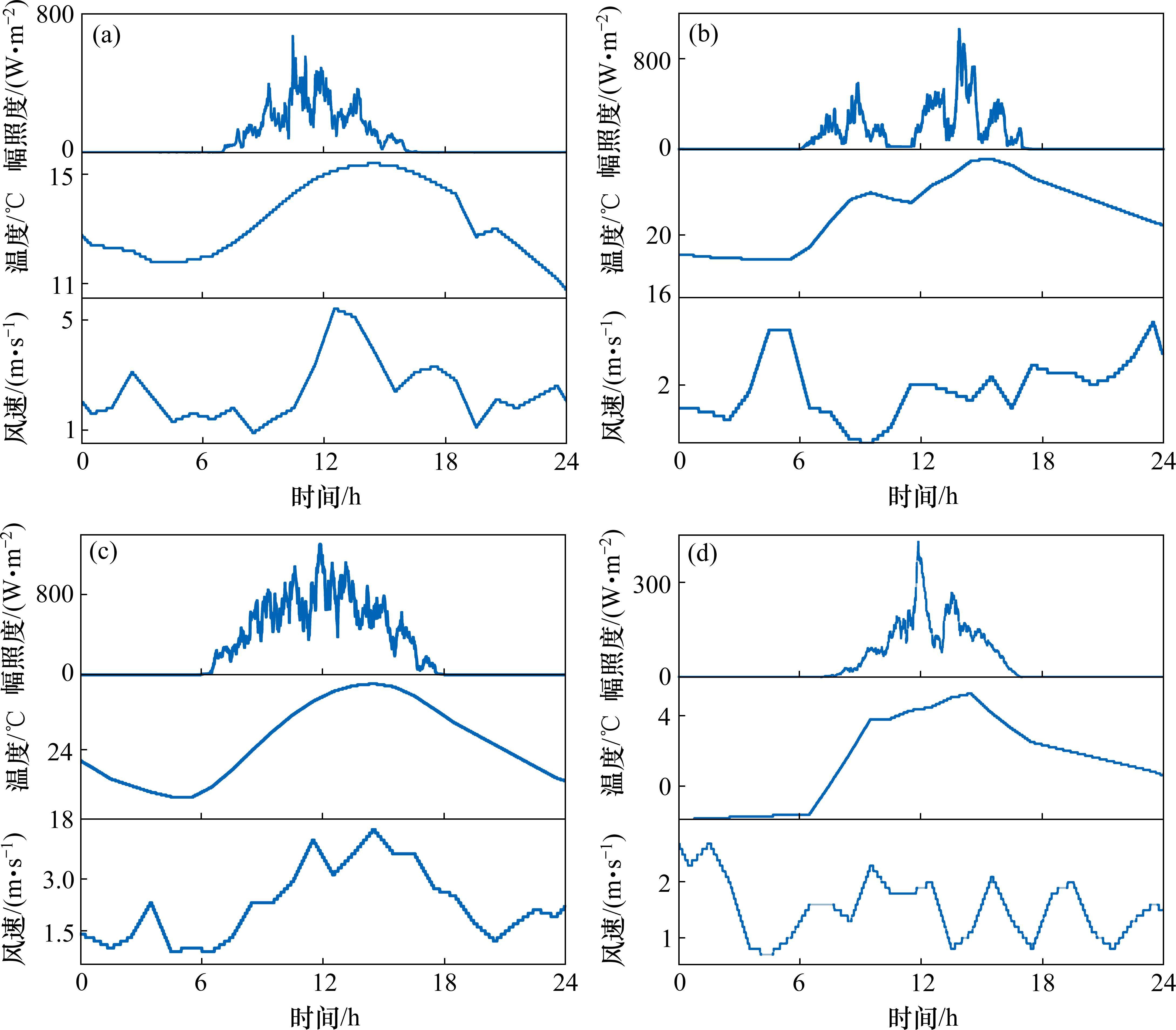
以我国某牵引变电所的实测数据进行算例分析,其牵引功率曲线如图3所示。该牵引变电所日返送再生制动能量高达13.8 MWh,牵引能耗为82.9 MWh,最大需量高达27.16 MW。该牵引变电所光伏可用面积为198 m2,设定光伏装机容量为20 kW,当地四季典型日气象数据如图9所示。
仿真算例中的各项参数如表2所示。
| 参数名称 | 数值 | 参数名称 | 数值 |
|---|---|---|---|
| 电池容量单价CE/(元∙Wh-1) | 5 | 占地成本/% | 33 |
| 电池功率单价CP/(元∙W-1) | 0.15 | 基本电费单价Bcap/(元∙月-1∙kVA-1) | 0.01 |
| 光伏功率单价Cpv/(元∙W-1) | 3.8 | 电度电费单价Bele/(元∙kWh-1) | 0.43 |
| 接口装置容量单价CRPC/(元∙W-1) | 0.65 | 全寿命周期n/年 | 20 |
NSGA-II算法参数设置如下:种群规模为100,最大迭代次数为100,交叉概率为0.9,变异概率为0.1。
4.2 不同能量管理策略运行效果对比
1) 运行效果对比
将自适应多阈值能量管理策略与固定阈值能量管理策略下储能系统的运行效果进行对比,储能系统容量设置为516.1 kWh/3.097 MW,充电和放电效率设为90%,接口装置容量设为2×2 MVA。不同能量管理策略下的运行结果如表3所示。
| 固定阈值 | 自适应多阈值 | |
|---|---|---|
| 充电阈值/MW | 0 | 0 |
| 放电阈值1、2/MW | 18.3 | 26.7、14.5 |
| 放电阈值调整基准/MW | — | 6 |
| 高需量时段/h | — | 9~15 |
| 最大需量降低值/MW | 0.83 | 1.20 |
| 再生制动回收率/% | 18.14 | 18.14 |
| 年节约基本电费/万元 | 32.93 | 47.48 |
| 年节约电度电费/万元 | 31.77 | 31.77 |
从表3可以看出,自适应多阈值能量管理策略下储能系统的运行效果更好,牵引变电所年电费支出更少。再生制动能量利用率均为18.14%时,固定阈值能量管理策略下最大需量仅下降0.96 MW,而自适应能量管理策略下最大需量下降1.20 MW,主要原因是自适应多阈值方案仅在9:00~15:00间维持较高的阈值进行最大需量削减,其他时间段维持较低的阈值回收再生制动能量。固定阈值能量管理策略受制于再生制动能量利用率和最大需量削减间耦合性,需采用折中的放电阈值进行削峰填谷,故其最大需量削减能力不如多阈值方案。
2) 阈值调整分析
储能放电阈值的变化主要受牵引功率和SOC的影响,如图10所示。
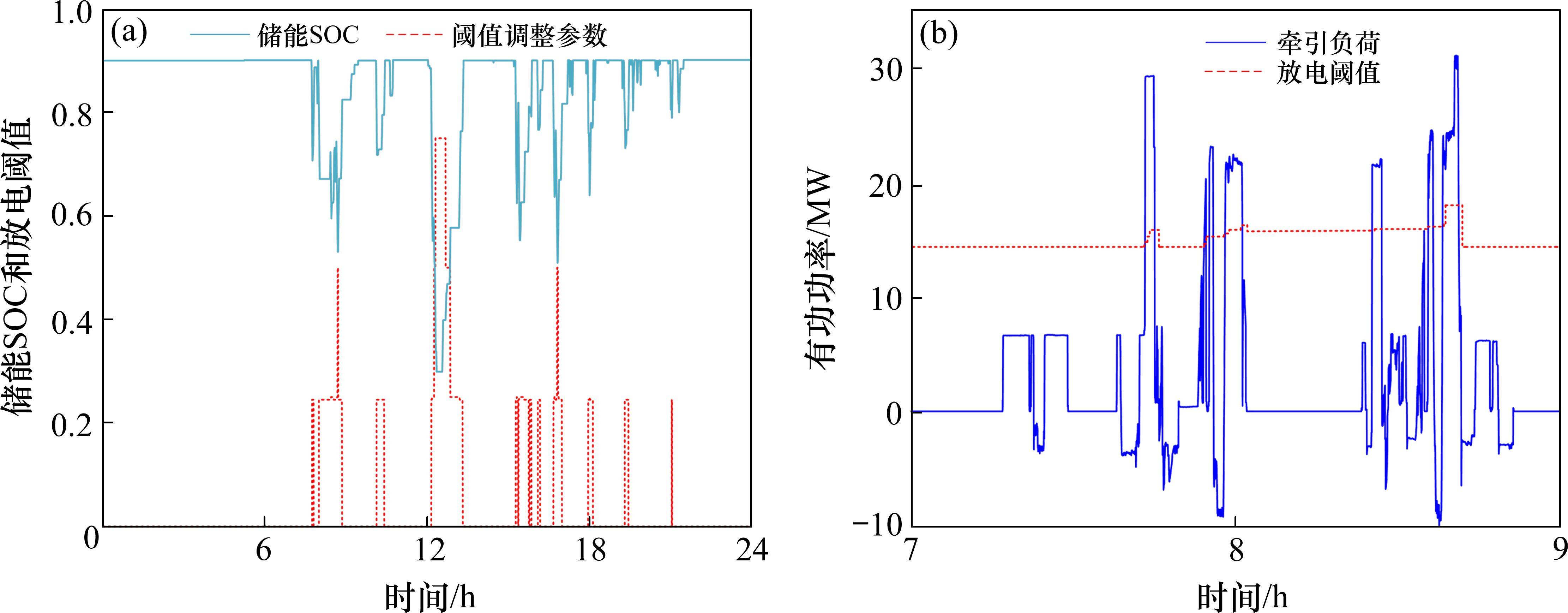
从图10可看出,储能放电启动阈值可根据SOC和牵引功率的变化进行自适应调整,当牵引负荷增大且储能SOC降低时,阈值调整系数U会逐渐升高,进而提高储能放电启动阈值,避免储能频繁放电,进入过放状态。
3) 储能寿命对比分析
储能系统长期运行下存在明显的寿命衰减,为观察固定放电阈值和自适应放电阈值对储能系统寿命的影响,本文将储能系统日寿命损失提升至其1 000倍模拟其长期运行,并以15 min为一个采样区间,利用雨流计数法统计其放电循环深度,采用经验公式[20]计算储能系统剩余寿命。储能放电深度和寿命变换如图11所示。
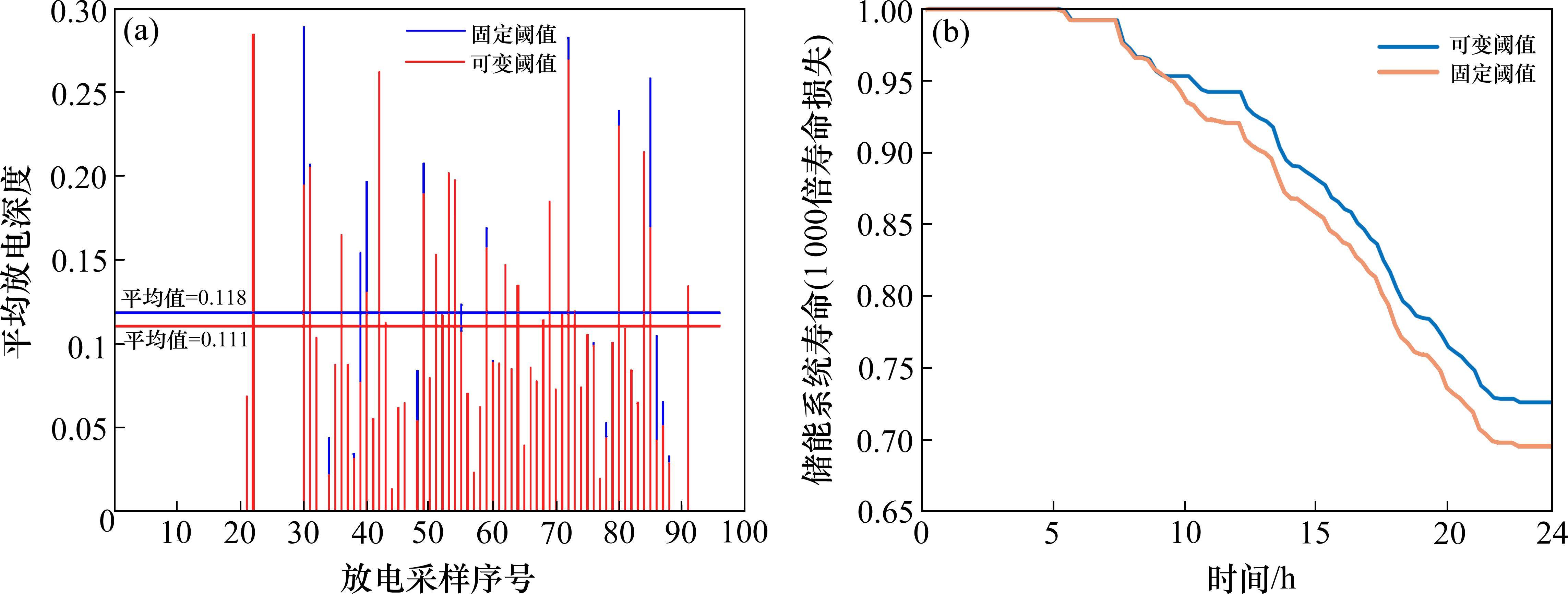
图11(a)中自适应多阈值能量管理策略下储能系统的平均放电深度低于固定阈值能量管理策略,图11(b)中自适应多阈值能量管理策略下的储能系统寿命衰减低于固定阈值能量管理策略。这表明自适应多阈值能量管理策略可以通过调整放电阈值,避免储能进入过充和过放状态,降低储能系统的平均放电深度,延长储能使用寿命。
4.3 协同优化结果分析
将求解出的第一支配等级的优化结果作为帕累托解集,如图12所示。
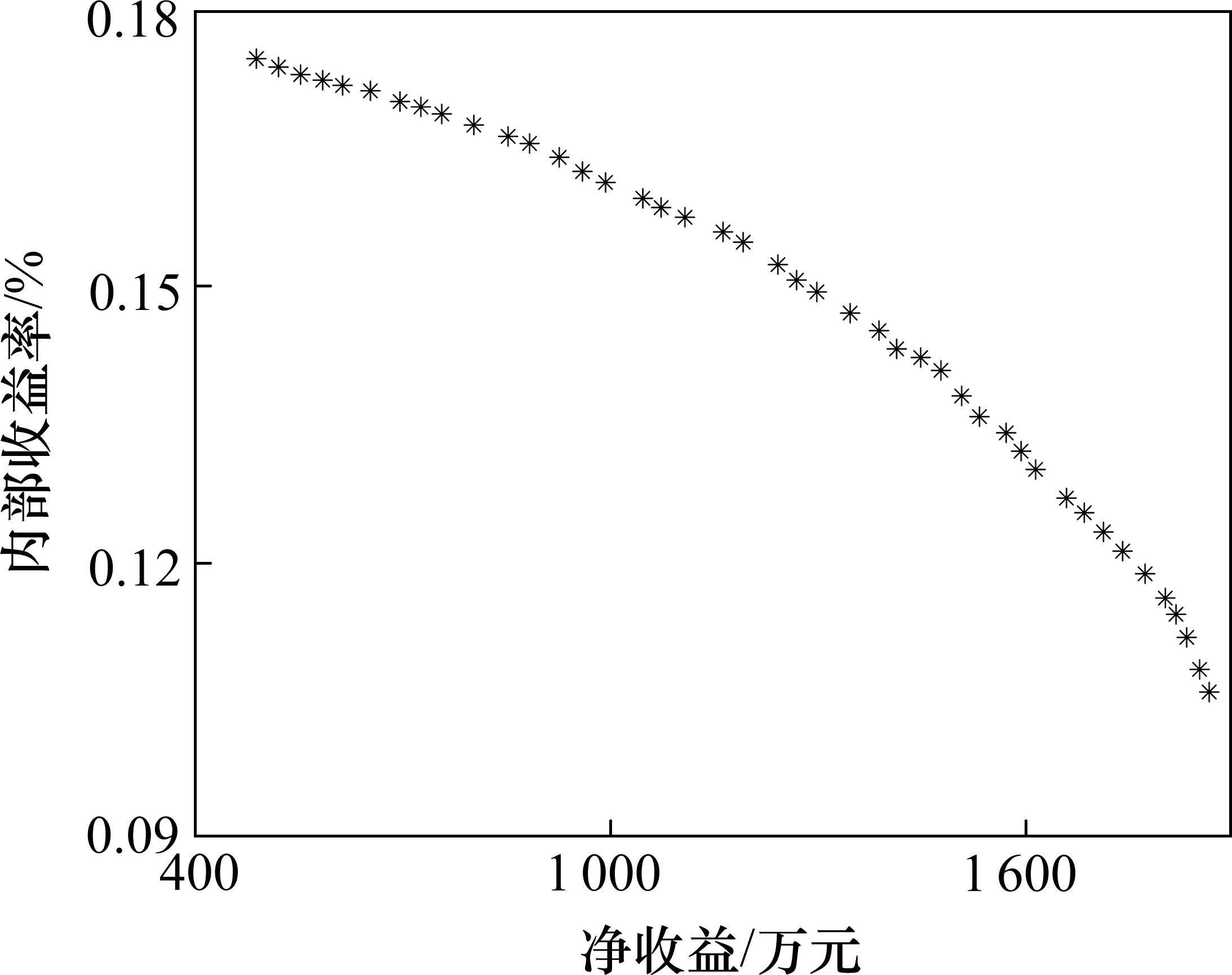
以模糊决策法选取折中解作为最优配置方案,其容量配置结果和运行效果如表4所示。
| 类别 | 参数 | 数值 |
|---|---|---|
| 容量配置 | 储能容量/kWh | 480 |
| RPC容量/MW | 2*2 | |
| 运行效果 | 初始投资成本/万元 | 683.7 |
| 净收益/万元 | 1 364.1 | |
| 投资回收期/年 | 6 | |
| 内部收益率/% | 14.60 | |
| 制动能量利用率/% | 45.3 | |
| 最大需量削减/MW | 1.15 |
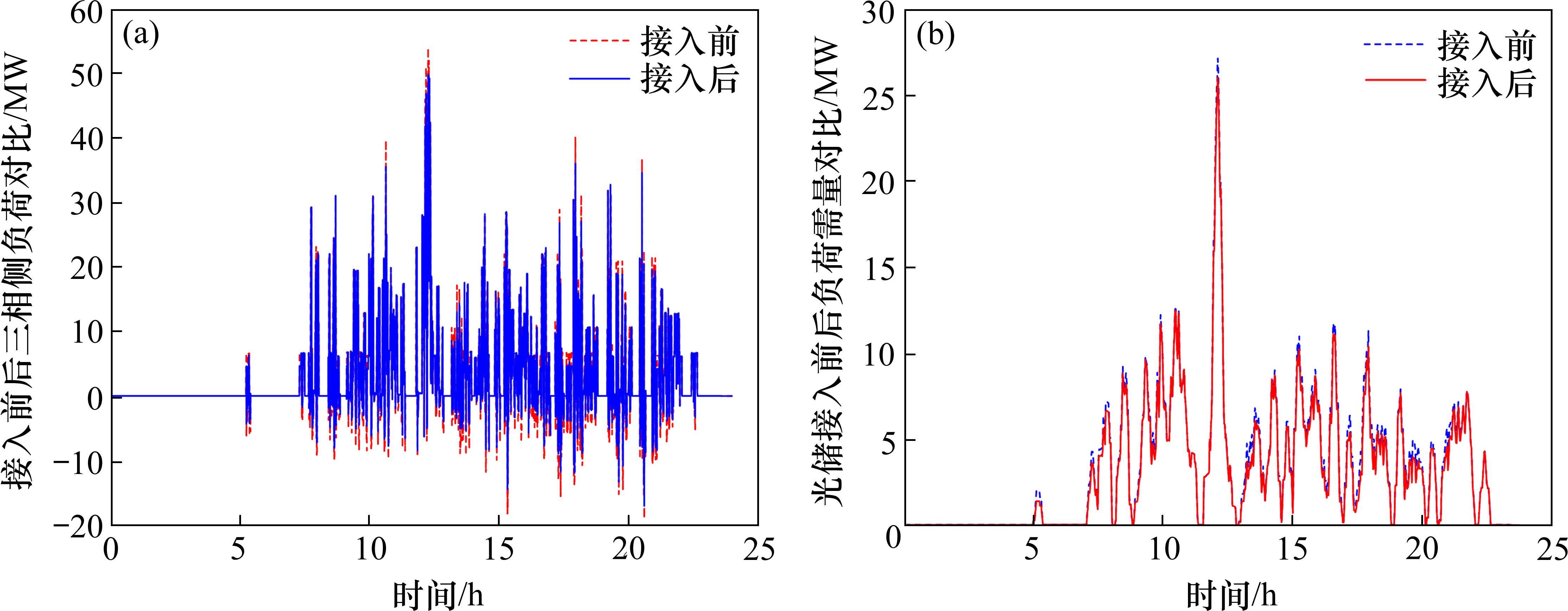
图13为接入光伏储能系统前后,牵引变电所三相侧有功功率和需量曲线对比。结合图13和表4可知,光伏储能系统接入后,牵引能耗降低,返送再生制动能量减少,再生制动能量利用率约为45.3%,最大需量下降1.15 MW,验证本文所提策略的有效性。该牵引变电所接入光伏储能后全寿命周期净收益约为1 364.1万元,相应的投资回收期为6年,对应的IRR为14.60%,高于电力行业的常规取值,该所接入光伏储能具备较好的经济效益。
4.4 不同方案运行效果对比
将方案与2种不同的储能方案进行对比,所有方案以系统全寿命周期净收益和内部收益率为优化目标。方案1是本文方案;方案2为超级电容储能方案;方案3为磷酸铁锂储能方案。磷酸铁锂和超级电容相关参数参考文献[10]。3种储能方案最优配置下的运行效果如表5所示。
| 方案1 | 方案2 | 方案3 | |
|---|---|---|---|
| 最大需量削减/MW | 1.15 | 0.17 | 1.17 |
| 制动能量利用率/% | 45.3 | 14.6 | 23.0 |
| 投资回收期/年 | 6 | 11 | 7 |
| 净收益/万元 | 1 364.1 | 347.8 | 859.3 |
| 内部收益率/% | 14.60 | 7.15 | 13.74 |
由表5结果对比可知:基于FLC自适应多阈值的钛酸锂储能方案在运行效益上优于其他方案。通过与方案2的对比可知,超级电容受制于其能量密度小、成本高的劣势,无法有效削减最大需量,难以适应牵引负荷能量高的特点。通过与方案3的对比可知,磷酸铁锂受制于功率密度低、循环寿命短的劣势,再生制动能量利用率较低,难以满足牵引负荷功率大的需求。
5 结论
1) 针对单一储能介质提出了基于FLC的自适应多阈值能量管理策略,相较于传统方法可以更好地发挥储能运行效果,制动能量利用率相同时其最大需量的削减效果更优,牵引变电所电费支出更少。
2) 本文所提配置与能量管理协同优化方法下牵引用光伏储能系统全寿命周期内的净收益为1 343万元,投资回收期为6年,对应的内部收益率达到14.6%,相较于其他储能方案经济性更优。
吴磊,舒洋浩,周斌彬等.基于配置与能量管理协同的铁路光储系统经济性提升策略[J].铁道科学与工程学报,2024,21(11):4711-4723.
WU Lei,SHU Yanghao,ZHOU Binbin,et al.Economic enhancement strategy for railway photovoltaic energy storage system based on collaborative configuration and energy management[J].Journal of Railway Science and Engineering,2024,21(11):4711-4723.