随着城轨系统逐渐实现供电资源共享,在解决电能均衡分配的同时,也为故障期间的应急恢复带来了新的挑战。目前,针对区域化失电等故障情形,为降低故障影响范围,一般以牺牲部分运营需求为代价,直接采取本线路支援供电方案,或者是通过闭合线间联络环网,形成多线路联合支援供电,这大大增加了故障期间的候选恢复方案数量,如果缺乏可靠的方案评估方法,可能会导致供电资源浪费,甚至二次支援的后果。因此,研究大面积停电时的应急恢复方案[1-2],对增强城轨供电系统韧性、快速完成灾后应急恢复具有重要意义。支援供电的实质是牵引供电系统的应急重构与综合调度[3-5]问题,目前已有大量智能算法应用于这类问题的求解。CHEN等[6]提出一种基于有向图遍历的配电网快速故障恢复方法,在有效利用分布式电源输出功率的基础上,最大程度地恢复失电负荷。SUN等[7]根据主动配电网中故障电流的特点建立故障恢复模型,采用人工蜂群算法搜索故障区域的并网路径。刘满君等[8]提出一种基于改进证据理论的元件运行可靠性模型,通过评估元件在短期内的故障风险,快速找到高可靠性的供电路径完成故障恢复。韩思宁等[9]建立了一种考虑可靠性约束的舰船电力系统故障重构模型,基于二阶锥松弛将故障重构模型转化为凸优化问题,并利用多面体逼近算法加速模型求解。李娟等[10]提出一种基于量子萤火虫算法的配电网故障恢复策略,能够通过控制配电网系统的开关通断,有效保证重要负荷恢复供电。张沛等[11]提出一种基于图强化学习的故障恢复决策方法,利用图神经网络对变化拓扑的处理能力提高对配电网拓扑变化的适应性,提升模型求解效率。针对候选应急恢复方案,需要采用客观合理的评价方法评估其供电能力。目前的主流方法是采用改进AHP法、熵权法等计算指标权重,利用TOPSIS等方法建立方案评分机制。陈鹏冲等[12]均采用层次分析—熵权法计算供电性能指标权重,完成了指标体系构建,能够直观展示指标间相对重要程度。林熹东等[13]提出一种基于贝叶斯模型的牵引设备风险源定量等级划分方法,在准确追溯风险源的同时,能有效量化其危害程度。SONG等[14]提出一种结合改进TOPSIS法和德尔菲—熵权综合权重法的电网规划方案综合决策方法,能够有效解决决策过程中客观数据利用不充分和权重分配不合理的问题。YU等[15]基于重要单位用户停电损失、应急资源响应等指标,建立了重要单位应急保障能力指标和应急用户损失模型,解决全市重要单位应急保障能力评价方法存在的问题。QIU等[16]设计了一种基于LCC思想的变电站供电方案评价方法,利用熵值法确定指标权重并计算相对贴近度确定方案排序。谷卫星等[17]提出一种基于秩和比的TOPSIS评价方法,不仅避免了评价过程中的信息丢失,而且克服了传统电能质量分级评价中随机性和模糊性的问题。肖志恒等[18-19]利用TOPSIS法对节点脆弱性量化计算并排序,从而有效发掘配电网系统中的薄弱节点。LUO等[20]提出一种基于加权马氏距离的变电站跳闸风险评估模型,能够根据数据分布特征准确划分风险等级。刘炜等[21-22]以系统附加网损为优化目标,采用潮流分析法循环迭代计算,筛选出最佳支援供电方案,实现了线网结构的优化。但是,目前应用于电网恢复方案中的评价算法对于指标数值变化不够敏感,难以体现方案间的差异性,并且无法实现对稀疏指标矩阵的有效评估。此外,应急恢复方案的筛选过程中并未考虑馈线容量及甩负荷量,难以证实最优复电方案的可行性。针对上述不足,本文根据复杂网络系统的拓扑简化原则和表示形式,建立了网络化运营模式下的城轨供电系统拓扑模型。利用多叉树拓扑搜索算法搜索需要断开的分段开关及闭合的联络开关,形成候选支援供电方案集。利用线路负荷及电压偏差等指标校验方案可行性,综合考量负荷切除量及开关操作次数,建立方案打分机制,筛选出故障模式下的最优复电方案。选取上海轨道交通网络典型线路,验证了本文所提出应急恢复策略的有效性。
1 城轨供电系统拓扑模型
为分析线网连接状态,确定故障期间的应急恢复方案。本文将复杂的集中式供电系统抽象为含n个负荷节点、m个电源节点及k条线路的稀疏连通拓扑,具体原则如下。
1) 假设不同线路的供电系统在换乘站处存在联络线路,正常运行时保持断开状态。
2) 对系统中的节点分类,设定牵引变电所、降压变电所及牵混所母线为负荷节点,主变电所母线为电源节点。按照供电分区顺序对节点及线路编号,默认联络开关编号为所在线路编号。
简化后的拓扑模型可用G=(A, W, E)描述,其中A为(n+m)×(n+m)阶的节点邻接矩阵,W为(n+m)×5阶节点属性矩阵,E为(z×6)阶线路信息矩阵。节点连接矩阵A中元素如式(1)所示:

式中: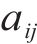
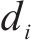
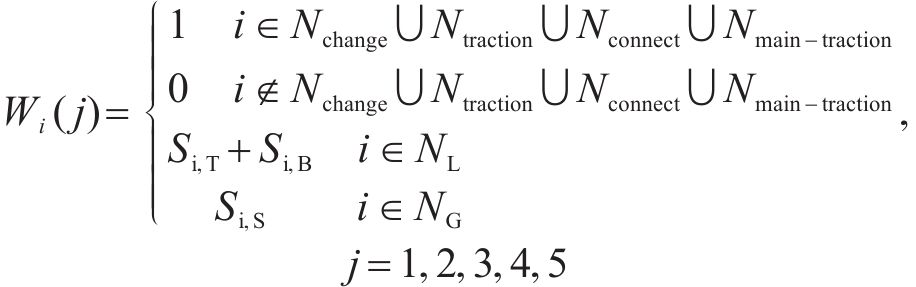
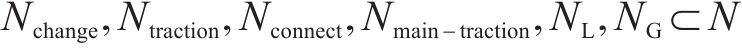
式中:i为节点编号;j为节点属性编号;Si,S为节点i对应主变压器的容量;Si,T、Si,B分别为节点i直连的牵引负荷功率和降压负荷功率;Nchange、Ntraction、Nconnect及Nmain-traction分别为换乘站节点集、牵引站节点集、本线路联络开关集及主变电所节点集;NL为负荷节点集;NG为电源节点集;N为全部节点集合。线路信息矩阵E中各元素如式(4)所示:
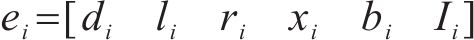
式中: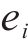
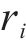
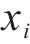
2 基于多叉树算法的应急恢复方案
2.1 方案设计
应急恢复方案的设计主要分为故障隔离与故障恢复两阶段,即通过断开分段开关隔离故障区域,搜索联络开关完成失电区域并网。
2.1.1 稀疏性处理
由于本文并不考虑潮流流向问题,基于式(5)对节点邻接矩阵做对称性处理,减少了大量无效连接信息。
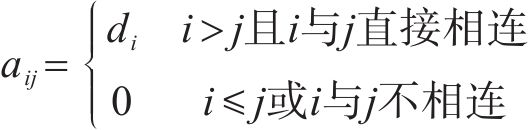
经式(5)处理后的矩阵A仍含有大量0元素,稀疏性较强。本文采用多向量存储方法,利用Ap,Ai及Ax这3个向量来表示维度为n×n,非零元数目为nz的稀疏矩阵。其中,Ap是长度为n+1的向量,Ap(i)表示矩阵第1至i-1行非零元数目之和,起始元素Ap(1)=0。Ai及Ax是长度为nz的向量,Ax中存储的是从第1行开始,列号由小到大的非零元的数值,Ai(i)中存储的是Ax(i)的列号。采用这样的存储方法,可以将稀疏矩阵A的存储空间从n×n降低为2×nz+n。
2.1.2 供电路径搜索
考虑到城轨供电系统的架构特征,本文采用多叉树算法搜索需要闭合的联络开关及需要断开的分段开关,步骤如下。
1) 设定多叉树节点类Nnode,包含叶子节点编号Lleafnodes,当前节点编号Vval,节点带电状态Sstate及供电电源Nnum。若当前节点含叶子节点,Lleafnodes为各叶子节点编号,反之为0。若当前节点带电,Sstate为1,反之为0。Nnum根据该节点由几路电源供电确定。
2) 基于Ap,Ai及Ax确定系统中各节点的Lleafnodes、Vval、Sstate及Nnum。将故障节点作为起始节点,依次判断其Lleafnodes的Nnum值,若大于1,则不失电,反之则判定为失电节点,断开起始节点与该节点间的连接线路。
3) 依次选择Lleafnodes中节点作为起始节点,重复步骤2中判断步骤,直至所有节点无Lleafnodes,则停止搜索,失电区域已形成。以16节点城轨供电系统为例,设定节点13发生故障。故障区域节点信息如表1所示,基于算法搜索结果形成的失电区域如图1所示。
| Vval | Lleafnodes | Sstate | Nnum | Vval | Lleafnodes | Sstate | Nnum |
|---|---|---|---|---|---|---|---|
| 1 | 4、5、6、7 | 1 | 0 | 9 | 0 | 0 | 1 |
| 2 | 6、8 | 1 | 0 | 10 | 9 | 0 | 1 |
| 3 | 0 | 1 | 1 | 11 | 10 | 0 | 2 |
| 4 | 3 | 1 | 1 | 12 | 0 | 1 | 2 |
| 5 | 0 | 1 | 2 | 13 | 14、15、16 | 0 | 2 |
| 6 | 0 | 1 | 1 | 14 | 0 | 0 | 1 |
| 7 | 11、12、13 | 1 | 1 | 15 | 0 | 0 | 1 |
| 8 | 11、12、13 | 1 | 1 | 16 | 0 | 0 | 1 |
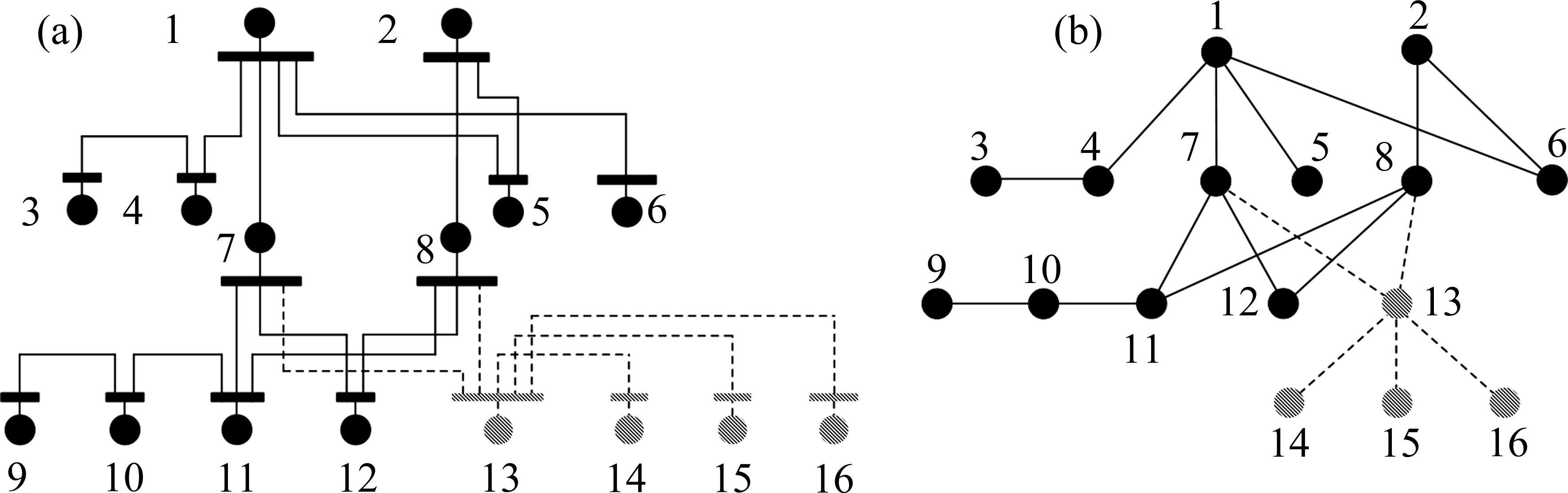
4) 搜索失电线路内部存在的联络开关,形成集合Kself。基于节点属性矩阵W确定失电区域中同时设置有换乘站与牵引站的节点,确定该失电孤岛与其他线路间的联络开关,形成集合Knet。
基于联络开关搜索结果可形成开关动作表,如式(6)所示。式中,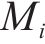
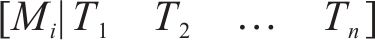
2.2 约束条件
应急恢复方案实施期间需满足一定约束条件,具体如下。
1) 电压偏差约束。支援供电期间各变电所中压母线电压偏差按照式(7)计算:
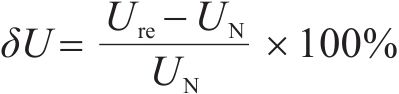
式(7)中: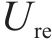

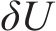
2) 线路负荷约束。支援供电期间,由于正常供电分区要承担失电区域的部分负荷,致使其馈线电流增大,各馈线流经电流应满足式(8)。式中,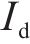
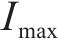
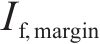
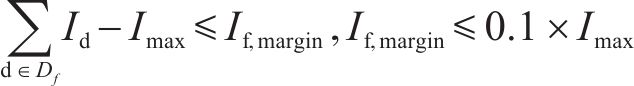
3) 主变容量约束。故障恢复期间,支援线路的主变容量应大于与其直接相连母线所承载的负荷,即满足式(9),式中,P、Q为正常运行时支援线路的系统损耗;Sz为主变容量;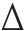
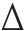
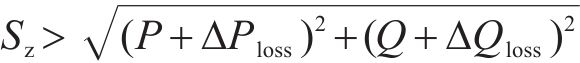
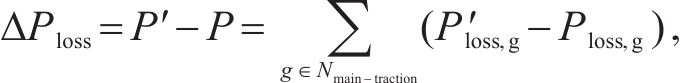
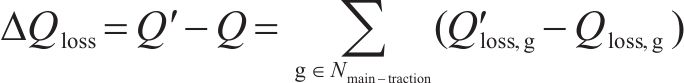
式(10)中: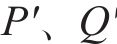
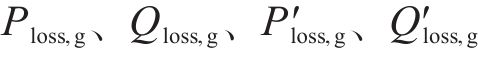
4) 输送容量约束。联络线路的输送功率应当小于其输送容量,即满足式(11)。式中,Dloss为故障区域的失电母线集;Sconnect为联络线路输送容量;Smargin为容量裕度。
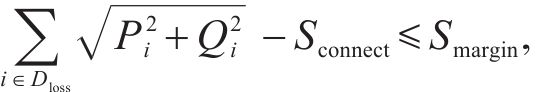
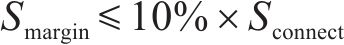
2.3 目标函数
应急恢复方案的筛选实质是支援成本与支援速度的综合评估问题,恢复过程中所涉及的评价指标主要为负荷切除量及开关操作次数,具体如下。
1) 负荷切除量f1,f2,f3,f4。由于供电能力限制,故障期间一般会减少支援线路或被支援线路的部分负荷实现降级支援。其中,牵引负荷切除量f1,f2及配电负荷切除量f3,f4可由式(12)~(13)求得。
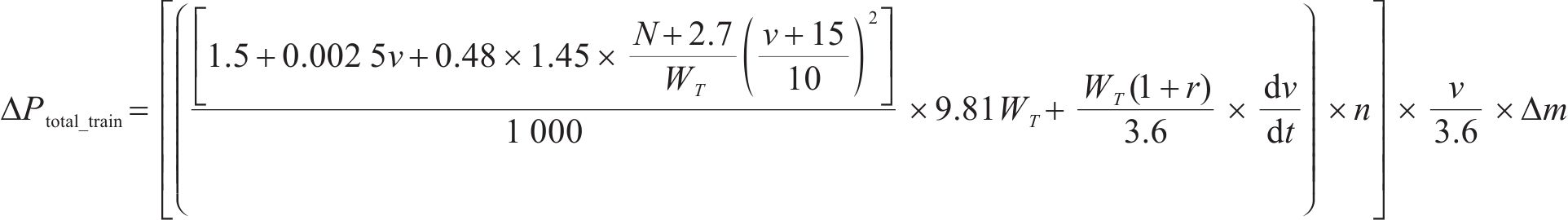
式(12)中:v代表当前运行速度;N为列车编组数;WT代表列车总重量;r代表列车回转系数;n为动车轴数;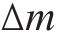
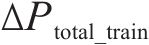
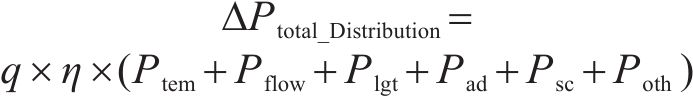
式(13)中:Plgt、Pad、Psc、Poth分别为照明负荷、商业负荷、通信系统负荷及其他小负荷;Ptem为环境变化所引起的负荷变化;Pflow为客流产生热功率。η为地铁配电负荷切除系数;q为降压变电站数量;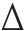
2) 开关操作次数f5。支援供电的快速性可以用开关操作次数衡量,如式(14)所示,式中,yi为故障线路内部联络开关i的动作情况;Zj为线路间联络开关j的动作情况。
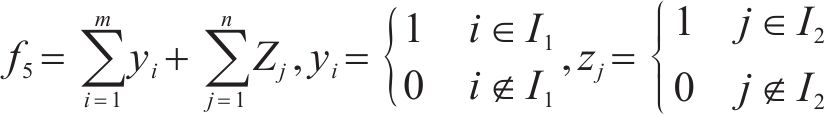
根据负荷切除量f1,f2,f3,f4及开关操作次数f5可确定目标函数,如式(15)所示。式中,vali代表评价指标值;ai为评价指标权重;Dcur为当前方案各评价指标值组成的向量;Dmin、Dmax分别为最差方案、最优方案的指标向量,S为当前方案得分。
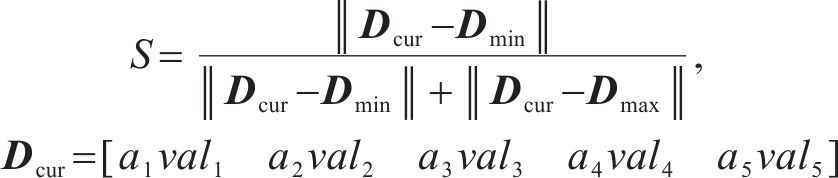
3 基于熵权—余弦相似度的多阶段联合模型求解
3.1 约束条件校验
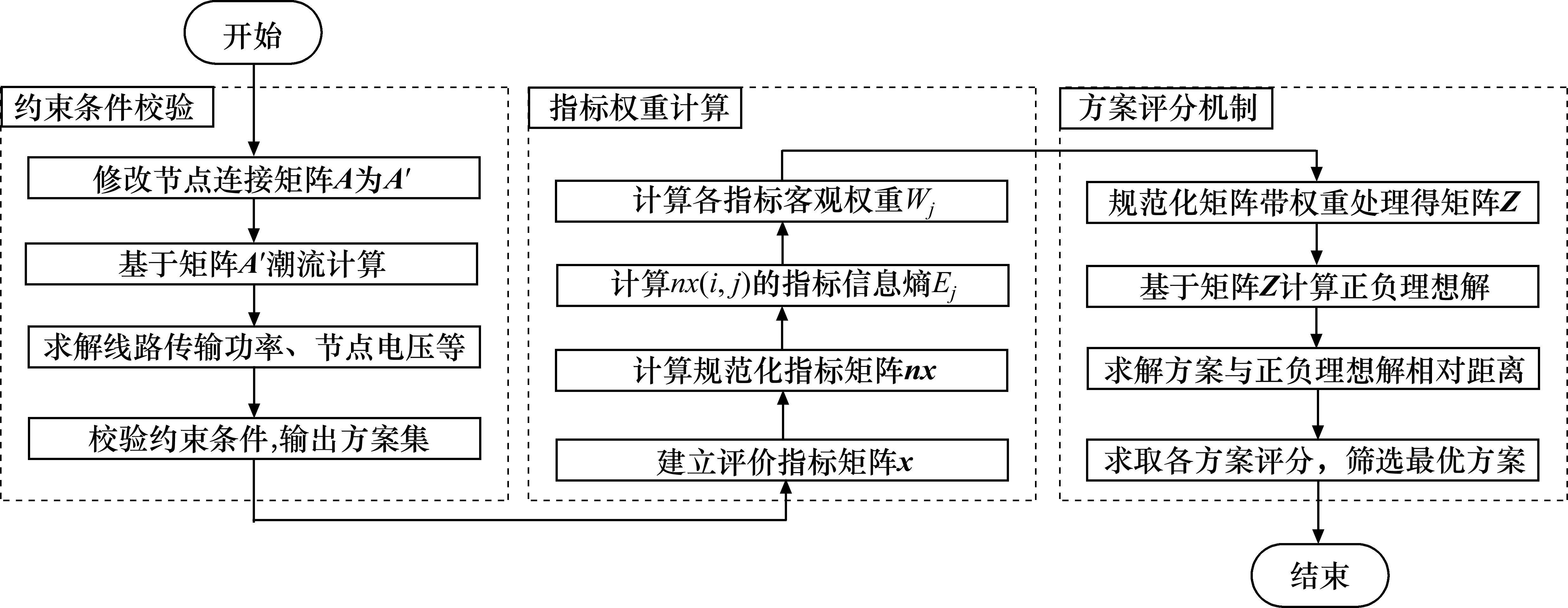
模型求解流程如图2所示,首先基于各支援供电方案下的节点连接矩阵
1) 根据
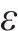
2) 设定节点电压初值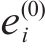
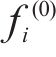
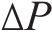
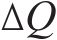
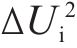
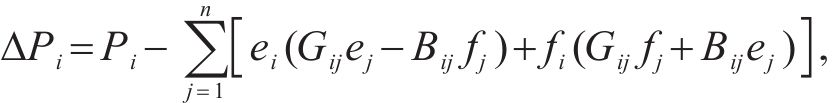
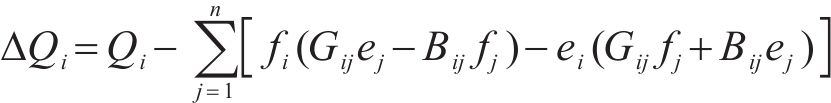
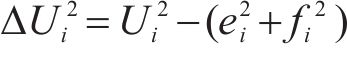
3) 根据雅可比矩阵J求取修正量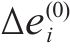
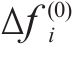
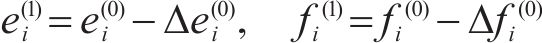
4) 重复步骤3,直至满足式(18)的退出条件,并根据式(19)求得节点功率。
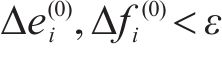
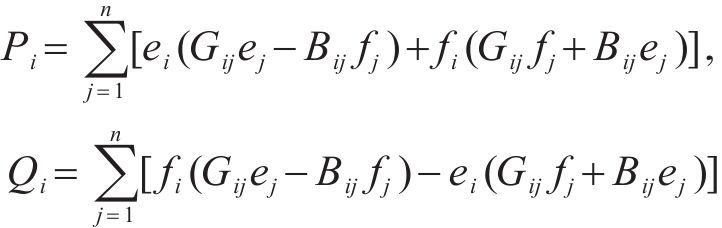
5) 根据计算结果校验约束条件,输出满足要求的方案集。
3.2 指标权重计算
为保证指标权重的客观性,尽量避免人为因素干扰,本文采用熵权法计算指标权重。具体步骤如下。
1) 建立评价指标矩阵,横坐标为方案编号i,纵坐标为评价指标编号j,矩阵中各元素为x(i,j)。利用极差变换法得到规范化数据矩阵nx,如式(20)所示。式中,x(:,j)代表指标矩阵中第j列的数据;m为方案数量;n为评价指标数量。
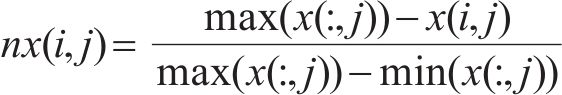
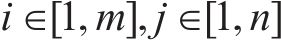
2) 基于式(21)计算nx(i,j)的指标信息熵,通过式(22)计算各评价指标客观权重。
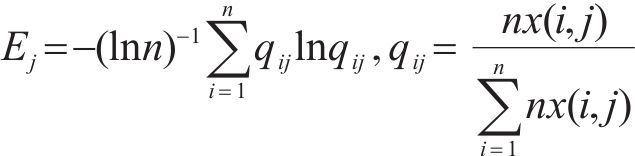
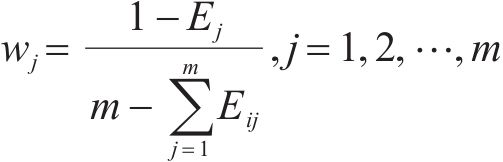
3.3 方案评分机制
针对规范化矩阵按式(23)带权重处理,形成矩阵z。由于负荷切除量及开关操作次数均为成本型指标,按照式(24)形成正理想解z+及z-与负理想解。
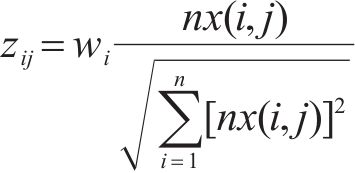
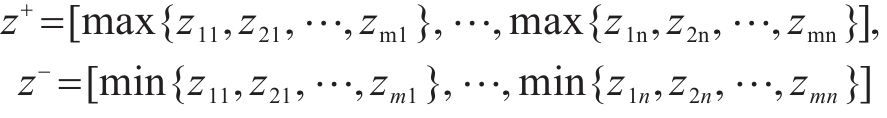
利用余弦相似度分别求取各评价方案到正理想解及负理想解的距离,如式(25)~(26)所示,并按照式(27)求方案最终评分。
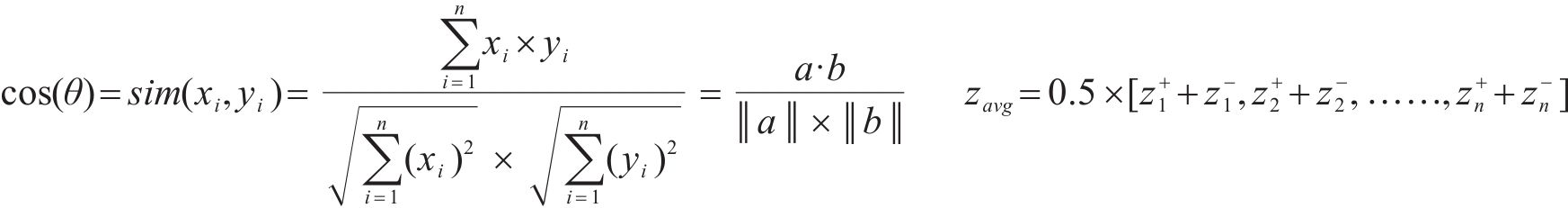
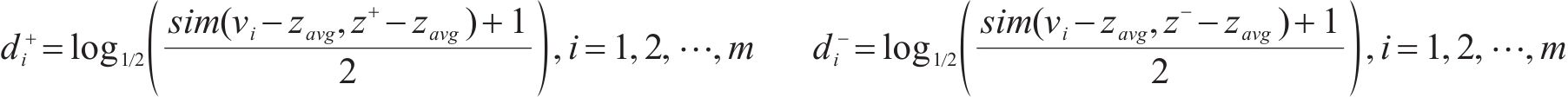
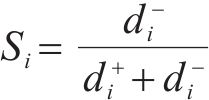
4 算例分析
4.1 应急恢复方案设计
本文以上海轨道交通网络为背景,基于式(1)~(4)对1、2、3、7、8、10号线的供电系统进行拓扑化建模,并按顺序对节点及线路进行编号,得到一个含34个电源节点,457个负荷节点及531条线路的简化拓扑[22-23]。为了验证所提出的应急恢复方案优化模型求解策略的有效性,本文设置了一种主变退出运行的故障模式。在计算负荷功率时,参考高峰时段的发车间隔,牵引变压器的负载率设置为85%,功率因数设置为0.95。根据切除三级负荷后的降压负荷,配电变压器的负载率设置为40%,功率因数设置为0.85。计算各中压线路参数时,35 kV进线电缆的电阻为0.047 Ω/km,电感为0.36×10-3 H/km,电纳为0.21×10-6 S/km。10 kV电缆的电阻为0.075 4 Ω/km,电感为0.296×10-3 H/km,电纳为0.129×10-6 S/km。计算线路输送容量时,截面积为240 mm2电缆的经济输送容量为16.7 M∙VA,极限输送容量为37 M∙VA,截面积为400 mm2电缆的经济输送容量为27.8 M∙VA,极限输送容量为50 M∙VA。
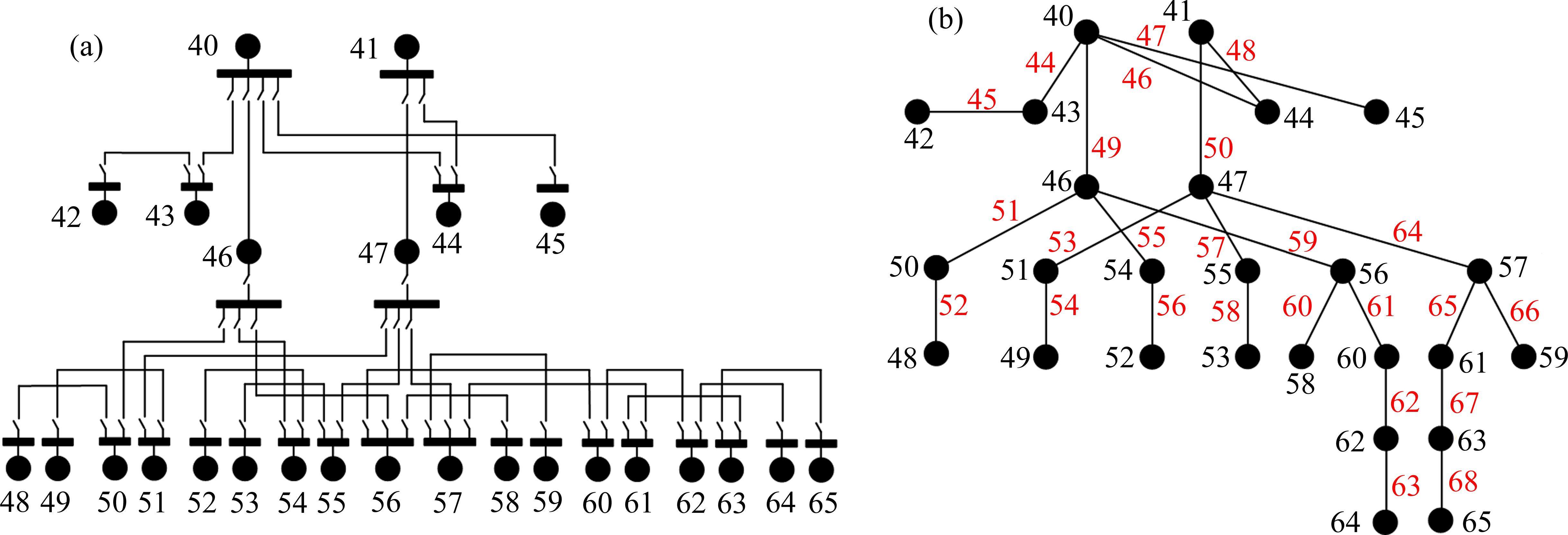
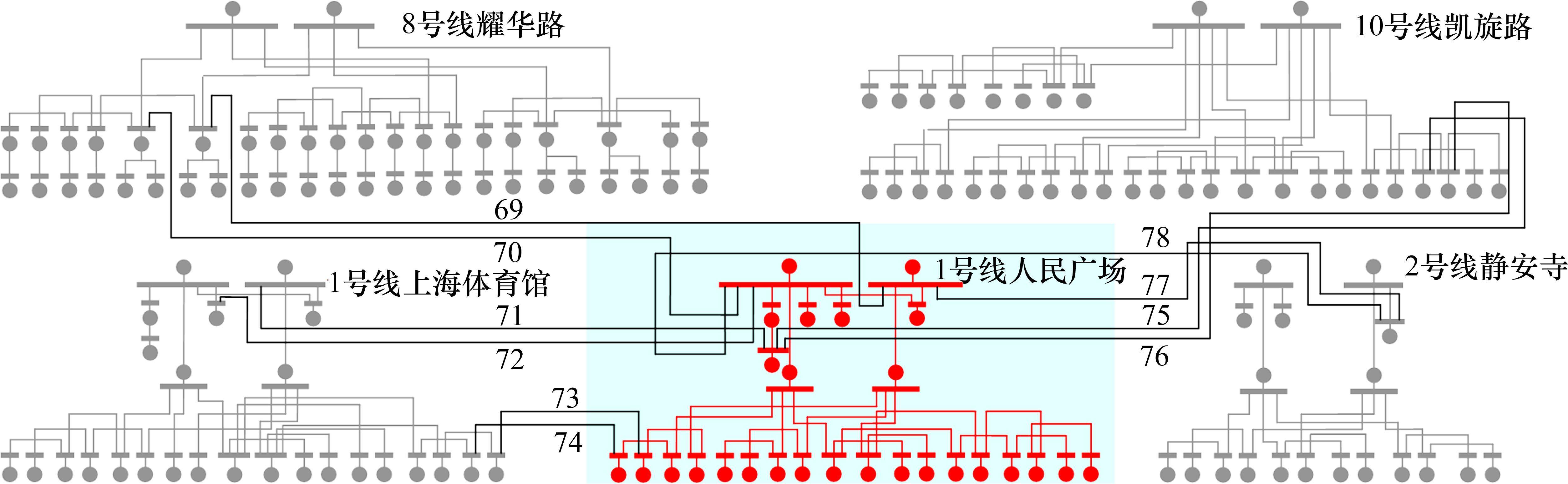
模拟1号线人民广场供电分区、2号线静安寺供电分区、8号线耀华路供电分区主变退出运行的故障情形,采用不同的支援供电方式完成应急故障恢复。以1号线供电分区失电为例说明求解过程,该分区内节点属性矩阵W如表2所示。利用多叉树算法搜索需断开的分段开关,结果如图3所示,图中线路编号代表需断开的分段开关。将失电区域视为孤岛,通过搜索并网路径完成支援供电,可闭合的联络开关如图4所示。根据搜索结果共得到1种本线路支援供电方案及4种跨线支援供电方案。依据该方法可完成2、8号线主变退出运行下的应急恢复方案设计,各方案下联络开关动作情况如表3所示。
| 编号 | wchange | wtraction | wmain-traction | wconnect | wcapacity | 编号 | wchange | wtraction | wmain-traction | wconnect | wcapacity |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 40 | 1 | 0 | 1 | 0 | 31.5MVA | 46~47 | 1 | 0 | 0 | 0 | 12.5MVA |
| 41 | 1 | 0 | 1 | 0 | 31.5MVA | 48~49 | 1 | 0 | 0 | 1 | 0.4 MVA |
| 42 | 1 | 1 | 0 | 1 | 3.5MVA | 50~51 | 0 | 0 | 0 | 0 | 0.4 MVA |
| 43 | 1 | 0 | 0 | 1 | 3.5MVA | 52~53 | 1 | 0 | 0 | 0 | 0.4 MVA |
| 44 | 0 | 1 | 0 | 0 | 3.5MVA | 54~65 | 0 | 0 | 0 | 0 | 0.4 MVA |
| 45 | 1 | 1 | 0 | 1 | 3.5MVA |
| 编号 | 方案名称 | 需动作的联络开关 | 编号 | 方案名称 | 需动作的联络开关 |
|---|---|---|---|---|---|
| 1 | 1号线本线路支援供电 | 71、72、73、74 | 9 | 1号线支援供电2号线 | 175、176 |
| 2 | 2号线支援供电1号线 | 77、78 | 10 | 7号线支援供电2号线 | 181、182 |
| 3 | 8号线支援供电1号线 | 69、70 | 11 | 1、8号线支援供电2号线 | 175、176、177、178 |
| 4 | 10号线支援供电1号线 | 75、76、70 | 12 | 8号线本线路支援供电 | 448、449 |
| 5 | 2、8号线支援供电1号线 | 69、70、77、78 | 13 | 1号线支援供电8号线 | 444、445 |
| 6 | 2号线本线路支援供电 | 133、135、150、151 | 14 | 2号线支援供电8号线 | 446、447 |
| 7 | 8号线支援供电2号线 | 177、178 | 15 | 1、2号线支援供电8号线 | 444、445、446、447 |
| 8 | 10号线支援供电2号线 | 179、180 |
4.2 最优方案筛选
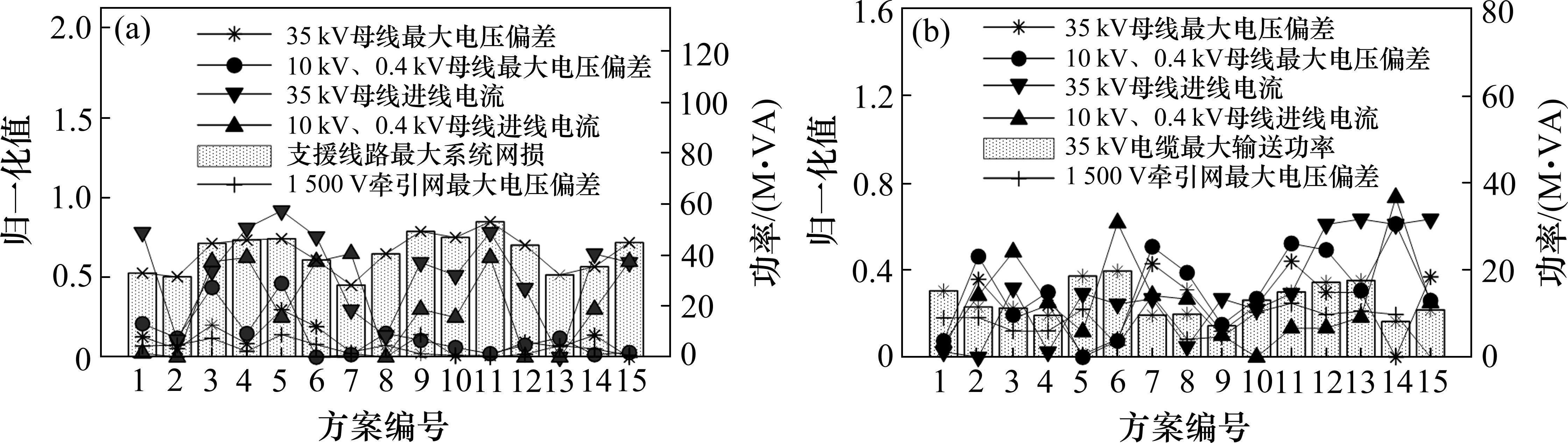
根据最优应急恢复方案的求解流程,首先校验各方案的约束条件。针对各方案下的系统架构进行潮流计算,并将电压偏差及线路负荷做归一化处理,计算结果如图5所示,发现各方案均满足约束要求。其次,根据式(12)~(14)计算各方案下的负荷切除量及开关操作次数,如图6(a)所示,结果表明在3种故障情形下,多线路联合支援供电方案的负荷切除量均为0,即采用该应急恢复方式在故障期间仍能满足线路基本运营需求。基于式(20)~(22)计算评价指标客观权重,结果如图6(b)所示,发现被支援线路的牵引负荷切除量f1及配电负荷切除量f4所占权重较大,对方案评价结果影响较大,在后续设计方支援供电方案过程中应尽可能少的切除被支援线路的牵引及配电负荷。
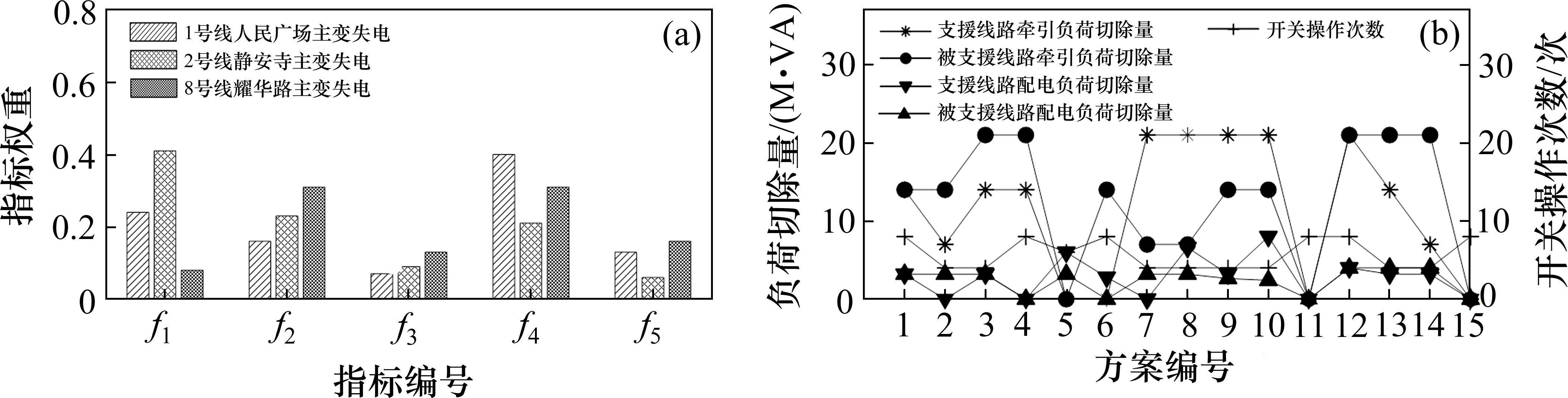
按照式(25)~(27)计算各故障情形下的方案评分,结果如表4所示。分析可知:
| 编号 | 方案名称 | 方案评分 |
|---|---|---|
| 1 | 1号线本线路支援供电方案 | 0.37 |
| 2 | 2号线支援供电1号线 | 9.27 |
| 3 | 8号线支援供电1号线 | 2.42 |
| 4 | 10号线支援供电1号线 | 2.17 |
| 5 | 2、8号线支援供电1号线 | 97.83 |
| 6 | 2号线本线路支援供电方案 | 76.01 |
| 7 | 8号线支援供电2号线 | 10.48 |
| 8 | 10号线支援供电2号线 | 7.22 |
| 9 | 1号线支援供电2号线 | 3.82 |
| 10 | 7号线支援供电2号线 | 3.32 |
| 11 | 1、8号线支援供电2号线 | 97.47 |
| 12 | 8号线本线路支援供电 | 0.03 |
| 13 | 1号线支援供电8号线 | 4.99 |
| 14 | 2号线支援供电8号线 | 5.67 |
| 15 | 1、2号线支援供电8号线 | 95.64 |
1) 本线路支援供电方案的应急恢复能力较跨线支援供电方案明显不足。尤其在1、8号线发生故障时,方案评分几乎为0,此时,正常供电分区母线承载负荷较重,难以完成故障期间的应急救援。
2) 在跨线支援供电方案中,单线支援的评分结果相较于多线支援平均相差了68.52,其故障恢复能力明显不足,难以满足故障线路的电能需求。
3) 在3种故障情形下,采用2号线支援供电的方案评分均较高,即该线路应急恢复能力较强,在后续故障处理过程中,可优先考虑采用该线路进行临时复电。
综上,若要缩小故障影响范围,即仅考虑单供电分区支援,可适当提升跨线支援供电方案的优先级,将本线路支援供电方案作为备选。若考虑在故障期间尽量不影响线路正常运营,可优先选择多线路联合支援供电。
4.3 算法验证
为了验证本文采用的熵权—余弦相似度算法的优势,采用改进AHP—TOPSIS法及熵权—TOPSIS法对比分析,各评价算法计算结果如图7所示。结果表明:
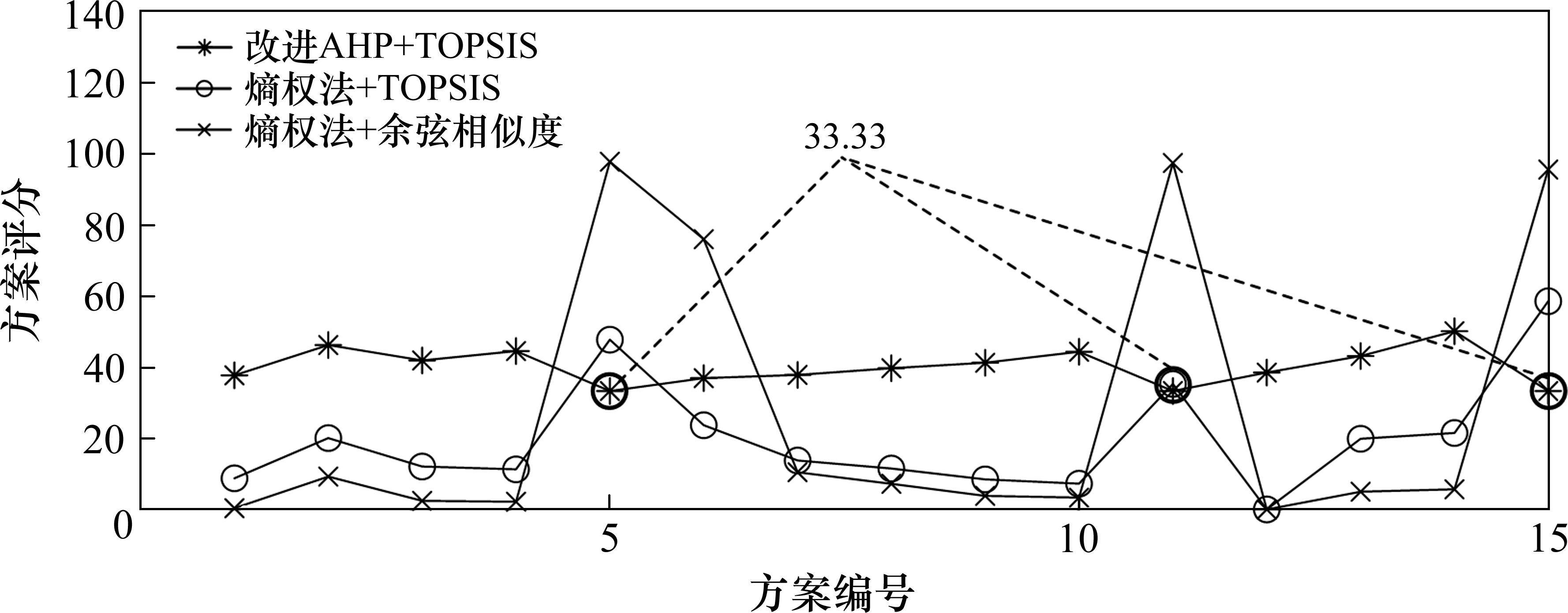
1) 改进AHP—TOPSIS受稀疏矩阵影响较大,评估结果不准确。如采用多线路支援供电时,其负荷切除量均为0,此时评分将不受指标权重影响,固定为0.33。
2) 采用熵权—TOPSIS法评估时,方案间的评分差异性不足。例如,采用1、8号线联合支援2号线时,其负荷切除量比2号线本线路支援供电方式减少了16.8 MVA,然而评分仅相差9.61。若不同方案下的指标值相近,使用该评估方法将难以直观显示得分差距,为调度人员的故障救援决策带来困难。
3) 熵权—余弦相似度法相较于其余2种算法,不仅能够有效避免零元素对评分结果造成的影响,而且能有效增强评分差异性,在不同故障情形下的平均最大得分差距为95.75,能够准确筛选出不同故障模式下的最优复电方案,最大程度地量化不同方案间的应急恢复能力差异。
5 结论
1) 基于本文采用的多叉树拓扑路径搜索算法,不仅能快速实现电网健康部位与故障点的电气隔离,且能准确搜索出应急联络开关,有效完成故障救援决策的前期工作。
2) 针对本文提出的应急恢复方案优化策略,在评分准确度层面,能够有效避免稀疏矩阵产生的影响。在评分精度层面,能增强方案间的评分差异性,降低方案误判率。
3) 针对大面积停电事故,多线路联合支援的应急恢复能力更强,在快速完成故障区域临时复电的同时,仍能满足线路基本运营需求。对于已实现城轨系统供电资源共享的城市具有很强的参考意义,能够有效提升其抵御极端故障的能力,实现故障后的快速恢复。
Fault location method of active distribution network based on improved artificial bee colony algorithm
[C]//城市轨道跨换乘站资源共享供电方案优化设计
[J/OL]. 西南交通大学学报, 1-9[张明锐,曹庭嵩,王小峰等.基于熵权—余弦相似度的城轨供电系统复电策略[J].铁道科学与工程学报,2024,21(11):4724-4734.
ZHANG Mingrui,CAO Tingsong,WANG Xiaofeng,et al.Restoration strategy of urban rail power supply system based on entropy weight cosine similarity[J].Journal of Railway Science and Engineering,2024,21(11):4724-4734.

