在建筑固废资源化利用背景下,再生粗骨料作为混凝土的原材料,在工程中逐渐得到应用[1-2]。相比较天然碎石粗骨料,再生粗骨料的强度更低且形状更不规则,具有表面棱角复杂和质地粗糙等特点[3],通过物理整形可以改善再生粗骨料的强度和形态特征[4]。形态特征是粗骨料的基本特征,对混凝土的工作性、力学性能和耐久性能有着重要影响[5-8]。在实际过程应用中,对混凝土用天然粗骨料形态特征通常用针片状和扁平状含量表示[8],无法精确量化。随着数字图像处理技术和三维重构技术的发展,现有研究主要围绕形状、棱角度和粗糙度3个尺度表征粗骨料的形态特征[9-15],并就每个尺度提出大量计算方法,张雪芹等[8]总结了棱角度的计算方法有轮廓曲率、轮廓梯度、多边形拟合、椭球拟合和腐蚀膨胀法等近十种。除了上述3个尺度外,分形理论也被用于量化粗骨料的形态特征,常用方法包括面积-周长法和计盒维数法等[16-17]。可见,粗骨料形态特征指标的计算方法不统一且计算复杂,影响了形态特征指标的量化应用。主成分分析方法是一种从高维变量中提取相互独立的公共变量从而降低输入维度的一种多元统计学方法[18]。骆行文等[19]采用主成分分析方法对岩石的5个性能指标进行分析,最终得到了一个综合指标评价岩石的质量。肖柏林等[20]对7种矿山充填粗骨料的形状和棱角度进行评价,并通过主成分分析方法得到了2组新的指标。目前,还没有简单明确的指标能直接反映再生粗骨料的形态特征,对再生粗骨料形态特征的系统研究还需要进一步开展。因此,考虑再生粗骨料和天然粗骨料的形态特征差异,从众多形态特征指标中找出合适的指标表征再生粗骨料形态特征,这作为再生粗骨料的基础性研究对再生粗骨料进一步推广应用具有积极意义。基于此,本文对再生粗骨料进行物理整形,采集了再生粗骨料在整形过程中圆度、棱角度、扁平度、细长度、球度、粗糙度和分形维数等形态特征参数,并采用主成分分析法研究物理整形对再生粗骨料形态特征综合形态的影响并提出了评价指标,以期为再生粗骨料的生产制备及高品质应用提供基础性研究。
1 原材料及试验
1.1 原材料
试验选用原材料包括天然碎石粗骨料(G)、道路混凝土再生粗骨料(RCA1)和砖混再生粗骨料(B-RCA),其中RCA1和B-RCA的原生混凝土强度分别为C30和C20,B-RCA中砖含量约为35%。再生粗骨料均由拆除后的建筑垃圾经实验室小型颚式破碎机破碎筛分得到,粗骨料照片如图1所示。采用4.75~9.5 mm粒径粗骨料测试基本物理性能,如表1所示。

| 粗骨料类型 | 表观密度/ (g∙cm-3) | 堆积密度/(g∙cm-3) | 空隙率/% | 吸水率/% | 压碎指标/% |
|---|---|---|---|---|---|
| G | 2.74 | 1.65 | 39.57 | 1.65 | 8.3 |
| RCA1 | 2.61 | 1.30 | 50.04 | 6.20 | 17.8 |
| B-RCA | 2.57 | 1.24 | 51.92 | 8.99 | 32.3 |
1.2 试验方案
1.2.1 粗骨料物理整形
本文采用洛杉矶磨耗仪进行物理整形,洛杉矶磨耗仪为浙江路达机械仪器有限公司生产的DM-Ⅱ型,尺寸710 mm×510 mm,转速30~33 r/min,模拟反击式破碎机的动能冲击作用环境整形再生粗骨料[13]。每次试验称取固定质量4.75~19.5 mm的粗骨料倒入料筒中,并放入6个钢球强化整形效果,以5 min间隔逐次递增。当整形时间为15 min时,再生粗骨料出现严重破碎,最终将试验整形时间设置为0、5、10和15 min。由于再生粗骨料整形过程中粒径会发生变化,影响形态特征测试结果,因此将整形后的粗骨料筛分取样为4.75~9.5 mm粒径,并进行物理性能和形态特征测试。
1.2.2 粗骨料形态特征测试
试验粗骨料种类包括3种粗骨料(G、RCA1和B-RCA),每种粗骨料有4种整形时间(0、5、10和15 min),因此共有12种类型粗骨料。使用集料图像测量系统(AIMS)采集粗骨料的形态特征,每种粗骨料均随机选取100颗进行试验,试验过程图2所示。为从形状、棱角度和粗糙度3个尺度表征再生粗骨料,采用圆度、棱角度、扁平度、细长度、球度、粗糙度和分形维数计算粗骨料的形态特征,计算方法如表2所示。

| 特征参数 | 计算公式 | 特征描述 | |
|---|---|---|---|
| 圆度 | 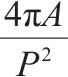 | 圆度越大,粗骨料的形状越趋近圆形。 式中:A为粗骨料的投影面积;P为投影周长。 | |
| 棱角度 | 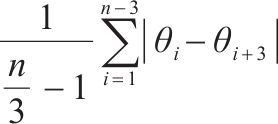 | 棱角度越大,粗骨料的棱角性越明显。 式中:θ为图像边缘某点的梯度向量角度;n为边缘点的总数量;i为边缘的第i个点。 | |
| 球度 | 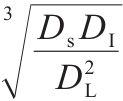 | 球度越大,粗骨料形状越接近球形。 式中:DS、DI和DL分别为粗骨料的短轴、中轴和长轴长。 | |
| 扁平度 | 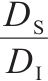 | 扁平度越小,粗骨料形状越趋于片状。 | |
| 细长度 | 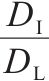 | 细长度越小,粗骨料形状越趋于针状。 | |
| 粗糙度 | 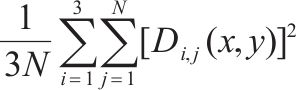 | 粗糙度越小,粗骨料表面越光滑。 式中:N为图像中细节系数的数量;i为i张图像;j为小波系数;D为分解函数;x,y为转换域中的位置坐标。 | |
| 分形维数 | 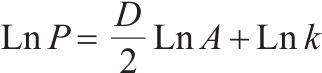 | 分形维数越大,粗骨料的形状轮廓越复杂。式中:D为分形维数,k为尺度常数。 | |
2 试验结果
2.1 粗骨料物理性能
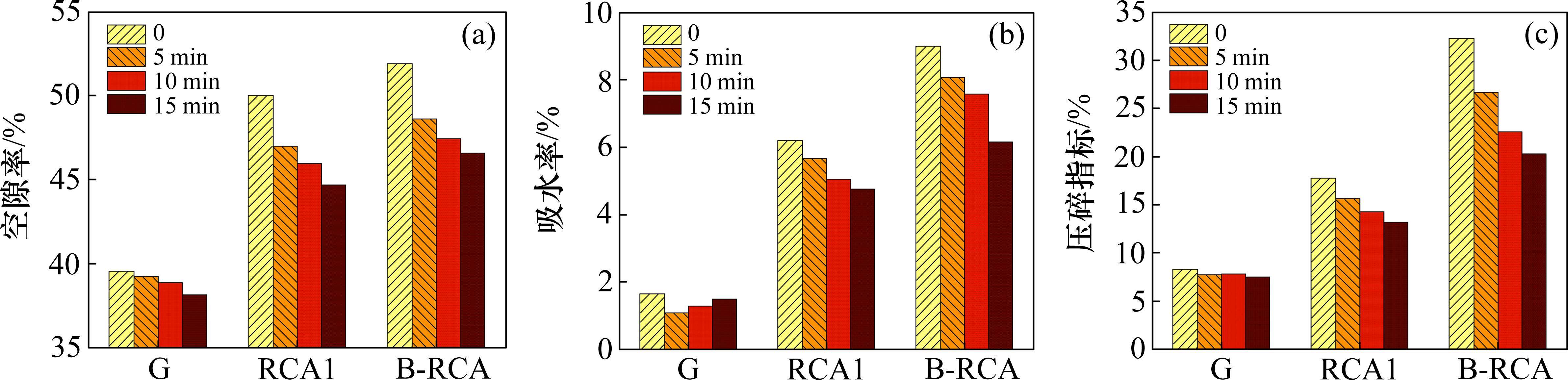
图3为不同整形时间时粗骨料的物理性能的变化。由图3可知,随着整形时间的增加,再生粗骨料的空隙率、吸水率和压碎指标均不断降低,当整形时间为15 min时,RCA1和B-RCA的空隙率较整形前分别降低了10.67%和10.24%、吸水率降低了23.23%和37.59%、压碎指标降低了25.84%和37.15%,表明物理整形能显著提高再生粗骨料的物理性能。这主要是由于在整形过程中,再生粗骨料表面的浆体在摩擦碰撞作用下不断剥落,附着浆体含量降低使得再生粗骨料物理性能得到提升。
2.2 粗骨料形态特征
表3为不同整形时间下粗骨料的粒形指标,由表3可知,随着整形时间的增加,再生粗骨料的圆度、扁平度、细长度和球度出现不同程度的增加,而棱角度、粗糙度和分形维数则出现降低。当整形时间为15 min时,RCA1、B-RCA的圆度分别增加了10.11%和7.03%;扁平度分别增加了7.43%和1.62%;细长度分别增加了14.39%和8.49%;球度分别增加了8.81%和7.38%;棱角度分别降低了24.82%和23.70%;粗糙度分别降低了13.59%和24.74%;分形维数分别降低了1.53%和1.06%。这表明再生粗骨料经过物理整形后,针片状含量减少、形状更趋于球形、表面更光滑、轮廓更规则,整形显著改善了再生粗骨料的形态特征。
| 粗骨料类型 | 球磨时间/min | 圆度 | 棱角度 | 扁平率 | 细长度 | 球度 | 粗糙度 | 分形维数 |
|---|---|---|---|---|---|---|---|---|
| G | 0 | 0.830 | 2 726.2 | 0.642 | 0.725 | 0.688 | 170.5 | 1.001 |
| 5 | 0.843 | 2 404.3 | 0.630 | 0.731 | 0.683 | 170.1 | 1.010 | |
| 10 | 0.843 | 2 371.6 | 0.663 | 0.711 | 0.688 | 169.9 | 1.006 | |
| 15 | 0.851 | 2 305.0 | 0.646 | 0.731 | 0.687 | 167.9 | 1.005 | |
| RCA1 | 0 | 0.790 | 3 380.4 | 0.646 | 0.667 | 0.647 | 212.6 | 1.046 |
| 5 | 0.853 | 2 857.5 | 0.668 | 0.720 | 0.691 | 198.9 | 1.015 | |
| 10 | 0.857 | 2 681.1 | 0.682 | 0.724 | 0.700 | 207.1 | 1.010 | |
| 15 | 0.870 | 2 541.3 | 0.694 | 0.763 | 0.704 | 183.7 | 1.030 | |
| B-RCA | 0 | 0.807 | 3 478.7 | 0.680 | 0.695 | 0.682 | 267.6 | 1.035 |
| 5 | 0.844 | 2 792.5 | 0.676 | 0.725 | 0.698 | 220.2 | 1.021 | |
| 10 | 0.855 | 2 596.7 | 0.683 | 0.732 | 0.705 | 184.5 | 1.024 | |
| 15 | 0.864 | 2 654.3 | 0.691 | 0.754 | 0.732 | 201.4 | 1.024 |
3 主成分分析
由于每个粒形指标仅在单方面描述粗骨料的形态特征,当粒形指标种类较多时,复杂的高维信息不利于直观反映粗骨料颗粒形态。因此本文使用主成分分析方法将粒形指标重新组合,用少量几个主成分来反映多数粒形指标的信息,简洁高效地描述整形过程中再生粗骨料形态特征的变化规律。
3.1 数据预处理
主成分分析前需要通过KMO(Kaiser-Meyer-Olkin,KMO)和Bartlett球形检验方法(Bartlett’s Test of Sphericity)验证粒形指标间的相关性,使用SPSS 25.0软件(Statistical Product and Service Solutions 25.0)进行计算,得到粒形指标的KMO值为0.690(>0.5),Bartlett球形检验指标为71.361(p<0.05),这说明不同粒形指标间的相关性较好,可以使用主成分分析方法。由于不同粒形指标的计算公式不同,为了消除量纲对试验结果的影响,按式(1)采用标准差标准化方法计算表3中的原始粒形指标数据,标准化后的数据均值为0,标准差为1,计算结果如表4所示。
| 粗骨料种类 | 球磨时间/min | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 |
|---|---|---|---|---|---|---|---|---|
| G | 0 | -0.527 | -0.017 | -1.169 | 0.073 | -0.207 | -0.888 | -1.320 |
| 5 | 0.032 | -0.895 | -1.736 | 0.314 | -0.461 | -0.901 | -0.657 | |
| 10 | 0.032 | -0.984 | -0.177 | -0.487 | -0.207 | -0.908 | -0.952 | |
| 15 | 0.376 | -1.165 | -0.980 | 0.314 | -0.258 | -0.977 | -1.025 | |
| RCA1 | 0 | -2.248 | 1.766 | -0.980 | -2.250 | -2.286 | 0.566 | 1.995 |
| 5 | 0.463 | 0.341 | 0.059 | -0.127 | -0.055 | 0.093 | -0.289 | |
| 10 | 0.635 | -0.140 | 0.720 | 0.033 | 0.401 | 0.376 | -0.657 | |
| 15 | 1.194 | -0.521 | 1.287 | 1.596 | 0.604 | -0.432 | 0.816 | |
| B-RCA | 0 | -1.517 | 2.034 | 0.626 | -1.129 | -0.511 | 2.466 | 1.185 |
| 5 | 0.075 | 0.164 | 0.437 | 0.073 | 0.300 | 0.829 | 0.153 | |
| 10 | 0.549 | -0.370 | 0.768 | 0.354 | 0.655 | -0.404 | 0.374 | |
| 15 | 0.936 | -0.213 | 1.146 | 1.235 | 2.024 | 0.180 | 0.374 |
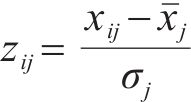
式中: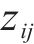
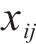
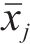
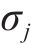
3.2 粒形指标相关性分析
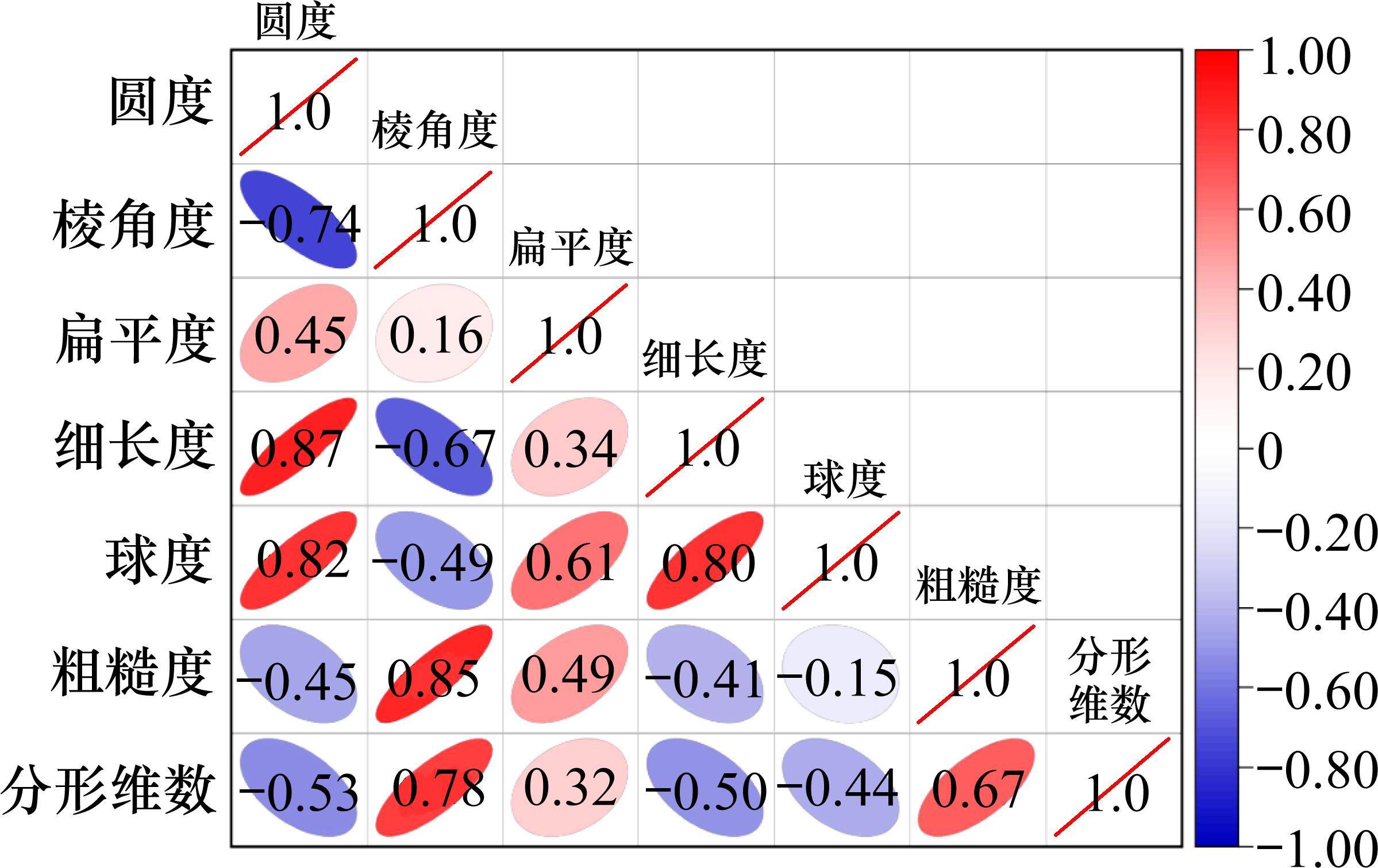
将表4的标准化数据按式(2)计算所有粒形指标间的相关系数,计算结果如图4所示。
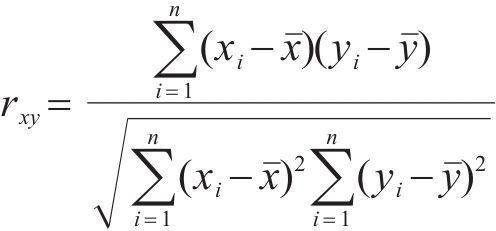
式中:rxy为2个粒形指标x、y的相关系数;n为样本容量;xi、yi分别为2个粒形的指标样本值;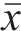
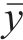
图4为不同粒形指标间的相关系数矩阵(R),由图4可知,正相关性较好的粒形指标分别有圆度和细长度、圆度和球度、细长度和球度、棱角度和粗糙度以及棱角度和分形维数。相关系数分别为0.87、0.82、0.80、0.85和0.78。负相关性较好的粒形指标有圆度和棱角度,相关系数为-0.74。这表明当粗骨料越趋于球形时,其针状和片状的含量会越少;当粗骨料表面的棱角越多时,其表面会越粗糙,轮廓会越不规则。
3.3 综合形态指标分析
将相关系数矩阵R按式(3)计算特征值λi,并将结果列于表5中。
| 组分 | 初始特征值 | 提取荷载 | ||||
|---|---|---|---|---|---|---|
| 特征值 | 解释量/% | 累积量/% | 特征值 | 解释量/% | 累积量/% | |
| 1 | 4.05 | 57.85 | 57.85 | 4.05 | 57.85 | 57.85 |
| 2 | 2.19 | 31.23 | 89.08 | 2.19 | 31.23 | 89.08 |
| 3 | 0.41 | 5.82 | 94.90 | |||
| 4 | 0.18 | 2.51 | 97.40 | |||
| 5 | 0.09 | 1.28 | 98.68 | |||
| 6 | 0.06 | 0.85 | 99.53 | |||
| 7 | 0.03 | 0.47 | 100.00 | |||
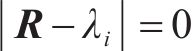
主成分贡献率反映出对原始数据信息的包含程度。按照特征值大于1的原则,提取出主成分1和主成分2,累计贡献率之和达到89.08%,说明能全面反映原始信息。为解释2个主成分的物理意义,采用最大方差法正交旋转初始载荷矩阵,计算出因子载荷矩阵,如表6所示。
| 因子 | 圆度 | 棱角度 | 扁平率 | 细长度 | 球度 | 粗糙度 | 分形维数 |
|---|---|---|---|---|---|---|---|
| 1 | 0.867 | -0.429 | 0.793 | 0.860 | 0.950 | -0.060 | -0.106 |
| 2 | -0.450 | 0.870 | 0.545 | -0.405 | -0.106 | 0.926 | 0.852 |
表6为主成分旋转因子载荷矩阵。由表6可知,因子1(F1)反映了再生骨料的圆度、扁平度、细长度和球度,载荷值分别为0.867、0.793、0.860和0.950,这4个粒形指标均侧重于描述粗骨料的整体形状特性,即判断粗骨料的形状是否接近球形,将因子1命名为整体形态因子。因子2(F2)中反映了棱角度、粗糙度和分形维数,载荷值分别为0.870、0.926和0.852。由于棱角度和粗糙度均可理解为粗骨料表面的形态规则程度,棱角度较大说明表面凸起较多,粗糙度较大说明表面凹凸不平的程度较大,将因子2命名为表面形态因子。
为了比较不同种类粗骨料的形态因子差异,使用SPSS对表6的因子载荷矩阵进行回归分析,计算得到因子得分系数矩阵,将其与标准化后的粒形指标值结合可得2个形态因子F1和F2的综合得分表达式,如式(4)和式(5)所示,F1越大说明粗骨料的整体形态越接近球形,F2越大说明粗骨料的表面形态越不规则。将表4中的数据代入式(4)和式(5)中便可得到粗骨料2个形态因子的综合得分,结果如图5所示。
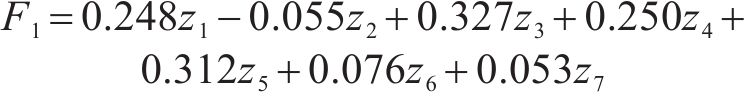
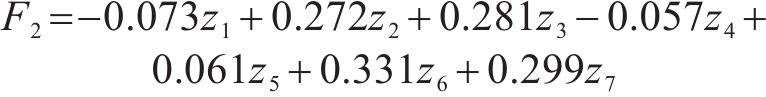
式中:Z1、Z2、Z3、Z4、Z5、Z6、Z7分别为不同种类和整形时间下粗骨料的圆度、棱角度、扁平度、细长度、球度、粗糙度、分形维数值的数据标准化值。
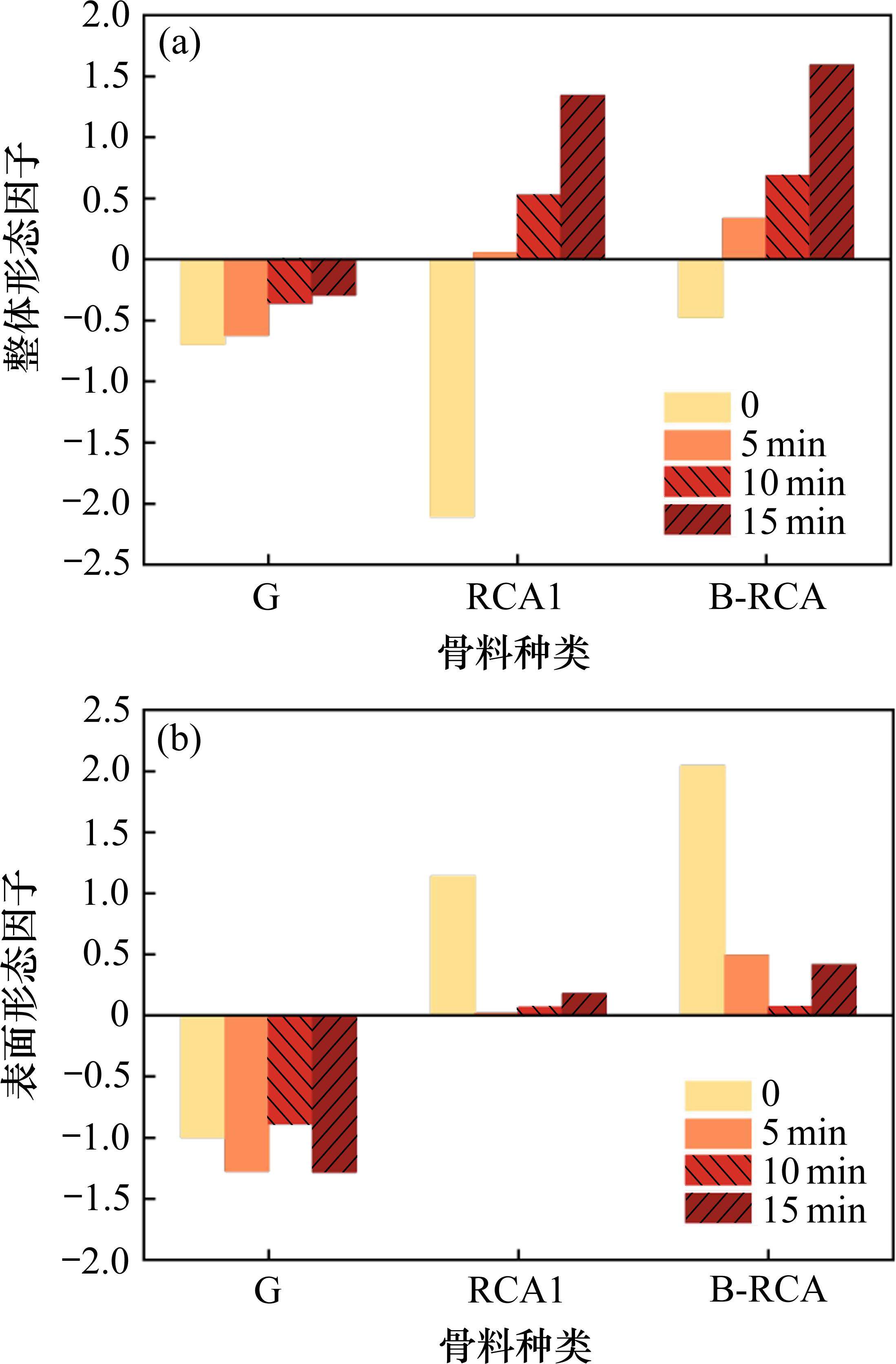
图5(a)为不同种类粗骨料的整体形态因子得分。由图5(a)可知,在整形前粗骨料的整体形态因子得分排序为RCA1<G<B-RCA。粗骨料的整体形状主要受母岩强度和破碎方法影响[8]。对于颚式破碎机,当母岩强度越高时,生产出的粗骨料针片状含量也越高[13],因此原生混凝土强度的差异导致了破碎后再生粗骨料整体形态的不同,强度较高的RCA1整体形态因子得分最低。而G在实际生产过程中会经过冲击式破碎机或反击式破碎机的多次破碎加工,因此改善后的形状优于RCA1。随着整形时间的增加,粗骨料的整体形态因子均呈增长趋势,但再生粗骨料的增长幅度均大于天然粗骨料,当整形时间为5 min时,再生粗骨料的整体形态因子得分均超过了天然粗骨料。这表明相比于天然粗骨料,再生粗骨料的整体形态在整形过程中更容易改善,其原因是粗骨料的强度越低,针片状颗粒在整形过程中越容易破碎,因此再生粗骨料经过短暂整形后,整体形状比天然粗骨料更接近球形。
图5(b)为不同种类粗骨料的表面形态因子得分。由图5(b)可知,在整形前粗骨料的表面形态因子得分排序为G<RCA1<B-RCA,再生粗骨料的表面形态因子均高于天然粗骨料,这是由于再生粗骨料表面附着的浆体有较多棱角和孔隙,使其表面形态较天然粗骨料相比更不规则[3]。此外,浆体强度越低时孔隙含量会越高,强度较低的原生混凝土破碎后会生产出表面更不规则的再生粗骨料,因此B-RCA的表面形态因子高于RCA1。随着整形时间的增加,不同种类粗骨料的表面形态因子得分出现不同程度的降低,但再生粗骨料的表面形态因子得分始终大于天然粗骨料。在整形过程中,再生粗骨料附着浆体含量的减少改善了其表面形态特征,但浆体中存在的孔隙仍使再生粗骨料的表面形态比天然粗骨料更不规则,这表明物理整形方法有利于改善再生粗骨料的表面形态,但无法使其达到近似于天然粗骨料的程度。此外,由图5还可知,整形时间超过10 min时,RCA1和B-RCA的因子得分均出现了增长趋势,研究表明整形时间过长会使再生粗骨料发生二次破碎,产生了微裂纹增加了表面形态的不规则程度[4]。因此本次试验条件下的最佳整形时间为10 min,在工程实际中可结合表面形态因子的变化规律来合理控制再生粗骨料的整形时间。
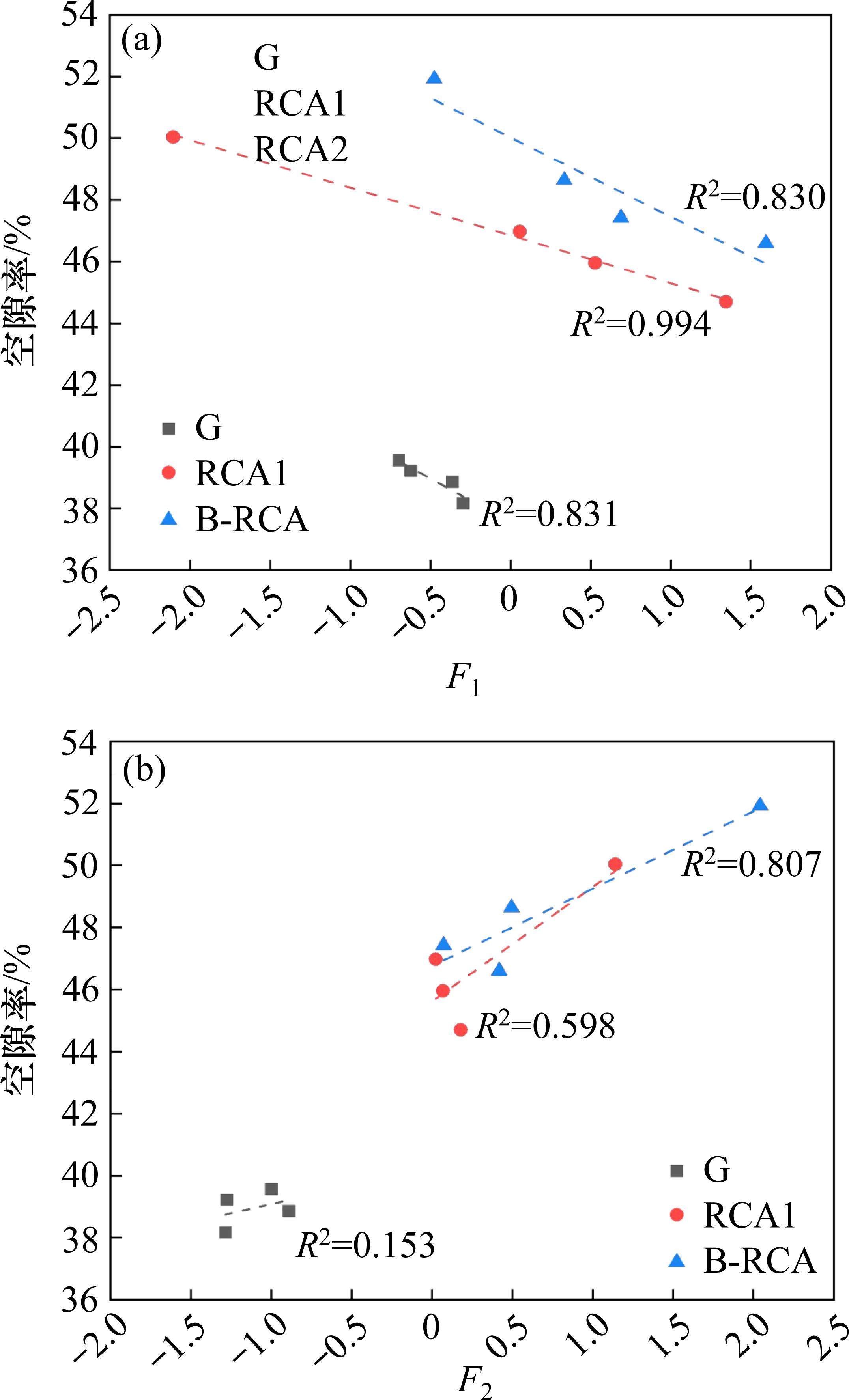
相关研究表明,骨料的空隙率主要决于级配和形态特征[19]。为探究骨料形态因子和空隙率的关系,将G、RCA1和B-RCA的2个因子得分和空隙率线性拟合,图6为将G、RCA1和B-RCA的2个因子得分和空隙率进行拟合,得到的粗骨料整体形态因子和表面形态因子对空隙率的影响。由图6可知,整体形态因子、堆积密度的线性拟合表面形态因子和堆积密度的线性拟合的系数。由图6(a)可知,随着整体形态因子的增加,骨料空隙率降低,这表明经过物理整形后,再生粗骨料整体形态因子增加,堆积密实程度也因此提高。由图6(b)可知,表面形态因子和堆积密度的线性相关性,表面形态因子对空隙率的影响规律不明显。
4 结论
1) 物理整形能有效改善再生粗骨料的物理性能和形态特征。本文实验条件下,整形时间为15 min时,RCA1和B-RCA的空隙率较整形前降低了10.67%和10.24%,吸水率降低了23.23%和37.59%,压碎指标降低了25.84%和37.15%,且再生粗骨料经过物理整形后,针片状含量减少,形状更趋于球形,表面更光滑,轮廓更规则,整形显著改善了再生粗骨料的形态特征。
2) 采用主成分析的方法能够将再生粗骨料的多个形态特征参数进行归一化简化。圆度、球度、细长度和扁平度可以组合成整体形态因子,从而更好地表征粗骨料的整体形状特征,而棱角度、粗糙度和分形维数则可以组合成了表面形态因子,则能够更好地表征粗骨料表面的规则程度。整体形态因子增大,则粗骨料的形状越趋于球形,粗骨料的堆积密实程度会越好,空隙率降低;表面形态因子增大,则粗骨料表面形态越不规则。
3) 随着物理整形时间的增加,再生粗骨料可能发生二次破碎,将导致再生粗骨料的表面形态因子增加,从而增大粗骨料表面的不规则程度,不利于再生粗骨料的使用,因此结合本文研究建议根据表面形态特征的变化合理控制整形时间。
申景涛,黄新宇,马昆林等.基于主成分分析的物理整形对再生粗骨料形貌特征影响的研究[J].铁道科学与工程学报,2025,22(03):1112-1120.
SHEN Jingtao,HUANG xinyu,MA Kunlin,et al.Influence of physical shaping on morphological characteristics of recycled coarse aggregates based on principal component analysis[J].Journal of Railway Science and Engineering,2025,22(03):1112-1120.

