隧道掘进机(Tunnel Boring Machine,简称TBM)因具有施工速度快、后期成本低、安全性好等诸多优点,在国内外长距离隧道(洞)施工中得到广泛应用。TBM掘进过程中产生的岩碴是岩~机作用的直接产物,不同掘进条件下岩碴粒径分布规律及形态特征均有差异,可有效地间接反馈围岩地质条件和TBM破岩效率[1]。许多学者对岩碴的形状、尺寸、粒径分布与TBM设备参数、破岩效率、围岩条件、能量消耗之间的内在联系开展了相关研究。周振国[2]对秦岭隧道TBM岩碴的形态、大小进行观测研究,分析了其与地质条件之间的关系并针对不同地质状态提出了相应的设备调整措施及支护方案。龚秋明等[3]利用室内滚刀线性切割试验,分析了刀间距、贯入度对岩碴形态特征的影响,认为岩碴既长又平时TBM破岩效率最高。孙金山等[4]采用颗粒流数值模拟分析了刀间距、岩体结构面数量、结构面方向对岩碴形态、粒径的影响。GONG等[5]探究了不同推力下的TBM破岩效率,发现随着推力增加,岩碴粒径增大,岩碴形状趋于细长扁平状。GENG等[6]研究了TBM岩碴形状对岩碴转移过程的影响,发现岩碴球形度是影响出碴过程的关键因素。李青蔚等[7]通过提取TBM岩碴二维形态特征信息,开展了围岩完整性预测。因此,TBM岩碴形态特征信息是TBM施工围岩感知、破岩效率评价等研究的重要基础支撑。岩碴破碎程度如何描述和表征是进行TBM破岩效率评价的关键。在岩石破碎学理论中,主要有3种学说解释了岩石破碎后岩碴块度与能量耗散之间的关系[8, 17],即新表面说、相似说和裂纹说。其中,新表面说认为机械破岩做功主要转化为岩碴的新增表面能。蔡成功等[9]通过室内煤岩落锤冲击试验,对比分析了以上3种学说与煤岩破碎的符合程度,结果表明新表面说可以较好地解释煤岩破碎过程中的能量消耗机制,煤岩破碎比功随煤岩破碎后新增表面积的增加而增加。GRADY[10]认为在冲击荷载作用下岩石断裂破碎形成新的表面需要消耗能量且岩屑新增的表面能和动能与岩石破碎消耗的能量成正比。SANCHIDRIAN等[11]利用爆破岩碴的粒径分布密度函数建立了一定体积岩体破碎新增表面积的计算方法并分析了爆破能耗与新增表面积的关系。苏国韶等[12]为研究岩爆碎块的能耗特征,提出了一种基于岩爆碎块单位面积表面能的总能耗计算方法,分析了破碎能耗与加载速率、质量分形维数的关系。尹岳降等[13]结合分形理论,推导了一种碎石骨料比表面积计算方法。李瑞泽等[14]结合粒径—比表面积曲线、岩碴粒径累计分布曲线绘制了比表面积累计分布曲线,为大粒径不规则岩碴的比表面积计算提供了新思路。目前,利用岩碴形态特征定量分析TBM破岩效率的研究成果较少。从岩-机作用机制出发,基于TBM破岩过程中的能量转化,利用岩石破碎后的岩碴表面积变化规律开展不同掘进条件下TBM掘进效能评价研究,尚处于初步探索阶段。樊明辉[15]基于岩石破碎理论分析了缩尺滚刀破岩试验中岩碴粒度与破碎比功之间的关系;闫长斌等[16]基于新表面说推导并定义了岩碴新表面理论指标,预测了比能耗与TBM最优推力区间。YAN等[17]依托2个TBM隧洞施工项目开展了现场筛分试验,根据筛分试验结果计算得到了岩碴质量分形维数,讨论了其与TBM掘进比能、岩碴粗糙度指数以及平均掘进推力的相关性。然而,需要指出的是,上述研究成果并未涉及岩碴表面积具体值的相关计算,而是用岩碴粒径分布与表面积的理论比例关系进行等效替代。此外,由于岩碴形状不规则,在计算岩碴表面积时通常将岩碴形状简化为球体或椭球体等规则图形,计算结果误差较大,导致岩碴表面积计算模型精度较低。因此,如何快速获取岩碴形态特征,准确计算岩碴比表面积并以此评价TBM破岩效率有待深入研究。基于此,在开展岩碴现场筛分试验和室内三维扫描试验的基础上,定量地分析TBM岩碴的形态特征及其随粒径的变化规律,提出一种基于岩碴粒径分布的比表面积计算方法,准确计算不同粒径分布条件下岩碴比表面积真实值。利用新表面理论指标验证岩碴比表面积计算结果,探讨岩碴比表面积与TBM破岩效率之间的内在联系,从而为TBM掘进效能评价提供一种新的途径。
1 工程概况与岩碴现场筛分试验
1.1 万安溪引水工程
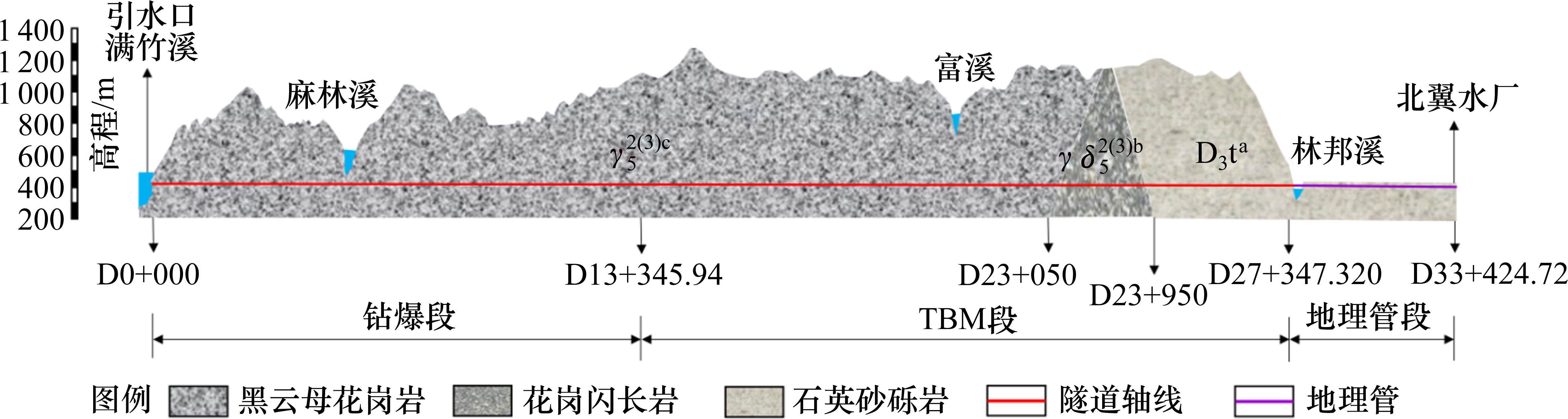
福建省龙岩市万安溪引水工程是保障龙岩城市供水安全的重大民生工程项目[16],位于龙岩市新罗区和连城县境内,采用钻爆法、敞开式TBM法、明挖法及顶管法等联合施工,引水线路总长34.31 km。输水隧洞沿途跨越麻林溪和林邦溪2条河流,其中林邦溪以北段采用隧洞输水,长约27.69 km,林邦溪以南段采用埋管输水,长约6.62 km。在隧洞输水段,以桩号D13+000.00为界,上游输水隧洞采用传统钻爆法施工,长约12.73 km;下游输水隧洞采用敞开式TBM施工,长约14.96 km,开挖断面为3.83 m,圆形。敞开式TBM主要设计参数见表1[16]。输水隧洞穿越地层岩性主要为燕山早期第3次侵入黑云母花岗岩(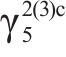
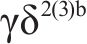
| 性能指标 | 开挖直径/mm | 中心滚刀/把 | 直径/mm | 正滚刀/把 | 直径/mm | 边滚刀/把 | 直径/mm |
|---|---|---|---|---|---|---|---|
| 参数 | 3 830 | 4 | 432 | 11 | 432 | 8 | 432 |
1.2 现场筛分试验
TBM掘进碴料携带着丰富的岩~机相互作用信息,可间接反馈隧洞围岩质量和TBM破岩效率,而岩碴筛分试验是当前准确获取岩碴粒径分布特征的有效手段之一。为了使得筛分试验中收集的岩碴更具代表性,BRULAND[18]认为应直接从TBM设备的传送带中取出,但是这种做法势必会影响TBM施工进度。因此,在隧洞施工现场TBM皮带机出碴口处或者出碴车弃碴处,针对不同岩性掘进段随机采取混合粒径的岩碴试样。根据集料粒径分布筛分测定相关规范[19],每组筛分试样需要的最小重量取决于集料的最大粒径尺寸(集料最大粒径为63 mm时样品至少需要40 kg),而TBM岩碴粒径的短边尺寸通常不会超过最大刀间距,因此为了使所取岩碴试样更具代表性,每组试样的岩碴质量不少于100 kg。
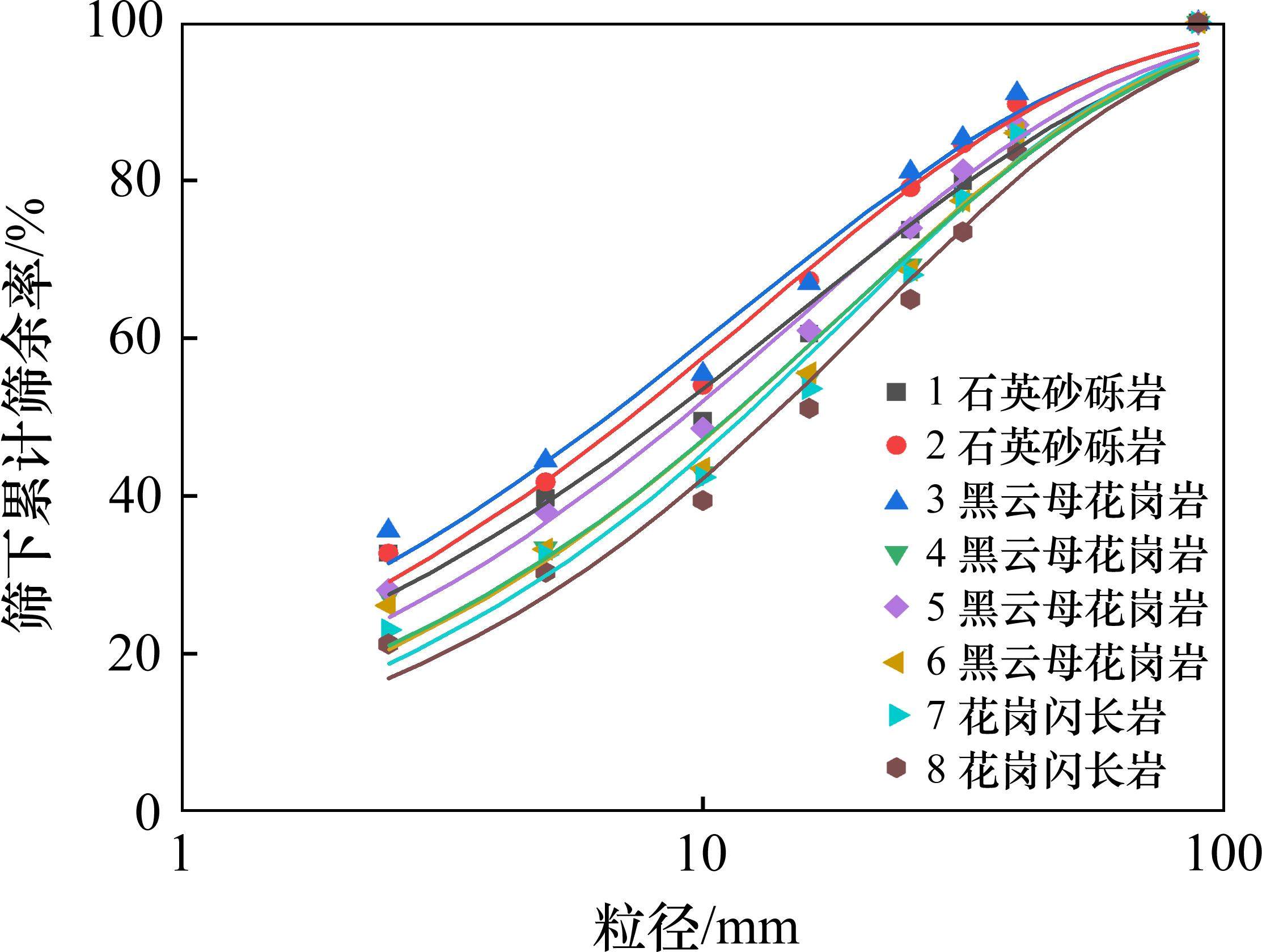
在龙岩万安溪引水隧洞TBM施工现场,选取围岩完整性好的不同岩性隧洞TBM掘进段,采用标准方孔筛(孔径为40、31.5、25、16、10、5和2.5 mm,共7级)进行岩碴筛分试验,共完成8组筛分试验。具体岩碴筛分情况见表2,统计结果见表3。
| 组号 | 掘进段岩性 | 取样质量/kg | 岩石坚硬程度 | 围岩等级 | 掘进段桩号/m |
|---|---|---|---|---|---|
| 1-1 | 石英砂砾岩 | 180.500 | 硬岩 | Ⅱ | D26+846.890~D26+842.040 |
| 1-2 | 174.300 | Ⅱ | D26+767.360~D26+753.750 | ||
| 2-1 | 黑云母花岗岩 | 99.810 | 硬岩 | Ⅱ | D23+561.010~D23+556.900 |
| 2-2 | 120.150 | Ⅱ | D23+519.510~D23+497.810 | ||
| 2-3 | 130.800 | Ⅱ | D23+497.810~D23+478.520 | ||
| 2-4 | 109.150 | Ⅱ | D23+478.520~D23+452.300 | ||
| 3-1 | 花岗闪长岩 | 109.950 | 硬岩 | Ⅱ | D23+653.930~D23+645.280 |
| 3-2 | 97.600 | Ⅱ | D23+645.280~D23+631.270 |
| 粒径/mm | 不同岩性掘进段岩碴的分计筛余率/% | |||||||
|---|---|---|---|---|---|---|---|---|
| 石英砂砾岩 | 黑云母花岗岩 | 花岗闪长岩 | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| >40.0 | 13.55 | 10.30 | 8.99 | 14.51 | 12.97 | 13.98 | 14.06 | 16.55 |
| 31.5~40.0 | 6.54 | 5.08 | 5.66 | 7.93 | 5.75 | 8.60 | 8.16 | 9.98 |
| 25.0~31.5 | 6.18 | 5.54 | 4.27 | 8.32 | 7.33 | 8.77 | 9.77 | 8.55 |
| 16.0~20.5 | 13.16 | 11.79 | 14.14 | 14.19 | 12.98 | 13.07 | 14.39 | 13.79 |
| 10.0~16.0 | 11.02 | 13.28 | 11.48 | 12.12 | 12.44 | 12.09 | 11.23 | 11.70 |
| 5.0~10.0 | 9.78 | 12.25 | 10.98 | 9.49 | 10.50 | 10.24 | 9.79 | 9.08 |
| 2.5~5.0 | 7.03 | 9.01 | 8.88 | 6.04 | 9.91 | 7.13 | 9.55 | 9.10 |
| <2.5 | 32.74 | 32.76 | 35.61 | 27.50 | 28.12 | 26.12 | 23.03 | 21.05 |
2 TBM破岩效率评价指标
比能与岩碴粗糙度指数是评价TBM破岩效率的常用指标。相关研究表明[3],片状岩碴含量越高,岩粉含量越低,粗糙度指数越大,比能越小,TBM破岩效率就越高。
2.1 比能
比能(Specific Energy, 简称Se)是TBM滚刀切削单位体积岩石所做的功,是用于衡量TBM破岩效率的重要指标之一[17]。比能越小,TBM破碎单位体积岩石所需的能量越少。其计算公式如下[20]:
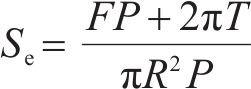
式中:Se为比能,kJ/m3;F为TBM掘进时的平均推力,kN;P为平均贯入度,mm/r;T为TBM平均扭矩,kN∙m;R为隧洞开挖半径,m。
2.2 粗糙度指数
粗糙度指数(Coarseness Index,简称Ci)是一个无量纲常数,可反映岩碴的破碎程度及其粒径分布规律,其概念最早由ROXBOROUG等[21]提出。根据筛分试验数据对岩碴粒径分布进行统计分析,得到各个筛网的累计筛余率,再将各个累计筛余率进行相加,即可得到粗糙度指数,具体表达式为[16]:
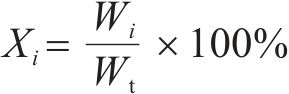
式中:Wi是现场筛分试验得到的大于某一粒径尺寸的岩碴总质量,kg;Wt是现场采取的TBM岩碴的总质量,kg;Xi是大于某一粒径尺寸的累计筛余率,%;Ci为岩碴粗糙度指数,%。
3 岩碴形态特征参数提取与分析
3.1 岩碴三维扫描重构
准确获取岩碴尺寸、表面积、体积等基础参数是定量研究岩碴形态特征的前提。然而,TBM掘进过程中产生的岩碴大小不一且形状不规则,难以通过理论计算或简单筛分获取准确的岩碴形态特征,而三维扫描技术可以对岩碴表面进行点云数据重建,得到岩碴三维模型,从而精准提取岩碴三维形态信息。为保证用于三维扫描重构的岩碴样品具有较好的代表性,这里选择岩性占比最大的黑云母花岗岩掘进段开展岩碴取样。此外,在筛分后的8个粒径段内共随机挑选出168块岩碴试样,以确保三维扫描结果中涵盖各个粒径区间的岩碴形态信息,不同粒径段的岩碴取样数量情况见表4。
| 粒径区间/mm | 取样个数 | 粒径区间/mm | 取样个数 |
|---|---|---|---|
| >50 | 15 | 16~25 | 24 |
| 40~50 | 21 | 10~16 | 21 |
| 31.5~40 | 23 | 5~10 | 22 |
| 25~31.5 | 24 | 2.5~5 | 18 |
手动量测可得到岩碴的长轴、短轴和厚度等信息,其中岩碴长轴长度主要为2~150 mm。而利用非接触式全自动三维扫描仪可较准确、便捷地获取该尺寸段的岩碴三维模型。Scan-T100是一款基于白光干涉原理,自带高集成全自动三维扫描系统的全自动双轴三维扫描仪,模型精度最高可达0.01 mm。在电脑端利用Jewel3D软件即可进行岩碴扫描并得到三维模型。
3.2 岩碴形态特征分析
目前,对于不规则岩碴的形态特征描述,尚无统一量化指标,常用的岩碴形态参数指标有伸长度、扁平度、球形度等[2, 5, 22-23]。利用三维扫描模型对岩碴信息进行提取,可得到岩碴相关形态特征参数。伸长度值越小表示岩碴越细长,扁平度越小表示岩碴越扁平,球形度越大说明岩碴三维形状越接近球体。根据形态特征参数,可将岩碴划分为长、平、既长又平、立方体等[3, 5],如图2(a)所示。将168块黑云母花岗岩的岩碴按照形状进行区间归类,结果如图2(b)所示。

由图2(b)可见,黑云母花岗岩掘进段岩碴形状特征分布不均,趋近于平状和立方体状,这是TBM破岩效率较低造成的。正如BRULAND[18]所述,除粒径分布信息外,岩碴形态特征也是反映破岩效率的重要手段。已有研究表明,TBM破岩效率较高时岩碴趋于长平状,而龙岩万安溪引水隧洞黑云母花岗岩掘进段岩石坚硬且完整性较好,当掘进推力为6 000 kN时,平均贯入度较小,仅为3 mm/r,这就使得滚刀破岩过程中岩石微裂纹无法充分向四周延伸贯通,因而少有较长岩碴出现。当岩体完整或裂隙较少时,在较小的贯入度下,岩碴缓慢剥落,形成较多的平坦片状岩碴;当岩体中节理裂隙较发育时,滚刀破岩产生的裂纹与节理裂隙相交,形成较多的块状或立方体状岩碴,使得岩碴形状集中分布于平状和立方体状。
由于图2(b)中数据点较多且离散,难以对不同粒径段的岩碴进行对比,为深入探究岩碴形态与粒径之间的关系,对不同粒径段岩碴的球形度、伸长度和扁平度的均值进行统计计算,如图3所示。由图3可见,岩碴的形态特征参数与其粒径大小有关。随着粒径增加,岩碴的球形度、扁平度逐渐减小,伸长度逐渐增大。这是因为岩碴的粒径越小,其形状越接近立方体状且针状棱角特征明显,从而导致球度、扁平度较大而伸长度较小。当岩碴粒径为2.5~5 mm时,球形度、扁平度最大,而伸长度最小,说明该粒径段岩碴最接近球状。随着粒径不断增加,岩碴形状结构逐渐“扁平化”,其相对厚度减小,棱角特征减弱,伸长度增大,从而球形度、扁平度减小。当岩碴粒径>40 mm时,伸长度最大,球形度、扁平度最小,说明该粒径段的岩碴最为扁平。不同粒径段岩碴图像及形态特征见表5所示。
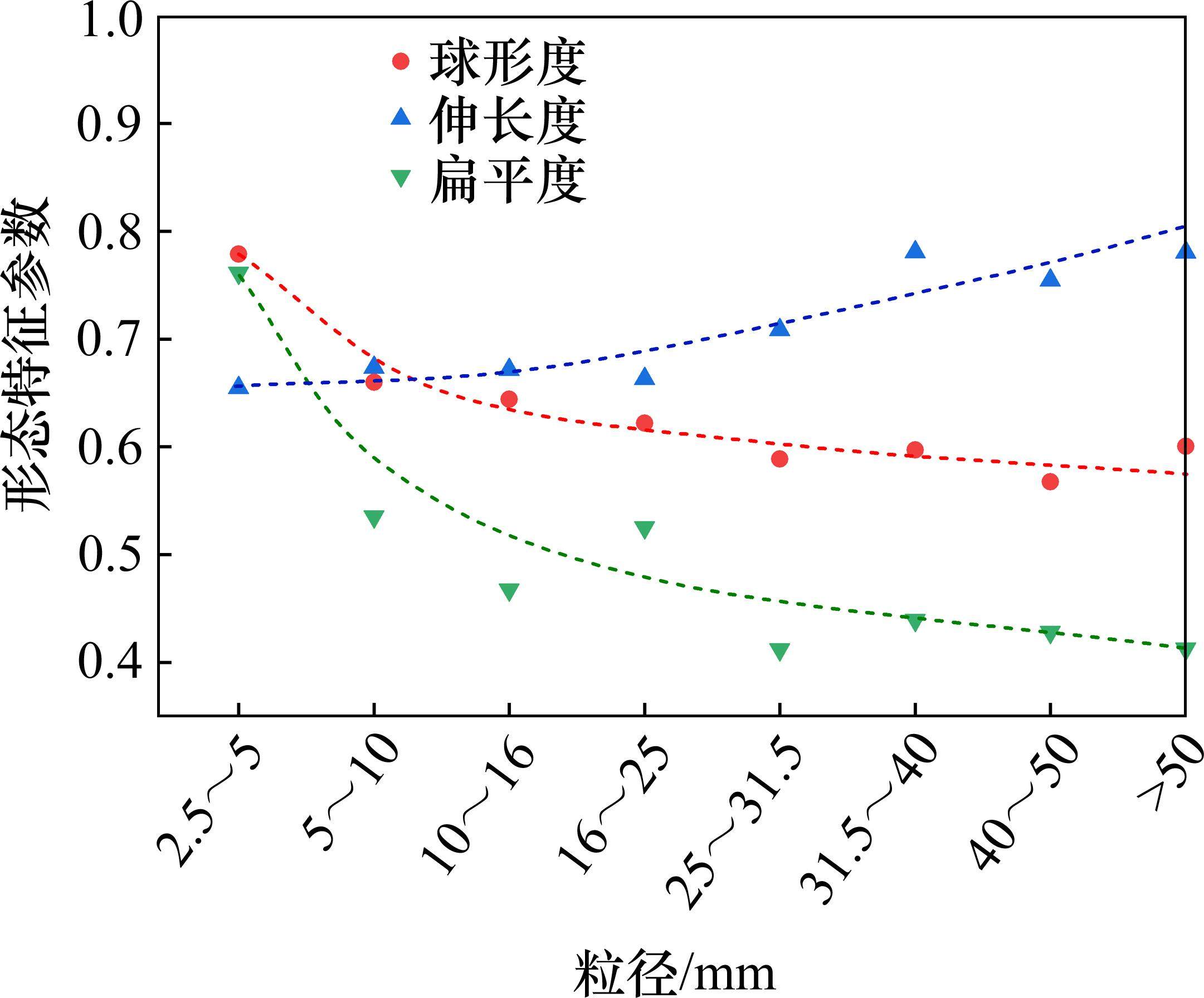
粒径区 间/mm | 典型岩 碴模型 | 伸长度e3D | 扁平度 f 3D | 球形度φ3D |
|---|---|---|---|---|
| 2.5~5 | 0.66 | 0.79 | 0.79 | |
| 5~10 | 0.67 | 0.60 | 0.67 | |
| 10~16 | 0.67 | 0.52 | 0.65 | |
| 16~25 | 0.65 | 0.49 | 0.64 | |
| 25~31.5 | 0.72 | 0.51 | 0.63 | |
| 31.5~40 | 0.76 | 0.43 | 0.61 | |
| 40~50 | 0.74 | 0.40 | 0.59 | |
| >50 | 0.77 | 0.39 | 0.58 |
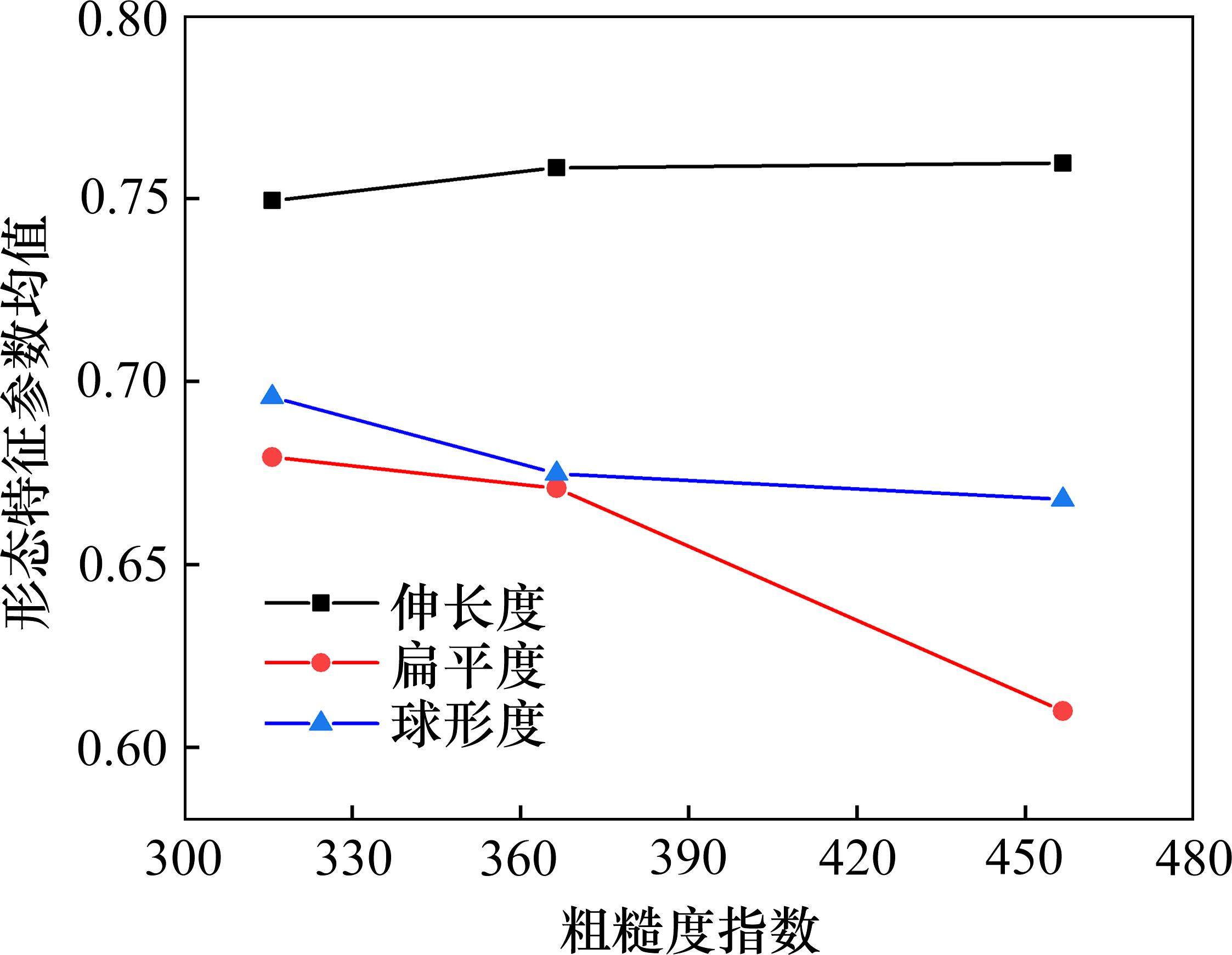
由于岩碴形态特征与粒径大小密切相关,因此岩碴形态特征参数包含一定粒径信息,其与TBM破岩效率之间必然存在某种联系。为进一步探究岩碴形态特征与TBM破岩效率之间的关系,同时兼顾三维扫描成本,从3组岩碴试样的各粒径段中随机抽取9块岩碴进行室内三维扫描试验,然后计算得到每组岩碴试样对应的形态特征参数均值,并将其与岩碴试样的粗糙度指数进行拟合分析,结果如图4所示。由图4可见,岩碴伸长度均值随粗糙度指数的增加而增大,扁平度和球形度均值随粗糙度指数的增加而减小,说明大块岩碴含量越高,岩碴整体上伸长度越大、扁平度和球形度越小,粗糙度指数就越大,TBM破岩效率也就随之越高。所以,岩碴的形态特征参数可以用于定量分析TBM破岩效率。由于地质条件、TBM设备参数等因素对岩碴粒径的影响,该结论仅适用于龙岩万安溪引水隧洞TBM施工中对应的地质条件和机械参数等。然而,该研究方法本身具有广泛适用性,后续研究将依托更多TBM工程开展岩碴三维扫描试验,扩充样本数据,深化分析岩碴形态特征与TBM破岩效率之间的关系。
4 TBM破岩效率分析
4.1 基于岩碴粒径分布的比表面积计算方法
岩体破碎形成自由表面需要能量,外荷载所做的功会转化为相应的表面能,可用岩碴的表面积来衡量能量的耗散。因此,了解不同掘进条件下TBM岩碴表面积变化情况对于降低能耗、提高设备利用率具有重要意义。然而,现场筛分试验中各组岩碴试样的质量均不相同,不同质量的岩碴表面积大小无法直接比较。基于此,可采用岩碴比表面积评价预测TBM能量耗散。岩碴比表面积计算式如下:
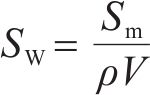
式中:SW为岩碴比表面积,cm2/g;Sm为岩碴表面积,cm2;ρ为岩碴密度,g/cm3;V为岩碴体积,cm3。
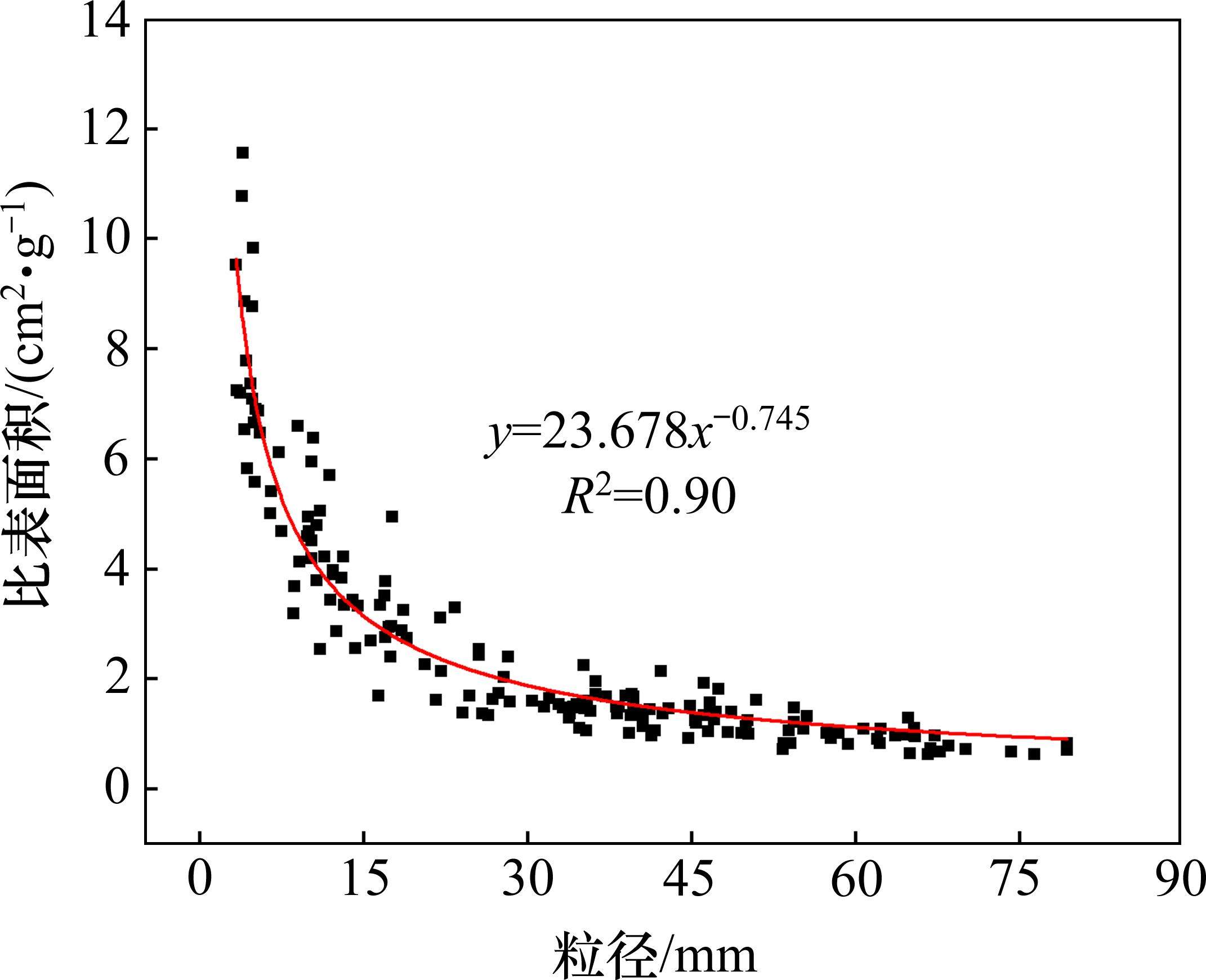
假设同一岩性的岩碴密度相同,根据勘察可知黑云母花岗岩岩碴天然密度均值为2.60 g/cm3,根据三维扫描模型提取到的体积、表面积值,利用式(4)即可得到不同粒径大小岩碴比表面积值。由于不同粒径大小岩碴的比表面积值有所差异,而岩碴粒径一般是由宽度(短轴)尺寸决定的[15],因此可对岩碴宽度与比表面积进行回归分析,所得结果即为岩碴粒径与比表面积的关系,如图5所示。由图5可见,随岩碴粒径增大,比表面积先快速减小后趋于平缓,二者呈明显的幂函数相关关系,相关系数R2为0.90。值得一提的是,这里在进行回归分析时并未考虑自变量与因变量之间的量纲问题,而是统计意义上的回归分析。
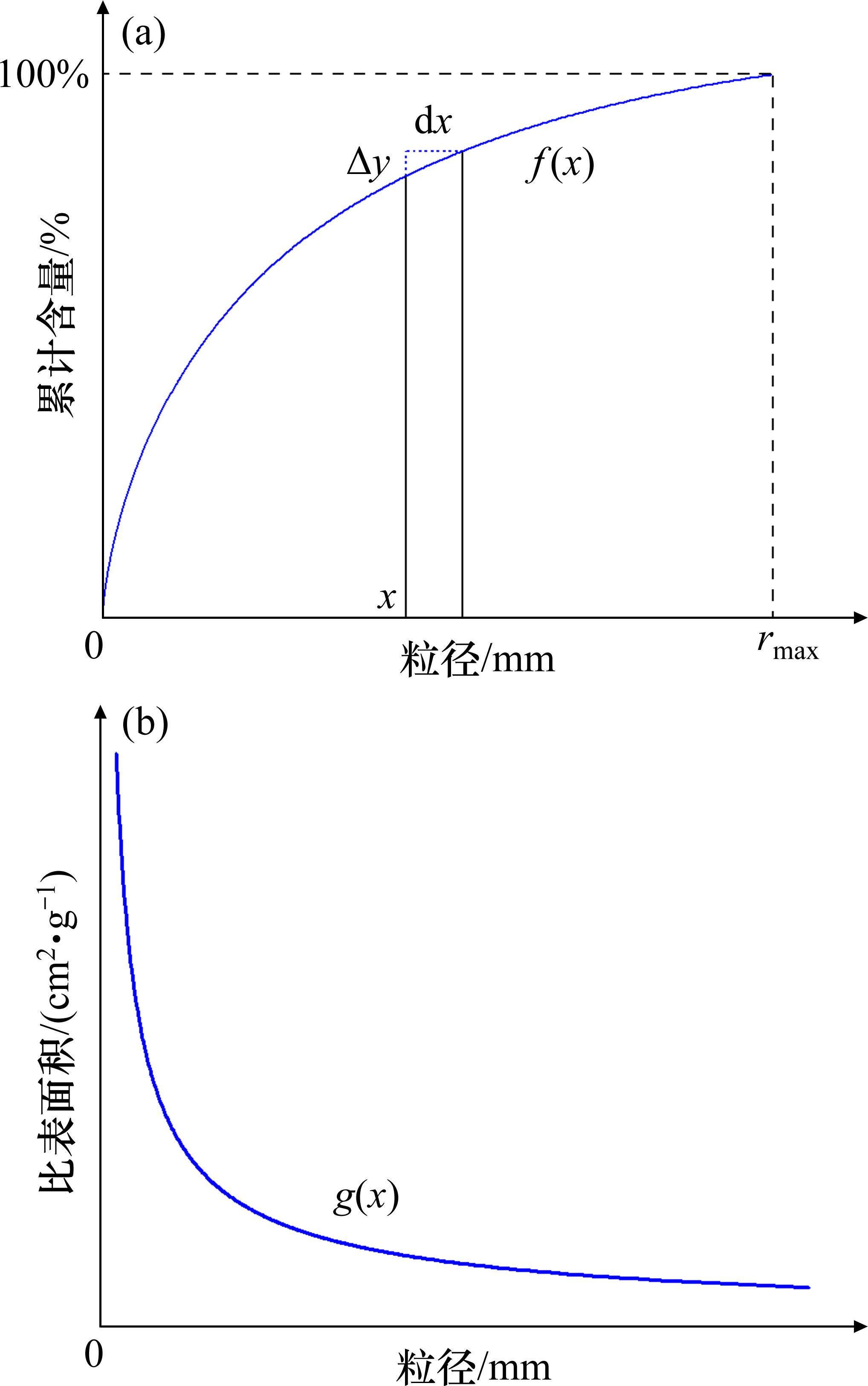
虽然利用岩碴粒径分布特征可以计算和预测其比表面积,然而目前尚无具体方法将其应用于TBM破岩效率分析。因此,基于岩碴粒径分布曲线,提出一种新的比表面积计算方法,具体如下。
1) 确定岩碴粒径分布函数,绘制岩碴粒径分布曲线,如图6所示。其中,f(x)为岩碴累计分布函数;g(x)为岩碴粒径与比表面积的关系函数。
研究发现,Rosin-Rammler分布函数(简称R-R函数)可较好地描述岩碴粒径分布规律[15],即f(x)可用R-R函数来表示。R-R函数的表达式为:
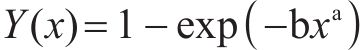
式中:x为岩碴粒径,mm;Y(x)为粒径小于x的岩碴质量占比;参数a为均匀分布系数,a越小则说明岩碴粒径分布范围越宽,粒径分布越均匀;参数b为拟合系数。
2) 计算岩碴比表面积。比表面积的含义为单位质量岩碴的总表面积(cm2/g),若假设某堆混合粒径岩碴的总质量为单位质量1g,则f(x)的值即为岩碴的累计质量,则这堆岩碴的比表面积即为粒径0~rmax岩碴的总表面积。那么,任意粒径区间段内x1~x2岩碴的质量Δy为:
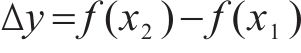
为计算x1~x2粒径区间段内岩碴总表面积,可将该部分岩碴粒径全部近似等效为(x1+x2)/2,则该粒径段岩碴的总表面积为:
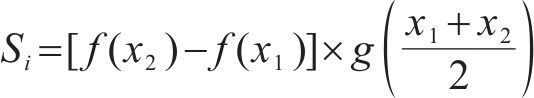
式中:Si为任意粒径区间段x1~x2内岩碴的总表面积,cm2。
以此为例,可将粒径区间划分为若干份,分别计算后累加求和即可获得总表面积,且每段区间划分越小,累加计算结果越接近真实值。现对粒径区间进行微分,每段长度为dx,则任一粒径区间段内x~x+dx岩碴的质量Δy为:
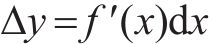
则x~x+dx粒径区间段岩碴的比表面积Si为:
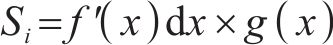
对0~rmax所有粒径区间段岩碴总表面积Si进行积分累加可以得到岩碴的比表面积SW:
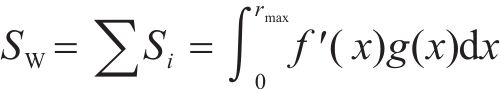
式中:SW为岩碴的比表面积,即单位质量岩碴的总表面积,cm2/g。
4.2 岩碴比表面积计算
利用式(5)对表3中的数据进行拟合分析,可以获取岩碴累计分布函数f(x)的表达式,结果如图7所示。g(x)可用图6中的回归函数来表示。在函数f(x)和g(x)已知的前提下,利用式(10),通过Matlab软件可以对积分进行求解,所得结果即为不同粒径分布条件下岩碴的比表面积值。
然而,函数g(x)在x=0处不可积,若从0开始计算积分函数,则会导致积分结果不收敛。实际上,岩石在研磨作用下产生的岩粉粒径并非无限趋近于0。蔡增辉[24]对大理岩、砂岩和煤岩试样进行研磨、筛分试验后发现,粒径小于75 μm的岩粉质量占比很小甚至为0;刘徐三等[25]在研究金刚石钻进破岩机理时发现,磨削状态下产生的岩粉粒径通常在2 μm以上。基于此,这里取岩粉的最小粒径为2 μm,岩碴最大粒径rmax可取最大刀间距89 mm。8组岩碴试样对应的比表面积SW计算结果见表6。
| 组号 | 比表面积 SW/(cm2∙g-1) | 新表面理论指标 Sa/10-2 mm-1 | 粗糙度指数 Ci | 比能Se/ (kJ∙m-3) | 贯入度指数/ (kN∙mm-1∙r-1) |
|---|---|---|---|---|---|
| 1-1 | 28.080 | 30.320 | 377.28 | 78 505.88 | 59.783 |
| 1-2 | 28.169 | 31.186 | 350.74 | 68 820.04 | 62.112 |
| 2-1 | 32.572 | 33.185 | 340.05 | 87 560.30 | 85.714 |
| 2-2 | 18.182 | 26.085 | 408.92 | 64 357.12 | 64.130 |
| 2-3 | 22.408 | 27.598 | 382.09 | 72 838.97 | 67.081 |
| 2-4 | 17.609 | 25.346 | 409.47 | 64 130.11 | 63.043 |
| 3-1 | 14.347 | 23.487 | 416.67 | 58 693.75 | 74.534 |
| 3-2 | 12.741 | 21.736 | 436.00 | 53 422.66 | 67.391 |
4.3 比表面积计算结果验证
根据8组岩碴筛分结果,利用文献[16-17]中的公式可计算得到每组岩碴对应的新表面理论指标Sa,结果见表6所示。岩碴比表面积SW与新表面理论指标Sa均可反馈TBM破岩过程中的能量耗散,为探究2个参数之间的内在联系,利用表6中数据,将SW与Sa进行回归分析,结果如图8所示。
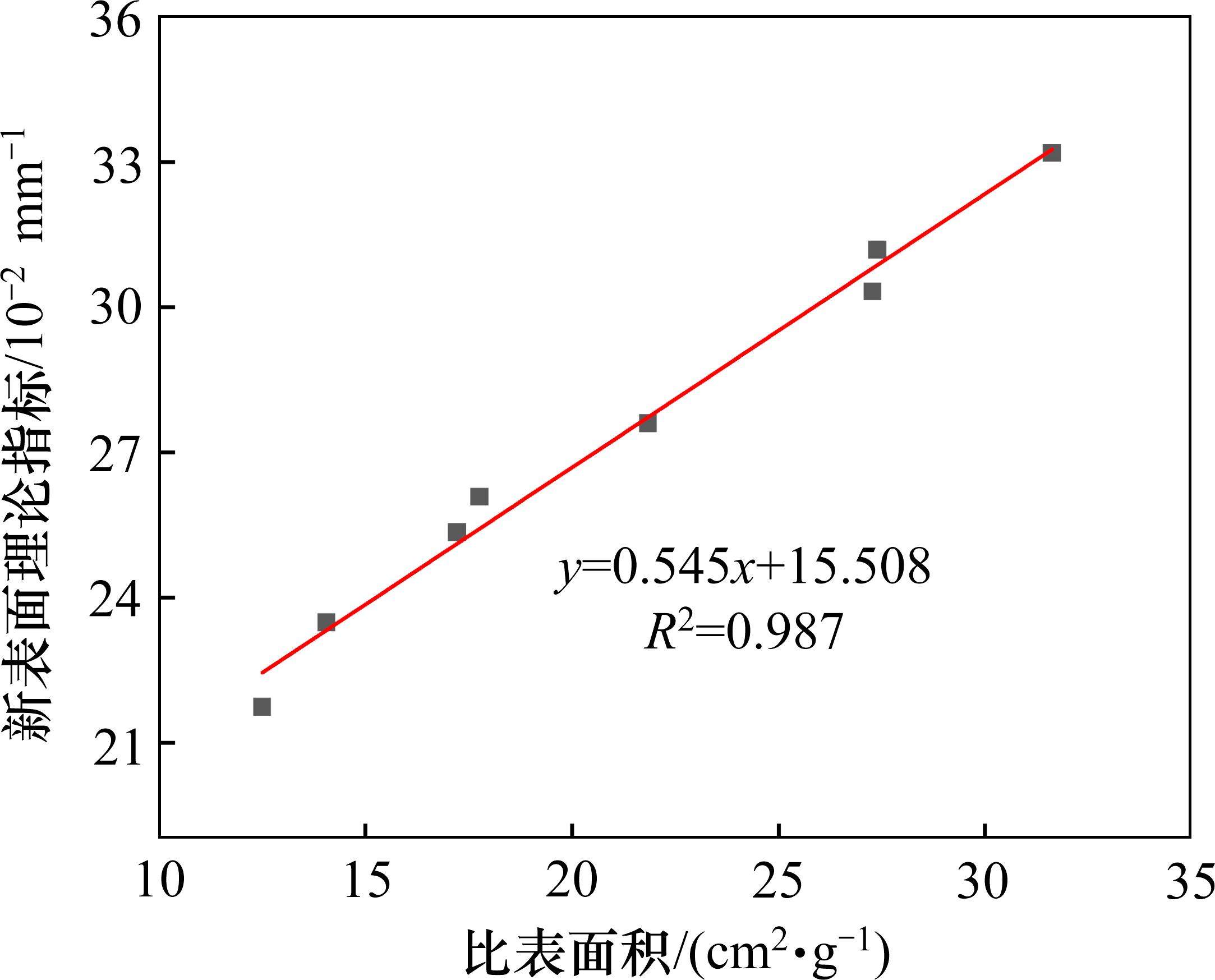
由图8可见,新表面理论指标Sa随着岩碴比表面积SW的增加而逐渐增大,且两者之间具有较好的线性相关关系,拟合相关系数R2为0.987。主要原因是,岩碴比表面积SW表示岩体破碎后单位质量岩碴具有的表面积大小,由于TBM掘进前隧洞中岩体质量大而裸露面小,其破碎前的岩体比表面积远小于破碎后的岩碴比表面积,可忽略不计,因此岩碴比表面积SW也可以近似表示单位质量岩体破碎后的新增表面积大小。而新表面理论指标Sa与单位体积岩石破碎后的新增表面积成正比,所以岩碴比表面积SW与新表面理论指标Sa均可衡量岩体破碎过程新增表面的多少,两者呈正比关系符合实际情况,这也验证了基于岩碴粒径分布规律得到的岩碴比表面积SW的准确性与合理性。此外,相比新表面理论指标Sa,比表面积SW具有更清晰的物理意义和更为直观的数字结果。因为Sa在理论推导过程中运用岩碴粒度与表面积、岩碴粒度与体积的理论比例关系替代推演,并未涉及岩碴表面积具体值的相关计算,而SW所得结果就是岩碴的比表面积真实值。通常,岩碴的真实表面积获取困难,利用新表面理论指标分析TBM岩碴也并未得到合理验证,这里采用三维扫描对表面积进行精确计算,同时也证明了新表面理论指标的准确性和可靠性。
4.4 岩碴比表面积与TBM破岩效率的关系
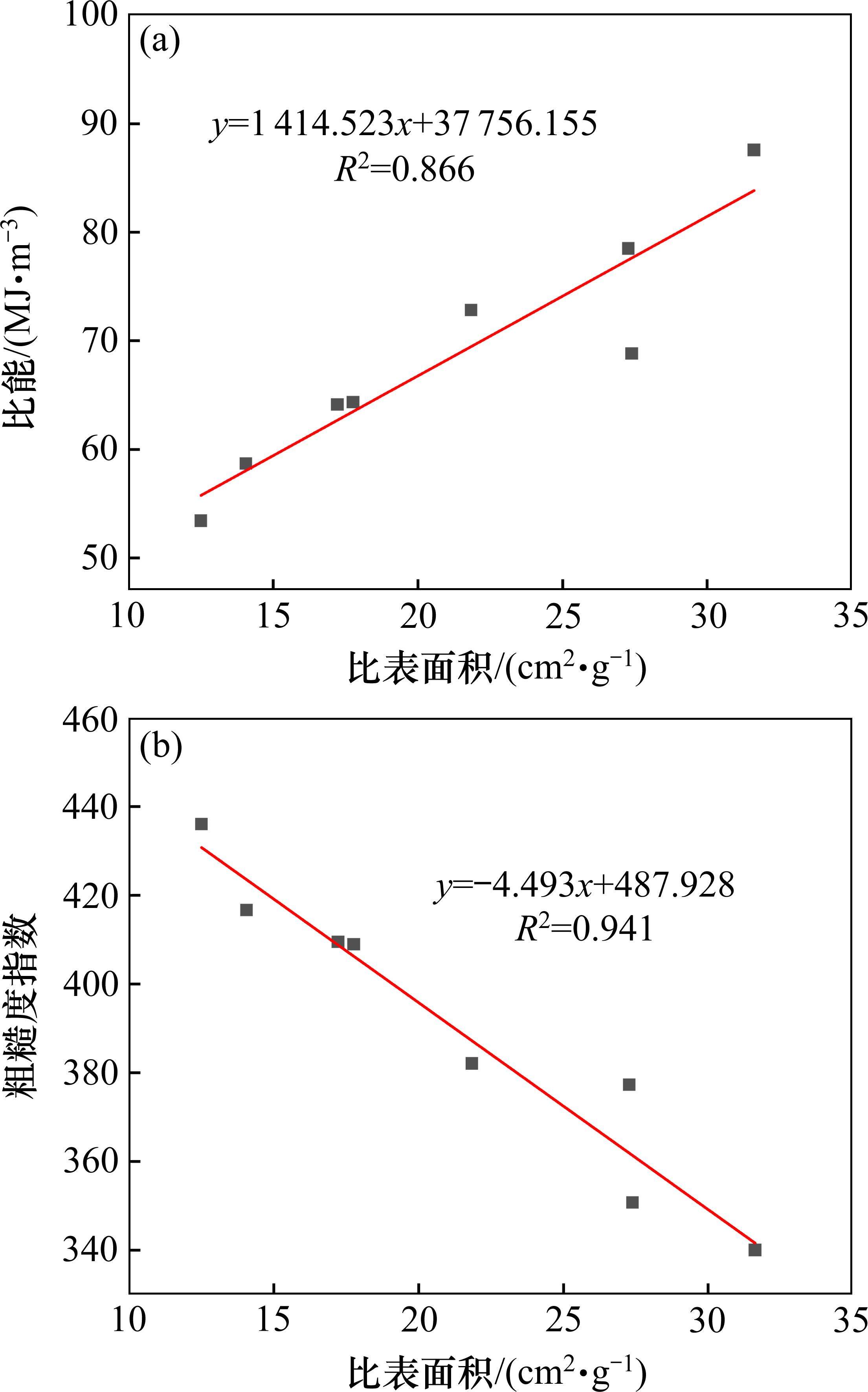
由前述分析已知,岩碴比表面积SW能够近似表示单位质量岩体破碎后的新增表面积大小。因此,比表面积SW也必然与比能Se成正相关关系。利用表6中的数据将岩碴比表面积SW与比能Se进行回归拟合分析,结果如图9(a)所示。由图9(a)可见,SW与Se之间具有较好的线性正相关性,说明随着岩碴比表面积增加,岩碴破碎程度增加,比能逐渐增大。此外,粗糙度指数可表征岩碴破碎程度,从而可反馈评价TBM破岩效率,将岩碴粗糙度指数与岩碴比表面积进行回归拟合分析,如图9(b)所示。由于粗糙度指数与比能呈负相关关系[26],粗糙度指数与比表面积也必然呈负相关关系。因此,岩碴的比表面积可以较好地描述岩碴破碎程度及能量消耗,且比表面积越大,岩碴越破碎,TBM破岩效率越低。
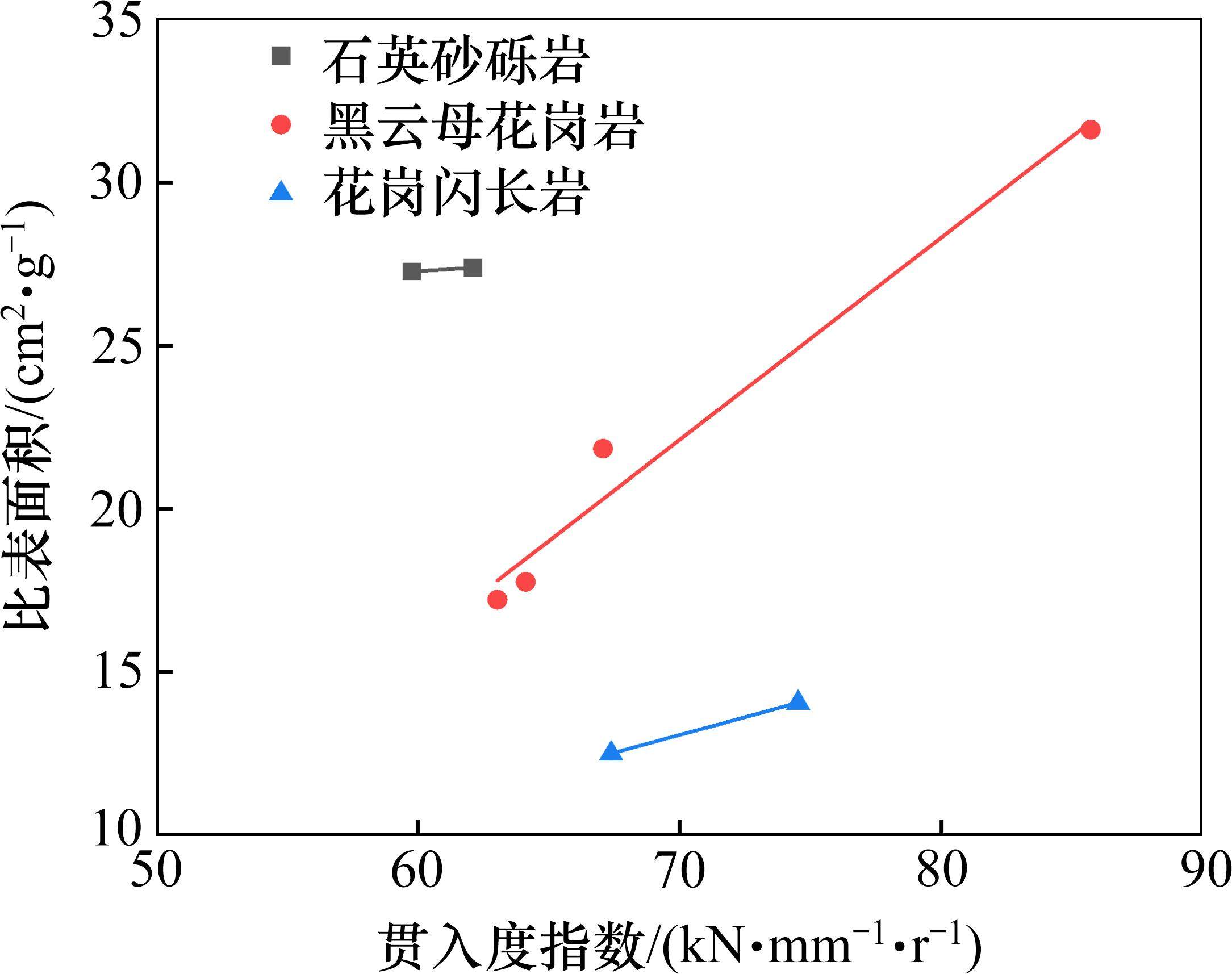
TBM掘进过程中贯入度指数(刀盘推力与贯入度的比值)是表征TBM掘进性能的另一重要参数,可用于评价岩体可掘性,其数值越大则说明岩体的可掘性越差,TBM掘进越困难,破岩效率越低。为探究不同贯入度指数与岩碴粒径分布规律之间的内在联系,利用龙岩万安溪引水隧洞TBM施工现场掘进记录有关数据,对岩碴比表面积与贯入度指数之间的关系进行回归拟合分析,如图10所示。由图10可见,图中的数据点整体上较散乱,不同岩性条件下的岩碴比表面积与贯入度指数之间并无显著相关性,这是因为贯入度指数除了受TBM掘进参数影响外,还受岩石抗压强度、岩体完整性、岩石耐磨性等其他参数的综合影响。对于相同岩性条件而言,岩碴比表面积与贯入度指数之间存在正相关性,随着贯入度指数增加,岩碴比表面积均呈增大趋势。原因在于:当贯入度指数逐渐增大时,岩体可掘性较差,刀盘推力较大而贯入度较小,滚刀的切削力无法稳定维持在岩石破坏临界荷载之上,因而TBM滚刀与岩石之间的研磨作用相对显著[17],小粒径岩粉生成量增加,从而导致岩碴比表面积增大,TBM破岩效率降低。
5 讨论
不同坚硬程度和完整程度的岩石,在相同破岩力情况下,将产生不同的破碎指标。如何合理定义岩石破碎指标并将其用于TBM破岩效率评价,值得深入探索。目前,关于岩石破碎指标及其定义,基本上都是从能量耗散角度开展的。除了前述提到的岩屑单位面积表面能[12]、岩碴粒径分布函数[15]、岩碴粗糙度指数[21]、新表面理论指标[16]、岩碴质量分形维数[17]外,郭连军等[27]将岩石破碎能耗分为岩石破碎生成新表面的消耗能(Ud)、未被破碎岩石中的剩余能量(Ue)和岩石塑性变形及损伤时消耗的能量(Ui),定义了一种与目标破碎尺度有关的岩石破碎指标Ku,认为Ku等于0时表示岩石处于完整状态,Ku等于1时表示该尺度下岩石达到了完全破碎状态,Ku大于1时表示岩石处于过破碎状。然而,在计算岩石破碎指标Ku时如何准确获取各部分能量占比,对于TBM破岩效率评价而言,无疑是难以实现的。
基于岩碴形态特征参数,利用积分原理计算得到的岩碴比表面积指标,与岩碴粒径分布函数、岩碴粗糙度指数、新表面理论指标以及岩碴质量分形维数等破碎指标类似,均以岩~机破岩过程中的能量耗散为基础,以机械做功转化为岩碴新增表面能为出发点,以岩碴新增表面积衡量能量转化效率,从而实现TBM破岩效率评价。由此可见,岩碴比表面积指标与上述其他岩石破碎指标具有相同的理论基础。
相比岩碴粒径分布函数、岩碴粗糙度指数、新表面理论指标及岩碴质量分形维数等岩石破碎指标,岩碴比表面积指标的优势在于:一是避免了不同岩石密度不同带来的影响,原因是现场筛分试验中各组岩碴试样的质量均不相同,不同质量的岩碴表面积大小无法直接比较。二是计算岩碴比表面积指标时不再完全依赖于筛分试验,采用三维扫描对表面积进行精确计算,避免了筛分试验的局限性以及计算过程中的体积比例换算不真实等问题,具有更清晰的物理意义和更为直观的计算结果。基于岩碴比表面积的TBM破岩效率评价结果表明,岩碴比表面积指标不但与比能(最常用的TBM破岩效率评价指标)具有较好的相关性,而且与贯入度指数存在良好的相关关系,可用于岩体可掘性及TBM破岩效率评价。
在实际工程应用时,可根据岩碴比表面积指标与比能之间的回归拟合结果,评价该掘进段的TBM破岩效率。在此基础上,可以比能最低为目标,选定岩碴比表面积范围值。以选定的岩碴比表面积范围值为基础,根据岩碴比表面积指标与贯入度指数之间的回归拟合结果,确定最优贯入度指数区间,从而为TBM掘进参数(推力、贯入度等)动态优化提供科学指导。
需要指出的是,本文提出的岩碴比表面积指标计算方法以及用于TBM破岩效率的思路是合理的,然而由于岩碴筛分试验和三维扫描数据有限,基于岩碴比表面积的TBM破岩效率评价分析效果还有待进一步验证。此外,如何考虑复杂岩体节理裂隙发育特征的影响,有待进一步深入研究。
6 结论
1) 岩碴形态特征参数与粒径大小有关,可用于评价TBM破岩效率。随着粒径增加,岩碴的球形度和扁平度逐渐减小,伸长度逐渐增大;岩碴伸长度越大、扁平度和球形度越小,粗糙度指数就越大,TBM破岩效率越高。
2) 利用积分原理,将岩碴比表面积预测函数与累积分布函数相结合,可准确计算得到岩碴试样的比表面积真实值且岩碴比表面积可近似表示单位质量岩体破碎后的新增表面积大小,与新表面理论指标呈很好的线性相关关系,两指标之间可相互验证,增加结果的可靠性与可信度。
3) 岩碴比表面积与比能成正比,与粗糙度指数成反比,可较好地反映岩碴破碎程度,客观地评价TBM破岩效率。岩碴比表面积越大,TBM破岩效率越低。相同岩性条件下,随贯入度指数不断增加,岩碴比表面积增大,此时岩体可掘性变差,TBM破岩效率降低。
岩石能量体概念及岩石破碎指标研究
[J/OL]. 金属矿山, 2023: 1-16. (闫长斌,石雨萱,李严等.基于岩碴比表面积的完整岩体TBM破岩效率分析[J].铁道科学与工程学报,2025,22(01):456-468.
YAN Changbin,SHI Yuxuan,LI Yan,et al.Analysis of TBM rock breaking efficiency based on the specific surface area of rock chips for intact rock mass[J].Journal of Railway Science and Engineering,2025,22(01):456-468.

