1 符号定义

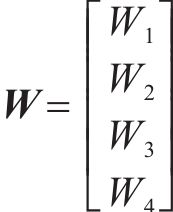
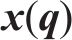
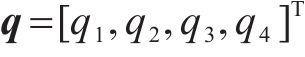
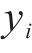
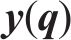
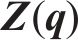
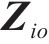
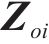
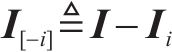
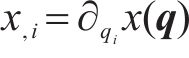
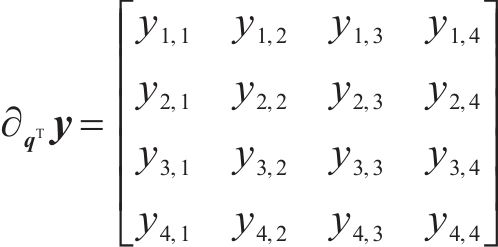
为方便公式的书写及推导步骤的清晰表示，用表示向量的函数，表示列向量函数的第个分量，为4阶方阵，、分别表示矩阵的第行与第列。为4阶单位矩阵，记矩阵和。若下文未进行特殊说明，上标符号优先于下标表示。此外，对于向量及矩阵求偏导数表示如下：

，，

。

2 单欠驱动度动车组模型的建立

动车组列车采用动力分散的驱动方式，为便于进行列车纵向动力学分析及控制算法设计，将一节动车与一节拖车(1M1T)组合为一个动力单元^[23]进行划分，则4M4T编组的动车组可看作由4个动力单元构成的4质点模型。各动力单元的纵向受力分析如图1所示。

图1全屏查看

动车组纵向动力学受力分析

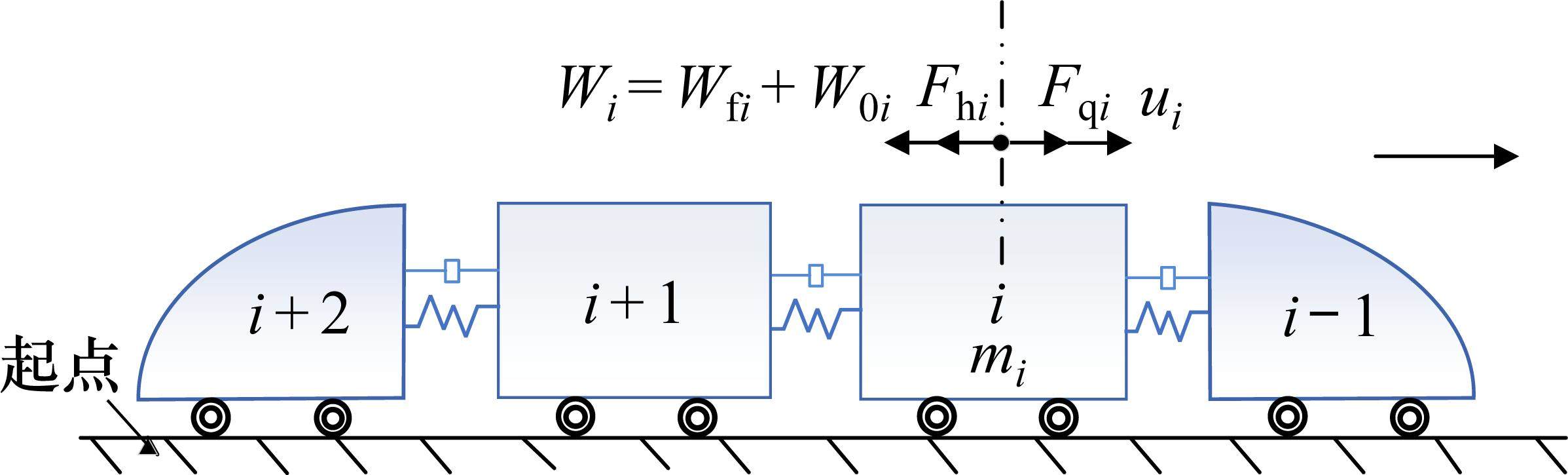
列车运行过程中，纵向方向受到牵引力/制动力、基本阻力、附加阻力、车间作用力及惯性力的共同作用。第个动力单元所受的基本阻力表示为，其中为单位滚动基本阻力参数，为单位机械基本阻力参数，为单位空气基本阻力系数，重力常数取为9.81 m/s²，代表各动力单元的实际载重。第个动力单元附加阻力为，附加阻力由线路运行环境导致，单位附加阻力，其中坡道附加阻力，曲线附加阻力，隧道空气附加阻力，其中为坡度角的大小，为坡度值，为曲线半径，为隧道长度。第个动力单元所受相邻单元的车间作用力为，其中、分别为相邻动力单元车钩系统的弹簧弹性系数和阻尼系数。车间作用力由相邻动力单元间的车钩缓冲器产生，只要车钩缓冲装置受到拉力或推力，该缓冲器就会工作，通常其缓冲器行程为45～67 mm^[24]。

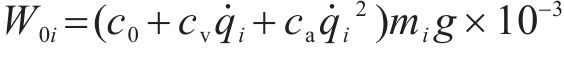
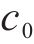
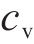
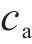
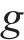
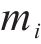
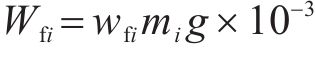
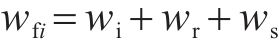
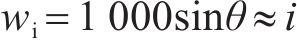
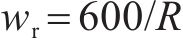
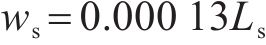
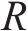
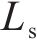
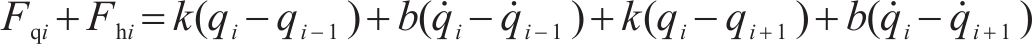
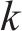
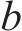
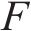
列车在运行过程中，各动力单元的牵引/制动相关设备都有可能发生故障并需要采取切除其牵引/制动的应急措施，从而导致某个单元出现动力完全缺失的现象。本文选取具有代表性的第2个动力单元发生此类故障的场景，即此时该单元的输入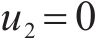，那么故障下的单欠驱动列车动力学方程可表示为：

(1)

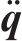
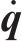
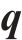
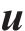
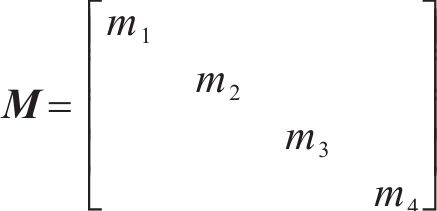
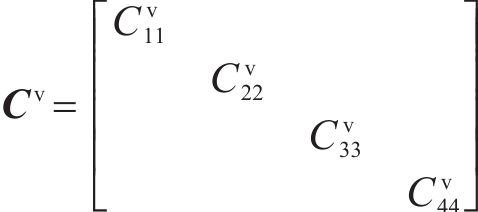
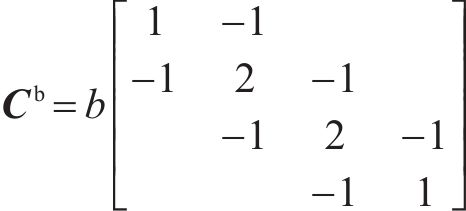
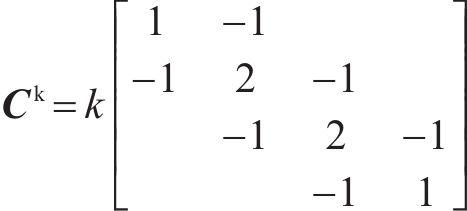
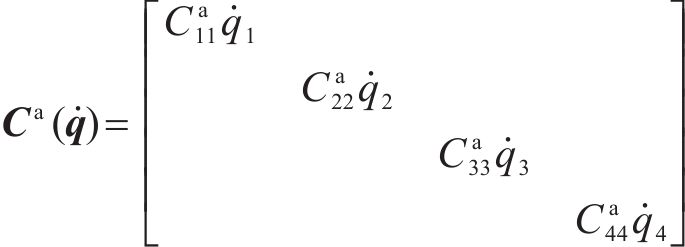
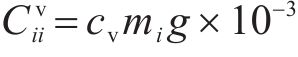
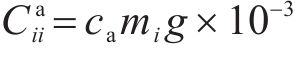
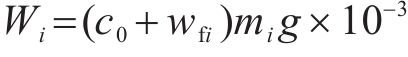
其中，、、为动车组各动力单元实际运行加速度、速度与位移；为控制输入。其余符号含义表示为：

，

，

，，

，，且其中，部分变量具体表示为，，。

3 跟踪控制器设计

本文的控制目标是利用CL法对故障下的单欠驱动动车组进行跟踪控制器设计，使故障列车系统通过剩余动力单元的执行器控制故障单元，继续跟踪期望运行曲线，从而保证整条线路按预定计划正常安全运行，并最终实现故障单元及所有正常单元的精准停车性能需求，以达到容错控制的目的。

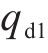
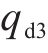
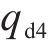
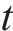
假设1：动车组各动力单元所跟踪的期望位移、、、是关于时间的连续函数，其满足3阶可导且这些导数在相应取值范围内都有界。

3.1　构造期望的受控系统

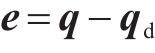
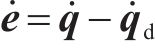
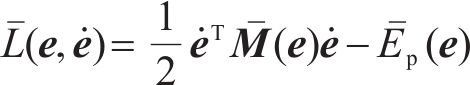
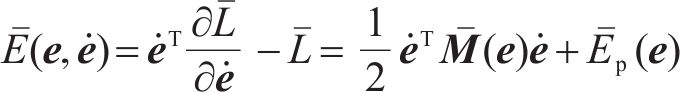
选取期望位移、速度与实际运行轨迹的偏差、作为受控系统的状态变量，则受控系统的受控拉格朗日函数和受控能量表示为：

(2) (3)

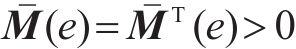
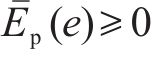
其中，受控惯性矩阵，受控势能满足。

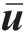
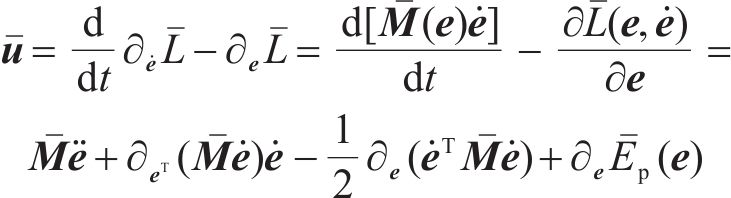
定义受控系统的受控广义力为，则利用Euler-Lagrange方程可得闭环系统动力学方程为：

(4)

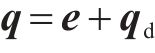
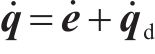
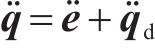
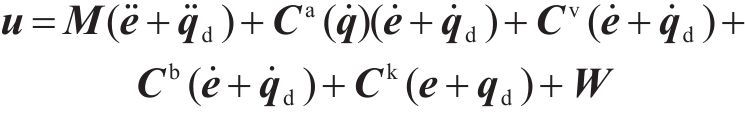
将、、代入原始系统方程式(1)中得到原始误差系统方程为：

(5)

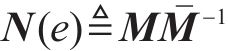
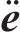
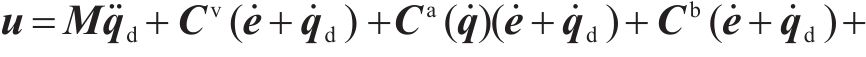
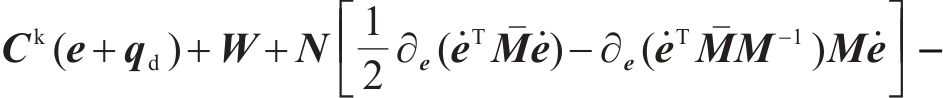
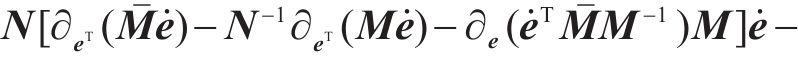
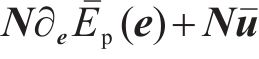
令矩阵，为使原始误差系统方程式(5)与期望受控系统方程式(4)相匹配，通过2个系统中加速度误差相等则可得系统等价方程为：

(6)

依据式(6)的结构特点，参考文献[25]中的引理2.1与引理2.2，首先定义一个反对称矩阵：

(7)

将式(7)代入式(6)可得：

(8)

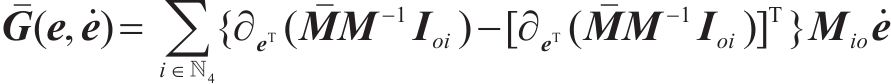
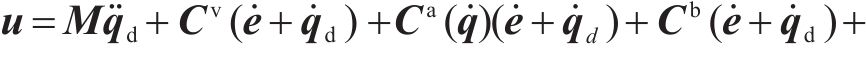
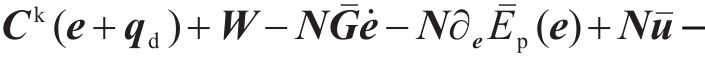
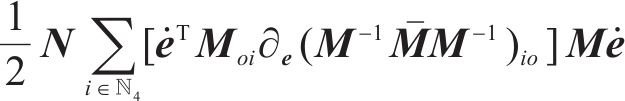
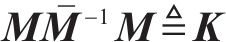
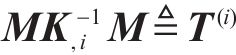
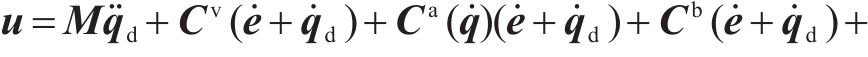
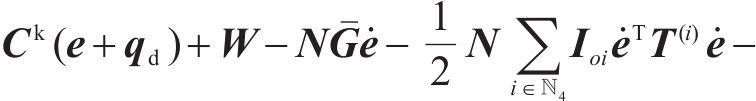
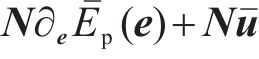
记，，则根据上述定义，式(8)可进一步简化为：

(9)

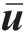
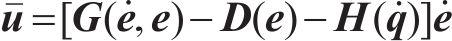
接下来，设计受控系统的广义力为：

(10)

其中，陀螺力矩阵，满足，；耗散力矩阵、满足、。

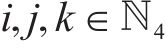
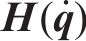
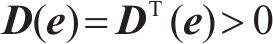
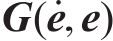
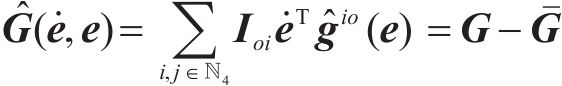
选取如下形式的矩阵表示为：

(11)

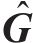
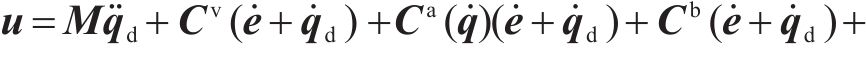
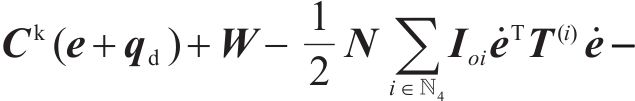
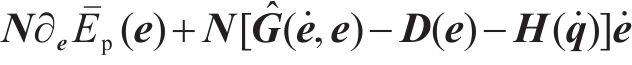
其中，具有与矩阵相同的结构形式。

将式(10)和式(11)代入式(9)可进一步简化得到：

(12)

3.2　匹配条件及匹配控制器形式的确定

如果受控方程式(4)与原始误差方程式(5)相匹配，则证明由式(6)确定的控制输入是满足要求的，那么由式(12)的第2行导出系统匹配条件表示为：

(13)

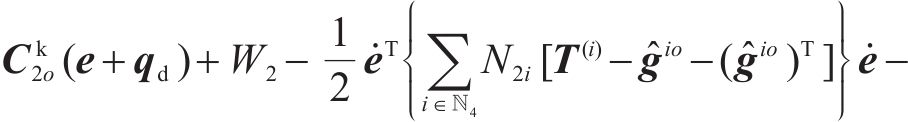
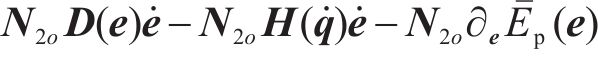
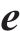
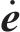
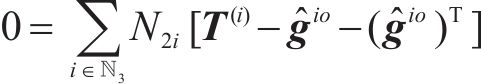
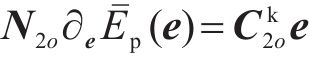
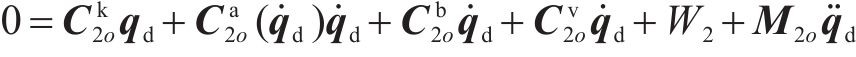
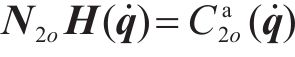
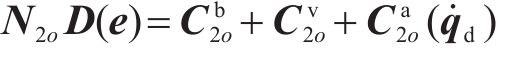
根据广义跟踪误差变量与的独立性，式(13)花括号中对称矩阵之和的二次型等于0，因而对称矩阵之和为0矩阵，则匹配条件(13)可分解为：

(14) (15) (16) (17) (18)

由矩阵、、的定义易知，是受控动能的正则条件。如果对，都有，则可以导出，因而至少存在一个使得。在式(14)的两边分别乘以向量和，则其可分解为一个新的动能方程式(19)和包含陀螺力项元素的其余动能方程式(20)，如下所示：

(19) (20)

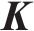
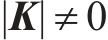
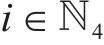
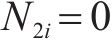
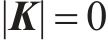
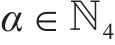
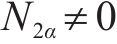
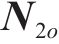
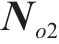
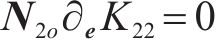
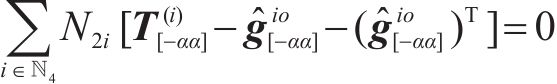
其中，式(19)是关于矩阵与的动能方程，而式(20)是包括9个有关陀螺力分量函数的线性代数方程。

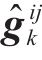
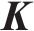
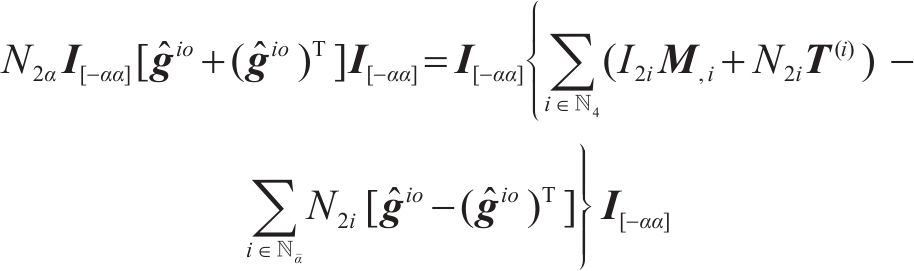
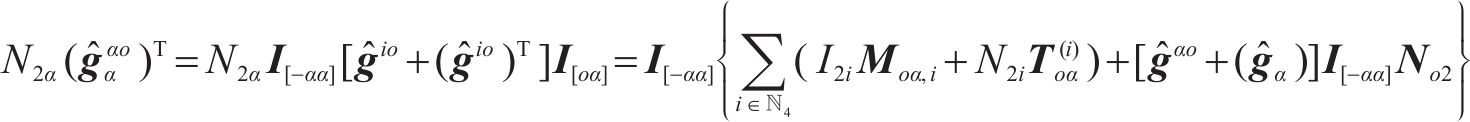
为求解其余动能方程式(20)，通过任意给定的正定矩阵，式(20)可进一步写为：

(21) (22)

其中，4阶矩阵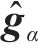是一个反对称矩阵。

引入一个函数行向量：

(23)

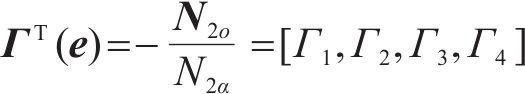
通过知，其中，，则可得：

(24)

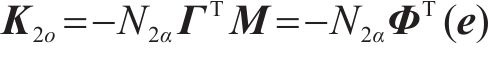
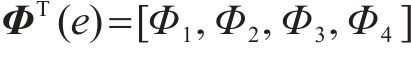
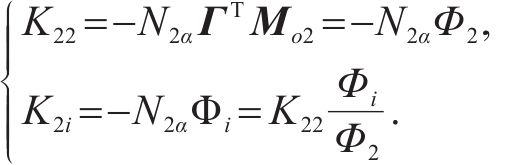
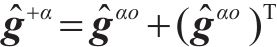
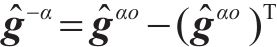
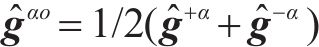
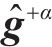
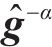
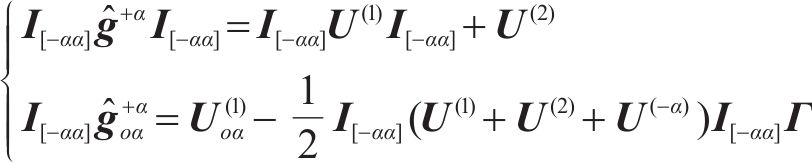
定义2个新的矩阵表示为和，则矩阵。将和代入式(21)和式(22)式得到以下方程组：

(25)

其中，， ，。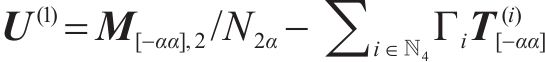

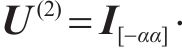
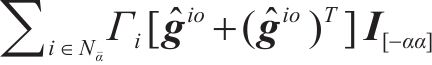
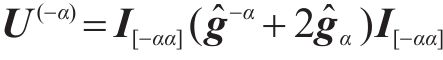
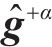
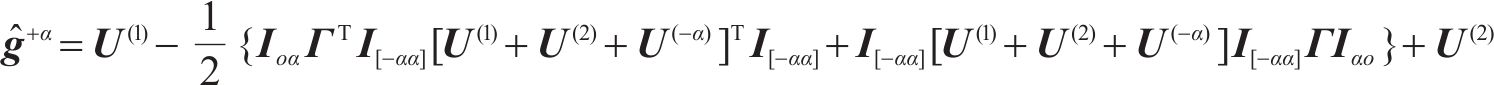
从式(25)确定出未知对称矩阵的形式为：

(26)

对于任意正则的受控动能，9个其余动能方程式(20)可被同等数量的独立函数满足，其由矩阵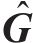元素的分量函数构造并被具有15个自由函数的式(26)决定。

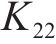
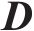
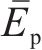
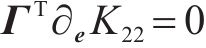
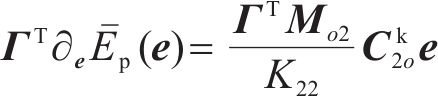
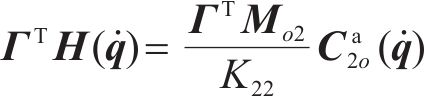
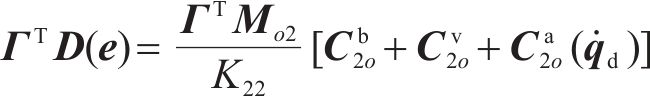
将匹配条件式(14)、式(15)、式(17)、式(18)用、、、、重新表示，可写为：

(27) (28) (29) (30)

综上所述，新的动能方程式(27)、势能方程式(28)、耗散力相关方程式(29)和式(30)、期望轨迹匹配方程式(16)，正则条件及显式陀螺力方程式(11)组合起来，即为原始误差系统与受控系统相等价的匹配条件。

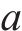
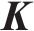
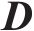
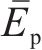
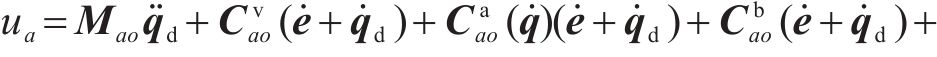
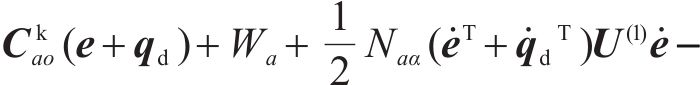
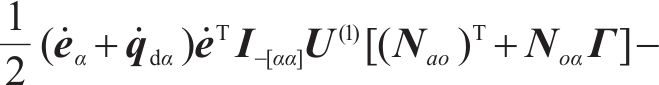
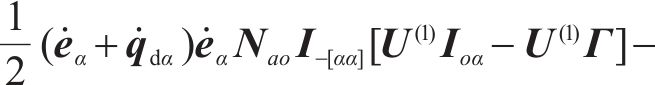
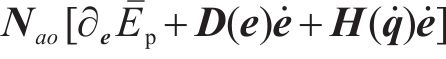
由上文可知，被控系统的第个自由度有控制输入，那么将求解出来的、、、、及代入式(12)得到匹配控制器形式为：

(31)

3.3　匹配条件及具体匹配控制律的求解

1) 受控动能的求解

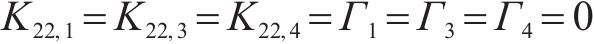
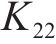
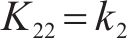
令，则可从式(27)得到的一个特解为：

(32)

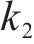
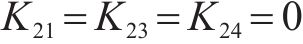
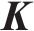
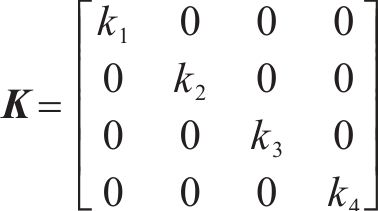
其中，为常数。利用式(24)可知，那么系统的矩阵表示如下：

(33)

矩阵的行列式为，为使，则其充分条件是：、、、。将与代入到中进一步可知，即陀螺力矩阵。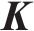

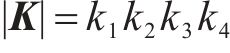
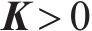
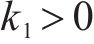
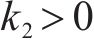
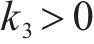
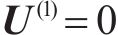
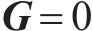
2) 受控势能的求解

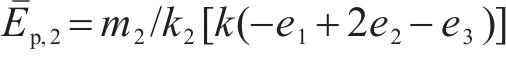
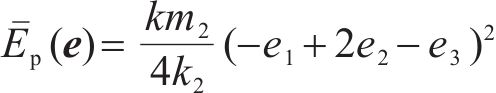
由式(28)可知，则受控势能的特解如下：

(34)

为满足受控势能的正定条件，取其通解为：

(35)

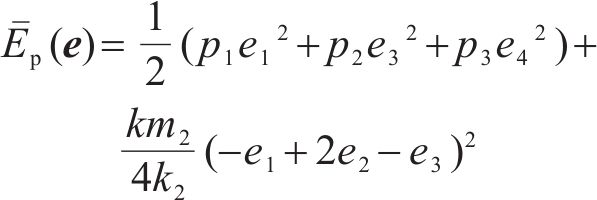
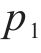
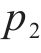
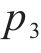
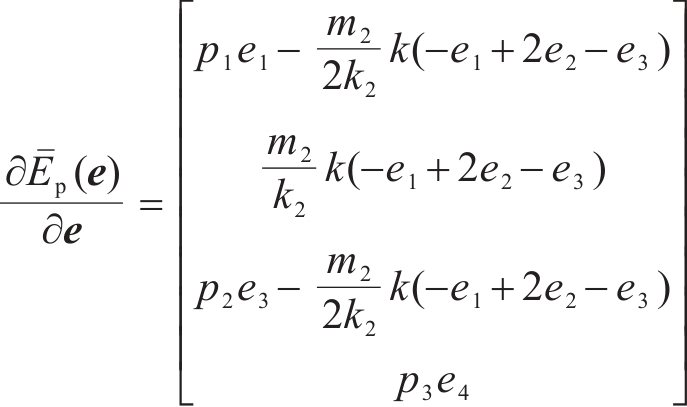
其中，、、为大于0的常数，那么：

(36)

通过直接计算得到受控势能的Hessian矩阵为：

(37)

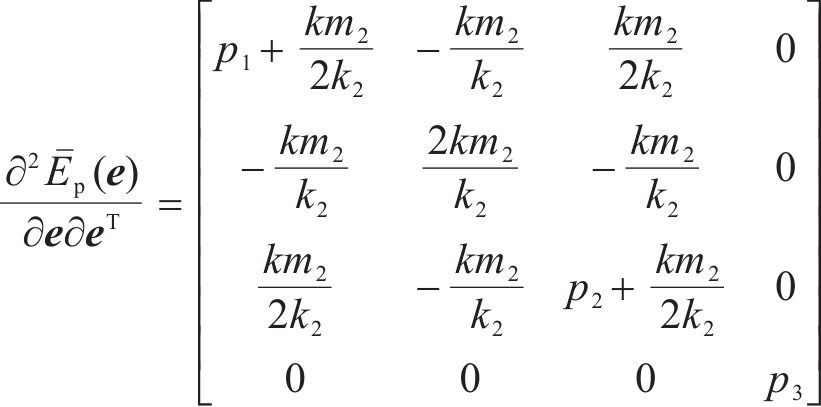
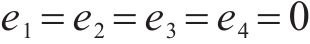
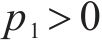
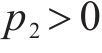
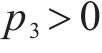
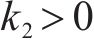
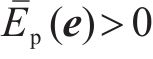
因为Hessian矩阵行列式大于0，则可知Hessian矩阵正定。当时，受控势能取极小值，其极值条件为、、、，这也是的充要条件。

3) 求解耗散力相关矩阵

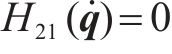
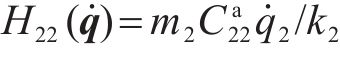
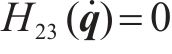
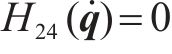
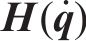
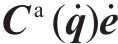
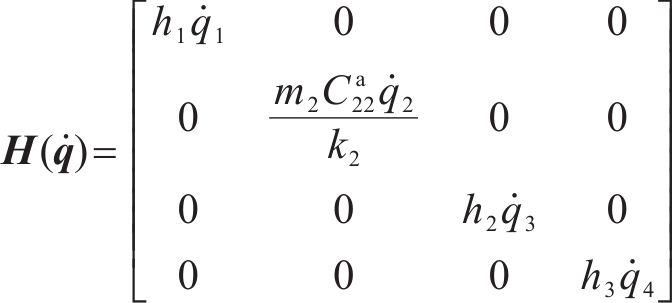
由式(29)可得、、、。因为矩阵是为与原始系统中的项进行匹配而设计的，则为方便计算矩阵可取为对角矩阵如下：

(38)

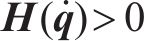
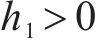
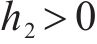
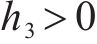
为满足成立，则、、。

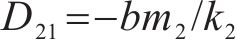
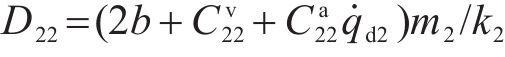
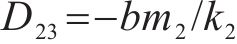
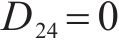
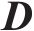
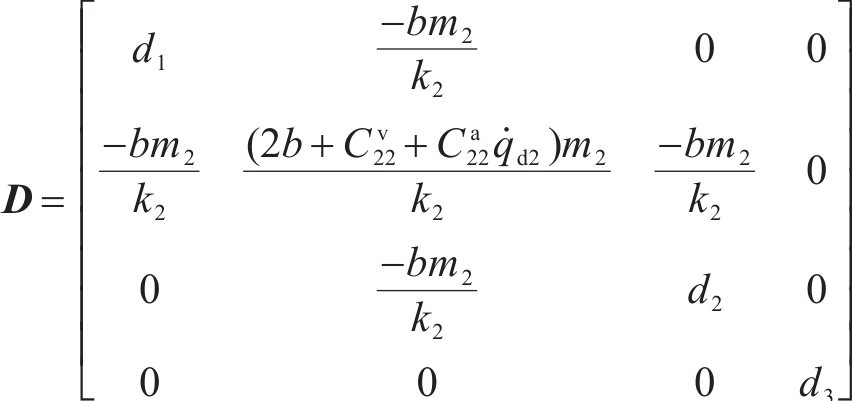
同理根据式(30)可以求得、、、，则矩阵具体形式可表示为：

(39)

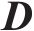
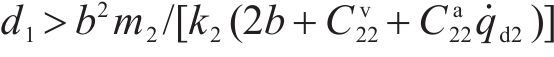
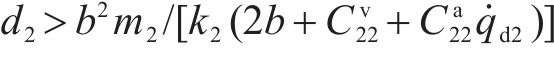
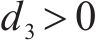
因耗散力矩阵为正定的对称矩阵，所以其内部各元素需满足条件、、。

4) 求解具体匹配控制律

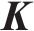
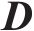
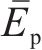
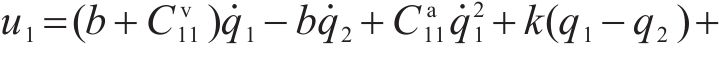
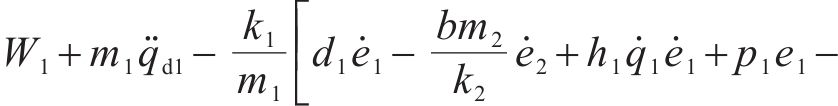
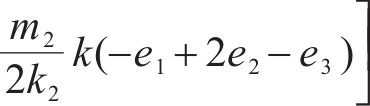
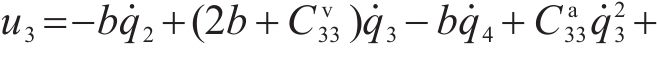
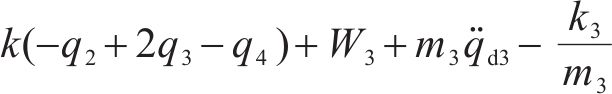
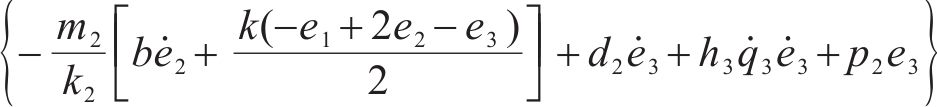
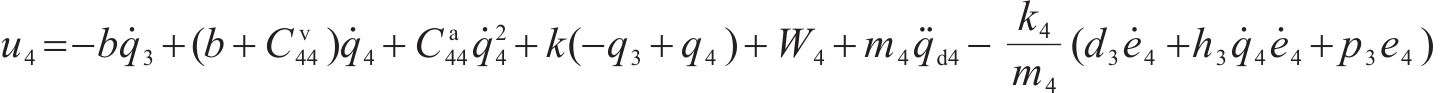
将求解出来的、、、及代入式(31)，得到具体的跟踪匹配控制律为：

(40)(41) (42)

4 稳定性证明

定理1：如果匹配控制律参数按如下要求设置：

(43)

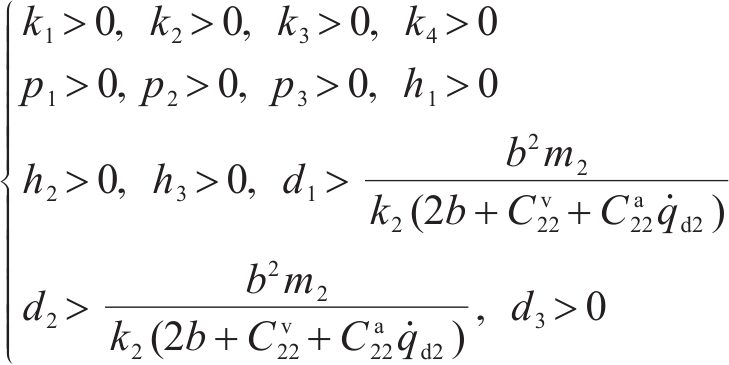
同时，期望参考轨迹的选取满足式(16)，那么由式(40)～式(42)确定的控制律可以在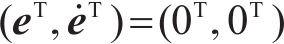实现系统的全局渐近稳定，从而使列车渐近跟踪期望速度与位移轨迹，达到精准停车的控制要求。

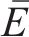
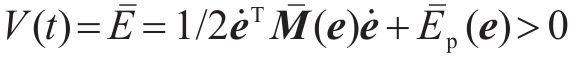
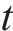
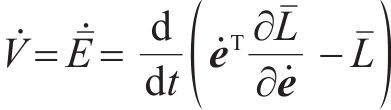
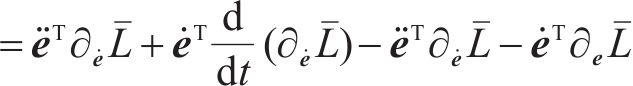
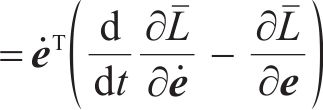
证明：直接选取受控能量作为Lyapunov函数，由其定义知，对其求关于时间的导数为：

(44)

通过Lyapunov稳定性可得期望的闭环受控系统稳定。接下来讨论系统的渐近稳定性，用反证法证明在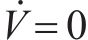的集合中只存在平衡点的轨迹。

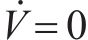
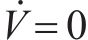
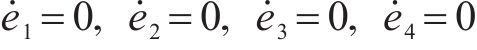
首先，假设在集合中存在非孤立点的轨迹，由条件可知：

(45)

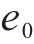
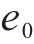
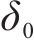
此时，在轨迹上应存在某点，同时在该点的某个邻域内同样也成立。对式(45)沿着轨线分别进行微分和积分计算得到：

(46)

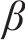
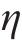
其中，、、、为常数。

将式(40)～式(42)、式(45)、式(46)及式(16)代入原始系统方程式(5)中可得：

(47)

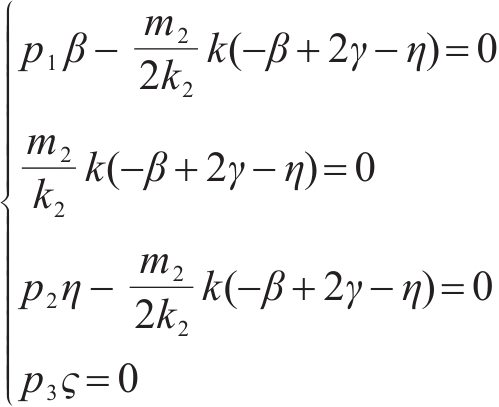
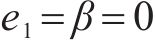
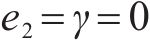
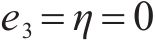
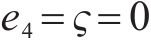
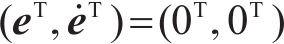
当且仅当距离误差满足、，、时，式(47)才成立，故假设不成立。同时由受控势能的Hessian矩阵正定，因此平衡点为受控能量的唯一的极小值点。根据LaSalle不变原理，该匹配控制律可在闭环系统期望的平衡点实现全局渐近稳定。

5 仿真结果分析

本节选取国内某线路实际运营编组方式为4M4T的CR400BF型高速列车作为研究对象，对其速度、位移轨迹跟踪情况及停车精度问题进行验证分析。考虑该列车的各动力单元的车长为50 m，将第四动力单元车尾所在位置视为距离原点，假设列车行驶在无隧道线路，线路外部环境坡道和曲线作用情况如图2所示。各动力单元的实际载重分别为120、110、115和120 t，根据新起草的铁道行业标准TB/T1407.2—202X中《列车牵引计算第2部分：动车组》，列车单位基本运行阻力参数及车间耦合作用力的参数取值如表1所示。

图2全屏查看

列车运行线路外部环境情况

取无故障的各动力单元的期望速度与位移轨迹都相同，选取其光滑的期望速度曲线如式(48)所示：

(48)

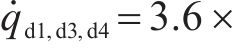
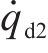
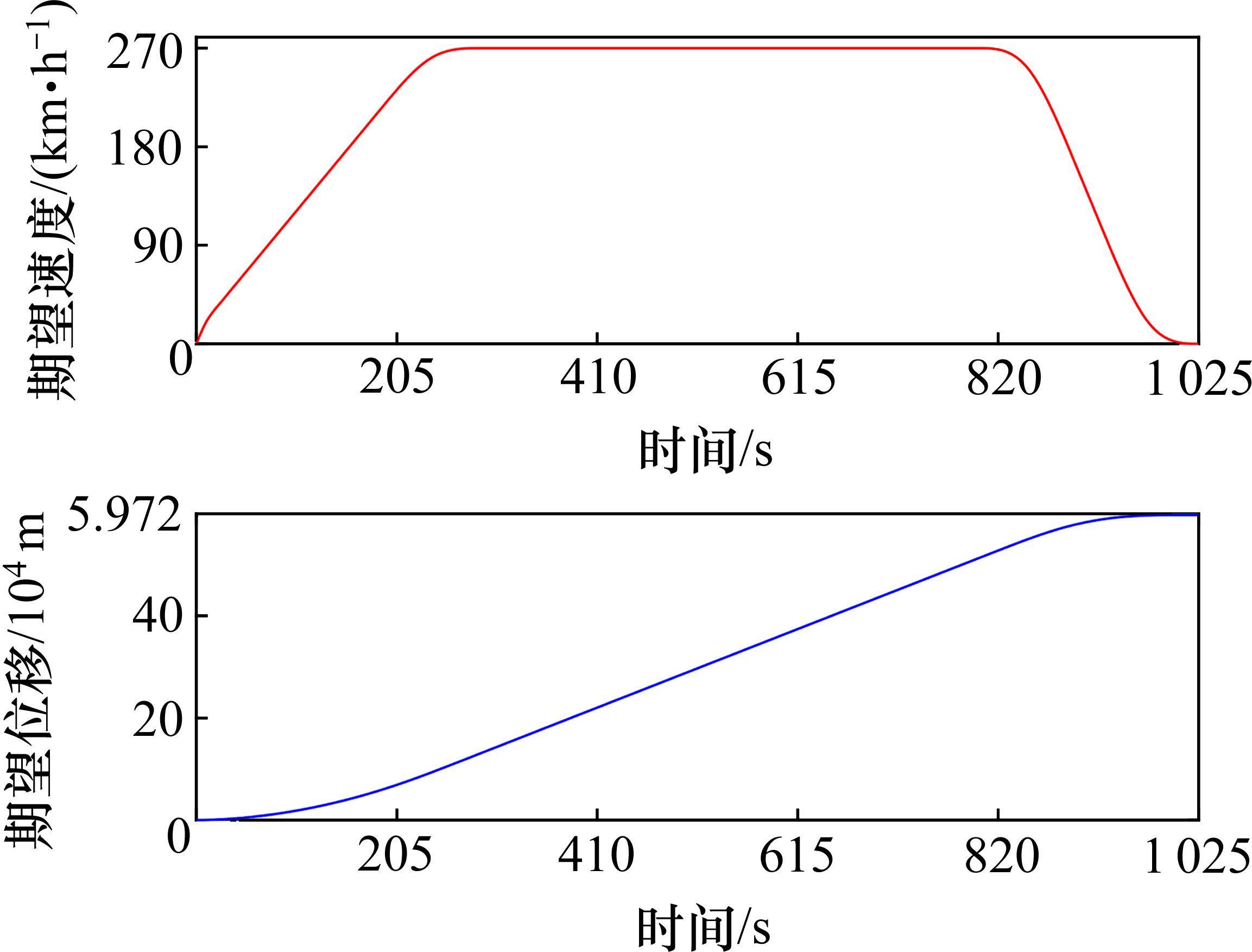
对于发生牵引/制动相关设备故障的动车组第二动力单元的期望轨迹、的选取需要满足轨迹匹配条件式(16)，而式(16)是2阶非线性非齐次微分方程，其求解相对困难，利用数值求解在给出无故障动力单元的期望轨迹的条件下，分析得到其故障单元的轨迹曲线如图3所示。

图3全屏查看

故障第二动力单元期望速度与位移曲线

为更好地体现所设计控制器对于跟踪效果的有效性，假设动车组在初始时刻及运行过程的第600 s时，因外界扰动使其实际位移与速度和期望位移与速度有较大偏差。将满足闭环系统控制目标要求的各跟踪控制器参数分别设置为：

(49)

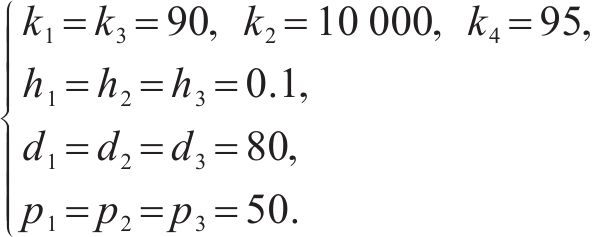
通过Matlab仿真得到动车组各动力单元的速度与位移曲线跟踪情况，速度、位移跟踪误差曲线及无故障的剩余动力单元控制输入曲线如图4～图7所示。

图4全屏查看

各动力单元位移曲线跟踪情况

图5全屏查看

各动力单元速度曲线跟踪情况

图6全屏查看

各动力单元位移跟踪误差

图7全屏查看

各动力单元速度跟踪误差

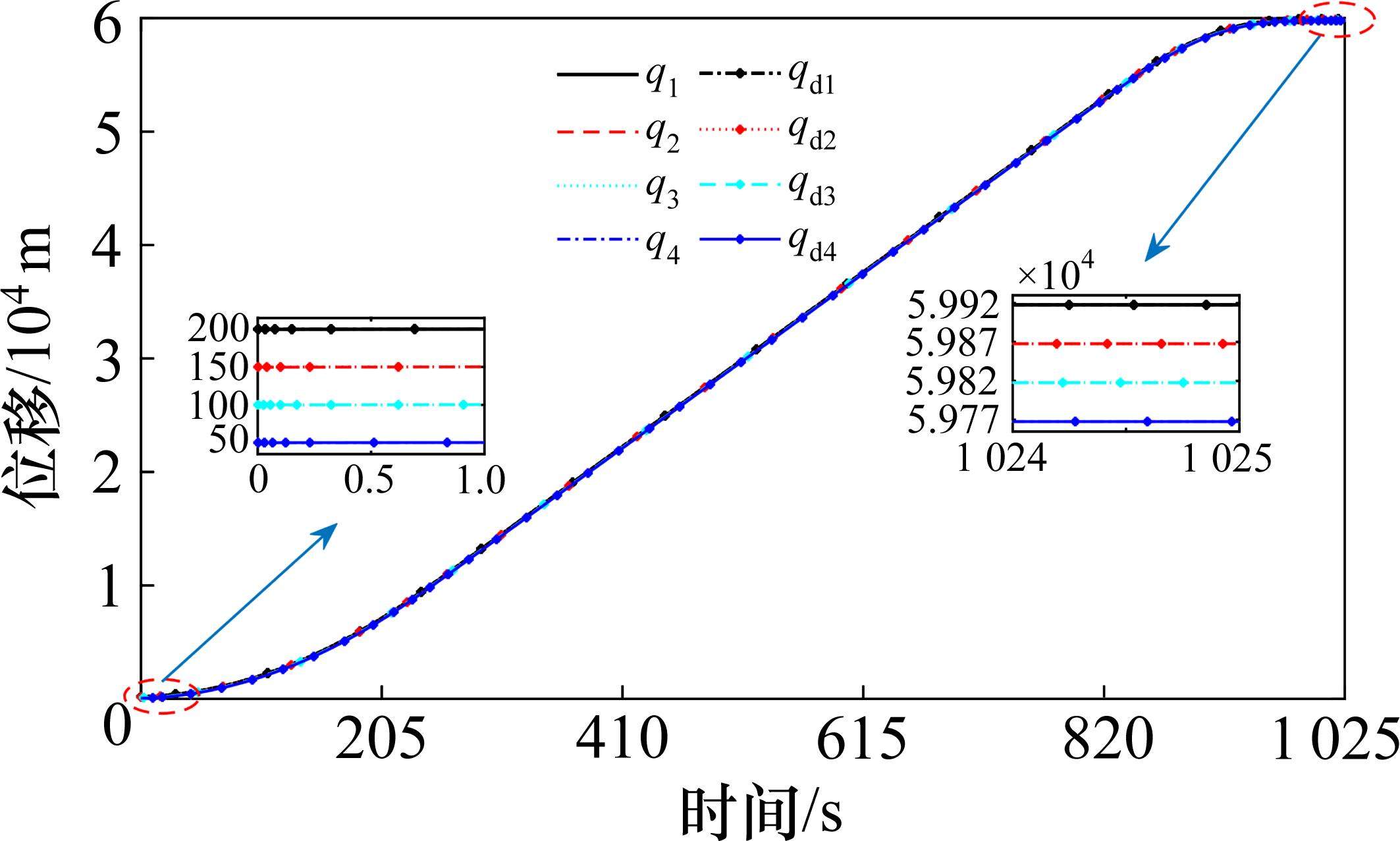
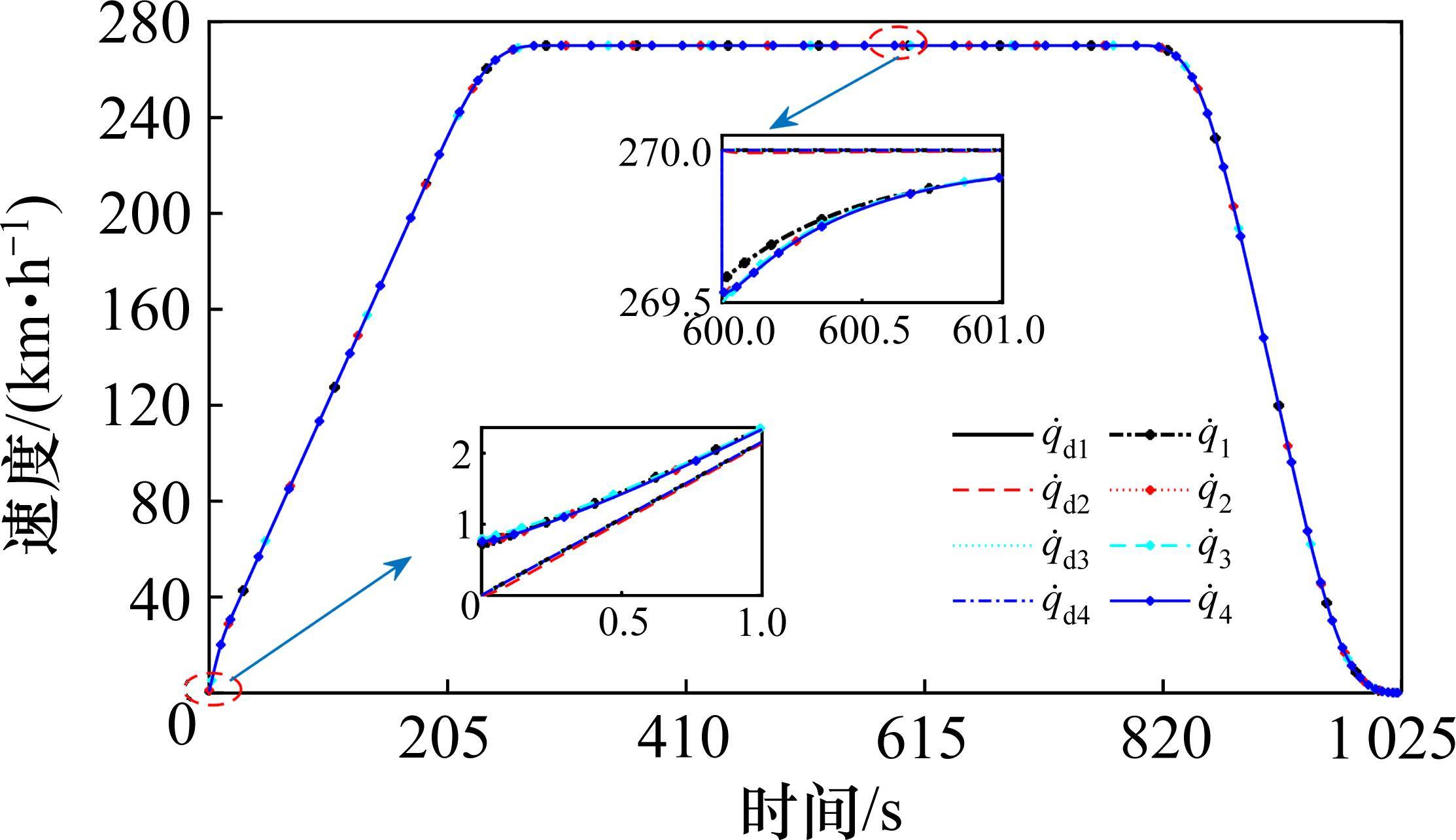
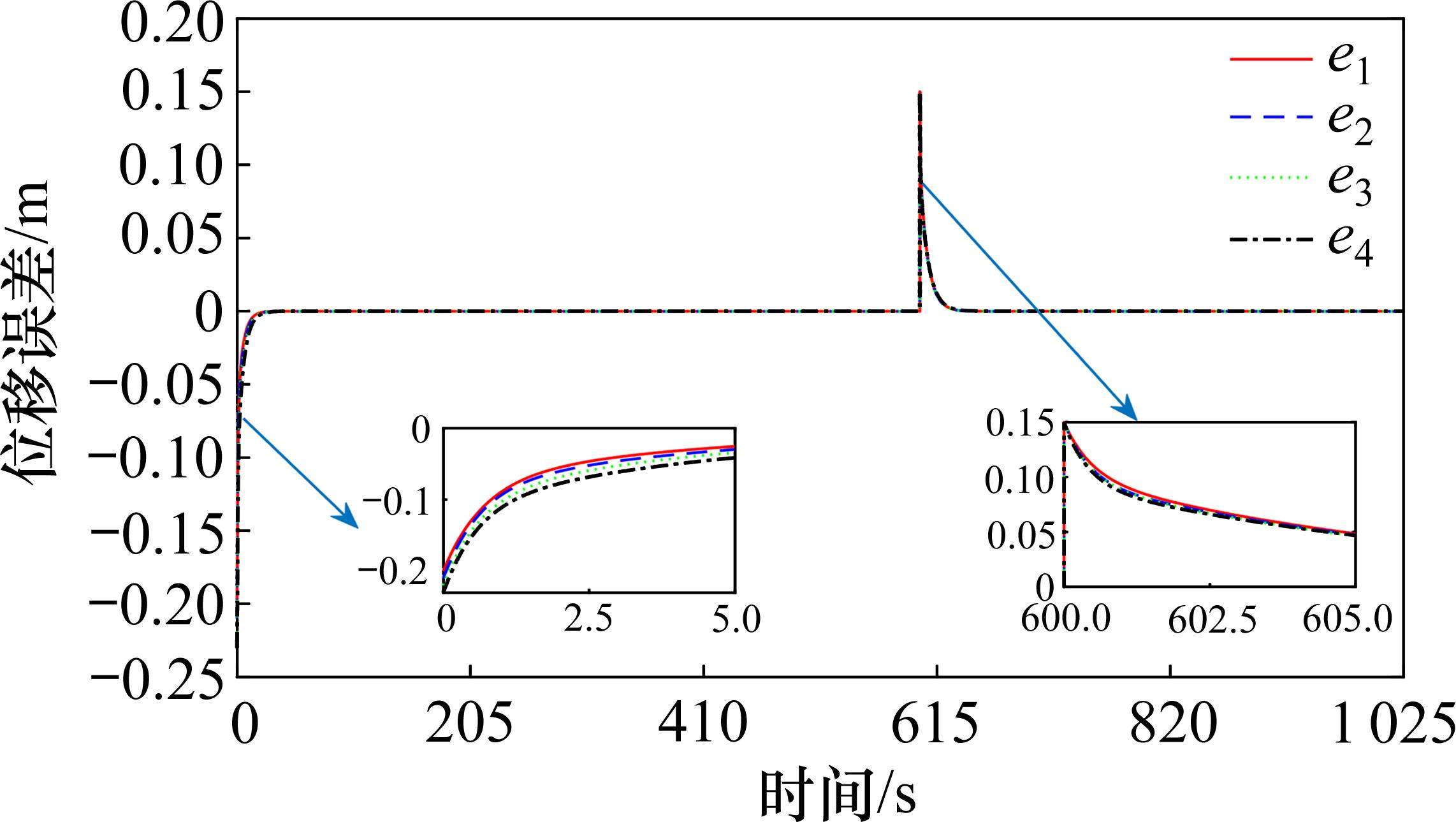
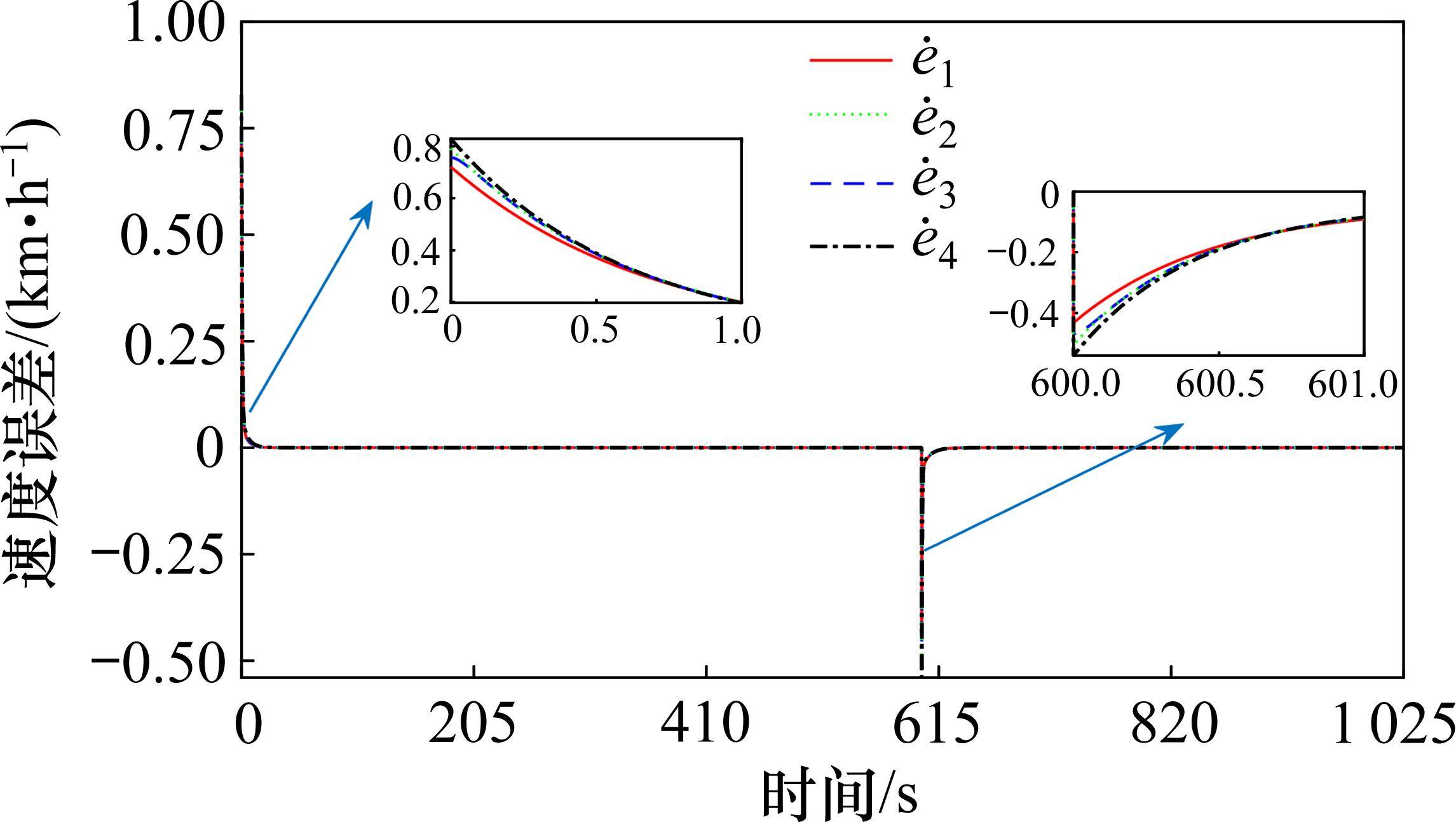
从图4～图7可以看出，初始时刻及第600 s时设置了由外界干扰产生的误差，在如图8所示的光滑反馈控制输入的作用下，各动力单元的实际位移及速度都稳定地跟踪着期望的位移与速度运行曲线轨迹，且速度与位移跟踪误差都快速趋于0，从而使全车实现速度追踪及精准停车的运行控制需求。由于所得控制律光滑，这将更有利于提高列车运行的平稳性，以此来保证运行中的乘客乘坐舒适度。

图8全屏查看

控制输入

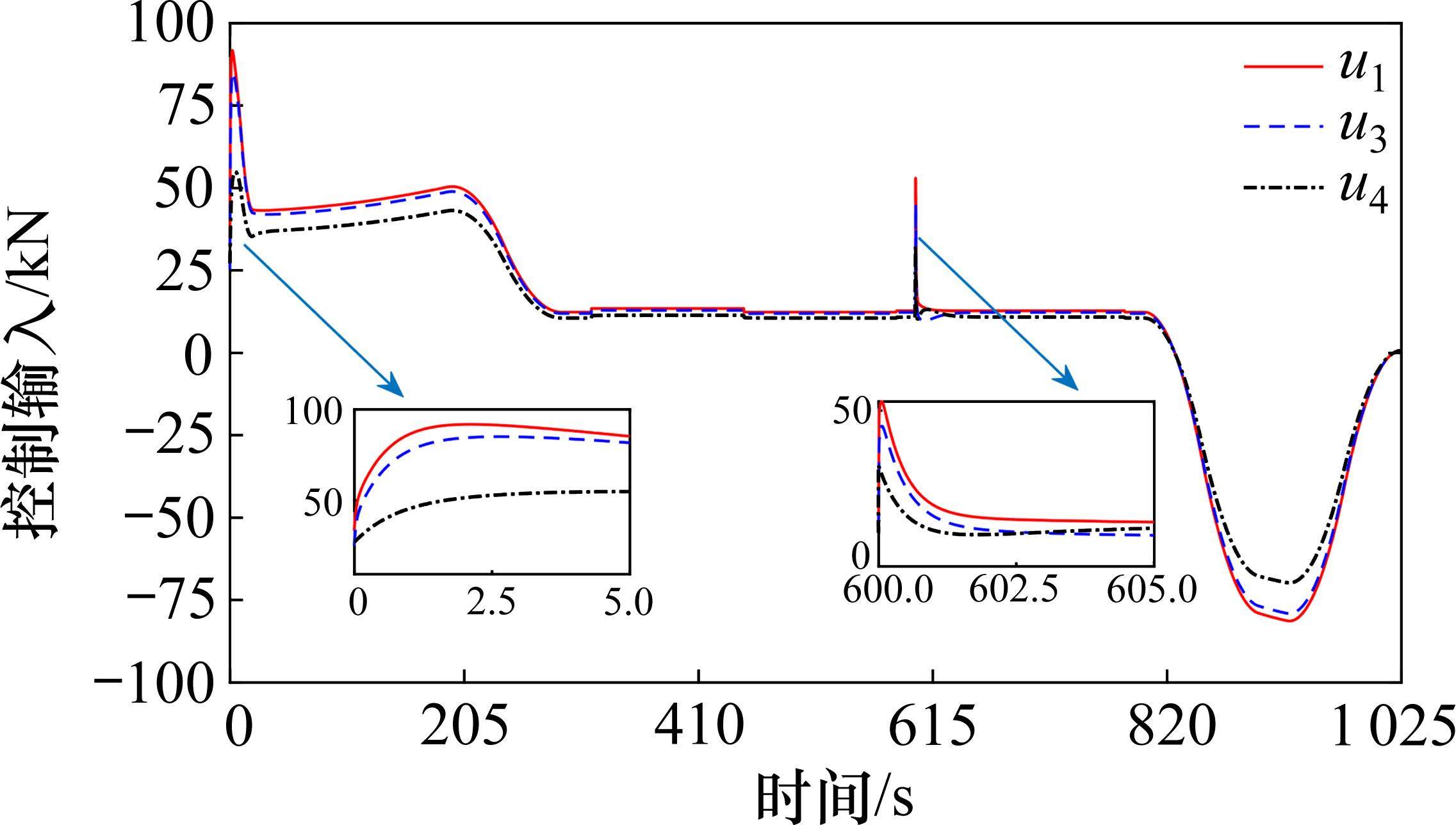
图9为相邻各动力单元间车钩力作用情况，可以看出初始时刻及第600 s时，各单元间车钩力纵向冲击力较大，而后随着运行工况的平稳变化，单元1-2、3-2的车钩力始终存在，这是因为故障第二动力单元的控制是通过与其直接相连的车钩力的耦合作用实现，同时从图9看出其车钩最大作用力远小于车钩最大纵向拉伸1 000 kN与纵向压缩1 500 kN^[24]。该仿真结果表明，所提跟踪控制器可以通过列车各动力单元的车间耦合连接，在直接控制剩余正常动力单元的同时利用相邻车钩力协调故障单元，从而保持有效控制。

图9全屏查看

相邻动力单元间车钩力

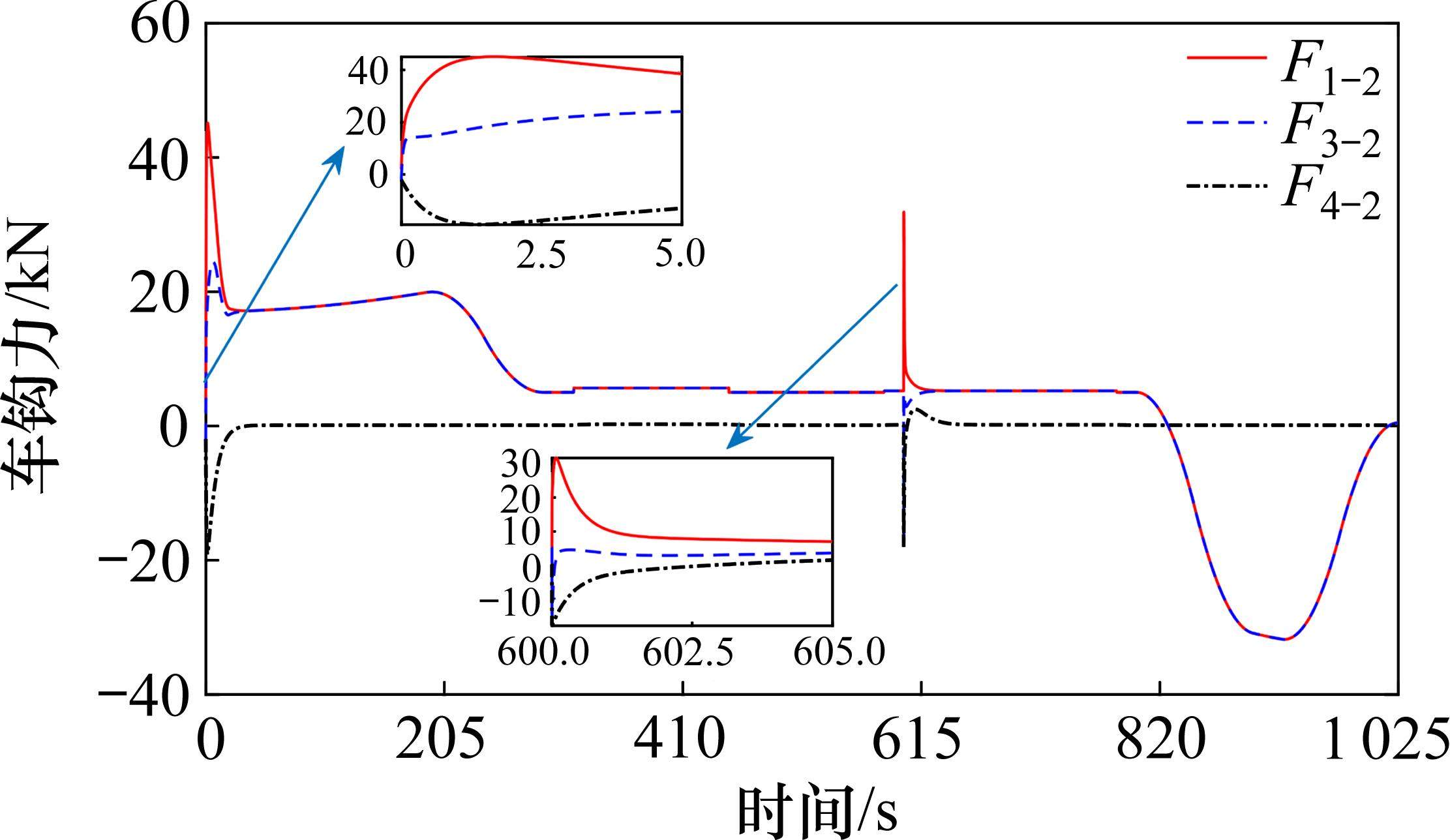
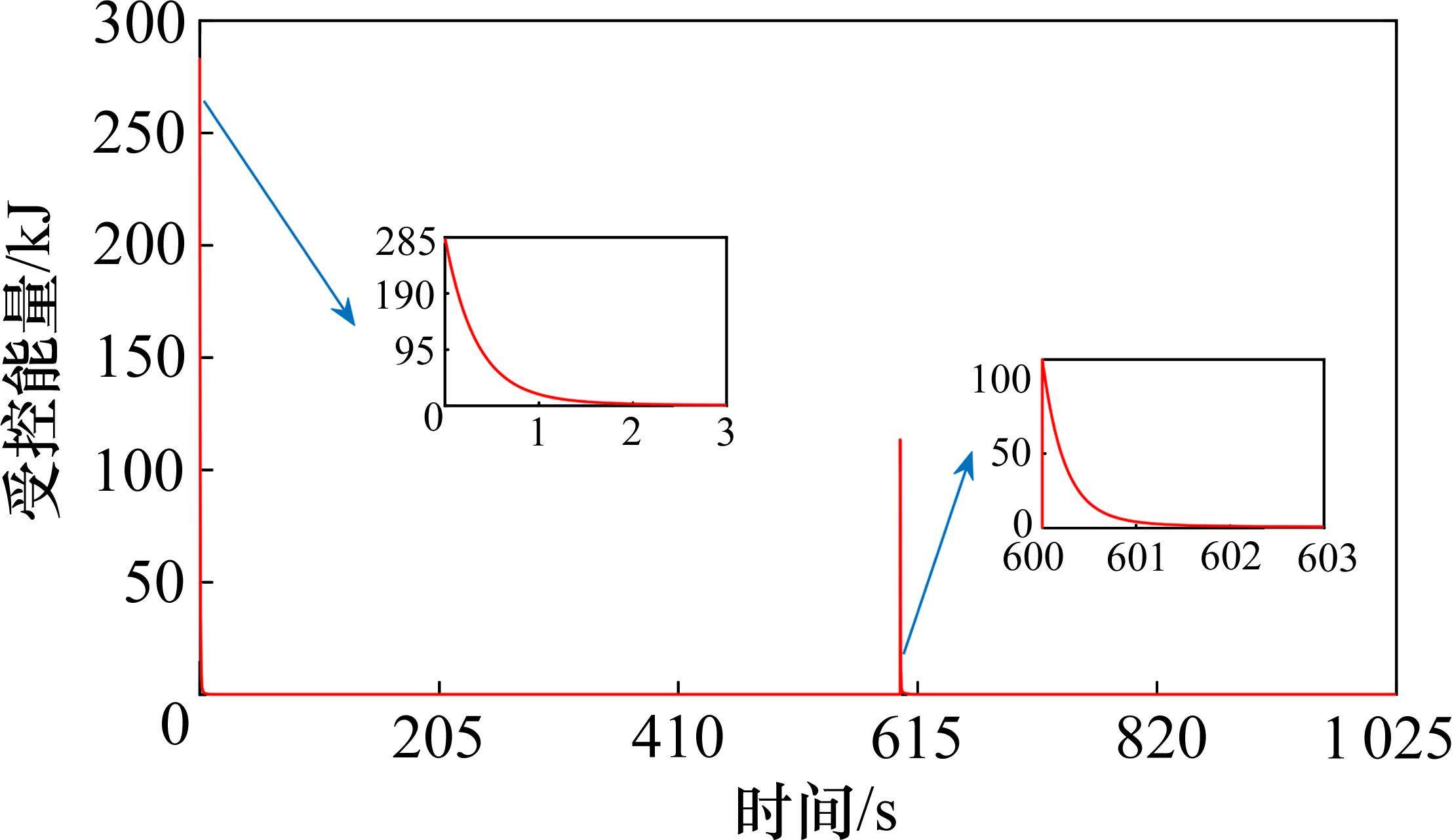
图10为所构造的受控系统能量的变化情况。根据定理1的分析，为保证受控系统稳定，受控能量正定且单调递减。从图10可以看出，在初始时刻及第600 s后，受控能量不断衰减并快速稳定收敛到0，这满足闭环误差系统能量的变化规律，使系统状态趋于期望的控制目标，以此达到精准的跟踪控制。

图10全屏查看

受控能量

6 结论

1) 将CL法扩展到因某个动力单元发生故障需切除该单元牵引/制动使单元动力完全缺失后呈现欠驱动特性的动车组自动驾驶跟踪控制问题上，通过设计相应的欠驱动光滑反馈跟踪控制律，从而增加列车运行的平顺性。

2) 理论分析和仿真结果表明，在控制输入减少的情况下，所得控制器仍然可以实现故障动车组系统速度与位移的渐近跟踪及精准停车的控制需求。

3) CL法在欠驱动系统中需要通过求解匹配条件才能获得控制律的具体形式，这使得其应用局限于能够精确建模且模型参数已知的机械系统。事实上，多数机械系统由于本身构造及运行环境等因素的影响，其模型参数未知，所以下一步将结合模型参考自适应控制^[26]处理参数不确定的优势，研究基于CL法的欠驱动系统自适应跟踪控制问题，并进一步将外部线路环境相关参数当作未知的时变参数进行鲁棒控制的研究，同时考虑输入受限的情况使研究更接近于实际运行要求。