1 Introduction
Geotechnical material, such as rock and soil, is always in layered structure, which will pose great influence on the thermo-mechanical (TM) coupling process in engineering activities, including exploitation of shale oil and gas [1, 2], storage of nuclear waste [3, 4], pipeline transportation of submarine gas [5-7], etc. BIOT [8] firstly introduced the linear thermal elastic theory and provided the solution of displacement field controlled by wave equation and temperature field controlled by diffusion equation. However, the propagation speed of the disturbed section was assumed as infinite. This is inconsistent with that in practical situation and in thermal conduction theory. Considering the above limitation, the classical Fourier thermal conduction theory was modified, and L-S theory [9, 10], G-L theory [11], G-N theory [12], non-local thermal shock theory [13], T-T theory based on double-temperature thermal conduction theory [14, 15], and general thermal elastic theory based on fractional derivative [16-18], have been proposed. The above modified general thermal elastic theory has laid a theoretical foundation for the analysis of the TM coupling process of multi-layered structure. In recent years, many scholars have studied the TM response of layered composite structure based on the above thermal elastic theory. YOUSSEF and EI-BARY [19] studied the thermal impact response of layered composite structure considering the variance of thermal conduction coefficient. HOSSEINI-TEHRANI et al [20] revealed the distribution pattern of temperature and stress at the interface between the elastic layer and stiff foundation. YU et al [21] analyzed the propagation pattern of thermal wave of the layered composite plate based on G-N thermal elastic model. EI-BARY and YOUSSEF [22] studied the thermal impact response of layered composite structure based on LS model. AMIRI DELOUEI et al [23] obtained the accurate solution of instant thermal conduction of cylindrical composite structure. AKBARZDEH and CHEN [24] obtained the semi-analytical solution of the complete and incomplete contact of 1D multi-layered material based on the Bessel and Laplace function. ABD EI-LATIEF and KHADER [25] studied the 1D dynamic response of double-thin-layer structure based on the fractal thermal elastic theory. However, the above research ignores the influence of boundary thermal contact on the dynamic response of composite structure.
The layered composite structure is always in the incomplete contact state, with tiny voids filled with air. Due to the significant difference of thermal conduction coefficient between the air and the contacting material, when the thermal wave propagates through, part of the thermal wave would be transmitted to the contacting layer, and another part would be reflected to the initial layer due to air resistance. The above propagation will induce significant contraction of thermal wave and further leads to large thermal gradient at the interface, which is known as thermal contact resistance [26]. Thermal contact resistance is related to the coupling interaction of temperature, mechanics and material [27] and is influenced by the interface roughness, interface load, soil property and particle size [28, 29]. JACKSON et al [30] concluded that the contacting area and surface roughness of the interface are two main factors that influence the thermal contact resistance. ROSHANKHAH et al [31] obtained the relationship between thermal contact resistance and stress state. It has also been reported that thermal contact resistance is the function of contacting area, average distance between interface and the thermal conduction coefficient [32, 33].
Considering the influence of thermal contact resistance, BALASUBRAMANIAN and PURI [34] studied the influence of multi-scale boundary effect when thermal wave transmits the interface of double-layered elastic structure. TIO and KOK CHUAN [35] studied the thermal contact resistance at the interface of cylindrical solid. KEK-KIONG and SADHAL [36] studied the influence of boundary condition and contacting geometry on thermal contact resistance. XUE et al [37, 38] studied the thermal impact response of double-layered structure based on GL and fractal thermal elastic theory. LI et al [39, 40] studied the thermal impact response of composite ceramic material. LOR and CHU [41] studied the influence of thermal contact resistance on the thermal conduction of composite material based on thermal wave model and radiation boundary condition. XUE et al [42] analyzed the thermal diffusion effect of the instant response of layered composite structure and the influence of thermal contact resistance on the thermal diffusion effect. WEN et al [43, 44] analyzed the influence of thermal contact resistance on the dynamic response of double-layered saturated porous material. However, the above thermal contact resistance model still has its limitations and is not suitable for situations where micro-cracks and local thermal conduction occur at the interface of composite structure [45].
In this paper, a new general incomplete thermal contact model is constructed by introducing the thermal resistance coefficient and local heat transfer coefficient. The instant response of layered composite structure under thermal load is analyzed and the expression of temperature and displacement of layered composite structure is obtained based on Laplace transform. Taking the double-layered rock mass as an example, the calculation results of four thermal contact models are analyzed and the relationship between thermal resistance coefficient and material properties, such as thermal conductivity coefficient and specific heat coefficient is revealed.
2 Problem formulation and governing equations
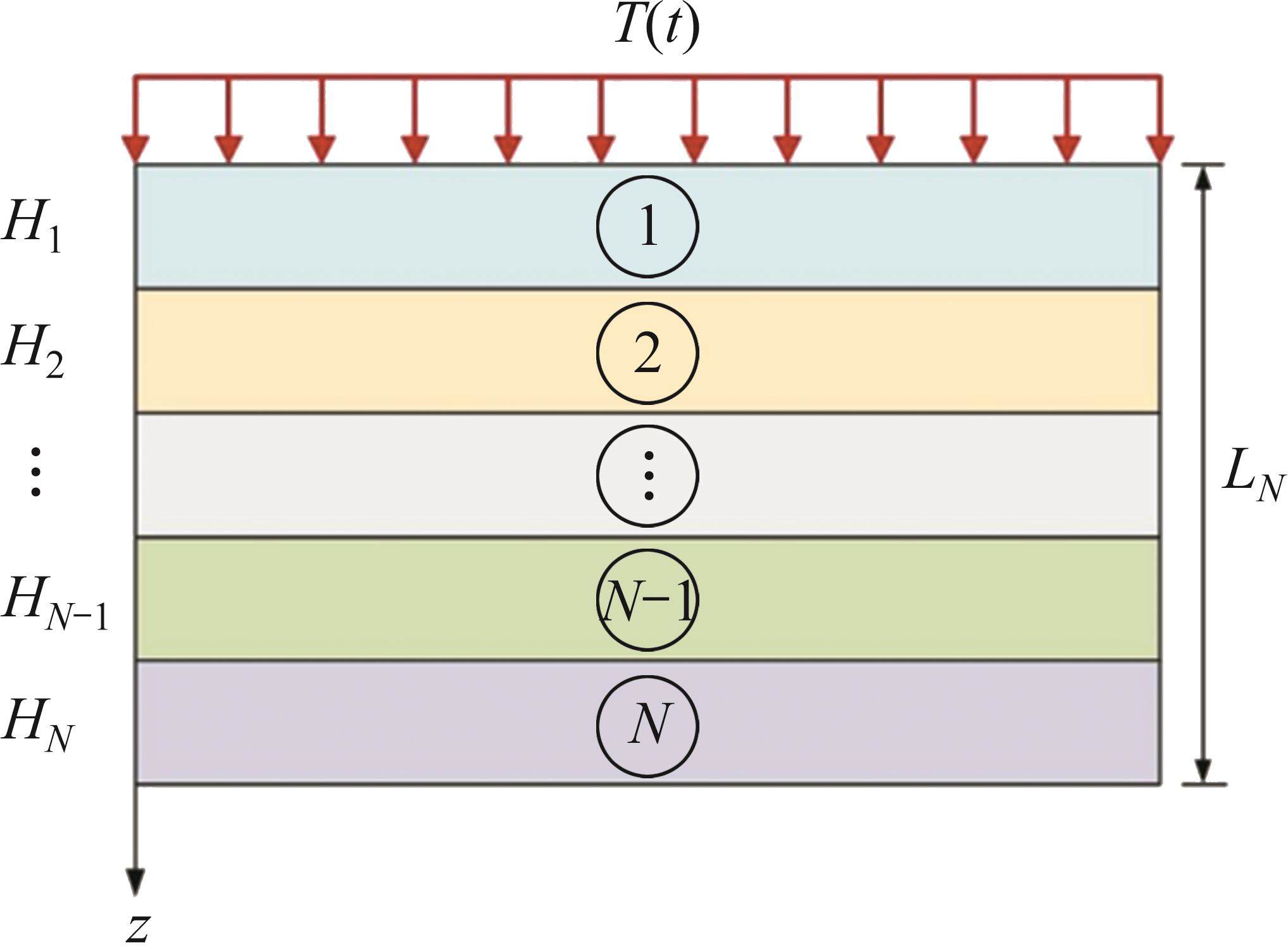
As shown in Figure 1, the multi-layered structure is divided into N layers of isotropic and homogeneous elastic material with different properties. The thickness of each layer is expressed as H1, H2 … HN-1, HN and the total thickness is LN=H1+H2+…+HN-1+HN. A thermal load T(t), which varies in step-wise mode with time, is applied on the top of the first layer. The bottom material of the Nth layer is thermal insulation, impermeable and without deformation. It is assumed that the interface between each layer is uneven and coarse, with tiny pores filled with air. Due to the significant difference of thermal conduction coefficient between the air and the contacting material, the propagation speed of thermal energy at the interface is different. When the thermal wave propagates through the air and contacting material, part of the thermal wave would be transmitted to the contacting layer, and another part would be reflected to the initial layer, which leads to large thermal gradient at the interface. As a result, the temperature increment at the interface is discontinuous and the air in the voids impedes the propagation of thermal wave, which is known as thermal contact resistance. According to geometrical and mechanical condition, the above model could be simplified as 1D thermal elastic problem.
According to the general elastic GL theory, the equation of motion is [11]:
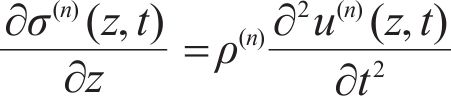
And the equations of local energy balance and heat conduction are as:
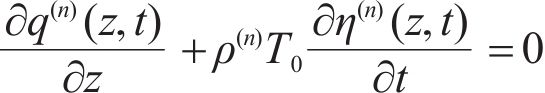
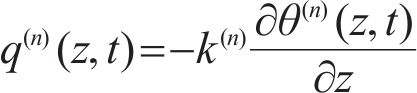
With the following constitutive equations [11]:
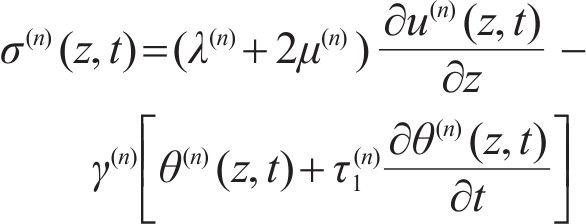
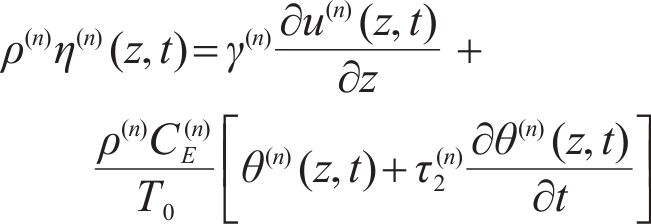
where 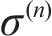
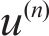
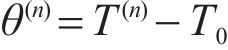
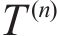
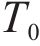
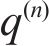
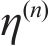
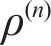
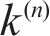
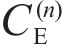
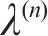
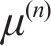
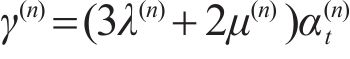
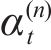
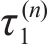
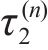
Substituting Eq. (4) into Eq. (1) produces:
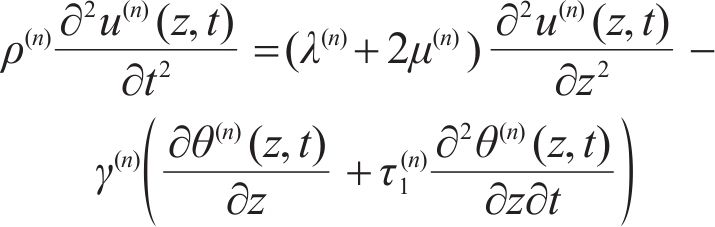
Combining Eqs. (2), (3) and (5) produces:
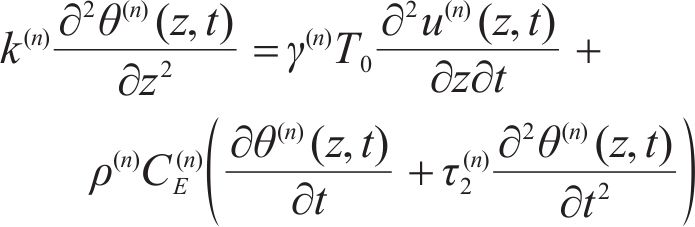
The Laplace transform of Eqs. (4), (6) and (7) is:
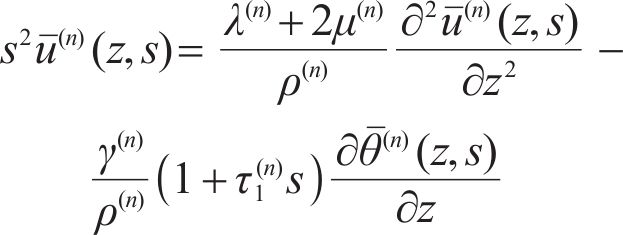
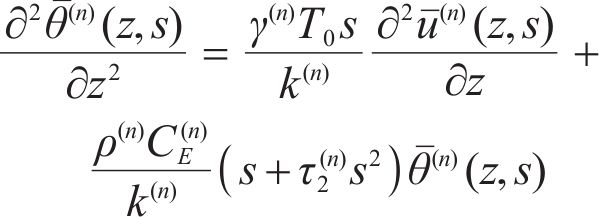
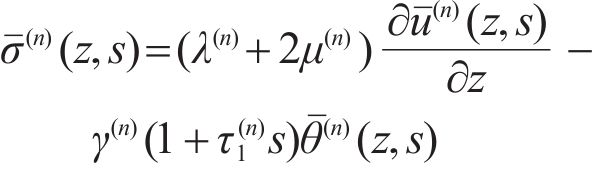
where s is Laplace transform variable; 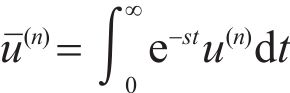
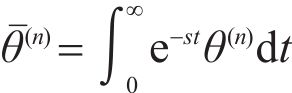
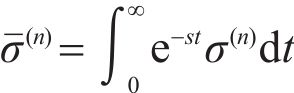
Equations (8)-(10) could be simplified as:
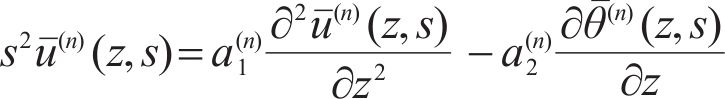
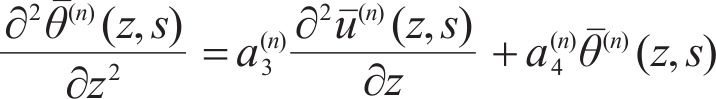
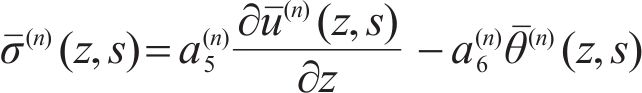
where
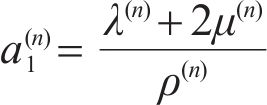
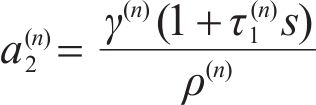
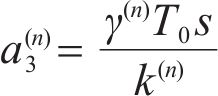
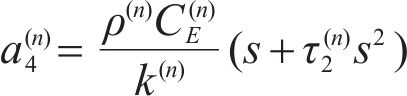
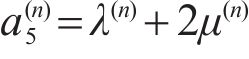
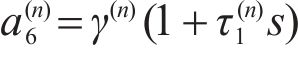
Combining Eqs. (11) and (12) and eliminating 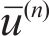
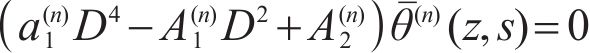
where 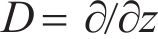
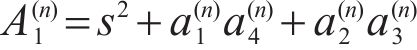
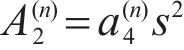
Equation (14) could be further decomposed into:
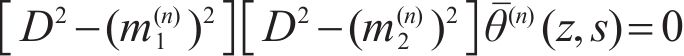
where 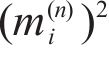
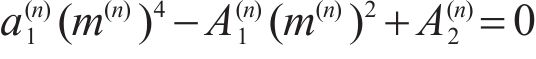
where 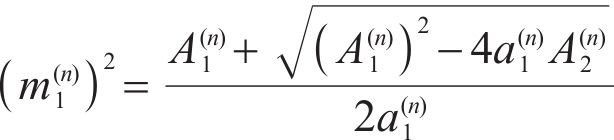
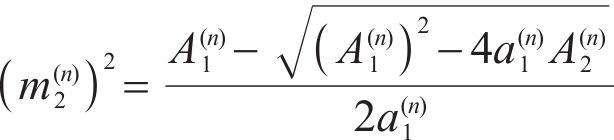
By solving Eq. (15), 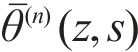
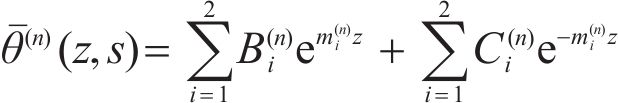
where 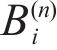
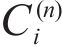
Then, 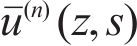
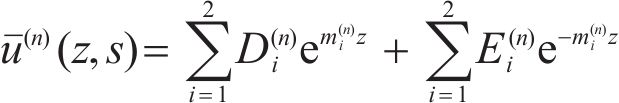
Substituting Eq. (17) and Eq. (18) into Eq. (12), the relationship of 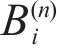
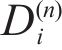
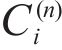
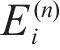
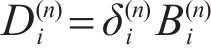
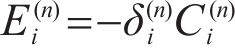
where 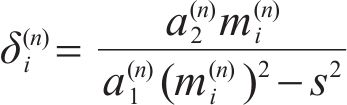
Substituting Eq. (19) and Eq. (20) into Eq. (18) produces 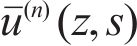
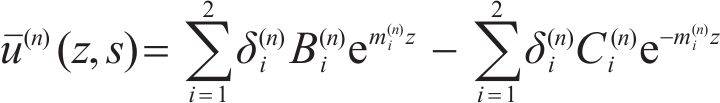
Substituting Eqs. (17) and (21) into Eq. (13) produces 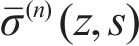
3 Solutions to governing equations
As shown in Figure 1, the following boundary conditions are given:
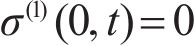
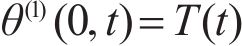
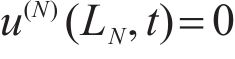
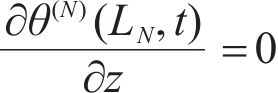
The interfacial conditions are given as:

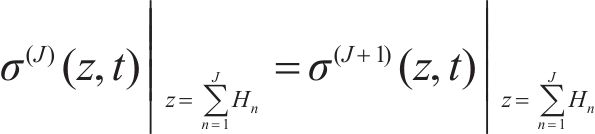
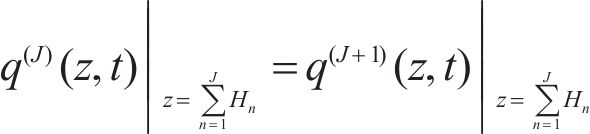
where J=1, 2, …, N-1.
When the interface of the layered structure is in complete contact, namely the temperature increment is continuous and the no thermal gradient exists at the interface, thermal energy is fully transmitted from the (N-1)th layer to the Nth layer, and the corresponding function [11, 12] is:
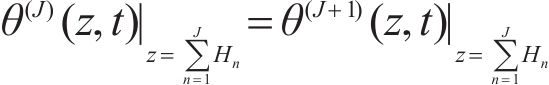
The above condition is the ideal continuous boundary condition, and the complete thermal contact model is applied by existing analytical and numerical solution to calculate the thermal response of layered composite structure.
When the interface of the layered composite structure is insulating, namely the temperature increment is discontinuous, part of the thermal wave is transmitted from the (N-1)th layer to the Nth layer, and another part is reflected to initial layer, and large thermal gradient exists at the interface, and the corresponding function [13, 15] is:
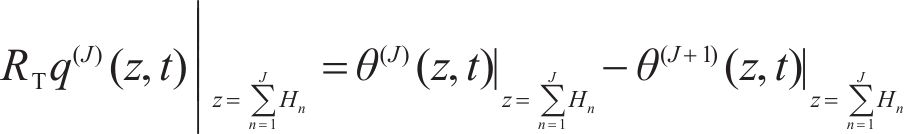
where RT is the thermal resistance coefficient, when 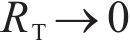
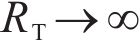
When the composite material is porous and has tiny cracks at the interface, part of the thermal wave is transmitted form the (N-1)th layer to the Nth layer, and another part is reflected to initial layer, and large thermal gradient exists at the interface, and the corresponding function [16] is:
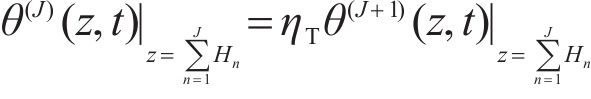
where 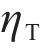
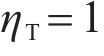
Assuming that the interface between each layer is uneven and coarse, with tiny pores filled with air. Due to the significant difference of thermal conduction coefficient between the air and contacting material, the propagation speed of thermal energy at the interface is different. When the thermal wave is transmitted from the (N-1)th layer to the interface, part of the energy is reflected to the boundary, and large thermal gradient forms at the interface. The model is applicable to layered composite materials with tiny cracks. Furthermore, it can effectively describe the impact of insulating interfaces on thermal transfer and analyze situations where there are discontinuities in temperature increments. Combining Eqs. (30b) and (30c), the general incomplete thermal contact model [17] is:
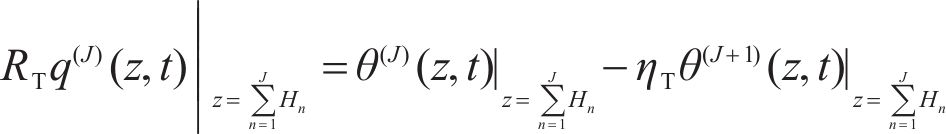
When 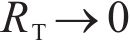
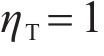
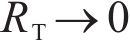
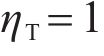
According to the Laplace transform of Eq. (23) to Eq. (30):
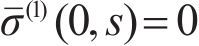
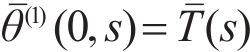
where 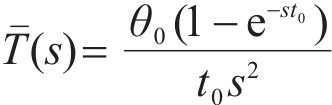
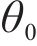
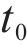
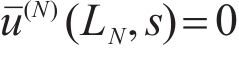
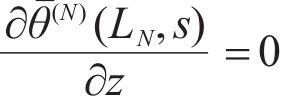
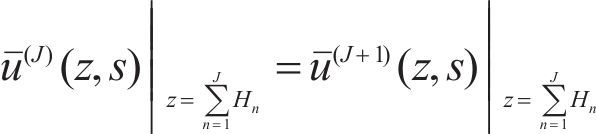
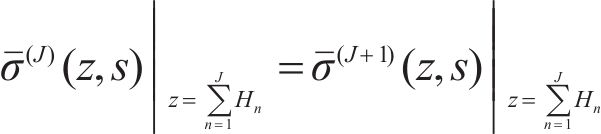
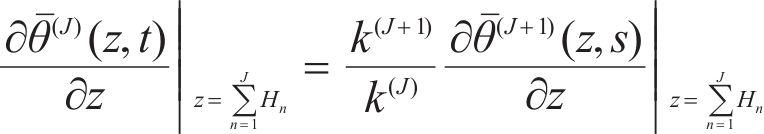
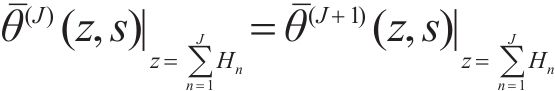
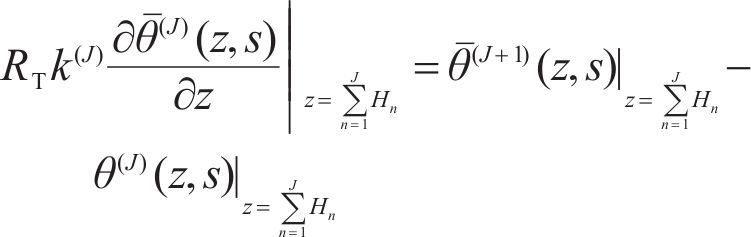
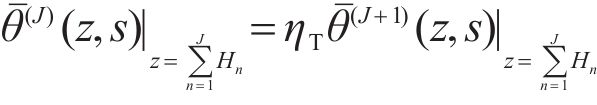
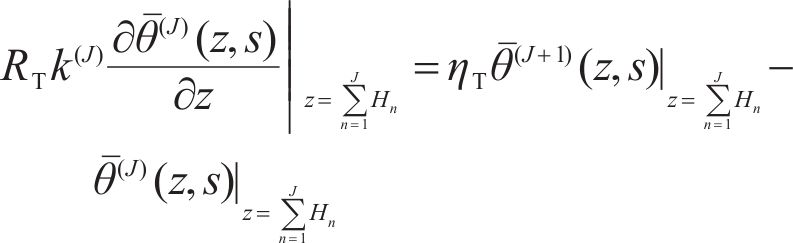
Substituting Eqs. (17), (21) and (22) into Eq. (31) to Eq. (38), the expression of undetermined parameter 
4 Numerical results and discussions
Taking the double-layered rock as an example, expression of the eight undetermined parameters, namely 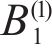
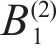
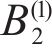
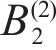
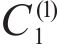
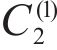
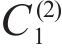
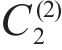
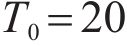
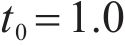
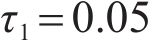
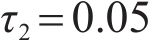
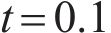
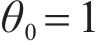
| Parameter | Value |
|---|---|
Mass density, 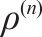 | 2320 |
Thermal conductivity, 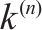 | 1.5 |
Heat capacity, 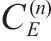 | 0.32 |
Lame’s constant, 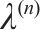 | 16.2 |
Lame’s constant,  | 9.1 |
Linear thermal expansion coefficient, 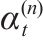 | 9×10-6 |
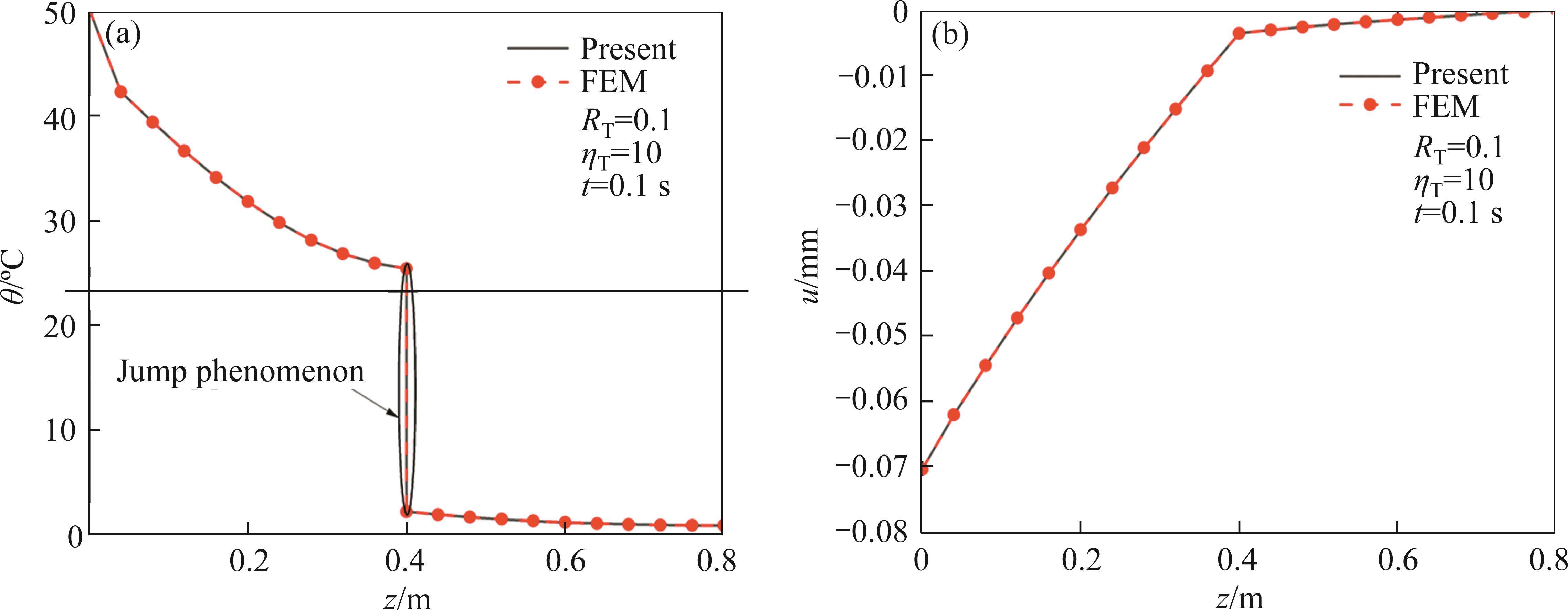
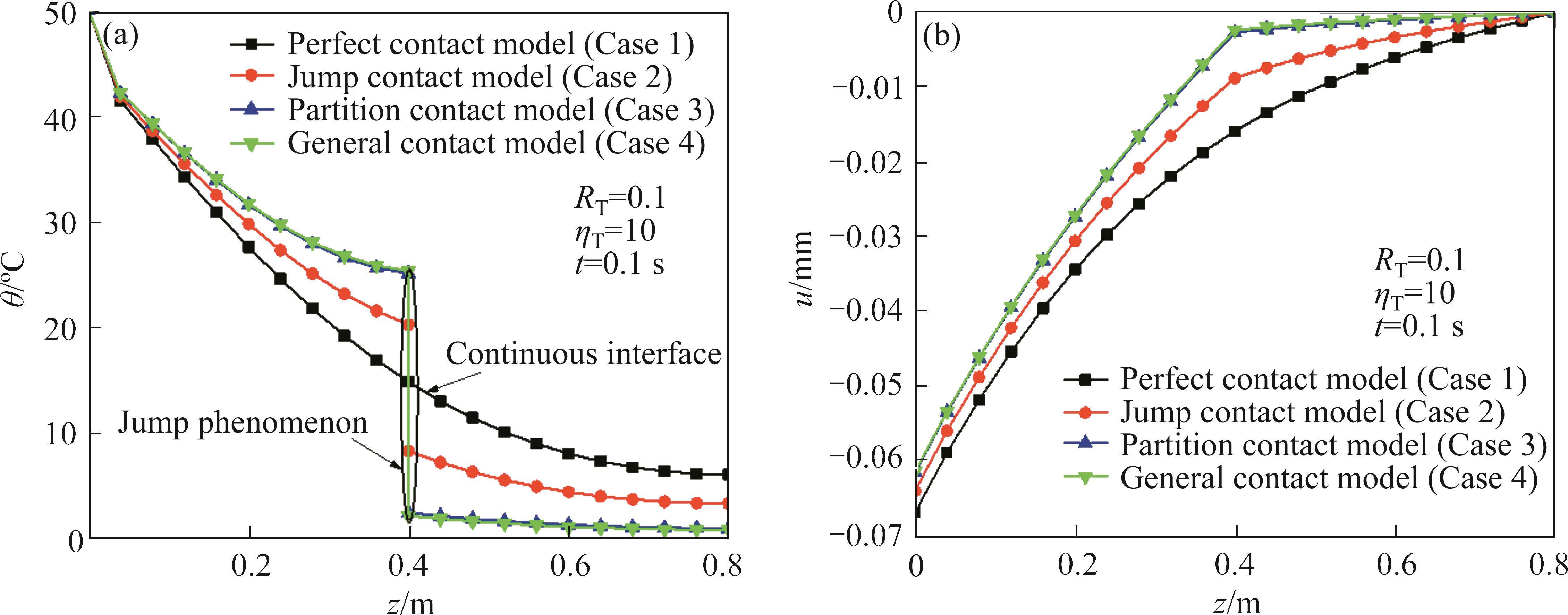
To validate the proposed model, numerical solution calculated based on finite element modelling (FEM) software COMSOL is compared with the result of the proposed model. The variation of temperature increment and displacement with depth of the double-layered rock material when RT=0.1, ηΤ=10, t=0.1 s is shown in Figure 2. It can be seen that the calculated result of the proposed method is basically consistent with the numerical result, which further proves the validity of the proposed model.
The calculation results of complete thermal contact model (Case 1), jump thermal contact model (Case 2), local thermal contact model (Case 3) and general incomplete thermal contact model (Case 4) are compared. The variance of temperature increment and displacement with depth when RT=0.1, ηΤ=10, t=0.1 s for the four thermal contact model is shown in Figure 3. As shown, the temperature increment in Case 1 is a smooth curve and decreases with increasing depth. This trend obeys the continuous boundary condition and the corresponding displacement is the largest. In Case 1, all the thermal energy is transferred to the next layer, while in Case 2, Case 3 and Case 4, jump phenomenon could be observed at the interface. This is induced by the decrease of displacement as large thermal gradient exists at the interface.
4.1 Effects of thermal resistance coefficient RT
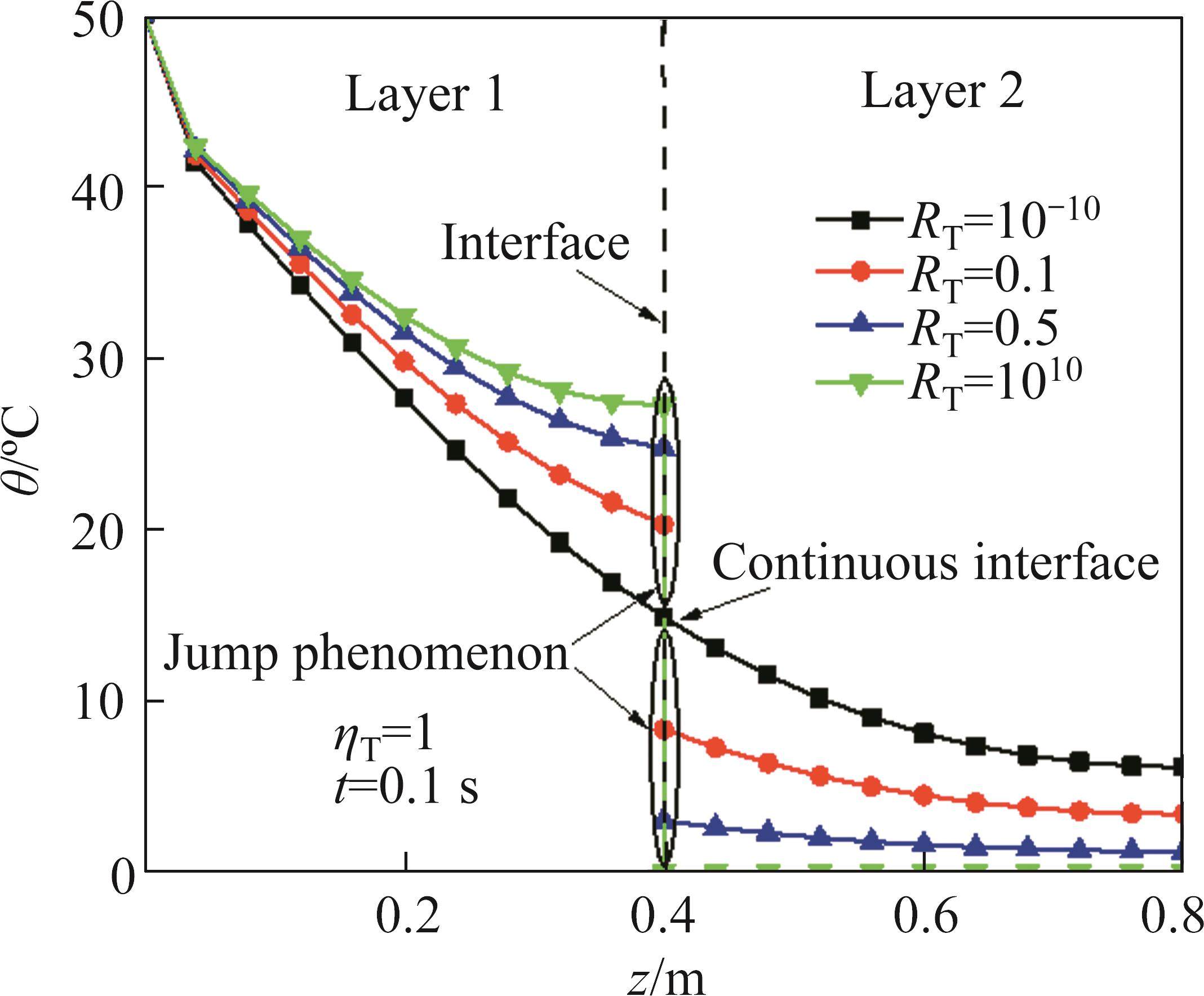
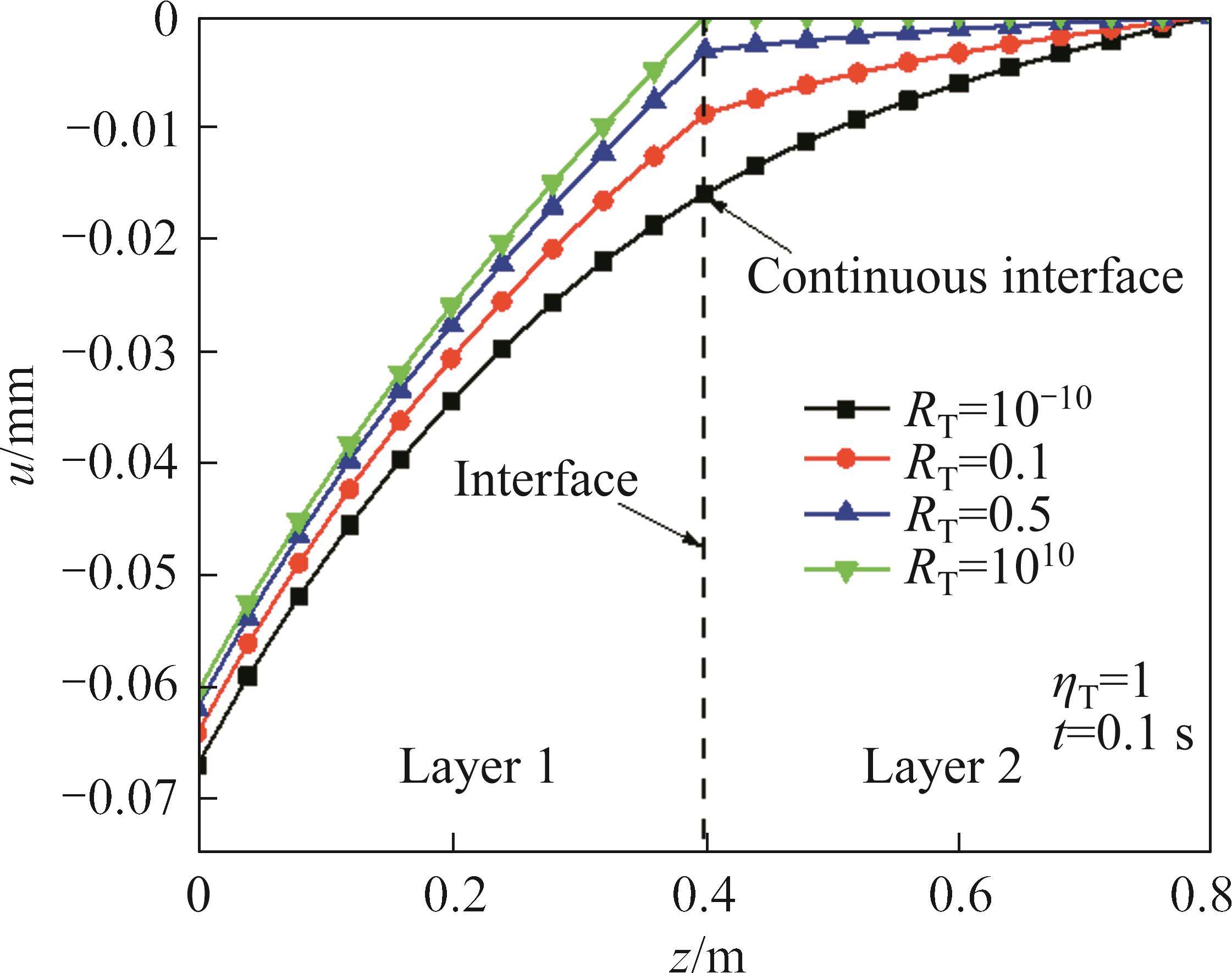
The influence of thermal resistance coefficient RT on the temperature increment and displacement at ηT=1 and t=0.1s is shown in Figures 4 and 5. As shown in Figure 4, when RT=10-10, the temperature increment curve is smooth and the boundary condition is continuous, and all the thermal energy is transferred to the next layer. With the increase of RT, the thermal resistance increases, and the jump phenomenon of temperature increment at the boundary is more obvious. At this time, part of the thermal wave is transmitted to the next layer, and part of the energy is reflected to the boundary, and large thermal gradient forms at the interface. When RT=1010, the temperature increment in the second layer is close to zero, the boundary is in the insulating condition and no thermal energy could be transferred to the second layer. At this time, the thermal gradient at the interface is the largest. As shown in Figure 5, when all the thermal wave is transferred to the second layer, the displacement is the largest. With the increase of RT, the thermal resistance increases and the displacement decreases. When the boundary is in insulating condition, the displacement in the second layer is close to zero.
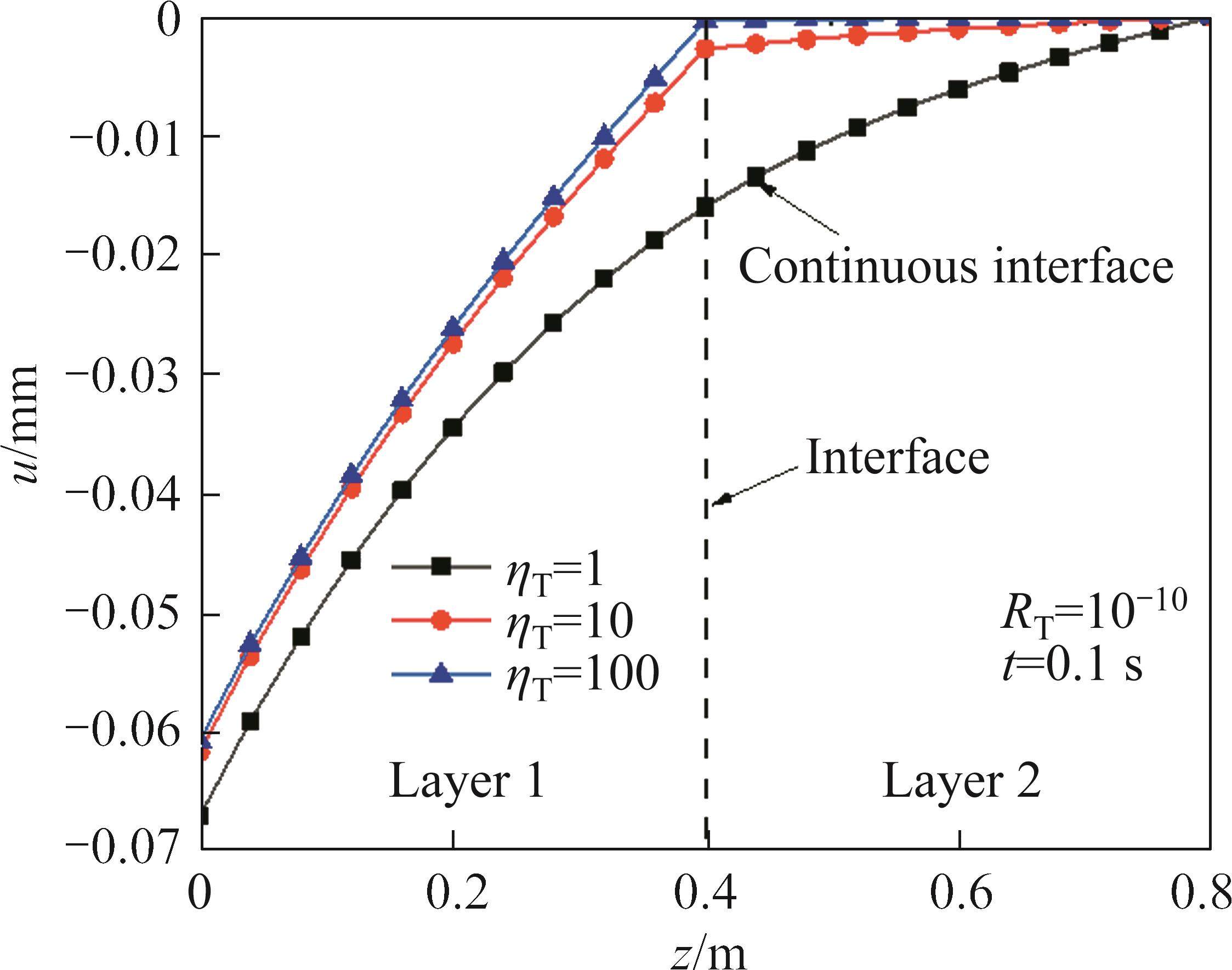
4.2 Effects of partition coefficient ηT
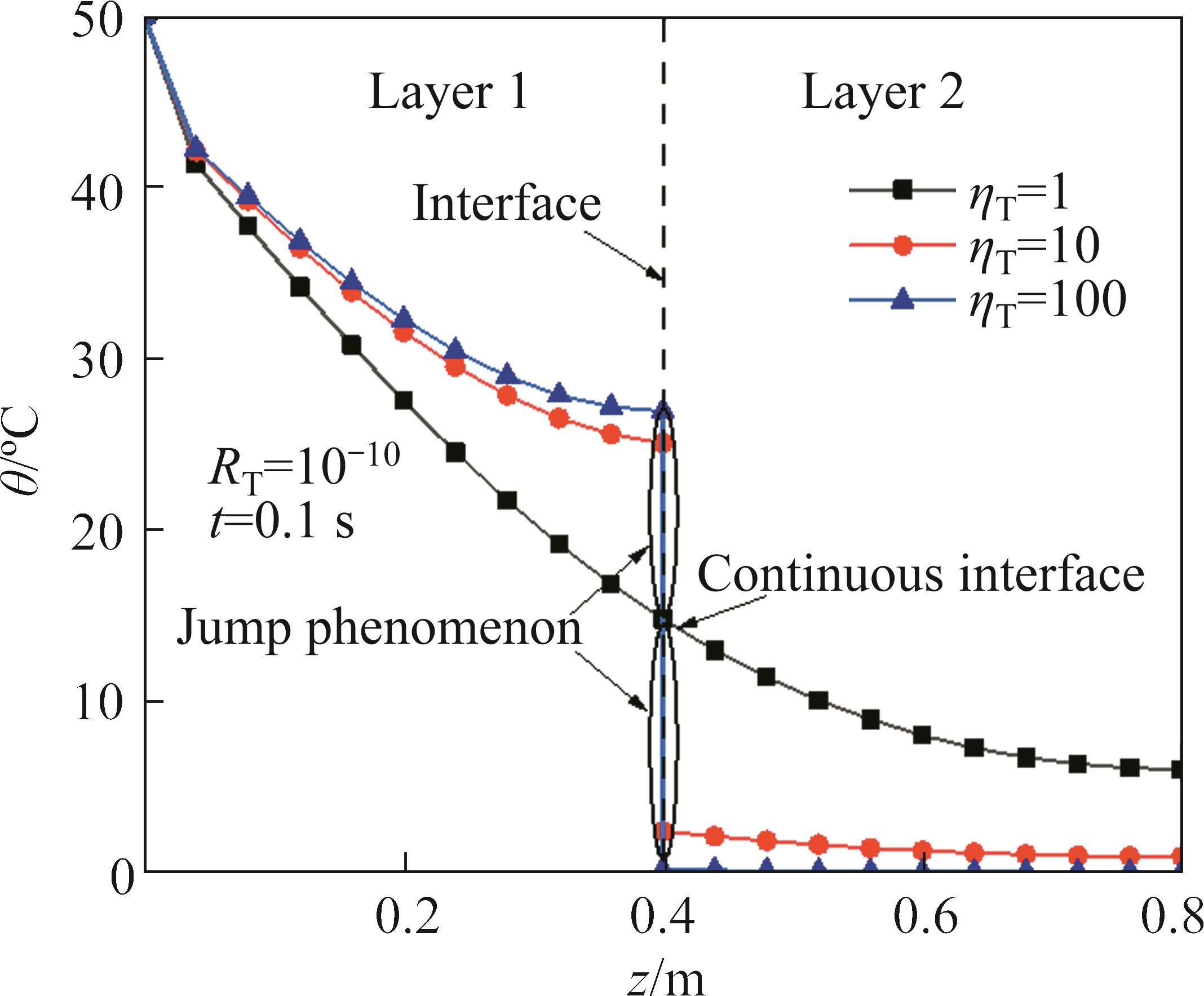
The influence of partition coefficient ηT on the temperature increment and displacement at RT=10-10 and t=0.1s is shown in Figures 6 and 7. As shown in Figure 6, when ηT=1, the temperature increment at the interface is continuous, at this time, all the thermal energy is transmitted to the second layer. With the increase of ηT, jump phenomenon of temperature increment at the interface is more obvious. When ηT=100, the temperature increment in the second layer is almost to zero and the thermal gradient at the interface is the largest. At this time, all the thermal energy is transferred to the initial layer. As shown in Figure 7, when all the thermal energy is transferred to the second layer, the displacement is the largest. With the increase of ηT, the thermal resistance increases and the displacement decreases. When the boundary is in insulating condition (ηT=100), the displacement in the second layer is close to zero.
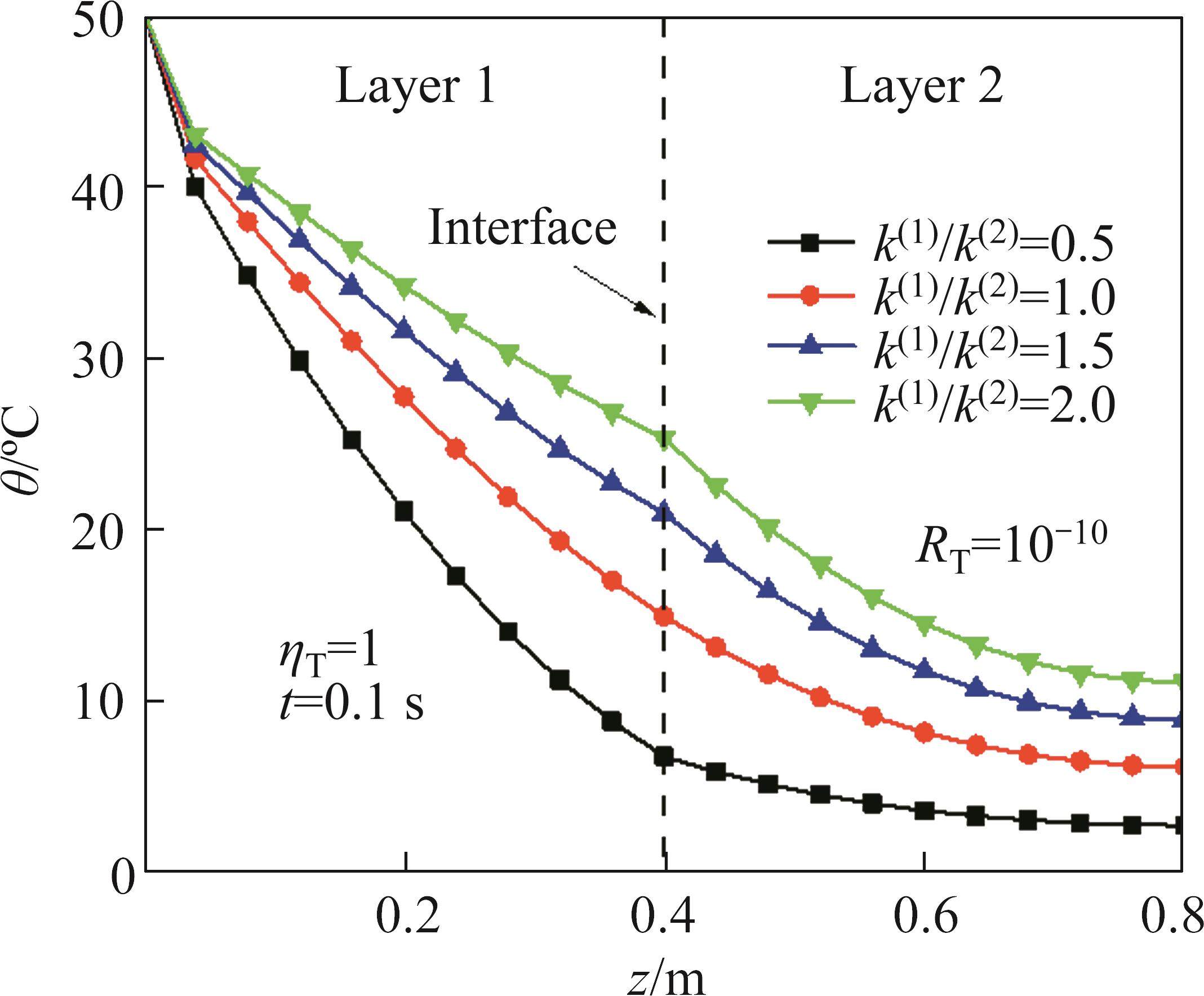
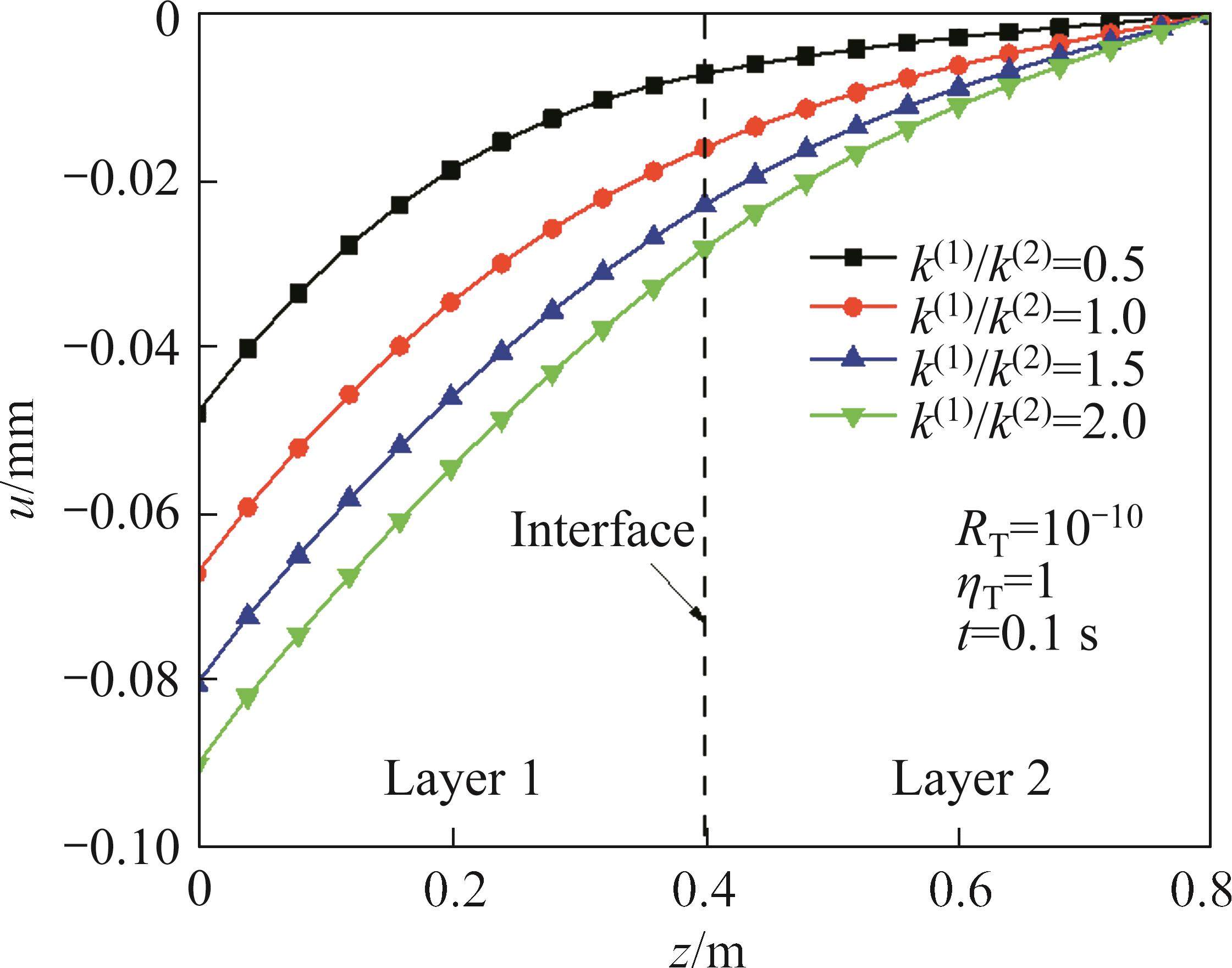
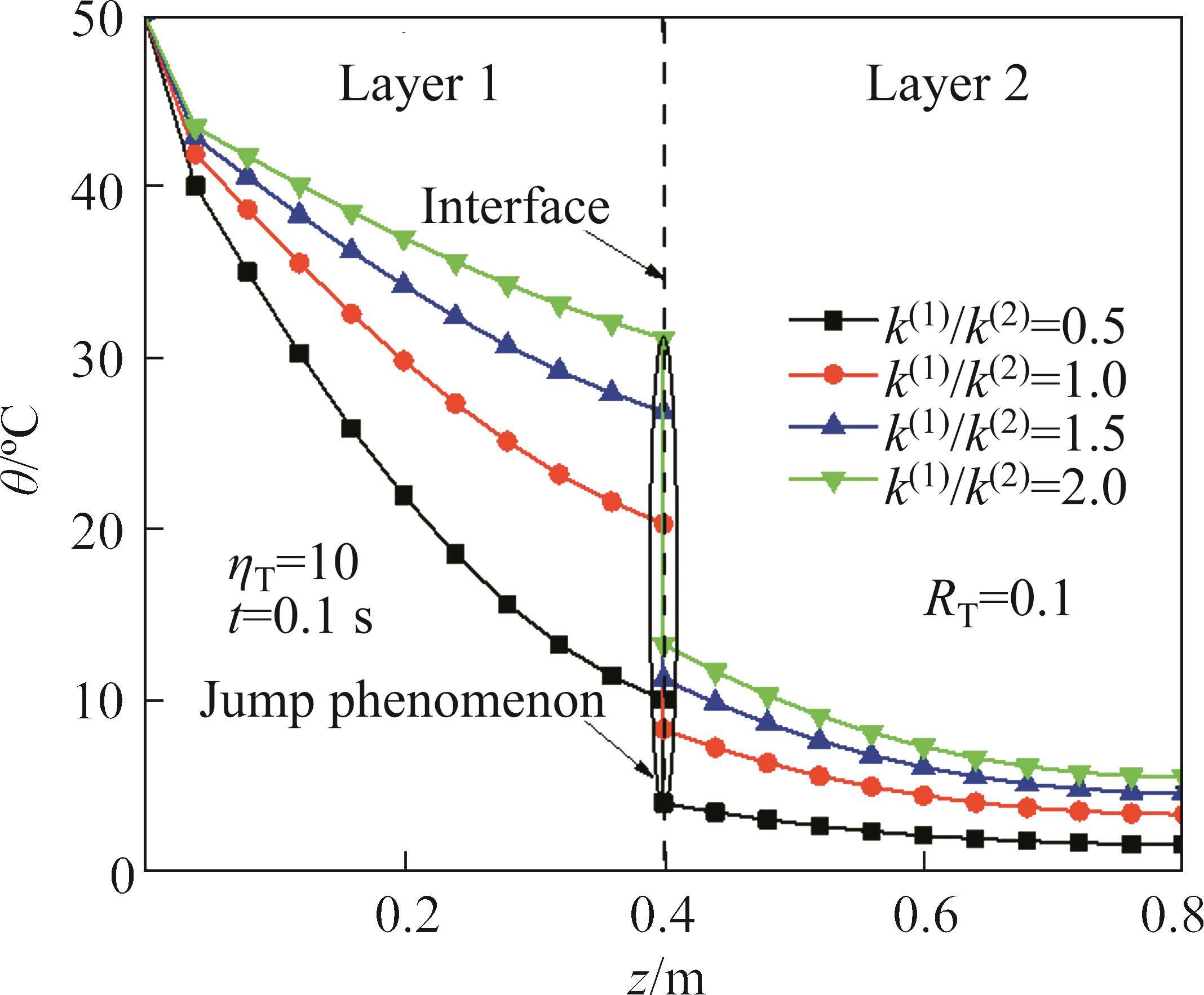
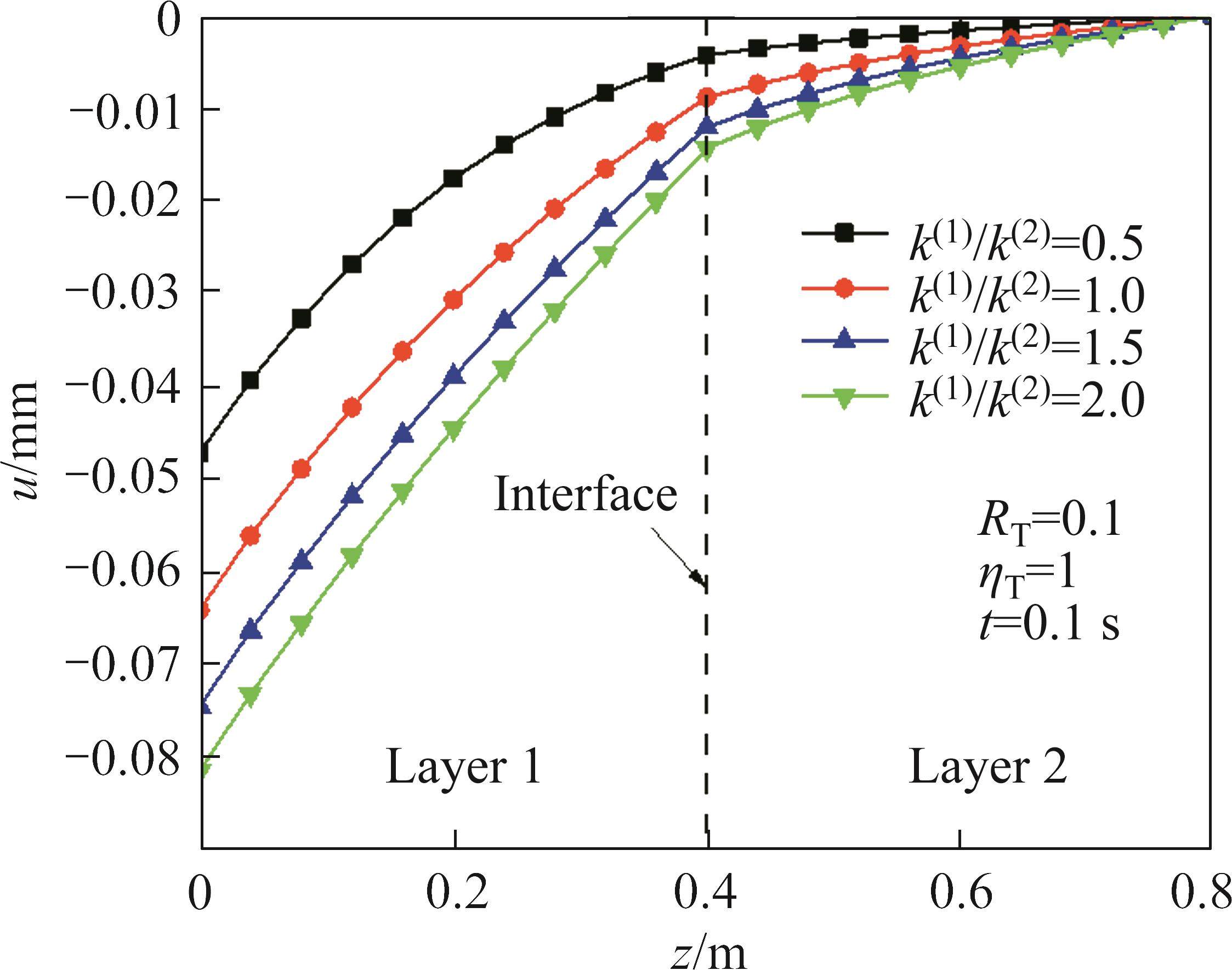
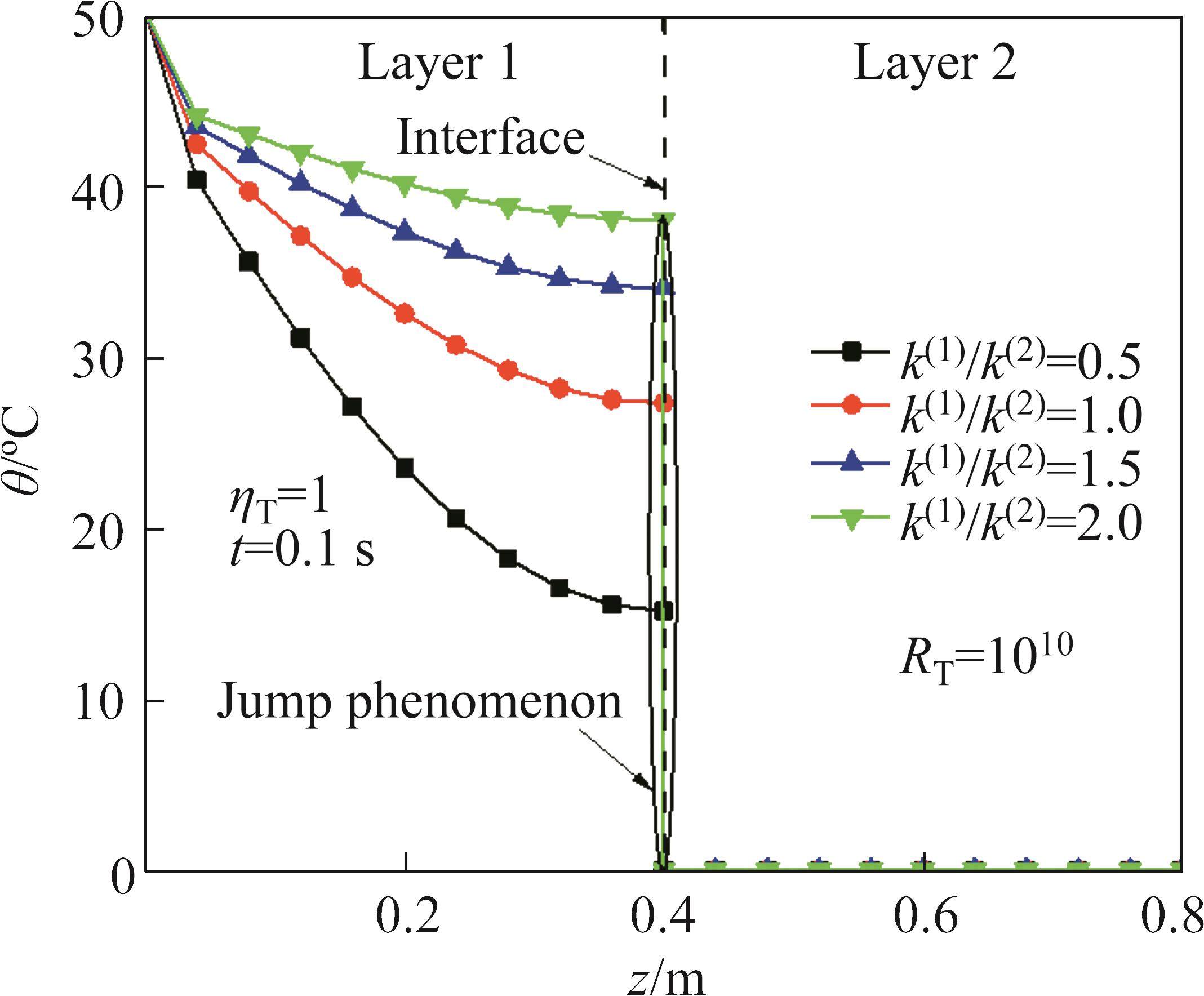
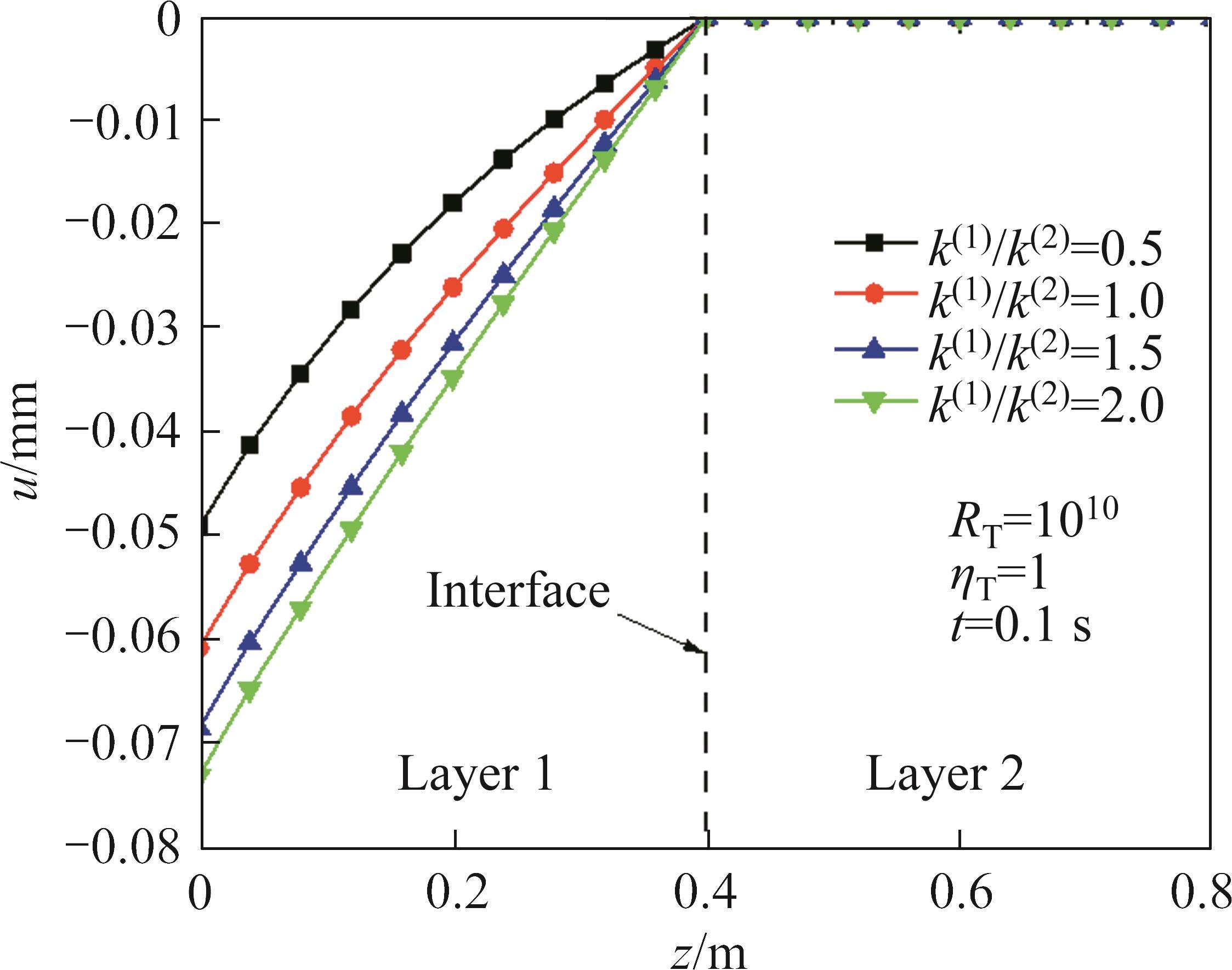
4.3 Effects of thermal conductivity ratio k(1)/k(2)
The influence of thermal conductivity ratio k(1)/k(2) on the temperature increment and displacement when RT=10-10, RT=0.1, RT=1010 and k(2)=1.5 W/(m·K) is shown in Figure 8 to Figure 13. With the increase of k(1)/k(2), the temperature increment and displacement increase. This is because the speed of thermal transfer increases as the k(1)/k(2) increases. Also, the influence of thermal conductivity ratio k(1)/k(2) on the temperature increment and displacement is related to the magnitude of RT. When thermal resistance exists at the interface, the thermal gradient increases with the increase of thermal conductivity ratio k(1)/k(2) and with increasing thermal coefficient, the thermal gradient at the interface increases. It can be seen that the influence of thermal contact resistance on the temperature increment and displacement is related to the propagation speed of thermal wave.
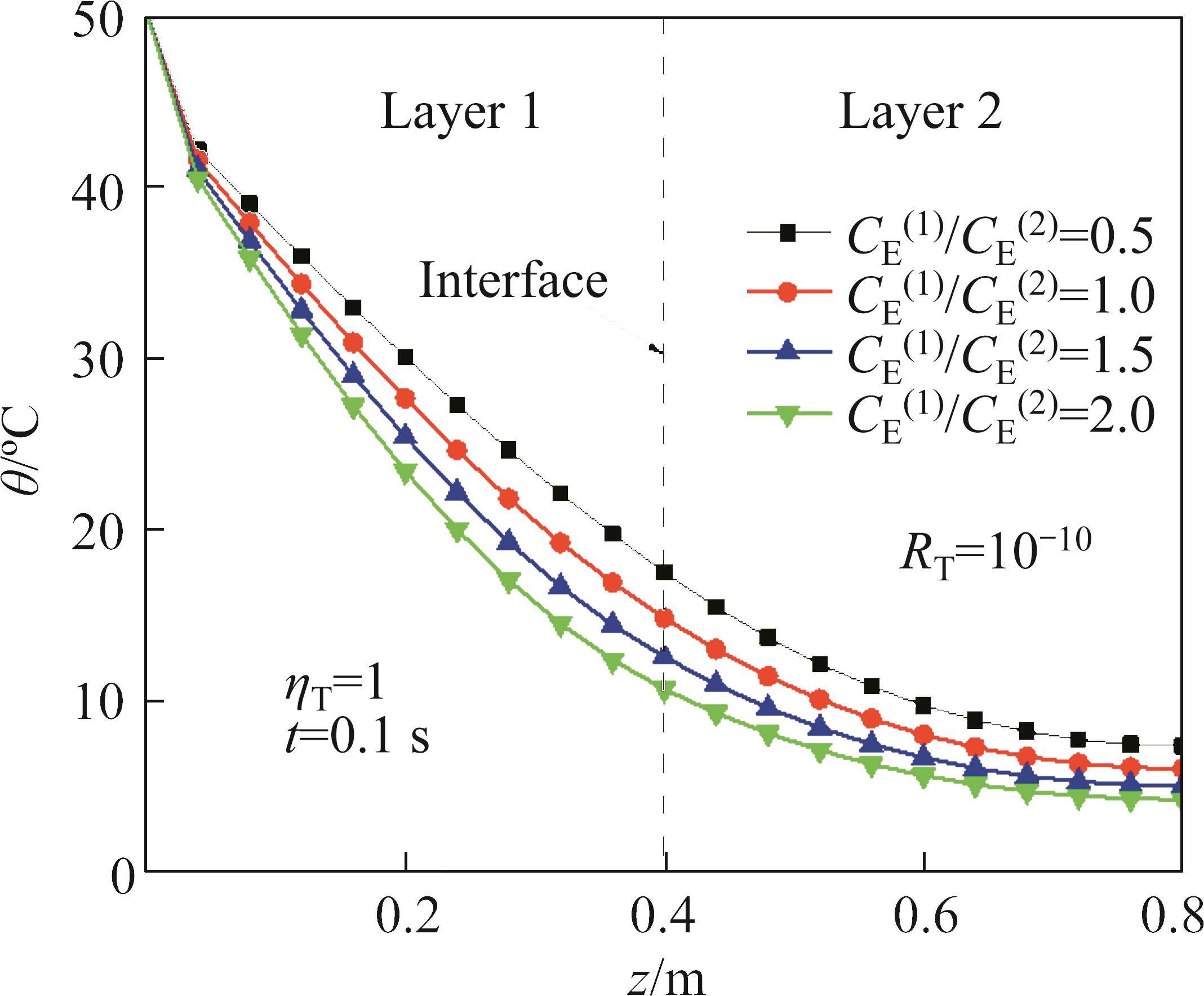
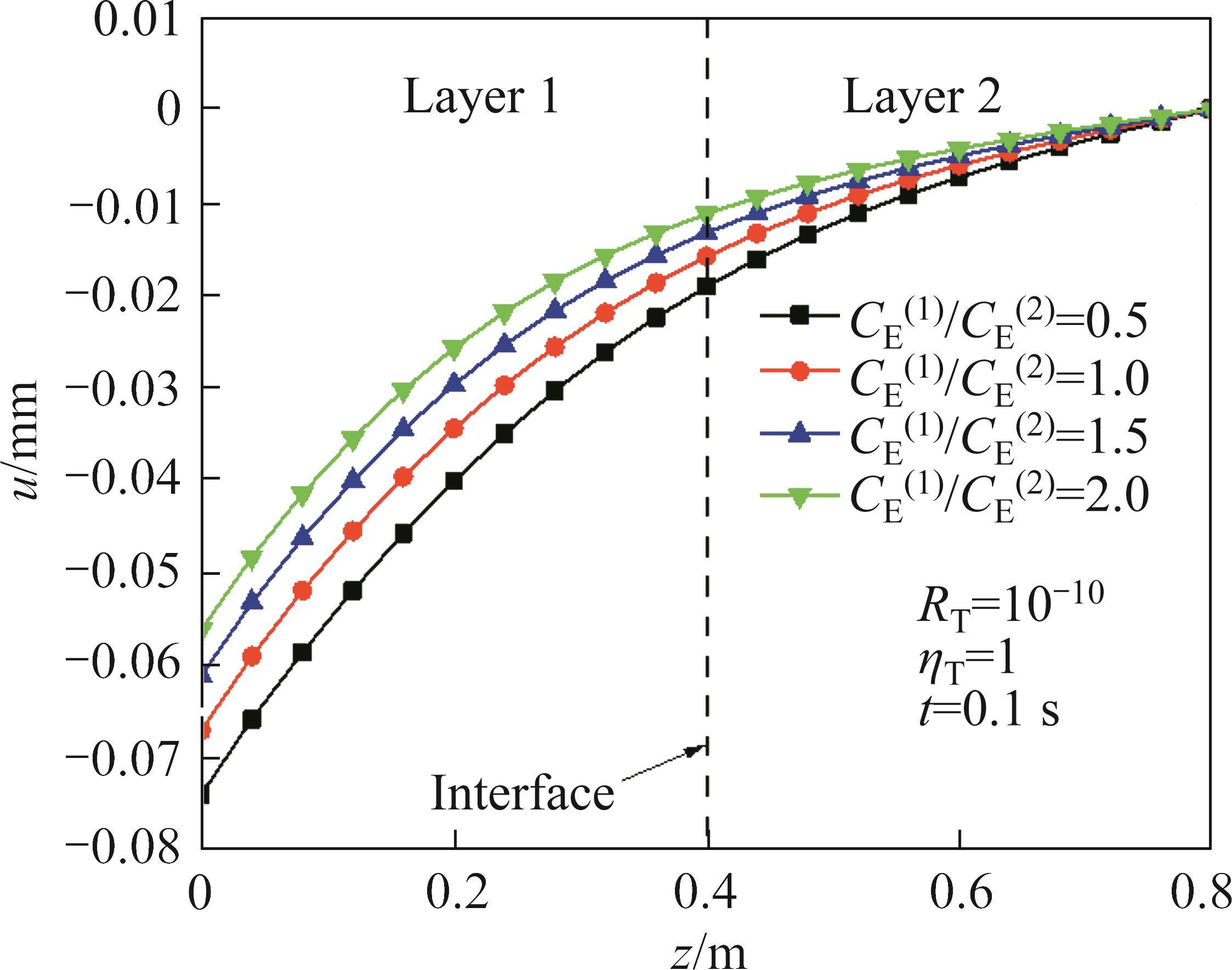
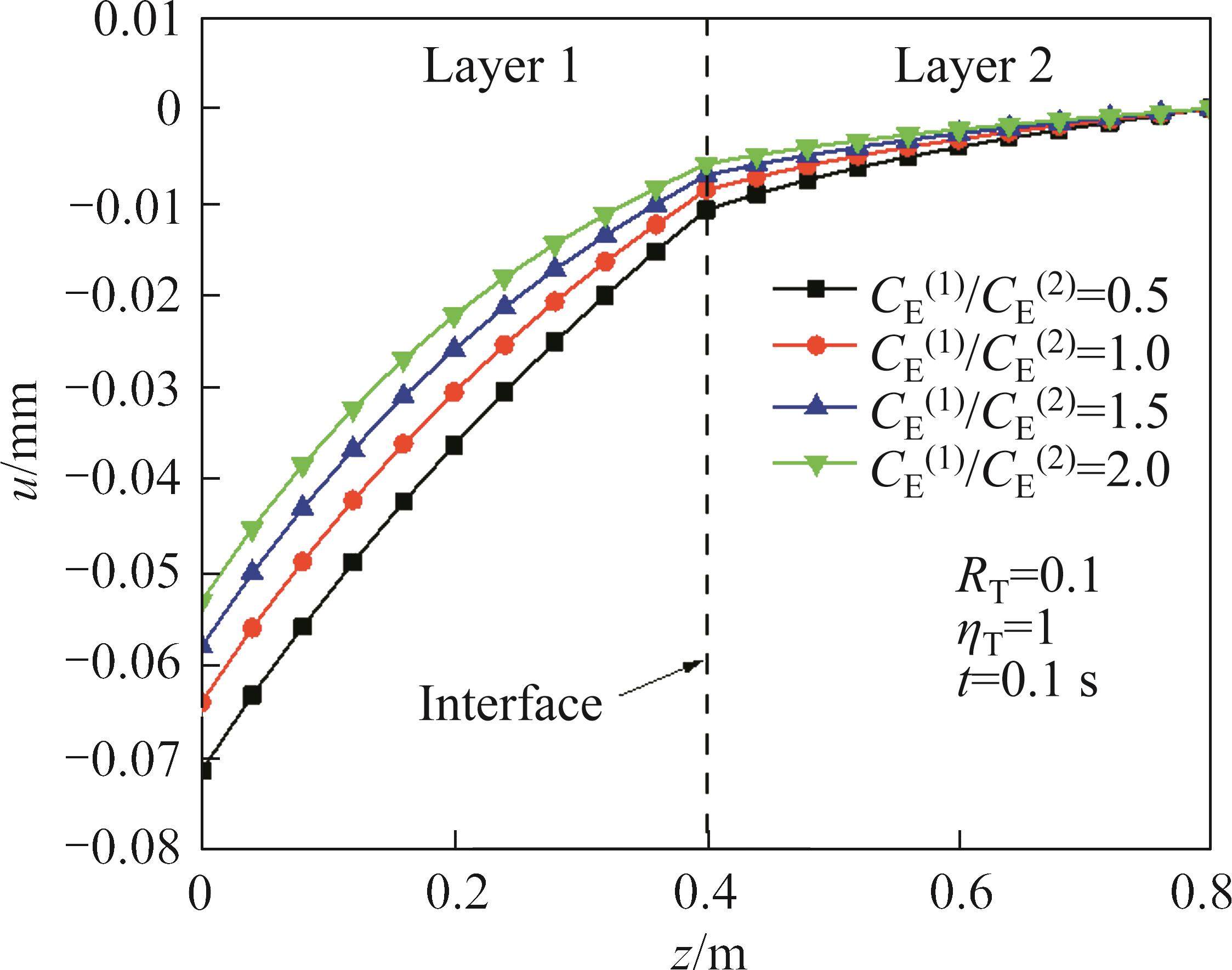
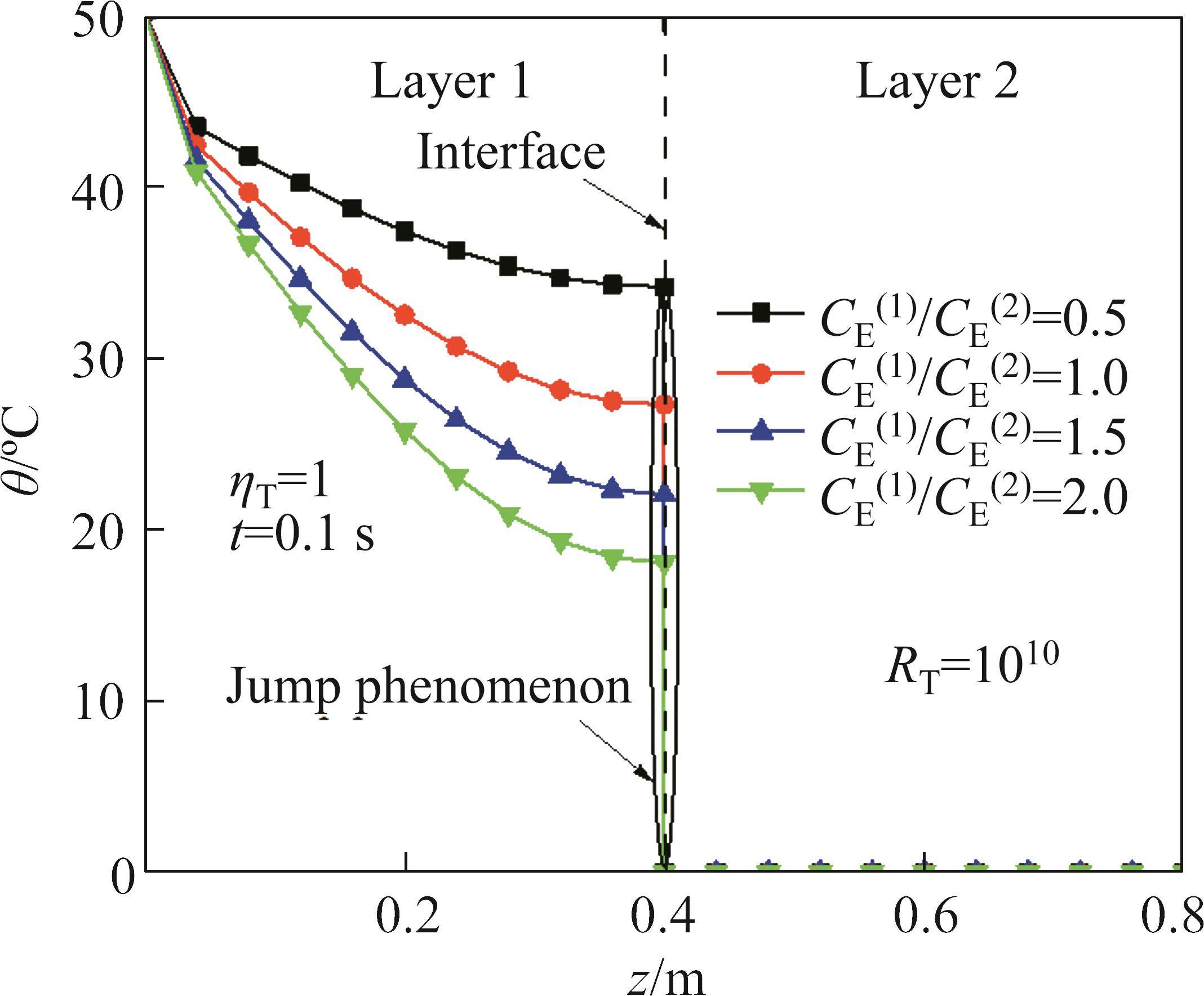
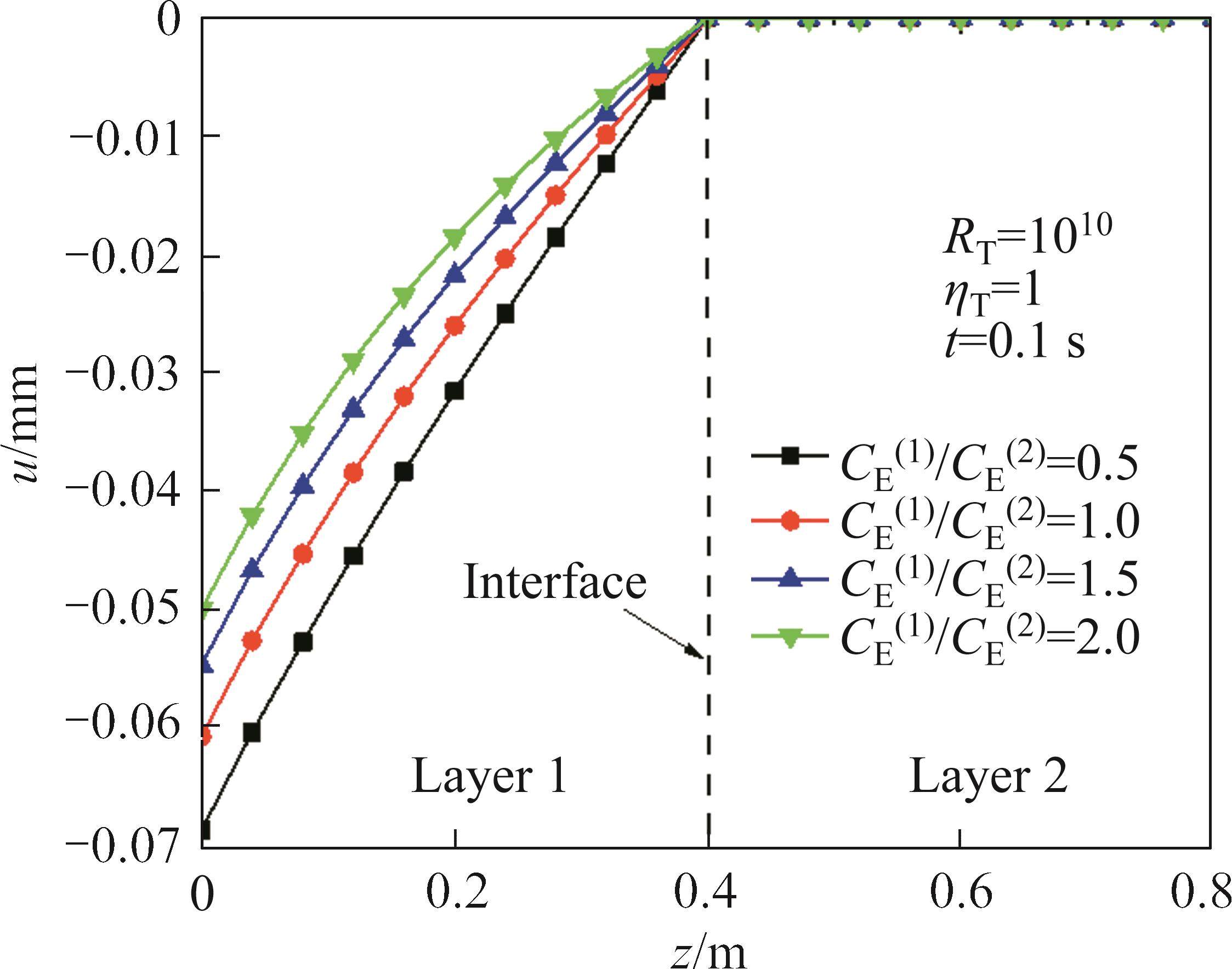
4.4 Effects of heat capacity ratio CE(1)/CE(2)
The influence of heat capacity ratio CE(1)/CE(2) on the temperature increment and displacement when RT=10-10,RT=0.1, RT=1010 and CE(2)= 0.32 J/(kg·K) is shown in Figure 14 to Figure 19. With the increase of CE(1)/CE(2), the temperature increment and displacement decrease. When thermal resistance exists at the interface, the thermal gradient decreases with the increase of CE(1)/CE(2), and the thermal gradient at the interface decreases with the increase of thermal resistance coefficient. It can be seen that the influence of heat capacity ratio CE(1)/CE(2) on the temperature increment and displacement is related to the thermal resistance coefficient RT.
5 Conclusions
In this paper, the instant response of layered composite structure under thermal load is studied. The general incomplete thermal contact model is proposed to predict the thermal resistance at the interface of layered composite structure. Based on GL thermal elastic theory, Laplace transform is applied to obtain the semi-analytical solution of temperature increment and displacement of the layered composite structure. The influence of thermal resistance coefficient, local coefficient, thermal conductivity ratio, heat capacity ratio on the dynamic response is analyzed. The main conclusions are as follows:
1) The general incomplete thermal contact model could be used to estimate the thermal contact resistance at the interface of layered composite structure; by adjusting the thermal resistance coefficient and local transfer coefficient, the proposed model could be degraded into three other thermal contact model.
2) With the increase of thermal resistance coefficient and local transfer coefficient, thermal resistance at the interface of the composite structure increases, the thermal gradient at the interface is more obvious and the displacement decreases.
3) With the increase of thermal conductivity ratio k(1)/k(2), the temperature increment and displacement increase; and the influence of thermal contact resistance on the temperature increment and displacement is related to the propagation speed of thermal wave.
4) With the increases of heat capacity ratio CE(1)/CE(2), the temperature increment and displacement decrease; the influence of heat capacity ratio CE(1)/CE(2) on the temperature increment and displacement is related to the thermal resistance coefficient RT.
A new model and analytical solutions for borehole and pile ground heat exchangers
[J]. International Journal of Heat and Mass Transfer, 2010, 53(13-14): 2593-2601. DOI: 10.1016/j.ijheatmasstransfer.2010.03.001.A review of transport mechanisms and models for unconventional tight shale gas reservoir systems
[J]. International Journal of Heat and Mass Transfer, 2021, 175: 121125. DOI: 10.1016/j.ijheatmasstransfer.2021.121125.Simultaneous features of soret and dufour in entropy optimized flow of Reiner-rivlin fluid considering thermal radiation
[J]. International Communications in Heat and Mass Transfer, 2022, 137: 106297. DOI: 10.1016/j.icheatmasstransfer.2022.106297.MHD fluid flow and heat transfer due to a shrinking rotating disk
[J]. Computers & Fluids, 2014, 90: 51-56. DOI: 10.1016/j.compfluid.2013.11.005.Lagrangian coupling two-phase flow model to simulate current-induced scour beneath marine pipelines
[J]. Applied Ocean Research, 2012, 38: 64-73. DOI: 10.1016/j.apor.2012.07.002.Heat transfer model of miniature heat pipe embedded in marine cabinet
[J]. Journal of Coastal Research, 2019, 97(sp1): 103. DOI: 10.2112/si97-014.1.Heat-transfer characteristics of subsea pipelines embedded in multilayered soils
[J]. SPE Journal, 2020, 25(3): 1128-1139. DOI: 10. 2118/199353-pa.Thermoelasticity and irreversible thermodynamics
[J]. Journal of Applied Physics, 1956, 27(3): 240-253. DOI: 10.1063/1.1722351.A generalized dynamical theory of thermoelasticity
[J]. Journal of the Mechanics and Physics of Solids, 1967, 15: 299-309. DOI: 10.1016/0022-5096(67)90024-5.Wave propagation due to impact through layered polymer composites
[J]. Composite Structures, 2014, 115: 1-11. DOI: 10.1016/j.compstruct.2014.03.037.Thermoelasticity
[J]. Journal of Elasticity, 1972, 2(1): 1-7. DOI: 10.1007/BF00045689.Thermoelasticity without energy dissipation
[J]. Journal of Elasticity, 1993, 31(3): 189-208. DOI: 10.1007/BF00044969.Buckling of nanobeams under nonuniform temperature based on nonlocal thermoelasticity
[J]. Composite Structures, 2016, 146: 108-113. DOI: 10.1016/j.compstruct.2016.03.014.Effects of two-temperature parameter and thermal nonlocal parameter on transient responses of a half-space subjected to ramp-type heating
[J]. Waves in Random and Complex Media, 2017, 27(3): 440-457. DOI: 10.1080/17455030.2016.1262974.Size-dependent thermoelasticity of a finite bi-layered nanoscale plate based on nonlocal dual-phase-lag heat conduction and Eringen’s nonlocal elasticity
[J]. Applied Mathematics and Mechanics, 2021, 42(1): 1-16. DOI: 10.1007/s10483-021-2692-5.Fractional order thermoelastic interactions in an infinite porous material due to distributed time-dependent heat sources
[J]. Meccanica, 2015, 50(8): 2167-2178. DOI: 10.1007/s11012-015-0152-x.Effect of variable thermal conductivity on a half-space under the fractional order theory of thermoelasticity
[J]. International Journal of Mechanical Sciences, 2013, 74: 185-189. DOI: 10.1016/j.ijmecsci.2013.05.016.A one-dimensional fractional order thermoelastic problem for a spherical cavity
[J]. Mathematics and Mechanics of Solids, 2015, 20(5): 512-521. DOI: 10.1177/1081286513505585.Thermal shock problem of a generalized thermoelastic layered composite material with variable thermal conductivity
[J]. Mathematical Problems in Engineering, 2006(1):Generalized thermoelastic analysis of layer interface excited by pulsed laser heating
[J]. Engineering Analysis with Boundary Elements, 2003, 27(9): 863-869. DOI: 10. 1016/S0955-7997(03)00069-9.Guided thermoelastic wave propagation in layered plates without energy dissipation
[J]. Acta Mechanica Solida Sinica, 2011, 24(2): 135-143. DOI: 10.1016/S0894-9166(11)60015-3.Thermal shock problem for one dimensional generalized thermoelastic layered composite material
[J]. Mathematical and Computational Applications, 2006, 11(2): 103-110. DOI: 10.3390/mca11020103.Exact analytical solution of unsteady axi-symmetric conductive heat transfer in cylindrical orthotropic composite laminates
[J]. International Journal of Heat and Mass Transfer, 2012, 55(15, 16): 4427-4436. DOI: 10.1016/j.ijheatmasstransfer. 2012.04.012.Heat conduction in one-dimensional functionally graded media based on the dual-phase-lag theory
[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2013, 227(4): 744-759. DOI: 10.1177/0954406212456651.Fractional model of thermoelasticity for a half-space overlaid by a thick layer
[J]. ZAMM - Journal of Applied Mathematics and Mechanics/Zeitschrift Für Angewandte Mathematik und Mechanik, 2015, 95(5): 511-518. DOI: 10.1002/zamm.201300174.Remarkably reduced thermal contact resistance of graphene/olefin block copolymer/paraffin form stable phase change thermal interface material
[J]. International Journal of Heat and Mass Transfer, 2020, 163: 120393. DOI: 10.1016/j.ijheatmasstransfer.2020.120393.Four decades of research on thermal contact, gap, and joint resistance in microelectronics
[J]. IEEE Transactions on Components and Packaging Technologies, 2005, 28(2): 182-206. DOI: 10.1109/TCAPT. 2005.848483.Effective thermal conductivity of granular porous materials
[J]. International Communications in Heat and Mass Transfer, 1996, 23(2): 169-176. DOI: 10.1016/0735-1933(96)00003-6.A theoretical model for effective thermal conductivity (ETC) of particulate beds under compression
[J]. Granular Matter, 2004, 6(2): 121-129. DOI: 10.1007/s10035-004-0170-1.A multiscale model of thermal contact resistance between rough surfaces
[J]. Journal of Heat Transfer, 2008, 130(8): 1. DOI: 10.1115/1.2927403.Engineered granular materials for heat conduction and load transfer in energy geotechnology
[J]. Géotechnique Letters, 2014, 4(2): 145-150. DOI: 10.1680/geolett.14.00001.Experimental measurements and theoretical predictions of the thermal conductivity of two phases glass beads
[J]. International Communications in Heat and Mass Transfer, 2001, 28(8): 1091-1102. DOI: 10.1016/S0735-1933(01)00312-8.Thermal conductivity of binary sand mixtures evaluated through full water content range
[J]. Soil Science Society of America Journal, 2016, 80: 592-603. DOI: 10.2136/SSSAJ2015. 11.0408.Heat conduction across a solid-solid interface: Understanding nanoscale interfacial effects on thermal resistance
[J]. 2011, 99(1):Thermal resistance of two solids in contact through a cylindrical joint
[J]. International Journal of Heat and Mass Transfer, 1998, 41(13): 2013-2024. DOI: 10.1016/s0017-9310(97)00259-7.Thermal constriction resistance: Effects of boundary conditions and contact geometries
[J]. International Journal of Heat and Mass Transfer, 1992, 35(6): 1533-1544. DOI: 10.1016/0017-9310(92)90043-r.Transient responses of bi-layered structure based on generalized thermoelasticity: Interfacial conditions
[J]. International Journal of Mechanical Sciences, 2015, 99: 179-186. DOI: 10.1016/j.ijmecsci.2015.05.016.Application of fractional order theory of thermoelasticity to a bilayered structure with interfacial conditions
[J]. Journal of Thermal Stresses, 2016, 39(9): 1017-1034. DOI: 10.1080/01495739. 2016.1192451.Modelling the effect of temperature and damage on the fracture strength of ultra-high temperature ceramics
[J]. International Journal of Fracture, 2012, 176(2): 181-188. DOI: 10.1007/s10704-012-9743-x.Effect of the cooling medium temperature on the thermal shock resistance of ceramic materials
[J]. Materials Letters, 2015, 138: 216-218. DOI: 10.1016/j.matlet.2014.09.137.Effect of interface thermal resistance on heat transfer in a composite medium using the thermal wave model
[J]. International Journal of Heat and Mass Transfer, 2000, 43(5): 653-663. DOI: 10.1016/S0017-9310(99)00178-7.Transient responses of multi-layered structures with interfacial conditions in the generalized thermoelastic diffusion theory
[J]. International Journal of Mechanical Sciences, 2017, 131: 63-74. DOI: 10.1016/j.ijmecsci.2017.05.054.Dynamic response of bilayered saturated porous media based on fractional thermoelastic theory
[J]. Journal of Zhejiang University: Science A, 2021, 22(12): 992-1004. DOI: 10. 1631/jzus.A2100084.Influence of thermal contact resistance on dynamic response of bilayered saturated porous strata
[J]. Journal of Central South University, 2022, 29(6): 1823-1839. DOI: 10.1007/s11771-022-5053-2.Semi-analytical solution of multilayer diffusion problems with time-varying boundary conditions and general interface conditions
[J]. Applied Mathematics and Computation, 2018, 333: 286-303. DOI: 10.1016/j.amc.2018.03.095.Numerical inversion of Laplace transforms using a Fourier series approximation
[J]. Journal of the ACM, 1976, 23(1): 89-96. DOI: 10.1145/321921.321931.WEN Min-jie, XIE Jia-hao, LI Li-chen, TIAN Yi, EL NAGGAR M. Hesham, MEI Guo-xiong, WU Wen-bing. An improved model for predicting thermal contact resistance at multi-layered rock interface [J]. Journal of Central South University, 2025, 32(1): 229-243. DOI: https://doi.org/10.1007/s11771-025-5865-y.
闻敏杰,谢家豪,李立辰等.预测多层岩石界面接触热阻的改进模型[J].中南大学学报(英文版),2025,32(1):229-243.

