我国轨道交通装备服役环境复杂,铁路裸露在户外或潮湿的隧道内,此类环境下液态水容易附着在轨道表面,其上的水介质会使黏着特性恶化导致制动和牵引力不足[1]。轨道表面的水膜可使黏着系数降低50%以上,轮轨间低黏着现象会降低列车安全性,导致列车晚点以及轨面擦伤等各种问题。我国地铁制动通常采用电制动和机械制动2种方式,在潮湿的地铁隧道中,轨道上的水膜会严重降低轮轨之间的黏着特性,导致牵引力和制动力的下降,从而导致地铁进站时车门与屏蔽门之间无法对齐,导致下一趟地铁延误,影响地铁的正常运行。轨道交通的高速化、轻量化发展对水介质下黏着特性的提升需求迫切,轮轨接触状态突然恶化时需采用增黏剂来提升轮轨黏着系数,撒砂是最常见的方法[2]。但撒砂对轮轨的损伤不可忽视[3]。超音速喷管用于灰尘和雪的清扫的应用与研究已有报道,但尚未用于轨道表面水膜的清扫。水膜吹除过程实际是高速气流与水膜间的相互作用,其在飞机结冰领域出现较多。檀妹静[4]对飞机在飞行过程中冰上水滴流动进行了研究,对于水膜模型的建立进行了详细的阐述。菅锦锦等[5]基于冰层表面薄水膜的功平衡分析方法,建立了角状冰表面水膜吹离的数学模型,并进行仿真,利用静止圆柱表面积冰模拟结果与实验结果对比,对该模型进行了验证,其使用的是“基于韦伯数的吹离/甩脱判据”,即当Wea>2时水膜吹离,对其进行变换得到临界水膜厚度,粗糙表面的水膜与不考虑粗糙度的表面水膜吹离速度不同,但本质都是气流剪切作用下的水膜运动,宏观的水膜吹除也符合此特征。拉瓦尔喷管几何是形成超音速流的关键,喷管前半段由大变小逐渐收缩至喉部,被称为收缩段,之后又由小变大向外扩张,被称为扩张段,气体受高压流入喷嘴收缩段,穿过窄喉后从扩张段逸出,因流道截面积的变化,从亚音速逐渐被加速至超音速[6]。喷管的性能与喷管出口速度、射流密度及喷管结构有关[7-8],喷管的出口速度和射流速度一般由其用途决定,设计过程中主要通过优化喷管的结构提升其性能。国内外学者为改善喷管的流场品质进行了大量的研究,喷管由收缩段和扩张段组成,气体在喷管中的流动直接受喷管型线的影响,其中又以扩张段的影响最大[9]。与直线型喷管相比,曲线型喷管出口处各项气流参数的均匀性都有明显的优势,基于特征线理论(Method of Characteristic, MOC)设计的曲线型喷管可减小喷管内部的机械能损失并优化喷管出口流场品质,提高工业生产工艺技术的效率和精确性[10]。锥形型线在微喷管中最为常用,基于MOC的Sivells方法多用于设计风洞,可以产生均匀试验段流场,短化喷管(Minimum Length Nozzle, MLN)则用于缩短喷管的长度,减小喷管的边界层效应[11]。喷管收缩和扩张的速率、型面类型对气流的流动特性也有较大影响,锥直形喷嘴的收缩角越小,涡流损失越小,出口平均速度越快,能量利用率越高[12],随着扩张段长径比以及扩张角的增大,喷管出口推力先增大后减小[13]。RESTREPO等[14]使用现代真实气体状态方程代替此前喷管型线设计中普遍使用的理想气体模型,设计得到的喷管相比其他结果发现不同的型线适用于不同的工况。仿真对微型超音速喷管内外流场还原最重要的点分别为黏性作用和连续性假设是否成立。CAI等[15]使用Sutherland模型来描述气体的黏性,并通过实验证明有较好的效果。DE GIORGI等[16]着重关注了拉瓦尔喷管的黏性作用对喷管分别在二维模型和三维模型仿真中对喷管效率的影响。微型超音速喷管的出口尺寸小,使用空气压缩机和加热器即可持续制备喷管入口所需的高压高温气源,制备好的气体平时可以存放在储气罐中,列车行驶中,当需要清扫水膜时再打开气罐出口,使喷管进入工作状态,喷管在列车上的安装位置如图1所示。

1 清扫轮轨水膜的超音速喷管设计
1.1 气流与水膜间的作用关系
当固液两相相互接触时,它们之间有一个固液相界面,具有一定的界面力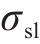
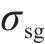
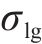
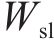
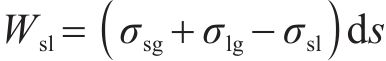
液相在空气中形成界面的表面张力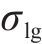
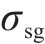
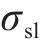
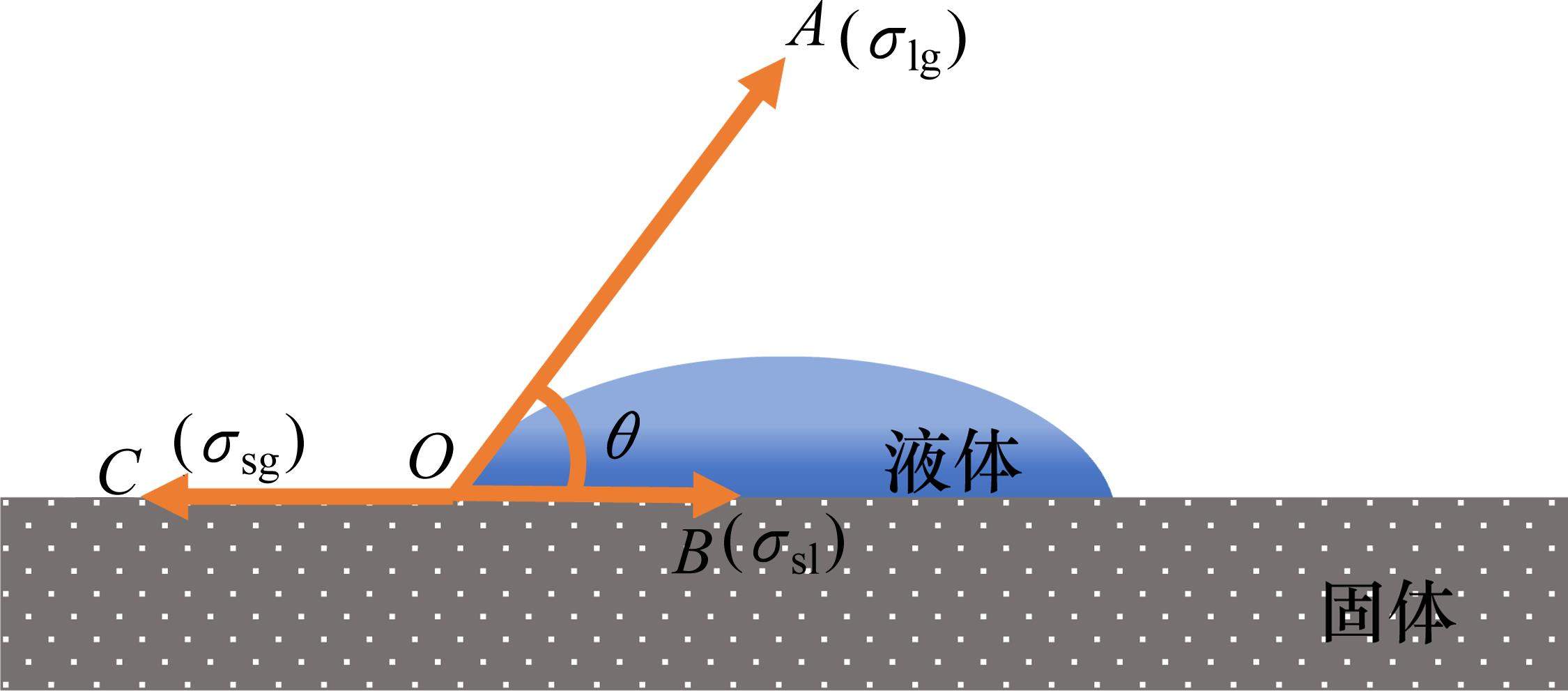
由接触点O沿气液界面作切线OA,与固液交界面OB间的夹角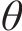
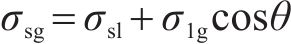
Young方程建立起了固液间作用力、固气间作用力和气液间作用力之间的联系,将式(1)与式(2)联立起来,可得:
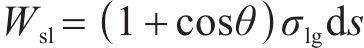
方程中黏附功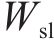
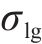
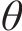
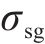
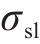
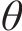
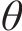
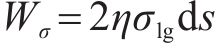
式中: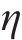
气流对水膜做功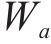
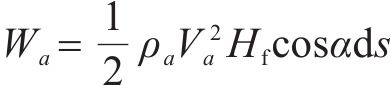
式中: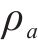
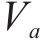
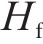
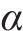
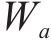
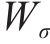
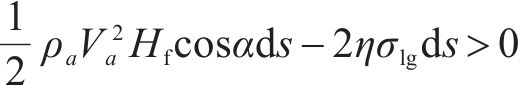
进一步化简,可以得到气流速度与水的表面张力、水膜厚度等水膜参数间的关系,如式(7)所示。
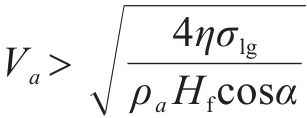
轨道表面对水膜的吸附作用随温度升高而减弱,在温度高时水膜更容易被去除,在设计产生高速气流的喷管时,使气流在喷管出口处恰好完全膨胀至环境温度和环境压力,考虑最恶劣的环境条件,采用0 ℃时的空气密度和水膜表面张力进行理论分析,气流的入射角度为30°,气流的密度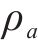
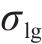
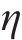
1.2 超音速喷管设计
气流在超音速喷管内流动时,喷管壁面上的热交换量远小于气流的内能,在设计绝大多数超音速喷管时,可将气流的流动过程视为绝热等熵过程,同时忽略不同截面上的具体流场分布,认为在同一截面上的参数均匀分布,基于这种假设的喷管内流动模型称为一维等熵模型。要使喷管达到最大性能,喷管喉部的马赫数恰好为1,再根据喷管内的截面积与马赫数的关系便可以得到喉部直径[18]。
喷管入口与喉部直径之比称为收缩段收缩比,统计数据表明,当收缩比小于3的情况下,收缩段内的流动才不会出现明显的分离。喷管收缩段的长度不能过短,以防止出现气流不均匀甚至气流分离的现象,增加能量损耗,从设备的经济性考虑,收缩段的长度也不应过长。经验表明,在保证收缩段性能的前提下,通常取0.5~1.0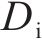
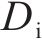
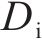
多位学者进行过轨道微表面粗糙度的现场试验,测量结果从2.2 μm到6 μm不等,结果显示钢轨表面存在着几个微米量级的表面粗糙度。为了精准获取本研究所关注钢轨表面的粗糙度,使用激光显微镜对钢轨表面粗糙度进行测量,获得了轮道表面完整的形貌和幅度参数,得到了轮轨接触区域的表面粗糙度。
表1为轨道表面粗糙度的测量结果,钢轨的平均表面粗糙高度为3.213 μm,而轮轨接触区域的平均表面粗糙高度为3.078 μm。因此,以轮轨接触区域的平均粗糙高度3.078 μm作为参考标准。
| 测试次数 | 粗糙度/μm | 测试次数 | 粗糙度/μm |
|---|---|---|---|
| 1 | 3.12 | 4 | 3.68 |
| 2 | 2.894 | 5 | 3.226 |
| 3 | 3.283 | 6 | 3.072 |
使用高速气流清扫轨道时,气流覆盖范围越宽清扫效果更好,但对喷管入口气源的温度和压力要求也越高,在满足清扫需求的前提下,尽量减小气流的覆盖宽度,可以有效降低清扫系统的功率和体积。轮轨接触斑是车轮与轨道之间的接触区域,是轨道上承载列车重量和传递牵引、制动力的关键部分,故只需要确定轮轨接触斑的宽度,即可确定最小的气流覆盖宽度。

在同样的几何型面下,喷管的型线设计也有众多方法,可分为收缩段型线设计和扩张段型线设计。收缩段的型线差异对喷管性能影响较小,本研究采用五次方曲线法设计喷管收缩段。扩张段型线设计则一直是喷管结构设计的重要研究方向,最简单的扩张段型线通过直线段连接喉部与出口,但这种喷管的流场品质较差,气体会在其内部损失很多的能量。以特征线法为基础的设计方法不断发展,用其设计的超音速喷管气流流动效果较好,基于其发展出的Sivells方法常用于风洞设计,可以产生较为均匀的流场,但该种喷管的长度较长,基于特征线法的MLN方法则可以大幅缩短喷管长度,并减弱壁面的边界层效应,MLN喷管更易于加工。赵宏星等[19]进行了研究,超音速气流进入外流场后速度呈波动衰减,MLN喷管相较于Sivells喷管较短的长度使其边界层效应的影响更小,在速度波动中能量耗散最少,性能最佳。
基于以上分析,本文采用MLN方法进行喷管设计。喷管的出口直径De为8 mm,入口直径Di为16 mm。收缩段长度li为14.08 mm。喉部直径Dt为6.535 mm,喷管额定入口压力Pi为0.713 MPa,额定温度Ti为477 K,喷管出口速度为640 m/s,马赫数是气流速度和当地声速的比值,当地声速又与当地温度和气体性质有关,其关系如式(8)所示。
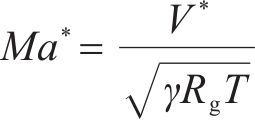
式中: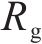
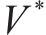
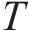
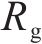
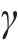
普朗特迈耶函数是气流折转角关于出口马赫数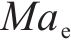
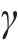
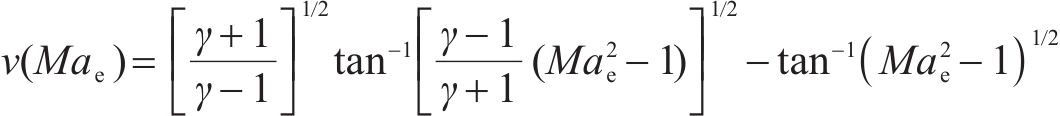
式中: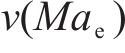
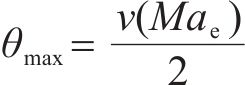
式中: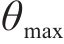
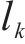
使用MLN方法设计的喷管在喉部处转折剧烈,生成一道很强的膨胀波,此波到达喷管轴线后发生反射,与喉部处的直音速线包围形成一个非简单波区的核心区,反射波与扩张段壁面间的过渡区也是非简单波区。MLN喷管的型线需使用数值方法进行求解,壁面根据壁面斜率与流动角关系方程确定,使用欧拉预测修正方案迭代求解[20]。
使用一维等熵理论和MOC方法得到的喷管按照无黏流动设计,考虑到空气的黏性作用,实际喷管流道中紧贴壁面附近的薄层存在边界层流动。喷管内的复杂波系会与边界层发生相互干扰,不但对边界层内的流动有影响,而且会改变喷管壁上波系的生成和反射,最终影响喷管出口气流的速度和均匀性,因此需要对得到的喷管型线进行边界层修正。
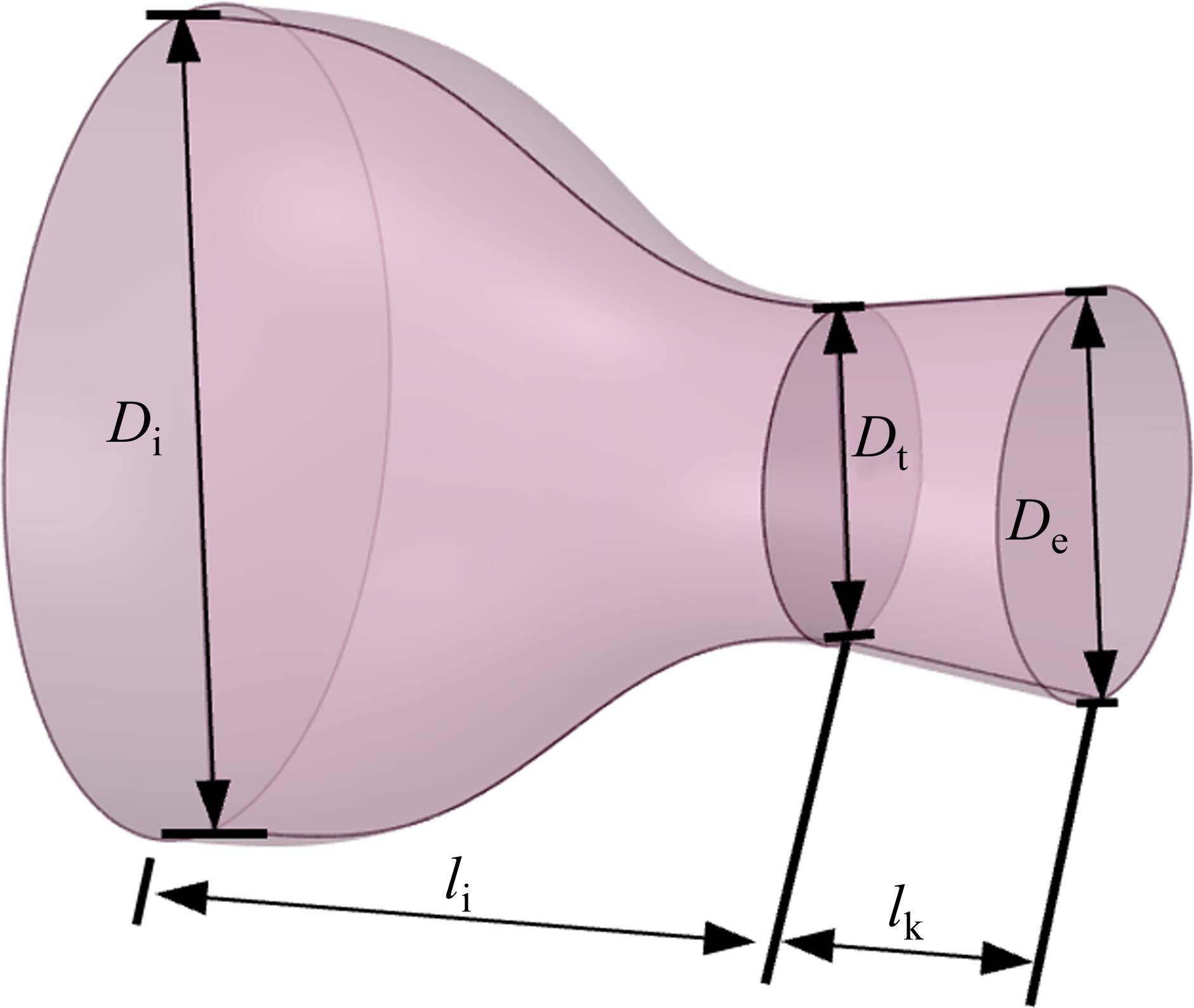
| 参数 | Di /mm | li/mm | Dt /mm | lk/mm | De/mm | Pi/MPa | Ti /K | Mae | 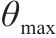 |
|---|---|---|---|---|---|---|---|---|---|
| \\ | 16 | 14.08 | 6.535 | 3.375 | 8 | 0.713 | 477 | 1.932 | 12.241 9 |
喷管型线修正完成后,建立了喷管的几何模型,修正后的喷管如图4。
1.3 喷管CFD建模
本文采用ICEM软件进行网格划分,运用Fluent软件进行仿真模拟,超音速喷管内流场雷诺数较高,大涡模拟(LES)将N-S方程进行滤波后的方程进行求解,在时间上是非均匀的,可以用于非稳态湍流流场量(大尺度涡)的直接求解[21]。大涡模拟有2个重要过程,首先是根据数学滤波模型,从湍流瞬时运动方程中将尺度比滤波函数的尺度小的涡过滤掉,从而分解出描写大涡流的方程,其次考虑被滤掉的小涡对大涡的影响,这可以通过在大涡流场的运动方程中引入附加应力项实现,这些数学模型称为亚格子尺度模型,WALE模型可以更准确模拟地涡环结构和涡的破碎范围,基于Favre滤波的可压缩流动控制方程具体可参考文献[22],本研究采用该模型进行亚格子建模。
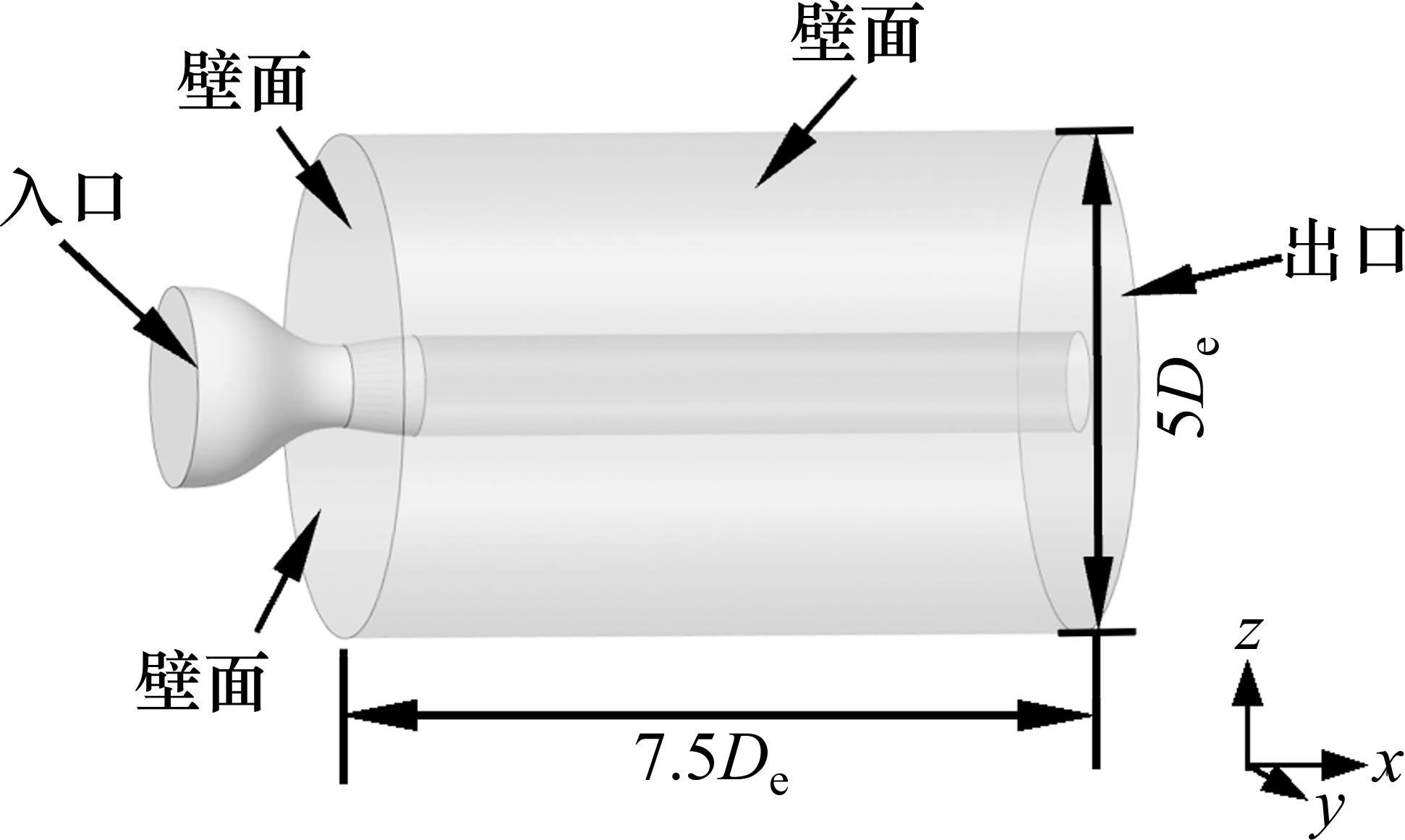
计算域的流场均使用压力出口入口,壁面设置为绝热。为了消除计算域大小对计算结果的影响,将计算域从喷管喉部处开始分别沿轴向和径向扩展7.5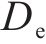
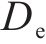
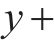
采用2阶迎风差分对各个方程进行离散,使用密度基隐式耦合双精度求解器。通过计算几个方程的残差判断仿真是否收敛,认为所有方程的残差小于1×10-5时计算收敛。使用隐式求解器求解,仿真时的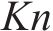
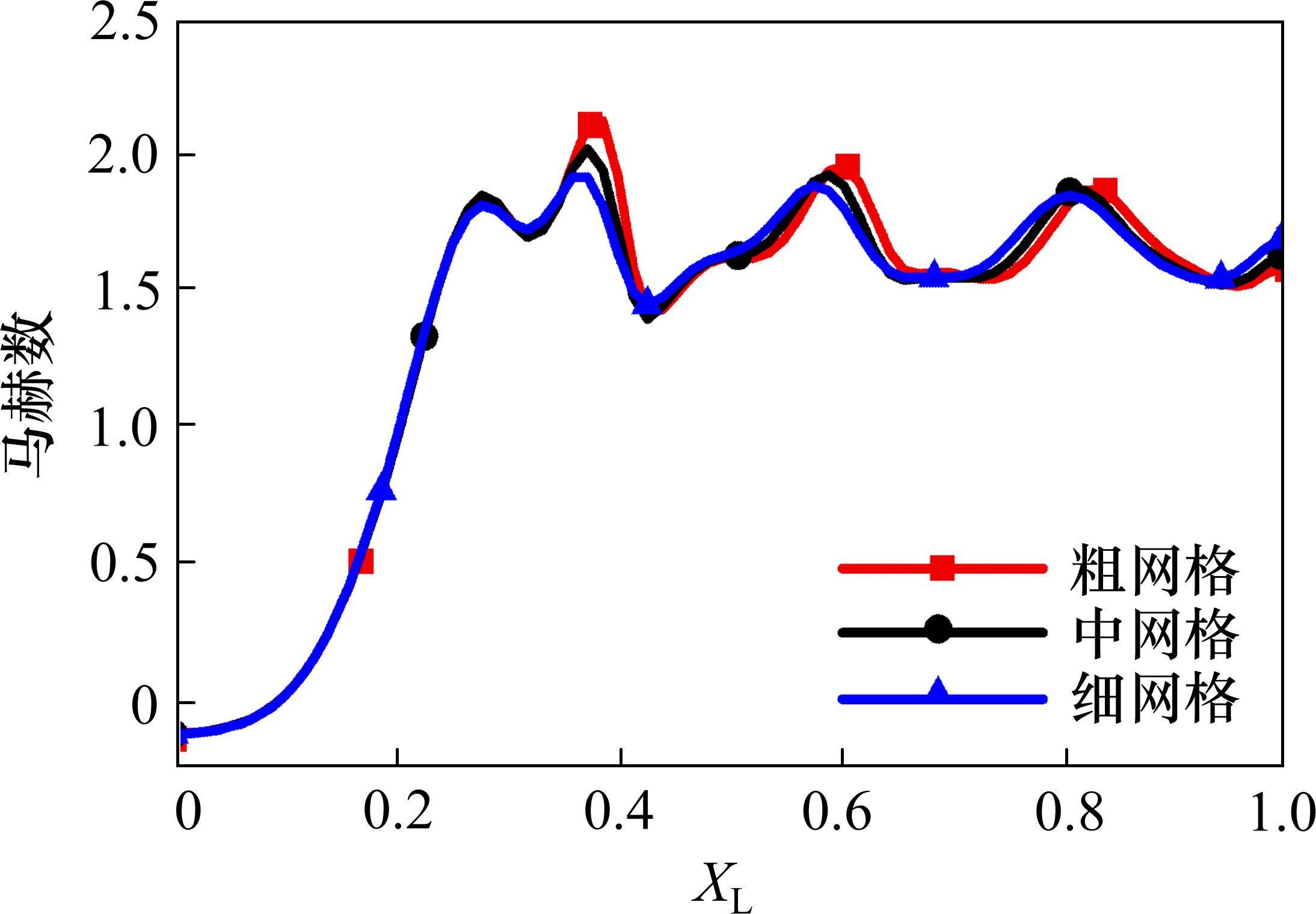
选用了3套网格进行网格无关性验证,粗网格模型中气流核心区域的网格平均尺寸为5×10-4 m,中网格为2×10-4 m,细网格为1×10-4 m。如图5所示,粗网格和中网格模型计算的喷管轴线上马赫数均值的误差为7.196%,中网格模型计算结果和细网格模型计算结果的误差为0.095%,中网格和细网格模型对马赫波处气流参数的细微变化捕捉效果更好。最终选用中网格尺寸进行仿真计算,网格数为74万。划分的网格如图6所示。
采用与ZHANG等[24]的试验中相同的参数,建立与其完全一致的微型喷管,使用本研究的仿真建模方法建立CFD模型,按照其试验中的边界条件进行仿真,仿真结果与试验结果对比如图7所示。

将仿真结果的密度梯度与试验的纹影图进行对比,仿真得到的马赫波的位置、从中心区域向周围的衰减情况等与试验结果吻合很好如图8所示。本研究基于LES方法建立的喷管内外流场仿真模型,其计算准确度高,可以用于研究喷管内外流场结构以及气流参数的波动情况。

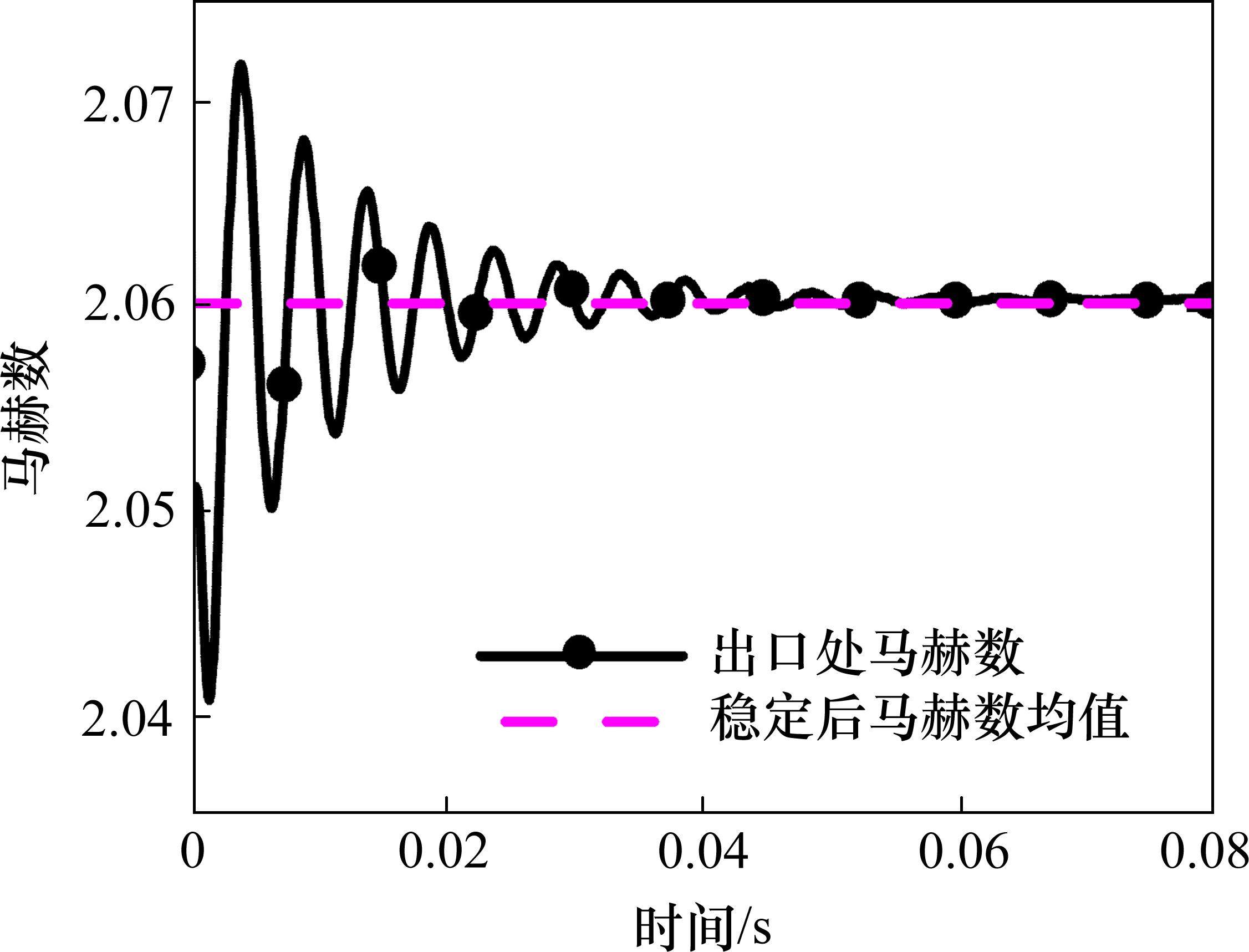
仿真计算过程中,流场入口和出口采用恒定边界条件,计算刚开始时得到的流场结构及气流参数与实际值误差很大,当计算逐渐收敛,流场进入稳态或者稳定波动后,才能对喷管的流场结构和气流参数进行分析,分析时间步的选取如图8所示,选择气流流动稳定后的时刻进行分析。
2 不同气源条件下喷管清扫能力分析
2.1 气源工况的确定
以概率论和数理统计理论为基础,通过在设计空间上选取合理、有效的有限样本点来对设计空间的特性进行研究的方法称作试验设计(Design of Experiment, DOE)。为了对额定气源条件(P=0.7 MPa,T=477 K)进行优化,并尽可能降低试验成本的前提下,尽可能提高代理模型的精度和可靠性,本研究采用最优拉丁超立方试验设计(Optimal Latin hyper cube design, OptLHD)方法进行抽样,抽取的样本点如表3所示。
| 编号 | 压力/MPa | 温度/K |
|---|---|---|
| PT1 | 0.6 | 466 |
| PT2 | 0.64 | 482 |
| PT3 | 0.68 | 450 |
| PT4 | 0.72 | 474 |
| PT5 | 0.76 | 490 |
| PT6 | 0.8 | 458 |
OptLHD方法使抽取的试验点尽量均匀地分布在设计空间内,该方法具有非常好的空间填充性和均衡性,具有设计空间均匀性好、试验次数少、设计空间探索精度高等诸多优点。
2.2 构建代理模型及优化结果
代理模型是通过数学模型的方法逼近变量与响应之间的关系,常用的代理模型有响应面模型、径向基神经网络模型和克里金(Kriging)模型,响应面模型适用于简单的数据情况,能够在有限数据下提供较好的预测效果,容易解释。径向基神经网络模型适用于复杂的非线性关系,能够捕捉数据中的复杂模式和趋势,但需要大量数据进行训练,并且可能比较复杂。克里金模型适用于空间相关性较强的数据,能够考虑数据点之间的空间布局和相互影响,适用于地理信息系统等领域。本文基于Kriging方法构建了喷管气源入口压力、入口温度与清扫后水膜厚度间的高精度代理模型。
Kriging方法又称空间局部插值法,是一种包括了函数创建、变异和创建表面等在内的多方向的算法,它以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计,可以保证构建的模型通过所有的样本点,并适用于对当前数据已知存在空间相关距离和方向存在偏差的情况。Kriging代理模型由全局模型和局部偏差2部分组成,其表达式如式(11)所示。
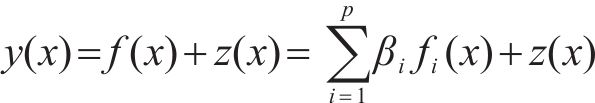
式中: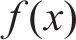
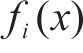
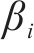
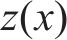
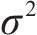
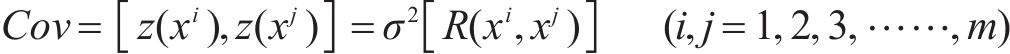
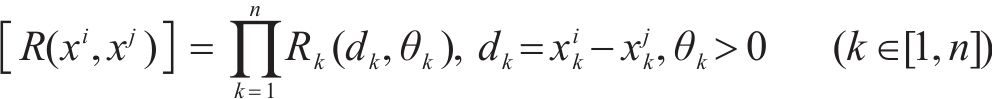
将样本点及其对应的数值分析结果组成数据集,用来构建代理模型。为了对喷管不同气源条件下的清扫增黏效果进行评估,考虑到喷管实际安装位置的影响,为了最大化提升喷管的使用效果,选择距离喷管出口16 mm的轨面位置作为研究点,通过公式(7)对气流覆盖区域的剩余水膜厚度进行分析,对比仿真分析后不同气源条件下剩余的水膜厚度,剩余的水膜厚度越低,说明该种气源条件的清扫效果越好。本研究采集的6组不同气源入口压力和入口温度样本的仿真结果如表4所示。
| 编号 | 剩余水膜厚度/μm | 编号 | 剩余水膜厚度/μm |
|---|---|---|---|
| PT1 | 2.07 | PT4 | 1.55 |
| PT2 | 1.95 | PT5 | 1.46 |
| PT3 | 1.75 | PT6 | 1.45 |
构建代理模型方法的选择取决于具体的应用场景、数据特点和需求。每种代理模型都有其优势和适用范围,没有一种模型能够适用于所有情况。常通过代理模型误差分析,分析构建的代理模型在样本集上的拟合精度,进而判断构建的代理模型是否满足参数优化的要求。代理模型常用的评价指标主要有相对均方根误差RMSE以及决定系数R2。
决定系数R2是样本集利用所建代理模型进行回归分析的离差平方和在总离差平方和中所占的比重,R2越大说明构建的代理模型的拟合精度越高,各样本观测点与回归线拟合得越贴近,通常要求R2的值高于0.9。基于Kriging代理模型及喷管不同安装形态下清扫后的水膜厚度仿真结果,构建了喷管入口气源条件和清扫后水膜厚度间的高精度代理模型,拟合的结果如图10所示。
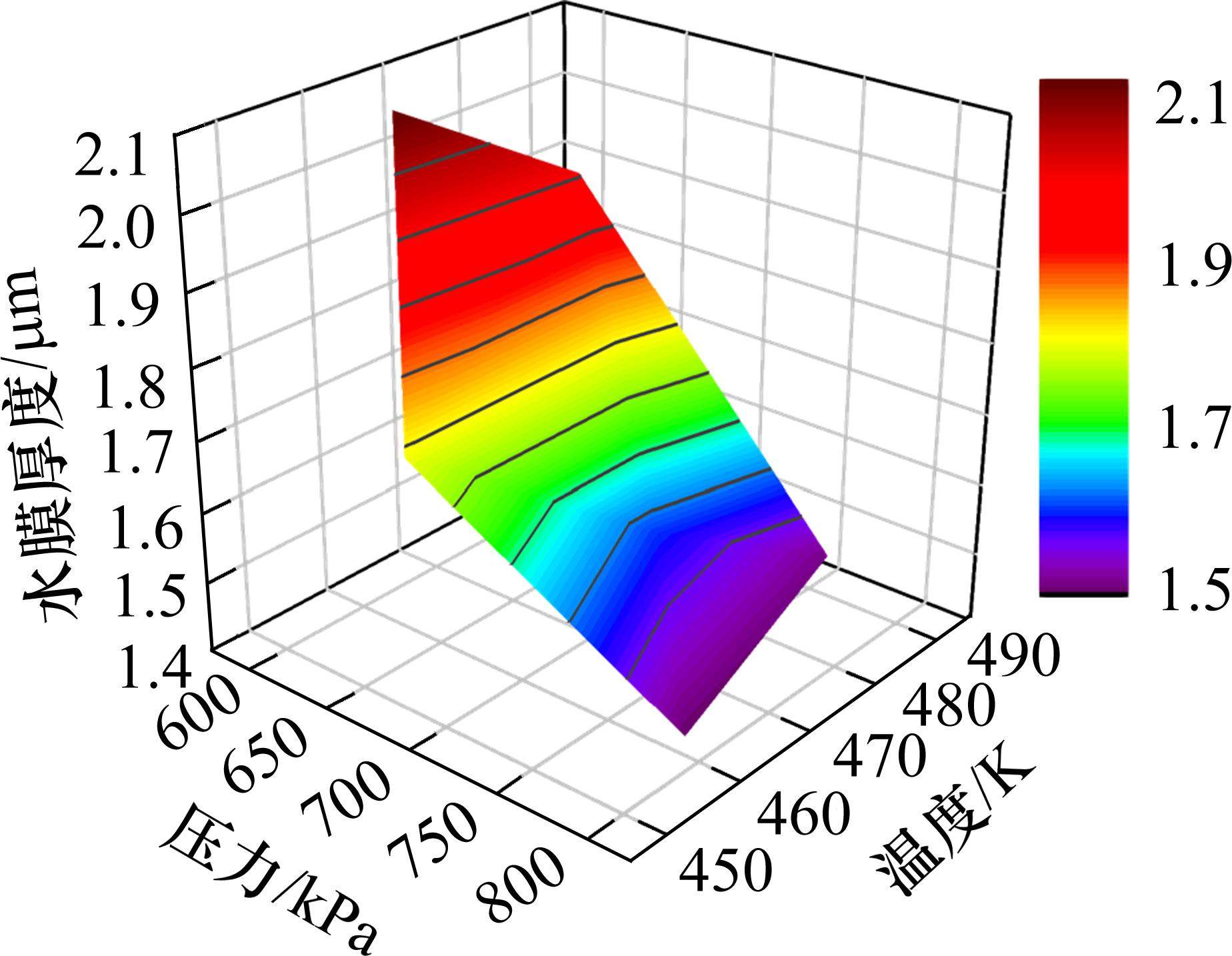
本研究构建的代理模型R2为0.987,高于可接受水平,构建的代理模型的均方根误差值RMSE为0.038,小于0.2,构建的代理模型精度高,符合要求。
多岛遗传算法是遗传算法的一种变体,它引入了多个独立的种群(岛屿)并通过迁移操作连接它们,属于进化算法的一种。该算法具有种群结构多、迁移操作、竞争与合作和参数调整等优点,与其他算法相比,具有增强多样性、加快收敛速度和更好的全局搜索等优势[25],因此本文选用多岛遗传算法进行参数优化。基于已构建的高精度代理模型,以清扫后剩余的水膜厚度最小化为目标,使用多岛遗传算法进行求解,优化算法的控制参数如下:群岛个体数为20,群岛数为20,进化的迭代次数为20。
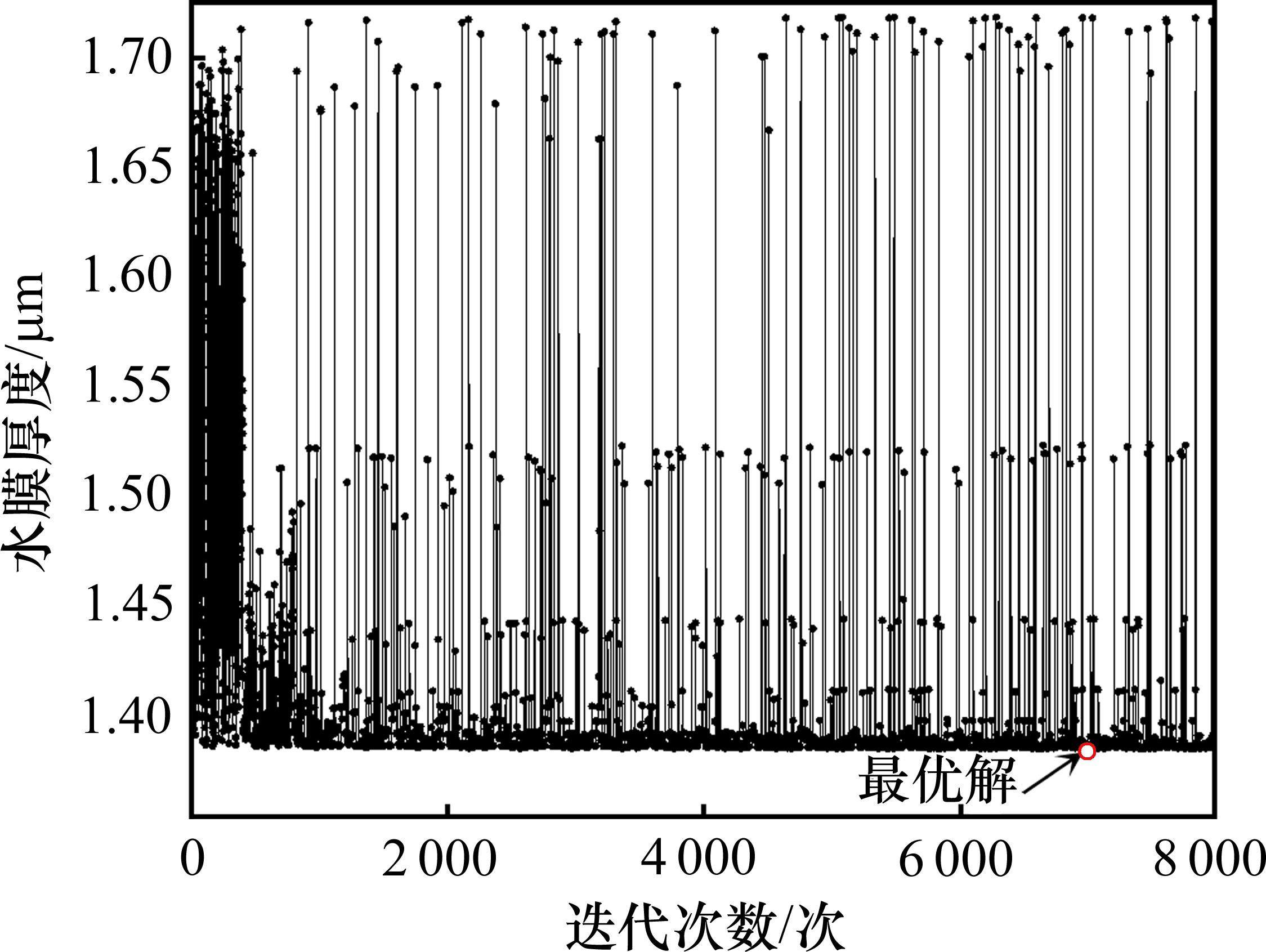
经过8 000次迭代计算,在第6 976次迭代时得到最优解,搜索历程如图12所示。优化结果显示喷管的最佳入口气源压力为0.78 MPa,最佳温度为450 K,在最优的喷管入口气源条件下,使用高速气流清扫轨道表面后,剩余水膜的厚度为1.386 μm。
2.3 气源条件优化前后结果对比
为了验证优化结果的准确性,使用喷管仿真模型对喷管在优化后的气源条件下再次进行模拟,并与优化前入口气源压力0.7 MPa、温度477 K的仿真结果进行了对比。
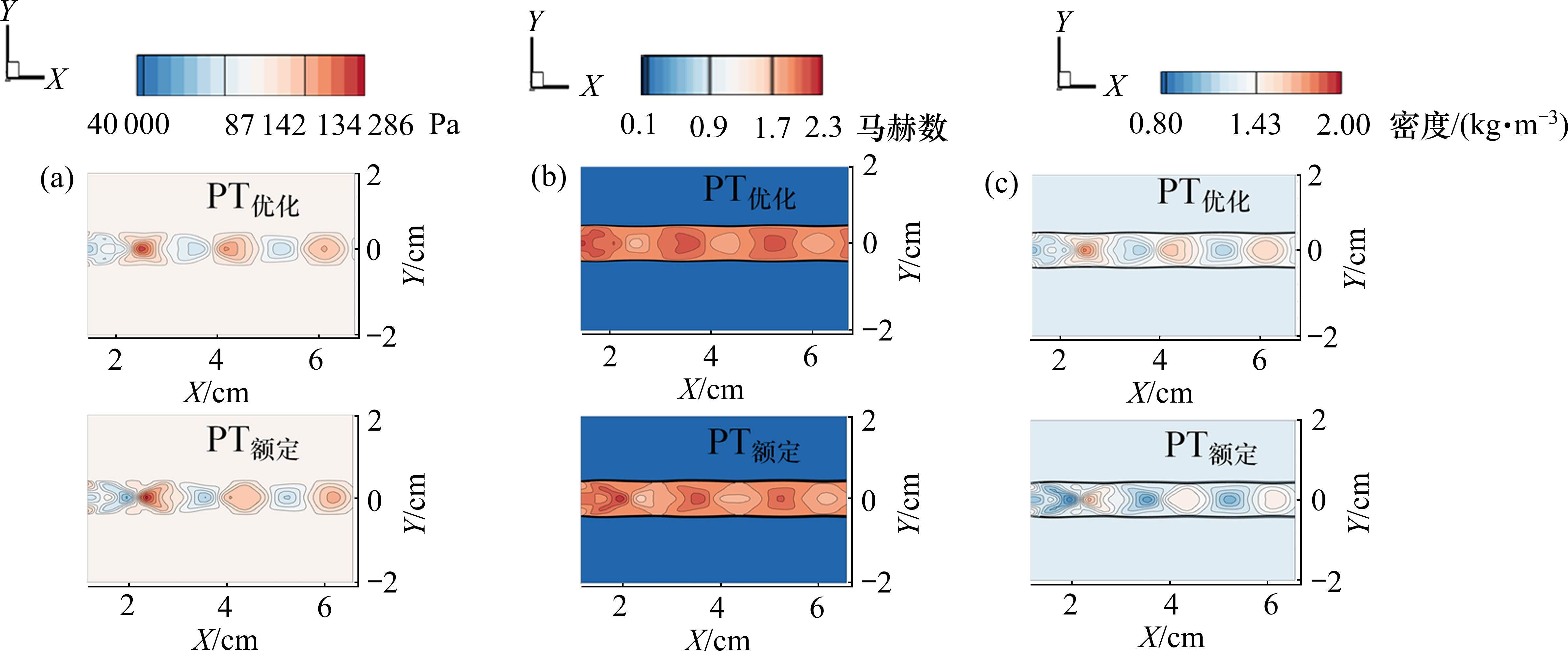
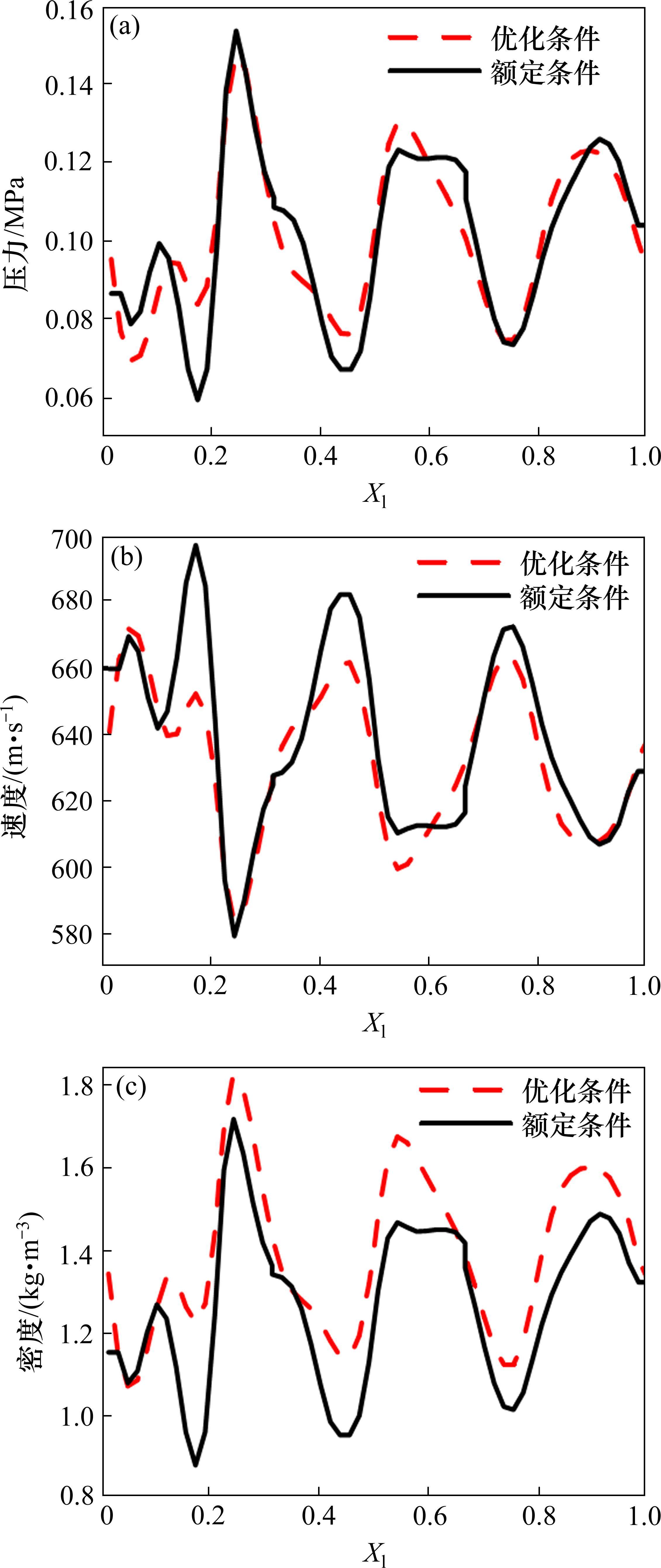
图12为优化前后喷管外流场压力、马赫数和密度云图,其中图12(a)为优化前后喷管外流场压力云图,图12(b)为优化前后喷管外流场马赫数云图,从这2个云图来看,优化前后喷管外流场压力和马赫数没有明显区别,由图12(c)来看,优化后的喷管外流场密度大于额定条件下喷管外流场的密度。
为了评价喷管在优化前后喷管性能的差别,将各喷管的出口对齐后进行无量纲化处理。其中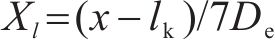
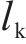
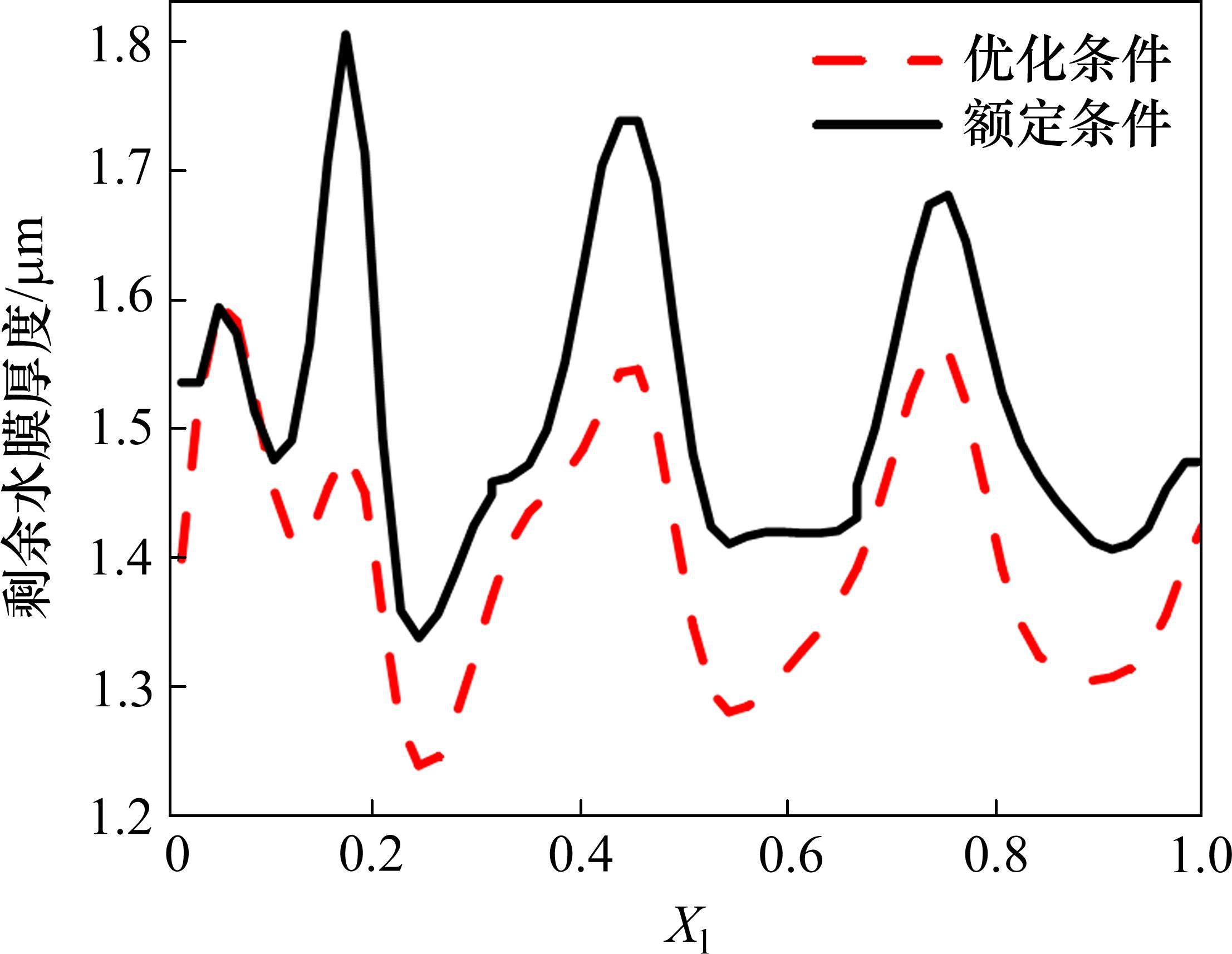
为了更精准地评价喷管在气源条件优化前后清扫水膜的能力,根据气流速度、密度等参数与水膜厚度间的关系,得到了从喷管出口开始,到下游不同位置气流清扫水膜的能力。剩余水膜厚度越小说明喷管清扫能力越强。由图14可知,在喷管入口气源条件优化后,喷管清扫水膜的能力从喷管出口到下游各位置都有所提升。在额定入口气源条件下,轨面处气流温度为283.2 K,清扫后剩余水膜厚度为1.45 μm;在喷管入口气源条件优化后,轨面处气流温度为271.6 K,清扫后剩余水膜厚度为1.27 μm,在气源条件优化后喷管清扫水膜能力提升了12.4%。
3 结论
1) 通过对喷管清扫水膜的动力学分析,得到了判别水膜吹离的方法和喷管清扫水膜的性能判别指标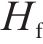
2) 在额定入口气源条件P=0.7 MPa、T=477 K时,轨清扫后剩余水膜厚度为1.45 μm;在喷管入口气源条件优化后,P=0.78 MPa、T=450 K,清扫后剩余水膜厚度为1.27 μm,在气源条件优化后喷管清扫水膜能力提升了12.4%。
刘洋,王北昆,卢耀辉等.气源对超音速喷管清扫轮轨增黏的影响分析[J].铁道科学与工程学报,2025,22(04):1747-1758.
LIU Yang,WANG Beikun,LU Yaohui,et al.Analysis of the influence of air source cleaning wheel and rail on increasing viscosity using supersonic nozzle[J].Journal of Railway Science and Engineering,2025,22(04):1747-1758.

