为缓解我国城市物流以公路运输为主造成的道路拥堵、城市污染及物流能耗高等问题,国务院办公厅印发的《推进运输结构调整三年行动计划》中明确提出推进城市生活性物资公铁联运,构建“外集内配、绿色联运”的公铁联运城市物流体系。该模式通过铁路连接城市外围的物流基地与城市内部的铁路货运站点,再通过卡车进行末端配送,有效发挥了铁路绿色高效的特点[1]。客户属性是地理区位、需求量等客户端对物流成本造成难以忽略影响的因素,因此在客户属性的基础上对城市公铁联运物流选址-路径优化进行研究成为亟待解决的关键问题。优化模型构建方面,选址分配与路径优化2个方面的研究较为丰富。选址分配方面,WANG等[2]视公铁联运网络为轴辐式网络[3],将问题描述为混合整数非线性非凸规划,运用拥堵效应、分段线性成本函数和定点约束等理论进行选址研究。在此基础上,李孟良等[4]针对公铁联运网络建立基于总费用最小的多分配p-枢纽中位选址模型并设计启发式算法求解;MOSTERT等[5]将碳排放等多因素纳入考虑,进一步完善公铁联运枢纽选址的研究内容并设计启发式算法求解。路径规划方面,除考虑经济效益[6]外,SUN等[7]考虑了碳排放与时间窗等因素,在此基础上,贾晓燕等[8]将危险货物等特殊货物因素纳入考虑;基于以上单目标研究优化,王超等[9]基于熵权-TOPSIS方法对公铁联运路径进行双目标优化;SUN等[10]使用精确式算法求解公铁联运路径多目标优化的Pareto解。单一的选址分配与路径优化模型无法准确反映客户属性对于整体系统的影响,而选址分配-路径联合优化模型能解决整体系统中枢纽与路径协同优化问题,有效地弥补上述研究的不足。研究者将选址分配-路径联合优化模型与客户属性研究相结合,广泛应用于流动医疗服务[11]、大型企业的物流服务[12-14]、城市物流服务[15-16]以及绿色物流配送[17]等方面。在此基础上,研究者将其应用于公铁联运城市物流服务研究中:周晓晔等[18]考虑地铁剩余运能、货车容量、客户服务时间窗等因素对地铁-货车联运网络进行研究,设计改进自适应遗传算法求解。LI等[19]在超大型城市配送中的小运转列车路径优化中加入碳排放约束建立联运模型并设计启发式算法进行求解。张得志等[1]在考虑客户地理区位与需求量的基础上,对超大型城市物流网络布局与小运转列车路径优化问题进行研究并设计改进的遗传算法求解。目前相关文献仅将客户属性作为基本参数[1, 20]对模型进行求解,缺乏其对于配送方案及物流成本影响规律的研究。且大多研究的组织优化模型较少考虑小运转列车货物装载、铁路网络节点连通度分析等关键因素,未有效体现该模式中小运转列车运行组织特点。基于此,以北京市为例,构建了一个改进的包含3级物流节点的两阶段公铁联运城市物流配送选址分配-路径优化模型,设计外集内配公铁联运城市物流模式规划方案并挖掘客户属性对于物流成本的影响规律。
1 问题描述
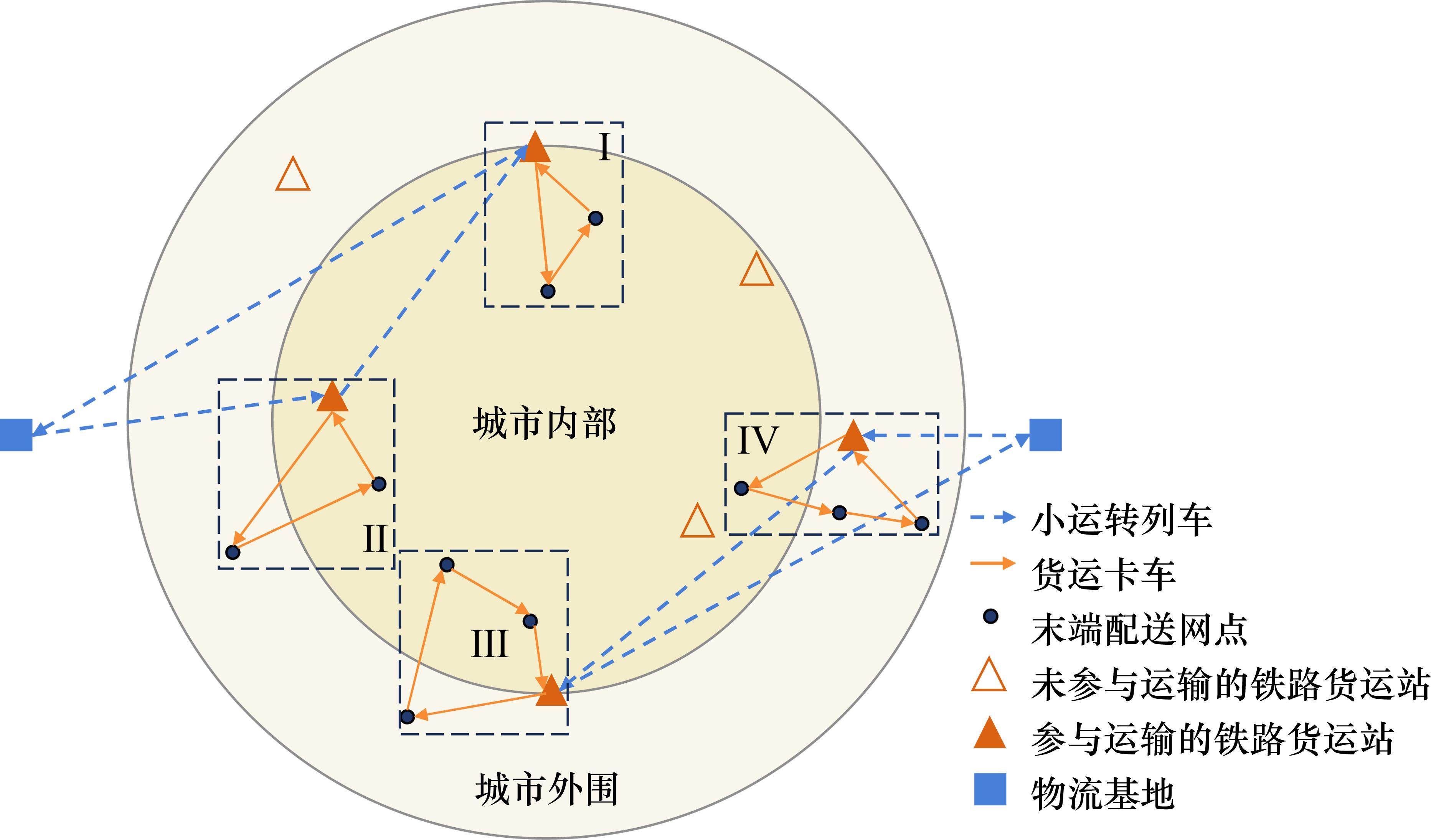
城市物资通过铁路运输到城市外围的物流基地(1级节点)进行集结后实现“外集”功能;再通过小运转列车(物流基地与各铁路货运站之间灵活开行的短距离货运列车)向城市内部各铁路货运站(2级节点)进行运输,最后在各站点中转后通过城市公路系统向各末端配送网点(3级节点)进行运输实现“内配”功能。
为提高铁路与公路之间的货物中转效率,小运转列车需要在各2级节点卡车发车前到达完成货物装卸;这要求小运转列车作业组织需要在2级节点向3级节点配送计划的基础上进行规划,而2级节点的配送计划则由3级节点的客户属性决定。由于在规划时无法直接通过3级节点客户属性直接推导出1级节点与2级节点间的小运转列车运行组织,因此本文设计了一种依托客户属性的逆序规划,根据已知的客户属性规划2级与3级节点间城市公路货运组织,再根据组织结果对小运转列车运行组织进行规划。如图1所示,选取地理区位、需求量与服务时间窗作为主要客户属性作为指标进行聚类与选址分配。第1阶段根据以上3种客户属性进行聚类与选址分配,图1中虚线部分表示根据客户属性聚类后的选址分配结果,每个虚线部分内包含1个2级节点与若干3级节点,其中的3级节点客户属性具有一定的相似性;第2阶段基于第1阶段的选址结果对2、3级节点之间的城市物流配送路径进行规划;第3阶段基于第2阶段规划结果对1、2级节点之间的小运转列车作业组织进行规划。
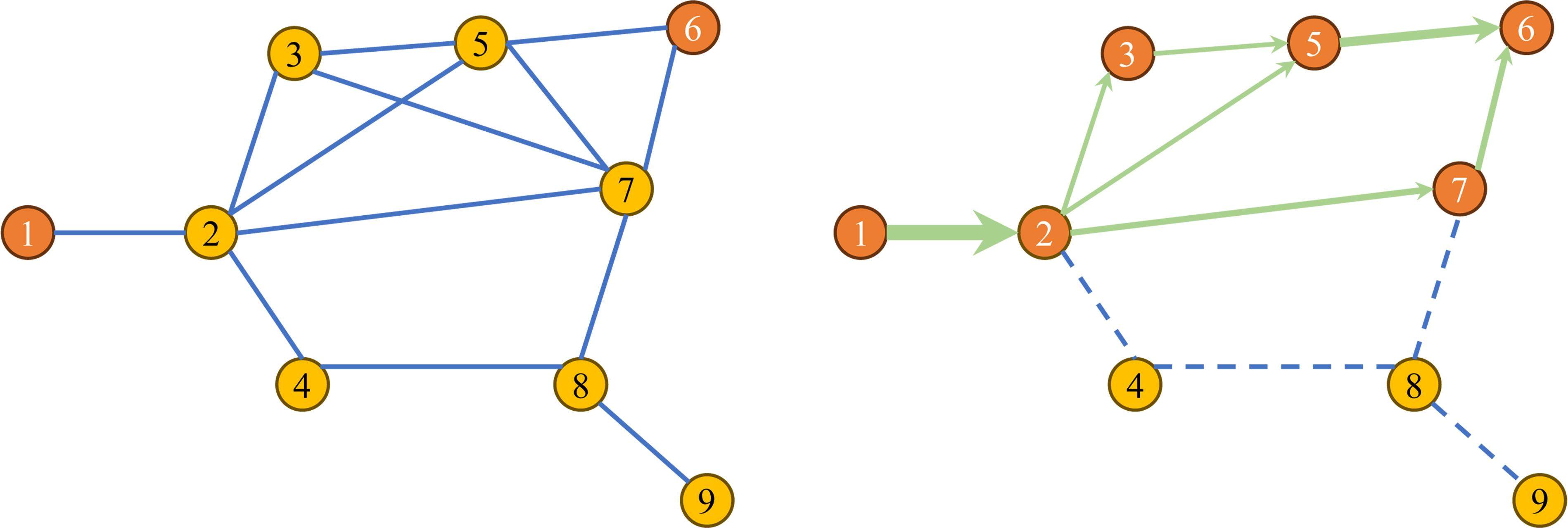
该模型中存在少数1级节点及多个2级节点,模型中城市内部货运站间小运转列车在物流配送时需要依托于既有铁路网布局,其可以看作一个无向连通图(undirected connected graph),以图2为例,对小运转列车进行节点1与节点6间的运输组织规划,虽然小运转列车并不服务节点2、节点3、节点5及节点7,但需经过这些节点完成节点1到节点6的运输。
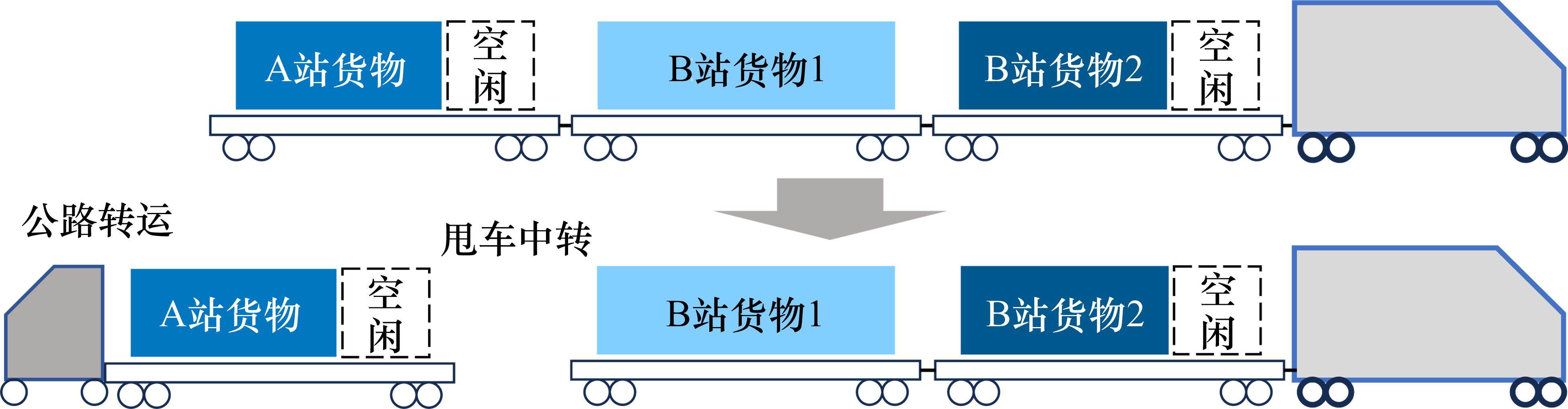
如图3所示,在物流基地发车前,小运转列车根据运输计划提前进行编组并采用模块化编组策略,即使某一站点所需物资装车后无法满载,仍按照满载进行编组以快速拼接成列车。在列车抵达计划站点时,仅通过甩车作业完成卸货,剩余列车继续在机车的牵引下进行配送作业,直到送至最后一个站点后返回出发基地。
综上所述,模型可看作一个涉及2种物流系统的选址分配-路径优化问题,拟解决的关键问题可描述为:1) 根据客户属性优化选址方案,即确定最佳的2级节点与其对应的3级节点;2) 根据选址方案,优化1级节点与2级节点之间的小运转列车运输组织与2级节点与3级节点之间的城市物流配送路径。
2 数学模型
2.1 假设条件
1) 允许每个2级节点由多个1级节点配送,并服务多个3级节点且每个3级节点只能由一个2级节点服务。
2) 每个3级节点只能由一个2级节点负责服务。
3) 每个2级节点能被小运转列车服务多次。
4) 每列小运转列车对应一条路线,在运行过程中不会出现路线冲突的情况。
2.2 参数说明
2.2.1 模型集合
涉及模型的集合如表1所示。
| 集合 | 集合解释 |
|---|---|
| G(N1, N2, N3, P1, P2) | 表示城市物流配送网络 |
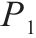 | 表示小运转列车运行路径 |
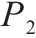 | 表示货运卡车运行路径 |
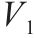 | 表示1级节点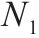 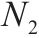 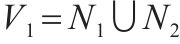 |
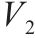 | 表示2级节点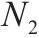 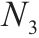 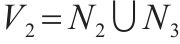 |
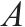 | 表示小运转列车集合 |
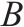 | 表示货运卡车集合 |
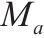 | 表示需要编入小运转列车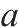 |
2.2.2 模型参数
涉及模型的参数如表2所示。
| 参数 | 参数解释 |
|---|---|
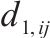 | 小运转列车在节点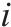 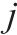 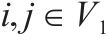 |
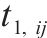 | 小运转列车在节点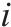 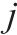 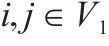 |
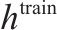 | 机车牵引定数 |
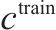 | 小运转列车单位运输成本 |
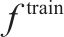 | 小运转列车发车固定成本 |
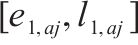 | 小运转列车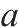 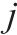 |
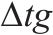 | 追踪列车时间间隔 |
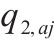 | 小运转列车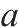 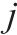 |
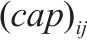 | 节点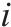 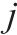 |
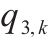 | 节点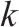 |
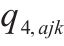 | 通过小运转列车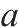 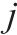 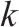 |
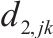 | 卡车在节点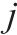 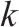 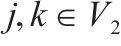 |
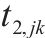 | 卡车在节点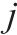 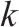 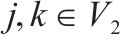 |
 | 货运卡车最大载重量 |
 | 货运卡车单位运输成本 |
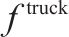 | 货运卡车发车固定成本 |
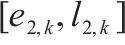 | 节点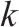 |
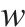 | 卡车单位等待时间 |
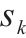 | 节点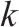 |
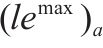 | 小运转列车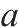 |
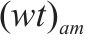 | 小运转列车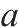 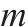 |
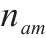 | 小运转列车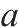 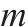 |
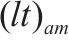 | 小运转列车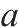 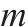 |
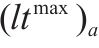 | 小运转列车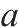 |
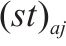 | 列车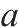 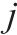 |
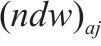 | 小运转列车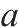 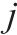 |
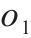 | 2级节点中转作业的单位货物费用 |
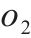 | 2级节点甩车作业的单位货车费用 |
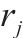 | 2级节点能够中转的货物量上限 |
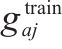 | 小运转列车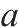 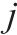 |
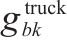 | 卡车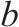 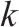 |
2.2.3 决策变量
模型涉及的决策变量如表3所示。
| 变量 | 变量解释 |
|---|---|
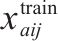 | 0-1决策变量,若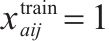 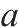 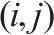 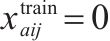 |
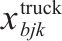 | 0-1决策变量,若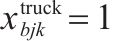 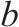 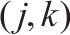 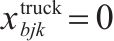 |
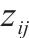 | 0-1决策变量,若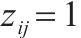 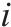 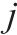 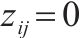 |
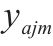 | 0-1决策变量,若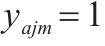 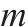 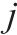 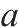 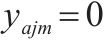 |
2.3 模型构建
本文外集内配公铁联运决策优化模型可拆分为小运转列车运输组织优化模型与城市货运车辆配送路径优化模型2个子模型,其中,小运转列车运行成本表示为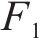
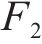
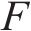
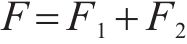
2.3.1 小运转列车运输组织优化模型
基于上述研究,可构建以下目标函数与约束条件。
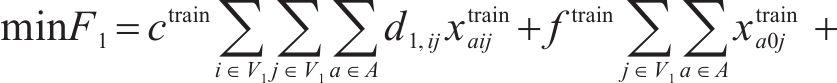
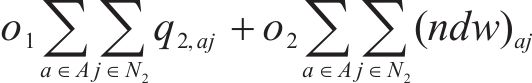
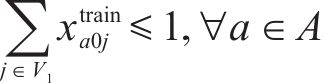
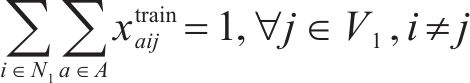
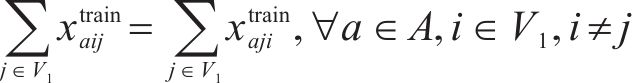
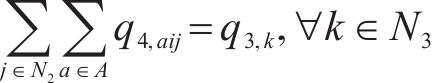
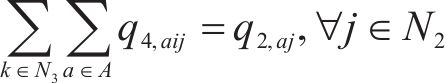
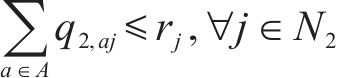
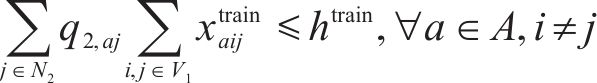
目标函数(2)表示模型目标为总成本最小化,前2项分别为小运转列车运行成本与固定成本,后2项表示小运转列车在2级节点办理中转作业的费用,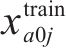
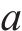
根据本文图2设计的编组模式,可构建以下约束条件。
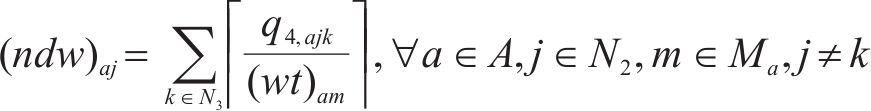
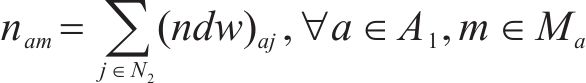
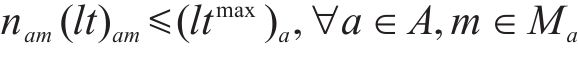
式(10)与式(11)通过计算编入小运转列车的货车数目,进而得出其编组出发总长度,约束(12)表示编组后小运转列车机车的最大牵引长度约束。为简化计算步骤,牵引长度约束(12)可直接由变量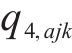
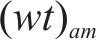
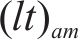
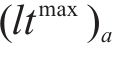
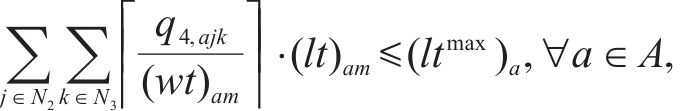
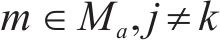
由于在该中转作业组织模式下无仓储环境,因此规定小运转列车必须在硬时间窗内在指定货运站完成到站、甩车、出发等作业流程;而公路运输较难完成高度精确的配送计划,允许有一定的变动余地,即在时间窗内完成配送则不会产生额外成本,若提前到达或延后到达将分别产生等待成本与迟到成本,故存在以下约束条件。
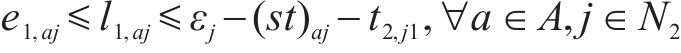
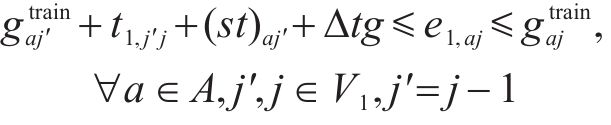
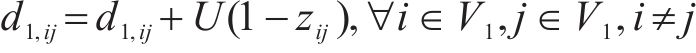

式(14)与式(15)为小运转列车的时间窗约束,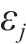
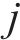
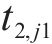
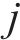
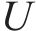
2.3.2 城市货运车辆配送路径优化模型
该部分模型可以看作一个多车场带时间窗的容量限制车辆路径问题(Multi-Depot Capacitated Vehicle Routing Problem with Time Windows, MD-CVRPTW),存在多个2级节点与3级节点,各2级节点车辆服务完成后返回出发点。
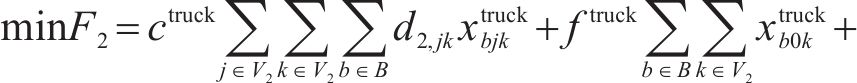
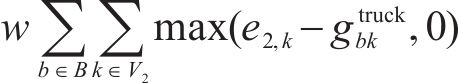
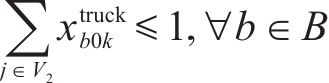
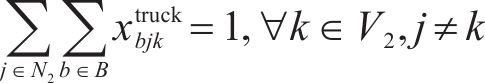
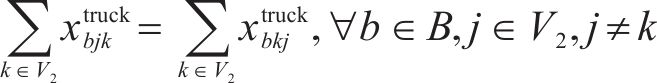
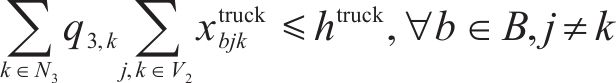
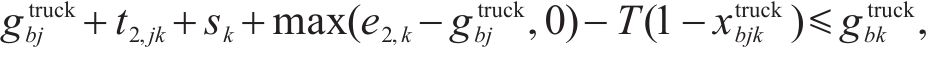
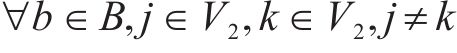
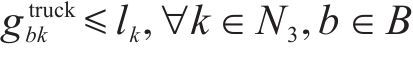
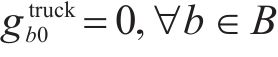
目标函数(18)表示模型目标是总成本最小化,第1项为车辆行驶成本;第2项为车辆开行产生的固定成本,包括司机工资、维修费用等;第3项为违反时间窗产生的惩罚成本。式(19)与式(20)分别表示每辆卡车是否派遣及对每个节点仅服务一次,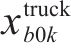
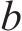
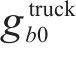
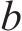
2.4 非线性约束线性化处理
为方便求解,对非线性化的方程(13)、(18)、(23)进行线性化处理。对于约束(13),引入变量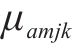
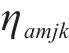
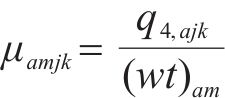
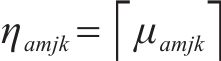
对于变量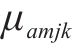
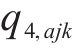
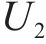
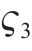
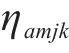
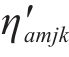
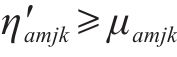
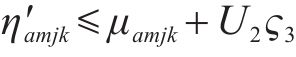
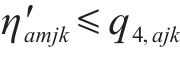
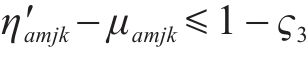
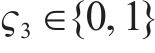
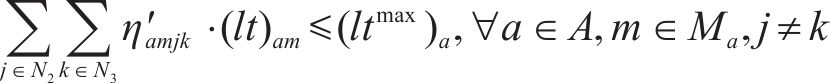
对于方程(18),引入新变量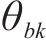
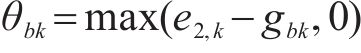
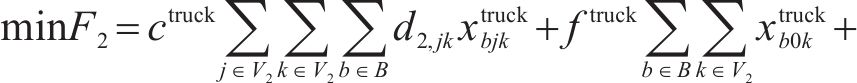

式(34)可等价为约束(36)与约束(37)。
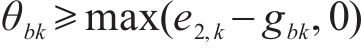
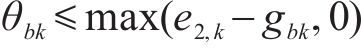
引入二进制变量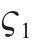
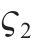
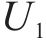
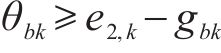
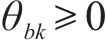
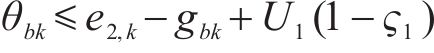
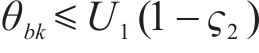
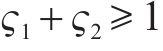
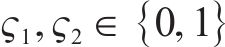
3 模型算法设计
本文基于外集内配公铁联运城市物流配送进行选址分配与2种运输服务方式的服务路径优化问题进行研究。为精确表征客户属性对于选址分配结果的影响,设计结合手肘法的加权k-means聚类算法进行选址分配;在服务路径优化方面,启发式算法虽然具有较高的运算速度,但精准度较差,无法准确体现各方案下物流成本的差异,因此使用Matlab调用CPLEX求解器对服务路径优化模型进行求解。
3.1 选址分配算法设计
3.1.1 加权k-means聚类算法
选择k-means聚类算法对2级节点与3级节点进行选址分配。针对多因子多量纲的k-means聚类,需要先对数据进行去量纲化处理。处理过程如式(44)所示,其中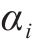
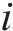
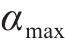
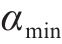
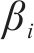
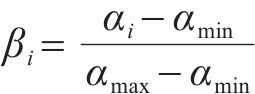
对处理后的数据加权处理,记第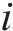
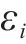
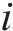
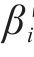
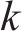
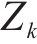
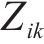
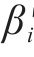
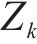
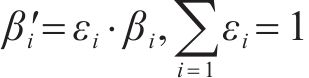
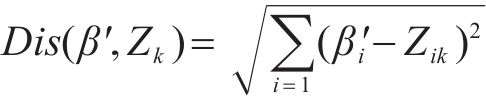
通过误差平方和(Sum of squared errors)判定是否达到停止迭代的标准,如式(47)所示。
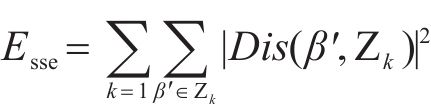
3.1.2 手肘法
在本文选址分配设计的k-means算法中,确定聚类中心数量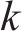
对于一个类,畸变程度[21]可以代表类内成员的紧密程度,且畸变程度会随着分类数目的增加而降低,当分类数目增加到一定数目时,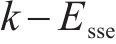

3.2 算法框架
本文采用结合手肘法的加权k-means聚类算法与CPLEX求解器相结合的方法进行求解,对于各个独立策略,模型求解算法框架如图4所示。
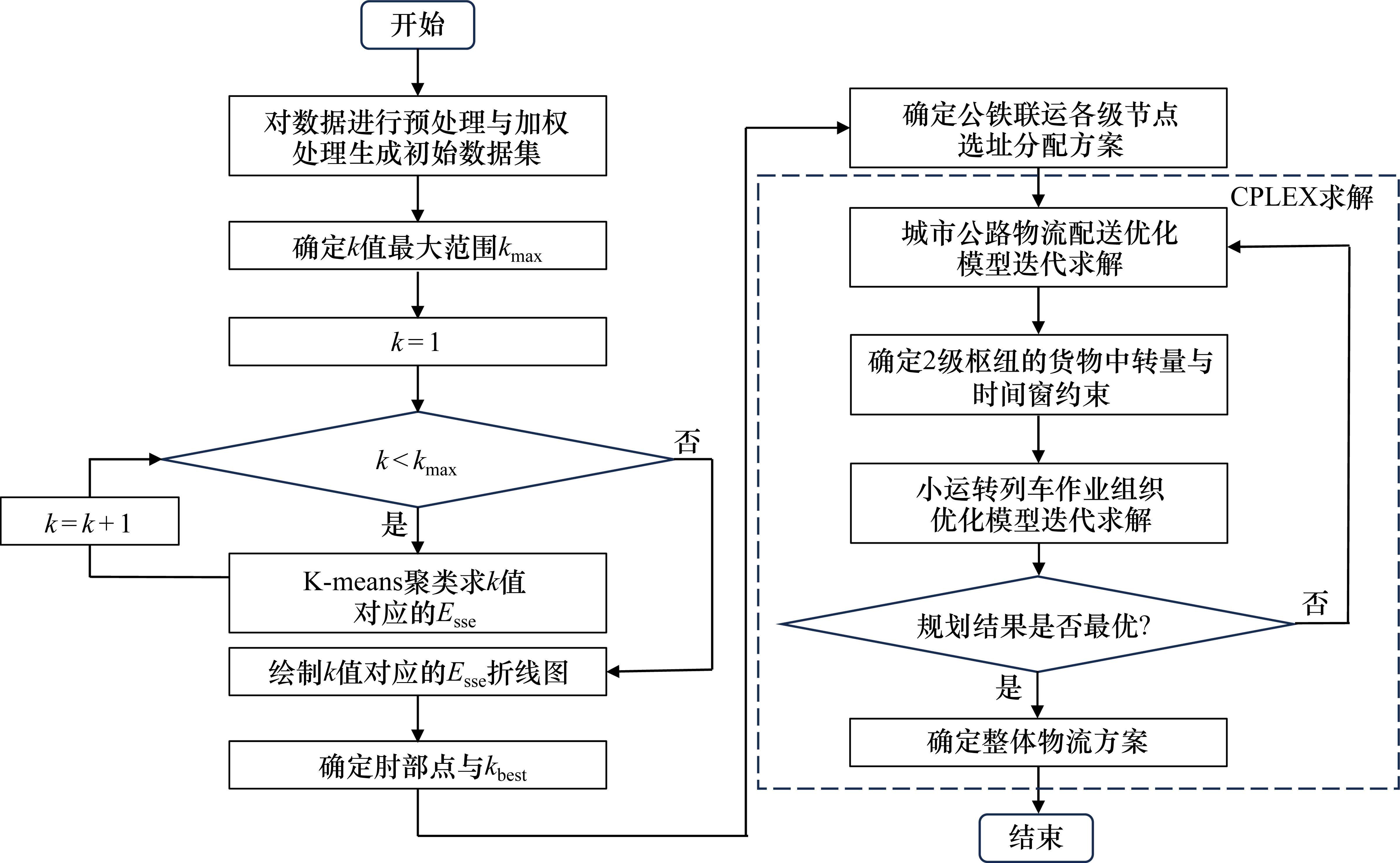
4 实例求解
4.1 算例说明
本文算法均采用Matlab R2021b编程实现,在11th Gen Intel(R) Core(TM) i7-11800H @ 2.30 GHz,内存16.0 GB,操作系统为win10的环境下运行算法程序。求解算例来源于文献[20],服务对象包括北京市6个城区(东城区、西城区、朝阳区、海淀区、丰台区和石景山区),算例包括各级节点区位,2级节点服务能力以及3级节点需求量及时间窗等数据以及小运转列车与货运卡车装载量、单位运输成本等运载工具相关数据,对各级节点的经纬度数据进行处理,得到节点地理位置关系如图5所示。
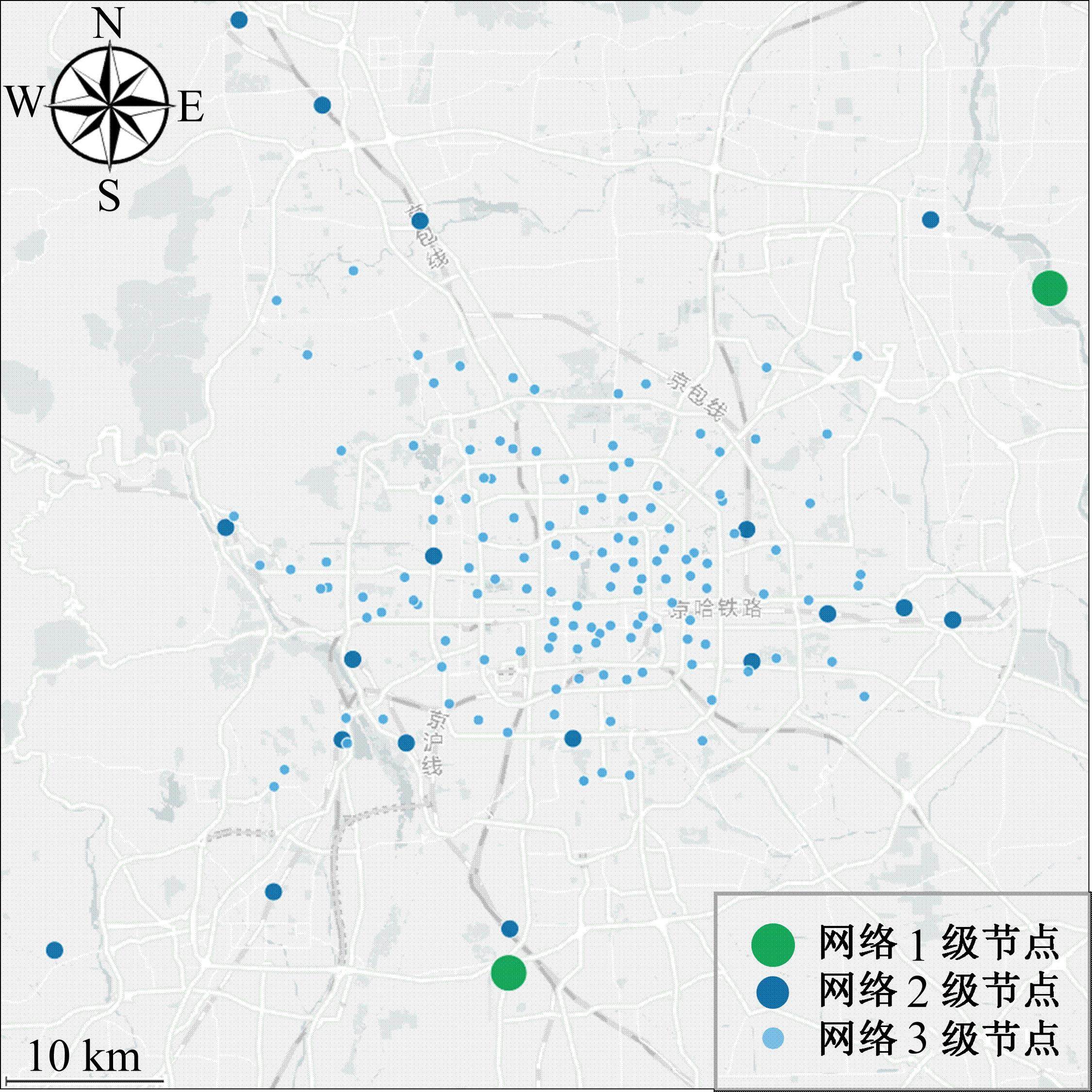
4.2 2级节点连通度分析
根据实际地理数据4对2级节点间连通度进行分析并确定决策变量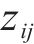
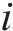
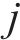
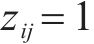
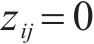
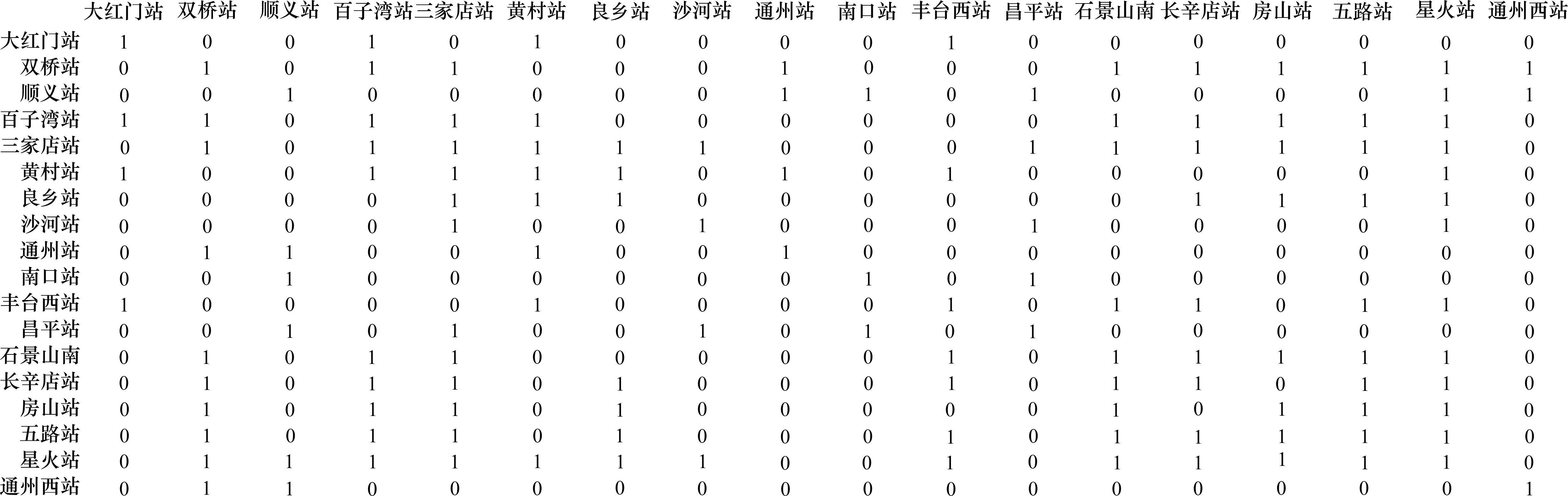
4.3 实验测试
4.3.1 选址分配
如表4所示,基于客户属性对数据集中3级节点加权聚类,制定以下6种策略,聚类策略1到聚类策略3仅探讨3级节点区位信息与时间窗影响下的聚类策略;聚类策略4到聚类策略6主要探讨3级节点区位信息、需求量与时间窗3个影响因素下的聚类策略。
| 策略 | 区位信息 | 需求量 | 时间窗 |
|---|---|---|---|
| 1 | 100 | 0 | 0 |
| 2 | 50 | 0 | 50 |
| 3 | 66 | 0 | 33 |
| 4 | 33 | 33 | 33 |
| 5 | 40 | 20 | 40 |
| 6 | 50 | 25 | 25 |
通过手肘法确定各聚类策略的最佳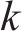
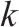
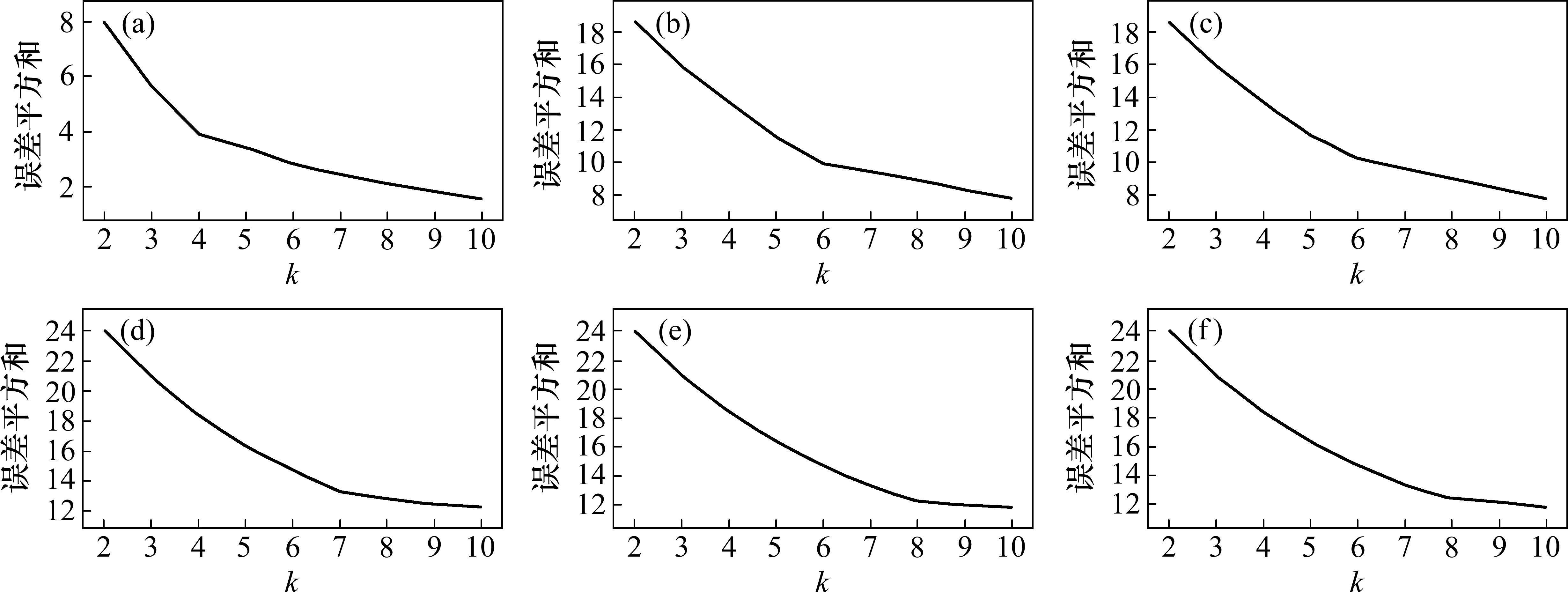
4.3.2 路径优化
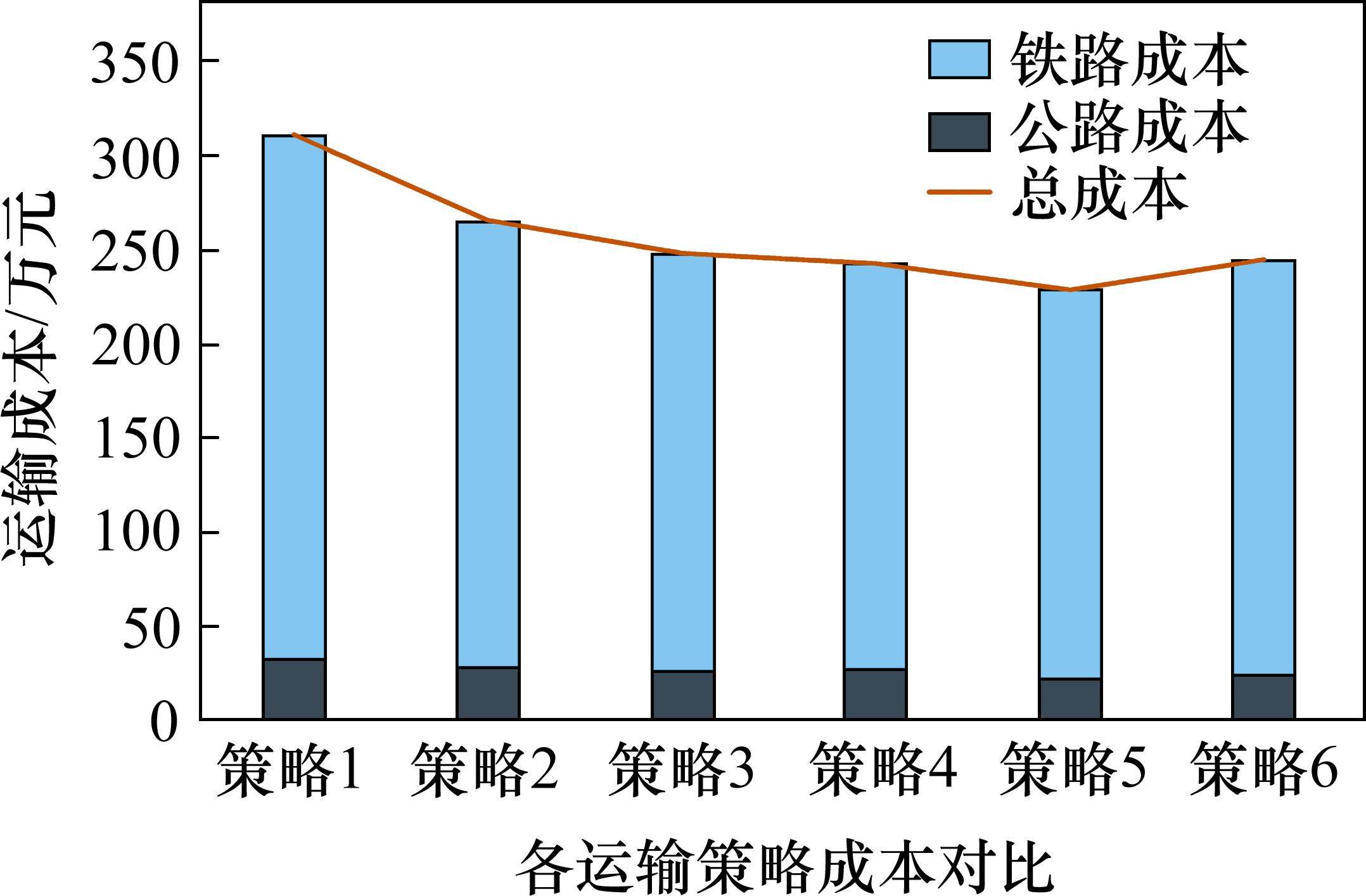
基于聚类结果,将各个聚类结果作为独立模型,采用逆序求解策略进行小运转列车与城市货运卡车配送服务路径优化,各聚类策略下物流成本如表5所示。策略5的总成本最低,其小运转列车成本为23.00万元,公路成本为205.48万元,总成本为228.48万元。
| 策略 | 铁路成本/万元 | Gap/% | 公路成本/万元 | Gap/% | 总成本/万元 |
|---|---|---|---|---|---|
| 1 | 33.31 | 0.92 | 277.64 | 6.42 | 310.95 |
| 2 | 28.49 | 0.94 | 236.95 | 6.32 | 265.44 |
| 3 | 26.28 | 1.24 | 221.64 | 5.34 | 247.92 |
| 4 | 28.24 | 1.85 | 214.31 | 4.45 | 242.55 |
| 5 | 23.00 | 2.69 | 205.48 | 4.48 | 228.48 |
| 6 | 24.52 | 2.77 | 220.08 | 4.44 | 244.6 |
如图8所示为最佳选址结果,参与运输的货运站为大红门站(聚类1中心)、双桥站(聚类2中心)、顺义站(聚类3中心)、五路站(聚类4中心)、百子湾站(聚类5中心)、三家店站(聚类6中心)、石景山南站(聚类7中心)、沙河站(聚类8中心)。
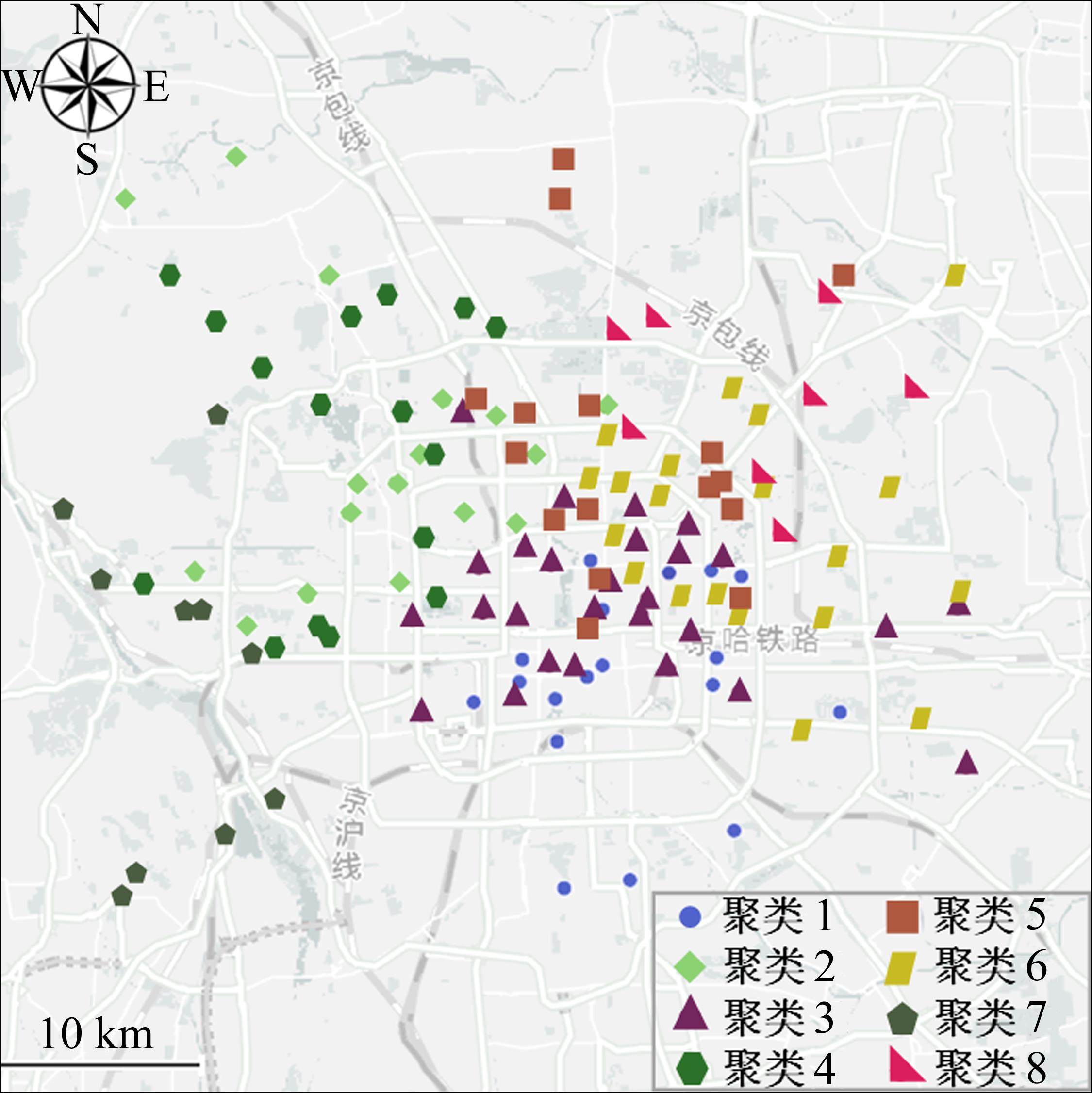
策略5中小运转列车运行路线如图9所示。
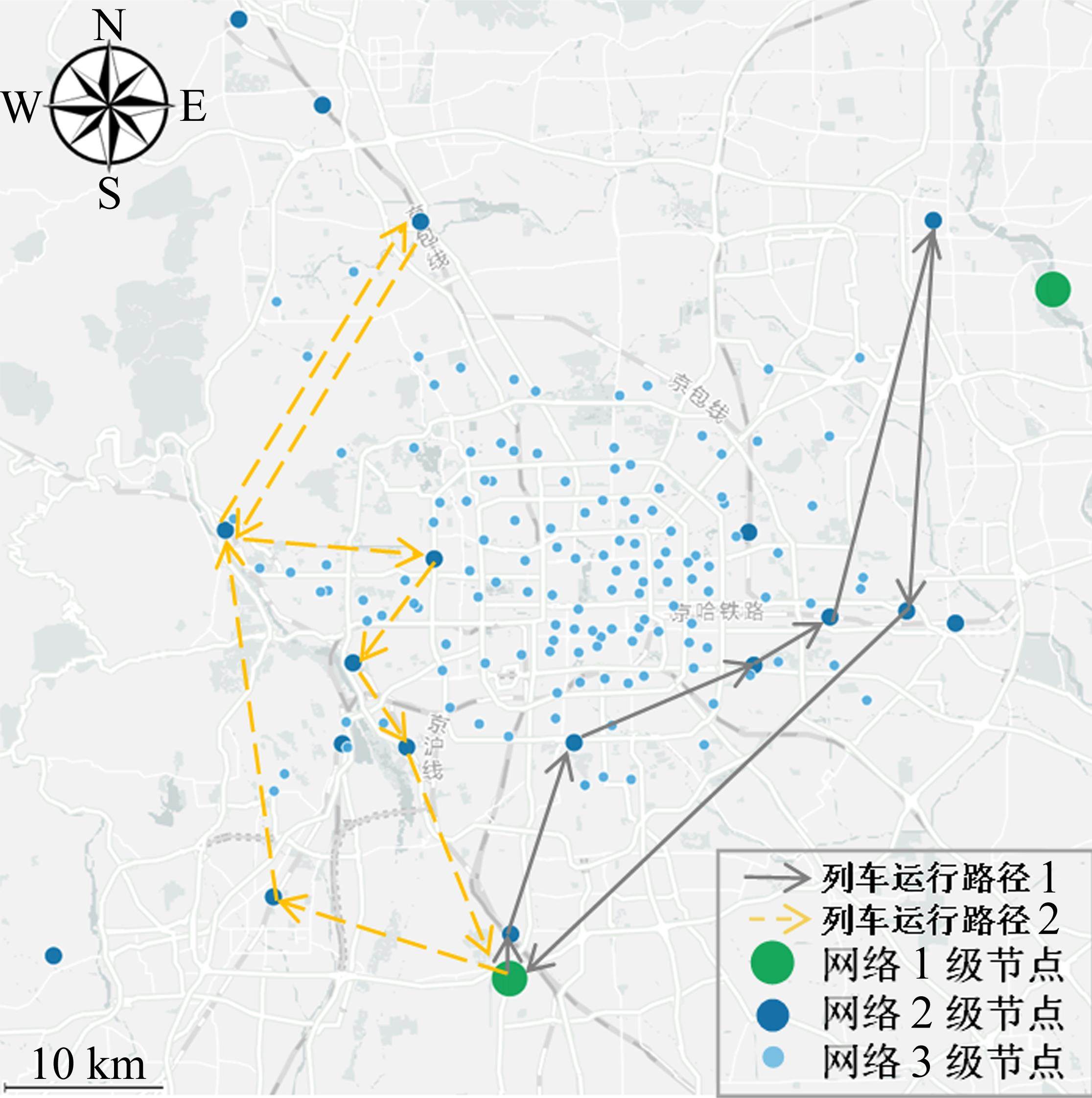
第1列小运转列车运行路线为:京南物流基地→黄村站(途径)→大红门站→百子湾站→双桥站→顺义站→通州西站(途径)→京南物流基地。
第2列小运转列车运行路线为:京南物流基地→良乡站(途径)→三家店站→沙河站→三家店站(途径)→五路站→石景山南站→长辛店站(途径)→京南物流基地。
4.4 结果分析
4.4.1 聚类策略成本对比分析
在识别影响物流运输的主要客户属性的基础上为其分配不同的权重来反映各属性在选址和路径规划中的相对重要性并生成6种不同的聚类策略,每种策略代表不同的客户分类和运输路径规划。
统计不同策略对于成本的影响程度如表6与图10所示,与只考虑客户区位的聚类策略1进行对比,聚类策略2~聚类策略6考虑了更多的聚类类别,相较于策略1,其配送成本降低了14.64%~26.52%。相较于策略1~策略3,策略4~策略6更反映了精细化管理仍能有效地控制物流运输的成本。
| 策略 | 类别数目 | 降低比例/% |
|---|---|---|
| 1 | 4 | 0 |
| 2 | 6 | 14.64 |
| 3 | 6 | 20.27 |
| 4 | 7 | 21.99 |
| 5 | 8 | 26.52 |
| 6 | 8 | 21.34 |
4.4.2 连通度对比分析
对比连通度分析对铁路运输成本的影响,如表7所示,连通度极大影响了小运转列车运行成本,伴随着考虑因素增多,影响程度逐渐减小。该步骤也在一定程度上影响了其运输组织规划,以策略5为例,若未进行连通度分析,则负责物流运输的小运转列车则只有一辆,其路线为:京南物流基地→大红门站→百子湾站→双桥站→三家店站→顺义站→沙河站→五路站→石景山南站→京南物流基地。这仅仅反映了小运转列车的站点服务顺序,并不代表小运转列车的真实运输路线,这与需考虑节点连通度的现实情况相差甚远。
| 策略 | 考虑连通度成本/万元 | 未考虑连通度成本/万元 |
|---|---|---|
| 1 | 33.31 | 22.31 |
| 2 | 28.49 | 19.49 |
| 3 | 26.28 | 18.28 |
| 4 | 28.24 | 23.24 |
| 5 | 23.00 | 18.01 |
| 6 | 24.52 | 18.52 |
5 结论
1) 合理考虑客户属性的选址策略不仅减轻了不同区域的物流成本负担,还促进了物流资源在城市各部分的均衡分布。
2) 物流系统总成本与客户属性的选择及其赋权紧密相关,即便在客户属性不变的情况下,调整权重亦能显著影响成本效益,突显了精细化管理的重要性。
3)证实了连通度分析在该模式的优化运输组织中的重要作用,其有效提升了模型的真实性,弥补了先前研究优化模型的不足。
未来值得进一步研究的问题:1) 探索更多维度的客户属性并纳入模型,以适应更广泛的服务需求和市场变化。2) 深入研究不同城市形态和物流需求特征下,如何动态调整优化模型参数,以实现更灵活高效的物流解决方案。3) 结合新兴技术(如物联网、大数据分析)进一步优化模型预测精度,实现物流系统的实时监控与智能化决策支持。
张宇昂,陈静怡,张肖飞等.考虑客户属性的城市公铁联运物流选址-路径优化[J].铁道科学与工程学报,2025,22(04):1554-1565.
ZHANG Yuang,CHEN Jingyi,ZHANG Xiaofei,et al.Locating-Routing optimization of urban road-rail intermodal transportation network with consideration of customer attributes[J].Journal of Railway Science and Engineering,2025,22(04):1554-1565.

