1 预制节段梁生产工艺描述

就预制节段梁生产而言，作业和机器分别由不同类型的预制构件和生产流程来表示^[1]，如图1所示。节段梁的预制生产一般分为9个流程。首先，由于预制技术的标准化程度不高，在生产前需要制作模具。然后，在组装作业时进行边框的固定、模具表面的清洁和涂油。混凝土凝固后，模具将被剥离以重新使用，再进行节段梁的抛光和修补。最后，新浇筑梁段将转运至匹配梁段以完成匹配。

图1全屏查看

短线法节段梁预制工艺流程图

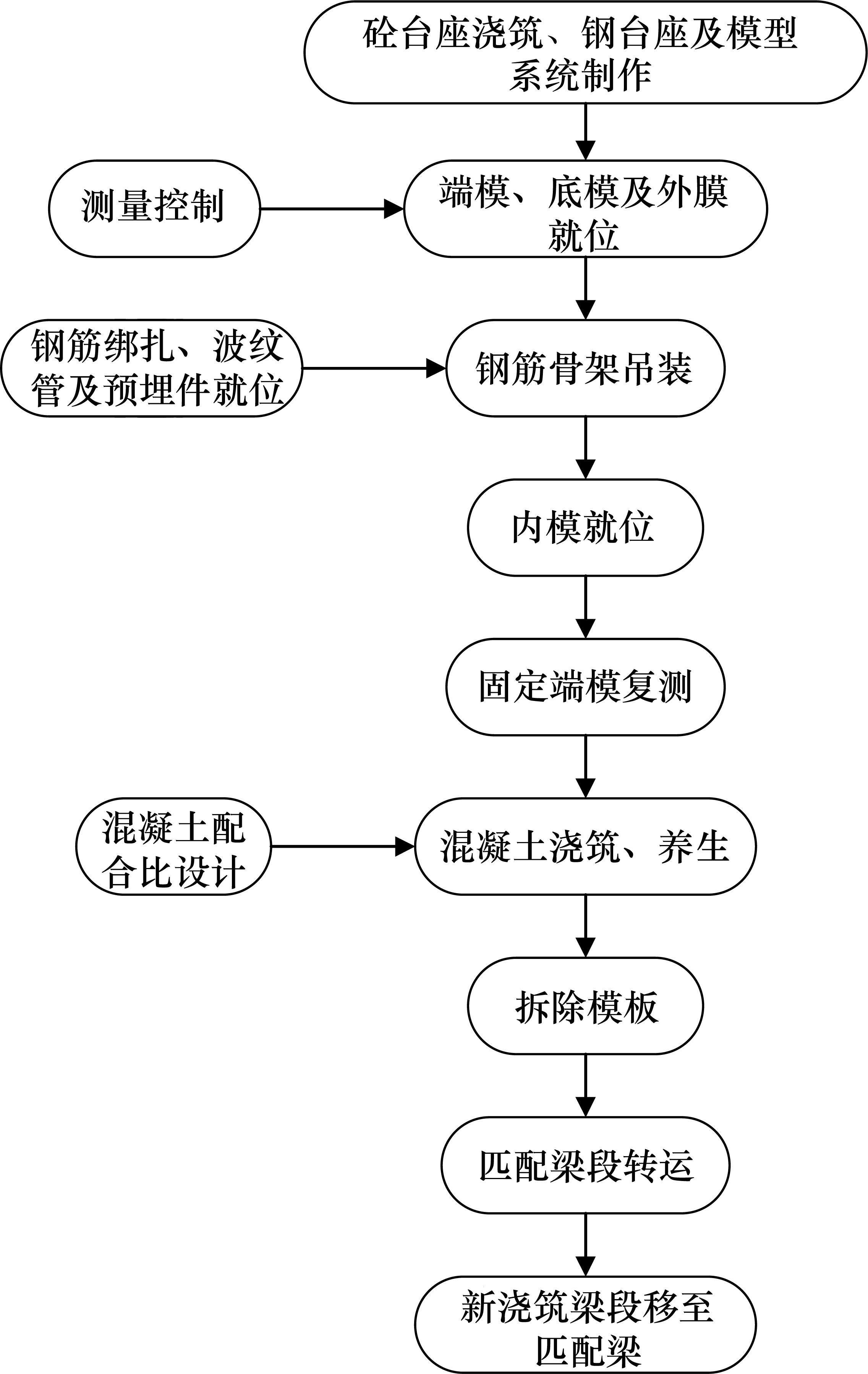
然而，预制过程中存在的不确定性通常会导致工期延误、成本超支、生产率损失和多方争议，假设生产过程考虑资源约束后的链路共包含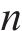项关键活动，由于每项活动工序时间和生产效率不一致，将会导致活动之间产生中断。因此，提高生产进度管理应对不确定性的能力非常重要。问题在于如何在不确定性和资源约束条件下计算和分析项目工期，以提供更可靠的项目进度，从而大幅降低成本超支的风险^[12]。本文引入关键链项目缓冲管理，从项目管理的角度考虑预制节段梁生产过程中存在的不确定性问题，通过设置缓冲吸收预制节段梁生产过程中不确定性。

2 基于工期-成本-质量目标优化的函数确定

首先需要研究工期、成本和质量三者之间的函数关系。节段梁生产过程中工期与成本、质量的关系，可分解为单个工序工期与成本、质量关系的累加。

2.1　工期-成本函数关系的确定

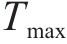
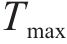
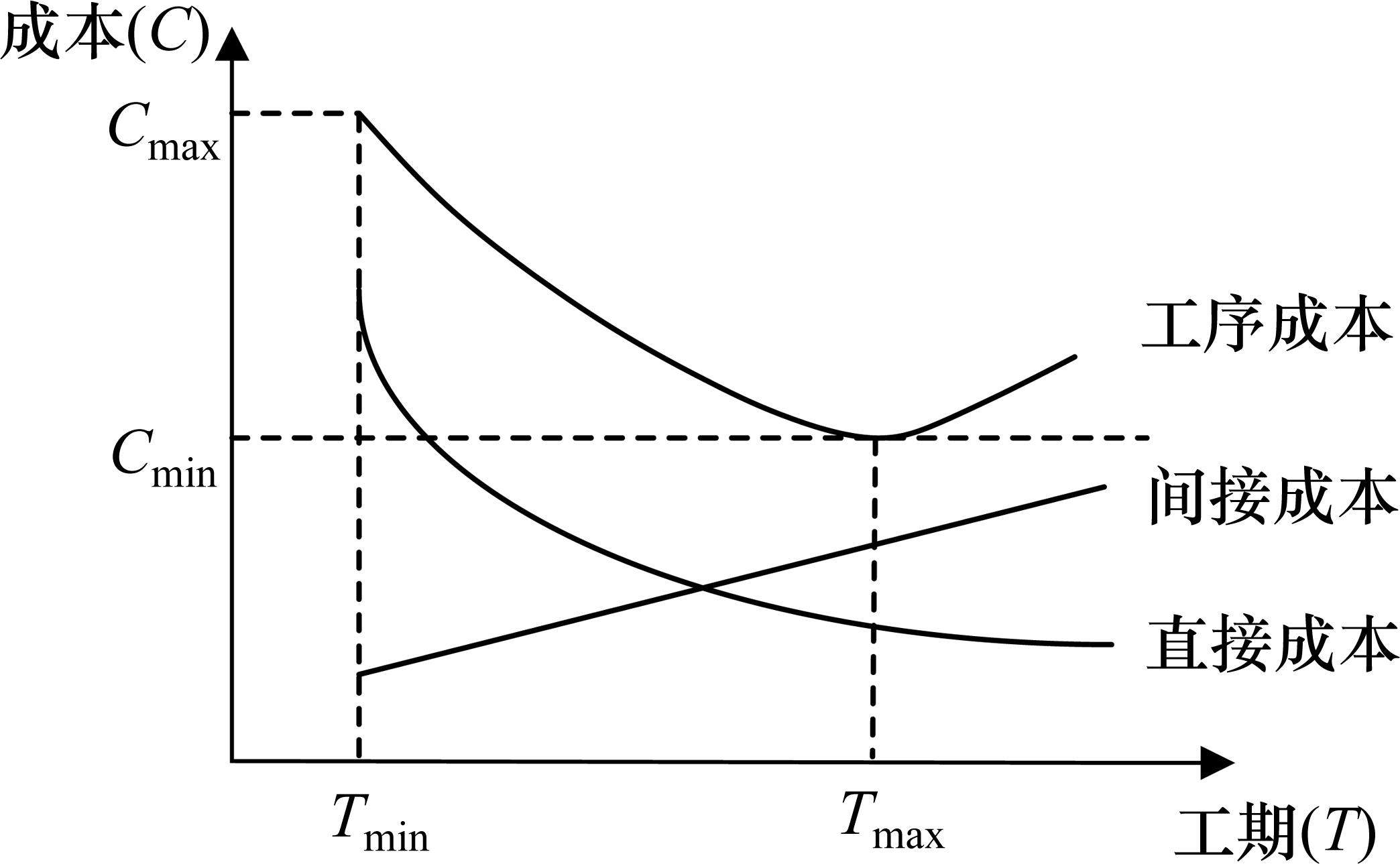
工序成本由直接成本和间接成本组成，直接成本包含固定成本和变动成本^[13]，其中，固定成本不随工期的变化而变化；变动成本随工期的缩短而增加。因此，直接成本随工期的增加而减少，与工期呈反比；间接成本随工期的增加而增加，与工期呈正比。综上，随着工期的增加，工序成本呈现如图2所示的先下降后上升趋势^[14]。在工期稳定于之前，工序成本随工期的增加而降低；工期在之后，成本随工期的增加而增加。

图2全屏查看

工期-成本关系曲线

因此，工序工期维持在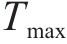左侧工序成本与工期达到最优。为简化成本计算，假定在正常时间和压缩时间范围内，工期与成本之间呈线性关系，且忽略环境、施工技术复杂度等不确定因素对工序成本的影响^[15]。由于预制节段梁在封闭的车间环境中进行生产，在车间环境中，生产过程可以受到更严格的控制，包括温度、湿度、气压等参数的调节^[16]，所以受外部环境因素(如天气、地形、资源供给等)影响较小，并且其标准化生产流程、专业化设备、规范化质量控制以及减少现场操作风险等特点，使得生产过程更加简化、可控，从而提高了生产效率并减少了技术方面的不确定性^[17]。

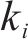
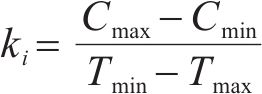
工期-成本函数关系斜率可表示为：

(1)

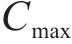
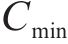
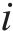
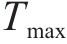
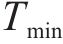
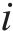
其中，和分别表示工序的最高成本和最低成本；和分别表示工序的最长工期和最短工期。

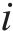
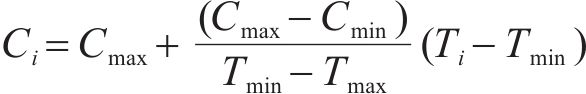
根据式(1)可得工序的成本为：

(2)

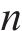
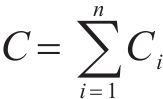
由于项目非关键链部分的接驳缓冲起到保护关键链上工序的作用，因此不考虑非关键链的影响。关键链上个工序的总成本为：

(3)

2.2　工期-质量函数关系的确定

在实际生产中，加快生产进度，会对项目生产质量造成无法避免的影响，质量会随工期的缩短而降低，与工期呈正比关系。本文参考国家标准《工厂预制混凝土构件质量管理标准》(JG/T 565—2018)、《装配式构件质量标准》和《装配式建筑预制混凝土构件质量检验标准》对预制节段梁的质量进行量化，将质量目标量化为一个介于0和1之间的数值范围内，数值接近于1表示工序的质量较高，而接近于0则表示工序的质量较低。假定工期与质量关系为线性关系，根据质量量化的数值范围，将最优质量定义为接近1的数值，表示工序质量达到最高水平，满足或超出所有质量目标和要求；将最低标准质量设置为0.6确保工序的质量达到基本可接受的水平，这意味着即使在项目或产品的质量要求较低的情况下，仍然能够保证一定程度的质量可靠性。函数图像如图3所示。

图3全屏查看

工期-质量关系曲线

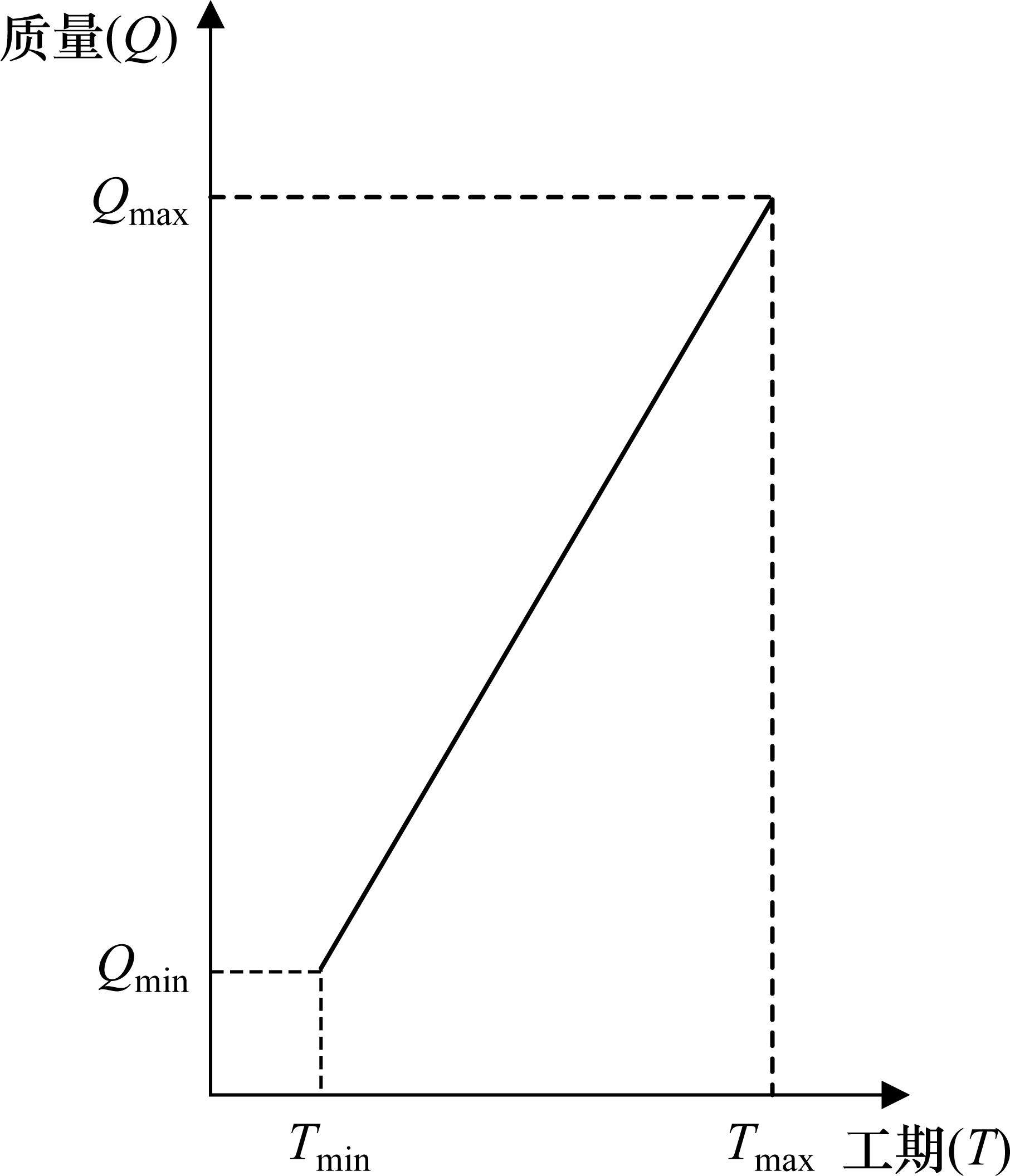
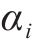
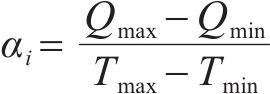
工序工期-质量函数关系斜率为：

(4)

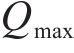
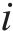
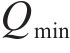
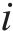
其中，是工序的最优质量；是工序的最低标准质量。

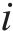
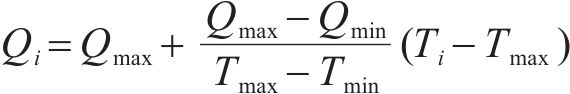
由式(4)可得工序的质量为：

(5)

根据每个工序对施工整体质量的影响程度不同，工序总质量可以用线性加权表示，如式(6)所示。

(6)

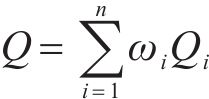
3 基于工期-成本-质量综合效用的项目缓冲确定

关键链指由优先关系和资源限量都可行的活动集合形成的一条虚拟链条^[18]。项目缓冲位于关键链末端，以吸收项目的不确定性，保证关键链的按时完工^[8]。基于工期-成本-质量多目标优化的方法确定缓冲，首先依据工序风险对工期、成本和质量的暴露度确定工期、成本、质量在综合效用中的权重；其次通过构建工期-成本-质量效用函数来确定最佳效用时间；最后利用时间弹性系数修正缓冲区，并运用根方差法将缓冲区集中在项目尾部。

3.1　基于风险事件的工期-成本-质量权重确定

鉴于生产工序的独特性，各个工序的工期、成本和质量对综合效用的贡献程度存在差异。要突出这些差异，就必须为工期、成本和质量分配适当的权重。过去，通常使用德尔菲法确定项目权重，这种方法简单易行。但是，它常常忽略了工序自身特性对工期、成本、质量效用权重的影响。

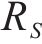
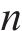
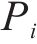
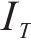
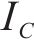
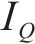
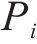
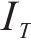
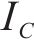
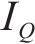
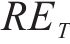
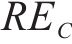
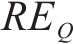
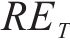
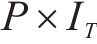
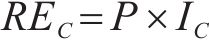
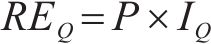
因此，本文通过识别不同工序中的风险，客观地确定工期、成本和质量的权重。风险识别有助于分析各个工序受到的风险对工期、成本和质量的影响程度。不同工序可能会受到不同风险事件的影响，即使是相同的风险事件，其对工期、成本和质量的影响程度也可能不同。这种影响程度通常反映了工期、成本和质量对项目总效用的重要程度。通过分析各工序风险事件对工期、成本和质量的暴露程度，依据其暴露度比例，客观地赋予工期、成本和质量在综合效用中的权重系数^[8]。假设项目的风险集合由个风险事件组成，每个事件包含的4个变量表示为：,,,。其中，是发生风险事件的概率，、、分别是总工期、总成本和总质量受风险影响的程度。此外，风险对工期、成本和质量的暴露度分别由、、表示，并且=，，。

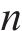
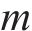
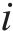
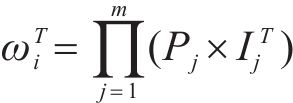
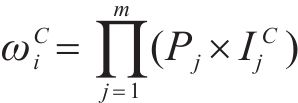
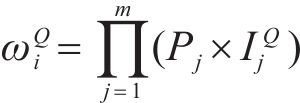
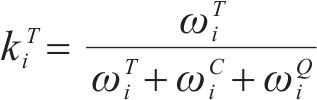
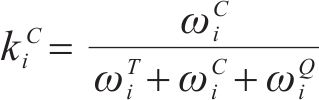
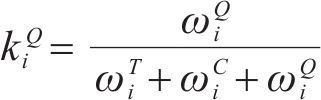
若关键链上有个工序，每个工序存在个潜在风险事件。那么，对于工序的工期、成本和质量权重分别表示为：

(7)(8)(9)(10)(11)(12)

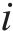
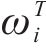
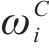
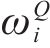
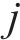
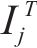
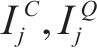
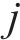
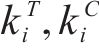
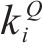
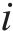
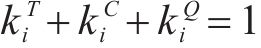
其中，风险对工序的工期、成本、质量的影响分别由,和表示；风险发生的概率由表示；,分别表示风险对工期、成本、质量产生的影响；和分别是工序的工期、成本、质量权重系数，并且。

3.2　工期-成本-质量综合效用的函数确定

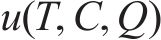
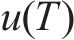
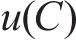
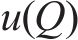
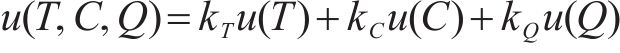
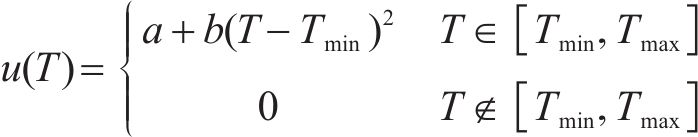
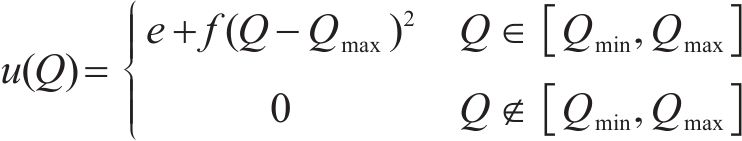
效用是指在一段时期内，消费者对某一产品或服务的消费所得到的满意度。效用函数反映顾客在消费过程中所得到的效用与其所消费的各种产品数量之间的关系，它是一种无量纲的尺度，常在消费需求理论、经济学等领域的研究中发挥作用^[19]。在本文中，引入多属性效用函数，将多目标问题转化为求工期-成本-质量综合效用最大的单目标优化问题^[9]。即将综合效用表示为单属性效用函数、、的加权和，即：

(13)(14)(15)(16)

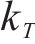
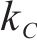
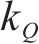
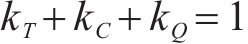
其中，工期、成本和质量的权重系数分别由、、表示，且。

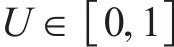
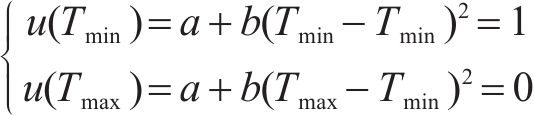
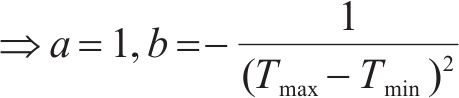
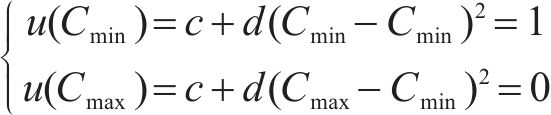
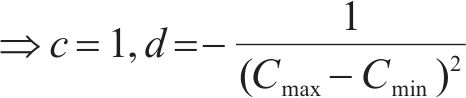
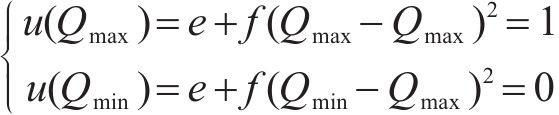
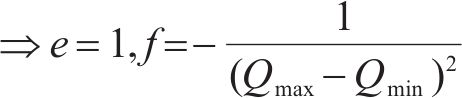
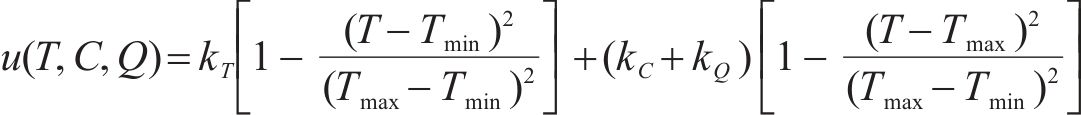
在项目生产过程中，3个目标要求为：工期尽量短，成本尽量低，质量尽量优，反映在效用函数上是工期-成本-质量综合效用最大。效用表示满意度水平，其中，效用值越大表示变量的取值对项目管理者的满意度越高。即：

(17)(18)(19)

由式(2)、(5)、(17)、(18)、(19)整理得：

(20)

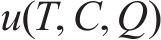
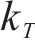
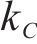
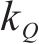
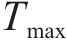
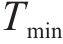
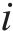
式中：是综合效用函数；，，分别表示工期、成本和质量的权重系数；和分别表示工序的最长工期和最短工期。

3.3　确定项目缓冲

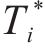
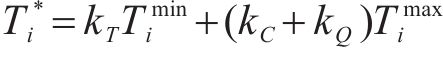
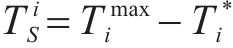
项目缓冲区的设置主要是为了消除不确定因素对工程进度的不利影响。安全时间是指在特定环境下，为确保任务、工作或活动能够顺利完成而提前预留的一段时间。这段时间通常用于处理意外情况、突发事件或不可预测的延迟，以确保整个过程不会因为意外情况而中断或延误^[20]。在全面考虑工期、成本、质量和风险等对综合效用影响的基础上，各工序的最佳效用时间及安全时间为：

(21)(22)

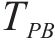
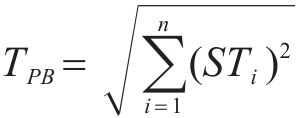
基于根方差法^[21]的思想，设为项目缓冲，确定缓冲大小的模型为：

(23)

4 实验模拟

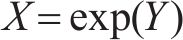
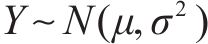
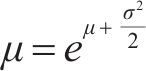
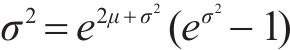
为检验项目缓冲模型的有效性，对黄茅海大桥的单个节段梁生产进行模拟验证。按照进度要求，黄茅海大桥的节段梁计划于2021年7月1日开始批量预制，2023年4月25日全部预制完成，总工期664 d。工期服从右偏的对数正态分布^[22]，，则均值和方差如式(24)和式(25)所示。

(24)

(25)

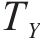
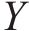
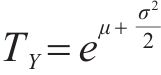
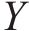
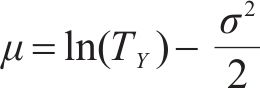
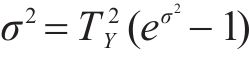
设工序时间为的均值，，则对有^[23]

(26)

(27)

工序标准差是通过随机函数来产生，即：

(28)

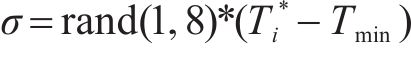
节段梁生产的关键链网络图如图4所示，假设在节段梁生产过程中每个工序的台班数是固定的，同时在考虑工序搭接关系和资源限制的共同影响下，关键链确定为：A→C→E→F→G→I→J→K，单个节段梁生产的关键链工序基本信息如表1所示。

图4全屏查看

关键链网络图

表1全屏查看

关键链工序基本信息

工序	/h	/h	/万元	/万元
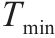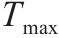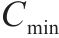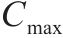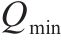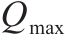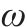A	8	10	1.05	1.31	0.60	1.00	0.128
C	6	9	0.78	1.18	0.60	1.00	0.127
E	14	15	1.83	1.96	0.60	1.00	0.128
F	11	13	1.44	1.70	0.60	1.00	0.124
G	5	6	0.65	0.78	0.60	1.00	0.125
I	144	160	18.82	20.91	0.60	1.00	0.124
J	6	8	0.78	1.05	0.60	1.00	0.123
K	5	6	0.65	0.78	0.60	1.00	0.121

展开更多

由风险事件确定节段梁生产过程中发生风险的概率，根据其发生后对工期、成本和质量的影响程度确定效用权重。节段梁生产过程中的风险事件及其对生产的影响如表2所示。

表2全屏查看

节段梁生产风险事件识别

风险事件		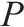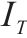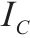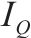/%	/%	/%	风险事件		/%	/%	/%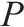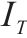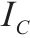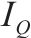
1	0.02	3	3	2	5	0.15	10	8	10
2	0.08	2	5	5	6	0.18	10	10	15
3	0.12	5	5	5	7	0.01	2	2	2
4	0.06	4	3	4	8	0.10	5	5	5

展开更多

根据表2中对风险事件的识别，评估各工序的工期、成本和质量权重，计算最佳效用时间和安全时间。之后，通过最佳效用时间和效用函数关系，得到关键链工序的参数如表3所示。

表3全屏查看

关键链工序参数

工序名称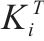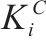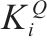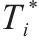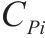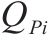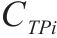
A	0.38	0.38	0.25	9.25	0.75	1.15	0.06	0.12
C	0.17	0.42	0.42	8.50	0.50	0.85	0.06	0.10
E	0.33	0.33	0.33	14.67	0.33	1.87	0.15	0.13
F	0.36	0.27	0.36	12.27	0.73	1.53	0.13	0.13
G	0.36	0.29	0.36	5.64	0.36	0.70	0.05	0.12
I	0.29	0.29	0.43	155.43	4.57	19.42	0.16	0.12
J	0.33	0.33	0.33	7.33	0.67	0.87	0.03	0.12
K	0.33	0.33	0.33	5.67	0.33	0.69	0.02	0.12

展开更多

注：为在最佳效用时间下计划成本；为在最佳效用时间下计划质量；为时平均成本。

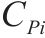
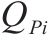
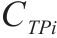
本研究借助MatlabR2022b软件进行蒙特卡洛模拟，将实验运行1 000次。根据项目期望和方差分别模拟本文方法、未含质量(工期-成本)法与RSEM法，对比结果如表4、图5、图6和图7所示。

表4全屏查看

本方法同传统方法对比结果

	缓冲/h	实际工期/h	实际成 本/万元	实际质量	缓冲消 耗率/%	超计划工期概率/%	超计划 成本概率/%	超计划质量概率/%	效用()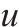
本文方法	5.13	217.32	27.27	0.96	51.19	57.69	58.74	63.25	0.70
未含质量	8.50	212.87	27.85	0.80	53.86	89.74	91.47	83.25	0.65
RSEM	1.88	216.16	27.42	0.82	90.81	68.54	88.10	76.32	0.44
C&PM	27.47	—	—	—	—	—	—	—	—

展开更多

注：RSEM为根方差法；C&PM为剪切-粘贴法。

图5全屏查看

实际工期和缓冲对比

图6全屏查看

实际成本和实际质量对比

图7全屏查看

综合效用和缓冲消耗比对比

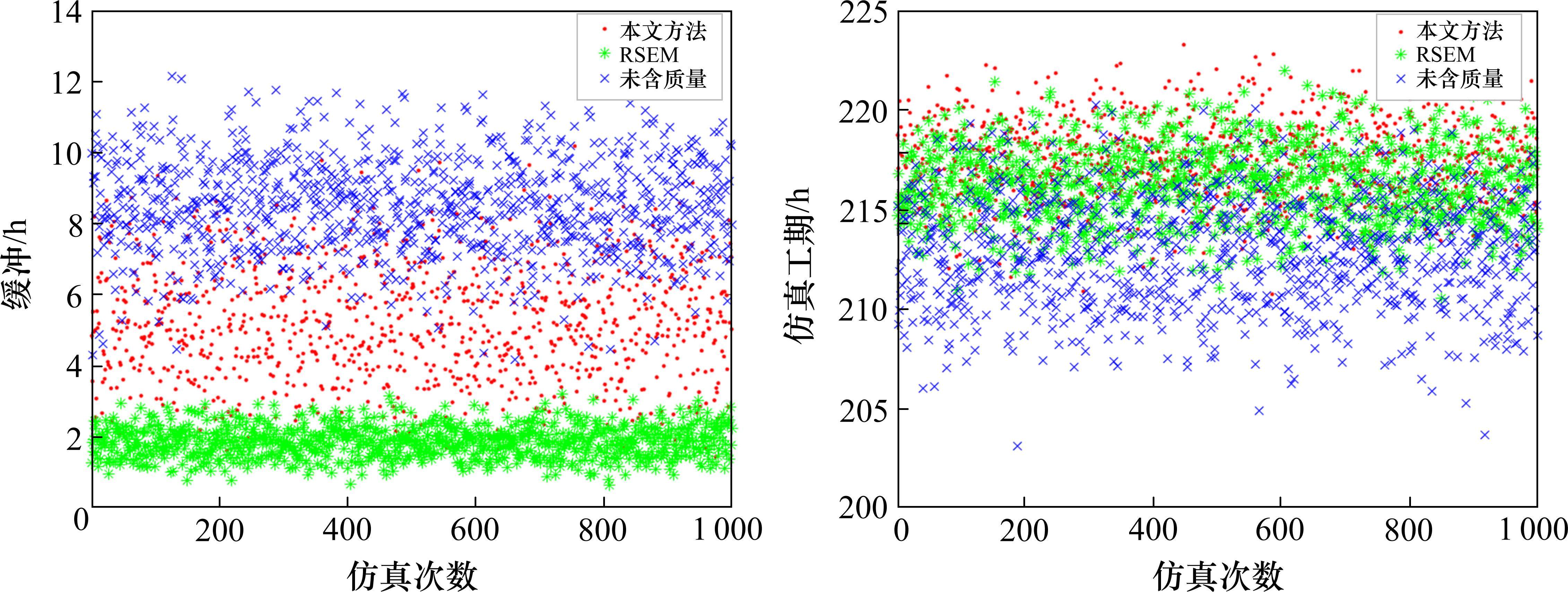
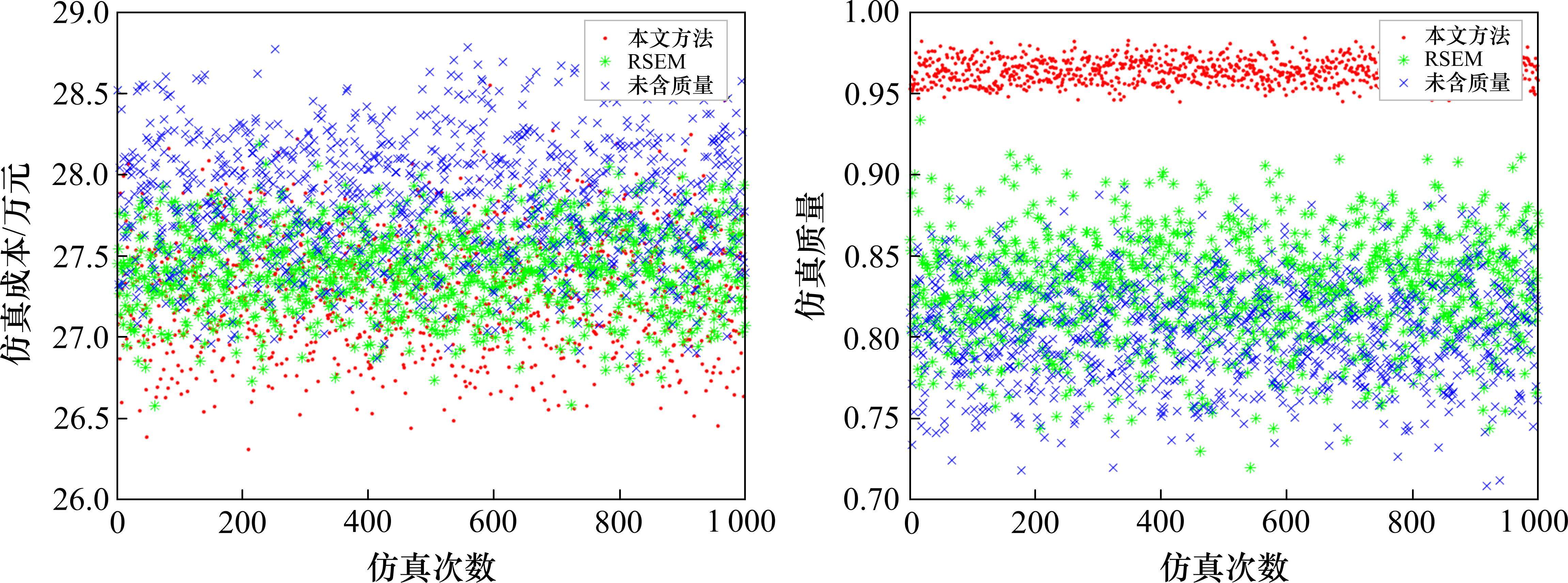
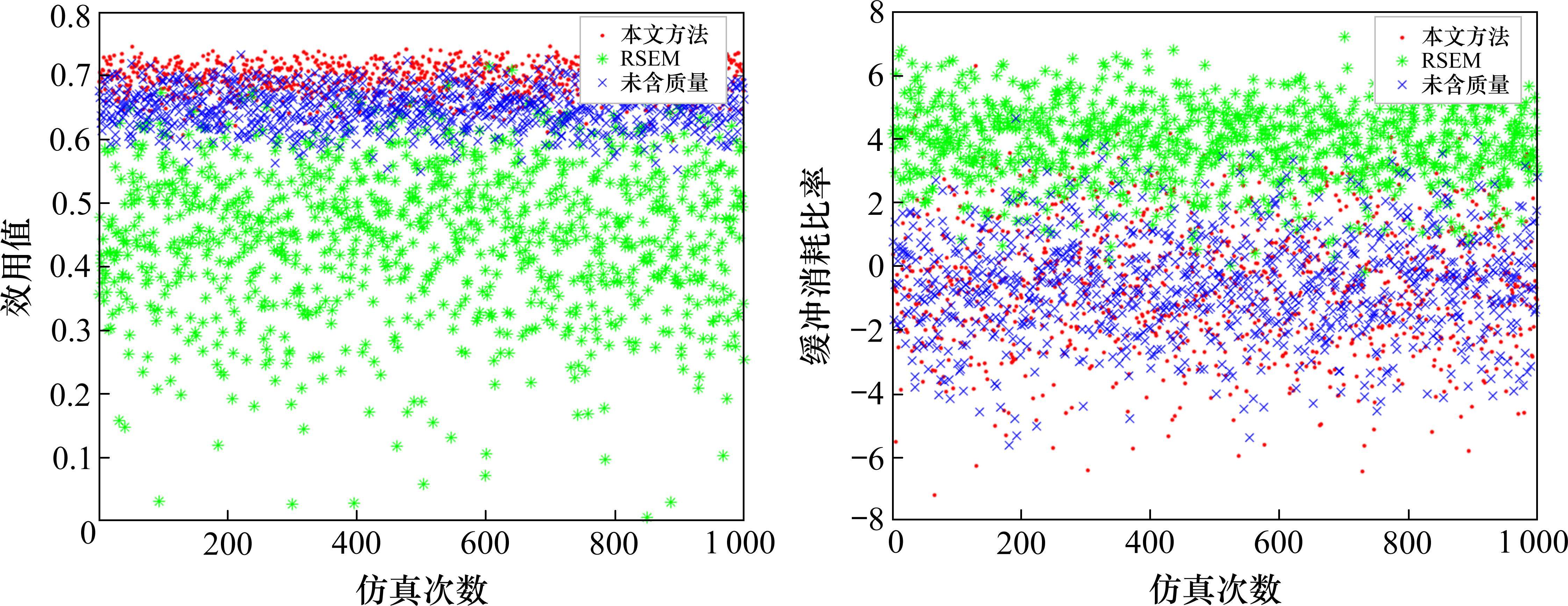
由上述结果可以得到以下结论：

1) 从表4和图5、图6的结果中可以看出，本文方法确定的缓冲区大小小于未含质量的，但本文方法和未含质量法确定的缓冲均介于RSEM和C&PM之间，这将从以下3个方面解释：第一，C&PM对链路上所有工序按50%的原则设置缓冲，使得缓冲区呈线性增长趋势，导致缓冲过大，对项目造成了过度保护^[24]；第二，RSEM法同样用“减半”的方法确定基准工期，缓冲区由根方差法确定，但该方法没有充分考虑人员因素，导致缓冲空间过小，具有一定的局限性；第三，本文方法充分考虑各工序实际情况，确定工期-成本-质量三者的关系，相较于考虑工期-成本而确定的缓冲更加合理，能够实现项目工期，成本和质量的三重优化。

2) 由表4和图5、图6可知，RSEM和本文提出的方法的工期分别为216.16和217.32，成本分别为27.42和27.27，本文方法确定的节段梁生产实际成本低于对比方法，实际工期和质量优于对比方法。这是由于：第一，传统的缓冲区确定方法在抽取安全时间时，常将因学生综合征而导致的作业过程中所耗费的大量时间进行计算，但实际中所能得到的安全时间并非完全受学生症候群和帕金森效应的影响；第二，本文所提出的缓冲提取方法在优化工期、成本和质量方面具有显著优势，以工期、成本和质量共同决定的效用最大化作为总目标，使其成本明显低于对比方法，而工期和质量则相对较优。

3) 由表4和图7可知，本文所提出的方法在缓冲消耗率方面较RSEM法更低，同时综合效用也更高于对比方法。这一结论的原因主要有以下几点：首先，RSEM法仅将工期最短作为目标，忽略了压缩工期对成本和质量的影响，从而导致综合效用降低；其次，本文方法的缓冲消耗率为51.19%，均低于对比方法，这是由于该方法以工期-成本-质量综合效用最大为目标，将安全时间抽取出来作为缓冲，减少各工序安全时间的浪费，降低项目缓冲的平均消耗。

综上所述，本文提出的方法根据综合效用优化节段梁生产工序的工期，成本和质量，设置的项目缓冲对关键链工序起到更好的保护作用，可减少项目延误风险，确保项目按计划完工。

5 结论

1) 通过实地考察黄茅海大桥，总结了节段梁生产工艺流程图，并考虑工期、成本和质量的三重约束，利用多属性效用理论构建了综合效用函数，将多目标优化问题转化为求解工期、成本和质量综合效用最大的单目标问题。

2) 基于风险识别的方法确定工期、成本和质量权重，并利用效用函数对3个指标进行归一化，确定最佳效用时间。

3) 引用工程实例—黄茅海大桥节段梁生产，进行实验模拟，验证缓冲确定对节段梁生产能提供有效的保护，可实现工期、成本和质量综合效用最大化。

在节段梁生产过程中，除工期、成本和质量因素外，仍存在其他因素，如需求变动、生产设备故障等，后续可研究这些因素的共同作用，决定项目的综合效用。此外，本文仅对单个节段梁生产进行了缓冲确定，未来的研究将探讨整个工程的节段梁生产缓冲设置情况，分析动态情况下缓冲区的确定和监控，以达到对节段梁生产进度实施动态控制的目的。