滑石(Talc)是一种无机非金属硅酸盐矿物,化学式为Mg3[Si4O10](OH)2。滑石通常由富镁矿物经热液蚀变形成,与硫化矿物有着相似的形成环境常伴生于硫化矿中。目前,滑石的存在极大地影响了目的矿物的浮选分离[1-5]。滑石对浮选过程带来的影响的主要原因是:1) 滑石具有良好的可浮性,有时候可浮性甚至比目的矿物还要强,造成滑石难以抑制,容易随气泡进入精矿产品中,进而降低选矿指标[6-10];2) 滑石硬度极低,在破碎、磨矿过程中容易发生泥化,导致滑石变为矿泥罩盖在矿物表面,阻碍了目的矿物与药剂的相互作用[11]。此外,滑石还会导致泡沫发黏、捕收剂选择性变差、浮选环境恶化、药剂用量增大、精矿指标下降等诸多问题[12-14]。
针对滑石可浮性好、泥化严重的特点,一般可以通过3种方法分离滑石与硫化矿:预先浮选脱除滑石;采用酸浸法去除精矿中滑石;在浮选中通过加入滑石抑制剂来抑制滑石[15]。对含滑石硫化矿,采用预选浮选工艺可以脱除大部分滑石,但也会导致目的矿物的损失;而酸浸法则需要大量的酸液,增加了环境治理难度以及处理成本,并对浮选设备造成腐蚀,所以,酸浸法的运用也较少。而在浮选过程中,加入无机类滑石抑制剂,例如水玻璃和六偏磷酸钠等,虽有效避免了对环境的严重污染以及对设备的腐蚀,但存在选择性差和用量大等缺点。陈桃等[16-19]对含滑石矿物浮选分离方法进行了研究,目前,采用常规工艺对于高滑石难选矿物的浮选仍难以获得良好指标,因此,分离滑石的热点转向了新型有机抑制剂的研究。
目前滑石常用的有机抑制剂有淀粉、瓜尔胶、壳聚糖、黄原胶、羧甲基纤维素及其衍生物等,这些有机抑制剂具有原料来源广泛、价格低廉、无毒性或毒性小、对环境污染小等特点,在矿物浮选领域有着广泛的应用[20-25]。ZHANG等[26]应用普鲁兰多糖为抑制剂分离滑石与辉钼矿,发现普鲁兰多糖对滑石具有较好的抑制作用,并且通过红外光谱的测试结果推测普鲁兰多糖与滑石表面之间发生了氢键作用。XIE等[27]为降低滑石的疏水性,将淀粉改性试剂羟丙基磷酸二淀粉(HDP)作为抑制剂,并通过DFT计算发现HDP与滑石的吸附过程中存在氢键作用。铝离子对滑石浮选中羧甲基纤维素的抑制作用有增强的效果,LUO等[28]利用DFT计算方法研究了水合铝离子在滑石(001)的吸附并解释了吸附现象。不同抑制剂及其衍生物在滑石抑制方面表现不同,因此,需对新型有机抑制剂的应用与开发进行研究。
本文通过纯矿物及实际矿物浮选试验,考察4种多糖类抑制剂(羧甲基瓜尔胶、普鲁兰多糖、羧甲基纤维素、羧甲基壳聚糖)对滑石浮选行为的影响,并采用DFT计算以及分子动力学模拟,从分子尺度进一步阐明分子尺度的抑制剂作用机理。
1 试验材料与研究方法
1.1 试验药剂
试验中所使用药剂主要有抑制剂(羧甲基瓜尔胶、普鲁兰多糖、羧甲基纤维素、羧甲基壳聚糖)、捕收剂(Y89)、起泡剂(甲基异丁基甲醇)。其中,羧甲基瓜尔胶为分析纯,购自福晨化学试剂有公司;普鲁兰多糖为分析纯,购自上海江莱生物科技有限公司;羧甲基纤维素为分析纯,购自天津奥普升化工有限公司;羧甲基壳聚糖为分析纯,购自合肥巴斯夫生物科技有限公司;Y89为化学纯,购自湖南明珠浮选药剂有限公司;甲基异丁基甲醇为化学纯,购自上海一研生物科技有限公司。
1.2 试验原料
本试验所用滑石纯矿物来自桂林市临桂县桂广滑石开发有限公司,细度为45 μm,纯度约为98%,仅含少量杂质,故认为试验所用原料为滑石纯矿物。
实际矿物试验所用原料取自刚果某高滑石铜硫矿,其主要化学多元素分析结果如表1所示。由表1及物相分析结果可知:该铜硫矿所含杂质众多,伴生硫化矿物有黄铁矿、磁黄铁矿,脉石主要有滑石、石英、蛇纹石等,故实际矿物原料属于难选矿物。矿石组成以硅酸盐主,质量分数为54.96%;氧化物次之,质量分数为26.42%;硫化物质量分数为15.78%。矿石中的铜主要以独立矿物的形式赋存于黄铜矿、斑铜矿、辉铜矿、硫砷铜矿、铜蓝、孔雀石、铋车轮矿中(占铜分配率的89.35%),其中以黄铜矿占比最高(占铜分配率的72.05%),少量以类质同象或机械混入(铜矿物的次显微、超显微包裹体)的形式赋存于闪锌矿、黄铁矿、磁铁矿、普通角闪石、金/黑云母、绿泥石、滑石、蛇纹石、透闪石、绿帘石和石英、长石中(占铜分配率的10.65%)。最终对以磨矿细度为小于74 μm、占72%的高滑石铜硫矿进行浮选试验。
| Cu | Mo | S | As | Pb | Zn | K2O | Fe |
|---|---|---|---|---|---|---|---|
| 0.45 | 0.01 | 6.79 | 0.10 | 0.01 | 0.35 | 2.60 | 10.14 |
| Na2O | SiO2 | Al2O3 | CaO | MgO | P | F | Mn |
| 0.29 | 50.47 | 8.69 | 3.01 | 11.54 | 0.14 | 0.22 | 0.20 |
1.3 研究方法
1.3.1 DFT模拟方法
模型的优化计算由Materials Studio中的CASTEP模块完成。使用超软赝势来近似表征原子核与电子的相互作用。采用广义梯度近似(GGA)和PBE泛函来描述电子的关联交换。原子最大位移、原子间最大内应力、能量最大变化、自洽迭代 精度的收敛值分别设置为0.03 eV/(10-10 m)、 0.05 GPa、1.0×10-5 eV/个、2.0×10-5 eV/个。此外,在计算过程中采用DFT-D校正。
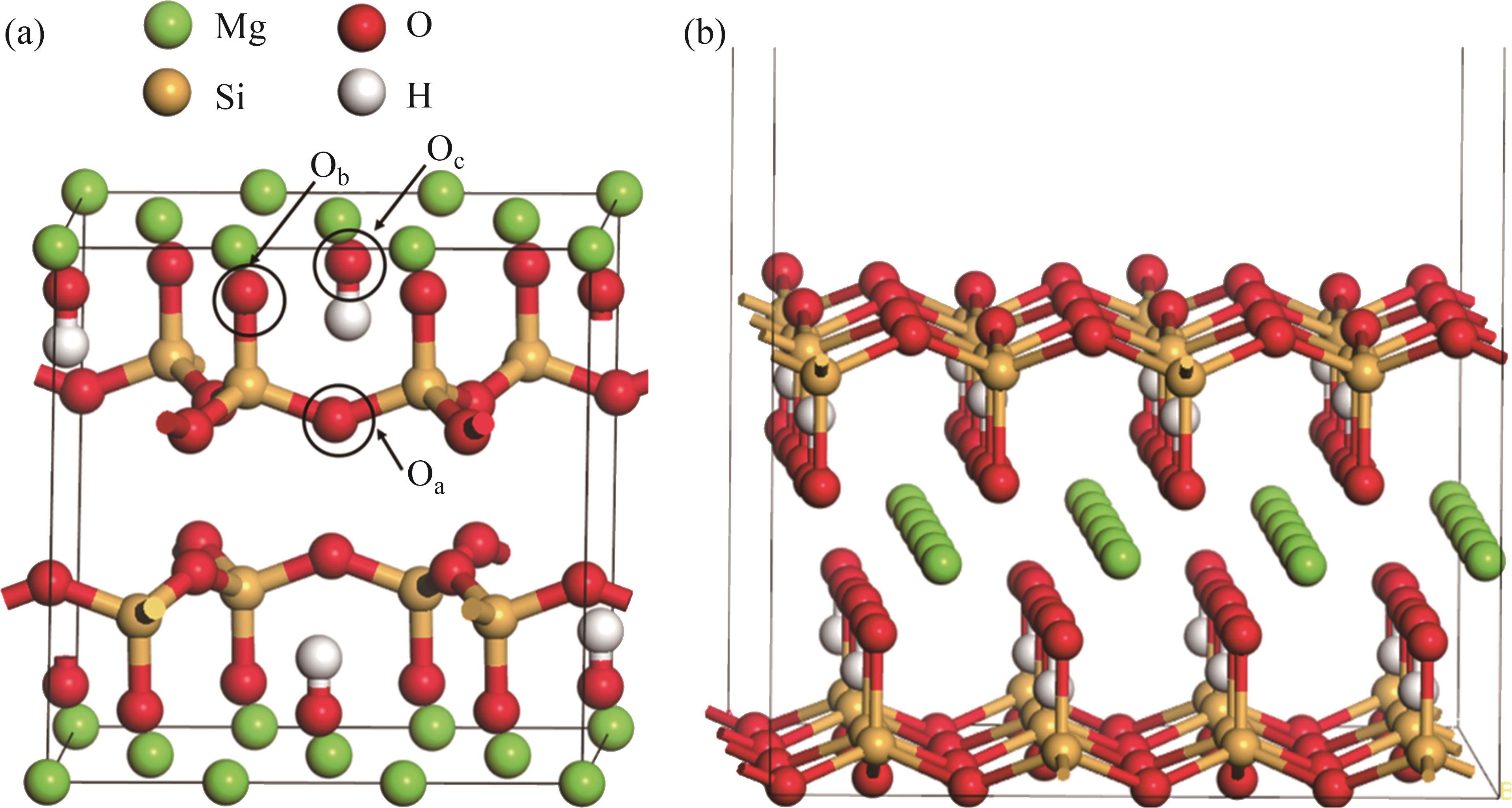
图1(a)所示为滑石晶体的单胞模型,模型来自美国矿物学家晶体结构数据库(AMCSD)。滑石的(001)表面表面能最低[29],因此,选择该解理面构建出2×1×1的滑石(001)表面构型。该表面构型由9层原子组成,在优化过程中仅允许最外4层原子弛豫。优化后的滑石(001)表面构型如图1(b)所示,滑石(001)表面由重复的氧硅六边形相连组成,并且每个氧硅六边形中心存在1个—OH基团。
本研究中,前线轨道计算通过DMol3模块完成。在计算过程中,采用GGA-PW91交换相关泛函。自洽场(SCF)迭代的精度和截断能的精度均被设置为中等。在布里渊区的采样计算中,使用Gamma点。电子处理方面,选择全电子计算的方法。基组选用双数值极化基组。此外,为了确保计算的收敛性,SCF循环次数设为1 000次。
根据分子轨道理论,分子的诸多性质主要由前线轨道决定[30],计算前线轨道的能量差可以判断浮选药剂与矿物作用的强度。前线轨道能量差计算公式如下:
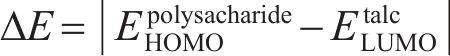
式中:ΔE代表抑制剂分子最高占据轨道(HOMO)与滑石最低占据轨道(LUMO)能量差值的绝对值;

1.3.2 MD模拟方法
分子动力学模拟是通过Materials Studio的Forcite模块中的分子动力学方法进行的,使用Amorphous Cell构建了由200个水分子和1个药剂单体组成的溶液模型,固液界面模型由Build layers工具构建。表面模型和溶液模型的电荷由DMol3模块计算得到,随后,通过Forcite模块使用Compass Ⅲ力场对表面模型和溶液模型进行优化。在298 K温度下,使用Nosé控温方式,在NVT系综下进行动力学计算,计算时间为500 ps,步长积分为1 fs。同时,静电力和范德华力使用PPPM和Atom base方法计算。选择NVT系综的最后100 ps计算结果进行分析。
均方位移(RMSD)可以用来描述溶液中水分子的动态特性,它表示经过时间t后,粒子距离其初始时刻位置的平均距离[31]。RMSD的计算公式如下:
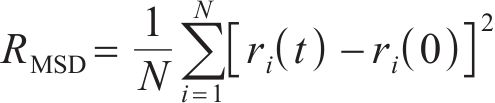
式中:N为水分子数;t为统计时间;

由均方位移公式可以计算得到体系内粒子的扩散系数D。
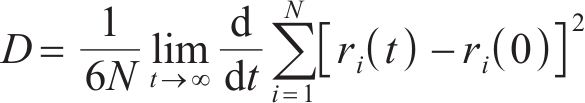
结合式(2)和(3)可以进一步得到均方位移与扩散系数以及时间的关系:
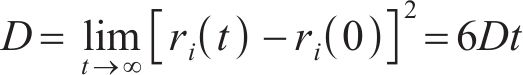
为了更加方便地比较不同体系的原子扩散程度,可将式(4)进行变形处理,得到
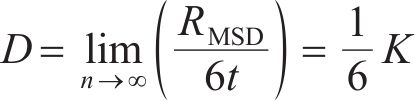
式中:K为曲线斜率,通过图像斜率的比较,能够更加直观地分析体系模拟结果。
径向分布函数
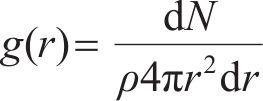
式中:ρ为粒子密度;r为参考粒子与作用粒子间距离;dN为参考粒子r到r+dr范围内的粒子数。
2 结果与讨论
2.1 滑石纯矿物浮选试验
为探究滑石的可浮性,采用捕收剂Y89(10 g/t)和起泡剂甲基异丁基甲醇(14 g/t)进行了滑石纯矿物的浮选试验,滑石的回收率高达65.79%,表明滑石具有良好的可浮性。为探究多糖类抑制剂对滑石的抑制效果,进行滑石纯矿物的浮选试验。选用羧甲基纤维素、普鲁兰多糖、羧甲基瓜尔胶、羧甲基壳聚糖作为滑石抑制剂,考察不同用量下的抑制剂对滑石回收率的影响,试验结果如图2所示。
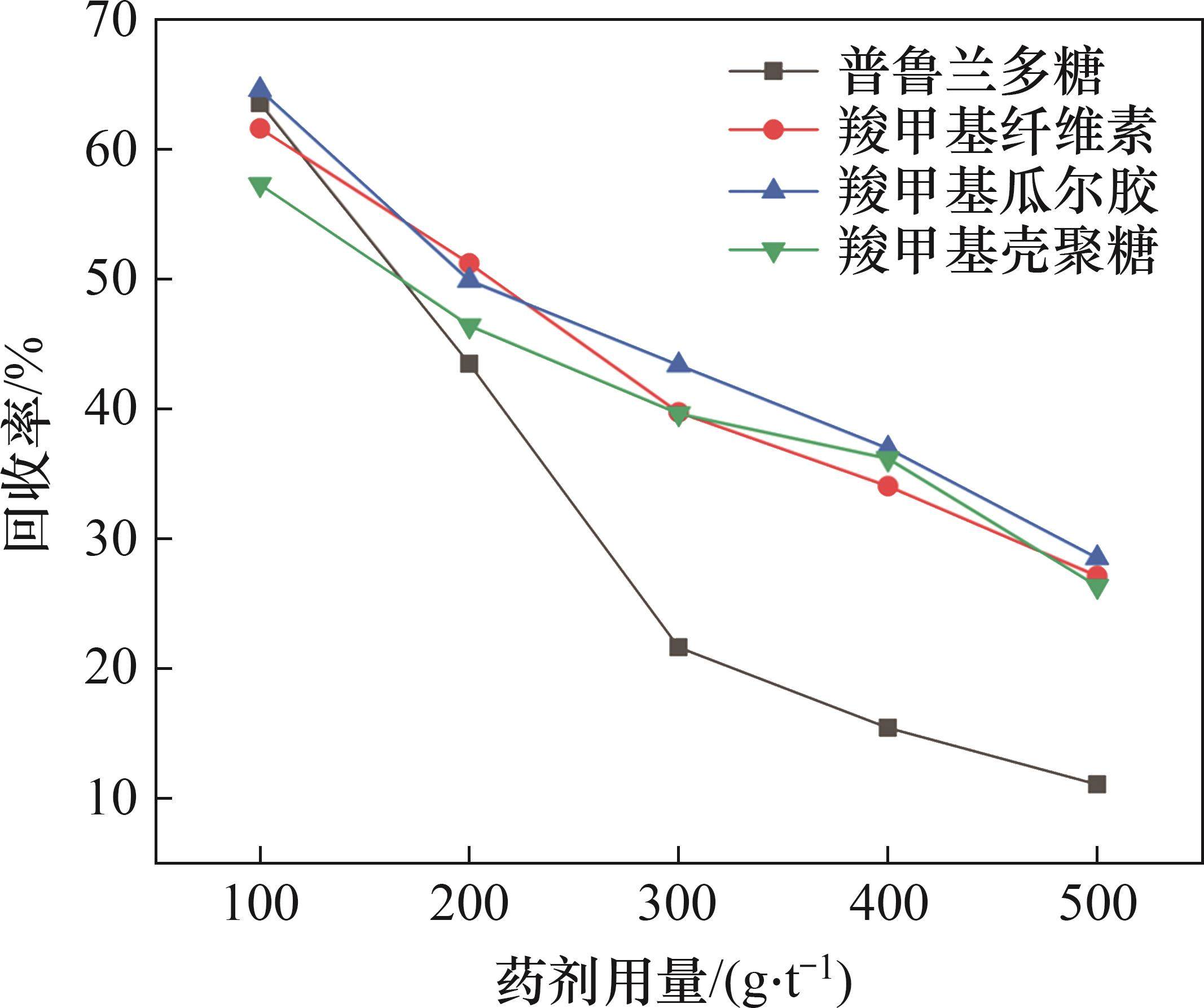
由图2可以看出:在低药剂用量(100 g/t)下, 4种药剂得到的滑石回收率相差不大,对滑石的抑制效果不明显;当药剂用量超过300 g/t后,普鲁兰多糖对滑石的抑制效果显著增强;当用量增加到400 g/t时,滑石回收率为15.43%,表现出良好的抑制效果;而当药剂用量从400 g/t提高到500 g/t时普鲁兰多糖,对滑石抑制效果的提升不大,因此,选定400 g/t为最佳药剂用量。
2.2 高滑石铜硫矿浮选试验
2.2.1 抑制剂种类对滑石浮选的影响
高滑石铜硫矿的抑制剂不仅需要对滑石具有良好的抑制效果,还需要保证铜精矿中的铜不被抑制。为考察羧甲基纤维素、普鲁兰多糖、羧甲基瓜尔胶、羧甲基壳聚糖这4种多糖类抑制剂对高滑石铜硫矿的抑制效果,本次试验以400 g/t的药剂用量探究所选4种抑制剂对铜硫矿中滑石回收率的影响,试验结果如图3所示。
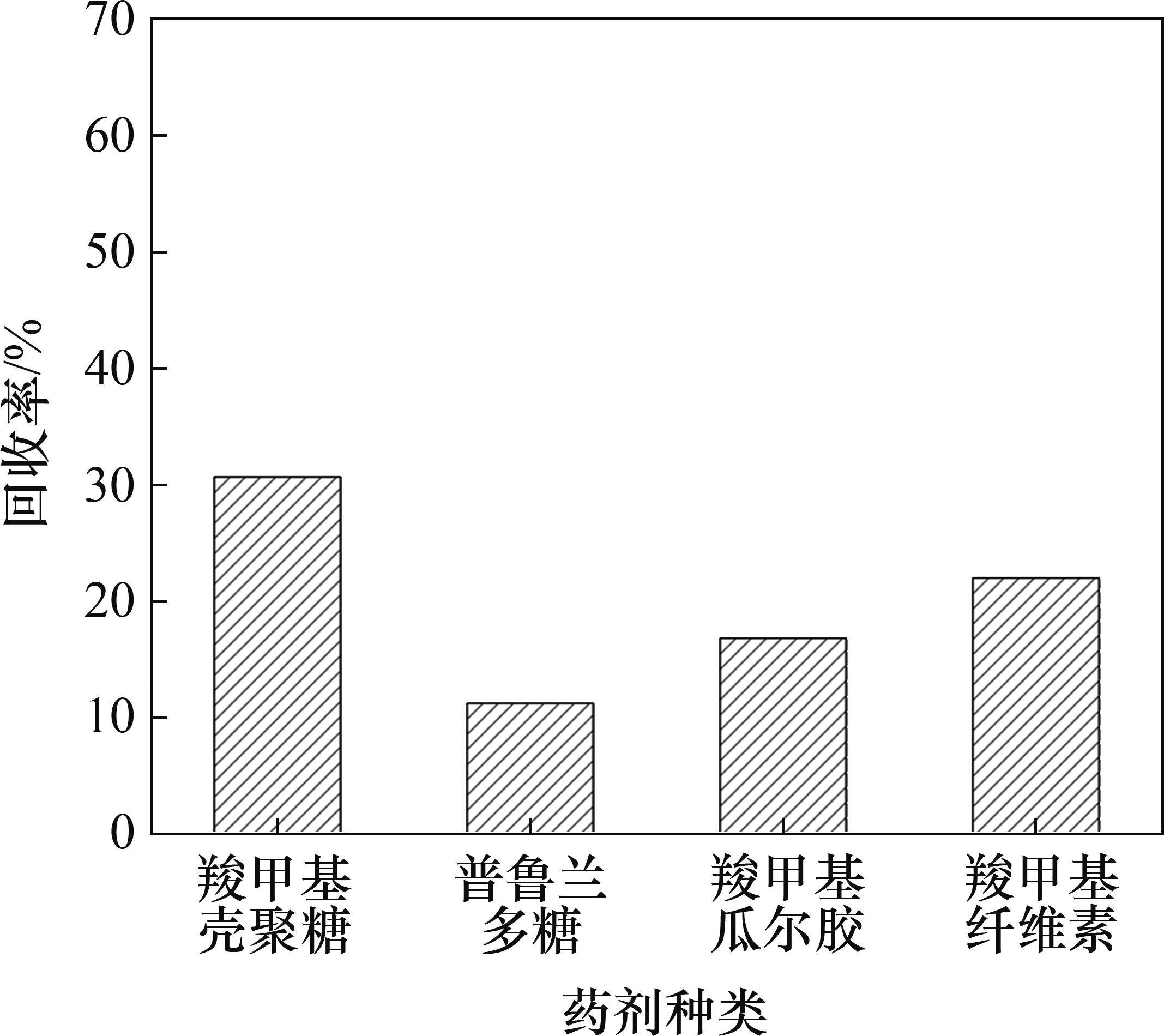
由图3可知:采用羧甲基壳聚糖、普鲁兰多糖、羧甲基瓜尔、羧甲基纤维素胶这4种多糖类抑制剂浮选获得精矿滑石回收率分别为30.68%、11.24%、16.83%、22.01%,可见,羧甲基壳聚糖对滑石的抑制效果最差,普鲁兰多糖对滑石的抑制效果最好。这4种滑石多糖类抑制剂在纯矿物和实际矿物浮选试验中的抑制效果不同,但普鲁兰多糖在纯矿物和实际矿物浮选试验都具有良好的抑制效果。
2.2.2 抑制剂种类对铜浮选的影响
取药剂用量为400 g/t,考察了羧甲基纤维素、普鲁兰多糖、羧甲基瓜尔胶、羧甲基壳聚糖4种多糖类抑制剂对高滑石铜硫矿铜浮选指标的影响,试验结果如图4所示。
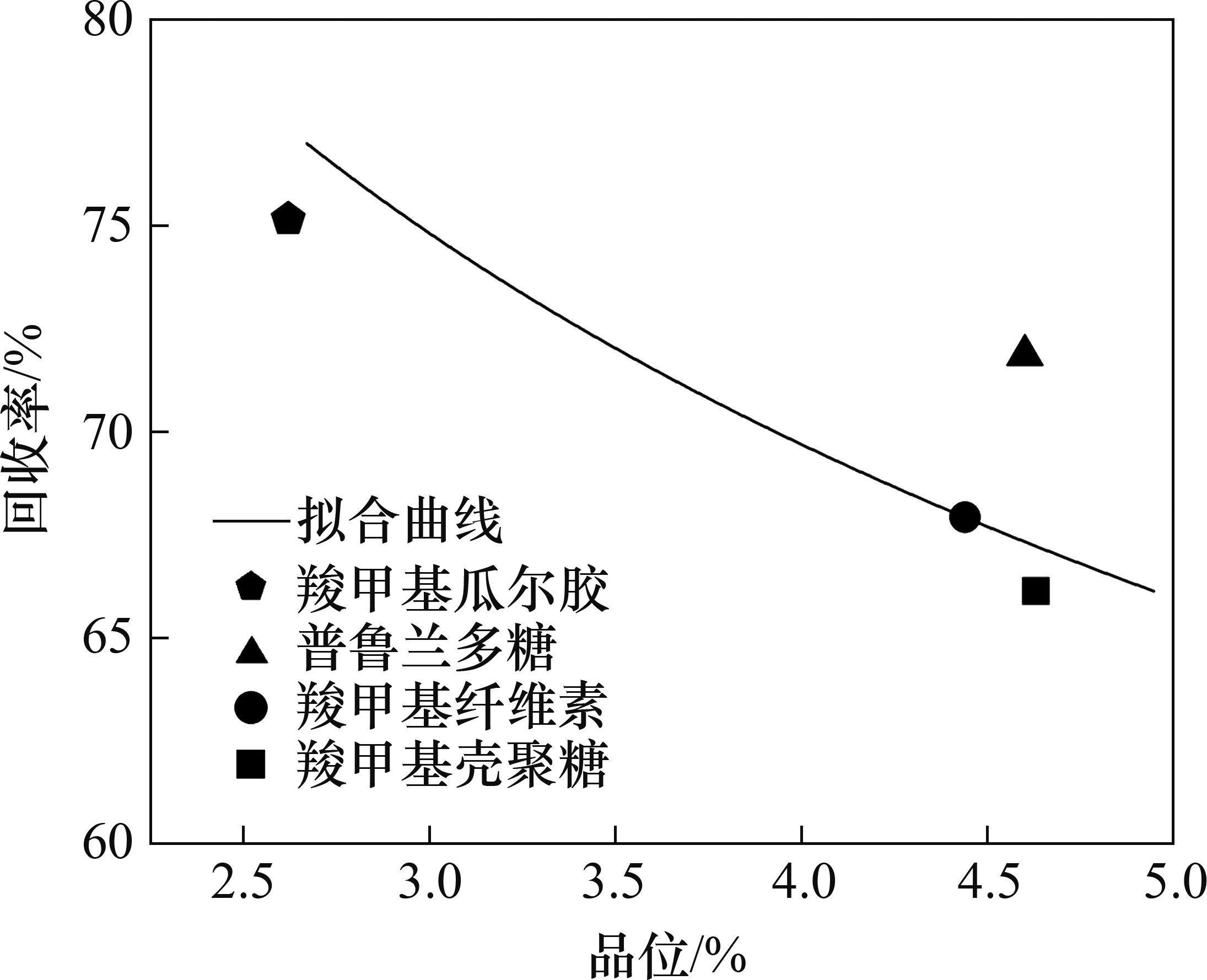
当处于某一确定品位时,若精矿回收率高于拟合线,则说明该精矿的铜回收率高于平均值。由图4可知:当采用羧甲基瓜尔胶与羧甲基纤维素作为抑制剂时,铜回收率位于拟合线上;而采用羧甲基壳聚糖作为抑制剂时,铜回收率在拟合线之下;当普鲁兰多糖作为抑制剂时,铜回收率在拟合线之上。铜硫矿浮选试验结果表明,普鲁兰多糖在选择性抑制滑石的同时,还能同时获得较高的精矿铜回收率以及品位。
2.3 滑石晶体的电子性质
2.3.1 滑石能带结构及态密度分析
理想滑石晶体的能带结构和总态密度如图5所示,取费米能级(EF)为能量零点。由图5可知:滑石晶体的价带主要由氧原子组成,导带主要由镁原子组成。计算所得滑石晶体的带隙值为5.19 eV,禁带宽度较大,电子较难发生跃迁,表明滑石是绝缘体。
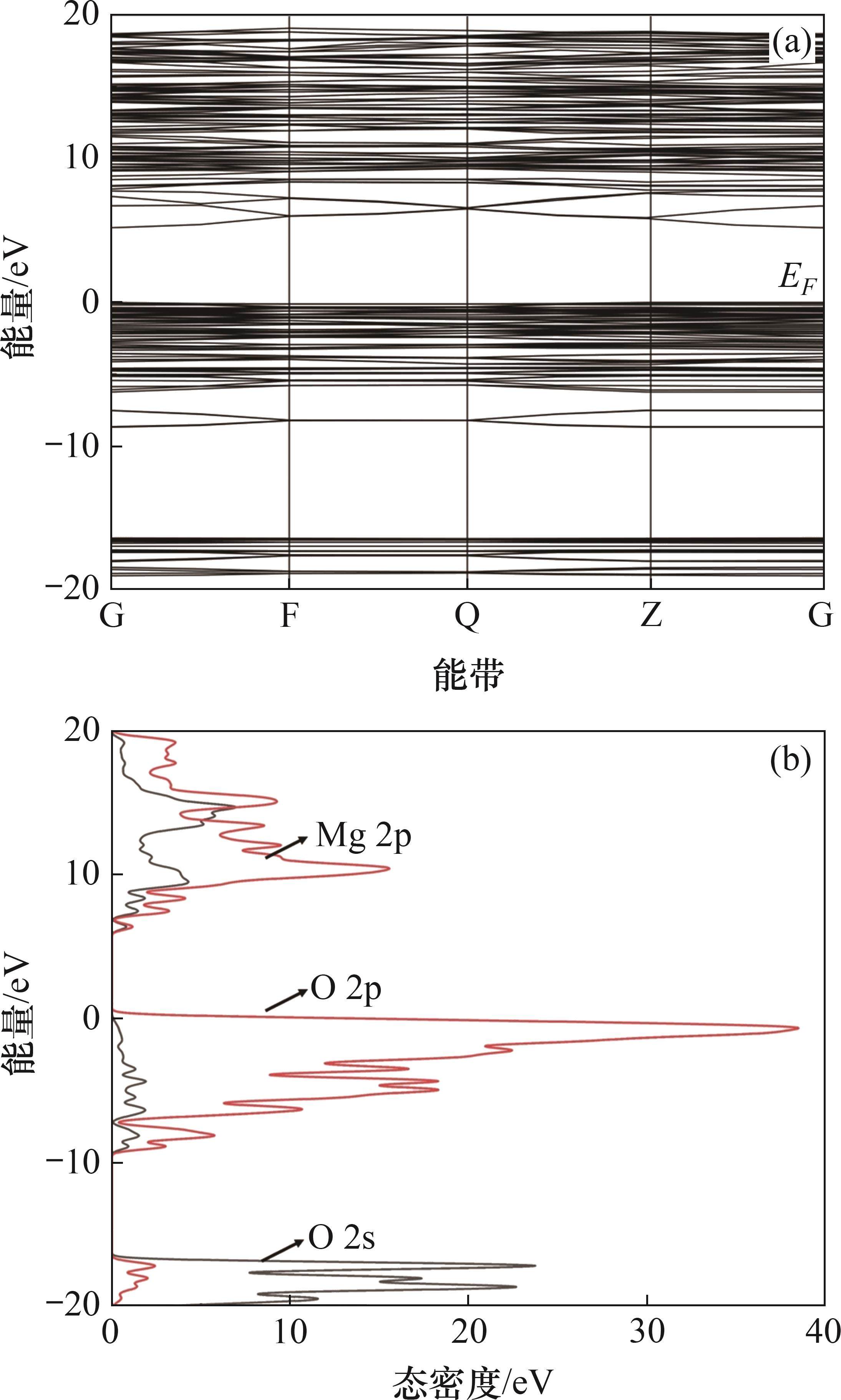
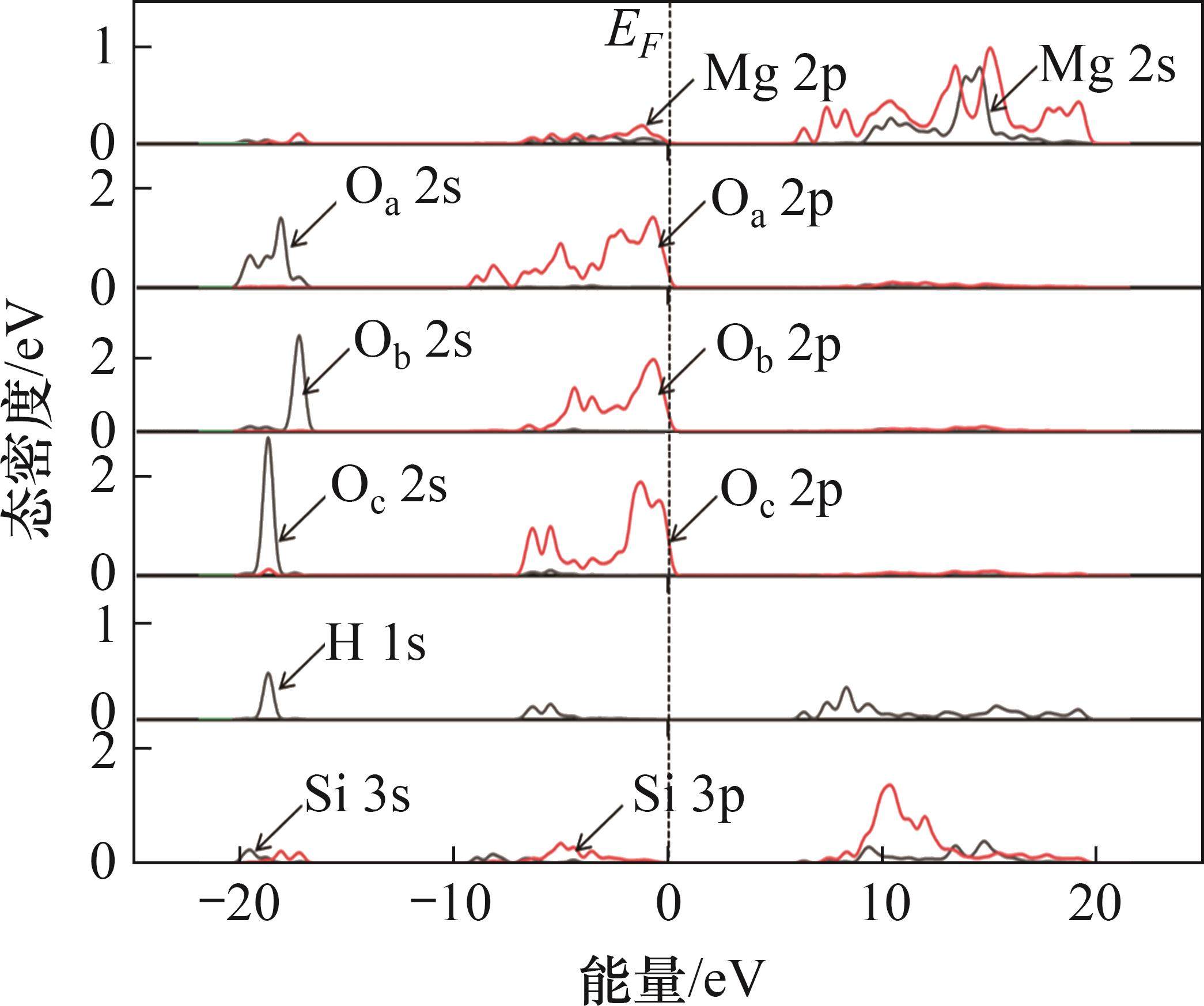
图6所示为滑石晶体各原子的态密度分布图,其中,Oa是氧硅四面体中处于同一平面的氧原子,Ob是在硅原子和镁原子之间共用的氧原子,Oc是与氢原子成键的羟基氧,Ob与Oc暴露在滑石(001)表面最先与药剂接触。滑石晶体低能区以s轨道为主。滑石晶体的费米能级位于价带顶部,价带以下的这部分能带主要由O 2p轨道组成。因此,氧原子最容易失去电子,是与浮选药剂发生吸附的主要活性靶点。
2.3.2 前线轨道分析
为研究多糖类抑制剂与滑石(001)表面的吸附机理,本文对滑石和抑制剂分子的前线轨道进行了计算和分析。图7所示为4种抑制剂的HOMO轨道分布。由图7可知:羧甲基瓜尔胶和羧甲基纤维素的HOMO轨道主要分布在羟基以及羧基上;普鲁兰多糖的HOMO轨道主要集中在羟基上;羧甲基壳聚糖的HOMO轨道分布在氨基。
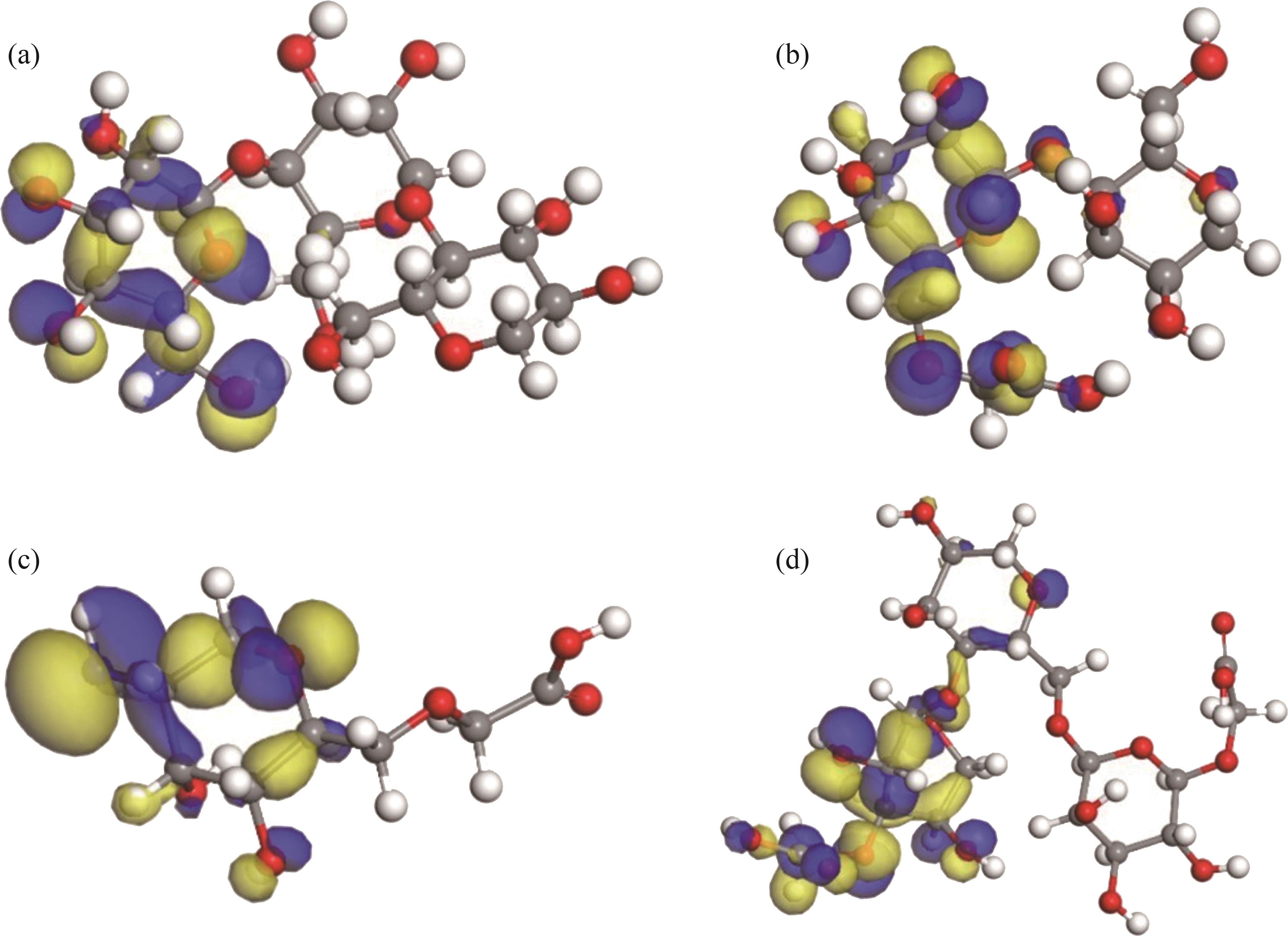
当多糖类抑制剂与滑石表面发生相互作用时,抑制剂的HOMO轨道容易失去电子,滑石的LUMO轨道容易得到电子。因此,抑制剂的HOMO轨道与滑石LUMO轨道能级间的能量差值的绝对值(







| 矿物及药剂 | 前线轨道 | 前线轨道能量/eV |  |
|---|---|---|---|
| 滑石 | HOMO | -8.15 | — |
| LUMO | -2.59 | ||
| 普鲁兰多糖 | HOMO | -5.62 | 3.03 |
| LUMO | -0.36 | ||
| 羧甲基壳聚糖 | HOMO | -5.55 | 2.96 |
| LUMO | -1.29 | ||
| 羧甲基瓜尔胶 | HOMO | -5.92 | 3.34 |
| LUMO | -1.30 | ||
| 羧甲基纤维素 | HOMO | -5.83 | 3.24 |
| LUMO | -1.32 |
2.4 MD模拟
2.4.1 径向分布函数
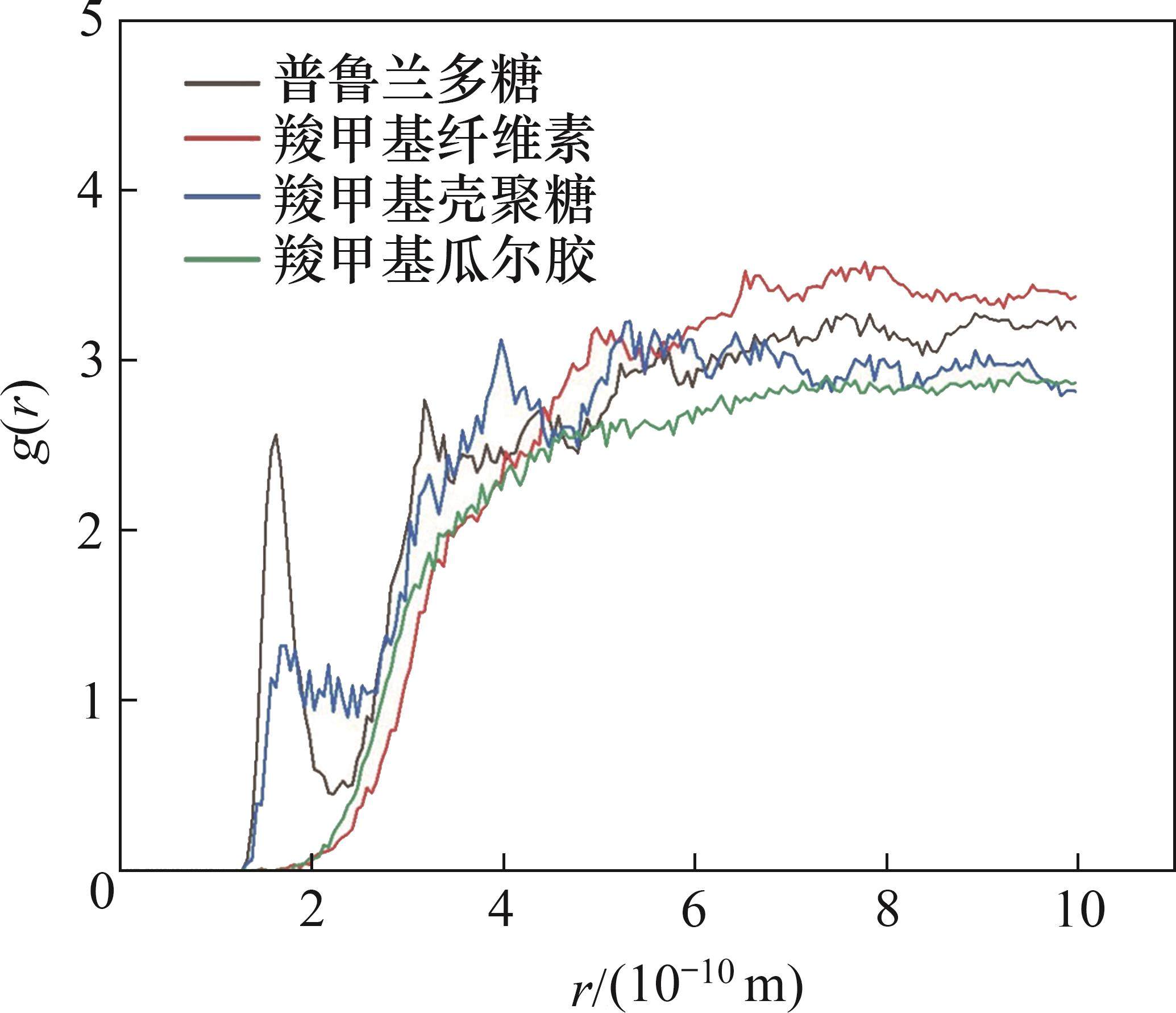
径向分布函数g(r)表示与某个原子距离为r的单位体积元内出现的相对分子数密度,通过径向分布函数可以分析不同药剂之间的亲疏水性差异。图8所示为不同药剂中氧原子(Op)与水分子中氢原子(Hw)之间的径向分布函数。函数峰值位置出现距离r越小,说明抑制剂对水分子的吸引力越强,并且峰值越高,说明吸引的水分子越多。由图8可知:第一处峰位于1.62×10-10 m,由普鲁兰多糖形成,第二处峰位于1.67×10-10 m,由羧甲基壳聚糖形成;而羧甲基纤维素与羧甲基瓜尔胶没有出现明显的峰,说明普鲁兰多糖对水分子的吸引力比其他3种抑制剂的强;并且普鲁兰多糖与羧甲基壳聚糖的两处峰值距离约为1.8×10-10 m(处于氢键键长范围内),说明上述2处峰值由氢键形成。另外,普鲁兰多糖体系的径向分布函数峰高约为羧甲基壳聚糖的2倍,这说明相比于其他药剂,普鲁兰多糖分子与水分子之间存在更多氢键,表现出了更强的亲水性能。
2.4.2 均方位移分析
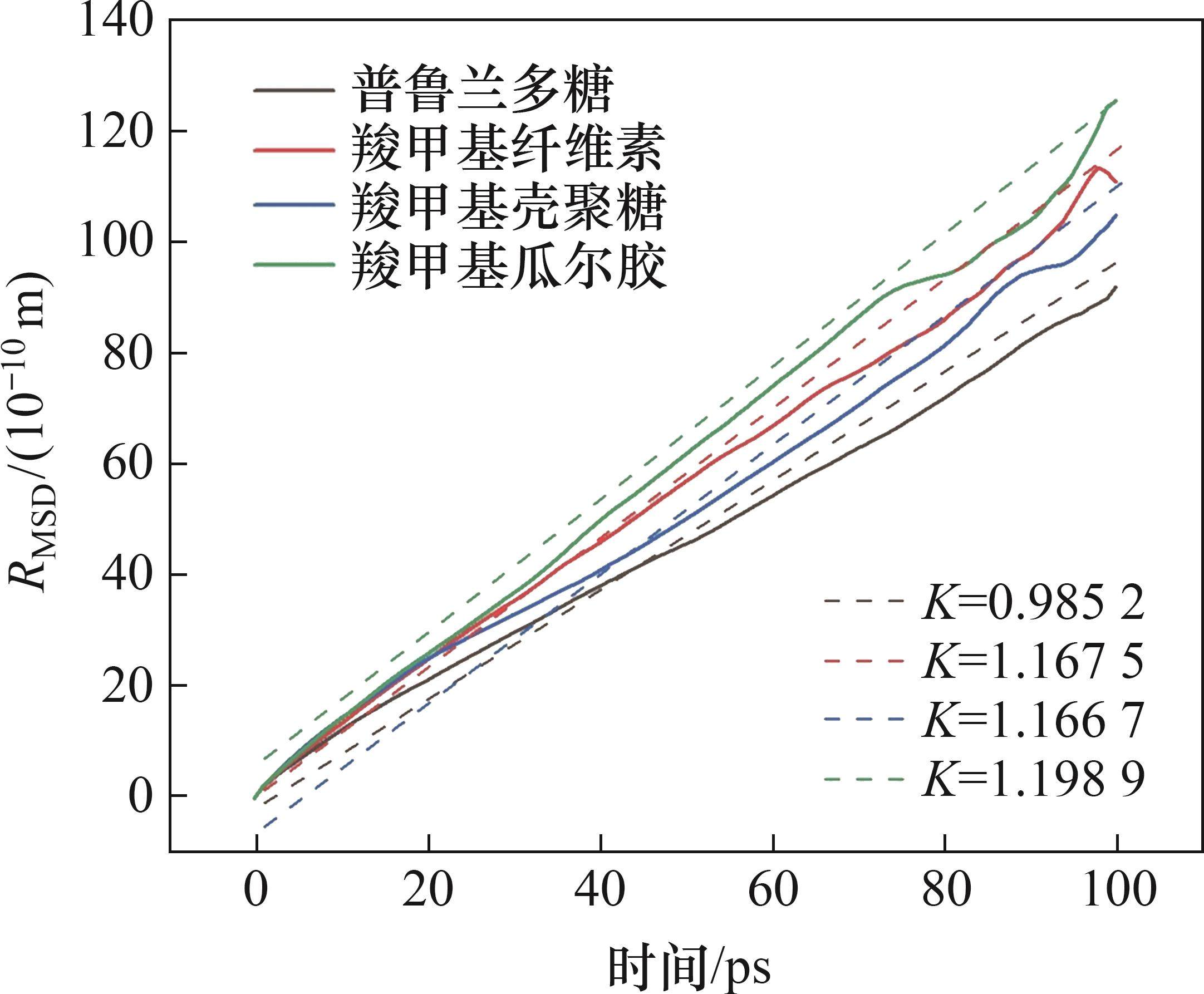
图9所示为水分子在滑石(001)表面的均方位移(RMSD),其中虚线为拟合线,不同拟合线的斜率(K)则代表了水分子在不同条件下的扩散系数(D)。通过分析扩散系数可以比较不同药剂对水分子扩散程度的影响。扩散的本质是物质克服自身能量壁垒的过程,水分子受到的束缚作用越强,则扩散系数越小、拟合线斜率越低[33]。由图9可知:抑制剂的加入改变了水分子在溶液中的聚集形态和分布状态。其中,不同体系的扩散系数由小到大抑制剂依次为普鲁兰多糖、羧甲基壳聚糖、羧甲基纤维素、羧甲基瓜尔胶。普鲁兰多糖体系中水分子的扩散程度最小,原因是普鲁兰多糖分子与水分子存在氢键,使水分子受到束缚。因此,结合RDF现象可以推断多糖类抑制剂的作用机理为:抑制剂吸附在滑石表面时能够与水分子形成氢键,并且被抑制剂吸引的水分子会在滑石表面形成亲水层,所以,降低了滑石的疏水性,从而达到了抑制滑石的效果。
2.4.3 氢键分析
氢键是一种特殊的非键相互作用力,通常在氢原子和相邻的高电负性原子之间形成。它的本质是原子之间的静电吸引,具有饱和性和方向性。氢键的定义可以按照能量标准和几何标准进行。能量标准是基于分子间相互作用能量来判断,而几何标准则是根据氢键供体、氢原子和氢键受体的几何关系来判断[34-35]。本文利用perl脚本参照几何标准计算模型中药剂与水分子之间氢键的数目,并统计了氢键的键长和键角。
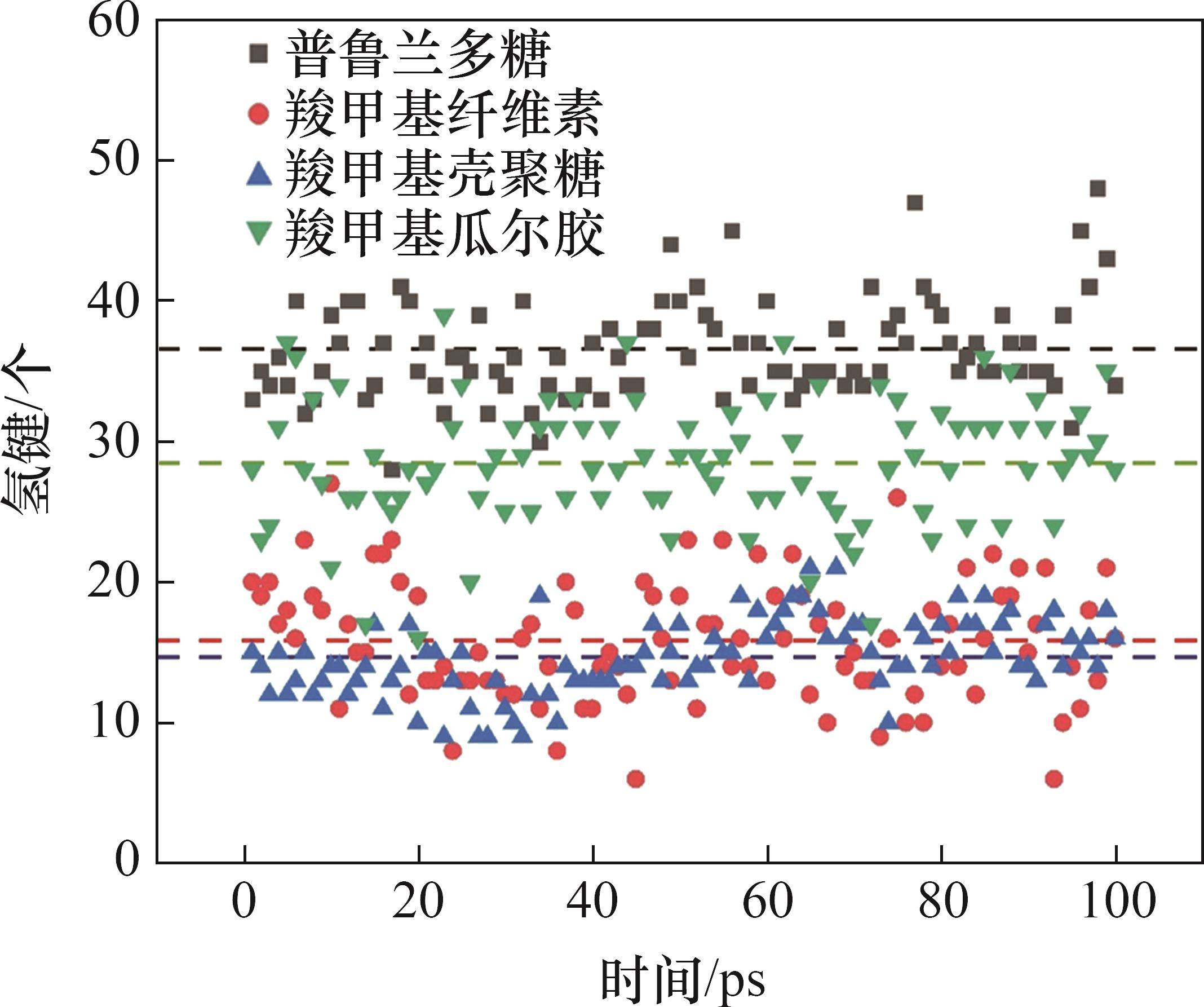
图10所示为溶液中抑制剂与水分子之间的氢键数量随时间的变化,表3所示为不同体系中的平均氢键数量、键长以及键角。氢键的键角越大,氢原子和受体原子越接近,说明氢键就越稳定。从图10和表3可以看出:羧甲基纤维素形成的平均氢键键长为2.83×10-10 m、键角为125.45°、平均氢键个数为15.82个,这表明羧甲基纤维素与水分子形成的氢键不稳定,亲水性较弱。羧甲基瓜尔胶虽然平均氢键个数为28.64个,但平均键角为121.97°,键长为2.76×10-10 m,氢键稳定性差,无法有效吸附水分子。羧甲基壳聚糖形成的平均键角为130.95°,键长为2.49×10-10 m,形成的氢键相对稳定,但其分子量较小形成的氢键个数仅14.64个,因此,亲水性不强。而普鲁兰多糖与水形成的氢键平均键角最大和键长最小,而且形成的平均氢键数目最多达36.54个,因此具有较强的亲水性能。氢键分析结果进一步解释了不同抑制剂之间的亲疏水性差异。
| 药剂 | 平均氢键数/个 | 平均键角/(°) | 平均键长/(10-10 m) |
|---|---|---|---|
| 普鲁兰多糖 | 36.54 | 132.06 | 2.37 |
| 羧甲基纤维素 | 15.82 | 125.45 | 2.83 |
| 羧甲基壳聚糖 | 14.64 | 130.95 | 2.49 |
| 羧甲基瓜尔胶 | 28.64 | 121.97 | 2.76 |
3 结论
1) 普鲁兰多糖、羧甲基纤维素、羧甲基壳聚糖、羧甲基瓜尔胶这4种抑制剂都对滑石具有较好的抑制性能。其中普鲁兰多糖对滑石的抑制效果最好,在400 g/t的用量下滑石回收率为15.43%。普鲁兰多糖对复杂铜硫矿中的滑石具有较好的选择性抑制效果,当其用量为400 g/t时,精矿铜回收率为71.86%,品位为4.60%,同时滑石回收率仅为11.24%。
2) 羧甲基壳聚糖和普鲁兰多糖的HOMO轨道与滑石LUMO轨道之间的能量差值较小,电子容易发生转移。其中,普鲁兰多糖在滑石表面的吸附是通过羟基与滑石表面氧原子成键实现的。
3) 普鲁兰多糖、羧甲基纤维素、羧甲基壳聚糖、羧甲基瓜尔胶这4种多糖类抑制剂与水分子之间均存在氢键,通过吸附在滑石表面形成了亲水层,从而降低了滑石的可浮性。其中,普鲁兰多糖对水分子的吸引力最强,体系中水分子受到束缚作用最明显,并且与其他3种抑制剂相比,普鲁兰多糖形成的氢键键长最短,键角最大,稳定性最强。
植物绝缘油中水对甲醇扩散影响的分子动力学模拟
[J/OL]. 绝缘材料, 1-7[离子影响油纸绝缘结合性能的分子动力学模拟研究
[J/OL]. 材料导报, 1-16[陆夏羿, 吴志强, 陈建华, 等. 滑石表面多糖类抑制剂作用机理的密度泛函理论和分子动力学研究[J]. 中南大学学报(自然科学版), 2024, 55(12): 4431-4441.
LU Xiayi, WU Zhiqiang, CHEN Jianhua, et al. Density functional theory and molecular dynamics studies on mechanism of polysaccharide depressants on talc surface[J]. Journal of Central South University(Science and Technology), 2024, 55(12): 4431-4441.

