随着我国隧道施工机械化水平不断提升,全断面硬岩隧道掘进机(TBM)以其安全、高效、环保等优势逐渐成为长大隧道施工的首选装备,广泛应用于水利、公路、铁路的工程建设中[1-3]。目前,TBM施工效率受地层条件影响较大,而受设备本身结构限制,现场作业人员难以像钻爆法施工那样及时根据掌子面围岩情况采取相对应的处理措施,这就导致了掘进参数与支护措施选择的随机性和盲目性,轻则容易造成刀具异常磨损,重则可能引发卡机事故,严重制约TBM的施工效率,亟需针对TBM隧道围岩感知这一卡脖子难题开展研究。传统的地质勘查手段如钻孔探测[4-5]、地震波探测[6-7]、地质雷达[8]等应用在TBM施工中一般都需要停机进行测试,对掘进施工影响较大,且成本高、耗时长,为避免对TBM掘进施工的影响,保证围岩感知的连续性和准确性,近年来许多学者尝试通过TBM掘进实时产生的掘进参数对围岩进行感知预测:ZHANG等[9]使用层次结构(BIRCH)算法,将12 038 636个TBM操作数据有效压缩到仅5 014个子节点条目,采用K-means++聚类算法从TBM大作业数据中识别潜在的岩体类型,利用岩体类型信息训练了3种分类器(SVC、随机森林和kNN),并对比了3种分类器的性能。LIU等[10-11]通过堆叠单目标(SST)技术改进了支持向量回归(SVR)算法,并用于建立岩体参数预测模型,还开发了一种将反向传播神经网络与模拟退火相结合的混合算法(SA-BPNN),建立SA-BPNN模型来预测岩体参数,该方法对岩体参数的预测结果比普通BPNN方法更加准确。朱梦琦等[12]采用基于集成CART算法的随机森林和AdaCost方法对岩体信息进行实时感知,结果表明相比传统掘进参数,采用刀盘转速、撑靴压力、撑靴俯仰角、推进速度和撑靴滚动角参数组合能更好反映围岩状况。WU等[13]提出一种基于数据挖掘(DM)的TBM-岩机互反馈感知方法,可实现TBM掘进过程中岩体状况的自动识别和掘进参数的动态调整。YAMAMOTO等[14]利用钻井测井结果和掘进机运行数据采用统计技术分析地质条件的三维时空分布,并建立了TBM挖掘控制系统,实现了对隧道掘进机工作面前方地质条件的预测。LIU等[15]引入并验证基于全局注意力机制的LSTM网络,用于利用TBM施工大数据进行长隧道掌子面岩性预测。李宏波[16]提出了一种结合自组织神经网络聚类和最小二乘支持向量机的围岩等级预测识别方法,经过现场数据验证,该方法能够较准确地预测围岩等级,并具有良好的鲁棒性。AYAWAH等[17]使用从马来西亚半岛PSRWT项目获得的TBM操作数据对6种机器学习模型进行训练和测试,并对测试结果进行了比较。张娜等[18]在分析TBM运行参数随围岩状态变化规律的基础上,通过聚类和分步回归等方法建立了TBM前方岩体状态预测模型,在石灰岩和花岗岩地层中岩体参数的预测误差少于18%。LI等[19]从掘进参数中提取出了一种新的岩石破碎指数RFI,建立了RFI与RC的映射关系以对RC进行预测。除TBM掘进参数外,TBM皮带岩渣也是岩机相互作用的产物,能够一定程度上反映在掘围岩的状态。随着图像识别技术以及计算机技术的发展,已经成为目前研究的热点[20-24]。但由于岩渣图像识别技术尚不成熟,现场补光、高速摄影等存在各种问题,数据获取困难且难以保证图像质量,目前已有成果较少。TBM主机振动主要由滚刀破岩产生,不同围岩条件通常导致不同的振动响应,因此TBM振动信号能够反映当前掌子面在掘岩体的状态[25-27]。然而,由于现场监测到的TBM振动信号成分复杂,难以直观分析其规律。但随着大数据技术在工程领域的广泛应用,基于TBM振动监测数据的围岩感知成为了可能,当前此类研究相对较少。综上所述,目前的围岩感知大多基于TBM掘进参数或室内试验建立预测公式,而掘进参数本身受TBM司机人为干扰较大,因此,其客观普适性可能会受到限制。而皮带岩渣与主机振动是滚刀与掌子面围岩直接作用的产物,更能直接反映掌子面的围岩状态,但数据采集与处理难度较大,研究成本较高。为深入探究TBM破岩振动应用在掌子面围岩感知领域的可行性,笔者依托新疆某工程TBM隧洞项目,采用高性能加速度传感器对刀仓内的主梁振动开展监测,通过小波阈值降噪方法对原始信号进行降噪处理,对振动数据的时域和频域特征进行分析,筛选出5项与围岩条件相关性最强的振动特征,并据此建立数据集,分别开发用于围岩感知的BP神经网络模型和SVM模型,通过验证集和测试集对模型的预测效果进行验证,并对2种模型的预测效果进行对比,研究成果可为TBM隧道围岩感知技术研究提供新的思路和借鉴。
1 依托工程
1.1 工程概况
新疆某工程XE隧洞全长139.04 km,采用5台Φ7.83 m敞开式TBM结合钻爆法施工,如图1所示。其中石英片岩长度约18.25 km,片麻花岗岩长度约43.89 km,花岗片麻岩长度约60.15 km,凝灰质砂岩长度约1.21 km,花岗岩长度约4.43 km,地质钻探取得的典型岩石样本如图2所示。


本文依托VIII标段TBM5开展研究,该标段主要穿越Ⅱ、Ⅲ类围岩,占比约96%,IV、V类围岩只占4%,84%的岩石单轴饱和抗压强度介于30~120 MPa。施工揭露的岩性包括华力西期花岗岩、黑云母石英片岩、黑云母角闪斜长岩、凝灰质砂岩等,其中华力西期花岗岩占比最高达90%以上。
依托工程采用北方重工设计制造的“奋进号”敞开式TBM施工,如图3所示。TBM总长190 m,总重约1 500 t,额定推力15 257 kN,额定扭矩8 800 kN∙m,其主要技术参数如表1所示。

| 项目 | TBM主机长度/m | TBM主机重量/t | TBM整机长度/m | TBM整机重量/t | 刀盘 直径/mm | 刀具数量/把 | 刀具额定载荷/kN | 最大刀盘功率/kW | 额定刀盘扭矩/(kN∙m) | 脱困刀 盘扭矩/(kN∙m) | 最大刀 盘转速/ (r∙min-1) | 额定推力/kN | 最大推力/kN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 参数 | 24 | 750 | 190 | 1500 | 7 830 | 53 | 311 | 3 500 | 8 800 | 17 600 | 21 | 15 257 | 22 450 |
1.2 振动监测系统布置
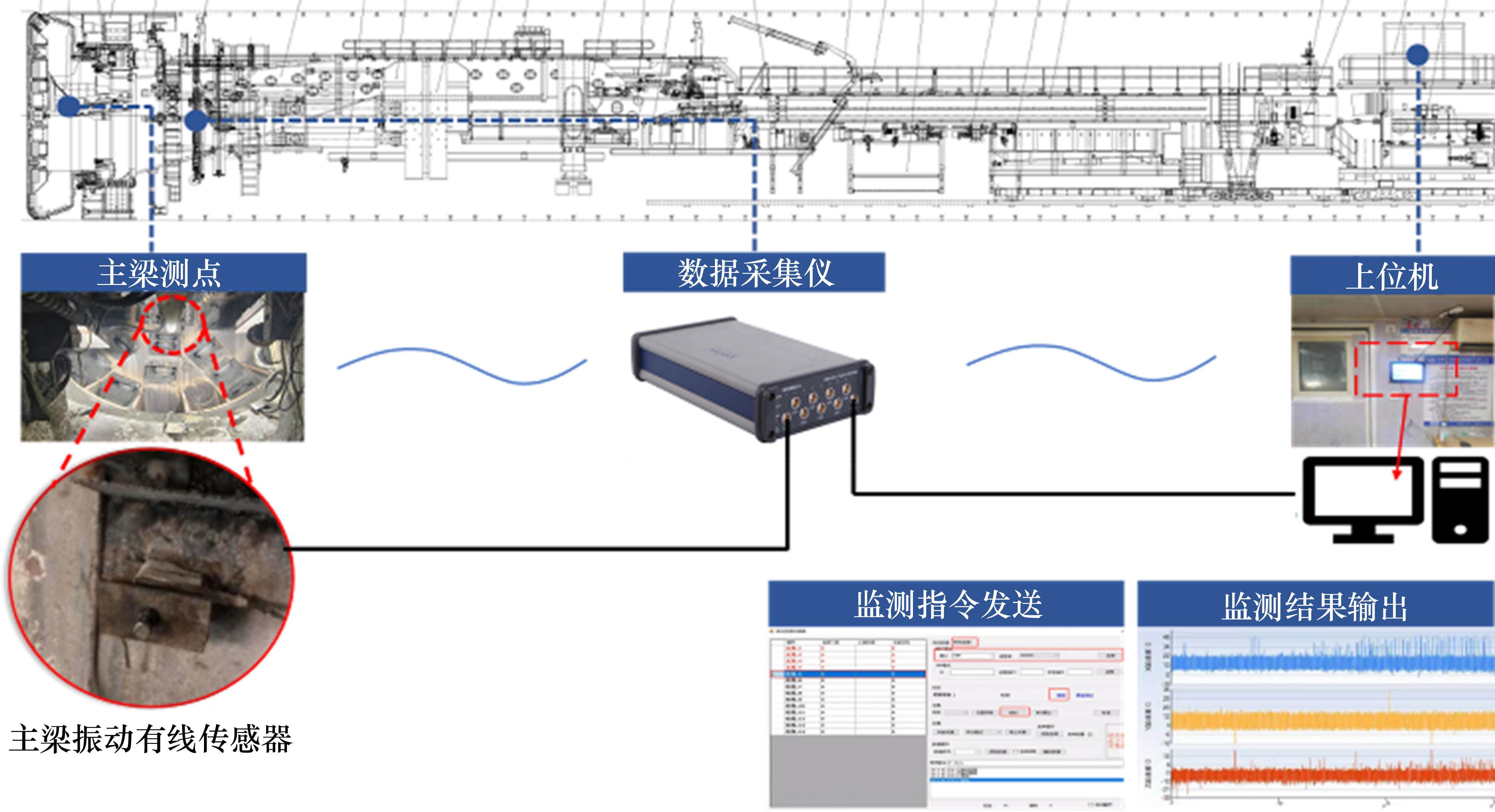
TBM振动监测系统包括振动传感器、中心端和上位机3部分,其中振动监测采用MEAS 3801A型加速度传感器,具有体积小、可靠性好、精度高等优势。测点布置方面,一方面测点要尽可能靠近刀盘,以求测得最真实的破岩振动信号,另一方面由于TBM掘进破岩时刀仓内环境恶劣,也要考虑测点传感器的保护与信号传输。综合考虑以上2个方面因素,最终将振动传感器安装在刀仓内的主梁末端(靠近刀盘位置),采用有线通讯方式将振动信号传递给安装在拱架安装机下部的中心端,中心端再通过RS485方式使用四芯屏蔽线连接到TBM主控室的上位机,由上位机控制主梁振动传感器的参数设置、数据采集与传输。TBM振动监测系统如图4所示,系统参数如表2所示。
| 项目 | 传感器类型 | 测量范围/G | 采样精度 | 精度/(mg∙LSB-1) | 采样频率/Hz | 传输方式 | 抗冲击能力/G |
|---|---|---|---|---|---|---|---|
| 参数 | 三轴加速度传感器 | 20 | 13位 | ≤4 | 默认采样频率1 024 | 有线 | 10 000 |
| 项目 | 工作温度/℃ | 供电情况 | 防护等级 | 系统安装 | 有线通信距离/m | 振动采集单元尺寸/mm | |
| 参数 | -40~80 | DC12 V AC220 V | IP68承压 2 MPa | 振动采集单元通过 焊接安装 | 最长1 000 | 100×100×40 | |
2 TBM振动信号降噪
TBM掘进时刀盘会产生剧烈振动,并通过各种连接件将振动传递给主梁、撑靴等部位,TBM主梁振动包含滚刀破岩冲击振动、主驱动电机振动、齿轮非线性啮合振动、锚杆钻机施工振动、混凝土喷射手施工振动等,频率成分极为复杂,其中只有滚刀破岩产生的冲击振动与掌子面围岩条件直接相关,为减小环境噪声对振动信号的干扰,需要对原始信号进行降噪。小波阈值方法作为一种经典降噪手段,在隧道工程施工振动监测领域应用广泛,本文使用小波阈值方法对TBM刀盘振动信号进行降噪。
2.1 小波阈值降噪原理
信号经过小波变换后,产生了包含关键信息的小波系数。通过对原始含噪信号进行小波分解,可以发现小波系数中的有用信号成分通常较大,而噪声成分则相对较小。此外,噪声的小波系数通常小于信号的小波系数。因此可以通过选择适当的阈值,将大于阈值的小波系数视为包含有用信号信息并保留,而小于阈值的小波系数则被认定为噪声并设为0,以实现去噪的目标。这个过程的实质在于抑制信号中的无用部分,同时增强有用部分。
2.2 小波阈值降噪步骤
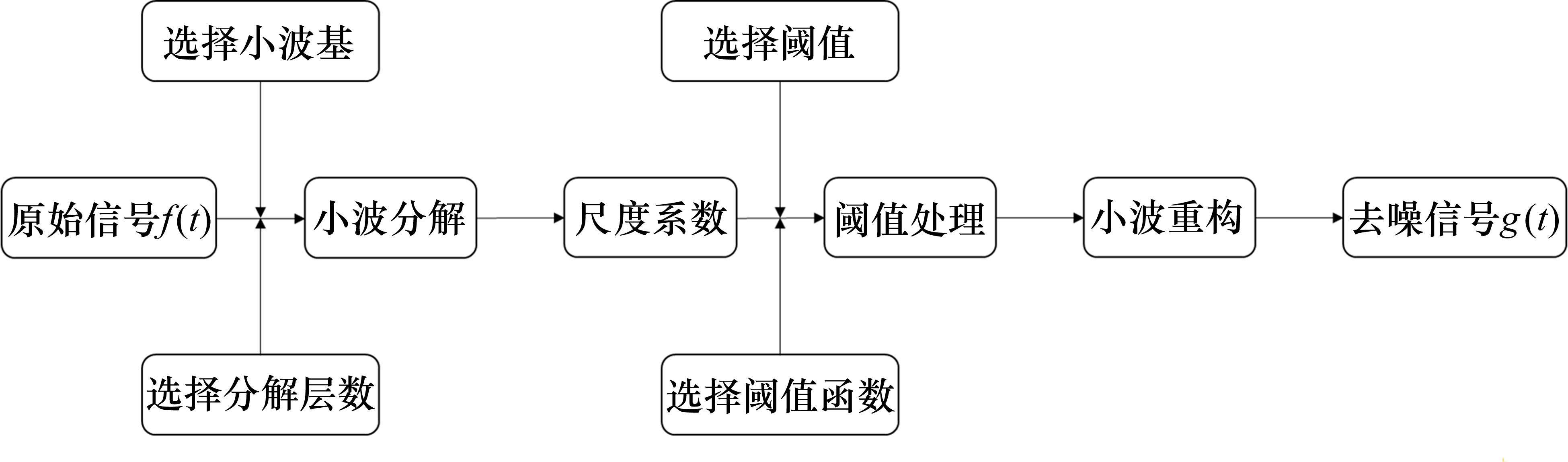
小波阈值降噪的一般步骤如图5所示,主要包括以下3个阶段:1) 小波分解,首先选择适合信号特征的小波基函数,分解信号,并根据研究需要确定分解的层数;2) 阈值处理,对分解后的各层系数进行阈值处理;3) 重构过程,根据经过去噪处理的各级小波系数进行信号重构,得到去噪后的信号。
2.3 降噪效果分析
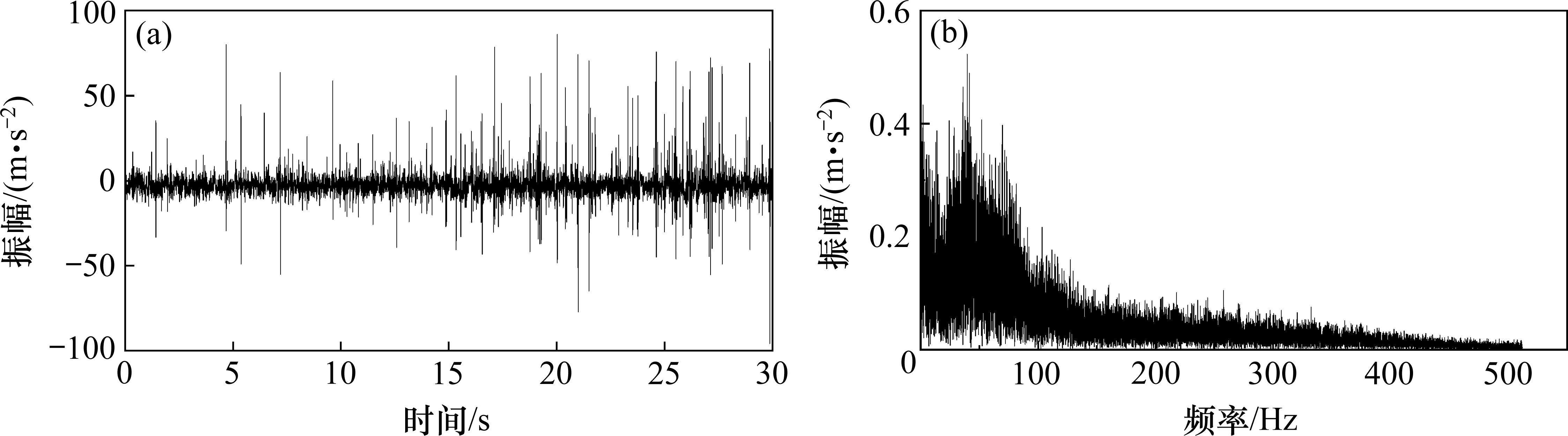
为了评估小波阈值方法对TBM破岩振动信号的去噪效果,首先从TBM破岩振动信号中提取了一段时长30 s的稳定信号作为原始信号,如图6(a)所示。采集这段信号时的掌子面围岩为Ⅱ类,振幅为-100~100 m/s2。图6(b)展示了对这一信号进行傅里叶变换后得到的频谱图,其中峰值频率主要出现在39.6、71.2、114.3和217.8 Hz等。在频谱中,峰值的幅度反映了对应频率的波能量,而40 Hz附近的峰值最高,其他峰值频率大约在40 Hz的整数倍附近,这表明40 Hz可能是振动的基频。随着峰值频率增加,振幅明显下降,特别是在90 Hz以上,大部分振幅都小于0.3 m/s2,这表明TBM破岩振动主要是低频振动。
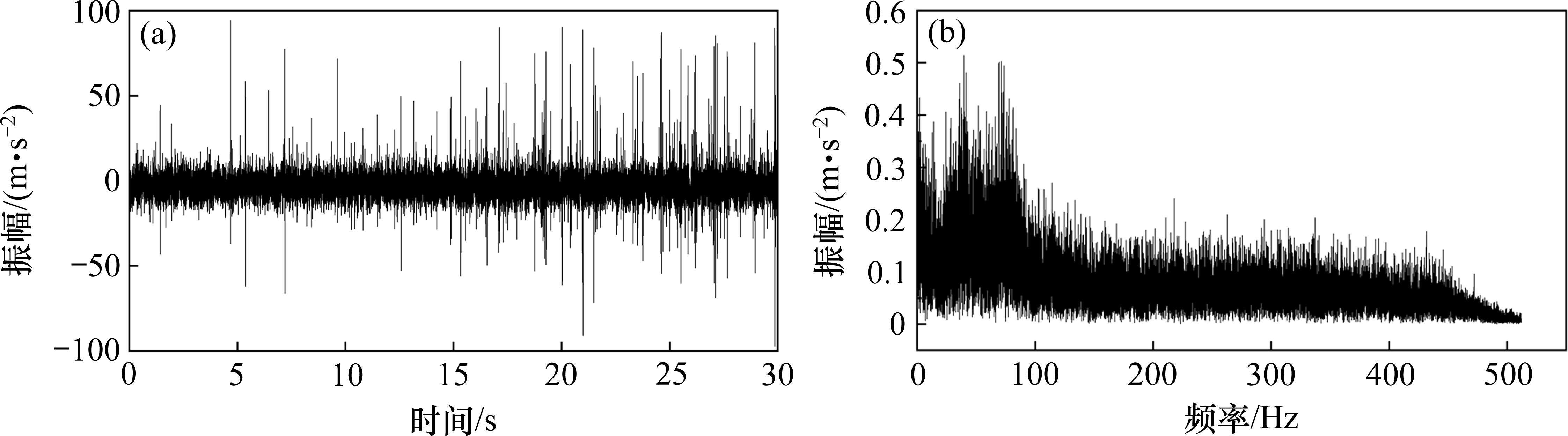
从图6(a)的振动波形可以看出,振动信号存在明显的冲击特征,信号中的冲击成分振幅较大且分布稀疏,分析其原因主要是滚刀破岩产生的冲击荷载以及掌子面破碎岩石与刀盘刀具撞击引起的。与破岩振动信号不同,噪声信号主要包含施工设备振动、齿轮啮合振动等,这些振动往往具有振幅小、频率成分复杂的特点。为分析滚刀破岩引起的冲击振动频率,对振动峰值进行了希尔伯特上包络,其包络曲线及包络谱如图7所示。在包络谱中,峰值频率主要分布在0~50 Hz,特别在2 Hz附近达到最大值,接近于刀盘转频,这也进一步说明了滚刀破岩振动是低频振动。
在对原始信号进行小波阈值降噪之前,需要选定小波基函数、分解层数、阈值函数及阈值计算方法等参数。常见的小波基函数有Haar、Daubechies(dbN)、Symlet(symN)、Gaussian等,其中symN具有良好的对称性和更高的正则性,能够有效减少信号降噪时的相位失真问题,而在sym2~sym8中,sym7的计算复杂度更低,滤波长度也较为适中,因此本文选择sym7作为小波基函数,对原始信号进行3层小波分解,得到各阶小波系数如图8所示。其中d1~d3分别为第1~3层小波系数,代表的频带分别为256~512 Hz、128~256 Hz、64~128 Hz;a3是第3层细节小波系数,代表的频带为0~64 Hz。
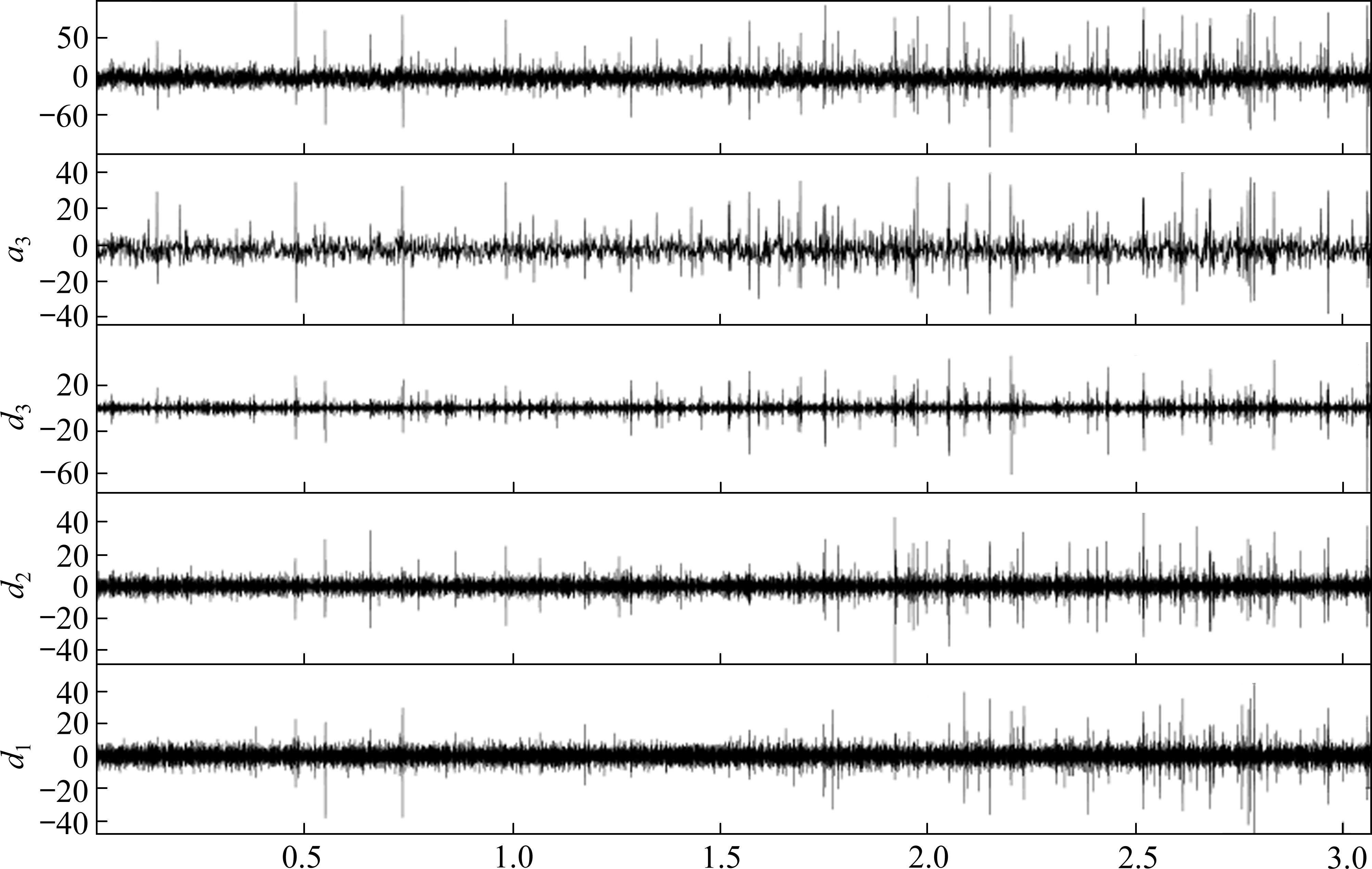
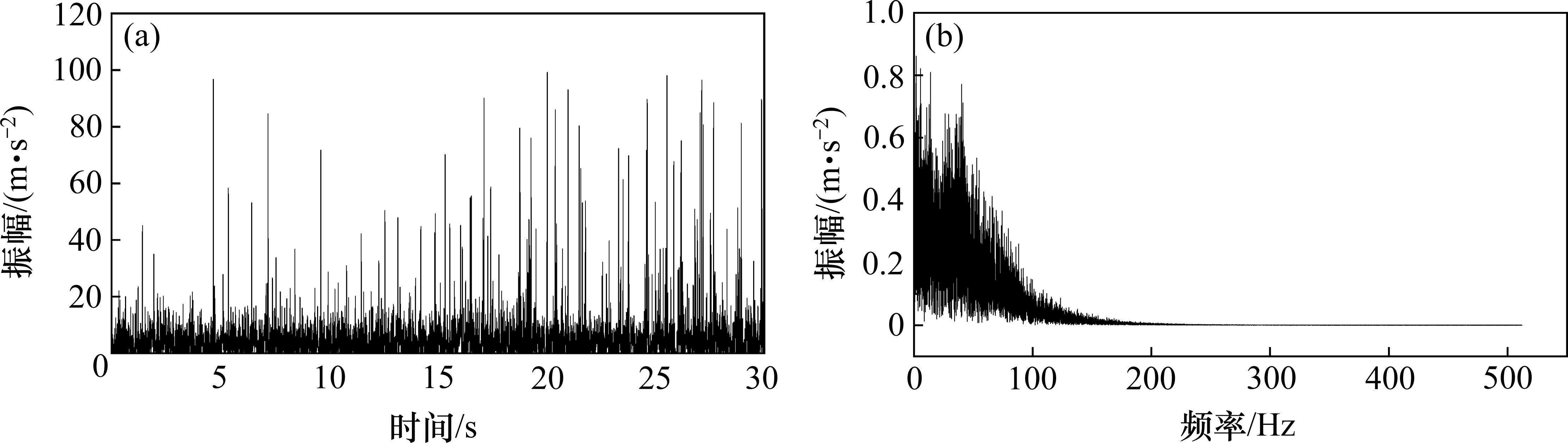
一般认为,TBM破岩振动主要表现为低频高幅振动,而噪声则主要表现为高频低幅振动。因此,对高频小波系数进行阈值处理,将低于特定阈值的小波系数设为0,以降低噪声的影响。同时,在处理振动信号时,选用软阈值函数,并采用基于固定阈值规则的方法来计算阈值。最后,对各级小波系数进行重构,以获得降噪后的信号。降噪后信号的时域和频域特性如图9所示。
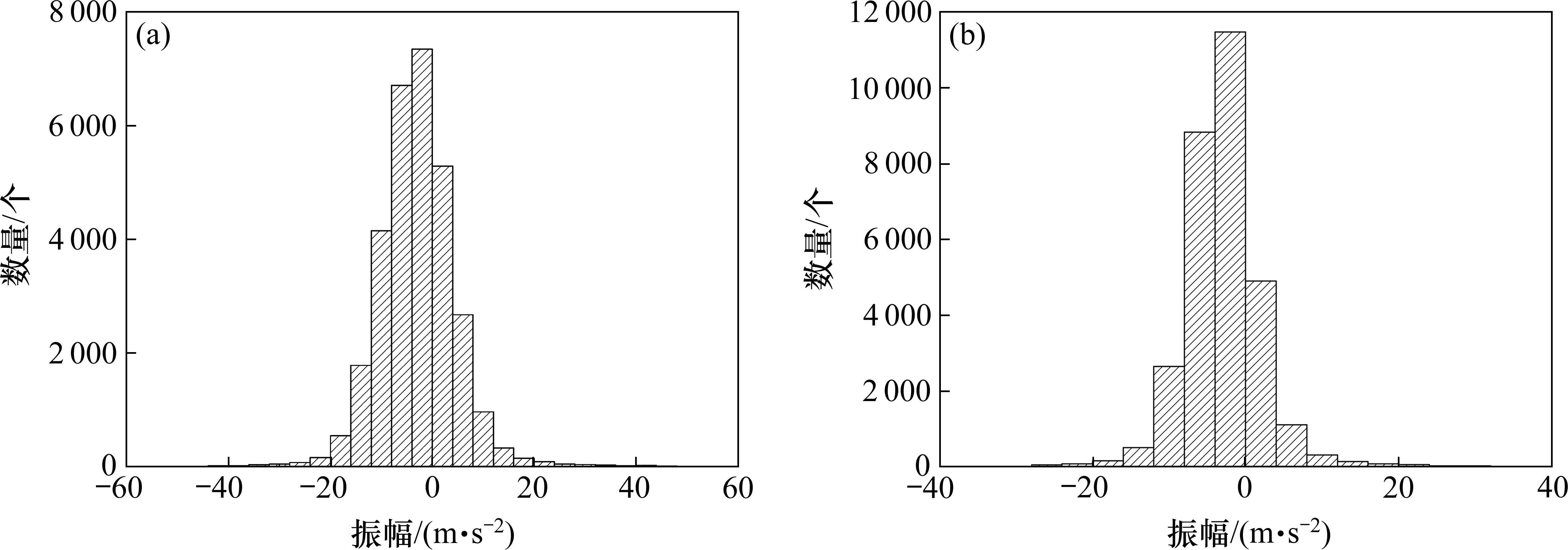
比较降噪前后的时域曲线可知,振动冲击信号的轮廓更加清晰,波峰的分辨率得到明显提高。降噪处理后,原始信号中低幅振动的强度明显减弱,这表明噪声的强度和能量受到了显著抑制。图10展示了降噪前后信号振动加速度幅值的直方图,在降噪后,振动加速度幅值集中在-8~8 m/s2范围内,高幅和低幅振动之间的差异更加明显,进一步突显了信号中的有用部分(振动强度较高的部分)。
对比降噪前后的时域特征参数,降噪前振动峰值为94.45 m/s2,降噪后为86.04 m/s2,峰值降低了8.90%;降噪前平均值为-2.83 m/s2,降噪后为-2.82 m/s2,基本不变;降噪前有效值为-3.09 m/s2,降噪后为-3.05 m/s2,降低了1.29%;降噪后峭度、偏度、波形因子、峰值因子、脉冲因子、裕度因子分别提高了7.21%、5.17%、2.91%、2.04%、5.20%、6.22%,表明降噪后信号的冲击性得到增强。
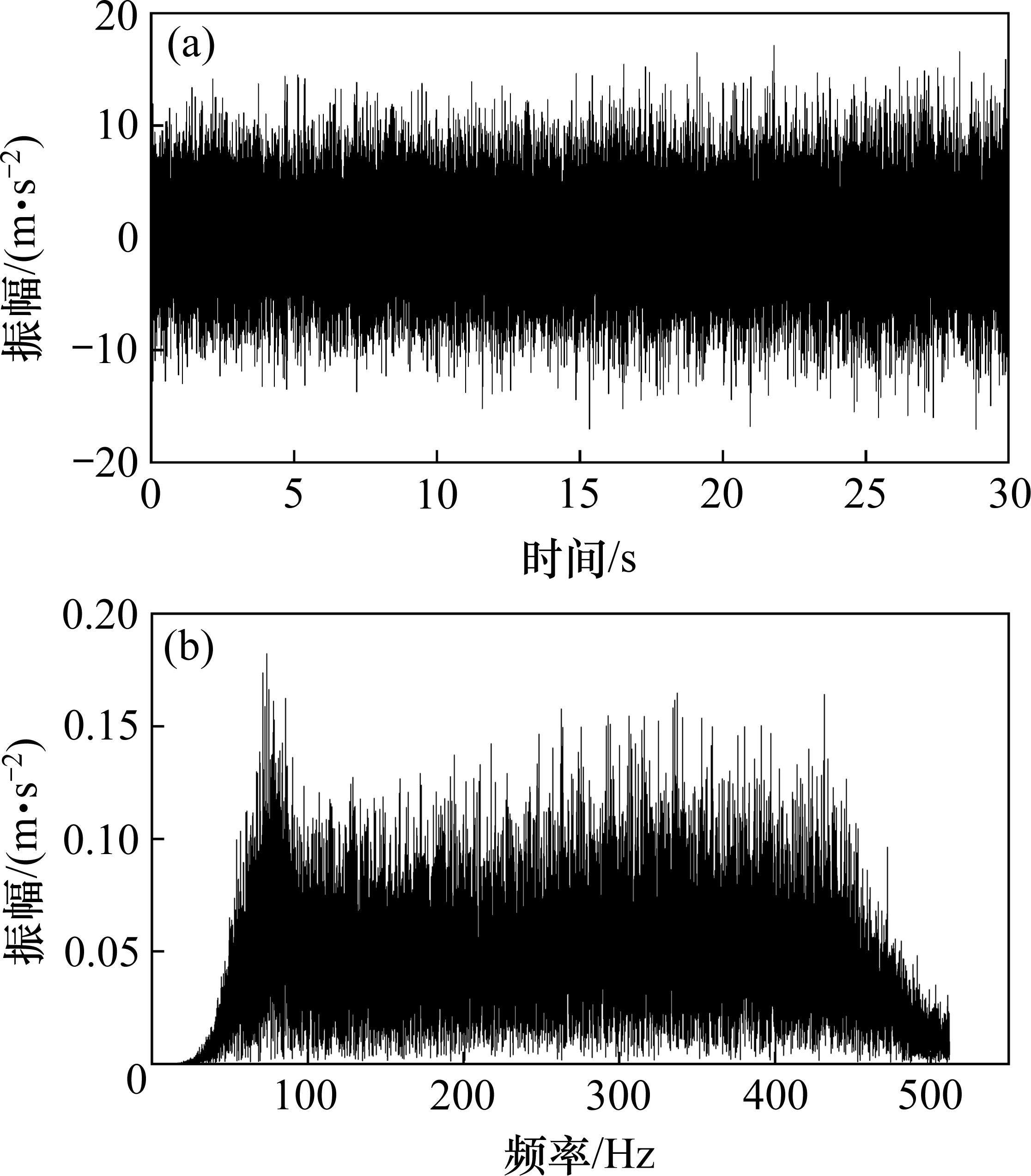
对比降噪前后的频域曲线,可以看出频域分布基本不变,峰值频率也变化不大,高频信号幅值略有下降。图11展示了经过降噪处理后产生的残差信号的时域和频域曲线。残差信号的时域曲线振幅范围为-20~20 m/s2,主要集中在-10~10 m/s2,其中部分峰值有所减小。在频域方面,残差信号主要分布在50~450 Hz,其峰值频率位于73 Hz左右。通过分析,被滤除的信号频率主要分布在50 Hz以上,而波峰包络谱的峰值主要位于50 Hz以下,这说明被过滤掉的成分属于滚刀破岩振动之外的振动,因此可以被视为噪声成分。
为进一步分析降噪效果,笔者按上述降噪方法对80组振动信号(其中II、IIIa、IIIb、IV类围岩段各设置20组)进行降噪处理,分别提取降噪前后的振动峰值及平均值,计算其与围岩等级的相关性。考虑到振动峰值和平均值是连续变量,而围岩类别属于离散变量,要分析二者间的相关性,不能使用常规的Pearson相关系数,而要改用Spearman秩相关系数(rs)进行分析,其计算公式如下。
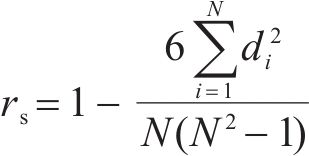
式中:rs为Spearman秩相关系数,值越大代表2组变量的相关性越强;di为每一组变量的秩次之差,即di =xi-yi,其中xi和yi分别为第i个变量值Xi在变量X中的排行秩次以及第i个变量值Yi在变量Y中的排行秩次;N为变量X或Y的元素个数(X和Y的元素个数相同)。
通过计算,降噪前振动峰值和平均值与围岩等级的相关性分别为0.701、0.787,降噪后振动峰值和平均值与围岩类别的相关性分别为0.754、0.883,相比降噪之前分别提高了7.56%和12.20%,说明该方法可有效实现TBM破岩振动信号降噪。
3 TBM破岩振动分析
3.1 时域及频域分析
在不同类别围岩中,TBM的岩-机相互作用也不同。考虑到TBM破岩振动与地质条件之间存在密切关联,为研究不同地质条件下的振动规律,选取不同类别围岩条件下TBM破岩产生的振动信号,并对其进行频域转换,图12展示了其时域曲线及频谱图。
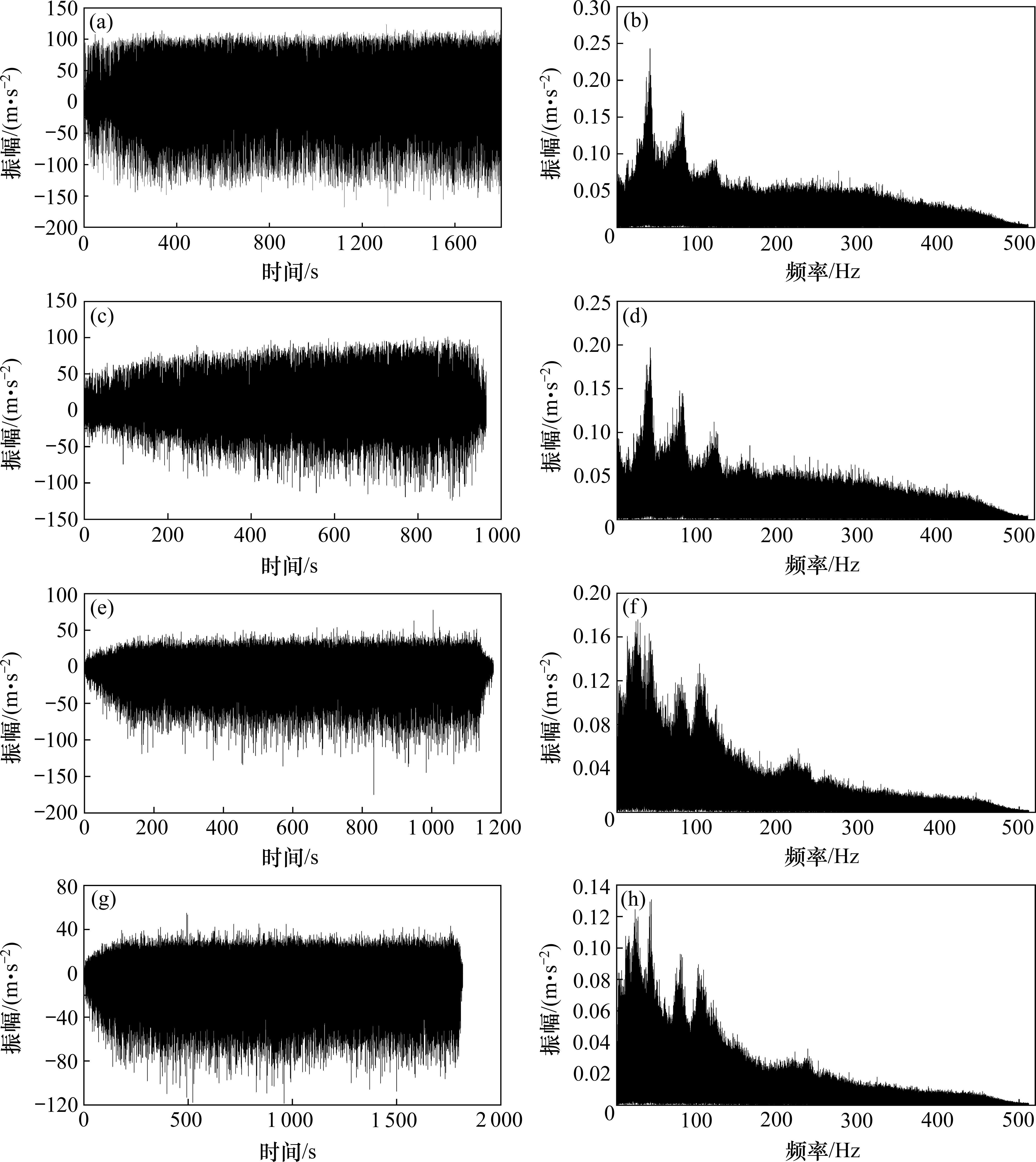
由图12可知,Ⅱ类围岩振动加速度主要分布在-150~100 m/s2,其峰值频率分别为41.0、80.4和123.2 Hz,其中最大峰值频率为41.0 Hz;Ⅲa类围岩振动加速度主要分布在-100~100 m/s2,其峰值频率分别为41.3、78.0、120.7和165.4 Hz,其中最大峰值频率为41.3 Hz;Ⅲb类围岩振动加速度主要分布在-100~50 m/s2,其峰值频率分别为25.9、40.1、80.1、102.5和225.1 Hz,其中最大峰值频率为43.2 Hz;Ⅳ类围岩振动加速度主要分布在-80~40 m/s2,其峰值频率分别为22.9、43.2、78.8、101.5和237.5 Hz,其中最大峰值频率为25.9 Hz。
分析可知,不同围岩条件下的TBM破岩振动在时域和频域方面都表现出明显差异。随着围岩条件变差,TBM破岩振动强度逐渐减小,各类围岩峰值频率的振幅也随之减小,说明围岩条件越好,振动越强烈。从峰值频率的组成来看,IIIb类和Ⅳ类围岩的峰值频率成分更加复杂,且低频成分能量占比较大、高频成分占比较小,Ⅱ类和IIIa类围岩的峰值频率成分相对稳定且数量较少,其中高频能量占比相对IIIb类和Ⅳ类围岩更高,表明随着围岩条件变好,TBM破岩振动更加稳定,高频成分的能量也随之增大。
3.2 时频分析
传统信号处理通常采用傅里叶变换对信号进行整体转换,这种方法不具备对信号在时间和频率上的定位能力,更适用于分析平稳信号。而TBM破岩振动信号是一种时变非平稳信号,传统方法很难准确反映其局部时变频率特性。时频分析则是一种新的方法,能够将一维时域信号转换为二维时频图像,在图像中描述了信号在不同时间和频率上的能量密度和强度分布,从而可以有效反映信号的时频特性。
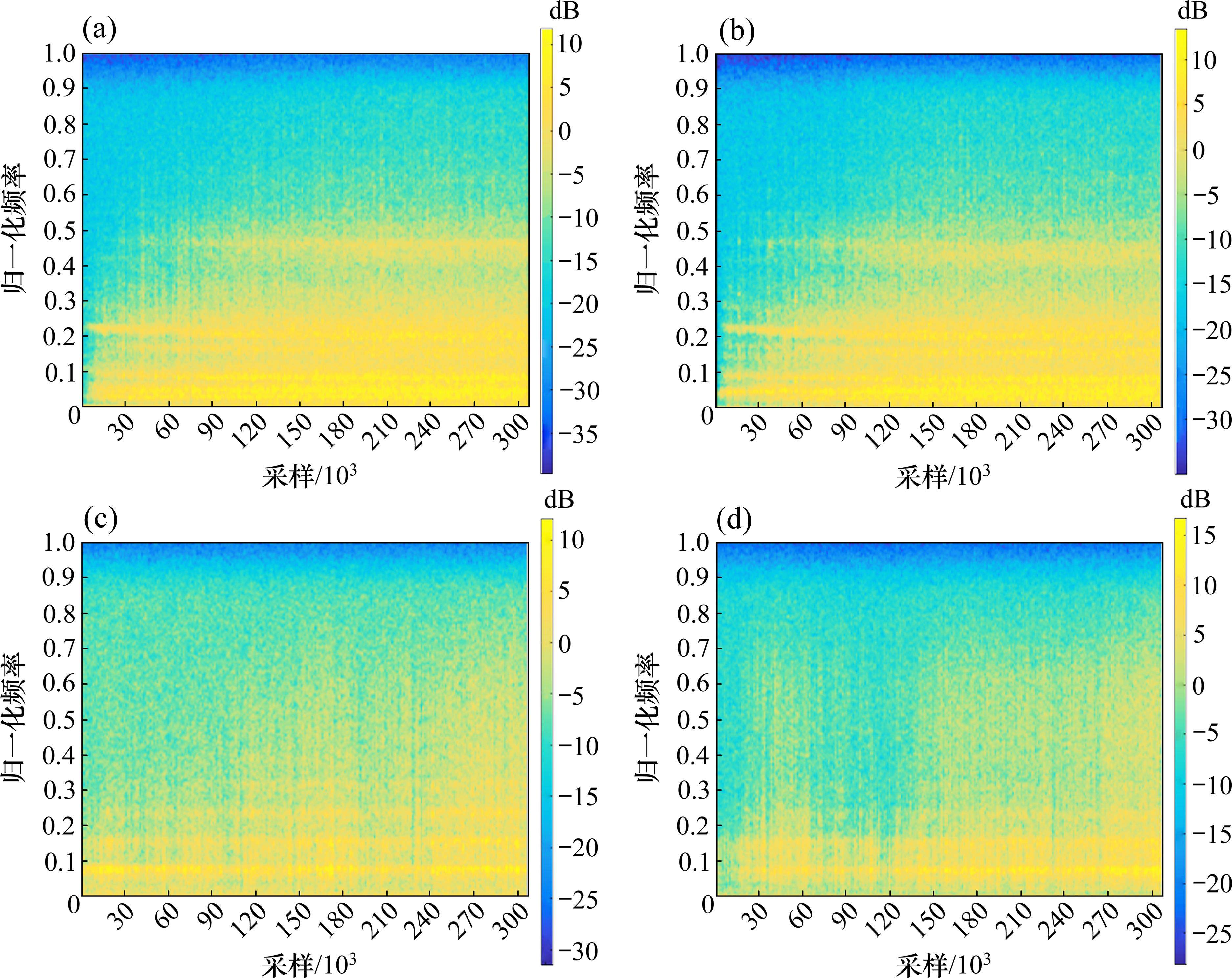
本文采用短时傅里叶变换进行TBM破岩振动信号的时频分析。从不同围岩类别的TBM破岩振动信号中分别选择5 min稳定段波形,并使用Matlab进行短时傅里叶变换,得到的时频图如图13所示。时频图中的颜色明暗表示能量值的大小,将不同类别围岩的破岩振动信号时频图能量值调整为相同区间范围后,可以看到,从Ⅱ类围岩到Ⅳ类围岩,高频范围的横向条纹基本不变且色彩偏暗,而低频范围的横向条纹逐渐由亮变暗,由密变疏,这表明TBM破岩振动的能量主要集中在低频范围内,且随着围岩条件变差,破岩能量逐渐减弱。
4 基于机器学习的围岩感知方法
4.1 数据集建立
为建立基于TBM破岩振动的围岩参数预测模型,需要构建包含振动特征和围岩参数的数据集。
4.1.1 围岩参数获取
围岩参数主要包括岩石单轴饱和抗压强度(UCS)和岩体体积节理数(Jv)。UCS通过现场钻孔取芯进行单轴压缩实验(图14)或现场拾取岩块进行点荷载试验(图15)获取。


当使用点荷载试验方式时,需要根据式(1)[28]将(50±35) mm的立方体岩渣试样的点荷载强度转换为UCS。
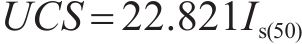
式中:UCS为岩石单轴饱和抗压强度,MPa;Is(50)为标准岩石点荷载强度,MPa;Jv通过隧道现场地质勘察资料获取,应根据岩体节理数的统计结果按式(2) [28]计算。
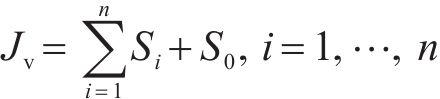
式中:Jv为岩体体积节理数,条/m3;n为统计区域内的结构面组数;Si为第i组结构面沿法向每米测线上的节理条数;S0为每立方米岩体非成组节理条数。
4.1.2 振动特征值提取
振动特征参数包含的种类繁多,由第3节分析可知,不同类别围岩在TBM破岩振动信号的时域、频域方面均存在一定差异,因此本文分别从时域、频域及峭度图中提取特征,其中时域特征包括最大值、最小值、平均值、中位数、峰峰值、整流平均值、方差、标准差、峭度、偏度、均方根、均方值、方根幅值、波形因子、峰值因子、脉冲因子、裕度因子共17个;频域特征包括重心频率、均方频率、均方根频率、频率方差、频率标准差共5个;谱峭度特征包括谱峭度的均值、谱峭度的标准差、谱峭度的偏度、谱峭度的峭度共4个。最终提取到TBM破岩振动特征共26个,以5段典型破岩振动信号样本为例,其特征值如表3所示。
| 参数项 | 最大值 | 最小值 | 平均值 | 中位数 | 峰峰值 | 整流 平均值 | 方差 | 标准差 | 峭度 | 偏度 | 均方根 | 均方值 | 方根幅值 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 110.21 | -127.1 | -2.98 | -3.61 | 237.78 | 9.51 | 204.25 | 14.29 | 16.99 | 1.42 | 14.73 | 216.95 | 6.86 |
| 2 | 93.42 | -100.54 | -2.17 | -3.16 | 197.74 | 8.03 | 161.46 | 12.71 | 14.79 | 1.62 | 12.3 | 151.35 | 5.97 |
| 3 | 49.67 | -112.55 | -1.98 | -0.68 | 163.86 | 10.01 | 172.48 | 13.13 | 8.88 | 1.28 | 13.22 | 174.66 | 7.49 |
| 4 | 27.84 | -89.54 | -1.2 | -0.37 | 123.64 | 8.4 | 108.47 | 10.42 | 7.16 | 1.17 | 10.73 | 115.03 | 6.09 |
| 5 | 27.79 | -38.96 | -0.55 | -0.72 | 71.12 | 2.84 | 18.67 | 4.32 | 11.55 | 1.13 | 5.13 | 26.28 | 1.69 |
4.1.3 振动信号特征筛选
通过分析26个振动特征与UCS、Jv的相关性,筛选出最能表征岩机相互作用关系的TBM破岩振动特征。由于振动信号特征值、UCS和Jv都是连续变量,此处选择Pearson相关系数进行计算。
由图16可知,统计特征与UCS相关性大于0.8的有6个,分别为平均值、峰峰值、峭度、均方根、重心频率、均方根频率,相关性介于0.6和0.8之间的有13个;统计特征与Jv相关性大于0.7的有5个,分别为平均值、峰峰值、峭度、重心频率、均方根频率,相关性介于0.4和0.7之间的有10个,4个谱峭度统计特征与UCS和Jv的相关性都在0.3以下,可认为与围岩相关性较差。最终选择平均值、峰峰值、峭度、重心频率、均方根频率作为TBM破岩振动的特征参数。
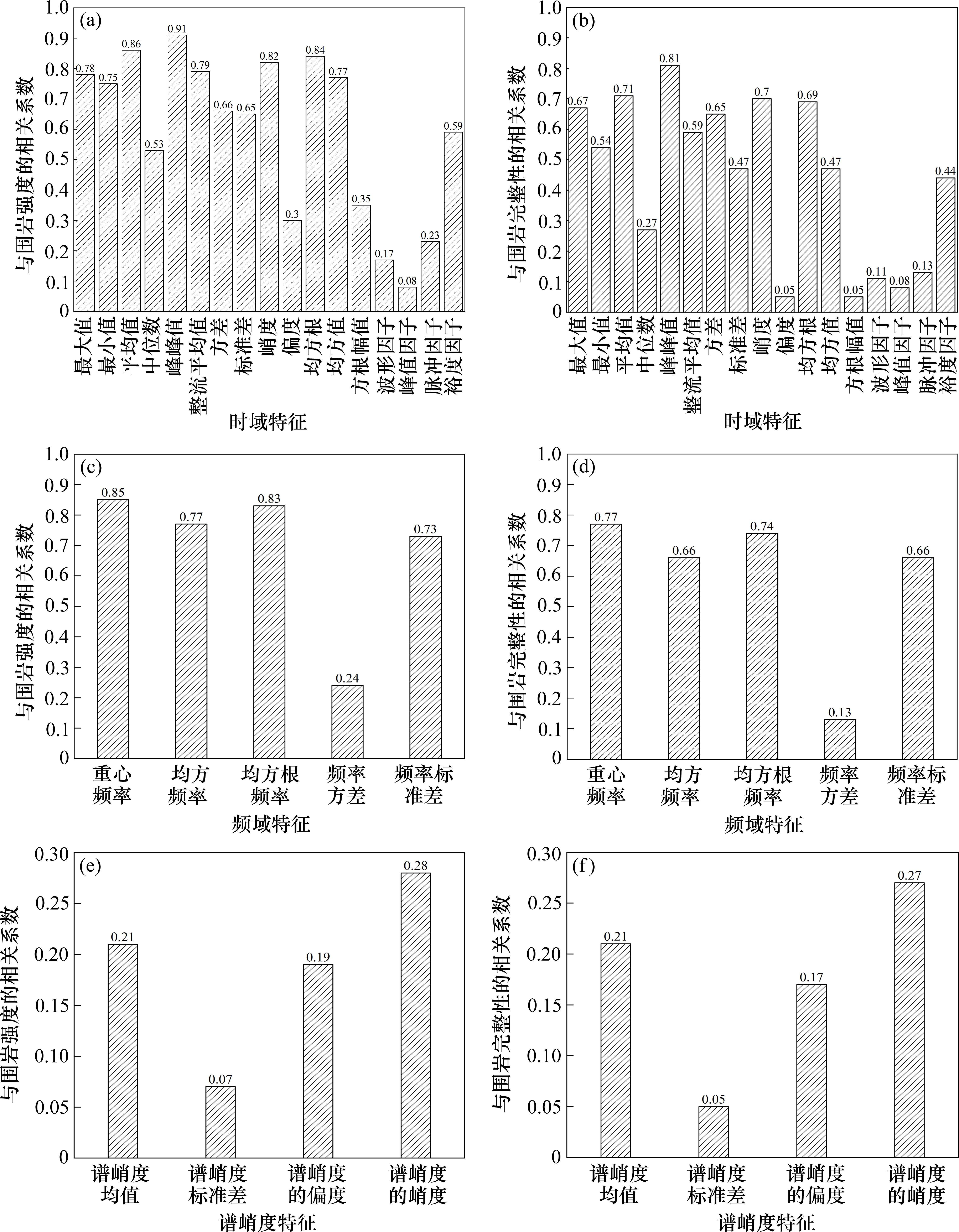
4.1.4 数据集分割
从现场监测所得数据中筛选出较为稳定的250组数据,其中II类围岩段50组,IIIa类围岩段75组,IIIb类围岩段95组,IV类围岩段30组,将数据集中的样本按第2节的方法进行降噪处理,并按7:2:1划分为训练集、测试集和验证集,其中训练集主要用来训练模型,测试集用于评估模型的泛化能力,验证集用于调整模型超参数和评估模型性能。训练集共计175组数据,测试集共计50组数据,验证集共计25组数据,每组振动特征参数与围岩参数一一对应,数据集统计特征如表4所示。
| 参数项 | 数量 | 极差 | 最大值 | 最小值 | 平均值 | 标准差 |
|---|---|---|---|---|---|---|
| UCS/MPa | 250 | 74.27 | 150.54 | 76.28 | 108.30 | 18.55 |
| Jv/(条∙m-3) | 250 | 39 | 39 | 0 | 16 | 12 |
| 平均值/(m∙s-2) | 250 | 23.88 | 28.45 | 4.57 | 15.40 | 6.24 |
| 峰峰值/(m∙s-2) | 250 | 236.91 | 292.83 | 55.92 | 167.35 | 48.28 |
| 峭度 | 250 | 7.20 | 14.89 | 7.69 | 11.94 | 3.83 |
| 重心频率/Hz | 250 | 115.01 | 144.07 | 29.06 | 83.85 | 37.77 |
| 均方根频率/Hz | 250 | 111.38 | 354.04 | 242.66 | 281.39 | 20.67 |
4.2 基于BP神经网络的围岩识别
BP神经网络是目前应用最广泛的神经网络模型之一,本节通过构建BP神经网络模型对围岩参数进行预测。BP神经网络的超参数主要包括激活函数种类、隐藏层数目和隐藏层单元数。本文采用网格搜索的方式寻找最优组合,激活函数方面选择Sigmoid、Relu和Tanh,隐藏层数方面选择1~5层,隐藏层单元数方面选择2~8个。由于网格搜索需要进行大量计算,本文仅展示一部分预测效果较好的正交结果,如表5所示。由表5可知,当选择Sigmoid激活函数、学习率设置为0.2、隐藏层数设置为1层、隐藏层单元数设置为5时,预测效果最佳。此时UCS的均方根误差(Erms)、平均绝对误差(Ema)和平均绝对百分比误差(Emap)分别为9.896、7.165和0.141;Jv的RMSE、MAE和MAPE分别为0.046、0.041和0.157。
| 学习率 | 激活函数 | 隐藏层数 | 隐藏层单元数 | UCS | Jv | ||||
|---|---|---|---|---|---|---|---|---|---|
| Erms | Ema | Emap | Erms | Ema | Emap | ||||
| 0.2 | Sigmoid | 1 | 2 | 9.958 | 8.536 | 0.124 | 0.046 | 0.038 | 0.149 |
| 0.2 | Sigmoid | 1 | 5 | 9.896 | 7.165 | 0.141 | 0.046 | 0.041 | 0.157 |
| 0.2 | Sigmoid | 1 | 4 | 7.905 | 9.057 | 0.134 | 0.053 | 0.040 | 0.134 |
| 0.1 | Sigmoid | 1 | 4 | 9.654 | 8.154 | 0.138 | 0.049 | 0.040 | 0.132 |
| 0.3 | Sigmoid | 1 | 4 | 9.350 | 7.897 | 0.146 | 0.049 | 0.045 | 0.139 |
| 0.2 | Relu | 2 | 4 | 11.183 | 8.431 | 0.148 | 0.058 | 0.038 | 0.139 |
| 0.2 | Tanh | 1 | 3 | 11.219 | 8.061 | 0.143 | 0.024 | 0.050 | 0.133 |
| 0.2 | Tanh | 2 | 4 | 10.754 | 8.228 | 0.152 | 0.063 | 0.035 | 0.126 |
以Sigmoid激活函数、学习率0.2、隐藏层数1层、隐藏层单元数5作为模型超参数,使用训练集数据对模型进行训练,将验证集和测试集中的TBM振动特征参数分别代入已建立的BP神经网络预测模型中,得到UCS、Jv的预测结果如图17所示,由图17可知该模型对UCS的预测效果较好,验证集预测误差少于1%,测试集预测误差少于2%;对Jv的预测效果相对较差,验证集预测误差少于4%,测试集预测误差少于8%。
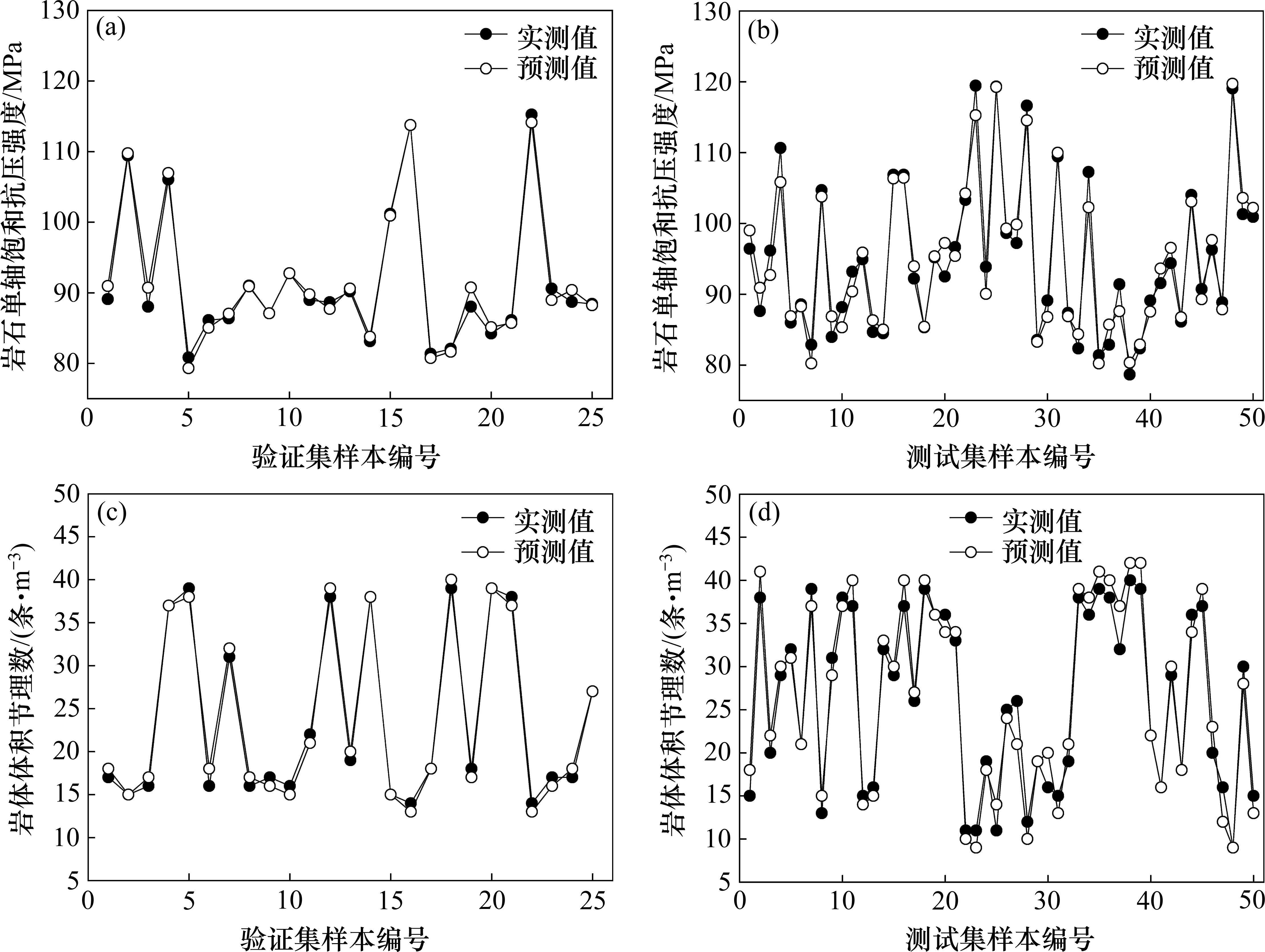
4.3 基于SVM的围岩识别
支持向量机(SVM)算法具有泛化能力强、鲁棒性好、适用于小样本数据等优点,本节通过构建SVM模型对围岩参数进行预测。SVM模型的主要参数包括核函数类型、核函数系数Gamma和惩罚因子c。核函数类型方面选择Poly、Rbf和Sigmoid,核函数系数Gamma取值越大,对训练集分类效果越好,对测试集的分类效果越差,越容易出现过拟合的情况。惩罚因子c表示模型允许的误差大小,c过小时,模型预测效果会变差,c过大时,模型容易出现过拟合。本文对核函数、核函数系数Gamma和惩罚因子c进行网格搜索,部分预测效果较好的网格搜索结果如表6所示。
| 核函数 | 核函数系数Gamma | 惩罚因子c | UCS | Jv | ||||
|---|---|---|---|---|---|---|---|---|
| Erms | Ema | Emap | Erms | Ema | Emap | |||
| Poly | 0.611 | 20 | 11.436 | 9.007 | 0.147 | 0.057 | 0.036 | 0.139 |
| Poly | 0.588 | 2 | 11.908 | 8.420 | 0.139 | 0.022 | 0.047 | 0.130 |
| Poly | 0.574 | 5 | 10.373 | 7.853 | 0.120 | 0.044 | 0.038 | 0.143 |
| Rbf | 0.521 | 10 | 9.348 | 8.572 | 0.138 | 0.052 | 0.042 | 0.132 |
| Rbf | 0.621 | 8 | 9.507 | 7.157 | 0.149 | 0.046 | 0.045 | 0.139 |
| Rbf | 0.564 | 6 | 7.471 | 8.229 | 0.114 | 0.044 | 0.040 | 0.132 |
| Sigmoid | 0.631 | 12 | 11.093 | 8.651 | 0.147 | 0.062 | 0.035 | 0.124 |
| Sigmoid | 0.556 | 11 | 9.583 | 8.146 | 0.143 | 0.045 | 0.035 | 0.161 |
由表6可知,当核函数选择Rbf、核函数系数为0.564,惩罚因子为6时,模型预测效果最优。此时UCS的Erms、Ema和Emap分别为7.471、8.229和0.114,Jv的Erms、Ema和Emap分别为0.044、0.040和0.132。将验证集和测试集中的TBM振动特征参数分别代入已建立的SVM预测模型中,得到UCS、Jv的预测结果如图18所示。
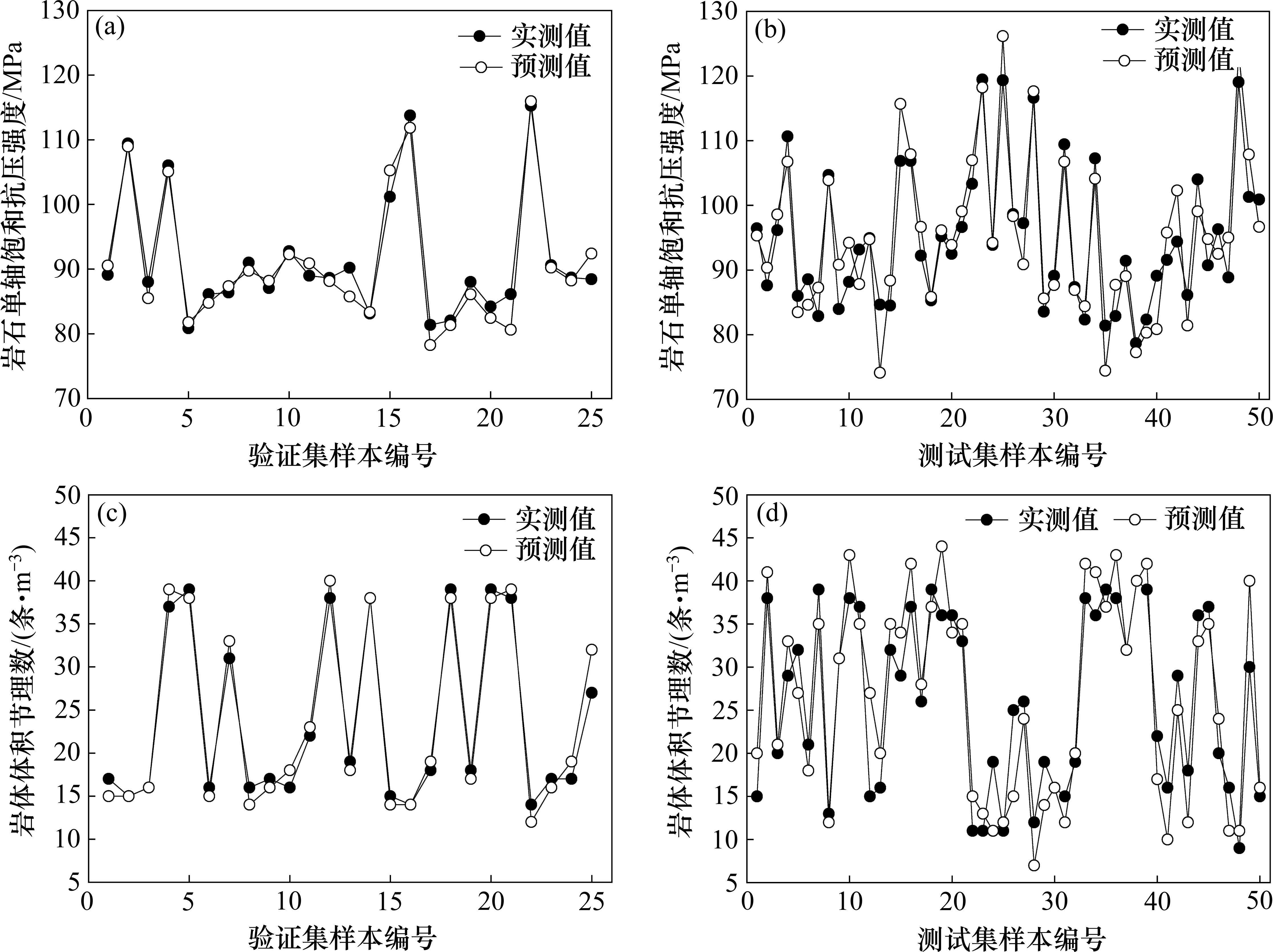
相比于BP神经网络预测模型,SVM模型的预测效果相对较差,验证集对UCS和Jv的预测误差分别为2%和6%,测试集对UCS和Jv的预测误差分别为4%和17%。与SVM模型相比,BP神经网络模型在测试集中对UCS的预测误差同比减少约50%,对Jv的预测误差同比减少约53%。此外,2种模型对UCS的预测效果均比对Jv的预测效果更好。
5 结论
1) 通过小波阈值方法对TBM破岩振动信号进行降噪,振动峰值、平均值与围岩类别的相关性分别提高了7.56%和12.20%。
2) 对各类围岩条件下的破岩振动分析可知,随着围岩条件变好,振动强度和振幅逐渐增加,破岩振动更加稳定且高频成分的振动能量随之增大。
3) 在26项振动特征值中,平均值、峰峰值、峭度、重心频率和均方根频率与UCS和Jv的相关性最高。
4) 相比于SVM模型,BP神经网络模型在掌子面围岩参数预测方面具有明显的优势,它在测试集中对UCS和Jv的预测误差同比分别减少了50%和53%,这也为后续开展更复杂的神经网络预测模型研究指明了方向。
李宗林,谭忠盛,周振梁等.基于TBM振动监测的围岩参数感知技术研究[J].铁道科学与工程学报,2025,22(04):1853-1869.
LI Zonglin,TAN Zhongsheng,ZHOU Zhenliang,et al.Research on surrounding rock parameter perception technology based on TBM vibration monitoring[J].Journal of Railway Science and Engineering,2025,22(04):1853-1869.

