随着人们对日常出行的准时性、安全性和舒适性的重视,城市轨道交通(以下简称“城轨”)系统已逐渐成为城市居民出行的首选。据中国城市轨道交通协会发布的数据显示,截至2023年底,北京地铁线路总长达836 km。2023年全年,北京地铁系统的日均客流量约946万人次,单日客运量甚至达到1 000万人次[1]。随着城轨线网的不断扩大和客流需求的不断攀升,其运营过程中运力运量不匹配、运营成本居高不下等一系列实际难题日益凸显。例如,北京、上海等城市轨道交通高峰时段部分列车满载率高达120%,严重影响乘客出行体验,但平峰时段部分列车平均满载率不足20%[2],导致运能大量浪费,严重依赖政府持续补贴,很大程度上影响了我国城市轨道交通的可持续发展。如何在保证服务水平的前提下,通过智慧化、数字化智能技术,优化运营组织和客流车流匹配度、降低系统运营成本已成为行业面临的重大实际需求。根据客流时空分布情况优化设计非等间隔的列车运行图,能够有效地提升列车运行效率和服务水平。例如,张矢宇等[3]和BLANCO等[4]设计了一种以最小化运营及乘客等待时间成本为目标的列车运行时刻表优化方法;许得杰等[5]和YUAN等[6]基于时变的客流需求,研究了多交路线路背景下的列车时刻表优化问题。WU等[7]将时变客流分组,以最小化各组中最长乘客等待时间为目标,优化列车时刻表和列车跳停站方案。在城市轨道交通列车运营中,列车时刻表和车底运用关系紧密,同时优化这两部分内容有利于求解系统更优的方案。YANG等[8]以最小化列车运营费用(列车购置费用和运行费用)和乘客出行费用(乘客等待时间和考虑拥挤感知的乘车时间)为目标研究了列车时刻表和车底运用整合优化问题;李思杰等[9]针对城市轨道交通时空分布不均衡的客流需求,构建了列车时刻表和车底运用协同优化的混合整数非线性规划模型;金波等[10]提出了一种考虑大小交路的城市轨道交通列车时刻表与车底运用计划协同优化方法。近年来,随着“虚拟编组”等概念的提出,以灵活编组解编、近距离追踪为特点的城轨列车群组运行模式得到国内外学者的广泛关注。例如,张英贵等[11]分析了虚拟连挂的城轨列车群组追踪运行过程,通过仿真实验验证群组列车运行能够在某些场景下显著提升系统运力。此外,李伟等[12]建立了在线编解模式下列车灵活编组的开行方案优化模型,以降低系统运营成本。钟林环等[13]针对城市轨道交通客流时空分布不均衡的问题,通过列车运行线候选集的建模方法,协同优化列车开行频率和编组方案,以降低乘客等待时间和企业运营成本,并提出基于可变邻域搜索的启发式优化算法。冉昕晨等[14]针对多编组列车混跑场景下的时刻表和车底周转问题,设计了基于遗传算法的变长度NSGA-II方法。朱昌峰等[15]构建了重联编组条件下城市轨道交通车底运用方案优化模型,针对模型的求解难题设计了多目标混沌粒子群优化算法。从以上研究和实验可以看出,群组列车运行模式已成为轨道交通发展的必然趋势。但现有研究主要集中于群组运行模式的可行性分析,面向客流车流耦合的列车运行图与车底接续研究较少;此外,由于该问题涉及列车到发时分、列车运行交路、列车编组类型等一系列变量,现有研究主要以其中一项为决策变量,通过启发式搜索和进化算法寻优,难以保证求解的全局最优性、无法实现多变量的一体优化。“时空网络”旨在将连续的时间离散为等间隔的时间段,从而直观地表示列车时空运行、客流时空演变,是近年来调度优化领域兴起的重要建模手段。本文面向城轨列车群组模式下的运行图与车底周转协同优化问题,以提升乘客服务质量和降低运营成本为双目标,基于高维网络构建一体化优化模型,并以北京地铁实际数据为例进行数值实验,进而为轨道交通运营部门实现“降本增效”提供科学的理论支撑。
1 问题描述
1.1 问题背景
如图1所示,本文研究的是包含N个车站的一条双向线路,分为上行(车站依次编号为1,2,…,N)和下行(车站依次编号为N+1,N+2,…,2N)2个运行方向。此外线路包含2个车场(车场1和2,编号分别为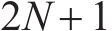
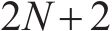
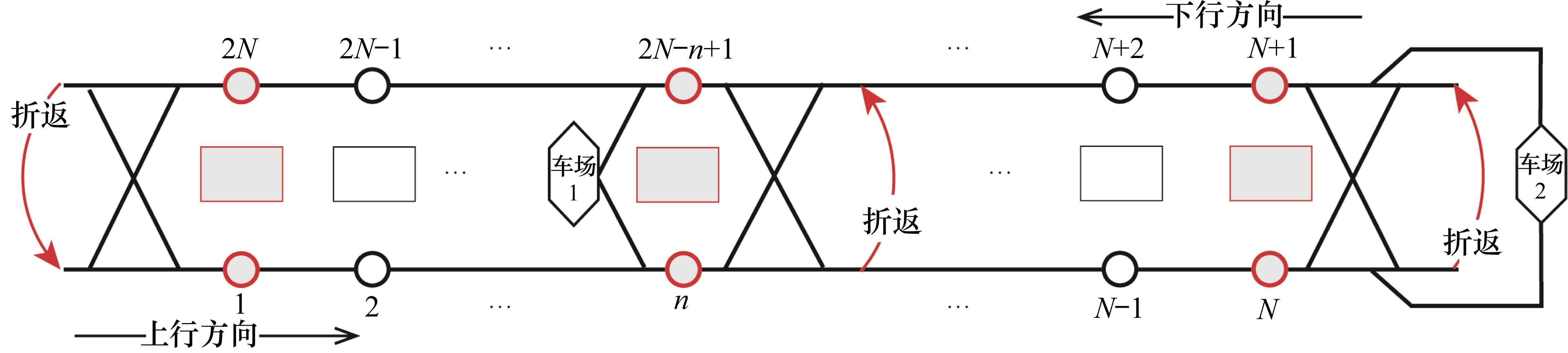
1.2 编组-位置-时间网络
时空网络作为一种有效的方法,被广泛地用于解决各种运输问题(YIN等[16-20])。不同于现有相关文献的直接建模方法,本文参照时空网络的创建思路,引入一类高维网络:编组-位置-时间网络构建模型。编组-位置-时间网络的3个维度如下:
1) 编组类型。例如4编组、6编组、8编组等,记为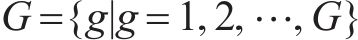
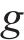
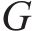
2) 车站和车场位置。记为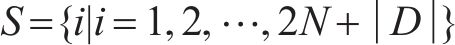
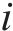
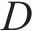
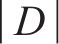
3) 离散的时间节点。将研究时段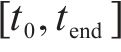
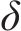

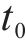
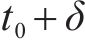
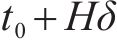
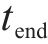
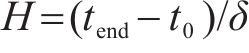
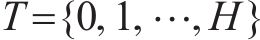
为叙述方便,记编组-位置-时间网络为G-S-T网络。如图2(为了更直观地描述,以包含车站A-F(其中A、D和F为具有折返能力的车站),及车场1和2的线路为例),G-S-T网络中的位置-时间平面(S-T平面)由节点集合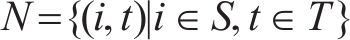

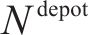
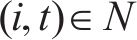
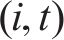
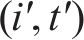
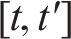
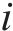
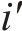
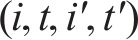
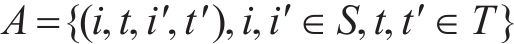
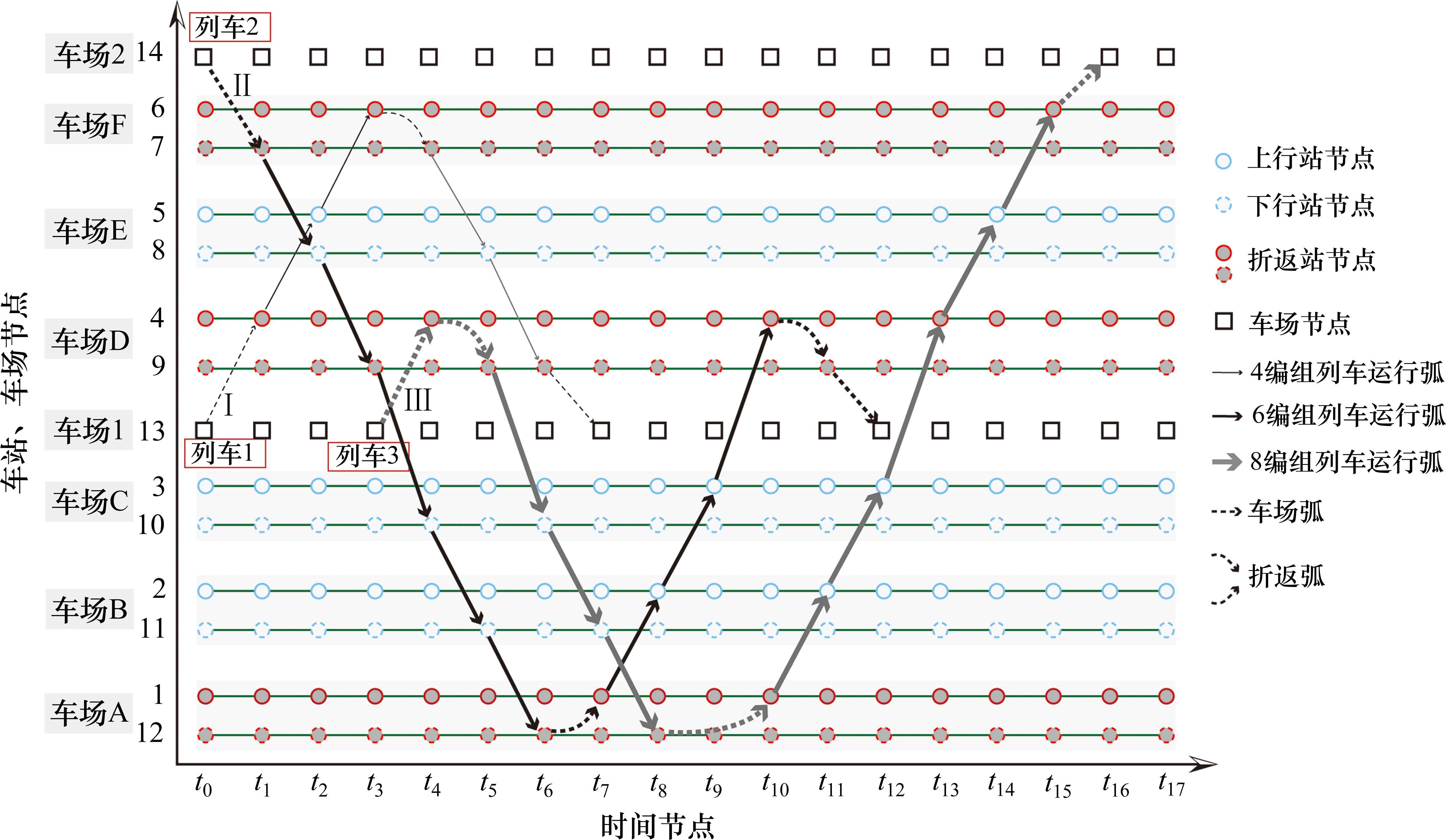
1) 运行弧(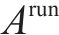
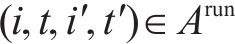
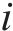
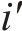
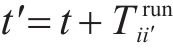
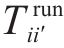
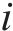
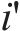
2) 折返弧(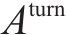
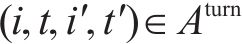
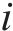
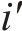
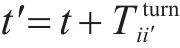
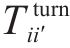
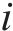
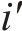
3) 车场弧(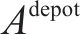
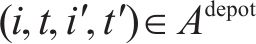
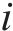
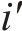
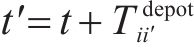
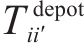
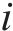
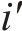
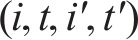
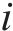
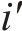
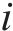
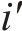
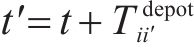
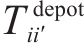
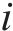
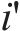
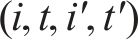
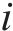
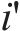
G-S-T网络中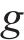
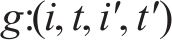
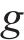
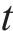
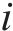
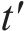
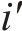
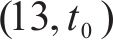
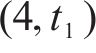
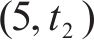
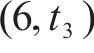
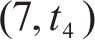
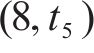
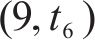
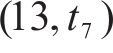
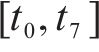
综上,时空网络中的弧选择过程可以决定:1) 编组类型动态变换。2) 列车在车站/车场间的到发时刻。3) 车底的衔接计划(包含列车折返、进出车场和编组变换等)。如列车到达折返站F后,可选择折返,继续下一个车次(列车1),也可选择驶入车场2(列车3)。由于折返站D为线路中段的车站,列车到达后,既可选择折返也可继续向下一站运行(列车3)。此外,列车在折返站的折返时间在最大和最小折返时间内可任意选择,如列车2和列车3在车站A的折返时间不同。借助G-S-T网络,将考虑灵活编组变换的城轨列车群组运行图和车底接续协同优化问题的核心转化成路径选择过程。值得指出的是,通过引入虚拟车场,基于G-S-T网络,本文所提方法可进一步解决列车在任意车站编组变换问题。
本文基于多车场、多交路的双向地铁线路,考虑时变的客流需求和灵活编组变换过程,研究了城轨列车群组运行图和车底接续问题。借助高维G-S-T网络,将问题转化为G-S-T网络中带资源约束的路径选择问题,并构建混合整数规划模型进行求解。在建模过程中,根据实际的运营情况给出如下几条合理假设:
1) 列车的编组类型可进行动态变换且变换过程须在车场(或虚拟车场)完成。基本车辆单元间依靠信号连接,即车辆单元间连接、断开的时间忽略不计。
2) 列车的折返过程均为站后折返,即列车到达折返站后,全部乘客下车,完成折返过程到达对向车站后,站台上等待的乘客上车。
3) 与以乘客起讫点(OD)数据作为输入的研究不同,本文采用了HUANG等[21]和YIN等[22]的研究方法,使用乘客进出站刷卡数据、站间断面客流作为模型的关键数据支撑,并假设下车乘客数量与列车上的乘客数量成正比。此外,假设与乘客数量相关的变量均为连续型变量。
2 模型构建
2.1 符号定义
为了便于描述,表1对本文涉及的主要参数和变量进行了定义。
| 符号 | 定义 | |
|---|---|---|
| 参数 | 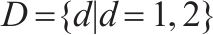 | 车场/车辆段集合,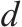 |
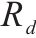 | 车场/车辆段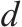 | |
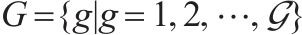 | 列车编组种类集合,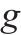 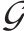 | |
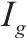 | 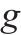 | |
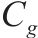 | 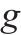 | |
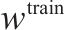 | 单列车辆单元的购置成本,单位:元 | |
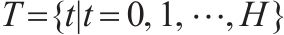 | 时间节点集合,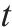 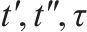 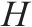 | |
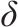 | 离散时间段长度,单位:秒 | |
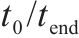 | 研究时段的起/终节点 | |
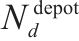 | G-S-T网络中车场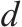 | |
 | G-S-T网络中车站节点集合 |
续表1
| 符号 | 定义 | |
|---|---|---|
| 参数 | 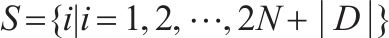 | 车站和车场节点集合,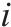 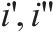 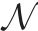 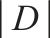 |
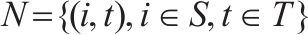 | G-S-T网络的节点集合,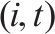 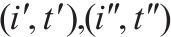 | |
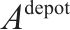 | G-S-T网络中表示列车进出车场的弧,简称为车场弧 | |
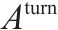 | G-S-T网络中表示列车折返的弧,简称为折返弧 | |
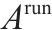 | G-S-T网络中表示列车在站间运行的弧,简称运行弧 | |
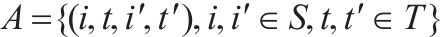 | G-S-T网络中的弧集合,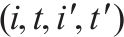 | |
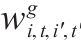 | 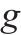 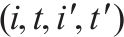 | |
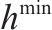 | 列车运行的最小安全间隔,单位:秒 | |
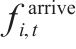 | 在时段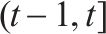 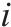 | |
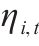 | 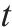 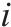 | |
| 变量 | 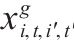 | 弧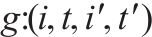 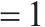 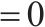 |
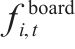 | 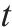 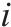 | |
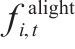 | 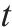 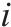 | |
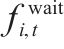 | 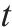 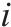 | |
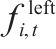 | 列车离开时,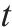 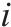 | |
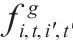 | 经过运行弧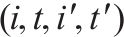 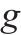 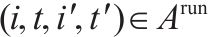 | |
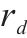 | 运营开始时,车场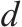 |
2.2 数学模型
借助G-S-T网络,将考虑灵活编组变换的城轨列车群组运行图和车底接续协同优化问题构建为一个混合整数规划模型。下面介绍模型的构建过程。
2.2.1 决策变量
根据研究内容,决策变量主要分为3类:
1) 整数变量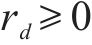

2) 0-1变量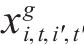
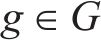
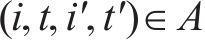

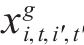
3) 连续变量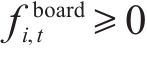
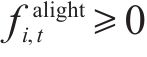
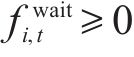
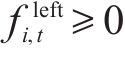
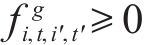
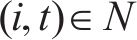
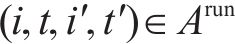
2.2.2 目标函数
目标函数包含列车购置成本、列车运行成本和乘客等待时间3部分。
列车购置成本是轨道交通运营成本的重要组成部分,表示为:
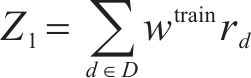
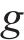
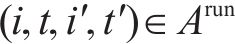
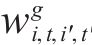
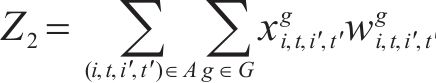
根据自动售检票系统(AFC系统)的历史刷卡数据,可得到时刻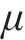
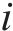
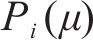
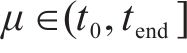
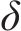
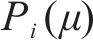
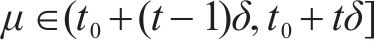
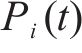
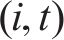
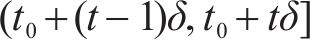
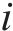
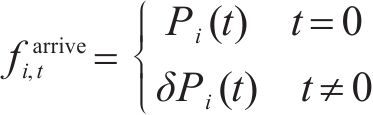
由于列车有容量限制,并不是所有等待的乘客都能成功乘坐到达的第1辆列车,未成功上车的乘客表示为:
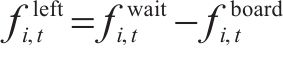
其中,
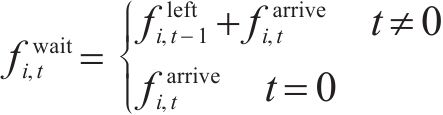
节点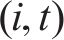
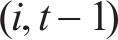
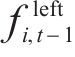
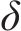
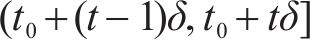
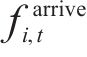
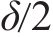
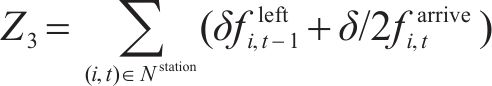
2.2.3 约束条件
1) 车场容量约束每个停车场存放的列车车辆单元数不能超过车场的容量,故
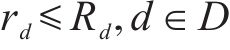
2) 车底循环约束每个时刻
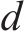
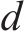

其中,

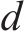


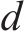
3) 车底平衡约束为保证列车时刻表的可循环性,要求运营结束时,各车场的列车车辆单元数与运营开始前相同,即
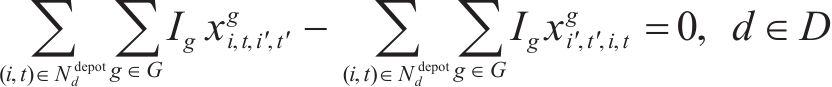
4) 列车流平衡约束如前所述,问题被转化成路径选择问题。因此,列车在节点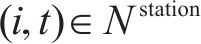
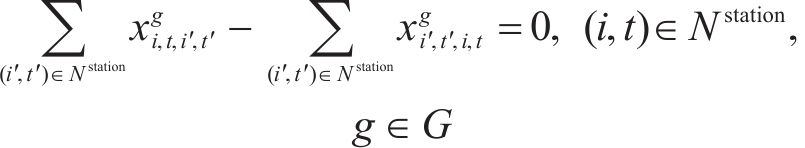
其中,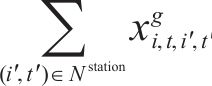
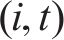
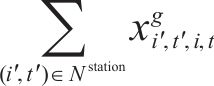
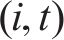
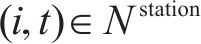
5) 安全运行约束列车运行需保证最小的安全间隔。设在G-S-T网络中,列车间的最小时间间隔为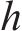
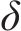
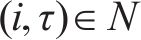
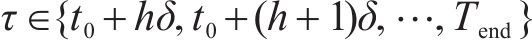
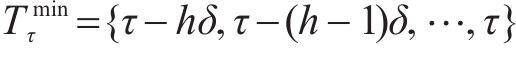
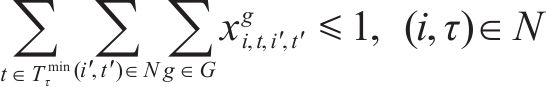
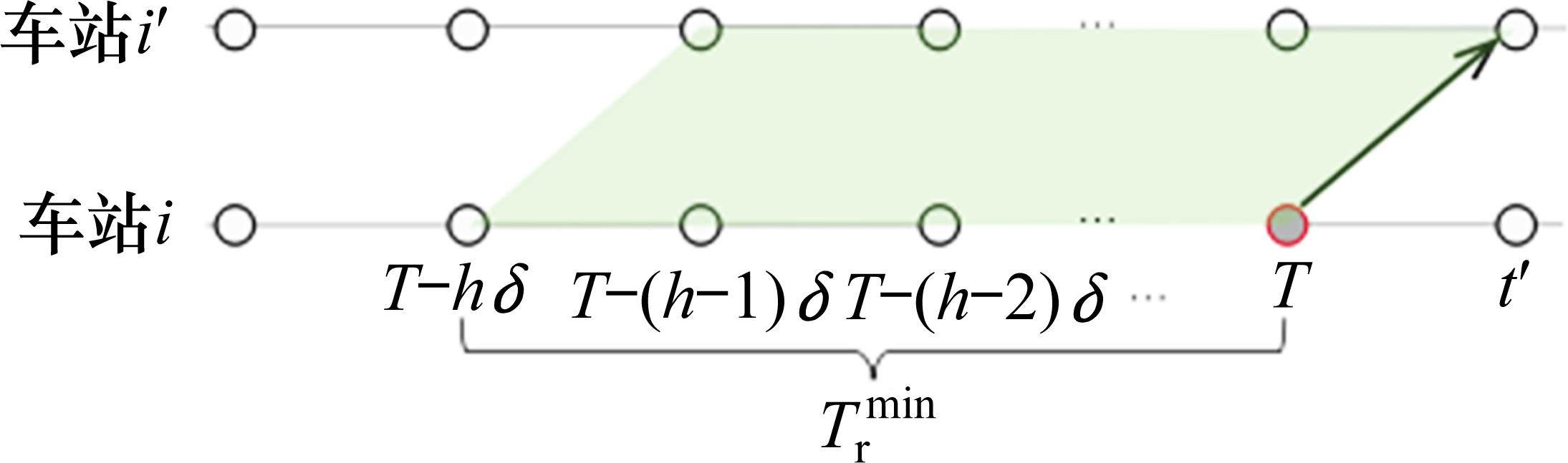
约束(11)不仅保证了列车在站间的安全运行,也保证了折返段和车场出入段的运用条件。
表示每个节点的最小时间间隔内,经过的列车不超过一辆,即图3阴影面积内,被选择的弧至多只有一条。
6) 列车上的乘客约束弧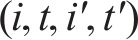
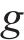
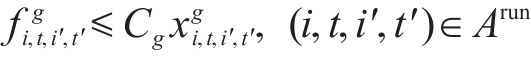
即,若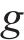
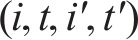
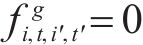
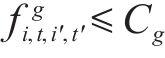
7) 上车乘客约束。a)上车人数须小于等于经过列车的剩余容量,即

b)上车人数应小于等于站台等待乘客数,即
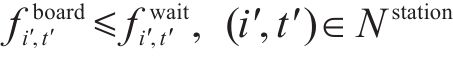
8) 下车乘客约束。a)要有列车经过才会有乘客下车,且下车人数不超过列车容量,即
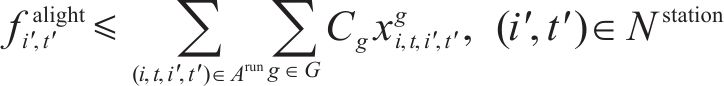
b) 为了简化模型,参照已有文献的处理方法,假设在节点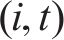
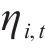
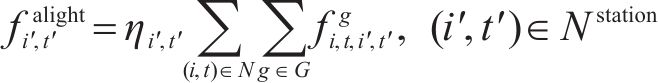
其中,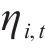
9) 客流平衡约束在节点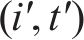
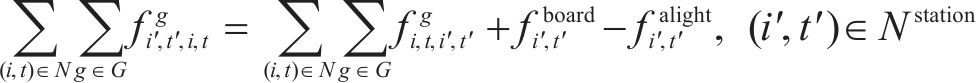
即列车驶离节点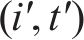
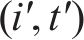
2.2.4 混合整数线性规划模型及性质分析
综上,得到一个多目标混合整数规划模型:
~
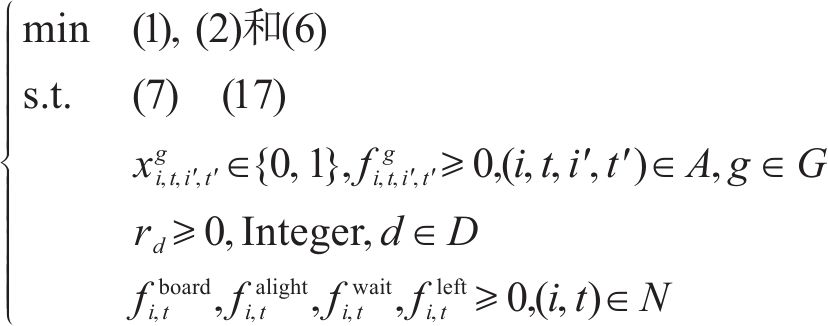
为了处理多目标问题,引入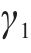
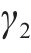
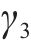
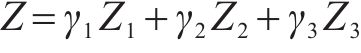
其中,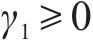
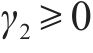
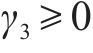
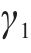
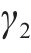
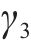
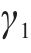
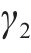
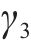
模型中目标函数和约束条件均为线性结构,因此该模型为一线性混合整数规划模型。与现有文献的非线性模型相比,本文构建的模型可以使用CPLEX、Gurobi等商业软件直接求解得到精确解。
3 实例分析
3.1 基础数据
本文以北京地铁15号线实际运营数据为基础进行实例分析。北京地铁15号线全长41.4 km,是一条途经海淀,朝阳,顺义3区的市郊线路。如图4所示,线路共包含20座车站(其中具有折返能力的车站5座),2个停车场/车辆段(位于中段的香江北路车辆段和末端的俸伯停车场)。15号线是双向运行的线路。由清华东路西口站到俸伯站为上行方向,反之为下行方向。
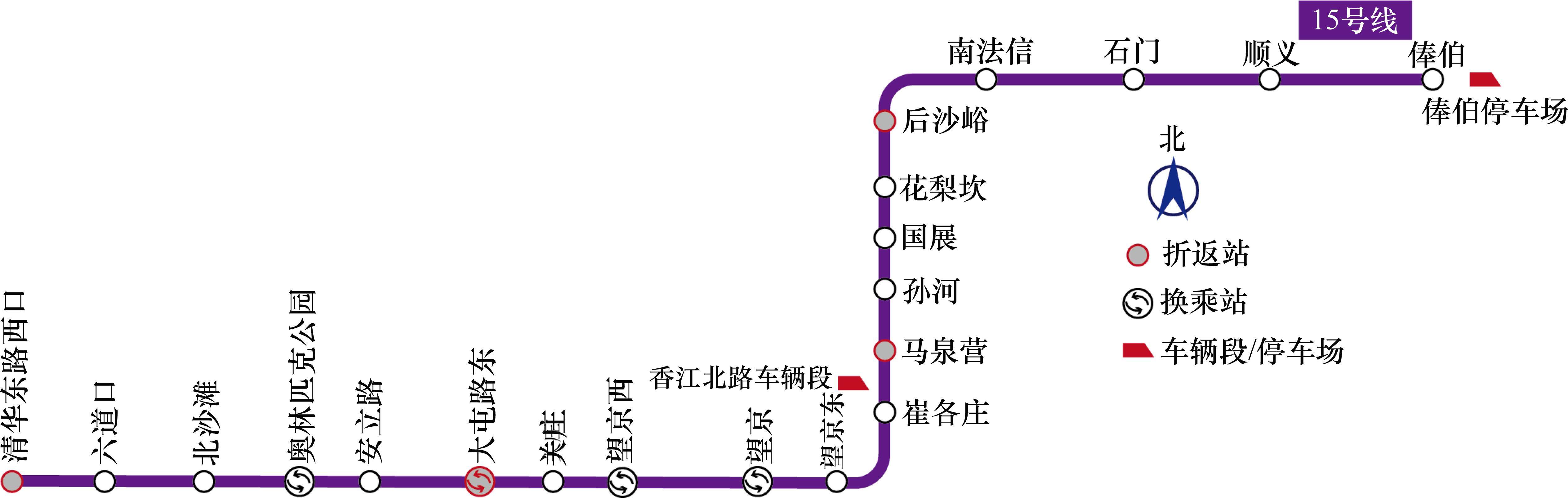
选取全天作为研究时段,即[5:00,次日1:00]。由于问题规模大、变量多,直接采用商用求解器甚至难以得到可行解,为了加速求解过程,将整个研究时段分为6个阶段,采用滚动优化方法进行求解。具体地,各个阶段的研究时段分别为[5:00,8:00]、[7:00,10:00]、[9:00, 14:00]、[13:00,1 8:00]、[17:00, 20:00和[19:00, 次日1:00]。除第1阶段外,每个阶段求解时均以前一阶段优化得到的部分解为约束。具体地,对于阶段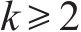
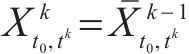
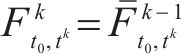
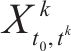
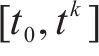
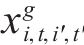
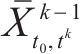
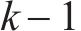
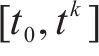
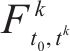
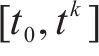
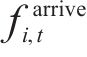
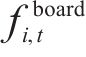
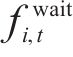
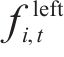
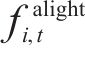
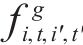
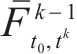
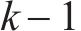
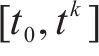
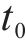
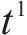
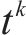
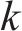
采用商业求解软件CPLEX进行求解,所有实验均在CPU为i5-10500-3.10 GHz的Windows10操作系统上进行。模型相关的其他参数列于表2和表3。
| 参数 | 取值 |
|---|---|
| 研究时段 | [5:00, 次日1:00] |
离散时间段长度(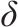 | 60 |
最小发车间隔(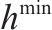 | 120 |
| 最小折返时间/s | 120 |
| 最大折返时间/s | 480 |
| 最大满载系数 | 1.1 |
香江北路车辆段容量(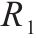 | 45 |
俸伯停车场容量(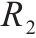 | 76 |
单列车辆单元的购置成本(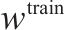 |  |
| 列车编组 | 4编组 | 6编组 | 8编组 |
|---|---|---|---|
| 额定载客量/人 | 960 | 1 440 | 1 920 |
| 单位时间运行成本/(元∙s-1) | 0.42 | 0.60 | 0.84 |
3.2 结果分析
为了验证协同优化方法的有效性及不同编组策略对优化结果的影响,设计了5组实验:1) 北京地铁15号线既有的运行方案,即优化前北京地铁15号线的实际运行方案(目前,15号线使用6编组列车);2) 仅考虑6编组列车的优化运行图;3) 同时考虑4和6编组列车的优化运行图;4) 同时考虑6和8编组列车的优化运行图;5) 同时考虑4和8编组列车的优化运行图。其中,实验1将既有列车时刻表作为参数,用本文所设计的优化模型进行评估,计算得到车场备车数、列车购置成本和目标函数值。实验2、3、4和5用优化模型求解,仅列车编组相关参数不同,其他均相同。为了更直观地比较各实验得到的运行方案,将实验结果,即各方案的车场备车数、列车购置成本、运行成本、乘客等待时间及目标函数值列于表4。
| 序号 | 方案 | 车场备车数/节 | 列车购置成本/元 | 运行成本/元 | 乘客等待时间/s | 目标函数值 | |
|---|---|---|---|---|---|---|---|
| 车场1 | 车场2 | ||||||
| 1 | 优化前(6编组) | 39 | 63 | 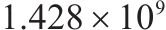 | 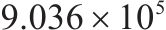 | 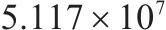 | 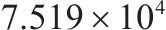 |
| 2 | 6编组 | 33 | 75 | 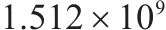 | 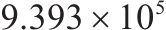 | 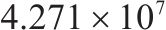 | 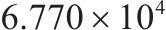 |
| 3 | 4和6编组 | 41 | 54 | 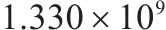 | 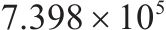 | 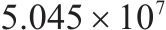 | 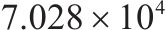 |
| 4 | 6和8编组 | 35 | 76 | 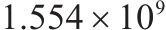 | 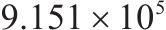 | 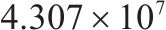 | 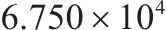 |
| 5 | 4和8编组 | 34 | 60 | 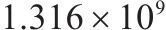 | 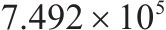 | 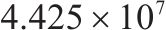 | 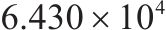 |
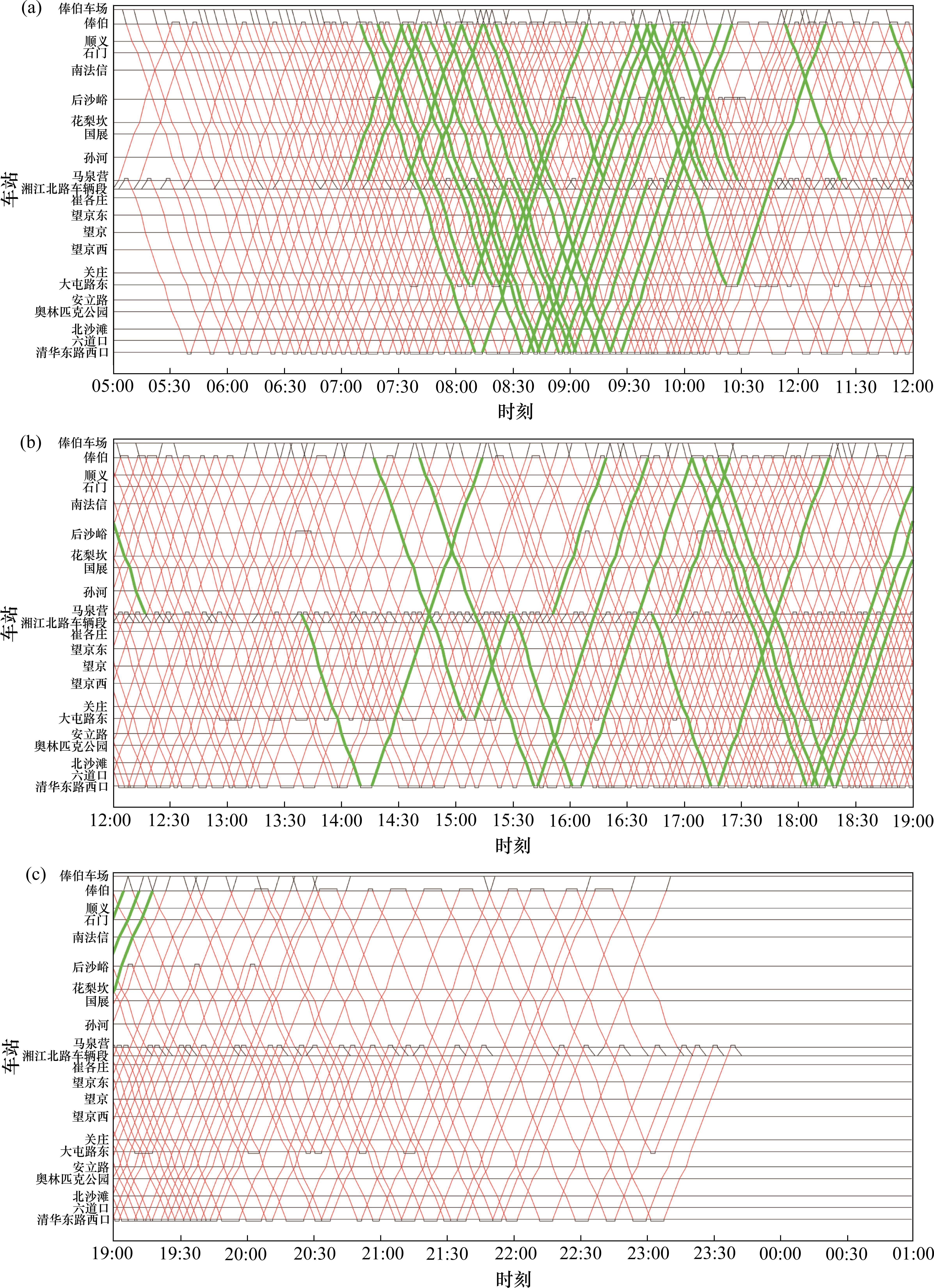
实验结果表明,优化后的方案2、3、4和5均优于方案1。与方案1比,方案2、3、4和5的目标函数值(综合成本)分别降低了10.0%、6.5%、10.2%和14.5%,说明了本文设计的优化方法的有效性。具体地,与方案1比,只考虑6编组列车的方案2和同时考虑6、8编组列车的方案4虽然分别减少了乘客等待时间16.5%,15.8%,但车辆购置和运行成本却高于优化前;同时考虑4和6编组列车的方案3车辆购置和运行成本有大幅减少,分别减少6.89%和18.1%,乘客等待时间仅减少1.4%。方案5是5个方案中最优的。方案5同时考虑4和8这2种编组类型的列车,运营开始前,在香江北路车辆段(车场1)放置34列车辆单元,在俸伯停车场(车场2)放置6列车辆单元。方案5与方案1比,列车购置成本减少7.8%,运行成本减少17.1%,乘客等待时间减少13.5%,有效降低了运营成本,提升了服务水平。图5为方案5优化后的列车运行图,包含列车进出车场,折返和站间运行情况。红色细线代表4编组列车,粗线代表8编组列车。由运行图可以看出,早、晚高峰时段[7:30, 9:00]、[17:00, 19:00]较其他时段列车车次比较密集,且8编组列车主要集中在这2个时段。
3.3 灵敏度分析
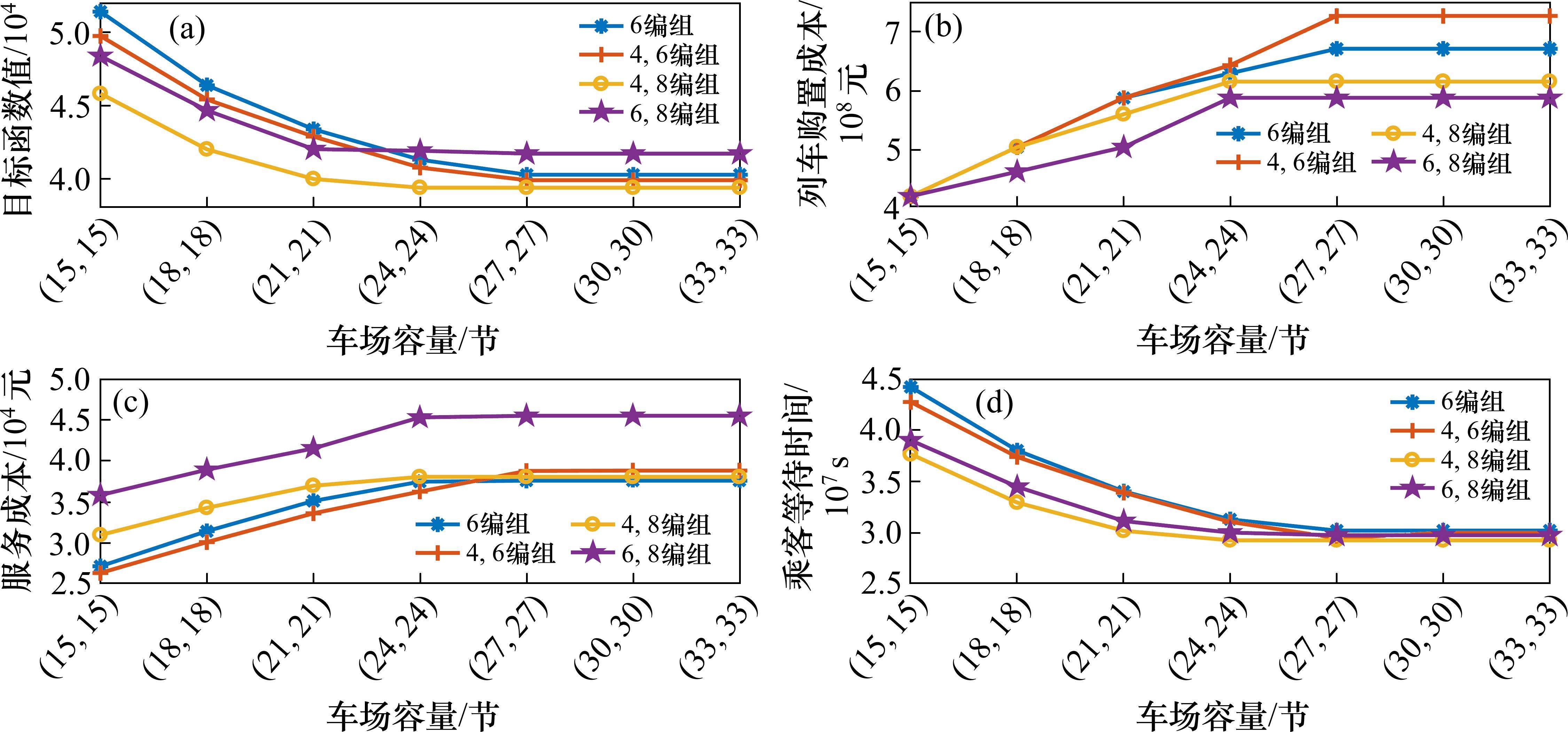
为进一步分析车场容量变化对不同编组方案优化结果的影响,在其他参数不变的情况下,将车场容量由小到大变化,得到不同场景下的优化结果,如图6。图6分别展示了不同编组方案下,目标函数值(车辆购置成本、服务成本和乘客等待时间的加权值,亦可称作综合成本)、车辆购置成本、服务成本和乘客等待时间随车场容量的变化趋势。随着车场容量不断增加,可使用的列车数增多,各方案的目标函数值(综合成本)和乘客等待时间先减小,最后保持不变(如图6(a)和图6(d))。对应的,车辆购置成本和服务成本随车场容量的增加先增加,后保持不变(如图6(b)和6(c))。这一优化结果与实际情况保持一致。开始时,由于车场容量较小,运力(可用列车数)远小于客流需求,随着车场容量的增加,乘客等待时间的减少幅度远大于车辆购置成本和服务成本增多的幅度,因此目标函数值(综合成本)减小。之后,随着车场容量的不断增加,目标函数值、车辆购置成本、服务成本和乘客等待时间保持不变的可能原因有二:1) 车辆购置成本、服务成本和乘客等待时间三者之间达到平衡(帕累托最优);2) 运营条件的限制,如最小发车间隔约束等使得开行列车数(服务频次)不能无限增加。
为了评估不同目标权重对优化结果的影响,对具有不同权重的实例进行了一系列实验。首先将目标函数权重标准化,即目标函数(19)被重构为:
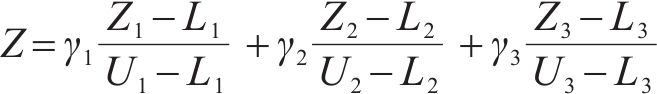
其中,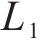
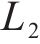
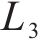
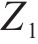
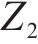
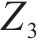
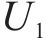
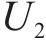
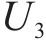
本组实验中,研究时段设置为2 h。车场1和2的容量分别设为20、40。固定其中2个权重的取值,另一个在0.1、0.5、2和5之间变化。实验结果展示在表5中,其中列出了与列车购置成本、运行成本和乘客等待时间相关的权重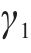
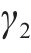
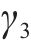
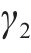
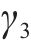
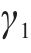
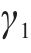
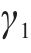
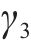
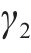
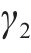
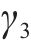
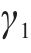
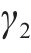
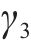
| 序号 | 权重系数 | 车场备车数/列 | 列车购置成本/元 | 运行成本/元 | 乘客等待时间/s | |||
|---|---|---|---|---|---|---|---|---|
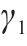 | 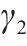 | 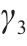 | 车场1 | 车场2 | ||||
| 1 | 0.1 | 1 | 1 | 12 | 32 | 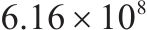 | 42 184.8 | 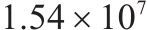 |
| 2 | 0.5 | 1 | 1 | 10 | 22 | 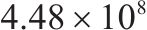 | 37 875.6 | 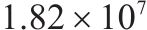 |
| 3 | 2 | 1 | 1 | 6 | 20 | 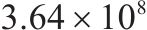 | 30 450.0 | 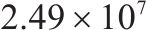 |
| 4 | 5 | 1 | 1 | 6 | 8 | 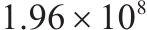 | 18 858.0 | 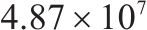 |
| 5 | 1 | 0.1 | 1 | 14 | 18 | 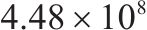 | 41 319.6 | 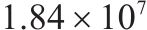 |
| 6 | 1 | 0.5 | 1 | 10 | 20 | 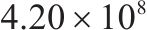 | 36 187.2 | 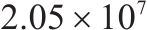 |
| 7 | 1 | 2 | 1 | 8 | 22 | 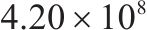 | 32 415.6 | 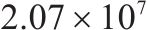 |
| 8 | 1 | 5 | 1 | 4 | 22 | 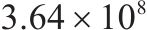 | 22 948.8 | 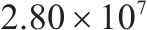 |
| 9 | 1 | 1 | 0.1 | 4 | 6 | 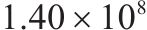 | 13 078.8 | 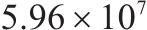 |
| 10 | 1 | 1 | 0.5 | 8 | 16 | 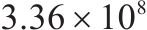 | 27 308.4 | 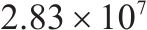 |
| 11 | 1 | 1 | 2 | 10 | 26 | 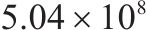 | 40 765.2 | 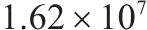 |
| 12 | 1 | 1 | 5 | 18 | 26 | 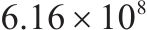 | 52 172.4 | 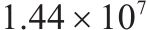 |
4 结论
1) 考虑灵活编组变换群组列车运行模式优化后的各列车运行方案(不同编组类型的方案)均优于北京地铁15号线实际运行方案,能够提高客流-车流的匹配度,有效降低列车购置、运行成本,缩短乘客总等待时间。
2) 考虑不同编组类型组合的优化结果也不同。其中,同时考虑4和8这2种编组类型列车的优化方案最优。列车购置成本,车辆运行成本和乘客等待时间较实际运行方案均有明显减少,分别减少了7.8%、17.1%和13.5%,说明了考虑列车群组灵活编组变换的必要性。
城市轨道交通2023年度统计和分析报告
[EB/OL].程育,阴佳腾,杨立兴等.考虑灵活编组变换的城轨列车群组运行图和车底接续协同优化[J].铁道科学与工程学报,2025,22(04):1506-1518.
CHENG Yu,YIN Jiateng,YANG Lixing,et al.Collaborative optimization of urban rail train group schedules and rolling stock circulation considering flexible train composition[J].Journal of Railway Science and Engineering,2025,22(04):1506-1518.

