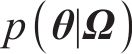钢筋锈蚀引起的混凝土保护层开裂主要包括两个阶段[1]:一是锈蚀开裂,即钢筋混凝土内部钢筋锈蚀膨胀至混凝土保护层与钢筋接触的内表面开始开裂;二是裂缝扩展,即裂缝在混凝土保护层中向外扩展至保护层表面开裂。在锈蚀开裂阶段,可采用均匀腐蚀的厚壁圆筒模型来表征初期的钢筋锈蚀[1]。然而,在实际环境中,钢筋锈蚀并不是均匀膨胀的,根据腐蚀产物的不均匀分布特点,常采用非均匀腐蚀模型如线性衰减腐蚀模型[2]、二次函数腐蚀模型[3]、部分均匀腐蚀模型[4]、椭圆腐蚀模型[5]、高斯腐蚀模型[6]和Von Mises腐蚀模型[7]等表征。在裂缝扩展阶段,SU等[8]提出了一种弹性旋转体模型,采用参数化方法分析混凝土斜裂缝的开裂。该方法将混凝土视为弹性体,仅进行简单的几何分析,没有对应力进行分析,得到的结果与实际结果存在较大误差。杨显华[9]基于黏聚裂纹的混凝土断裂力学模型,分析了混凝土裂缝的扩展形式,通过断裂过程区的黏聚力分布和双K准则研究了外加荷载与裂缝扩展之间的关系。
钢筋锈蚀引起的混凝土保护层开裂时间是反映锈蚀钢筋混凝土(RC)结构使用寿命的关键因素之一。对于混凝土保护层开裂时间的预测,EL MAADDAWY等[10]采用厚壁圆筒模型,利用法拉第定律从检测的腐蚀电流密度中估计钢筋的质量损失,预测从腐蚀开始到混凝土保护层表面开裂的时间。该方法将腐蚀电流密度看成一个常数,这与实际情况不符,因此,预测的混凝土保护层开裂时间与实际开裂时间误差较大。LI等[11]采用厚壁圆筒模型,基于混凝土保护层中的裂缝扩展程度与钢筋锈蚀损失量之间的关系,推导了混凝土保护层开裂时间、混凝土保护层开裂宽度随时间的变化规律,该方法能够较好地预测混凝土保护层的开裂时间。
需指出的是,对不同腐蚀环境中混凝土的腐蚀退化过程的认识具有很大的不确定性[12-14]:一方面,对混凝土保护层开裂扩展的复杂机理认识不足;另一方面,腐蚀电流密度物理模型表征具有经验性。因此,仅靠物理方法预测得到的锈蚀钢筋混凝土结构保护层开裂时间存在较大误差。可采用贝叶斯方法对腐蚀电流密度的物理模型参数进行推断,量化并传递其不确定性,以减小物理模型表征产生的经验性,提高预测结果的准确性。GUO等[15]针对海洋环境中受氯离子侵蚀的混凝土结构,将耐久性评估框架和考虑环境参数变化、氯离子对流传输以及混凝土腐蚀开裂的退化模型相结合,通过动态贝叶斯网络推断模型参数,量化并传递其不确定性,较好地评估了氯离子侵蚀混凝土结构的耐久性,但此方法只考虑了氯离子传输对混凝土结构性能退化的影响,没有考虑钢筋锈蚀。FAROZ等[16]基于钢筋锈蚀损失量,采用贝叶斯方法对钢筋锈蚀损失量物理模型中的2个参数进行推断得到其后验分布,根据其不确定性得到预测模型,并利用预测模型对结构进行时变可靠度分析。据该方法获取的钢筋锈蚀损失量需通过结构破坏试验得到,难以对钢筋混凝土结构保护层开裂时间进行预测。
针对上述问题,本文提出一种基于贝叶斯修正的锈蚀RC结构保护层开裂时间预测方法。首先,基于无损检测腐蚀电流密度的实测值,采用贝叶斯方法推断RC结构腐蚀开裂过程中的腐蚀电流密度物理模型的参数,采用马尔科夫蒙特卡罗方法中的Metropolis-Hastings算法进行采样,得到参数的后验分布;然后,利用后验分布传递参数的不确定性得到腐蚀电流密度的预测模型;最后,利用锈蚀产物质量相等将非均匀腐蚀的钢筋锈蚀椭圆模型转换成均匀腐蚀的厚壁圆筒模型来计算混凝土保护层中的应力,通过钢筋损失量与腐蚀电流密度预测值之间的关系,预测混凝土保护层开裂时间,并通过2个试验试件验证所提方法预测开裂时间的有效性。
1 混凝土保护层开裂时间预测物理模型
氯盐侵蚀环境下锈蚀钢筋混凝土结构的承载力退化过程如图1所示,主要包括5个阶段[17]。
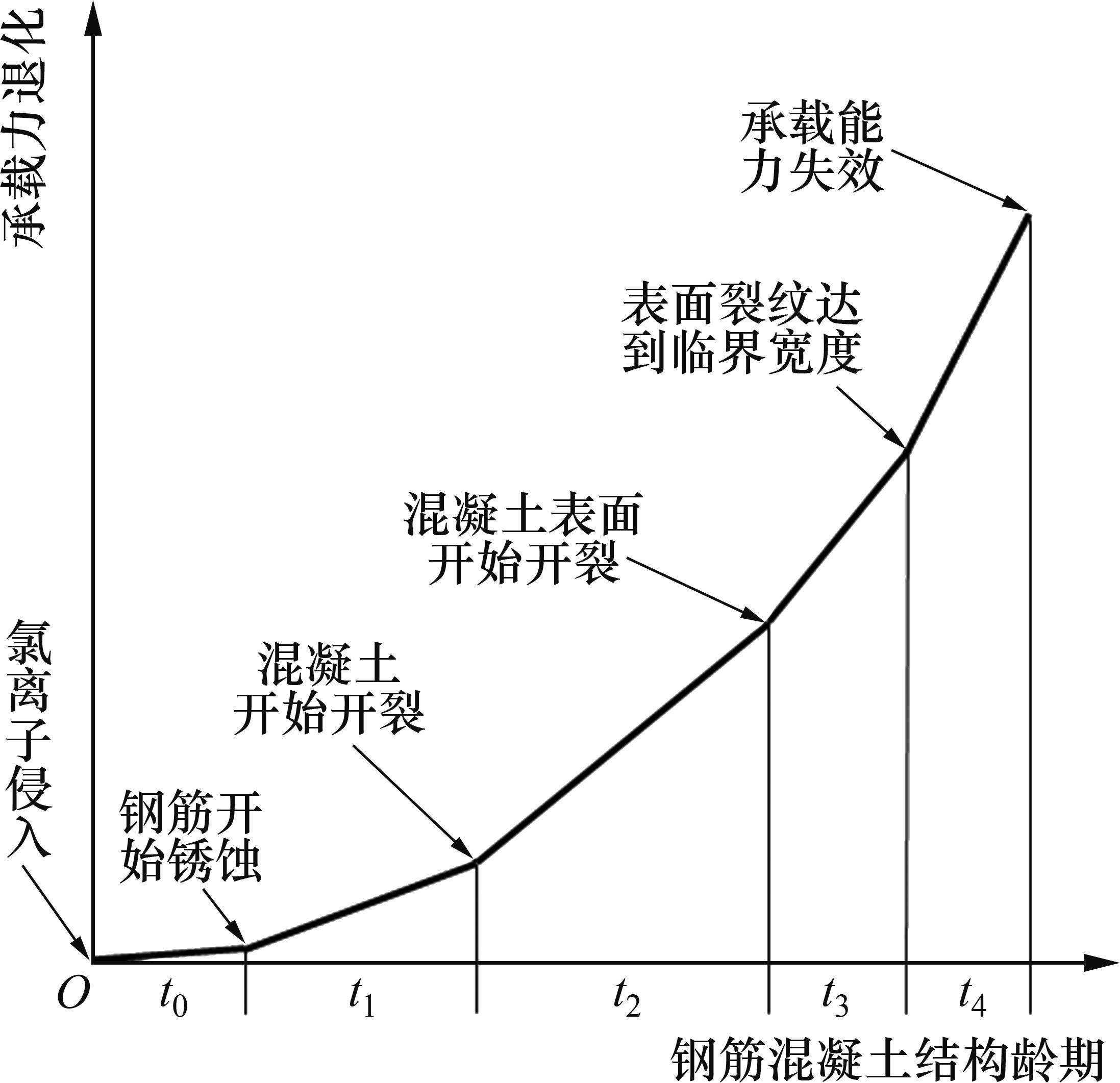
阶段1:从氯离子侵入到钢筋开始锈蚀。在这个阶段,钢筋周围的氯离子浓度逐渐升高,钢筋还未锈蚀,钢筋混凝土结构承载力退化缓慢。本阶段时间为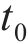
阶段2:钢筋开始锈蚀到混凝土保护层内部开裂。随着钢筋表面氯离子浓度达到临界值,钢筋开始锈蚀膨胀,锈胀产物逐步充满钢筋与混凝土之间的间隙;然后继续膨胀,应力增加到混凝土的极限抗拉强度时致使保护层开始开裂。在这个阶段,结构承载力开始加快退化。本阶段时间为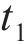
阶段3:混凝土保护层中裂缝扩展至表面。钢筋继续锈胀,混凝土保护层内的应力不断增大,裂缝不断向外扩展,到达混凝土保护层表面开裂的临界点,结构承载力退化继续加快。本阶段时间为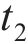
阶段4:混凝土保护层表面裂缝宽度扩展到临界宽度,结构承载力速度增大退化。本阶段时间为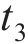
阶段5:结构承载力继续退化直至失效。本阶段时间为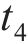
定义第2和第3阶段时间总和为钢筋锈蚀引起的混凝土保护层开裂时间,即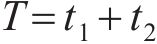
1.1 钢筋锈蚀椭圆模型
YUAN等[5]基于室内人工环境的钢筋混凝土构件钢筋锈蚀试验结果,即钢筋锈蚀产物在钢筋周围堆积并呈半椭圆形分布,提出了钢筋锈蚀椭圆模型,如图2所示。该模型假定钢筋锈蚀产物满足以下条件:
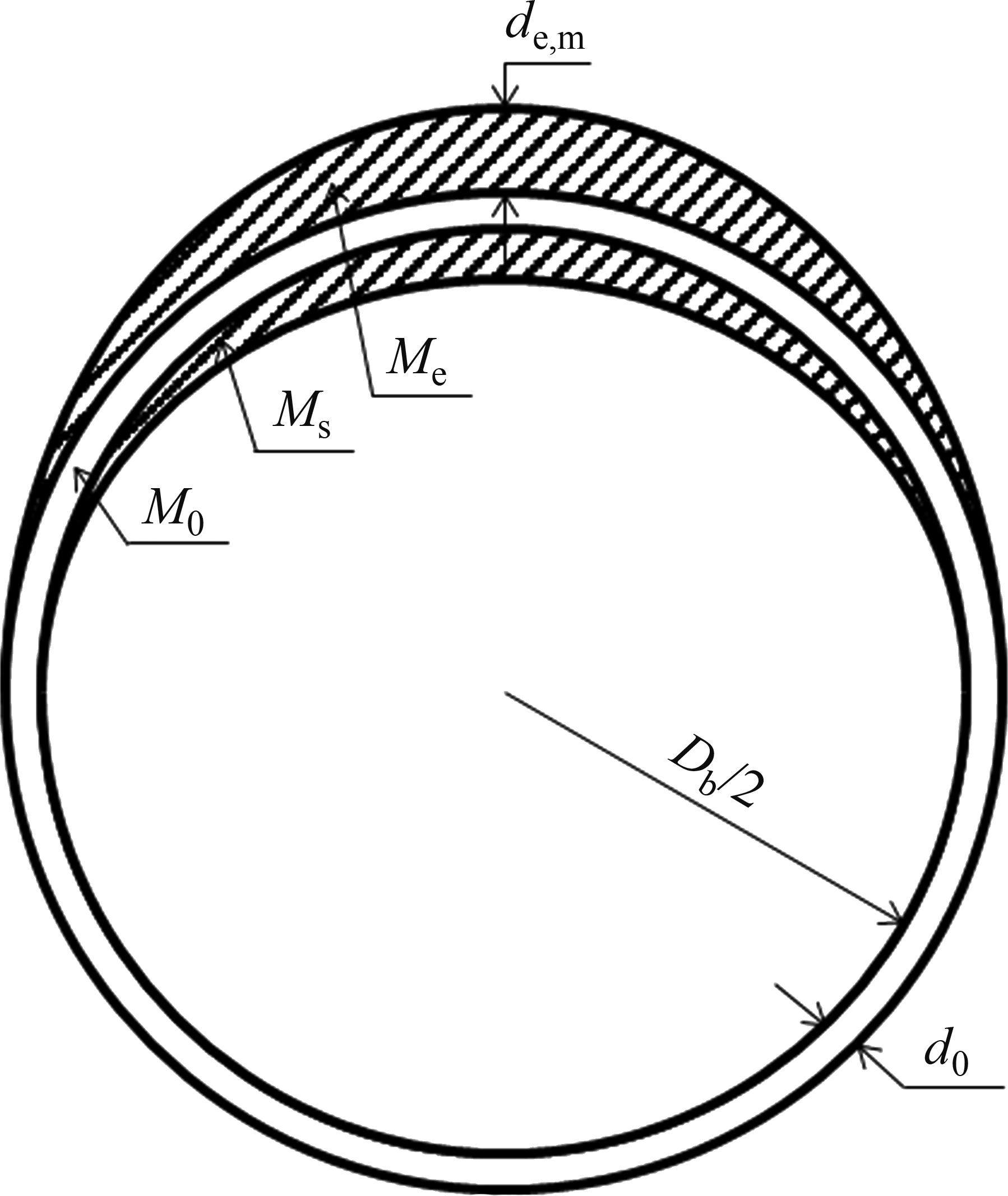
1) 锈蚀产物只在平面内扩张,RC结构纵向无应变,钢筋锈蚀引起的混凝土保护层开裂的力学问题可简化为平面应变问题;
2) 锈蚀产物充满整个孔隙;
3) 锈蚀产物充满整个孔隙后,继续膨胀产生锈胀力[18-19]。
沿纵向取单位长度钢筋,其锈蚀产物总质量
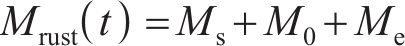
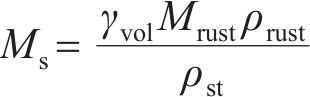

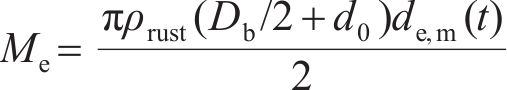
式中: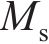
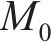
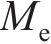
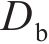
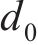
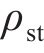
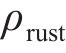
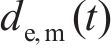
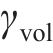
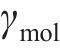

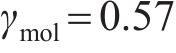
由式(1)~(4)可知,钢筋椭圆形锈蚀产物膨胀位移量最大值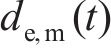
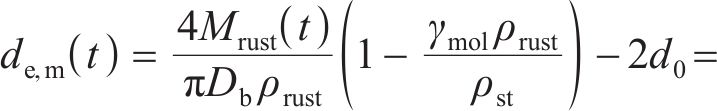
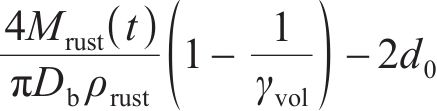
1.2 腐蚀开裂和裂缝扩展过程
1.2.1 腐蚀开裂过程
均匀腐蚀的厚壁圆筒模型[11]如图3(a)所示。基于该模型,钢筋锈蚀产物分布满足与上述非均匀腐蚀相同的假设条件,其厚度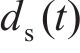
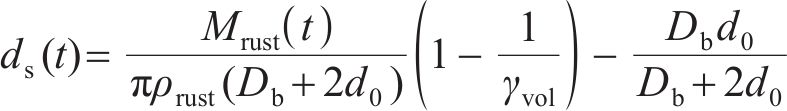
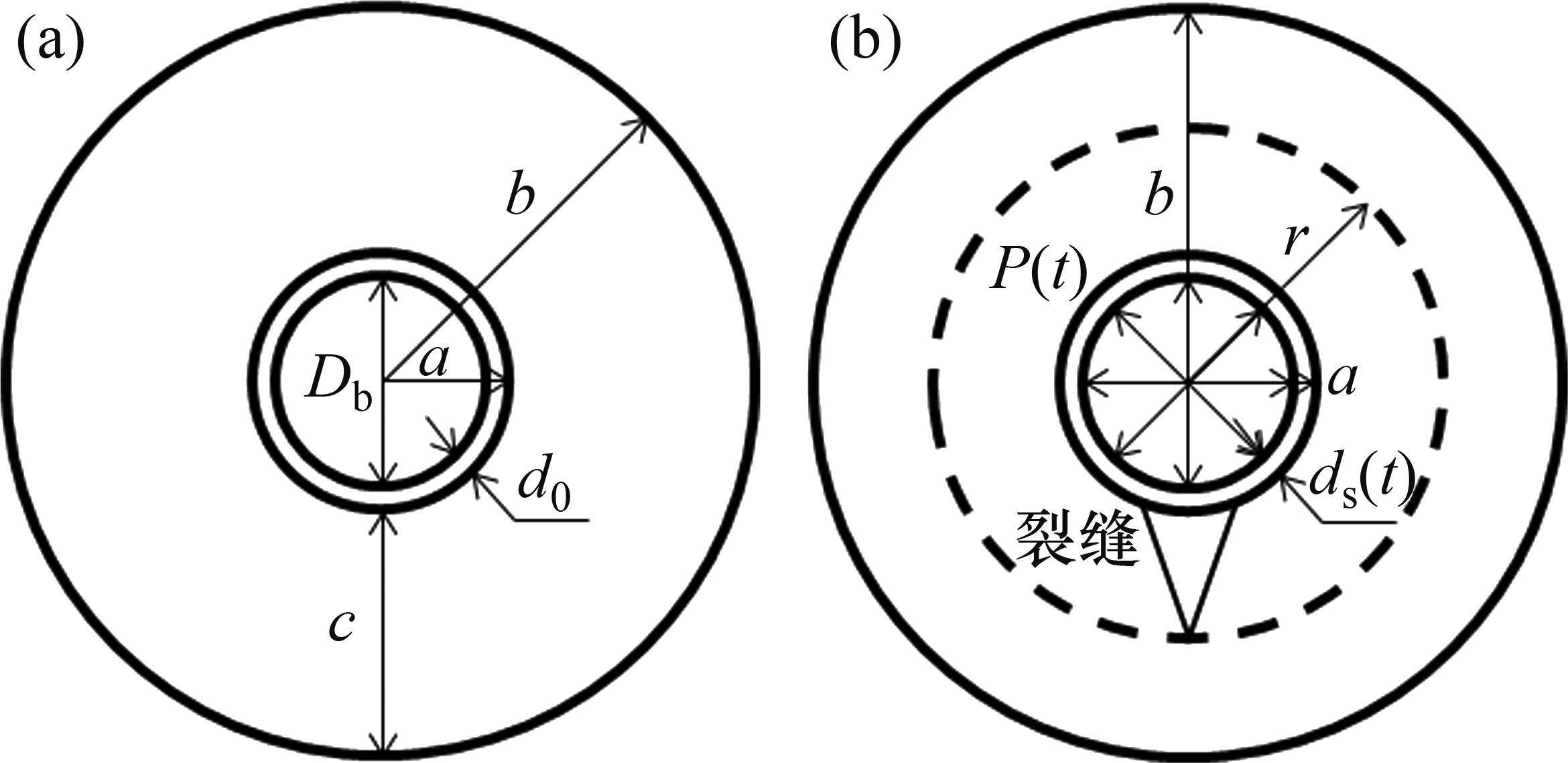
钢筋锈蚀产物先充满整个孔隙,随后继续锈蚀膨胀,直至混凝土保护层中的环向应力达到混凝土最大拉应力时,在钢筋结合处,混凝土保护层开始开裂。
由于目前尚未明确非均匀腐蚀的钢筋锈蚀椭圆模型中的应力变化机理,本文利用锈蚀产物质量相等将非均匀腐蚀的钢筋锈蚀椭圆模型转换成均匀腐蚀的厚壁圆筒模型来计算混凝土保护层中的应力。由此得到非均匀腐蚀钢筋锈蚀膨胀位移最大值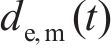
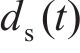
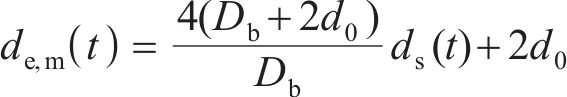
1.2.2 裂缝扩展过程
裂缝扩展模型(图3(b))假定裂缝在均匀腐蚀圆周上均匀分布,且混凝土为准脆性材料,利用断裂力学可确定均匀腐蚀厚壁圆筒模型中的应力分布。
研究表明[11],开裂混凝土中存在残余切向刚度,且裂纹表面每个点沿径向方向的残余切向刚度取决于该点的切向应变。理论上,残余切向刚度为径向坐标r的函数。本文不考虑残余切向刚度的径向变化,将其简化为常数,即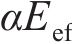
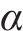
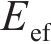
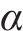
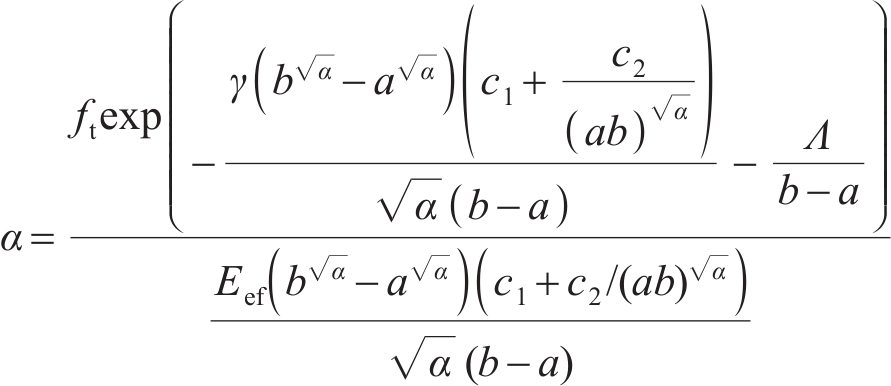
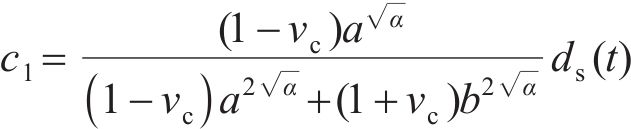
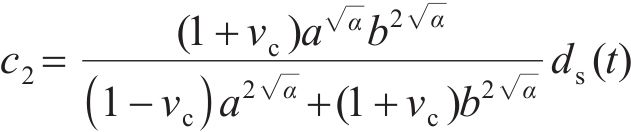
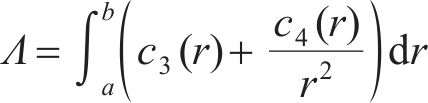
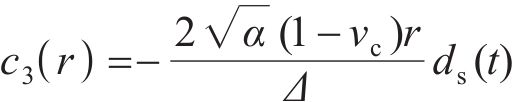
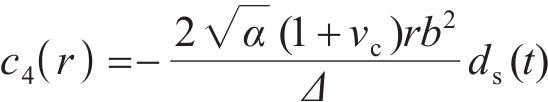
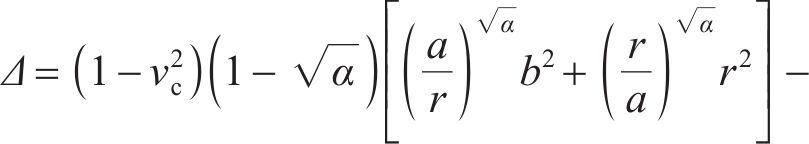
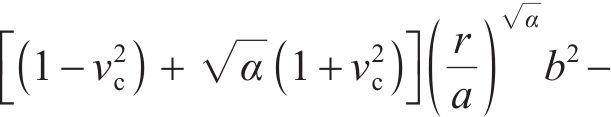
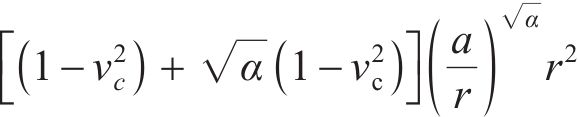
式中:a为混凝土保护层内圈的径向半径,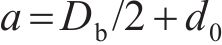
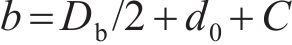
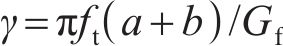
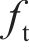
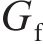
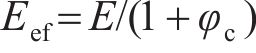
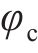
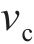
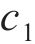
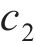
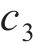
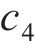
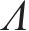
当混凝土保护层表面(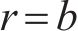
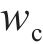
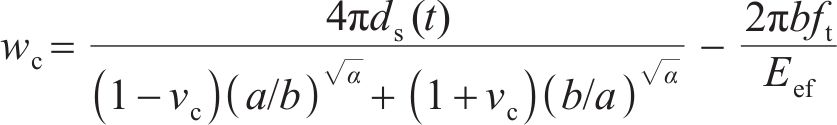
当混凝土保护层表面刚出现裂缝时,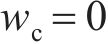
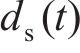
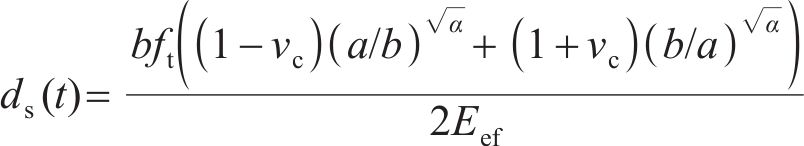
联立式(8)~(14)、(16),求解得到混凝土保护层开始开裂时的均匀腐蚀钢筋锈蚀产物厚度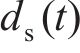
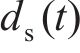
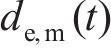
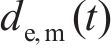

1.3 混凝土保护层开裂时间预测物理模型
通过无损检测得到的腐蚀电流密度,利用法拉第定律估计钢筋的质量损失,预测从钢筋锈蚀开始到混凝土保护层表面开裂的时间。LIU等[21]通过实验确定的钢筋锈蚀产物质量与腐蚀电流密度之间的经验关系式为
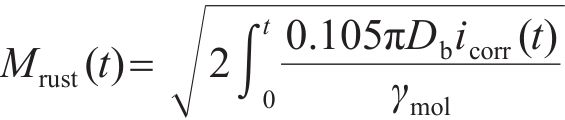
式中:
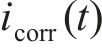
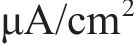
LIU等[21]对5年室内和室外不同氯离子浓度的钢筋混凝土试件进行试验,基于2种设备实测的腐蚀电流密度,得出腐蚀电流密度随时间变化的一般预测公式,即
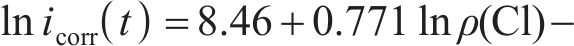
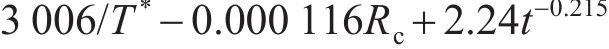
式中: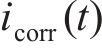
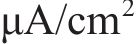

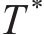
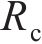
式(18)中氯离子浓度、温度和混凝土电阻都是随时间变化的参数,上述3个参数的均值代入式(18),本文不考虑其随时间的变化,只考虑腐蚀电流密度随时间的变化,得到腐蚀电流密度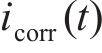
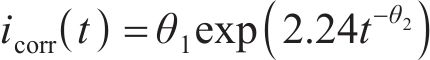
式中: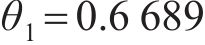
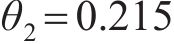
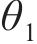
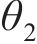
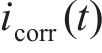
2 基于贝叶斯修正的混凝土保护层开裂时间预测
2.1 贝叶斯方法
贝叶斯方法认为任何参数都是概率化的,基于先验信息并融合样本信息,可得到参数的后验信息[22]。根据实测数据集Ω,采用贝叶斯方法对参数θ进行推断,量化参数θ的不确定性。根据贝叶斯定理,结合由联合概率密度函数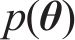
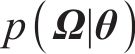
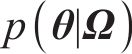
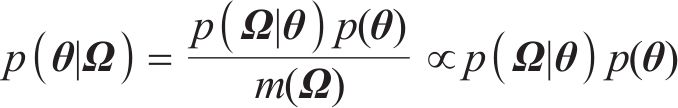
式中: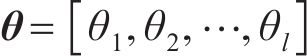
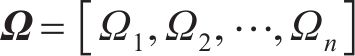
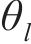
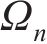
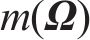
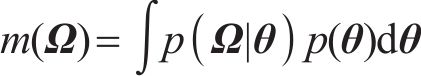
由式(21)可知,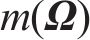
2.2 腐蚀电流密度的概率模型
由于腐蚀电流密度测量存在误差,采用式(17)预测混凝土保护层开裂时间具有经验性,锈蚀RC结构的保护层开裂时间的预测值具有较大误差。
一方面,测量误差(包括仪器和方法误差)使得物理模型中的参数具有显著的不确定性,因此,选择式(19)中2个参数,即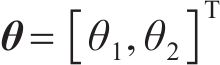
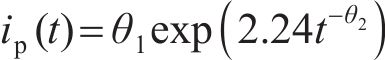
实测的腐蚀电流密度样本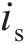
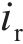
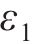
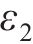
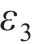
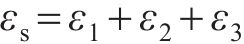
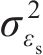
另一方面,由于式(19)具有经验性,式(22)得到的腐蚀电流密度预测值和真实值之间也存在预测误差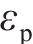
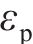
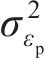
因此,腐蚀电流密度的真实值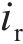
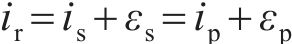
由式(23)可知,腐蚀电流密度的预测值与实测样本值之间的误差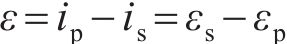
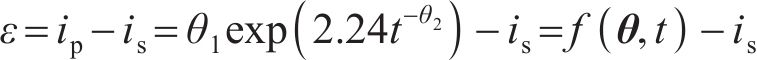
式中: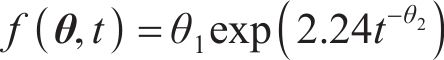
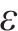
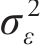
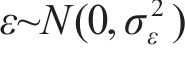
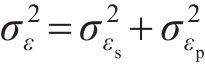
2.3 腐蚀电流密度概率模型的贝叶斯推断
基于腐蚀电流密度预测值与实测值之间误差的贝叶斯概率模型(式(24)),得到腐蚀电流密度第i个实测数据中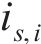
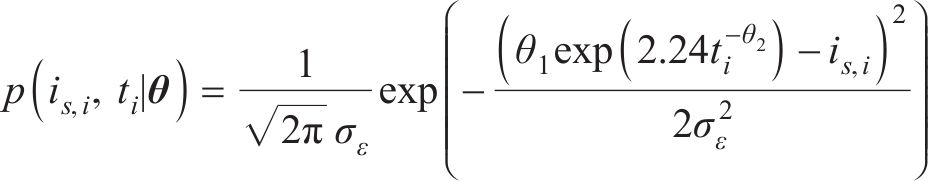
通过式(25),基于实际测量数据集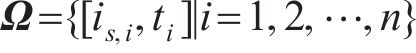
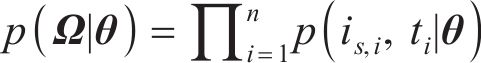
将式(26)代入式(20),量化参数θ的不确定性,得到后验分布:

需指出的是,式(27)是一个高维积分问题,直接求解非常困难。本文采用马尔可夫链蒙特卡罗(MCMC)方法,通过Metropolis-Hastings(MH)算法抽样得到参数后验分布的样本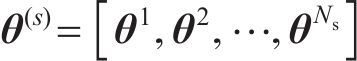
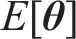
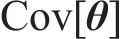
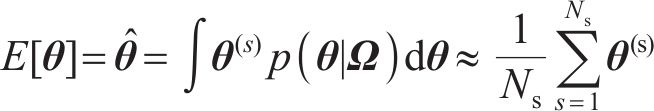
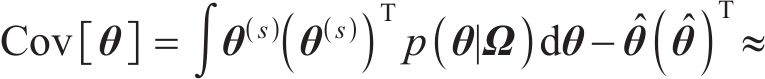
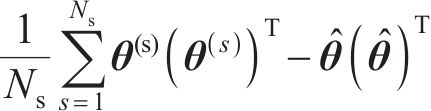
2.4 腐蚀电流密度和开裂时间预测
得到参数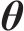
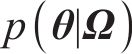
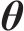
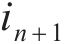
由式(24)得到
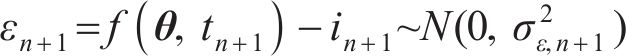
由式(30)得到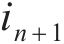
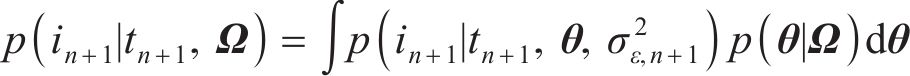
式中: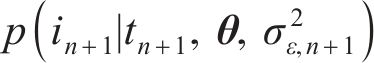
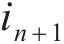
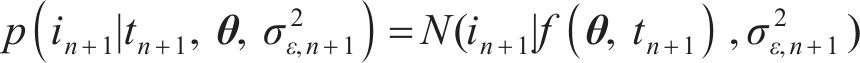
式中: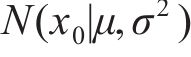
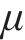
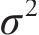
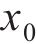
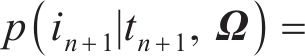
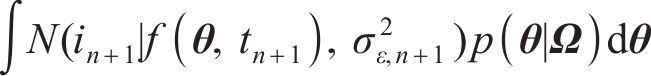
与式(27)相同的是,式(33)也是一个高维积分问题,直接求解非常困难,本文采用抽样方法进行积分求解,得到如下近似结果:
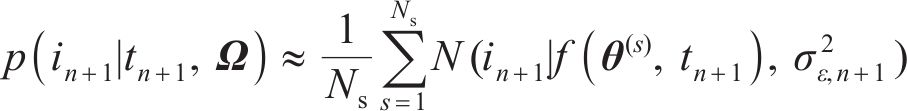
式中: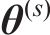
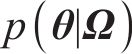
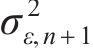
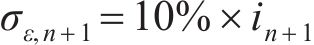
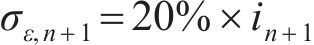
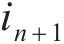
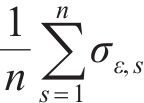
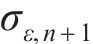
根据式(34),得到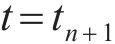
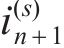
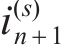
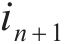
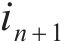
同时,利用后验分布抽样样本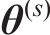
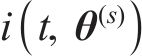
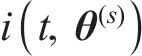
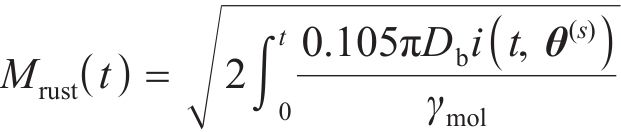
结合1.2节中求解得到的钢筋锈蚀产物质量
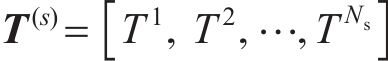
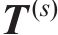
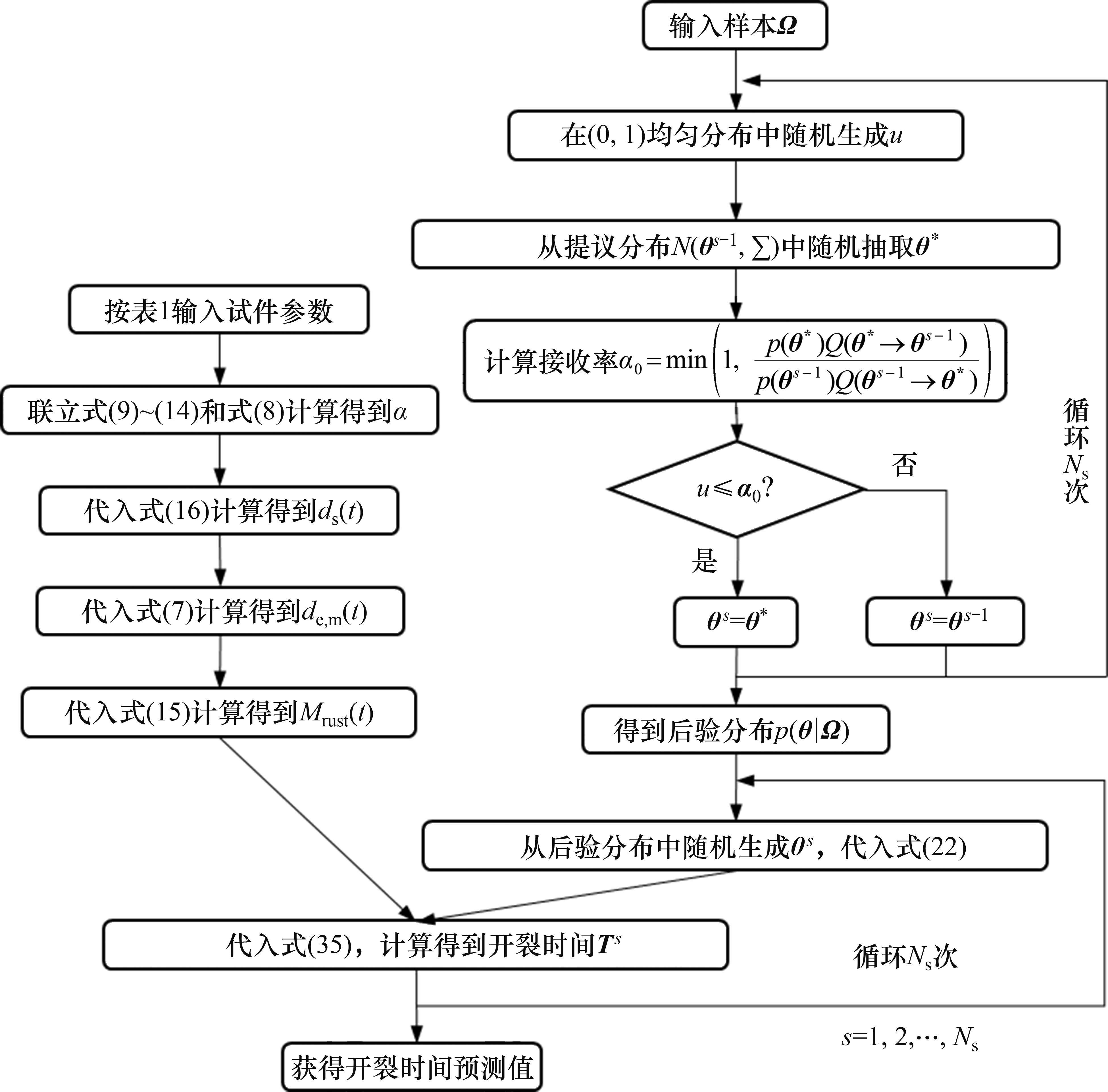
图4所示为本文提出的基于贝叶斯修正的锈蚀RC结构混凝土保护层开裂时间预测方法流程图,主要步骤包括采用马尔可夫链蒙特卡罗(MCMC)方法中的Metropolis-Hastings(MH)算法,量化参数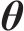
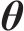
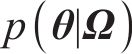
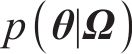
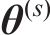
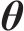
3 实例分析
选择LIU等[21]试验中的2个钢筋混凝土试验试件(OA2859.6和OB2859.6),采用实测得到的混凝土保护层开裂时间验证本文所提出的锈蚀RC结构混凝土保护层开裂时间预测方法。在氯离子质量浓度为5.7 kg/m3的室外环境下,试件OA2859.6和OB2859.6进行5年试验,试件的物理参数如表1所示,实测的这2个试件的腐蚀电流密度如表2所示。
| 参数 | 试样 | 参数 | 试样 | ||
|---|---|---|---|---|---|
| OA2859.6 | OB2859.6 | OA2859.6 | OB2859.6 | ||
| 钢筋直径Db/mm | 16.0 | 16.0 | 钢筋密度ρst /(kg·m-3) | 7 850 | 7 850 |
| 混凝土保护层厚度C/mm | 50.8 | 76.2 | 锈蚀产物平均密度ρrust /(kg·m-3) | 3 600 | 3 600 |
| 钢筋与混凝土间空隙厚度d0 /μm | 12.5 | 12.5 | 混凝土断裂能Gf /(N·m-1) | 88 | 88 |
| 混凝土标准抗拉强度ft /MPa | 3.3 | 3.3 | 混凝土泊松比νc | 0.18 | 0.18 |
| 混凝土有效弹性模量Eef /GPa | 9.0 | 9.0 | |||
| 试件 | 序号 | 时间/a | 实测电流密度/(μA·cm-2) | 样本数目/个 |
|---|---|---|---|---|
| OA2859.6 | 1 | 0.470 4 | 7.660 2、8.475 7、8.945 5、9.964 7 | 4 |
| 2* | 0.559 2 | 4.639 5、5.916 9、9.368 1、10.437 6、11.166 5、12.783 0 | 6 | |
| 3 | 1.970 8 | 2.214 9、3.020 4、3.342 0、3.599 3、3.902 7、4.036 5、4.260 3 | 7 | |
| OB2859.6 | 1* | 0.382 6 | 9.068 9、9.439 7、9.439 7、11.007 2、11.689 2、12.248 7、12.835 0 | 7 |
| 2 | 0.969 6 | 4.012 7、4.148 9、4.232 9、4.406 0、4.555 6、5.069 4 | 6 | |
| 3 | 1.800 0 | 2.141 7、2.320 4、2.497 3、2.634 4、2.873 4、3.605 9 | 6 |
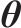
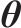
3.1 参数先验分布选取
对于参数先验分布的选取,贝叶斯方法一般采用专家建议的先验分布或根据已有统计信息得到先验分布信息。由于先验分布信息不足,本文采用无信息先验,采用对数正态分布描述参数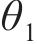
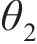
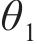
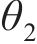
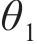
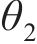
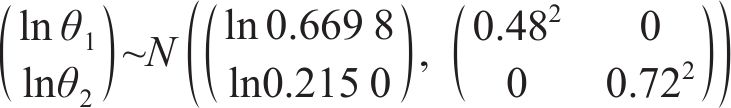
3.2 结果分析
3.2.1 参数后验分布
考虑接受率,针对式(25)中的标准差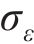
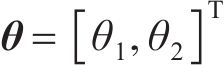
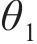
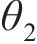
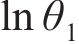
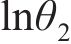
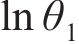
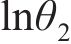
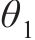
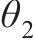
| 误差水平 | 试样OA2859.6 | 试样OB2859.6 | ||
|---|---|---|---|---|
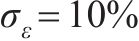 | 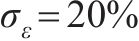 | 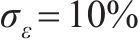 | 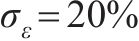 | |
| lnθ1均值 | ln0.416 0 | ln0.446 4 | ln0.506 0 | ln0.503 1 |
| lnθ1方差 | 0.102 7 | 0.0635 | 0.105 4 | 0.112 3 |
| lnθ2均值 | ln0.328 6 | ln0.307 0 | ln0.288 4 | ln0.283 6 |
| lnθ2方差 | 0.322 8 | 0.211 3 | 0.143 6 | 0.166 4 |
| lnθ1与lnθ2协方差 | -0.163 7 | -0.103 2 | -0.116 9 | -0.126 3 |
3.2.2 腐蚀电流密度预测模型
在后验分布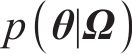
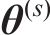
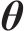
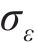
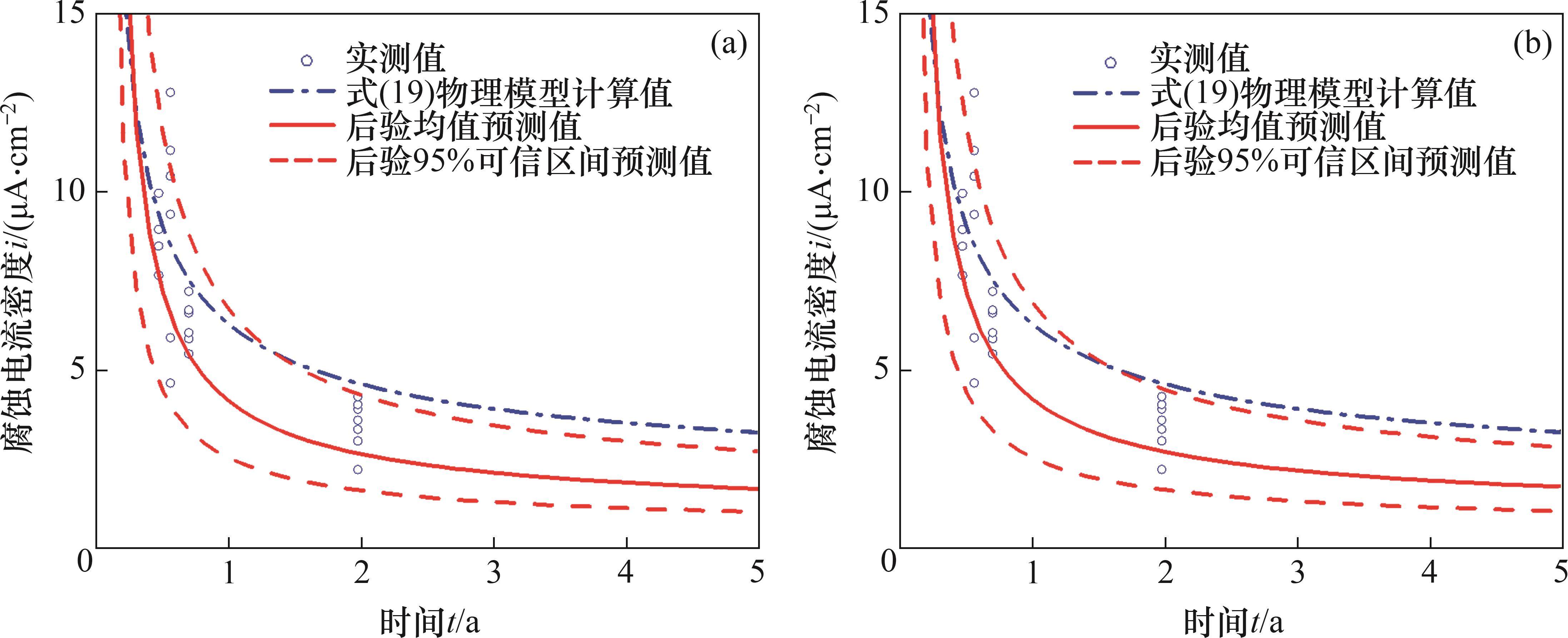
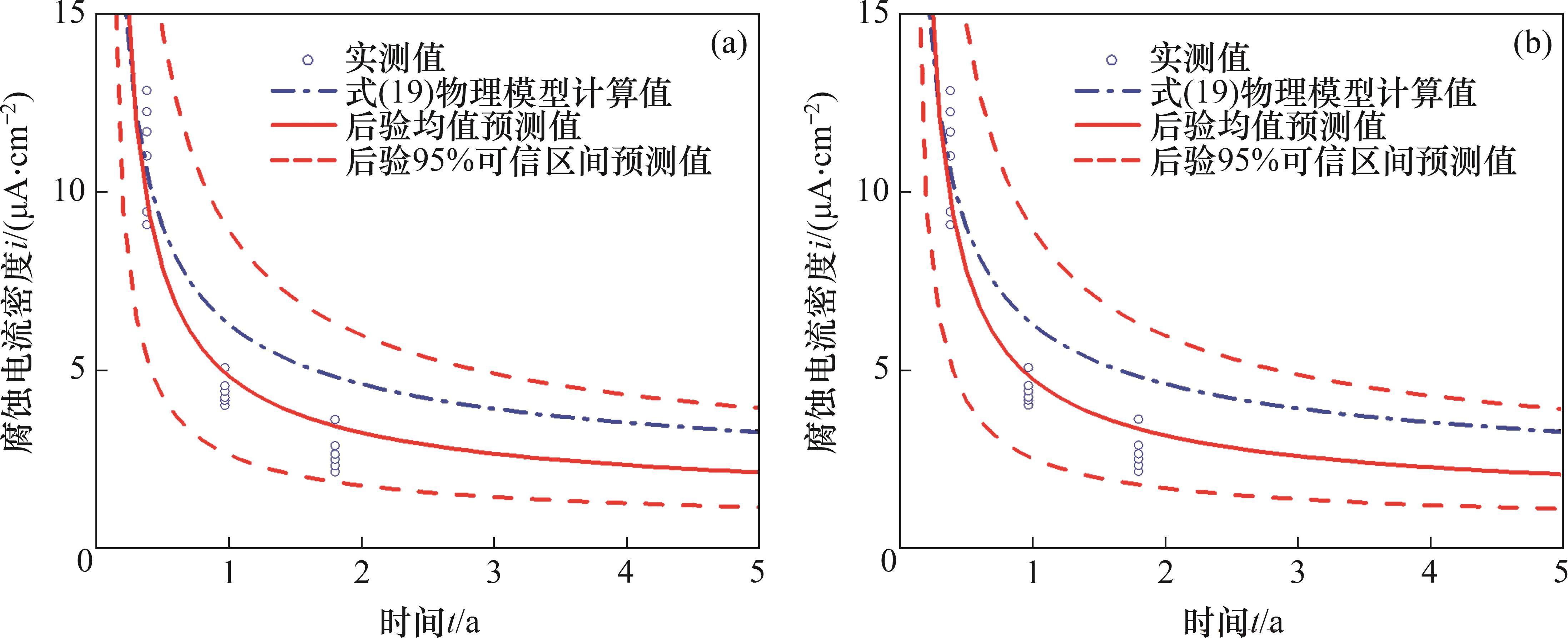
3.2.3 开裂时间预测
从标准差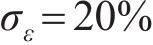
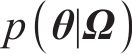
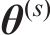
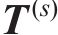
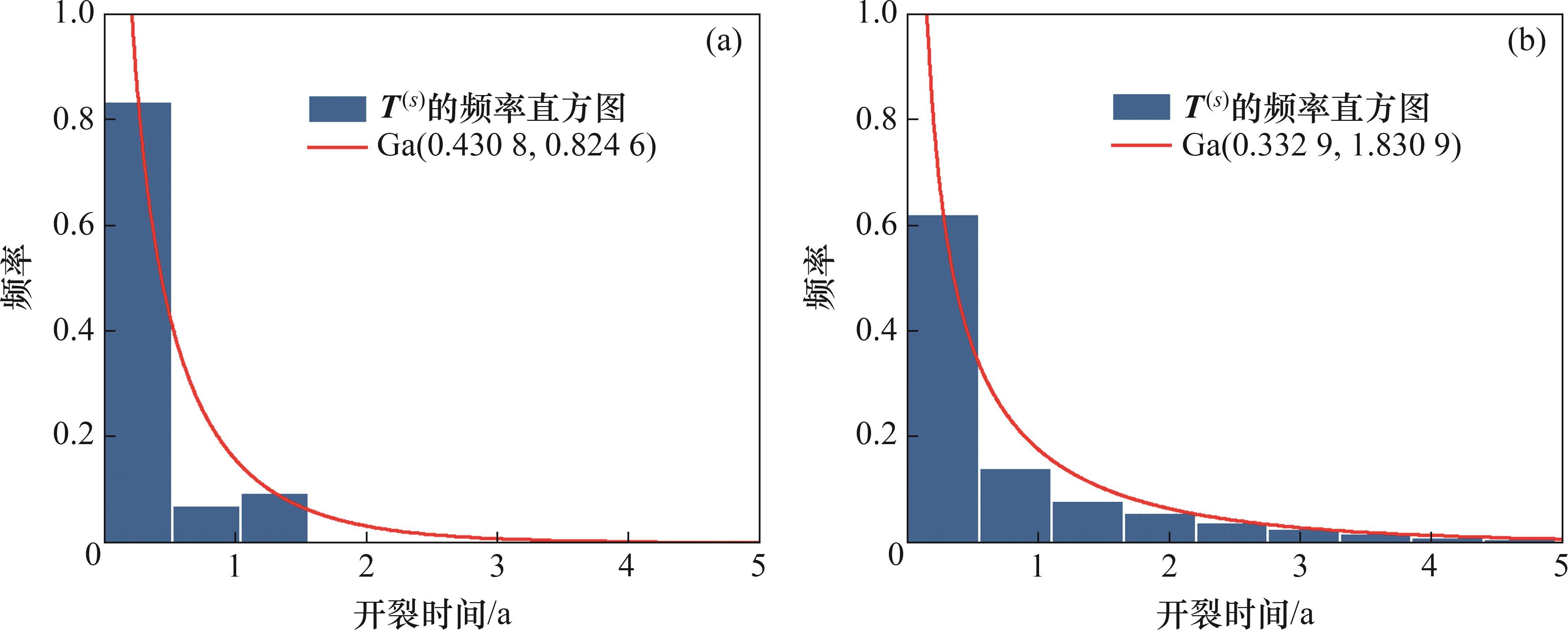
采用伽马分布拟合开裂时间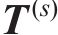
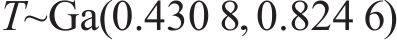
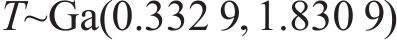
式中: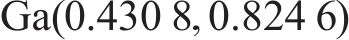
尺度参数为0.824 6的伽马分布,下同。
表4所示为试件OA2859.6和OB2859.6混凝土保护层开裂时间实测值和预测值。其中,预测值采用的是95%可信区间的上限值,即表示开裂时间不超过该值的概率为95%。从表4可以看出,两个试件的混凝土保护层开裂时间预测值与实测值之间的相对误差分别为3.8%和4.1%,均小于5.0%。由此表明,本文提出的方法能较准确地预测锈蚀RC结构的混凝土保护层开裂时间。
| 试件 | 实测值/a | 预测值/a | 相对误差/% |
|---|---|---|---|
| OA2859.6 | 1.840 0 | 1.910 1 | 3.8 |
| OB2859.6 | 3.540 0 | 3.684 4 | 4.1 |
4 结论
1) 提出了一种基于贝叶斯修正的锈蚀RC结构保护层开裂时间预测方法。该方法在采用贝叶斯方法推断RC结构腐蚀开裂过程中的腐蚀电流密度模型参数的基础上,结合无损检测实测的腐蚀电流密度,采用马尔科夫链蒙特卡洛模拟Metropolis-Hastings算法量化模型参数的不确定性,得到基于参数后验分布的腐蚀电流密度预测值,通过钢筋损失量与腐蚀电流密度预测值之间的关系,预测混凝土保护层开裂时间。
2) 2个锈蚀RC试件室外试验实测的混凝土保护层开裂时间验证了所提方法的正确性。基于贝叶斯修正后的腐蚀电流密度预测值能更准确地预测腐蚀电流密度,锈蚀RC结构保护层开裂时间的预测值与实测值之间的相对误差小于5.0%。
3) 提出的保护层开裂时间预测方法中采用腐蚀电流密度无损检测数据,不需要采用破坏试件方式获取钢筋锈蚀量数据。
黄天立, 李群, 陈龙, 等. 基于贝叶斯修正的锈蚀RC结构保护层开裂时间预测[J]. 中南大学学报(自然科学版), 2025, 56(2): 575-585.
HUANG Tianli, LI Qun, CHEN Long, et al. Prediction of cracking time of concrete cover in corroded reinforced concrete structures based on Bayesian updating[J]. Journal of Central South University(Science and Technology), 2025, 56(2): 575-585.