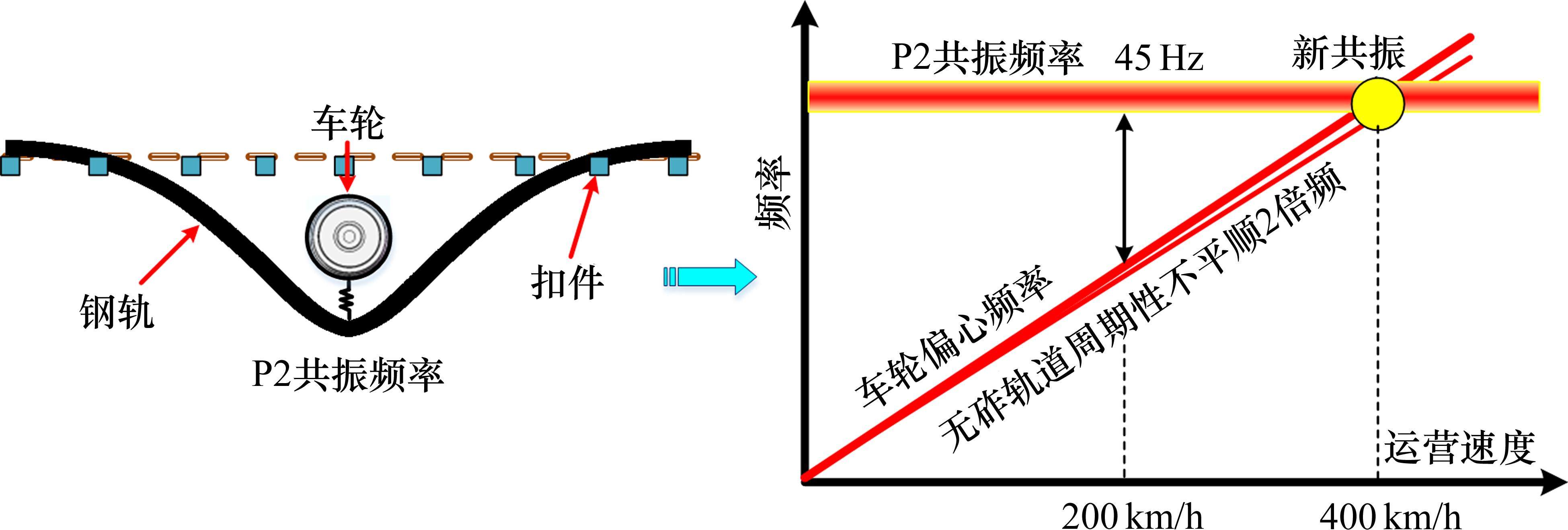
伴随着高铁大规模运营网络形成,我国掌握了具有自主知识产权的时速200~350 km高速铁路技术体系。以国家交通强国战略需求为导向,推进时速400 km级高速铁路研究是我国铁路领域的重点发展方向,并被列入《“十四五”铁路科技创新规划》。运营速度的提升带来的动力学影响是非线性增加的,良好的轮轨动力学性能是保障时速400 km级更高速高铁安全开行的关键。现阶段针对时速350 km及以下轮轨动态作用已开展了大量研究,如无砟轨道层间离缝、路基沉降等复杂服役状态下车轨中低频动态响应已被系统分析[1-5];针对车轮多边形、钢轨波磨等短波病害,轮轨高频荷载分布特征被初步探明[6-9];此外,结合测力轮对以及在钢轨上粘贴应变花,真实轮轨载荷的分布特征被统计分析[10-11]。针对时速400 km+更高速无砟轨道系统动力学问题,翟婉明等[12-13]研究了400 km/h下无砟轨道线路平面设计参数,并探讨了既有350 km/h高速铁路设计参数的适应性;王平等[14]对400 km/h更高速道岔设计关键技术和参数进行了研究;ZHANG等[15]研究了路基差异沉降对400 km/h车轨动力学响应的影响,表明在相同路基沉降条件下,运营速度的增加会显著加剧轮轨动态作用;ZHAO等[16]研究了双块式无砟轨道1~2 m短波不平顺对更高速轮轨动态响应的影响,并提出了更高速下短波不平顺的安全限值;李帅等[17]研究了400 km/h更高速下长波不平顺(30~200 m)的敏感波长和相应安全限值;韦强文等[18]研究了层间离缝对时速400 km高速铁路车辆-轨道动态响应的影响规律,表明无砟轨道离缝劣化会增大轮重减载率;涂英辉[19]开展了钢轨波磨、车轮多边形激励下更高速轮轨动态响应的现场测试和理论仿真分析,对更高速度下线路平纵断面、轨道不平顺等关键设计参数的安全限值开展了较为深入的研究。相较时速200~350 km运营条件,400 km/h+更高速度在车轮偏心[20]和无砟轨道周期性不平顺[21-22]等周期性激励下容易形成新的共振现象,如图1所示。无砟轨道周期性不平顺2倍频与车轮偏心频率接近,在时速400~450 km下激励频率均会增加至40 Hz以上,接近车轮与钢轨的P2共振模态频率,引发轮轨耦合共振。目前,对400 km/h更高速度下无砟轨道这一新的共振现象尚未研究,对车轨系统周期性激励作用与不同结构参数下无砟轨道系统模态间的相互关系仍不清楚,需要重点关注车轨系统周期性激励作用下更高速轮轨动态响应特征及其影响规律。本文针对更高速无砟轨道系统动力学问题,考虑复杂激励作用、不同结构参数影响,建立高速车辆-无砟轨道系统动力学模型。研究不同激励作用下400 km/h+更高速轮轨动态响应特征,分析更高速度下无砟轨道轮轨耦合共振响应变化规律,为进一步保障更高运营速度下车轨低动力相互作用提供基础。
1 模型及方法
1.1 高速车辆-无砟轨道系统动力学模型
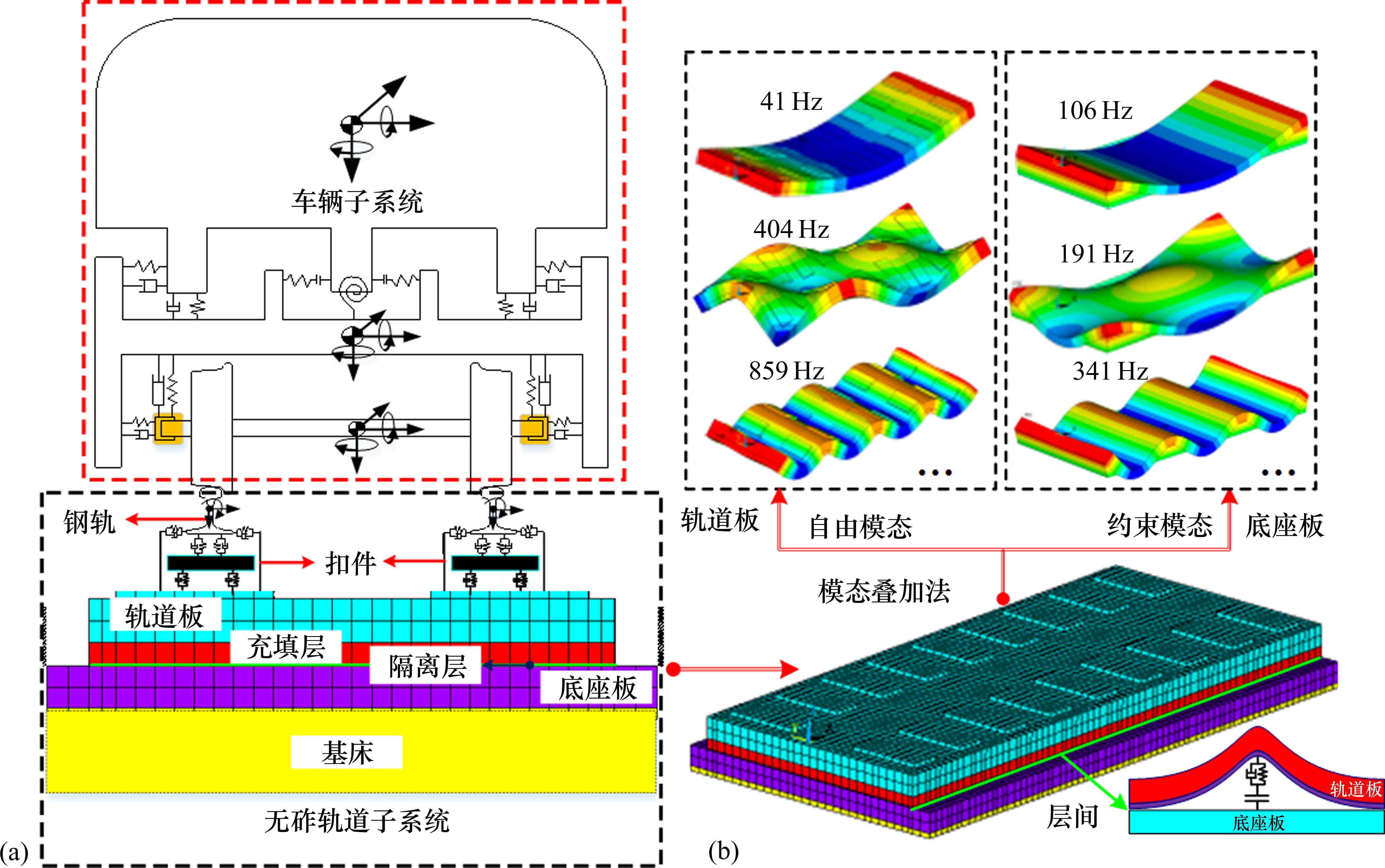
基于车辆-轨道耦合动力学理论[23],构建高速车辆-无砟轨道系统动力学模型,如图2所示。该模型由无砟轨道子系统、车辆子系统以及车辆与轨道间轮轨非线性接触作用等部分构成。
1.1.1 无砟轨道系统精细化模拟
无砟轨道系统是由钢轨、多部件装配扣件和多层异质无砟道床组成的复杂结构体系。基于无砟轨道系统各结构部件的力学参数和参振规律,提出了无砟轨道系统精细化模拟方法,考虑了温度翘曲变形影响下结构层间的非线性作用关系。具体如下。
钢轨采用具有周期离散支承的Timoshenko梁来模拟其垂向、横向及扭转动力学行为,并通过有限元法求解,其动力学方程如下所示:
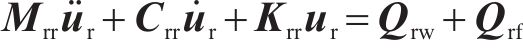
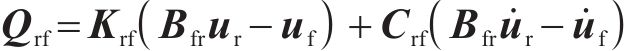
式中: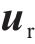
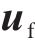
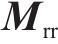

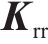
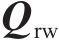
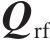
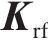

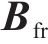
扣件是由上层橡胶垫板、中层铁垫板和下层弹性垫板组成的多部件装配结构。本文模拟考虑了铁垫板的振动,形成双层Kelvin-质量单元串联模型。详细扣件系统的动力学方程可参见文献[24]。
以CRTS III型板式无砟道床为例,其由轨道板、自密实混凝土充填层和底座板等主体结构构成,在充填层和底座板间铺设了土工布隔离层或缓冲垫层。由于结构温度翘曲变形的存在,充填层和底座板间部分区域存在脱空。为精细考虑这两结构层间相互作用,采用含不同间隙大小的非线性弹簧模拟,弹簧刚度由土工布隔离层或缓冲垫层的面刚度乘分摊面积等效获得。无砟道床结构及层间模拟如图2(b)所示。CRTS I型、II型板式无砟轨道CA砂浆充填层以及CRTS II型轨道板间宽窄接缝在层间板间良好黏结条件下采用线性弹簧-阻尼单元进行简化模拟。
轨道板(含充填层)的振动响应采用模态叠加法求解,在相同的分析频率范围内可显著减小计算自由度。首先基于有限元模型获取轨道板的自由模态参数,以该模态集通过坐标变换获取动力学控制方程,如式(3)和式(4)所示:
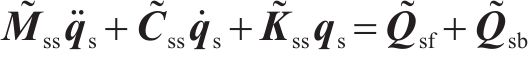

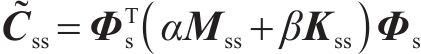
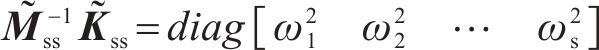

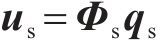
式中: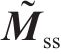

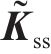
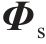
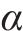
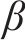
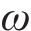

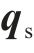
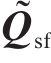
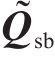
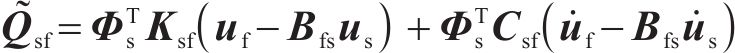
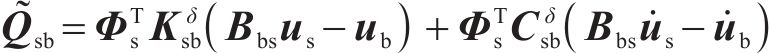
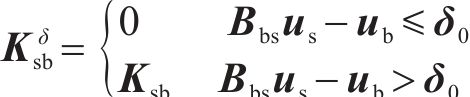
式中: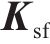

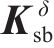
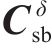
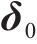
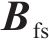
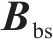
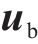
同理,底座板动态响应求解时,基于路基/隧道等下部基础弹性支承下的约束模态参数,通过坐标变换获得动力学控制方程如下所示:
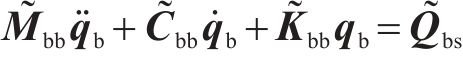
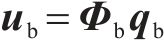
式中: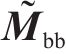
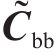
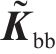
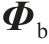
1.1.2 车辆多体系统及轮轨接触作用的模拟
车辆考虑了车体、构架、轴箱、轮对等多刚体间相互作用,系统的动力学控制方程如式(10)所示:
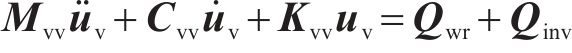
式中: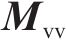
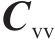
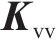
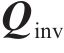
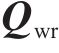
轮轨接触法向作用采用基于虚拟穿透的非Hertz接触算法求解[25],计算公式如式(11)和式(12)所示;切向蠕滑作用采用KALKER[26]的Fastsim算法求解。
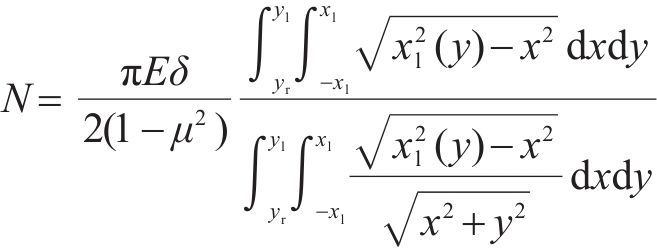
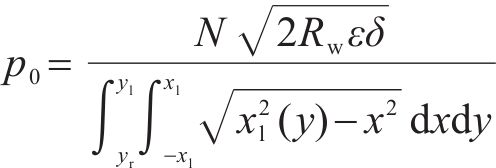
式中: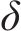
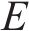
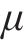
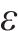
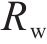
1.2 车辆-轨道系统激励的模拟
车轨系统激励是造成其剧烈振动的根源,本节主要就高速铁路实际运营中的轮轨宽频随机激励、车轮偏心激励和无砟轨道周期性不平顺激励展开分析。
1.2.1 轮轨宽频随机激励
轮轨宽频随机激励由高速铁路轨道长波不平顺和轮轨短波粗糙度组成。波长2.0 m以上的轨道长波不平顺由高速铁路综合检测列车检测获得,轮轨短波粗糙度选用Sato谱近似模拟,以此形成高速铁路轮轨系统的宽频随机激励,不平顺波长范围为0.03~120 m,详细模拟方法参见文献[7]。
1.2.2 车轮偏心激励
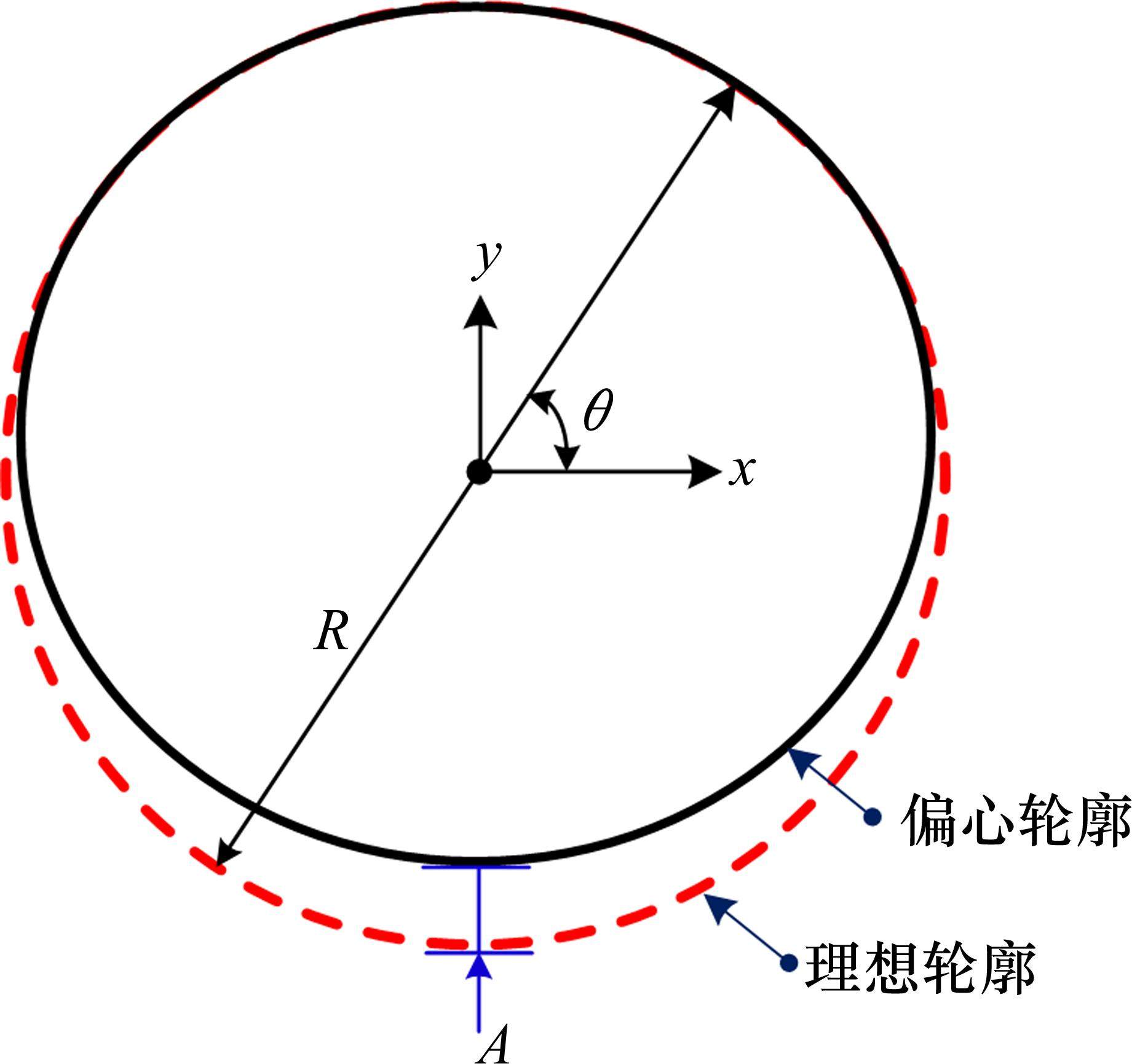
由于制造时加工工艺误差和运营时沿车轮纵向的不均匀磨耗,车轮偏心成为轮轨系统最主要的激励源之一,文献[27]研究表明,偏心磨损车轮占比非圆化磨耗车轮高达96%。车轮高速滚动时,微小的车轮偏心也会产生较大离心力并持续激励车轨系统,引发振动和噪声。车轮偏心激励可采用式(13)谐波模拟,其周期性激励频率fw如式(14)所示。车轮偏心激励几何特征如图3所示。
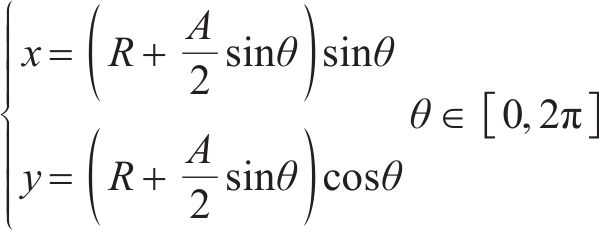
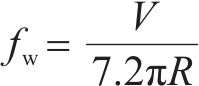
式中:x、y是轮廓一点的坐标;A是车轮偏心幅值;R是车轮名义滚动圆半径;θ是车轮的方位角;V是车辆的运营速度。
1.2.3 无砟轨道周期性不平顺
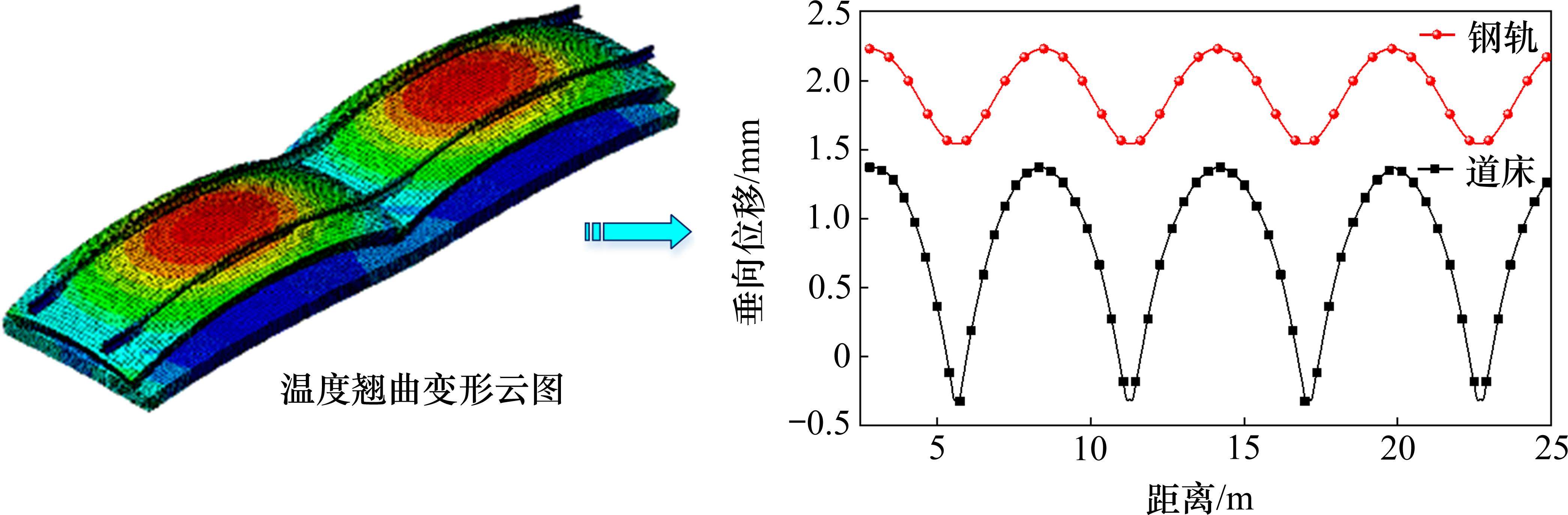
无砟轨道由于热胀冷缩、温度翘曲变形使其沿纵向产生以轨道板长为周期的不平顺,影响车辆的运营安全与舒适。昼间运营条件下,无砟轨道结构变形受正温度梯度作用影响显著。以CRTS III型无砟轨道为例,基于1.1节构建的无砟轨道多层结构精细化有限元模型,对轨道板和自密实混凝土组成的复合板施加正温度梯度90 ℃/m,获取了无砟道床温度翘曲变形以及映射至钢轨的不平顺特征,如图4所示。图4表明正温度梯度作用下,无砟轨道温度翘曲变形垂向上呈现板中高/板角低、纵向上呈现周期性变化的空间分布特征,波长以轨道板长5.6 m为一个周期。无砟道床的温度翘曲变形会带动钢轨变形呈现周期性波动。将结构层间脱空和钢轨几何变形状态作为初始边界条件,开展该激励下车轨系统动态响应仿真计算。
1.3 基于实测轴箱加速度的模型验证
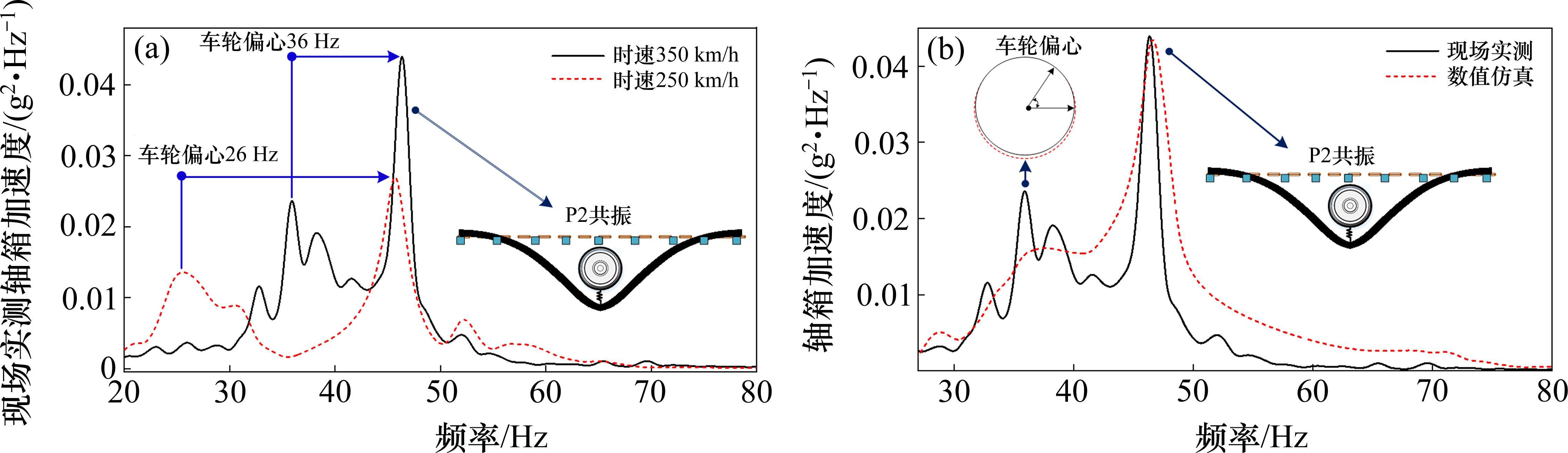
轴箱加速度可以直接反映轮轨动态作用特征,本节以轴箱加速度的数据来验证仿真结果的合理性。首先对250 km/h及350 km/h不同速度下高速铁路轴箱加速度进行现场实测,获得轴箱加速度测试结果及相应模型验证结果如图5所示。图5(a)表明,在100 Hz范围内轴箱加速度主要存在2处显著峰值:一个峰值对应频率为45 Hz,其不受行车速度影响,由轮轨P2共振模态引起;另一个峰值对应的频率随行车速度的变化而变化,在时速350 km和250 km下分别是36 Hz和26 Hz,根据式(14)推断这是由车轮偏心引起的。值得注意的是,在现行350 km运营时速下,车轮偏心激励频率和轮轨P2共振模态频率不重合,车轮偏心激励不会引发轮轨P2共振。但随着行车速度的提高,车轮偏心激励频率会贴近轮轨P2共振模态频率,当两者频率吻合时会引发显著共振。基于车轮踏面实测粗糙度,图5(b)为350 km/h轴箱加速度实测及模型仿真的对比结果,发现仿真模型和实测结果两者吻合较好,验证了模型的准确性。
2 不同激励作用下时速400 km+轮轨动态响应特征
本节研究轮轨宽频随机激励、车轮偏心激励以及无砟轨道周期性不平顺激励作用下时速400 km+轮轨动态响应特征。采用垂向力、磨耗功率来表征轮轨动态响应,磨耗功率
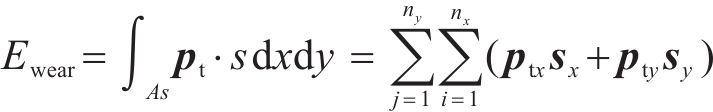
式中: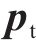
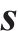
2.1 宽频随机激励下轮轨动态响应
宽频随机激励下轮轨动态响应特征如图6所示。图6表明,从时速300 km提升至时速450 km,轮轨动态响应的共振带分布规律没有改变,轮轨动态响应有效值(均方根值)增大约30%。这表明运营速度的提升不会造成轮轨共振频带的移动,仅显著加剧轮轨宽频动态响应。此外,40~50 Hz的共振响应在全频带能量中占据主要成分,这是由轮轨P2共振模态引发的。P2共振模态普遍存在于车辆轨道系统中,是轮轨耦合共振的主要表现形式。高速铁路无砟轨道轮轨P2共振模态频率在45 Hz附近,在高速铁路运营中应重点关注并控制这一共振。
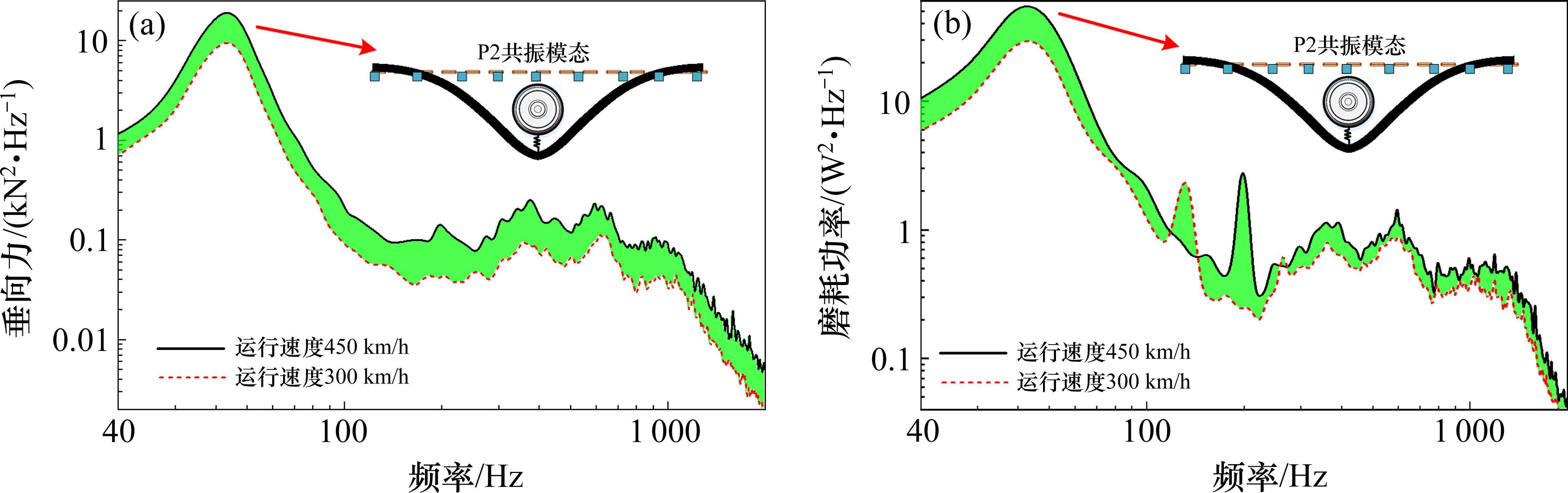
2.2 车轮偏心激励下轮轨动态响应
仿真分析了列车以时速400 km运营时0.03~0.5 mm不同车轮偏心激励下轮轨动态响应变化规律,如图7所示。接着选取车轮偏心0.3 mm,研究车轮偏心动态响应随列车运营速度的变化规律,如图8所示。
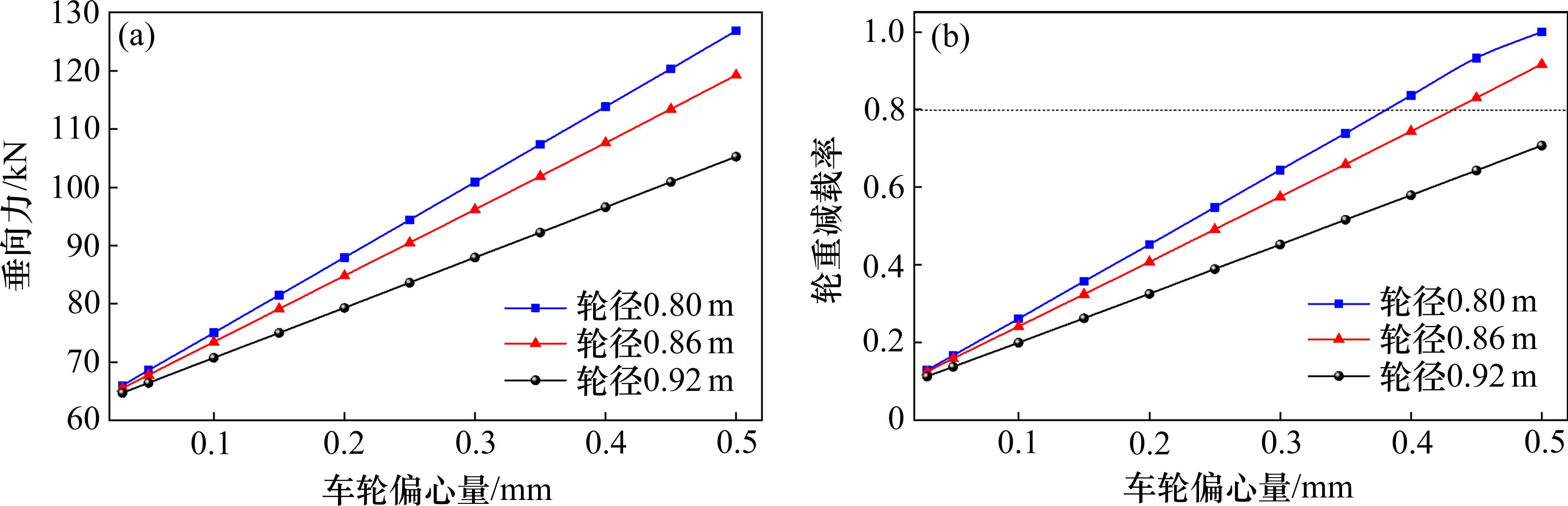
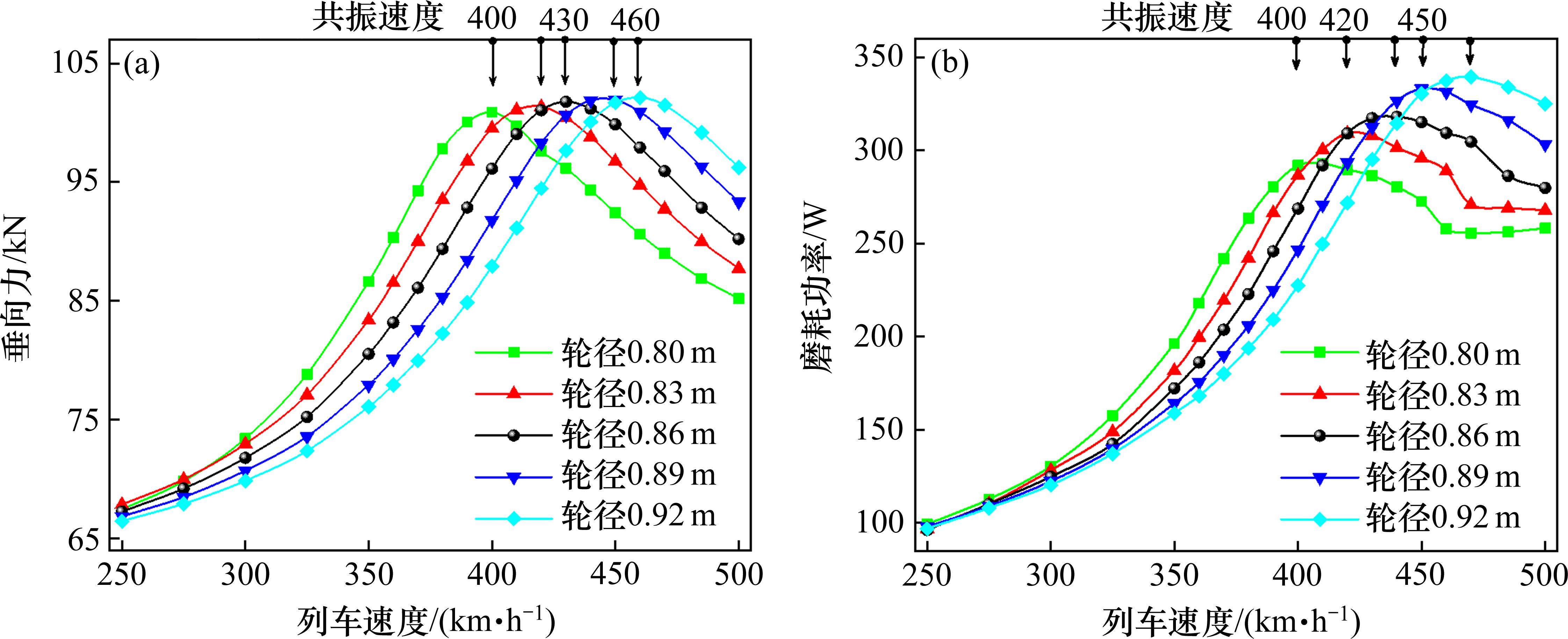
图7表明,轮轨垂向力和轮重减载率随着车轮偏心量的增加基本呈线性增大规律,且轮径越小,车轮偏心动态响应增大速率越快。从图8可以看出,随着车辆运营速度的增加,垂向力、磨耗功率等轮轨动态响应先增大后逐渐减小,在400~500 km/h范围内具有峰值,这是由更高速时车轮偏心激励频率和轮轨P2共振模态频率相等所引发的共振导致的。轮轨共振临界速度随着车轮直径的减小而降低,当车轮直径由0.92 m磨耗至0.80 m,轮轨共振临界速度由460 km/h降低至400 km/h。可以推断,更高速度运营时,小轮径车轮偏心激励更易引发轮轨耦合共振。为避免时速400 km运营时车轮偏心引发的轮轨耦合共振,应严苛控制车轮磨耗到限直径。
2.3 轨道周期性不平顺激励下轮轨动态响应
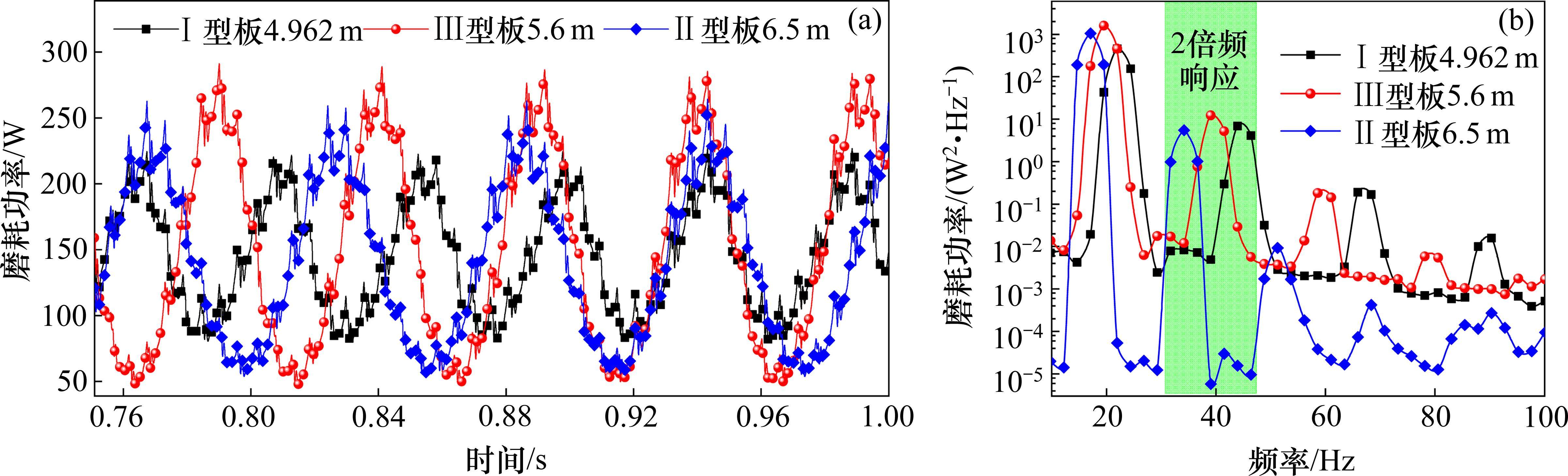
设置车辆运营速度为400 km/h,无砟轨道周期性不平顺幅值为1.2 mm。由于磨耗功率波动更为剧烈,以磨耗功率为例,获取无砟轨道周期性不平顺激励下轮轨动态响应,如图9所示。图9表明,时速400 km下CRTS I、CRTS II、CRTS III型无砟轨道周期性不平顺的激励频率分别为22.4、19.8和17.1 Hz;轮轨动态响应除在无砟轨道不平顺激励频率处存在显著尖峰外,在其2阶倍频处仍表现出较为显著的尖峰值,相应的2倍频分别为44.8、39.7和34.2 Hz,贴近轮轨P2共振模态频率。
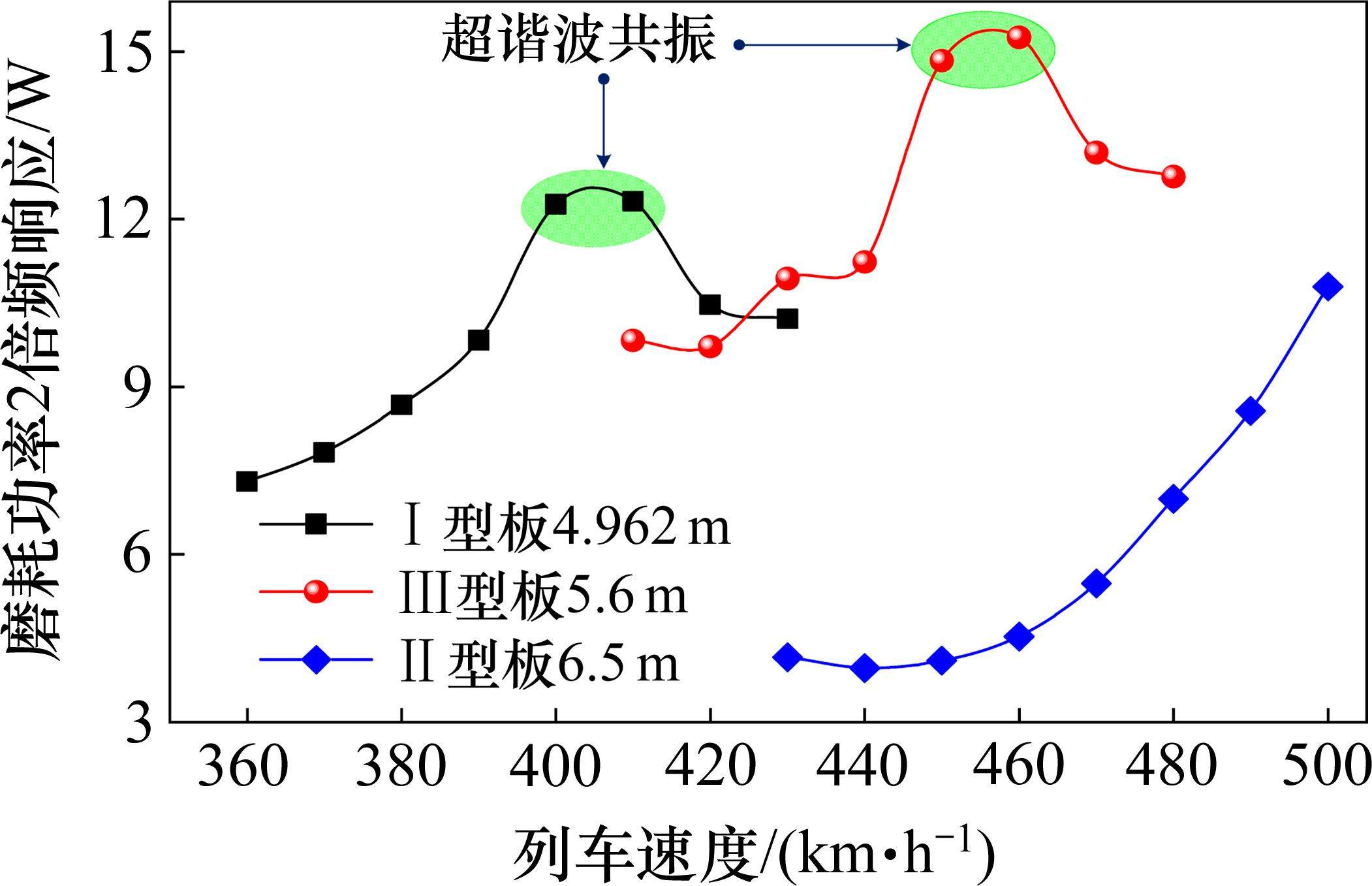
车轨系统的固有频率等于激励频率的整数倍时出现的共振现象称为超谐波共振。图10为无砟轨道周期性不平顺激励下磨耗功率2阶倍频响应随行车速度的变化规律。可以发现,在400~500 km/h范围内随着车辆运营速度的增加,CRTS I和CRTS III型无砟轨道的磨耗功率2阶倍频响应先增大达到峰值后减小,表明无砟轨道周期性不平顺激励下更高速轮轨耦合振动表现出超谐波共振现象。具体的,CRTS I型板式无砟轨道的超谐波共振临界速度为400 km/h,CRTS III型板式无砟轨道的超谐波共振临界速度为450 km/h。CRTS II型板式无砟轨道由于板长较长,在时速500 km范围内未表现出超谐波共振。
3 更高速度下无砟轨道轮轨耦合共振影响因素分析
更高速度下车轮偏心激励、无砟轨道周期性不平顺激励分别会引发轮轨共振和超谐波共振。由于轮轨耦合振动会受扣件刚度、道床下缓冲垫层以及下部基础类型等因素影响。本节以轮径0.92 m、偏心0.3 mm的车轮偏心为激励源,重点分析这些因素对更高速无砟轨道轮轨耦合共振的影响规律。
3.1 扣件刚度
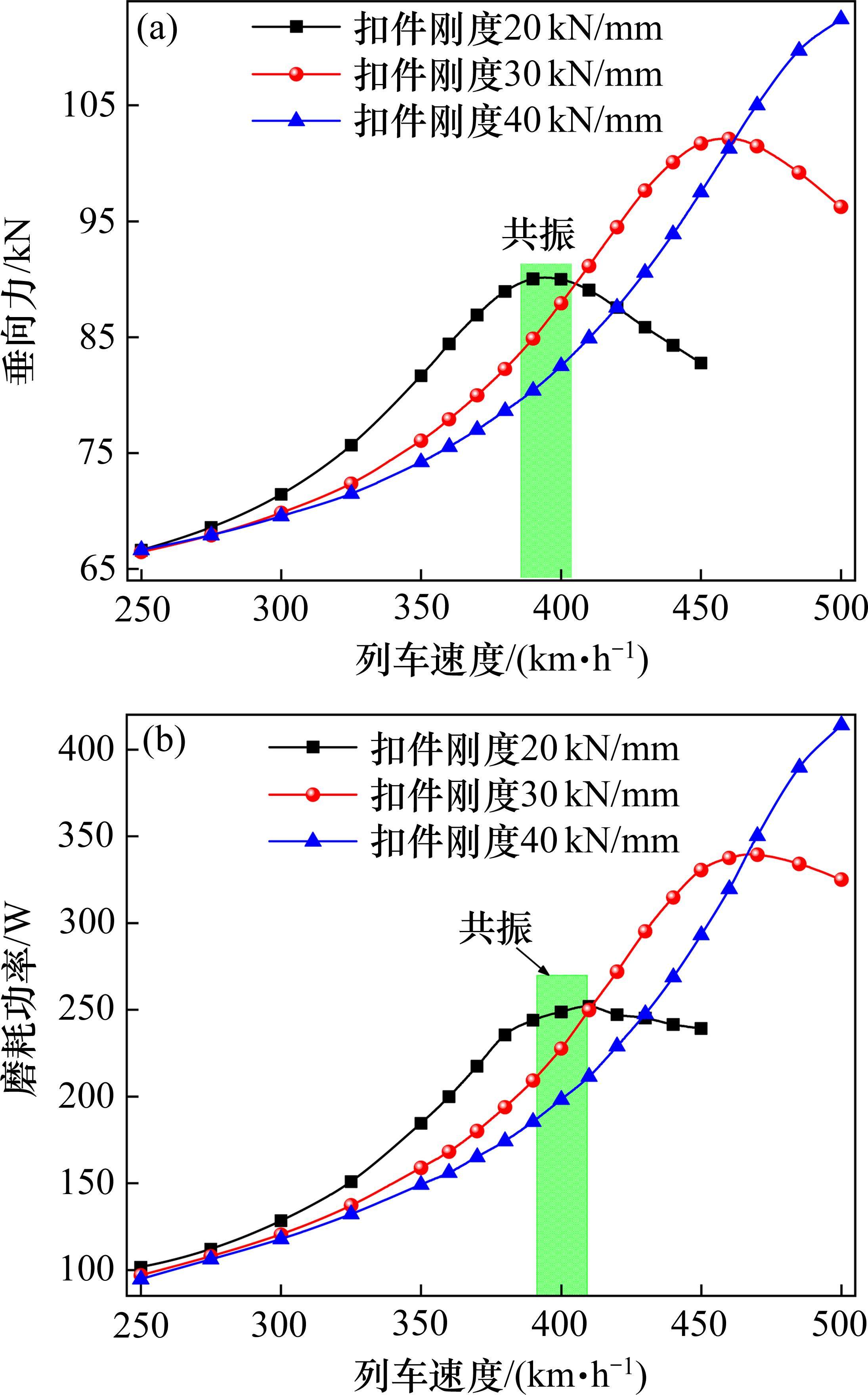
扣件刚度会改变轮轨P2共振模态频率,导致轮轨耦合共振特征发生改变。对比分析20、30及40 kN/mm这3种不同扣件刚度下轮轨动态响应,如图11所示。从图11可以看出,车轮偏心激励下,轮轨耦合共振临界速度随着扣件刚度的减小而降低。当扣件刚度为20 kN/mm时,轮轨共振临界速度为390~400 km/h。列车以更高时速400 km运营时,低扣件刚度会引发轮轨耦合共振并加剧轮轨动态响应,使得轮轨垂向力和磨耗功率相比高扣件刚度(40 kN/mm)分别增大12%和31%。为避免可能引发的轮轨耦合共振,400 km/h更高速运营时,扣件刚度不宜低于20 kN/mm。
3.2 大跨桥上无砟轨道缓冲垫层
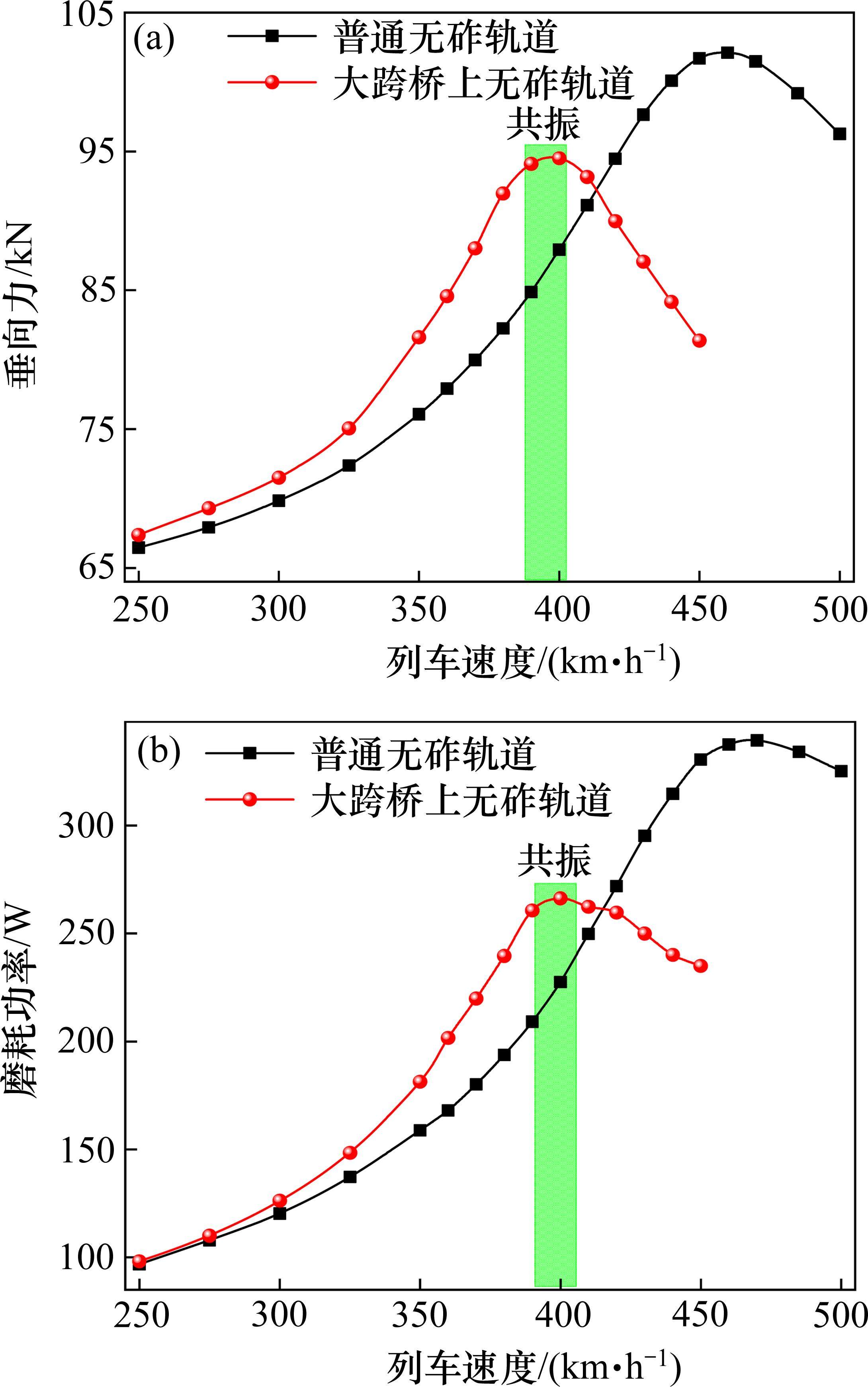
为协调无砟轨道和大跨桥梁结构间变形,大跨度桥梁上无砟轨道会采用隔离缓冲垫层代替土工布隔离层,缓冲垫层的面刚度[28]一般取为100 MPa/m。对比大跨桥上无砟轨道(铺设缓冲垫层)和普通无砟轨道(铺设土工布隔离层)在更高速时的轮轨耦合共振响应,如图12所示。从图12可以看出,当动车组由普通无砟轨道区段驶入大跨桥上无砟轨道时,轮轨耦合共振临界速度由460 km/h降低至400 km/h。这表明存在车轮偏心的列车以时速400 km驶入大跨桥上无砟轨道时会发生轮轨耦合共振并加剧轮轨动态响应,使得轮轨垂向力和磨耗功率相比普通无砟轨道区段分别增大11%和25%。
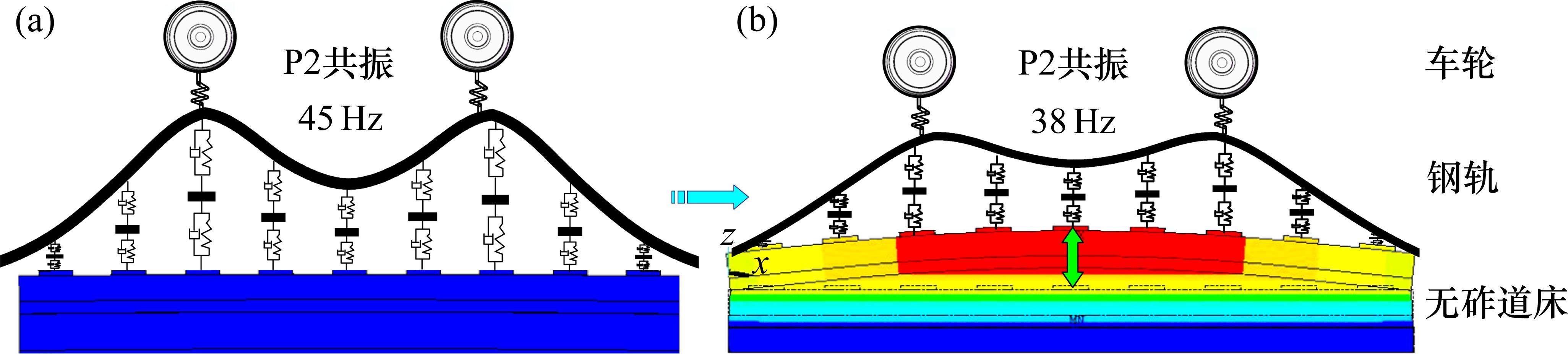
将转向架双轮对与无砟轨道采用线性化Hertz弹簧耦合,通过有限元模态分析获取轮轨P2共振模态,如图13所示。图13表明,未铺设缓冲垫层时,轮轨耦合共振主要表现为车轮与钢轨的P2共振模态;当铺设隔离缓冲垫层后,由于整体垂向刚度的降低使得无砟道床在轮轨P2共振频率附近产生弯曲振动,这会影响轮轨P2共振模态的振型,降低其模态频率至38 Hz。可以推断,轮轨耦合振动固有频率的减小是大跨桥上无砟轨道轮轨耦合共振临界速度降低的根本原因。为抑制列车400 km/h更高速运营时大跨桥上无砟轨道的轮轨耦合共振,宜适当提高隔离缓冲垫层的刚度,以此削弱大跨桥上更高速轮轨动态相互作用。
3.3 下部基础类型
我国高速铁路跨越不同地形、地质、地貌,存在路基、桥梁及隧道等多种下部基础类型,不同下部基础对无砟轨道的支承刚度差异显著。设置软土路基和隧道对无砟轨道的等效支承动刚度分别为200 MPa/m和2 000 MPa/m,参考文献[7]对桥梁进行建模以考虑32 m简支箱梁的弯曲振动,分析软土路基、桥梁和隧道支承下更高速轮轨耦合共振特征,如图14所示。
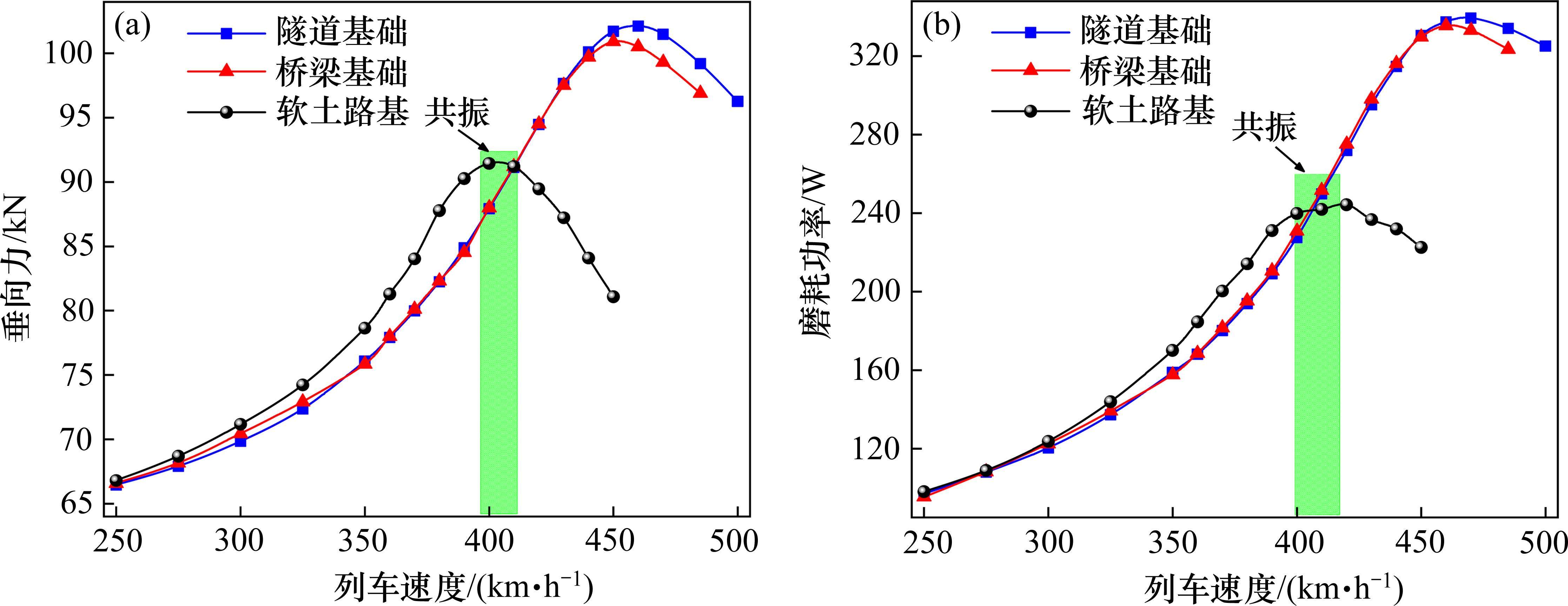
从图14可以看出,当偏心车轮高速通过不同类型的下部基础时,隧道和桥梁发生轮轨耦合共振的临界速度基本一致;软土路基发生轮轨耦合共振的临界速度低于隧道和桥梁,为400 km/h。这表明当列车以时速400 km/h通过软土路基区段时,车轮偏心激励会引发轮轨耦合共振,使得软土路基区段轮轨垂向力和磨耗功率相比桥隧区段分别增大6%和10%。由于轮轨耦合共振,列车从时速300 km增加至400 km时,软土路基上车轮偏心动态响应增幅高于隧道或桥梁。因此,更高速运营下需重点关注软土路基区段轮轨动态相互作用,避免更高速运营时可能引发的轮轨耦合共振。
3.4 不同因素下更高速轮轨耦合共振条件
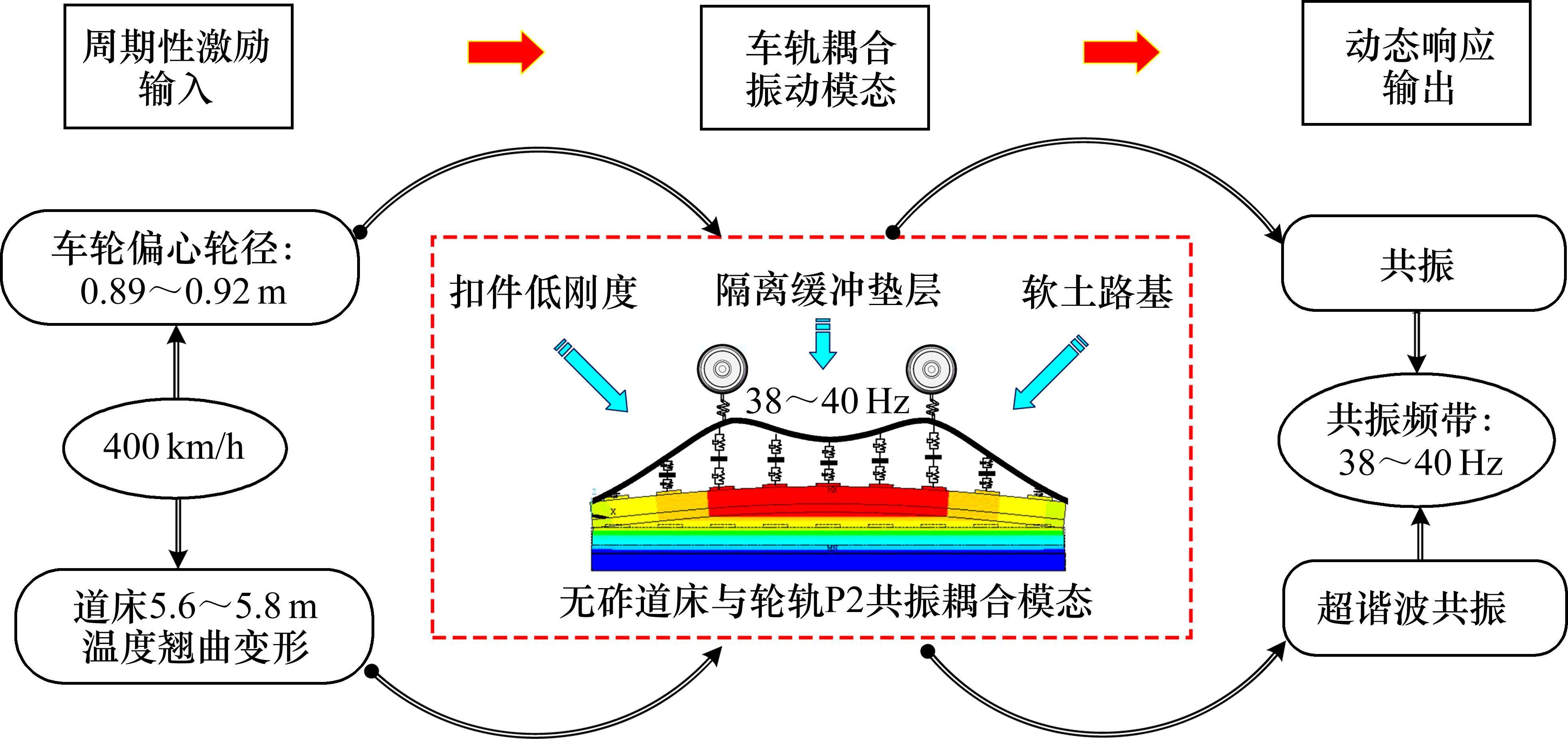
我国跨海或跨江特大桥上无砟轨道多采用CRTS III型板式无砟轨道和双块式无砟轨道结构,道床单元长度一般为5.6~5.8 m,动车组新轮轮径通常为0.92 m。基于上述关于扣件刚度、隔离缓冲垫层以及下部基础类型的影响因素分析结果,探明更高速无砟轨道轮轨耦合共振条件,如图15所示。图15表明,列车以时速400 km运营时,车轮偏心激励频率和无砟轨道周期性不平顺2倍频为38~40 Hz;低扣件刚度、隔离缓冲垫层以及软土路基会使得无砟轨道轮轨P2共振模态频率由45 Hz降低至38~40 Hz。因此,在车轮偏心和无砟轨道周期性不平顺持续激励下,激励频率和轮轨耦合振动固有频率相等,400 km/h更高速轮轨耦合系统分别会发生共振和超谐波共振,加剧这一运营速度下轮轨动态响应。
为保障400 km/h更高速运营时轮轨动态相互作用处于低动力水平,从避开车轨系统周期性激励与无砟轨道系统模态匹配的角度,可重点关注2个方面:一方面增大无砟轨道轮轨耦合系统的固有振动频率,比如适当提高扣件刚度或者大跨桥上隔离缓冲垫层刚度;另一方面减小车轨系统周期性激励频率,削弱其激励强度,如更高运营速度选用大轮径车轮,严苛控制车轮偏心及无砟轨道周期性不平顺限值。
4 结论
1) 宽频随机激励下运营速度的提升不会改变轮轨共振分布特征,仅显著加剧其动态响应幅值。
2) 车轮偏心和无砟轨道(CRTS I型、CRTS III型板式)周期性不平顺激励下,轮轨系统在时速400~500 km范围内分别会发生共振和超谐波共振。轮轨耦合共振临界速度随着轮径、轨道板长的减小而降低。针对普通无砟轨道区段,CRTS I型和CRTS III型板式无砟轨道的超谐波共振临界速度分别为400 km/h和450 km/h;CRTS II型板式无砟轨道由于板长较长,在时速500 km范围内未出现超谐波共振。
3) 低扣件刚度、大跨桥上缓冲垫层和软土路基会减少轮轨P2共振模态频率,降低轮轨耦合共振临界速度至400 km/h附近,加剧这一运营速度下轮轨动态响应。400 km/h更高速运营时应重点关注这些引发轮轨耦合共振的因素。
马超智,赵闻强,周鹏等.时速400 km级无砟轨道轮轨耦合共振及影响因素研究[J].铁道科学与工程学报,2025,22(04):1407-1419.
MA Chaozhi,ZHAO Wenqiang,ZHOU Peng,et al.Research on wheel-rail coupled resonance and influencing factors of 400 km/h ballastless track[J].Journal of Railway Science and Engineering,2025,22(04):1407-1419.

